Third-order effects in resonant sum-frequency-generation signals at electrified metal/liquid interfaces

Abstract

Vibrational sum-frequency-generation (SFG) spectroscopy experiments at electrified interfaces involve incident laser radiation at frequencies in the IR and near-IR/visible regions as well as a static electric field on the surface. Here we show that mixing the three fields present on the surface can result in third-order effects in resonant SFG signals. This was achieved for closed packed self-assembled monolayers (SAMs) with molecular groups of high optical nonlinearity and surface potentials similar to those typically applied in cyclic voltammograms. Broadband SFG spectroscopy was applied to study a hydrophobic well-ordered araliphatic SAM on a Au(111) surface using a thin-layer analysis cell for spectro-electrochemical investigations in a 100 mM NaOH electrolyte solution. Resonant contributions were experimentally separated from non-resonant contributions of the Au substrate and theoretically analyzed using a fitting function including third-order terms. The resulting ratio of third-order to second-order susceptibilities was estimated to be $\mathcal{O}$(10⁻¹⁰) m/V.

1. Introduction

Impinging light with su ciently high field amplitudes on surfaces can result in the generation of non-linear optical contributions involving frequency mixing of the incident radiation. One example for such higher-order effects is the mixing of two frequencies that may result, upon other contributions, in a signal at the sum-frequency of the two incident ones. This second-order process is typically used to study vibrational resonances of molecules at interfaces by mixing IR and visible light on the specimen of interest. Within dipole approximation, signals can only be generated in non-isotropic media in which inversion symmetry is broken. This scheme makes vibrational SFG spectroscopy inherently specific to interfaces which are buried by an adjacent isotropic medium, such as most liquids or gases [1].

Working on charged interfaces adds another interesting phenomenon, namely the interaction between the light fields and the static electric field at the interface. In this configuration, signals at the sum-frequency might not primarily be generated by second-order effects, but also third-order effects can emanate from interactions with the static electric field [2-5]. The corresponding intensity I of the signal at the sum-frequency ω_SFG is proportional to

$$I\left({\omega }_{\mathrm{SFG}}\right)\propto \mid \mid {\chi }^{\left(2\right)}\mid e^{i\varphi }+E_{\mathrm{pot}}{\mid {\chi }^{\left(3\right)}\mid e^{i\gamma }\mid }^2$$ (1)

where χ^(2,3) are the effective second- and third order susceptibilities for different polarization combinations of the optical fields (e.g. ssp or ppp polarization for SFG, NIR, and IR beams), φ and γ phases of the corresponding susceptibilities, and E_pot the static electric field. χ⁽²⁾ can have different contributions from vibrational (resonant) as well as electronic transitions in the metal (non-resonant).

According to Eq. 1 the magnitude of third-order effects depends on E_pot and |χ⁽³⁾|, whereas the phase γ can effectively switch the sign of the third-order effect, e.g. it could lead to increasing SFG signals at cathodic potentials (E_pot < 0 V) with γ ~ 180° and decreasing signals for γ ~ 0°. The magnitude of |χ⁽³⁾| has been the topic of several discussions, where it was usually concluded that for charged polymeric systems or solids in media with pH-values away from the point of zero charge, the effects are too small to be detected [3, 6-8]. In this context third order hyperpolarisability tensor elements were estimated to be 10 orders of magnitude smaller than the respective second order quantities [3].

Here we report on third-order contributions at su ciently high electric fields obtained within a combined vibrational SFG and electrochemical experiment. Broadband SFG signals from araliphatic SAMs of (4-(4-(4 pyridyl)phenyl)phenyl)methanethiol (PyPP1)(Fig. 1) on Au(111) were recorded over 10 cyclic voltammograms (CVs) in real-time and in situ. PyPP1 SAMs have been shown to posses an extraordinary electrochemical stability [9] that allows to isolate third-order effects from changes in orientation and/or surface density. Resonant SFG signals from the SAM were separated from non-resonant (Au) signals and analyzed utilizing Eq. 2.

Fig. 1.

Structure of (4-(4-(4 pyridyl)phenyl)phenyl)methanethiol (PyPP1).

2. Materials and Methods

2.A. Preparation of the aralphatic SAMs on Au(111) surfaces

PyPP1 organothiols were synthesized as described elsewhere [10]. Au(111) substrates were prepared by evaporating gold onto freshly cleaved mica sheets at a substrate temperature of 450° C in a Leybold Univex 450 system. Prior to use, the Au films were annealed in a H₂ flame. SAMs were formed by immersion of the Au substrates into 20 μM ethanolic thiol solutions for 12-15 h. After removal from solution, samples were thoroughly rinsed with ethanol and purged with nitrogen gas. All chemicals used were in reagent grade.

2.B. Broadband SFG Spectrometer

The broadband SFG spectrometer has been described in detail elsewhere [11]. The parameters used for the current experiments were incident angles for the 100 fs IR and etalon shaped narrowband 800 nm beams to be 55° and 60°, respectively. For the resonant measurements, the IR beam was centered at 1600 cm⁻¹ and for non-resonant recordings at 2800 cm⁻¹ During the cyclic voltammetry measurements, signals were accumulated in kinetic mode every 0.4 s (400 shots). All spectra were recorded in p polarizations for all beams (SFG, Vis, and IR) and no further data treatment such as smoothing was applied. Static delay-shifted spectra were recorded in air with an accumulation time of 4 s for each spectrum. All other spectra were recorded using a purpose-built variant of the thin-layer analysis (TLA) cell describe in the next section [11].

2.C. Measurement cell and electrochemical setup

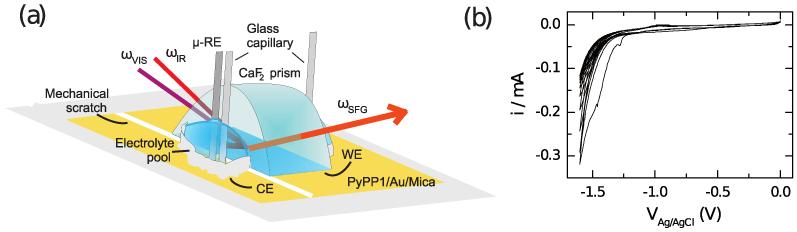
Modifications of the TLA cell are shown schematically in Fig. 2a. Electrolyte reservoirs (0.1 M NaOH) were built at the sides of the CaF₂ prism using a chemically resistive two-component adhesive (X60, HBM Inc., USA). Two glass capillaries containing a part of the electrolyte solution were dipped into each of the electrolyte pools and slowly released electrolyte into the reservoir during the measurements in order to compensate evaporation in dry air conditions. PyPP1/Au/Mica substrates underlying the prism were extended over the larger side of the prism into the reservoir. Au films on the substrates were separated into two parts at the boundary between the prism and reservoir by a mechanical scratch so that the part underneath the prism served as working electrode (WE) and the other part within the reservoir as counter electrode (CE). An Ag/AgCl (3 M KCl) microreference electrode (RE) was placed next to the prism in order to minimize the potential drops in the solution. Electrode potentials V_e in this work are reported as V_Ag/AgCl with respect to the Ag/AgCl reference system. After 10 recorded spectra at the open circuit potential (OCP), the Com-pactstat potentiostat (Ivium Technologies, The Netherlands) was switched on performing a CV starting from the first vertex at 0 V to the second vertex at −1.6 V with a scan rate of 50 mV/s (Fig. 2b). The SFG signal was then continuously recorded for 10 CVs.

Fig. 2.

(Color online) (a) Sketch of the beam path and the arrangement of the electrodes in the modified thinlayer analysis cell for SFG measurements. (b) Recorded CV for PyPP1 over 10 cycles.

3. Results and discussions

3.A. Separating resonant and non-resonant signals

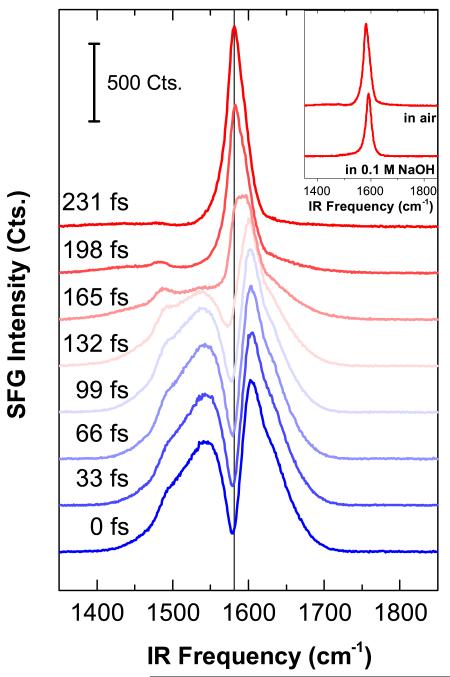
As previously mentioned, SFG signals are generated by both, the Au substrate (non-resonant) and, if the IR beam is in resonance with an SFG active mode, a vibrational band of PyPP1. These contributions sum up with individual phases for the effective resonant $\left({\chi }_{\mathrm{res}}^{(2,3)}\right)$ and non-resonant $\left({\chi }_{\mathrm{non}-\mathrm{res}}^{(2,3)}\right)$ susceptibilities $({\chi }^{(2,3)}={\chi }_{\mathrm{res}}^{(2,3)}+{\chi }_{\mathrm{non}-\mathrm{res}}^{(2,3)})$. In order to decouple phase effects of resonant and non-resonant signals from third-order effects as a result of the static field at the interface, we followed a measurement scheme first proposed by Dlott and co-workers [12]. It takes advantage of a time-asymmetrically etalon shaped pulse for the 800 nm beam having a steep rise in the beginning followed by a long fall in the signal intensity versus time. This allows to temporally separating the (100 fs) IR beam and the (~2 ps) 800 nm beam, but with a su cient population of excited states when the 800 nm beam reaches its maximum in intensity. Fig. 3 shows the corresponding SFG spectra recorded at different delay times between IR and 800 nm beam. At delay = 0 fs, both non-resonant and resonant contributions overlap; the constant non-resonant signal follows the IR intensity profile while the resonant signal appears as a dip in the spectrum (destructive interference between resonant and non-resonant signals). Increasing the delay time leads to the suppression of non-resonant signals up until only resonant contributions remain in the spectral trace at about 231 fs. Following this procedure also allows to identify that the resonant contribution is indeed a dip in the spectrum with a phase-difference of ~180° between resonant and non-resonant terms (see vertical line in Fig. 3).

Fig. 3.

(Color online) SFG spectra recorded at around 1600 cm⁻¹ at different delay times between IR and 800 nm beams. The vertical line at peak maximum is a guide to the eye for comparing resonant and non-resonant signals. The inset shows background suppressed SFG spectra (231 fs) in air and in 0.1 M NaOH.

The intensity of the resonant band at 1585 cm⁻¹ is associated to C—C vibrations specifically in the pyridine ring [13]. Its frequency is above phenyl vibrations and has a very strong SFG activity, comparable to the intensity of the non-resonant background. This can be related to delocalized electrons effectively supporting the up-conversion of vibrational resonant states to produce SFG signals. This strong optical nonlinearity is not only used to generate well-resolved peaks at accumulation times as low as 0.4 s (400 laser shots), but also provides high-enough e ciency towards |χ⁽³⁾| contributions. This might be an important parameter as e.g. alkanechains or water molecules have a much lower nonlinearity and |χ⁽³⁾| effects are potentially not that strong in comparison to the aromatic system within the araliphatic chains studied here.

Analyzing the film within the electrochemical cell does not significantly change its spectral shape (see inset in Fig. 3). The contribution from the pyridine ring is still clearly detectable, while bending vibrations of water molecules centered at 1645 cm⁻¹ are absent due to a comparably lower Raman tensor and IR cross section limiting its SFG intensity to be below signal-to-noise ratio.

3.B. Combining CV and SFG for resonant and non-resonant signals

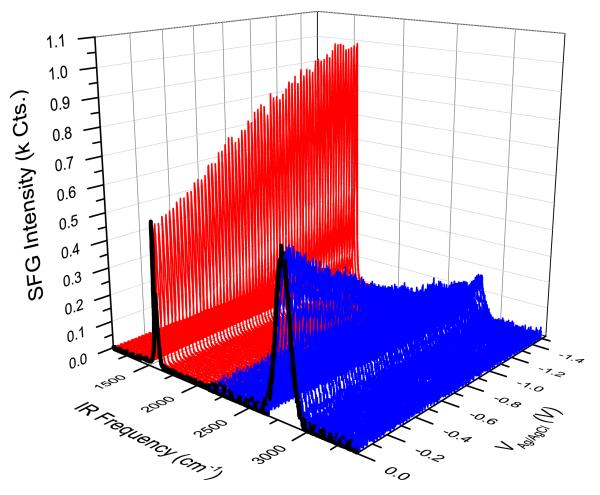
The background suppressed resonant signal of the band shown in Fig. 3 was recorded simultaneously during the acquisition of 10 CVs. The resulting first ramp of SFG spectra down to V_Ag/AgCl = −1.5 V is shown in Fig. 4 (red spectra). For the resonant signal, the intensity increases with decreasing V_Ag/AgCl. For non-resonant signals (blue spectra), the intensity has an opposing trend in that it decreases with decreasing V_Ag/AgCl. The fact that resonant signals increase while non-resonant signals decrease within the same potential sweep indicates that Fresnel coe cients cannot be accounted for describing these changes. If this is the case, both resonant and non-resonant signals should follow similar trends.

Fig. 4.

(Color online) SFG signals for the first ramp towards negative potentials for resonant (red, around 1600 cm⁻¹) and non-resonant (blue, around 2800 cm⁻¹) recordings.

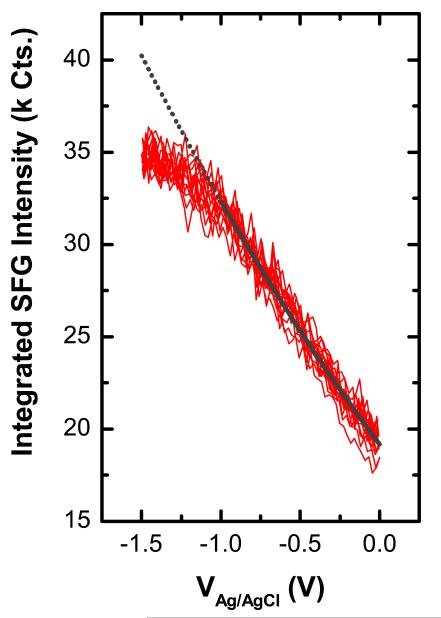
In order to further investigate the dependency of the resonant SFG signals on applied electrode potentials, all recorded spectra over 10 CVs were integrated (a total number of 2992 spectra) and are plotted versus V_e in Fig. 5. The integrated intensities are well reproduced from cycle to cycle. Similar results have been found for alkanethiols with longer chain length (16 and 18 carbon atoms) where the ex situ recorded SFG spectra after 30 cycles nearly matches the initial one [14].

Fig. 5.

(Color online) Integrated intensities of resonant SFG spectra recorded through 10 CVs. The gray line corresponds to a fit using Eq. 1, the grey dotted line is an extension of the fitting results towards more negative potentials.

The electric field E_pot generated by application of an electrode potential V_e at a metal electrode is given by the gradient of the electrostatic potential V, E_pot = −▽V. For SAM-covered electrodes, the potential has been shown by X-ray photoelectron spectroscopy to drop linearly over the SAM with 90 % of the overall potential drop occur within the SAM [15,16]. Therefore, the electric field inside the SAM at a SAM-covered electrode can in good approximation be estimated as

$$E_{\mathrm{pot}}\simeq (V_{\mathrm{e}}-V_{\mathrm{pzc}})∕\lambda ,$$ (2)

where λ is the layer thickness and V_pzc the electrode potential of zero charge. Assuming a SAM layer thicknesses around 1 nm, E_pot values on the order of 10⁹ V/m are easily obtained in standard electrochemical experiments. The range of V_e available in experiments is limited by gold oxidation on the anodic side and by reductive desorption on the cathodic side [17], which is typically accompanied by a significant loss in order for most thiols [18,19]. Accordingly, the first dip in the CV shown in Fig. 2b is around V_Ag/AgCl ~ −1.3 V where reductive desorption of the PyPP1 SAMs occurs [9]. At higher cathodic potentials, hydrogen evolution dominates the CVs. After reversal of the scan direction, readsorption of the thiols is observed at V_Ag/AgCl ~ −1 V through a current peak in the CVs. Therefore, for further analysis of the SFG intensities, we only used the range down to −1 V and did not consider spectral traces for V_Ag/AgCl < −1 V.

SFG intensities can depend on number density, orientation, and conformation of absorbed species. However, for V_Ag/AgCl < −1 V the observed behavior cannot originate from these influences. Intact PyPP1 SAMs are densely packed with an upright molecular orientation of the molecules [13]. In the adsorbed state, there is geometrically no room for a significant change in orientation and conformation. If changes occur in orientational order via changes in superstructure of the SAM, these should be visible as a peak in the CV [20], but in fact no such changes are observable. Furthermore, potential dependent spectroscopic ellipsometry shows no evidence for any change in the SAM in its adsorbed state [21]. Therefore, changes in number density, orientation and conformation can be ruled out as the source for the observed increase in SFG intensity with decreasing potential up to −1 V.

To consider third-order effects as described in Eq. 1 for a potential cause of changes in SFG intensity, constant values were assumed for χ^(2,3), φ, and γ in between 0 V > V_Ag/AgCl > −1 V, implying that conformation and order within the SAM is essentially not a ected by changes in V_e. Using Eq. 2 with V_pzc = 200 mV and λ = 1.44 nm [13] gives an estimate for the electric field as function of V_e. The data in Fig. 5 were then fitted using Eq. 1 with V_Ag/AgCl as the dependent variable. From the fit, the ratio χ⁽²⁾/χ⁽³⁾ for resonant contributions was determined to be (2.2±0.3)10⁻¹⁰ m/V with a phase between χ⁽²⁾ and χ⁽³⁾ signals of 180°

Fig. 5 also shows an extension for the fitting function obtained by using the values obtained for 0 V > V_Ag/AgCl > −1 V. Deviations to the extended fitting function can be observed that are indeed related to phenomena occurring at high cathodic potentials, such as change in orientation during reductive desorption. The important point to make is that increasing or decreasing SFG signals are not necessarily related to ordering or reorientation effects, but, in case of su ciently strong electric fields at the interface, can also be associated to interactions with this static field.

The non-delay-shifted intensity of SFG signals also depends on Fresnel coe cients of the Au substrate, which may change the spectral shape significantly, in particular when having a non-resonant background signal overlapped with spectral features that are as broad or broader than the spectral shape of the IR beam, such as those of water stretching vibrations. For these systems its experimentally not possible to separate resonant and non-resonant signals by delay-shifting. However, here we investigated a comparably narrow band and, therefore, separation of the resonant signals is possible. There might be a dependency for the real and imaginary part of the refractive index with surface potential, although we do not see a direct indication of this phenomenon for the system we studied here. We think that this issue warrants further investigation, but such an analysis lies beyond the scope of the present work.

4. Conclusion

SFG studies on coated metal surfaces usually involve resonant and non-resonant signals from the electrode material, which need to be disentangled when it comes to spectral analysis. Here we show that third-order effects can dominate trends in resonant SFG signals in a wide applied potential range. Contributions from vibrational signals of an araliphatic self-assembled monolayer on a single crystalline Au(111) surface and non-resonant signals from electronic transitions in the metal could be separated and, for resonant signals, χ⁽³⁾ contributions and phase relation between second-order and third-order susceptibilities were identified. Third-order effects are a result of mixing the incident laser fields and the static field at the surface and, depending on the phase value for each contribution to the polarization at the sum-frequency, can lead to increasing or decreasing trends in the non-linear optical signal. For systems with χ⁽²⁾/χ⁽³⁾ > $\mathcal{O}$(10⁻⁹) m/V, third-order effects become important at strong electric fields such as those generated at electrified interfaces (E_pot > 10⁹ V/m).

Our work is extending third-order effects in second-harmonic generation spectroscopy at charged interfaces originally introduced by Eisenthal and coworkers towards vibrational SFG spectroscopy at electrified interfaces. While here the focus is on resonant contributions, changes in the non-resonant signals may have additional causes such as changes in band occupation with potential and requires further attention, both experimentally and theoretically.