Dynamic Circadian Modulation in a Biomathematical Model for the Effects of Sleep and Sleep Loss on Waking Neurobehavioral Performance

Abstract

Recent experimental observations and theoretical advances have indicated that the homeostatic equilibrium for sleep/wake regulation—and thereby sensitivity to neurobehavioral impairment from sleep loss—is modulated by prior sleep/wake history. This phenomenon was predicted by a biomathematical model developed to explain changes in neurobehavioral performance across days in laboratory studies of total sleep deprivation and sustained sleep restriction. The present paper focuses on the dynamics of neurobehavioral performance within days in this biomathematical model of fatigue. Without increasing the number of model parameters, the model was updated by incorporating time-dependence in the amplitude of the circadian modulation of performance. The updated model was calibrated using a large dataset from three laboratory experiments on psychomotor vigilance test (PVT) performance, under conditions of sleep loss and circadian misalignment; and validated using another large dataset from three different laboratory experiments. The time-dependence of circadian amplitude resulted in improved goodness-of-fit in night shift schedules, nap sleep scenarios, and recovery from prior sleep loss. The updated model predicts that the homeostatic equilibrium for sleep/wake regulation—and thus sensitivity to sleep loss—depends not only on the duration but also on the circadian timing of prior sleep. This novel theoretical insight has important implications for predicting operator alertness during work schedules involving circadian misalignment such as night shift work.

Citation:

McCauley P; Kalachev LV; Mollicone DJ; Banks S; Dinges DF; Van Dongen HPA. Dynamic circadian modulation in a biomathematical model for the effects of sleep and sleep loss on waking neurobehavioral performance. SLEEP 2013;36(12):1987-1997.

INTRODUCTION

Building on the seminal two-process model of sleep regulation,^1,2 biomathematical models for the prediction of fatigue, behavioral alertness and performance during periods of sleep deprivation and/or circadian misalignment instantiate a homeostatic process seeking to balance time asleep with time awake, and a circadian process seeking to place wakefulness during the day and sleep during the night.³ Such fatigue models have become useful tools in modern fatigue risk management systems.⁴ To capture the temporal dynamics of waking neurobehavioral performance across a wide range of sleep/wake schedules, we recently introduced a new class of fatigue models, formulated in terms of coupled first-order ordinary differential equations (ODEs).⁵ A specific implementation of the new model class, using scheduled time in bed (TIB) as input, was calibrated and validated⁵ with large datasets of neurobehavioral performance from laboratory-based dose-response studies of sleep loss.^6,7

The dynamics of this new fatigue model⁵ indicated that prior sleep history modulates the homeostatic equilibrium state for sleep/wake regulation,^8,9 and therefore the magnitude of the effect of subsequent sleep restriction on neurobehavioral performance.¹⁰ This prediction has since been corroborated experimentally.^11,12 The dependence on sleep history of the effects of sleep loss implies that sleep homeostatic effects on performance show integration of both chronic and acute sleep loss over time and should be modeled with (at least) two state variables. In our model,⁵ the state variables are p representing performance impairment over time (hours to days), and u modulating the sleep homeostatic equilibrium over time (days to weeks). The interplay of these two state variables in the model exhibits a bifurcation: for daily scheduled amounts of wakefulness less than a critical threshold estimated to be 20.2 h (i.e., more than 3.8 h TIB per day), performance deficits are predicted to converge across days to an asymptotically stable state of equilibrium; whereas for daily wakefulness extended beyond this critical threshold, performance deficits are predicted to escalate through divergence from an unstable state of equilibrium.⁵ This provides a unified explanation for the experimentally observed, differential dynamics of neurobehavioral performance under conditions of total sleep deprivation versus sustained nocturnal sleep restriction.^7,13

The general mathematical framework of our published model⁵ focused primarily on the temporal dynamics between sleep/wake cycles (i.e., across days). The dynamics of waking neurobehavioral performance within sleep/wake cycles are driven by an emergent property involving nonlinear interaction between the homeostatic process described by the homogeneous part of the differential equations and the circadian process encompassed in the non-homogeneous part.^14–16 It was shown that as long as the non-homogeneous part contains only oscillatory functions such as circadian rhythm, the dynamics across sleep/wake cycles do not depend on it. Recognizing this property, a detailed examination of the non-homogeneous part was left to be addressed in follow-up research.⁵

Inspired by the significant contributions of other groups to fatigue modeling,^2,17–23 we present the results of this follow-up research. Dropping the constraint for the non-homogeneous part to contain only oscillatory functions, we generalized the applicability of our model to also include night shift schedules and nap sleep scenarios. This was accomplished without increasing the net number of model parameters, by introducing time-dependence in the amplitude of the circadian modulation of neurobehavioral performance.

METHODS

Model Reformulation

The ODE system modeling neurobehavioral performance during wakefulness and (notionally) during sleep is given by Eqs. (1) in Table 1 (cf. Eqs. (9), (21) and (26) in ref. 5). These equations describe the two state variables p and u. The first state variable, p, represents the primary outcome variable, which denotes predicted performance impairment. This variable rises in a saturating exponential manner towards an upper asymptote during wakefulness and falls exponentially towards a lower asymptote during sleep, while being modulated continuously by circadian rhythm. The second state variable, u, represents a slow dynamic process that causes allostatic modulation of p over time (days to weeks). Specifically, during wakefulness u produces a slow exponential increase of the asymptote towards which p rises, and during sleep u produces a slow exponential decrease of the asymptote towards which p falls.

Table 1.

Biomathematical model equations. Eqs. (1) represent the earlier model version,⁵ and Eqs. (2)-(7) represent the present reformulation and update of the model

In Eqs. (1) in Table 1, the parameters α and σ in the homogeneous part of the ODE system govern the homeostatic changes in p and u and their interaction during wakefulness and sleep, respectively. The function c is a skewed sinusoidal (i.e., 5-harmonic oscillatory) function representing the circadian process of the two-process model.²⁴ In the model formulation of Eqs. (1), c is scaled by κ, offset by μ, and shifted in time by φ (see footnote of Table 1). Also, note that u is offset by a constant δ (not explicitly shown) during wakefulness compared to sleep⁵ to distinguish the upper and lower asymptotes to which p rises and falls, resulting in a discontinuity in the model at each sleep/wake and wake/ sleep transition.

Without changing any aspect of the model, Eqs. (1) can be written as a coupled non-homogeneous first-order ODE system for p (see supplemental material, section 1), which is given in Eqs. (2) and (3) in Table 1 (where the subscripts “w” and “s” stand for wakefulness and sleep, respectively). The parameters in this model formulation are described in Table 2. The functions g_w and g_s are bounded, and are described in more detail in the next section. In the formulation of Eqs. (2) and (3), both p and u are continuous over time across wake/sleep and sleep/ wake transitions, removing the discontinuity embedded in Eqs. (1). Note that Eqs. (2) in Table 1 can be reduced to the original homeostatic process of the two-process model²⁴ by setting α_w = −1/τ_r, α_s = −1/τ_d, β_w = 0, β_s = 0, g_w = −α_w, and g_s = 0.

Table 2.

Model parameters and their constraints and interpretations, as well as their estimates and standard errors as obtained using MCMC fitting to the data of studies A1-A3

As briefly discussed above, the model exhibits a bifurcation when comparing daily scheduled wakefulness greater versus smaller than a critical threshold. This critical threshold is given by A_c = W_c / T = η_s / (η_s – η_w). The published value for W_c is 20.2 h for a day length T of 24 h,⁵ such that A_c = 0.84. Postulating that this bifurcation is a generalizable neurobiological property with constant value of A_c, it follows that η_s can be derived from η_w through Eq. (4) in Table 1. This reduces the number of free parameters by one without changing the model.

Improved Circadian Dynamics

The functions g_w and g_s in Eqs. (2) in Table 1 are the main focus of this paper. They represent the non-homogeneous part of the ODE system, which includes circadian rhythm. Recent laboratory studies, in particular from simulated shift work schedules,²⁵ suggested that improvement was needed in the dynamics of the non-homogeneous part to better track circadian influences on performance.

In Eqs. (5) in Table 1 we introduce minor, yet important, changes in the mathematical form for the non-homogeneous part. Here the circadian process is represented by the function c(t) given in Eq. (6), with τ = 24 h representing the circadian period and time being denoted by t (expressed in hours). By including the term α_s β_s / η_s, Eq. (5b) is formulated such that performance impairment p in Eq. (2b) tends to zero for increasing sleep duration (see supplemental material, section 2). This constrains the model to converge to zero PVT lapses under the hypothetical condition of infinite sleep duration, as should theoretically be the case, and helps to improve the estimation of initial values for studies with different amounts of baseline sleep.

To capture findings that sleep/wake state moderates the electrophysiological activity level of the circadian pacemaker²⁶ and that the circadian modulation of neurobehavioral performance is small in well-rested individuals and larger in sleep-deprived individuals,^16,27 the time-dependent function κ in Eqs. (5) modulates the amplitude of the circadian process as a function of sleep/wake state. The function is specified in Eqs. (7) in Table 1, and produces a sigmoidal rise in circadian amplitude during wakefulness and an exponential fall during sleep. In future work, this dynamic behavior may be further refined to include a limit-cycle oscillator, in agreement with published biomathematical models of the human circadian pacemaker,²⁸ but this is not needed for the present purposes.

Datasets

Using data from previously published studies, we compiled two large datasets. The first, comprised of studies A1-A3, was used for estimation of the model parameters (i.e., for model calibration). The second, comprised of studies B1-B3, was used for model validation.

Study A1

47 healthy young adults were subjected to 1 of 4 different laboratory sleep deprivation protocols.⁷ Each protocol began with several baseline days involving 8 h TIB. Subsequently, 13 subjects were kept awake for 3 days continuously (i.e., 0 h TIB), for a total of 88 h of total sleep deprivation. Afterwards, they received varied amounts of recovery sleep (not considered here). The other 34 subjects underwent 1 of 3 doses of sustained sleep restriction for 14 consecutive days, followed by 2 recovery days with 8 h TIB. The sleep restriction schedule involved 4 h TIB per day for 13 subjects; 6 h TIB per day for another 13 subjects; and 8 h TIB per day for the remaining 8 subjects (control condition). Awakening was scheduled at 07:30 for every sleep period.

Performance on a 10-minute psychomotor vigilance test (PVT)^29,30 was tested every 2 h, starting at 07:30, during scheduled waking periods. The first 2 test bouts of each waking period were omitted in order to avoid confounds from sleep inertia.³¹

Study A2

27 healthy young adults participated in a laboratory study of simulated shift work.²⁵ Thirteen subjects were randomized to a night shift schedule, which began with a baseline day with 10 h TIB (22:00-08:00) and a subsequent prophylactic nap of 5 h TIB (15:00-20:00). Subjects were then on a night shift schedule for 5 days, with diurnal sleep of 10 h TIB (10:00-20:00) after the first 4 shifts and a transition nap of 5 h TIB (10:00-15:00) after the last. The transition nap commenced a 34 h “restart” or recycling break which also included a nocturnal sleep period of 10 h TIB (22:00-08:00) and a prophylactic nap of 5 h TIB (15:00-20:00). Subjects were then on a night shift schedule again for 5 days, which was identical to the first 5 days on night shift and ended with a transition nap of 5 h TIB (10:00-15:00). They subsequently had a final recovery sleep period of 10 h TIB (22:00-08:00).

The other 14 subjects in this study were randomized to a day shift schedule (control condition), which was equivalent to the night shift schedule but involved nocturnal sleep with 10 h TIB (22:00-08:00) every day and no napping. The second day in the laboratory was considered a rest day, not a shift day. Cumulative TIB during the study was identical between the 2 conditions.

In both conditions, performance on the 10-min PVT was tested before and after a 30-min session on a driving simulator occurring every 3 h during the baseline day (practice) and during each of the shift days. Only the pre-driving PVT bouts on the shift days are considered here—4 bouts daily starting at 21:00 or 22:00 (randomized over subjects) in the night shift condition, and at 09:00 or 10:00 (randomized over subjects) in the day shift condition. PVT performance was also tested once every 3 h during the first 5 h after baseline sleep (at 09:30 and 12:30), during scheduled wakefulness in the “restart” break (at 09:30, 12:30, 16:30, and 19:30), and after the final recovery sleep period (at 09:30 and 12:30). Sleep inertia was not an issue, as there was no significant sleep loss²⁵ and no test bout occurred close to awakening.

Study A3

90 healthy young adults were subjected to one of 18 different laboratory sleep restriction protocols.³² Each protocol began with 2 baseline days involving 8.2 h TIB (21:54-06:06). Subjects were then randomly assigned to one of 18 sleep restriction conditions, each involving a specific sleep regimen that was maintained for 10 consecutive days, the first 8 of which had sufficiently complete data to be considered here. The sleep regimen involved one of four nocturnal sleep durations: 8.2 h TIB (control condition), 6.2 h TIB, 5.2 h TIB, or 4.2 h TIB (all centered around 02:00), of which the 3 shorter ones were followed by one of 7 diurnal nap durations: 2.4, 2.0, 1.6, 1.2, 0.8, or 0.4 h TIB (all centered around 14:00) or 0.0 h TIB (i.e., no nap). The 2.4-h nap duration was paired only with the 4.2-h nocturnal sleep duration; the 2.0-h and 1.6-h nap durations were paired only with the 5.2-h and 4.2-h nocturnal sleep durations. Each of the 18 conditions had 5 subjects, which sufficed for the study's original objective to investigate dose-response relationships across different sleep regimens.

Performance on the 10-min PVT was tested every 2 h during scheduled wakefulness, starting at 04:10, 06:10, or 08:10, depending on the study condition. Focusing on test bouts that the conditions had in common and that were not potentially confounded by sleep inertia, only tests administered at 08:10, 10:10, 12:10, 16:10, 18:10, and 20:10 were considered.

Study B1

Twelve healthy young adults participated in a laboratory study of total sleep deprivation.³³ The study involved 2 baseline days each with 10 h TIB (22:00-08:00), then 62 h of sustained wakefulness, and then 2 recovery days each with 10 h TIB (22:00-08:00).

Performance on the 10-min PVT was tested every 2 h, starting at 09:30, throughout most of scheduled wakefulness. The first test bout of each waking period was omitted in order to avoid confounds from sleep inertia. Note that the presence of recovery days distinguishes the data of this study from the data of the total sleep deprivation condition in study A1.

Study B2

Fifteen healthy young adults were subjected to a laboratory study condition identical to the 88 h sustained wakefulness condition in study A1, except they were given a nap of 2 h TIB every 12 h during the 88 h period.³⁴ Nap start times alternated between 02:45 and 14:45.

Performance on the 10-min PVT was tested every 2 h, starting at 07:30, during scheduled wakefulness. The first 2 test bouts after each awakening were omitted in order to avoid confounds from sleep inertia.

Study B3

As part of a larger study, 142 healthy young adults were involved in a laboratory sleep restriction protocol similar to the 4 h TIB condition of study A1.³⁵ The study began with 2 baseline days each with 10 h TIB (22:00-08:00). Subsequently, subjects were given 4 h TIB (04:00-08:00) each day for 5 consecutive days. They were then randomized to one of 6 doses of sleep, all ending at 08:00 the next day: 0 h TIB (13 subjects), 2 h TIB (27 subjects), 4 h TIB (29 subjects), 6 h TIB (25 subjects), 8 h TIB (21 subjects), or 10 h TIB (27 subjects).

Performance on the 10-min PVT was tested every 2 h, starting at 08:00, during scheduled wakefulness. Data points through to 20:00 on the day after the night with the randomized sleep dose were considered. The first 2 test bouts after each awakening were omitted in order to avoid confounds from sleep inertia.

Model Evaluation

For each PVT test bout of every subject in studies A1-A3 and B1-B3, the number of lapses (reaction times > 500 ms)³⁶ was assessed. Day 0 was defined as the study day leading into the night when sleep loss first began, or the equivalent day for control conditions without sleep loss. Starting with day 0, the number of lapses was averaged over subjects by time point, separately for each condition in each study. The number of data points was 427 in study A1 (4 conditions), 96 in study A2 (2 conditions), 972 in study A3 (18 conditions), 31 in study B1 (1 condition), 28 in study B2 (1 condition), and 317 in study B3 (6 conditions).

Model parameter estimates and their standard errors (indicating the magnitude of the uncertainty in the parameter estimates) were obtained using the data from studies A1-A3 and applying state-of-the-art Metropolis-Hastings-type Markov chain Monte Carlo (MCMC) fitting^37,38 (with a chain length of 10,000). We posited that β_w = β_s and λ_w = −λ_s, leaving 9 free parameters to be estimated (see Table 2). For determining the initial values, we assumed steady state for the sleep/wake schedule of the baseline days in each study (see supplemental material, section 3).

For studies A1-A3 (calibration) and B1-B3 (validation), model goodness-of-fit was quantified using root mean square errors (RMSE) and explained variance. Statistical comparisons with our earlier model version⁵ were made using Akaike's Information Criterion (AIC).

RESULTS

Table 2 and Figures 1 and 2 show the results of parameter estimation for the model, Eqs. (2)-(7), based on the data from studies A1-A3. Judging by the standard errors (Table 2), all parameters are well defined by the data. This is largely corroborated by their pairwise correlations (see supplemental material, section 4).

Figure 1.

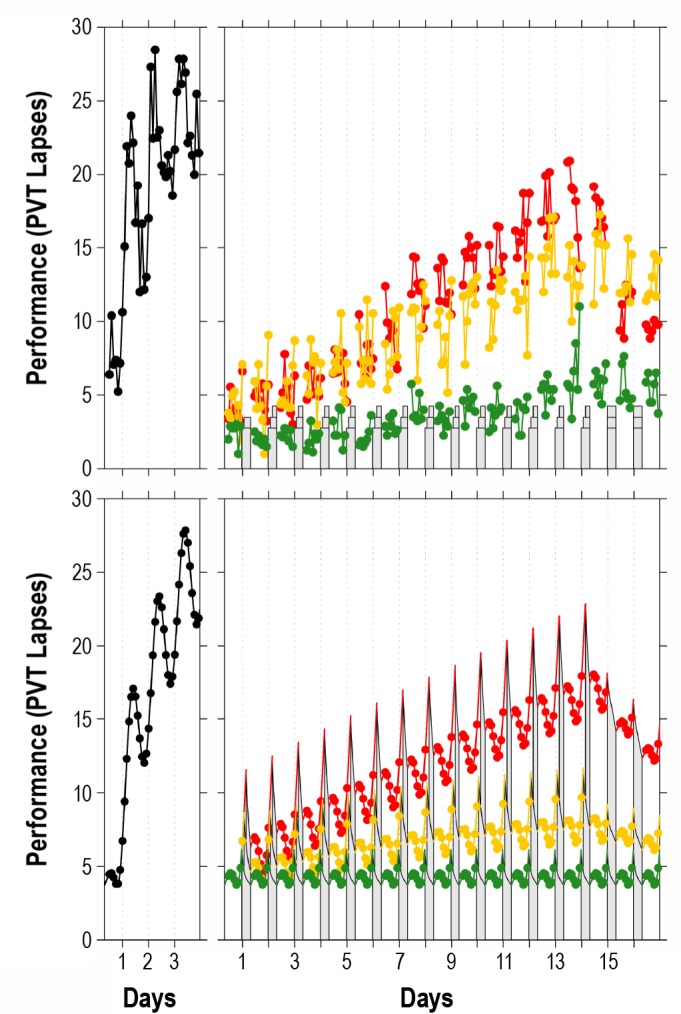
Performance observations for study A1 and predictions by the new version of the biomathematical model. Left panels show the 88-h total sleep deprivation condition; right panels show the conditions with 14 days of sustained sleep restriction followed by 2 recovery days. The sleep restriction conditions involved 8 h TIB per day (green), 6 h TIB per day (yellow), and 4 h TIB per day (red).⁷ Top panels: condition-average data by measurement time point. Bottom panels: predictions by the new model version. Gray bars indicate scheduled sleep periods. Tick marks indicate midnight of each day. Day 0 is the last baseline day (shown starting at scheduled awakening). Note that performance impairment in the sleep restriction condition with 6 h TIB per day (yellow) is relatively poorly predicted by the model because the condition-average impairment observed for this condition is inflated by a few outliers.⁷

Figure 2.

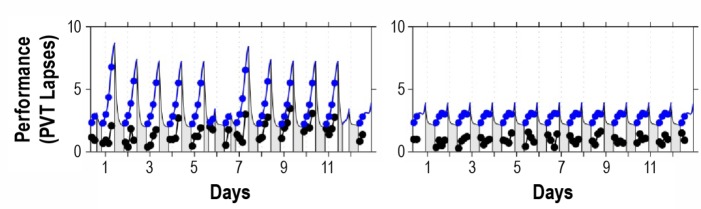
Performance observations and biomathematical model predictions for study A2. The left panel shows the night shift condition; the right panel shows the day shift condition.²⁵ Black: condition-average data by measurement time point. Blue: predictions by the new model. Gray bars indicate scheduled sleep periods. Tick marks indicate midnight of each day. Day 0 is the day leading into the first simulated shift for the night shift condition or the equivalent day for the day shift condition (shown starting at scheduled awakening). Although the model slightly overpredicts the magnitude of impairment in the observations, it captures the relative dynamics in the two study conditions well.

The estimated values for α_w and α_s are comparable to the corresponding parameters in the two-process model of sleep regulation,²⁴ −τ_r^-1 = −1 / 18.2 = −0.055 and −τ_d^-1 = −1 / 4.2 = −0.24. The estimate for the parameter η_w, which does not exist in the two-process model, is nearly identical to the equivalent parameter in our earlier model version,⁵ α₂₂ = 0.00743. The estimate for φ is also nearly identical to its equivalent in the earlier model,⁵ namely θ + t₀ = 12.7 + 8.6 = 21.3 (with θ = 12.7 taken from ref. 5 and t₀ = 8.6 defined in ref. 24). The other parameters in Table 2 are not directly comparable to either the two-process model parameters or the parameters in our earlier model version. Note that the new model version presented in this paper has only 9 free parameters (see Table 2), whereas the earlier model version had 10.

Figure 1 shows the data of the 4 conditions of study A1 (top panels), which had also been used for the calibration of our earlier model version,⁵ and the predictions of the new version of the model (bottom panels). The earlier model captured as much as 73.2% of the variance (RMSE: 3.06), leaving little room for improvement (see supplemental material, section 5). The new model, calibrated to fit the collective data of studies A1-A3, still captures almost the same amount of variance in study A1, namely 71.6% (RMSE: 3.15). Goodness-of-fit for sustained sleep restriction and recovery days, which was the main scientific advance achieved with the earlier model, is preserved in the new model (Figure 1, right panels).

Figure 2 shows the data and the predictions of the new model for the two conditions of study A2, which compares a night shift scenario (left panel) to a day shift scenario (right panel). The observed performance impairment in this study was remarkably low even in the night shift condition.²⁵ Nonetheless, although the model slightly overpredicts the magnitude of impairment, it captures the relative dynamics in the 2 conditions well. The dynamics are also well captured in the nap sleep conditions of study A3 (not shown in a figure because there were 18 different conditions; but see supplemental material, section 6).

For study A2, the new model represents a notable improvement over our earlier model version (see supplement material, section 5). The earlier model would have captured only 15.5% of the variance in study A2, but the new model captures 81.9% of the variance. For study A3, the new model likewise represents an improvement. The earlier model would have mispredicted the data and captured none of the variance in study A3, but the new model captures 34.9% of the variance. Indeed, considering studies A1-A3 together, the new model outperforms our earlier model version significantly. Whereas the earlier model would have captured 34.2% of the overall variance (RMSE: 4.08) in dataset A, the new model captures 60.0% of the variance (RMSE: 3.18, smaller is better).

It should be noted that besides model goodness-of-fit, variance explained and RMSE also reflect the magnitude of the variance in the experimental data (as affected, e.g., by the range of sleep loss and the circadian variability) and the signal-to-noise ratio. Even so, the improvement of the new model over the earlier model is confirmed by the AIC values, which are 4222.0 for the earlier model versus 3477.8 for the new model (smaller is better). For comparison, a null model predicting a straight line at the grand mean (predicting 0% of the variance) would have an AIC of 4830.3. AIC values cannot be interpreted in an absolute sense, but the relative improvement achieved with the new model version is substantial by any standard.

Figures 3 and 4 show the results of validation of the new model using the data from studies B1-B3. In study B1 (Figure 3, left panel), there is slight underprediction of the highest levels of impairment during total sleep deprivation (as expected based on metric nonlinearity³⁹), and slight overprediction of residual impairment following recovery. Peak impairment in the first 2 days of study B2 is also overpredicted (Figure 3, middle panel), which could potentially be overcome by dropping the assumption that λ_w = −λ_s (but more data would be needed to support the ensuing increase in the number of parameters). Regardless, the model does capture the relative dynamics within and between studies. Furthermore, the model predicts the recovery sleep dose-response curve for study B3 particularly well (Figure 4).

Figure 3.

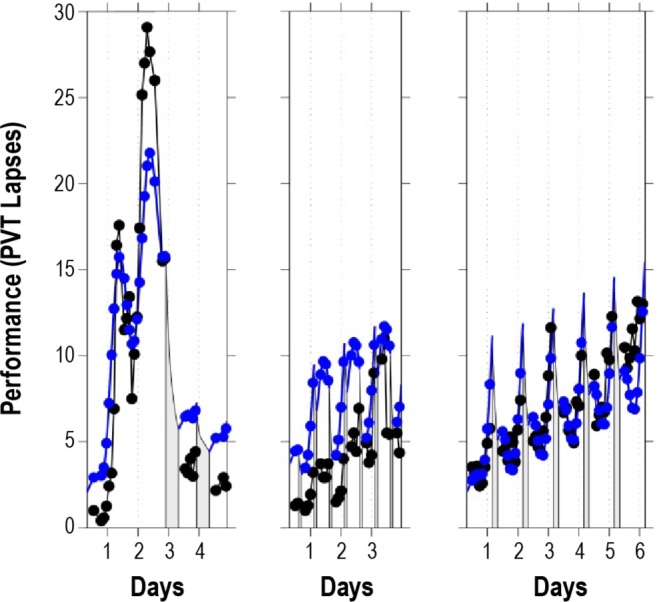
Performance observations and biomathematical model predictions for validation studies B1-B3. The left panel shows 62 h of total sleep deprivation followed by 2 recovery days (study B1).³³ The middle panel shows 88 h of extended wakefulness intervened by a 2-h nap opportunity every 12 h (study B2).³⁴ The right panel shows sustained sleep restriction to 4 h TIB per day for 5 days (the first 5 intervention days of study B3).³⁵ Black: study-average data by measurement time point. Blue: predictions by the new model. Gray bars indicate scheduled sleep periods. Tick marks indicate midnight of each study day. Day 0 is the last study day without prior sleep loss in each of the studies (shown starting at scheduled awakening). In study B1 (left panel), there is slight underprediction of the highest levels of impairment during total sleep deprivation and slight overprediction of residual impairment following recovery. In study B2 (middle panel), peak impairment in the first two days is overpredicted as well. Goodness-of-fit for study B3 (right panel) is high. Overall, the model captures the relative dynamics within and between studies well.

Figure 4.

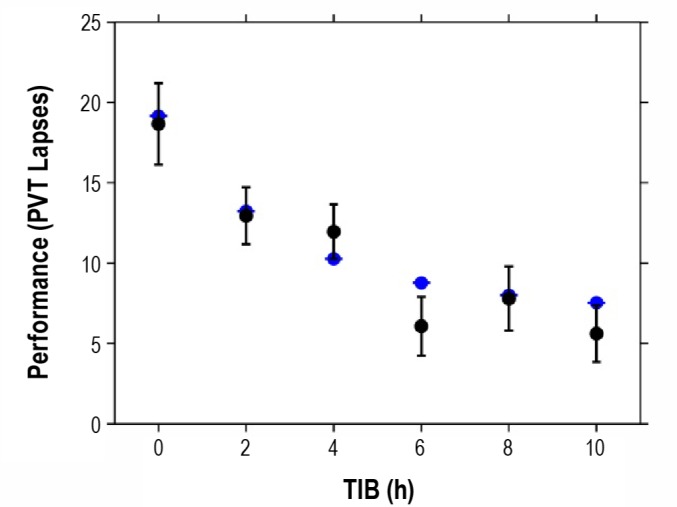
Dose-response predictions for the effectiveness of a single recovery night following 5 days of sleep restriction to 4 h TIB. The abscissa shows the sleep dose on the sixth day of study B3.³⁵ The ordinate shows PVT lapses averaged across hours 2-14 of subsequent wakefulness (following awakening at 08:00). Black: unadjusted condition-specific averages (and standard error bars) as computed with mixed-effects ANOVA.⁵⁹ Blue: predictions by the new model. The model predicts the overall dose-response curve well. Residual impairment following the 6 h TIB recovery dose is not well predicted, but the relevance of this outlier is uncertain given that the empirical data for this condition do not follow the expected monotonic relationship between recovery sleep duration and residual impairment.³⁵

Overall, the model performs well on the validation dataset, relatively closely matching the data of all 3 studies B1-B3. The model captures 75.1% of the variance in this dataset, although that number should be interpreted carefully—the model parameters are not re-estimated to fit the validation data and explained variance is then not a reliable statistic.⁴⁰ The excellent goodness-of-fit is confirmed by the RMSE though, which is 2.29 and near theoretical lower bounds derived in earlier fatigue model validation efforts.⁴⁰

DISCUSSION

Here we refined our previously published model⁵ on the temporal dynamics of neurobehavioral performance under conditions of sleep loss and circadian misalignment. A key feature retained from the earlier model version is the instantiation of a slow process (in the order of days to weeks) that modulates the waking neurobehavioral expression of sleep/wake homeostasis as a function of the prevailing sleep/wake ratio,⁵ with prior sleep insufficiency increasing the sensitivity to neurobehavioral impairment during subsequent sleep deprivation. The dynamics of the model indicate that prior sleep history modulates the homeostatic equilibrium state for sleep/wake regulation allostatically.^8,9 This implies that “optimal” neurobehavioral functioning is a moving target depending on prior sleep history⁶ as has been confirmed experimentally.^11,12,41,42 Such dynamics could potentially explain the discrepancy of temporal profiles in sustained sleep restriction scenarios⁷ between objective measurements of neurobehavioral performance and self-reports of subjective sleepiness. That is, the former are typically expressed in terms of absolute impairment and therefore display the effects of both short-term homeostatic and longer-term allostatic regulation, whereas the latter seem to be dominated by acute change and may primarily reflect short-term homeostatic regulation in response to deviations from the homeostatic equilibrium state.

The main refinement introduced in the present paper concerns the circadian modulation of neurobehavioral performance, for which we improved the dynamics and the prediction accuracy without increasing the total number of model parameters. To better capture the nonlinear interaction between circadian and homeostatic influences on neurobehavioral performance,^14,15 where the circadian modulation of neurobehavioral performance is small in well-rested individuals and larger in sleep-deprived individuals,^16,43 we implemented a sigmoidal rise in circadian amplitude during wakefulness and an exponential decline in circadian amplitude during sleep. The introduction of sigmoidal time-dependence for the circadian amplitude during wakefulness generalizes the scope of the model to include night shift schedules and nap sleep scenarios. Moreover, through the nonlinear interaction between circadian and homeostatic influences on neurobehavioral performance, the new model also produces good predictions for the neurobehavioral effects of recovery sleep following sustained sleep restriction (Figure 4).

The time it takes for the circadian amplitude to rise to and saturate near its asymptotic maximum during wakefulness, when initially well-rested, is estimated to be about 20 h (as derived by entering the estimate for λ_w in Table 2 into Eq. (7a) in Table 1). Sigmoidal dynamics for waking neurobehavioral functioning have been proposed previously,⁴⁴ with similar estimated saturation time, but were presumed to be associated principally with a decline in homeostatic influence on waking neurobehavioral performance.

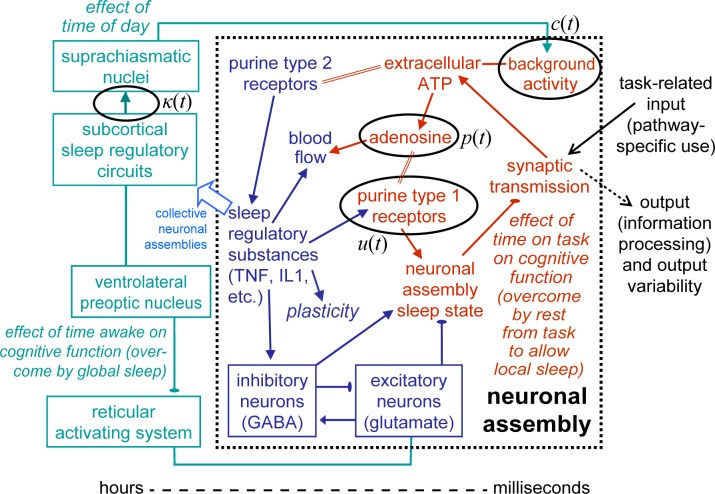
Goodness-of-fit statistics for both the calibration dataset and the independent validation dataset indicate that prediction accuracy across the extended scope of the new model is high. The model is grounded in mathematical characterization of the emergent dynamic behavior⁵ and in experimental studies and theory of the regulatory neurobiology. The recently proposed ATP-cytokine-adenosine hypothesis^45,46—the first theoretical advance to offer a neurobiological explanation for the cumulative deficits associated with sustained sleep restriction—has suggested specific connections between the time-dependent variables of our model and the neurobiology of sleep and wakefulness. These hypothesized connections are shown in Figure 5 (black ovals), placed in the framework of a broader theory proposing that sleep is fundamentally use-dependent and local to cortical columns and other neuronal assemblies.^47–49 Within that framework, we posit that p(t) corresponds to extra-cellular adenosine production rate in neuronal assemblies critically involved in task performance,⁴⁹ which may be proportional to the probability of local sleep and thereby underlie performance variability and impairment.⁵⁰ We posit that u(t) reflects the regulation of post-synaptic adenosine receptor density,⁴⁸ changes in which may embody allostatic control of the homeostatic equilibrium for sleep/wake regulation.⁹ We posit that c(t) represents global modulation of basal synaptic activity,⁵¹ which may be driven by peripheral oscillators in the brain⁵² orchestrated by the circadian pacemaker in the suprachiasmatic nuclei (SCN).⁵³ Lastly, we posit that κ(t) captures the influence of sleep homeostasis on SCN activity,²⁶ as may be induced by sleep regulatory substances and subcortical sleep regulatory circuits⁴⁹ (see Figure 5).

Figure 5.

Hypothesized connections between mathematical model variables and the neurobiology of sleep and wakefulness. The schematic is based on a theory of local, use-dependent sleep and provides speculative explanations of key phenomena of waking neurobehavioral impairment due to sleep loss, as follows⁴⁹: (A) On a time scale in the order of milliseconds to seconds, information processing in a cortical column or other neuronal assembly associated with a given performance task triggers a biochemical cascade (red elements), which induces a sleep-like state locally. When the neuronal assembly is in the wake state and stimulated by input, it responds with synaptic transmission to process the input signal and generate corresponding output. The synaptic transmission is associated with release of adenosine triphosphate (ATP) into the extracellular space. Breakdown of extracellular ATP results in increased extracellular adenosine production, at a rate approximately proportional to the amount of synaptic transmission in response to stimulation (i.e., use-dependent). Binding of extracellular adenosine at adenosine (purine type 1) receptors promotes the neuronal assembly sleep-like state, during which the assembly's synaptic transmission patterns are fundamentally altered. This functionally changes the contribution of the neuronal assembly to the coordinated response of the larger neuronal pathway involved in the performance task, causing degraded (delayed and/or impaired) information processing.⁴⁸ As such, the local sleep-like state causes output variability, which leads to stochastic cognitive performance variability and thus neurobehavioral performance impairment.⁶⁰ In this context, we posit that in our model, p(t) corresponds to extracellular adenosine production rate. (B) On a time scale of minutes to hours (blue elements), binding of ATP to purine type 2 X7 receptors⁴⁵ results in release of sleep regulatory substances (SRSs) such as tumor necrosis factor (TNF) and interleukin-1 (IL1).⁴⁶ The SRSs mediate neuronal plasticity, and promote the neuronal assembly sleep-like state through growth hormone releasing hormone (GHRH) mediated activation of GABAergic neurons.⁴⁸ These GABAergic neurons inhibit glutamatergic excitatory neurons, which prevents the glutamatergic neurons from promoting the local wake state. The SRSs together with adenosine also influence regional blood supply and thereby oxygen and metabolic supply. As a consequence of these SRS effects, the probability of entering the sleep-like state increases in a time- and use-dependent manner, giving rise at the cognitive level to habituation and the time-on-task effect. A rest break (or switching to a task that does not intensively use the same neuronal pathway) allows SRS and adenosine levels to decay, resetting the time-on-task effect.⁶⁰ (C) On a time scale of hours to days, basal synaptic activity in neuronal assemblies throughout the brain, and the associated release of ATP into the extracellular space, leads to a global build-up of SRSs over time awake. This is modulated by the suprachiasmatic nuclei (SCN), which orchestrate circadian rhythms in the cellular machinery and neuronal activation across the brain.⁵² As such, time awake and time of day independently and in interaction amplify use-dependent neurobehavioral impairment and the magnitude of the time-on-task effect.⁶¹ Sustained exposure to wake extension and repeated intensive use of neuronal assemblies over days to weeks cause the SRSs to accumulate and, via their receptors and nuclear factor κB, increase the density of post-synaptic adenosine A₁ (purine type 1) receptors.⁶² This leads to cumulative performance deficits across days of chronic sleep restriction and allostatic shifting of the homeostatic equilibrium for sleep/wake regulation. Conversely, across multiple days of recovery sleep the adenosine receptors downregulate, the homeostatic equilibrium point shifts back, and baseline performance capability is gradually restored.⁵ We posit that in our model, u(t) reflects adenosine receptor density, and c(t) represents global circadian modulation by the SCN. (D) Subcortical circuits involved in the coordination of whole-brain sleep (green elements) are influenced by the collective neuronal assembly states, integrated across the brain through mechanisms involving the SRSs.^63,64 The subcortical circuits concerned include the SCN, as well as the ventrolateral preoptic nucleus (VLPO), which can deactivate the wake-promoting (e.g., glutamatergic) neurons of the reticular activating system and other systems such as the cholinergic networks of the basal forebrain.⁶⁵ These subcortical systems thus nycthemerally and homeostatically balance and consolidate sleep/wake states globally, seeking to induce whole-brain sleep to prevent interaction with the environment when too many neuronal assemblies would otherwise be in the local sleep-like state. The global sleep state allows SRS concentrations to be restored, and adenosine receptors to be gradually downregulated, in a coordinated manner across all neuronal assemblies. This counteracts the effects of prior time awake both globally and locally.⁴⁹ We posit that in our model, κ(t) captures the homeostatic influence of the collective neuronal assembly states, as integrated across the brain through SRSs, on SCN activity. Figure adapted from ref. 60 with permission.

As the underlying neurobiology is increasingly well understood, confidence grows that predictions of our model generalize to sleep/wake/work scenarios not already included in the calibration and validation datasets.⁵⁴ Some specific predictions regarding the dynamics of neurobehavioral performance, in scenarios for which carefully controlled studies have yet to be published, are worth discussing. Consider, for example, the dynamics of neurobehavioral performance impairment across days of sustained sleep restriction when the restricted sleep is placed during the day. It could be expected that the build-up of neurobehavioral deficits across days of sleep restriction is accelerated under such conditions of circadian misalignment. However, that is not what the model predicts—see Figure 6. Although neurobehavioral performance is worse overall when sleep is placed during the day and wakefulness during the night, the predicted rate for the build-up of impairment is essentially the same regardless of the circadian placement of the restricted sleep. Preliminary analyses of laboratory data addressing this issue appear to tentatively confirm this.⁵⁵

Figure 6.

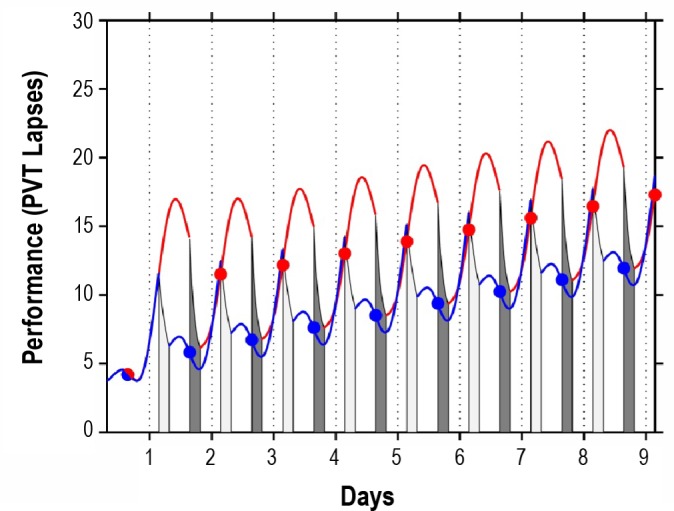
Model predictions for the effects of sustained sleep restriction on neurobehavioral performance when wakefulness is placed during the night as compared to during the day. The blue trajectory displays predicted performance (PVT lapses) across days with 20 h diurnal wakefulness and 4 h nocturnal sleep (dark gray bars; TIB: 03:30-07:30). The red trajectory displays predicted performance across days with the restricted sleep periods shifted 12 h later, i.e., with 20 h nocturnal wakefulness and 4 h diurnal sleep (light gray bars; TIB: 15:30-19:30). In both scenarios, baseline sleep is assumed to involve 8 h TIB at night (23:30-07:30) for several days prior. In agreement with preliminary laboratory findings,⁶⁶ circadian phase adjustment in the shifted scenario is assumed to be negligible. Circadian effects on sleep efficiency are accounted for in the model dynamics. Dots represent averages across the interval from 2 h to 14 h after scheduled awakening for each period of wakefulness.

The situation seems more complex following a “restart” (recycling) break with nocturnal recovery sleep—see Figure 7. Initially, the nocturnal recovery sleep is predicted to restore degraded performance more when prior restricted sleep is placed during the day (red trajectory) than during the night (blue trajectory), to about the same absolute level of performance. The relatively greater restorative benefit of nocturnal recovery sleep following restricted diurnal sleep appears to be short-lived, though—after a few days, predicted neurobehavioral performance is again worse overall when sleep is placed during the day, and with the same predicted rate for the build-up of impairment. In contrast, nocturnal recovery sleep immediately following a short period of acute sleep loss (with only a brief nap; black trajectory) is predicted to have a relatively large and more enduring restorative effect. The trajectories in the figure suggest that sustained circadian misalignment, similar to sustained sleep restriction, allostatically modulates the homeostatic equilibrium for sleep/wake regulation.

Figure 7.

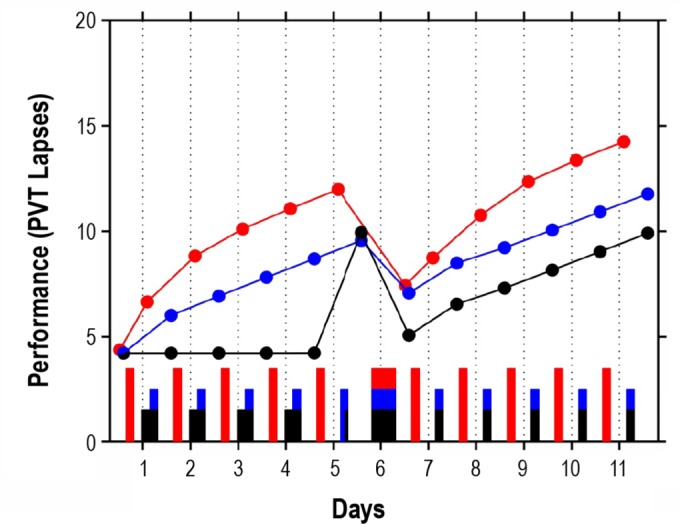
Model predictions for the effects of sustained sleep restriction comparing hypothetical schedules with nighttime versus daytime sleep and different sleep histories. The blue trajectory displays predicted performance (PVT lapses) for a scenario beginning with 5 days with 4 h nocturnal sleep (TIB: 03:30-07:30) and ending with a recovery day with 12 h nocturnal sleep (TIB: 19:30-07:30) followed by 5 days with 4 h nocturnal sleep (TIB: 03:30-07:30). The black trajectory displays predicted performance for a scenario also ending with a recovery day with 12 h nocturnal sleep and 5 days with 4 h nocturnal sleep, but beginning with 4 days with 8 h nocturnal sleep (TIB: 23:30-07:30) followed by a day with only a 1.5 h nap (TIB: 06:00-7:30). The red trajectory shows predicted performance for a scenario beginning with 5 days with 4 h diurnal sleep (TIB: 15:30-19:30) and ending with a recovery day with 12 h nocturnal sleep (TIB: 19:30-07:30) followed by 5 days with 4 h diurnal sleep (TIB: 15:30-19:30), where circadian phase adjustment is assumed to be negligible. In all three scenarios, baseline sleep is assumed to involve 8 h TIB at night (23:30-07:30) for several days prior. Dots represent averages across the interval from 2 h to (up to) 12 h after scheduled awakening for each period of wakefulness. Bars indicate sleep periods.

The present version of our model may be suitable for use in model-based fatigue risk management,⁴ comparable to if not more precise than other fatigue and performance models⁵⁶ currently in use for that purpose. Our model is distinct from other models in this context in that it uses time in bed (TIB) as a basis for predicting waking neurobehavioral function, and does not require information about or estimation of actual physiological sleep obtained. That is, homeostatic, circadian, and allostatic effects on sleep efficiency are implicitly accounted for in the predictions for neurobehavioral performance through the parameter estimates of the model. It should be noted that external factors that could markedly reduce sleep efficiency (such as environmental noise) cannot be accounted for this way unless actual sleep obtained is measured (e.g., through actigraphy). A reparameterization of the model to use measured sleep times as a basis for prediction is possible, and will be considered in the future.

Even though our model predicts performance impairment quantitatively, model predictions should generally not be interpreted as absolute measures of impairment, especially when used in sleep/wake scenario evaluation and model-based fatigue risk management.⁴ One reason is that there is increasing recognition of quantitative and qualitative differences in the effects of sleep loss across different tasks.^57,58 This issue can be partially addressed by building on a primary strength of fatigue and performance models, which is their focus on the temporal dynamics of neurobehavioral impairment. Model predictions can accordingly be used to compare the relative impairment associated with different sleep/wake schedules (see footnote following this section)—and select a schedule that is comparatively favorable with respect to fatigue and other operationally relevant criteria. Following the recent promulgation by the U.S. Federal Aviation Administration of a new rule on duty and rest requirements for flight crew members in commercial aviation (14 Code of Federal Regulations Parts 117, 119, and 121), which contains a provision for requests for exceptions from duty hour restrictions based on safety-relevant evidence including predictions from fatigue and performance models, the stakes are high to further develop model-based fatigue risk management methodology along these lines.⁴

While the work presented here constitutes a considerable expansion of the scope of our model, further improvements will be pursued. Data from additional studies on the effectiveness of recovery sleep that may become available in the future will be used to re-estimate the parameters of the model. In doing so, the correlation among some of the model parameters (see supplemental material, section 4) will likely be significantly reduced. Prediction of the effects of sleep inertia on neurobehavioral performance will be included in the model pending the better development of a theoretical basis for the phenomenon. Finally, there is a need for additional improvements to the circadian component of the model, particularly with regard to phase adjustments after circadian desynchronization. Although informative data on this issue relevant to real-world scenarios are scarce, it is a priority for our next model development efforts. Until then, the model in its present form should not be applied to scenarios involving transmeridian travel or otherwise systematically shifted circadian rhythmicity.

FOOTNOTE

Schedule-based comparisons of predicted fatigue by time point and by time spent above some threshold level⁴ are nominally invariant to what measure of fatigue is considered, provided a monotonic relationship between different fatigue measures may be assumed. Caution is warranted if schedule-based comparisons rely on temporal integration of predicted fatigue⁶⁷ (e.g., average or area under the curve), because outcomes may then vary depending on the fatigue measures considered if relationships between them are nonlinear.

DISCLOSURE STATEMENT

This was not an industry supported study. This work was supported by Air Force Office of Scientific Research grant FA9550-09-1-0136 (to Dr. Van Dongen); and in part by Office of Naval Research contracts N00014-10-C-0392 and N00014-11-C-0592 (to Dr. Mollicone), Naval Medical Logistics Command contract N62645-12-C-4004 (to Dr. Mollicone), Naval Warfare Development Command contract N65236-09-D-3809 (to Dr. Mollicone), National Institutes of Health grant NR04281 (to Dr. Dinges), Air Force Office of Scientific Research grant F49620-95-1-0388 (to Dr. Dinges), Federal Motor Carrier Safety Administration award DTMC75-07-D-00006 (to Dr. Van Dongen), Congressionally Directed Medical Research Program award W81XWH-05-1-0099 (Washington State University, Spokane, WA), and the National Space Biomedical Research Institute through NASA NCC 9-58 (to Dr. Dinges). This work was performed at Washington State University, the University of Montana, and the University of Pennsylvania. The paper does not address any off-label or investigational use.

SUPPLEMENTAL MATERIAL

1. Invariant reformulation of Eqs. (1) as a system of coupled non-homogeneous first-order ODEs

Reintroducing previously used notation where p and u are replaced by q and v and where wake/sleep cycles are indexed by n, we start with Eqs. (1) in the following form¹:

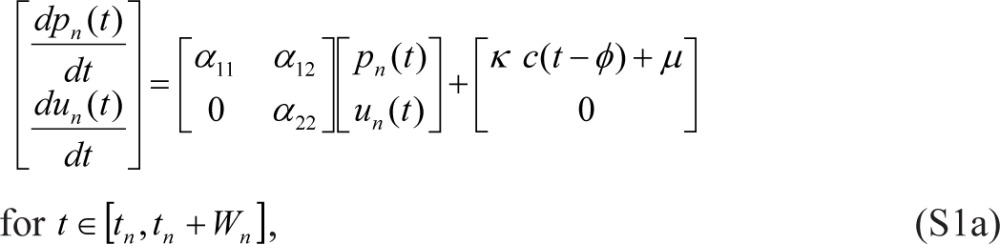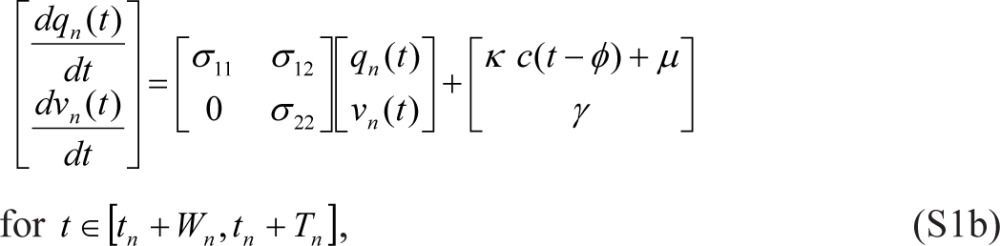where t_n denotes the beginning of scheduled wakefulness in the n^th wake/sleep cycle, W_n is the duration of scheduled wakefulness in the n^th cycle, T_n is the total duration of the n^th cycle (such that t_n+1 = t_n + T_n), and γ = 0. Eqs. (S1) are linked within and across days by:

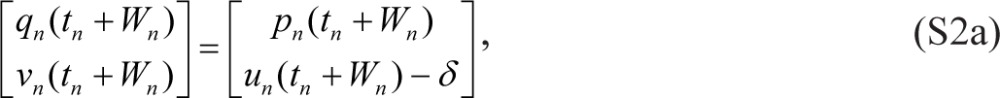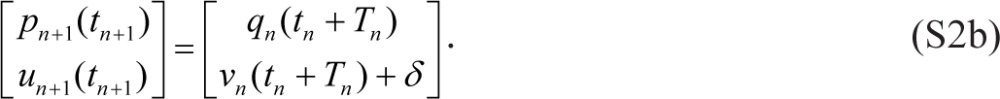The link between u_n(t) and v_n(t) in Eqs. (S2) can be made continuous by setting γ = −σ₂₂ δ in Eqs. (S1) and dropping δ from Eqs. (S2). However, the equation for dq_n(t)/dt then has to be adjusted as follows:

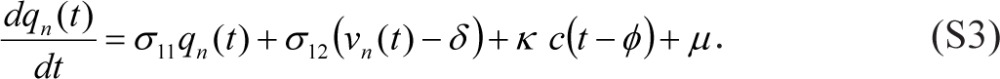Normalizing u_n(t) and v_n(t) through division by −σ₂₂ δ and making a number of trivial parameter substitutions puts the model in the following form:

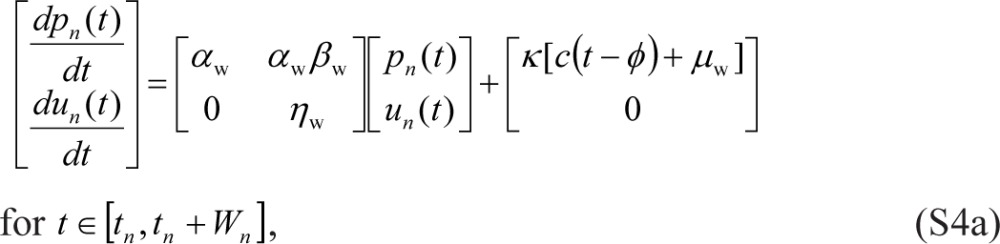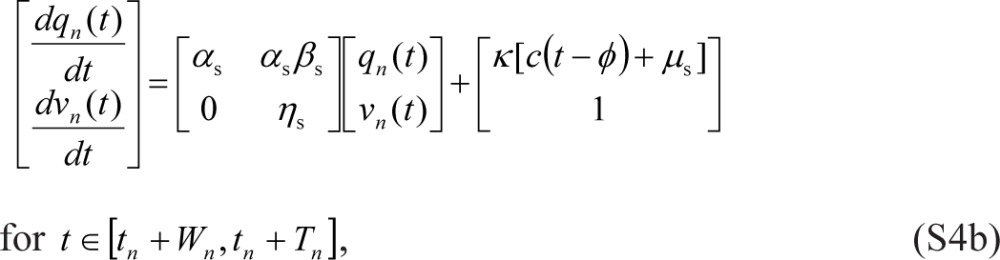which is equivalent to the form given in Eqs. (2) and (3).

2. Proof that performance impairment in Eq. (2b) tends to zero for increasing sleep duration

The solutions for Eqs. (7b) and (3b) with arbitrary initial conditions have the form:

respectively. Substituting Eqs. (S5) and (S6) into Eq. (2b), and taking into account Eqs. (5b) and (6), we arrive at:

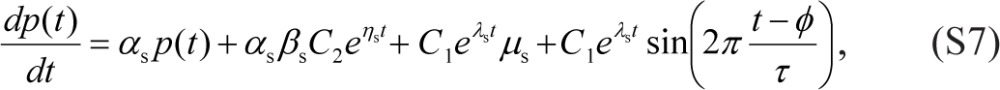or

where the non-homogeneous term is a linear combination of the functions e^η_st, e^λ_st, and e^λ_st $\sin \left(2\pi \frac{t-\phi }{\tau }\right)$.

The solution of Eq. (S8) with arbitrary initial condition has the form:

where F(t) is a particular solution of the non-homogeneous Eq. (S8) which, under conditions α_s ≠ β_s and α_s ≠ λ_s, is also a linear combination of e^η_st, e^λ_st, and e^λ_st $\sin \left(2\pi \frac{t-\phi }{\tau }\right)$. If α_s = β_s and/or α_s = λ_s, then F(t) also contains terms proportional to te^η_st and/or te^λ_st. Since α_s < 0, β_s < 0 and λ_s < 0, each term on the right hand side of Eq. (S9) tends to zero as t → ∞, and thus lim_{t → ∞} p(t) = 0. That is, p(t) tends to zero for increasing time asleep.

3. Initial values for the ODE system of Eqs. (2), (3) and (7)

For a wake/sleep schedule of constant wake duration W and constant day length T, where T = τ (i.e., circadian entrainment), we assume steady state (of a periodic map with period T). The initial values for p(t) and u(t) in Eqs. (2a) and (3a) at the onset of scheduled wakefulness t₀ are then given by¹:

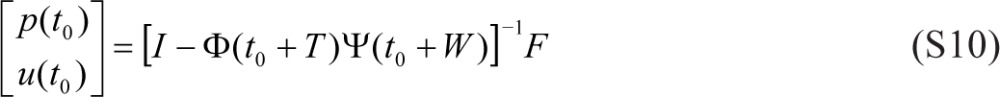where Ф(t) = φ(t)φ^-1 (t₀ + W) and Ψ(t) = ψ(t)ψ^-1(t₀) with

and

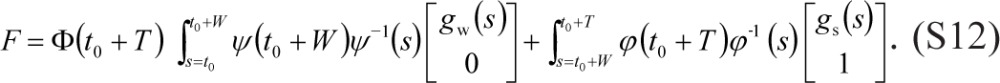The corresponding initial value for κ(t) in Eq. (7a) is given by:

Note that under the steady state (of the periodic map), the time-dependent trajectory for κ(t) is bounded and oscillatory, and thus the non-homogeneities given by Eqs. (5) are bounded and oscillatory and the integrals in Eq. (S12) are constant. Previously provided proofs² about states of equilibrium, stability, and the bifurcation property of the model are therefore applicable to the present version of the model.

4. Pairwise correlations among the estimated model parameters

Figure S1 shows the one- and two-dimensional marginal probability distributions of the model parameters, obtained through MCMC, and gives the pairwise correlations among the estimated model parameters. While some correlation among model parameters is unavoidable in non-linear models, substantive correlations were found only among α_s, β_w and η_w. It suggests some potential redundancy in the model parameterization given the data at hand, which may be resolvable with the inclusion of data from additional studies focusing on recovery sleep.

Figure S1

Approximate one- and two-dimensional marginal probability distributions of the model parameters as obtained with MCMC fitting. The red dots are pairs of parameter estimates from the MCMC chain. The blue curves over the clouds of red dots represent contours of the approximate 50% and 95% reliability regions. The black curves anchored on the axes are the one-dimensional marginal distributions. Numbers in bold are correlation coefficients between pairs of parameter estimates as derived from the MCMC chain.

5. Predictions by the earlier version of the biomathematical model

In the publication on the earlier version of our biomathematical model,¹ we focused primarily on the temporal dynamics between sleep/wake cycles (i.e., across days). Figure S2 shows the predictions of the earlier model version for study A1, which had also been used for the calibration of that model version. Comparison with the predictions of the new model version (main paper, Figure 1, bottom panels) illustrates that goodness-of-fit between sleep/wake cycles has been preserved from the earlier version to the new version of the model.

Figure S2

Predictions by the earlier version of the biomathematical model for study A1. See Figure 1 in the main paper for details.

It was demonstrated that as long as the non-homogeneous part of the model contains only oscillatory functions such as circadian rhythm, the dynamics across sleep/wake cycles do not depend on it.¹ A detailed examination of the non-homogeneous part of the earlier model version was left to be addressed in the present paper, and involved inclusion of additional calibration data sets such as those of study A2. The earlier model version was not meant to be used for the night shift schedule of study A2. For comparison with the predictions of the new model version, however, Figure S3 shows the predictions of the earlier model version for study A2. The magnitude of the changes within sleep/wake cycles in the night shift condition was much too large in the earlier model version; this has been fixed in the new model version by means of the time-dependent function κ, which modulates the amplitude of the circadian process as a function of sleep/wake state.

Figure S3

Predictions by the earlier version of the biomathematical model for study A2. See Figure 2 in the main paper for details (but note the difference in the range of the ordinate).

6. Dose response curve for build-up of impairment across days with restricted, split sleep

In study A3, a dose-response experiment involving 18 different conditions with chronically restricted nocturnal sleep augmented with a diurnal nap, it was found that the rate of PVT performance degradation across days is primarily a function of total TIB per 24 h—in the range from 4.2 h to 8.2 h—regardless of whether and how sleep is split between a nocturnal sleep period and a diurnal nap.³ Based on previously developed methodology for statistical modeling of changes in average performance impairment across days,⁴ the data of each condition were normalized to baseline and then fitted with a function β t^θ, where t denotes time in days, θ is a curvature parameter, and β is an index of the rate of the (non-linear) build-up of performance impairment across days. The study revealed that β could be adequately described by a linear function of total TIB per 24 h.³

We applied the same analytical strategy to our new model estimates for study A3, averaging them over the time points 08:10, 10:10, 12:10, 16:10, 18:10, and 20:10 for each of days 0 (baseline) through 8 (see study A3 description in the methods section of the paper). After subtracting the day 0 average from the other day averages, β was assessed for each study condition by fitting the function β t^θ (where θ was shared among conditions and estimated to be θ = 0.74, indicating near-linearity across days as previously reported^3,4). The results for β are shown as a function of total TIB per 24 h in Figure S4 (blue dots).

Figure S4

Dose-response relationship between daily sleep amounts and the build-up of performance impairment across days with restricted, split sleep. The blue dots show model-based estimates for β, an index of the build-up rate of impairment across days, plotted against total TIB for nighttime sleep and daytime naps per 24 h for each of the 18 conditions in study A3. The blue dashed curve shows a parabolic dose-response approximation thereof. The black dashed line displays a linear dose-response relationship as estimated originally with statistical modeling of the study data.

To derive a dose-response curve approximation, the analysis of the model estimates was repeated with β constrained as a parabolic function of total TIB per 24 h. Figure S4 (blue dashed curve) shows that the dose-response curve approximation is near-linear, reaching zero (i.e., no build-up of impairment across days) near 8.2 h TIB (in agreement with an earlier estimate⁴ based on statistical modeling in study A1).

The originally estimated dose-response relationship (Figure S4, black dashed line),³ based on statistical modeling of the study A3 data, was linear. It was anchored at nearly the same β value for the lowest sleep dose of 4.2 h TIB in the experiment. However, the improvement as a linear function of increasing total TIB per 24 h was underestimated – seemingly implying that much more than 9 h TIB per day would be needed to maintain baseline performance across days, which is inconsistent with other laboratory study findings.^4,5 Here, the model-based estimates appear to reflect a more realistic account of the dose-response relationship between daily sleep amounts and the build-up of performance impairment across days with restricted, split sleep.