On the interpretation of subgroup analyses in randomized trials: heterogeneity versus secondary interventions

Abstract

In randomized trials with subgroup analyses, the primary treatment or intervention of interest is randomized but the secondary factors defining subgroups are not. The commentary clarifies when confounding is or is not an issue in subgroup analyses. If investigators are simply interested in targeting subpopulations for intervention, control for confounding does not need to be made. If investigators are interested in intervening on the secondary factor defining the subgroup in order to increase the treatment effect or in attributing the subgroup differences to the secondary factor itself then confounding is relevant and must be controlled for. The point is illustrated using randomized trials published in the literature.

Background

Prior commentary on subgroup analyses (1–6) has focused on data analysis and reporting rather than on the interpretation of effect heterogeneity itself when clinically and statistically significant. This past literature has pointed out the importance of specifying subgroup analyses a priori, the issue of multiple testing and proper statistical procedures for subgroup analyses. Others have noted the possibility of confounding in subgroup analyses, but these authors have not discussed when such confounding is or is not relevant (4,7). Here we clarify in what settings confounding for the secondary factor defining subgroups is important in interpreting subgroup analyses. As will be seen throughout the course of this commentary a distinction should be drawn between whether (i) it is simply the case that the effect of an intervention varies across strata of a secondary factor, referred to as “effect heterogeneity”, or (ii) it is the case that an intervention on the secondary factor would actually change the effect of the primary intervention, referred to as “causal interaction”. If the first is in view, confounding for the secondary factor is not relevant; if the second is in view, confounding for the secondary factor must be controlled.

Confounding in subgroup analyses

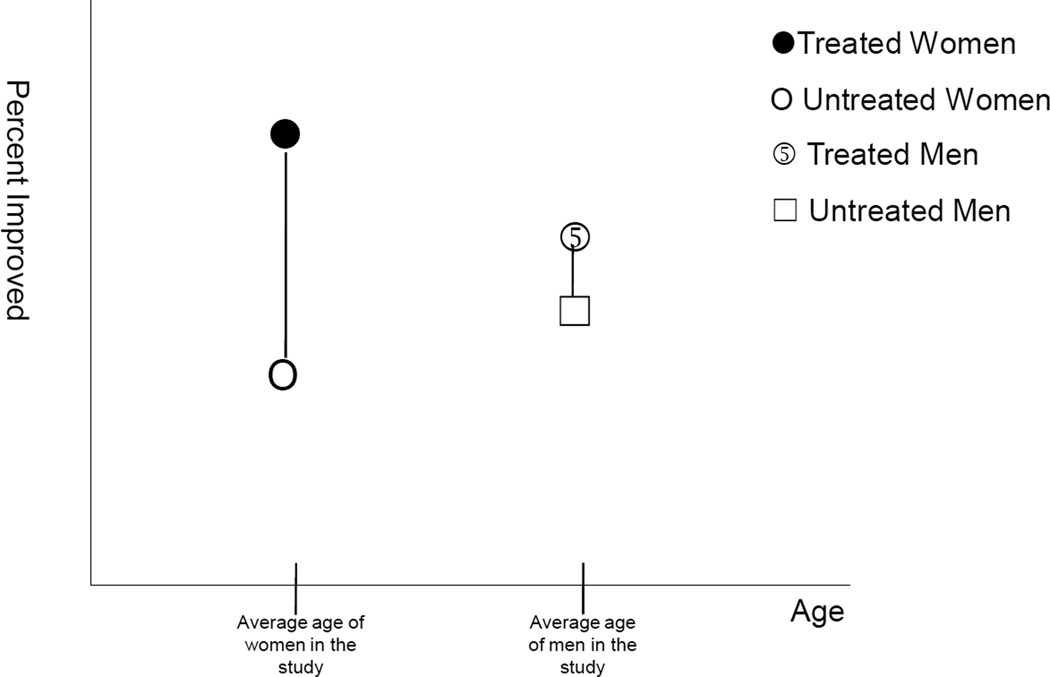
Consider a subgroup analysis of a randomized trial that indicated that the effect of treatment was larger for women than men. If the men in the study were substantially older than the women and if treatment were more effective at younger ages, then it might be age rather than sex that is responsible for the differences in treatment effects when comparing men and women. This possibility raises the question of when confounding is relevant in subgroup analyses. On the one hand, treatment is randomized and the treatment groups should be comparable, even when divided into subgroups using baseline characteristics. On the other hand, the subgroups themselves (e.g. men and women) may not be comparable to one another on other baseline characteristics (e.g. age).

Because treatment is randomized, a comparison of treatment and placebo for men and for women will give valid estimates of the treatment effects in these two subgroups (assuming also no differential loss to follow-up and adherence to study protocol). The difference between these two estimates will give a valid measure of effect heterogeneity comparing the men and women in the sample. What we cannot do, however, is necessarily attribute the difference in treatment effects as being due to sex itself. As illustrated in Figure 1, we might see a difference in treatment effects comparing men and women simply because men and women differed in age. Conceived of another way, at least in large samples, the effect of treatment within subgroups will not be confounded because treatment is randomized; but the effect of the secondary factor defining subgroups might be confounded since it is not randomized. If we are simply interested in assessing the treatment effect within subgroups, control does not need to be made for confounding. If we are interested in attributing the differences in treatment effect to the secondary factor itself, then control must be made for confounding of the secondary factor. If we controlled for age in the subgroup analysis and still found a difference in treatment effects comparing men and women, we would have evidence that the effect heterogeneity was not due to age. However, we could not definitively conclude that the effect heterogeneity was attributable to sex itself unless we were able to control for the relevant differences (a sufficient set of confounders) between the men and women in the study.

Figure 1.

Confounding in subgroup analyses: Valid estimates of treatment effect for men and women in the study; but these differences in treatment effect might be attributable to age rather than to sex itself

Examples

The distinction concerning when confounding is important becomes especially apparent if we consider possible interventions on the secondary factor. Consider a randomized trial (8) on the effects of tiotropium on forced expiratory volume in patients with chronic obstructive pulmonary disease. In subgroup analyses, the investigators found a statistically significant decline in mean postbronchodilator forced expiratory volume comparing tiotropium versus placebo only in the subgroup of patients who were not receiving either inhaled corticosteroids or long-acting beta-agonists at baseline. The subgroup of those not receiving either inhaled corticosteroids or long-acting beta-agonists at baseline consisted of 1554 of the 2554 patients included in the main analysis. The subgroup analysis was post hoc but let us suppose that it indicates an accurate and replicable finding. If one were simply interested in targeting groups for which treatment was most effective, the subgroup analysis would validly indicate that, in comparable samples, the effect of treatment will be larger for those not receiving corticosteroid/beta-agonists at baseline than for those receiving them. Suppose, however, we considered ceasing the use of corticosteroid/beta-agonist for those receiving them. The subgroup analysis does not give definitive evidence that intervening on corticosteroid or beta-agonist use itself would render triotropium more effective. Individuals not receiving corticosteroids or beta-agonists may be healthier at baseline and it may be the case that tiotropium is more effective for these healthier individuals. We do not know whether we can attribute the effect heterogeneity across corticosteroid/beta-agonist subgroups to corticosteroid/beta-agonist use itself or to some other factor confounded with it. To answer this question, control would have to be made for a set of factors that suffice to control for confounding of the relationship between corticosteroid/beta-agonist use and forced expiratory volume.

Essentially, if we are simply interested in targeting subgroups to better maximize the treatment effect, confounding for the secondary factor defining the subgroups need not be taken into account. If we are interested in intervening on the secondary factor to increase the treatment effect (or desire to attribute the effect heterogeneity to the secondary factor) then we need to take into account confounding of the secondary factor. The secondary factor has not been randomized. Control for factors confounding the effect of the secondary factor could be done by multivariate adjustment or by stratifying on the confounders for the secondary factor. However, to produce valid estimates of how intervening on the secondary factor would change the effect of the primary intervention, all such factors would have to be controlled for in the analysis. Note that simply stratifying randomization on the secondary factor does not suffice to control for confounding of the secondary factor. This would simply increase the likelihood of comparable numbers of treated and control subjects in each strata of the secondary factor. The secondary factor itself, since it is not randomized, may still be correlated with other covariates at baseline. If it were possible to randomize the secondary factor then we could use a factorial experiment in which both the primary intervention and the secondary factor were randomized; such an approach would eliminate confounding for the secondary factor.

As another example where such concerns may be relevant, Sadowski et al. (9) report results from a trial of supportive housing for homeless adults with chronic illness. Suppose it were found that the effect of supportive housing on the number of hospital days were larger for homeless adults with at least part-time employment. This would imply that the effectiveness of treatment could be increased by targeting individuals with employment. However, the subgroup analysis would not imply that if individuals were given employment, along with the supportive housing program, that this would increase the effect of the housing program itself. It may be the case that employment may be confounded by mental health so that employment is effectively serving as a proxy for mental health. Supportive housing may be more effective for those without mental illness. Intervening on employment without changing mental health status may make no difference to the effectiveness of supportive housing. If this were the case, a subgroup analysis for employment that controlled for mental health status might find the effect heterogeneity for employment vanish indicating no causal interaction between employment and the housing program. Control for confounding is not necessary for targeting subgroups; it is necessary if we consider interventions on the secondary factor, e.g. employment.

Additional remarks

Several further points merit attention. First, the remarks made above are also relevant in observational studies. In an observational study, neither the primary exposure nor the secondary factor has been randomized. When effect heterogeneity is in view, only one set of confounding factors (for exposure) need be controlled for; when interventions on both exposure and the secondary factor are considered, adjustment needs to be made for both sets of confounding factors. In the context of observational studies, we have elsewhere (10) discussed the distinction between referred to the former setting as one of “effect modification/heterogeneity” and the latter as “causal interaction.”

Second, even when the aim of the subgroup analysis is simply establishing effect heterogeneity, all of the prior cautionary points concerning the analysis and reporting of subgroup results (1–6) should be heeded. To ensure validity of results, pre-specified subgroup analyses are preferable to post-hoc analyses; issues of multiple testing should be corrected for (5,6); formal interaction tests should be undertaken; subgroup analyses with some biologically plausibility are to be preferred. All of these points are relevant irrespective of whether effect heterogeneity or potential interventions on the secondary variable are in view.

Third, although confounding control via multivariate adjustment is not necessary for targeting subpopulations (assessing “effect heterogeneity”), it may still be useful in correcting chance imbalances between treatment and control subjects within each subgroup and in generalizing findings and identifying factors that are most relevant.

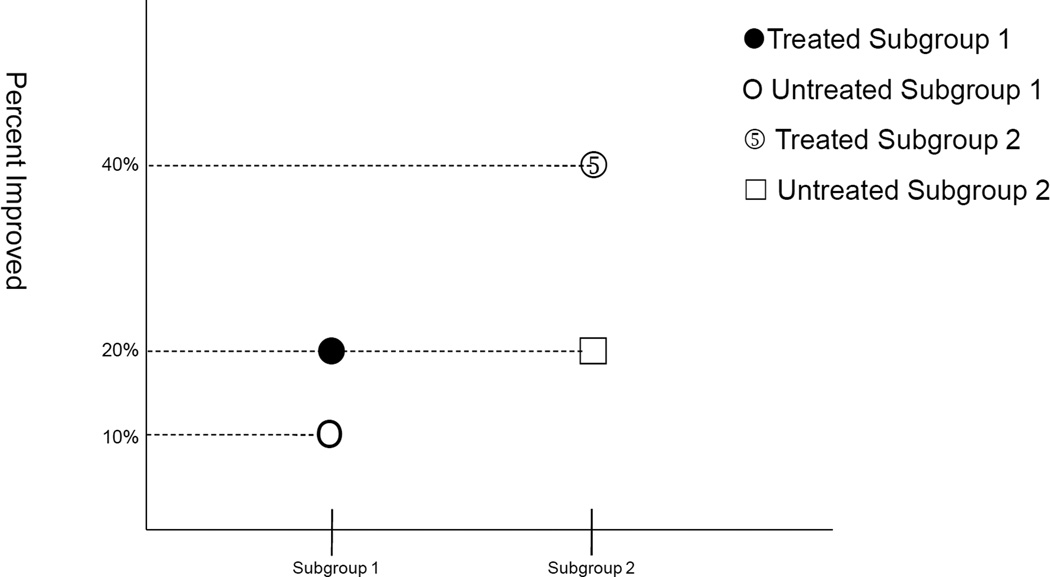
Fourth, when targeting subgroups to maximize the effect, differences in absolute risk are often most relevant for assessing public health importance (4,11–13). Statistical tests for testing effect heterogeneity for absolute risk have been described elsewhere (14). It should be noted that important differences in absolute risk may exist even in the absence of effect heterogeneity on the relative risk scale. Consider for example a case in which effect estimates were those shown in Figure 2. On a ratio scale, the effect of treatment in subgroup 1 is to increase the percentage of patients improved by 2 fold (from 10% to 20%). Likewise, on the ratio scale, the effect of treatment in subgroup 2 is to increase the percentage of patients improved by 2 fold (from 20% to 40%). There is no effect heterogeneity on the relative risk scale. However, there is effect heterogeneity on the absolute risk scale. In subgroup 1, treatment increases the percentage of patients improved by 10 percentage points (from 10% to 20%); in subgroup 2, treatment increases the percentage of patients improved by 20 percentage points (from 20% to 40%). If resources were limited, subgroup 2 would be the appropriate subgroup to target. There would be a larger proportion of patients helped in subgroup 2 if this subgroup were given treatment than if subgroup 1 were given treatment. Differences in absolute risk are more relevant for assessing public health importance (4,11–13) and may also give greater evidence of mechanistic interaction (13,15). Investigators who use logistic or proportional hazards models may want to convert estimates to the absolute risk difference scale when implementing subgroup analyses. Methods for testing and calculating measures of effect heterogeneity on the absolute risk scale from logistic or proportional hazards models have been described elsewhere (16–18). These points about absolute risk versus relative risk are relevant for both effect heterogeneity and for interventions on the secondary factor (“causal interaction”).

Figure 2.

Illustration of the presence of effect heterogeneity for absolute risk differences but not for risk ratios

Finally, when interventions on the secondary factor are in view (“causal interaction”), findings should be assessed with the same considerations as those from observational studies because the secondary factor has not been randomized. It is difficult to know whether adequate adjustment has been made for confounding for a variable that has not been randomized. Subgroup analyses should be interpreted as instances of causal interaction only with caution.

Key Summary Table.

1. In subgroup analyses in randomized trials, the primary treatment is randomized but the secondary factor defining subgroups is generally not. The potential need to control for confounding variables for the secondary factor depends on how we desire to interpret the subgroup analysis results.

2. If we are simply interested in whether the effect of treatment varies across subgroups (“effect heterogeneity”) so as to target specific subgroups to better maximize the treatment effect, confounding for the secondary factor defining the subgroups needs not be taken into account.

3. If we are interested in intervening on the secondary factor to increase the treatment effect or desire to attribute the effect heterogeneity to the secondary factor itself (“causal interaction”) rather than some other factor potentiall related to it then we need to control for confounding variables for the secondary factor.