Experimental Design and Primary Data Analysis Methods for Comparing Adaptive Interventions

Abstract

In recent years, research in the area of intervention development is shifting from the traditional fixed-intervention approach to adaptive interventions, which allow greater individualization and adaptation of intervention options (i.e., intervention type and/or dosage) over time. Adaptive interventions are operationalized via a sequence of decision rules that specify how intervention options should be adapted to an individual’s characteristics and changing needs, with the general aim to optimize the long-term effectiveness of the intervention. Here, we review adaptive interventions, discussing the potential contribution of this concept to research in the behavioral and social sciences. We then propose the sequential multiple assignment randomized trial (SMART), an experimental design useful for addressing research questions that inform the construction of high-quality adaptive interventions. To clarify the SMART approach and its advantages, we compare SMART with other experimental approaches. We also provide methods for analyzing data from SMART to address primary research questions that inform the construction of a high-quality adaptive intervention.

Introduction

In adaptive interventions the type or the dosage of the intervention offered to participants is individualized based on participants’ characteristics or clinical presentation, and then repeatedly adjusted over time in response to their ongoing performance (see, e.g., Bierman, Nix, Maples, & Murphy, 2006; Marlowe et al., 2008; McKay, 2005). This approach is based on the notion that individuals differ in their responses to interventions: in order for an intervention to be most effective, it should be individualized and, over time, repeatedly adapted to individual progress. An adaptive intervention is a multi-stage process that adapts to the dynamics of the “system” of interest (e.g., individuals, couples, families or organizations) via a sequence of decision rules that recommend when and how the intervention should be modified in order to maximize long-term primary outcomes. These recommendations are based not only on the participant’s characteristics but also on intermediate outcomes collected during the intervention, such as the participant’s response and adherence. Adaptive interventions are also known as dynamic treatment regimes (Murphy, van der Laan, Robins, & CPPR, 2001; Robins, 1986), adaptive treatment strategies (Lavori & Dawson, 2000; Murphy, 2005), multi-stage treatment strategies (Thall, Sung, & Estey, 2002; Thall & Wathen 2005) and treatment policies (Lunceford, Davidian, & Tsiatis, 2002; Wahed & Tsiatis 2004, 2006).

The conceptual advantages of adaptive interventions over a fixed-intervention approach (in which all participants are offered the same type or dosage of the intervention) have long been recognized by behavioral and social scientists. For example, in the area of organizational behavior, Martocchio and Webster (1992) studied the effect of feedback on employee performance in software training, stressing the need to develop training programs in which training design characteristics are adapted to employee level of cognitive playfulness (cognitive spontaneity in human-computer interactions). Recently, in their study of career goal setting, Hirschi and Vondracek (2009) discussed the development and adaptation of goals as a dynamic process, in which individuals have to select goals according to personal preferences and environmental opportunities and limitations, optimize their behavior to achieve those goals, and compensate and adjust if goals become unattainable or unattractive (also see Abele & Wiese, 2008; Baltes & Baltes, 1990). In the area of psychotherapy, Laurenceau, Hayes and Feldman (2007), conceptualized individuals’ growth and change during therapy as a dynamic (i.e., nonlinear and discontinuous) process and highlighted the need to use experimental designs that improve the ability of practitioners to effectively adjust therapy over time in response to the dynamics of change (Laurenceau et al., 2007).

Here, we discuss an experimental design and data analysis methods useful for developing (i.e., for constructing or revising) adaptive interventions in the social and behavioral sciences. First we review how adaptive interventions use decision rules to operationalize the individualization of intervention options (i.e., intervention type and dosage) based on participants’ characteristics, and the repeated adaptation of intervention options over time in response to the ongoing performance of participants. Next we discuss how the sequential multiple assignment randomized trial (SMART; Murphy, 2005; Murphy, Collins, & Rush, 2007; see also Lavori & Dawson, 2000; 2004 for related ideas), an experimental design approach used across the medical fields (e.g., Fava et al., 2003; Lavori et al., 2001; Schneider et al., 2001; Stone et al., 1995), can be used to develop adaptive interventions in the social and behavioral sciences. More specifically, we discuss how data from SMART designs is useful in addressing key research questions that inform the construction of a high-quality adaptive intervention. Building on ideas from the clinical literature, we compare the SMART design with other common experimental approaches. We also provide data analysis methods that can be used with the resulting SMART data to compare the effectiveness of intervention options at different stages of the adaptive intervention, and to compare the effectiveness of adaptive interventions that are embedded in the SMART design. To clarify ideas and illustrate the data analysis methods we employ data from the Adaptive Interventions for Children with ADHD SMART study (Center for Children and Families, SUNY at Buffalo, William E. Pelham, PI). Finally, we discuss directions for future research for social and behavioral scientists aiming to develop adaptive interventions.

Adaptive Interventions

Adaptive interventions are conceptualized as sequential treatment processes in which the varying needs of participants are taken into consideration (Collins, Murphy, & Bierman, 2004). This conceptualization has two components: (1) the intervention is individualized based on the characteristics and specific needs of participants; and (2) the intervention is time-varying; that is, it repeatedly adapts over time in response to participants’ ongoing performance and changing needs.

Sackett, Rosenberg, Gray, Haynes and Richardson (1996, p. 71) define evidence-based practice as “the conscientious, explicit, and judicious use of current best practice evidence in making decisions about the care of individual patients.” The practical appeal of the adaptive approach is outlined in Weisz, Chu and Polo’s (2004, p. 302) discussion of dissemination and evidence-based practice in clinical psychology, which suggests that evidence-based practice should ideally consist of much more than simply obtaining an initial diagnosis and choosing a matching treatment. Evidence-based practice

…is not a specific treatment or a set of treatments, but rather an orientation or a value system that relies on evidence to guide the entire treatment process. Thus, a critical element of evidence-based care is periodic assessment to gauge whether the treatment selected initially is in fact proving helpful. If it is not, adjustments in procedures will be necessary, perhaps several times over the course of the treatment (p. 302).

In fact, many behavioral and cognitive therapies can be seen as adaptive interventions (Bierman et al., 2006). For example, group therapy processes are adjusted over time based on group dynamics and the developmental stage of the group (Cole, 2005; Yalom, 1995). Cognitive therapy is tailored to address the unique cognitive conceptualization of the patient and to respond to his/her progress or regression during the process, with therapists basing the format, content, duration and intensity of the upcoming sessions on the results of the prior sessions (Beck, Liese & Najavits, 2005). While in practice the idea of adaptive interventions is not new, limited attention was given to developing research designs and methods that help scientists and practitioners decide how to individualize and repeatedly adapt intervention options (i.e., intervention type and/or dosage) in order to optimize long term outcome. In recent years, intervention scientists are becoming increasingly interested in experimental designs that explicitly incorporate the adaptive aspects of the intervention. The general aim is to obtain data useful for addressing key questions concerning the individualization and adaptation of intervention options so as to inform the construction of high-quality (i.e., highly efficacious) adaptive interventions.

Decision Rules and Tailoring Variables

One approach to operationalizing the conceptual idea of an adaptive intervention is to use decision rules (Bierman et al., 2006) that link individuals’ characteristics and ongoing performance with specific intervention options. The aim of these decision rules is to guide practitioners in deciding which intervention options to use at each stage of the adaptive intervention, using available information relating to the characteristics and/or ongoing performance of the participant. This approach is conceptually appealing because it mimics decision processes in real life, in which decision makers select their actions based on information obtained from the environment and modify their actions based on this information with the general aim to achieve good long-term outcomes.

In an adaptive intervention, the adaptation of the intervention options is based on the participant’s values on tailoring variables. These variables strongly moderate the effect of intervention options, such that the type or dosage of the intervention should be tailored according to values of these variables. Not all moderators are tailoring variables (Gunter, Zhu & Murphy, 2011). Consider an example in which both men and women respond better to high intensity than to low-intensity behavioral intervention, but high intensity behavioral intervention is more beneficial for women. In this case, although gender is a moderator, both men and women should be offered high intensity behavioral intervention because both groups are likely to benefit. Thus, gender is not a tailoring variable (otherwise different genders should be offered different levels of intervention intensity).

Although the list of candidate tailoring variables depends on the problem at hand, potential tailoring variables include individual, group, or contextual characteristics representing risk or protective factors that influence responsiveness to (or need for) intervention type or dosage. For example, assume an investigator is interested in evaluating an intervention (i.e., assessing the effectiveness of the intervention compared to control) that includes 13 weekly group sessions for improving perceived social support among community residents. Suppose the investigator considers two types of intervention: one in which group sessions emphasize cognitive restructuring (e.g., positive assertions to self and others, conflict resolution strategies, active listening), and one in which group sessions emphasize developing social skills (e.g., identifying and correcting dysfunctional attitudes in relationships, positive self-statements, and self-acceptance). Assume that prior scientific evidence suggests that community residents who are characterized by particular risk factors, for example low self-esteem, are more likely to benefit from an intervention that emphasizes cognitive restructuring than on social skills training. Those with high self-esteem, on the other hand, might find other interventions more beneficial. Accordingly, the investigator might choose to offer a supportive intervention in which the type of the intervention is individualized based on baseline levels of self-esteem (i.e., to offer different types of intervention to community residents with different baseline levels of self-esteem).

Participants’ responsiveness might also be an important tailoring variable. For example, assume the investigator conjectures that community residents who do not adequately respond (report low levels of support) to the support intervention within a certain period of time (e.g., six weeks), might need a more intensive subsequent intervention (e.g., during the last 7 weeks of the intervention), rather than more of the same. In this case, the investigator might choose to offer a supportive intervention that adapts to community residents’ response to the first six weeks of the intervention.

The choice of intervention options can also be tailored by the intervention options the individual has already received. For example, assume the investigator conjectures that intensifying the intervention for non-responders might be more effective for those residents who received cognitive restructuring during the first 6 weeks of the intervention. However, it is better to add a cognitive component to those non-responders who received social skills training during the first 6 weeks of the intervention. In this case, the investigator might choose to offer a supportive intervention in which the decision of whether to intensify the support intervention for non-responders to the first six weeks of the intervention varies depending on the type of support intervention given during the first 6-weeks.

To demonstrate the way decision rules link the tailoring variables to intervention options, assume the investigator decided to offer a supportive intervention that begins with 6 weekly sessions of social skills training (denoted as the first stage of the intervention) and then the sessions offered during the subsequent seven weeks (denoted as the second stage of the intervention) are tailored according to the participant’s response to the first stage of the intervention. In this case, the decision rule can be expressed as

• First-stage intervention = {social skill development}

  • IF evaluation = {non-response}

    • THEN second-stage intervention = {intensify first-stage intervention}
  • ELSE IF evaluation = {response}

    • THEN at second stage= {continue on present intervention}

Notice that the IF and ELSE IF parts of the rule contain the tailoring variables; intervention options are expressed in the THEN parts of this rule. To develop high-quality adaptive interventions, we focus on constructing good decision rules.

Researchers have used decision rules to operationalize adaptive interventions in several existing programs. In the Fast Track adaptive intervention for preventing conduct problems among high-risk children (Conduct Problems Prevention Research Group, 1992), the frequency of home visits were adapted, and at half-year intervals re-adapted. The tailoring variables were two types of clinical judgment: ratings of parental functioning and global assessments of family need for services. Program guidelines were used to link these two tailoring variables to three prescribed levels of home visiting (e.g., weekly home visits for low-functioning families; biweekly home visits for moderate-functioning families, and monthly home visits for high-functioning families (see Bierman et al., 2006). In the misdemeanor drug court adaptive intervention developed by Marlowe and colleagues (Marlowe et al., 2008), the frequency of court hearings and type of counseling session were adapted using pretreatment tailoring variables (history of formal drug abuse treatment and evidence of antisocial personality disorder) as well as time-varying tailoring variables (participants’ compliance with the drug court program and results of drug tests). McKay (2005) evaluated the effectiveness of an adaptive intervention for patients who are alcohol dependent. This intervention was built around brief telephone contacts, consisting of risk-for-relapse assessment and problem-focused counseling. When risk levels increased above specified criteria, participants received stepped-up care, such as more frequent telephone sessions and sessions of motivational interviewing.

In these programs, the sequence of decision rules that operationalized the adaptive intervention was pre-specified based on clinical experience and scientific evidence. However, in many cases, there is not enough evidence a priori to inform the construction of high-quality sequences of decision rules. There might be open questions (or even debates in the literature) concerning the best intervention option at specific intervention stages, or other important questions relating to which tailoring variables to use. For example, consider the previous example concerning the group-based intervention for improving the social support of community residents. Suppose the investigator is interested in developing a two-stage adaptive intervention but there is not enough scientific evidence to determine (a) whether the group sessions at the first stage of the intervention should focus on cognitive restructuring or social skills development; and (b) what is the most efficacious intervention option for participants who do not respond to the first six sessions. In this case, the investigator might be interested in obtaining data that informs the development of an adaptive intervention prior to its evaluation (i.e., assessing the effectiveness of the intervention compared to control). More specifically, the investigator might be interested in collecting data that enables him/her to compare the effectiveness of various intervention options at different stages of the intervention, as well as to compare different sequences of decision rules (i.e., different adaptive interventions). To better understand this, consider the following example, based on the Adaptive Interventions for Children with ADHD study (Center for Children and Families, SUNY at Buffalo, William E. Pelham, PI).

Adaptive Interventions for Children with ADHD Example

Suppose an investigator is interested in planning an adaptive two-stage intervention to improve the school performance of children with ADHD. There are two critical decisions confronting the development of this adaptive intervention: “Which intervention option should be provided initially?” and “Which intervention option should be provided to children whose ADHD symptoms did not sufficiently decrease during the first-stage intervention (i.e., nonresponders)?” First, the researcher considers two possible first-stage intervention options: low-intensity behavioral intervention, or low-dose medication. Second, the researcher considers two possible second-stage intervention options for the non-responding children: to increase the dose of the initial intervention or to add the alternative type of intervention. More specifically, if the child is not responding to low dose of medication, the dose of medication can be increased or medication can be augmented with behavioral intervention. If the child is not responding to behavioral intervention, the intensity of the behavioral intervention can be enhanced or the behavioral intervention can be augmented with medication. Table 1 presents four simple adaptive interventions and the four associated decision rules drawn from this example.

Table 1.

Four Adaptive Interventions and Decision Rules Based on ADHD Example

Adaptive intervention3	Decision rule
(1, −1) First, offer low-intensity behavioral intervention; then add medication for non-responders and continue low-intensity behavioral intervention for responders.	First-stage intervention option = {BMOD}   IF evaluation = {non-response}     THEN second-stage intervention option ={AUGMENT}   ELSE continue on first-stage intervention option
(−1, −1) First, offer low-dose medication; then add behavioral intervention for non-responders, and continue low-dose medication for responders.	First-stage intervention option = {MED}   IF evaluation = {non-response}     THEN second-stage intervention option={AUGMENT}   ELSE continue on first-stage intervention option
(1, 1) First, offer low-intensity behavioral intervention; then increase the intensity of behavioral intervention for non-responders and continue low-intensity behavioral intervention for responders.	First-stage intervention option= {BMOD}   IF evaluation = {non-response}     THEN second-stage intervention option={INTENSIFY}   ELSE continue on first-stage intervention option
(−1, 1) First, offer low-dose medication; then increase the dose of medication for non-responders and continue low-dose of medication for responders.	First-stage intervention option = {MED}   IF evaluation = {non-response}     THEN second-stage intervention option={INTENSIFY}   ELSE continue on first-stage intervention option

Assuming that an investigator considers the four adaptive interventions presented in Table 1, the question is how to obtain high-quality data that can be used to contrast these four adaptive interventions and that, beyond this simple comparison, more deeply informs the construction of an adaptive intervention for children with ADHD.

Sequential Multiple Assignment Randomized Trial

A SMART is a multi-stage randomized trial, in which each stage corresponds to a critical decision. Each participant progresses through the stages and is randomly assigned to one of several intervention options at each stage (Murphy 2005). The SMART was designed specifically to aid in the development of adaptive interventions. Data from a SMART design can be used to address primary research questions concerning (a) the comparison of different intervention options at different stages of the intervention (e.g., the difference between the firs-tstage intervention options, or the difference between the second-stage intervention options for non-responding participants); (b) the comparison of adaptive interventions (i.e., sequences of decision rules) that are embedded in the SMART design (e.g., the difference between the four adaptive interventions specified in Table 1; Oetting, Levy, Weiss & Murphy, 2007); and (c) as described in the companion article (Nahum-Shani, et al, 2011) to construct more deeply tailored adaptive interventions that go beyond those explicitly embedded as part of the SMART design.

Trials in which each participant is randomized multiple times have been widely used across the medical fields. Precursors of SMART include the CALGB study 8923 for treating elderly patients with primary acute myelogenous leukemia (Stone et al., 1995), and the STAR*D for treatment of depression (Lavori et al., 2001; Fava et al., 2003). In recent years, a number of SMART trials have been conducted. These include trials for treating cancer at the University of Texas MD Anderson Cancer Center (for more details see Thall, Millikan, & Sung, 2000; Thall et al., 2007); the National Institute of Mental Health Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) study concerning antipsychotic drug effectiveness for persons with schizophrenia (for more details see Stroup et al., 2003); and the Adaptive Interventions for Children with ADHD conducted by one of the authors (W. Pelham) at SUNY-Buffalo. The latter SMART study is discussed above and in the following.

The ADHD SMART Study

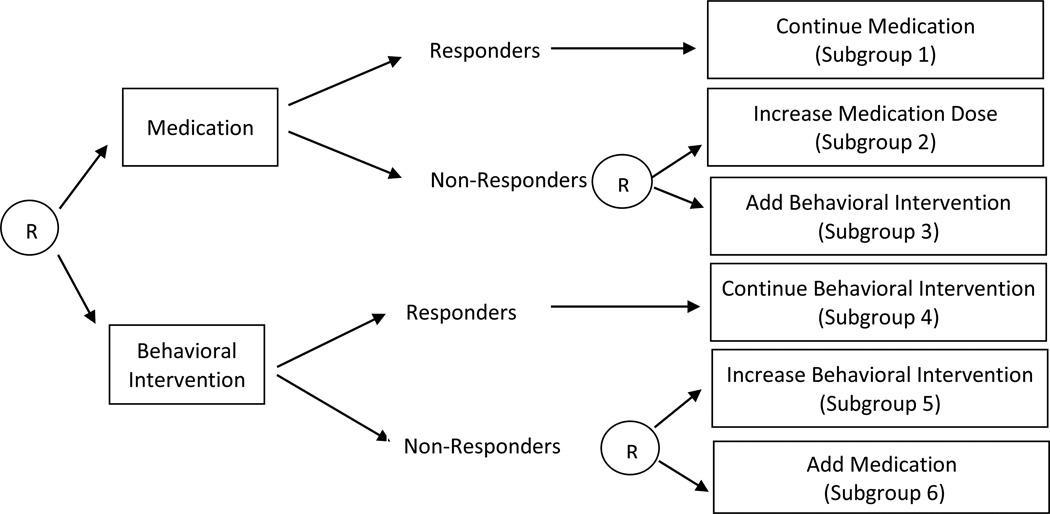
In the first stage of the ADHD SMART study (beginning of the school year), children were randomly assigned (with probability .5) to a low dose of medication or a low dose of behavioral intervention. Beginning at eight weeks, children’s response to the first-stage intervention was evaluated monthly until the end of the school year. Monthly ratings from the Impairment Rating Scale (IRS; Fabiano et al., 2006) and an individualized list of target behaviors (ITB; e.g., Pelham , Evans, Gnagy, & Greenslade, 1992; Pelham et al., 2002) were used to evaluate response. At each monthly assessment, children whose average performance on the ITB was less than 75% and who were rated by teachers as impaired on the IRS in at least one domain were designated as non-responders to the first-stage intervention and entered into the second stage of the adaptive intervention. These children were then re-randomized (with probability .5) to one of two second-stage intervention options, either to increasing the dose of the first-stage intervention option or to augmenting the first-stage intervention option with the other type of intervention (i.e., adding behavioral intervention for those who started with medication, or adding medication for those who started with behavioral intervention). Children categorized as responders continued with the assigned first-stage intervention option. Consistent with each randomization, this trial was designed to investigate two critical decisions: the decision regarding the first-stage intervention, and then the decision regarding the second-stage intervention for those not responding satisfactorily to the first-stage intervention.

The structure of this SMART study is illustrated in Figure 1. The four adaptive interventions listed in Table 1 are embedded in this SMART study. Notice that each adaptive intervention embedded in this design is operationalized by a sequence of decision rules that specifies the intervention options at each stage for both responders and non-responders. Accordingly, there are responding and non-responding children who are consistent with each adaptive intervention (i.e., who were assigned to experimental conditions that form a specific sequence of decision rules). More specifically, each responding child receives only the initially assigned intervention and thus the child would have received the same treatment under two different adaptive interventions; these two adaptive interventions differ in only how nonresponding children are treated. As illustrated in Figure 1, children in subgroups 1 and 2 are consistent with an adaptive intervention that begins with low dose of medication and then non-responders receive increased dose of medication (subgroup 2) whereas responders continue with the same low dose of medication (subgroup 1); children in subgroups 1 and 3 are consistent with an adaptive intervention that begins with a low dose of medication and then behavioral intervention is added to non-responders (subgroup 3) whereas responders continue with the same low dose of medication (subgroup 1). Notice that responders to a low dose of medication (subgroup 1) are consistent with the two adaptive interventions specified above (i.e., the two adaptive interventions that begin with low dose of medication). Figure 1 also illustrates that children in subgroups 4 and 5 are consistent with an adaptive intervention that begins with low-intensity behavioral intervention and then the intensity of the behavioral intervention is increased for non-responders (subgroup 5) and responders continue with the same low-intensity behavioral intervention (subgroup 4); children in subgroups 4 and 6 are consistent with an adaptive intervention that begins with low-intensity behavioral intervention and then medication is added to non-responders (subgroup 6) and responders (subgroup 5) continue with the same low-intensity behavioral intervention. Notice that responders to low-intensity behavioral intervention (subgroup 4) are consistent with 2 adaptive interventions (the two adaptive interventions that begin with low-intensity behavioral intervention).

Figure 1.

Sequential multiple assignment randomized trial for ADHD study.

Other Types of SMART Designs

The ADHD study described above is a SMART study in which re-randomization to the second-stage intervention options depends on an intermediate outcome (i.e., response/non-response to first-stage intervention). Other types of SMART designs might vary in the extent and form of the tailoring that is incorporated in the design. Such aspects of the design are determined by the investigator based on scientific evidence, as well as ethical considerations. In the following we describe three other common types of SMART studies: SMART designs with no embedded tailoring variables; SMART designs in which participants are re-randomized to different second-stage intervention options depending on an intermediate outcome; and SMART designs in which whether to re-randomize or not depends on an intermediate outcome and prior treatment.

SMARTs with no embedded tailoring variables

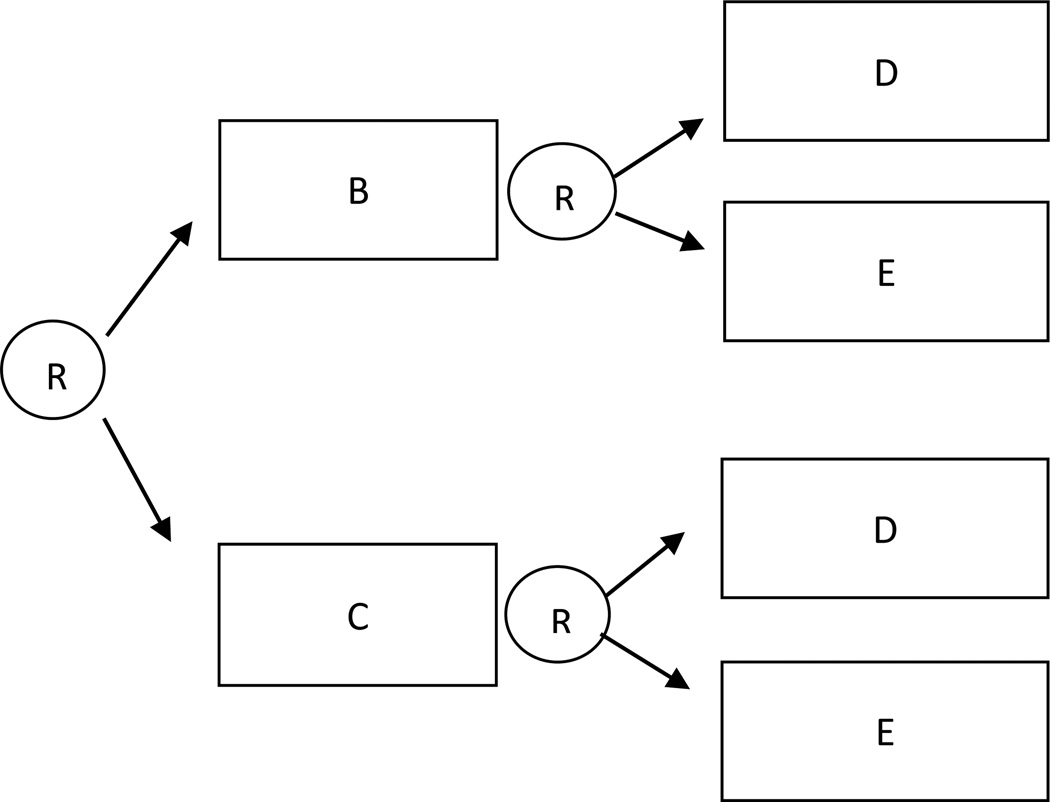
In these SMART designs participants are first randomized to two different first-stage intervention options (e.g., B or C), and then (e.g., after 12 weeks) all participants are re-randomized to two second-stage intervention options (e.g., D or E) regardless of any information observed prior to the second-stage randomization (i.e., regardless of any intermediate outcome or prior treatment). This design is illustrated in Figure 2. Because there are no embedded tailoring variables in this SMART design, the embedded interventions are non-adaptive. More specifically, there are four non-adaptive interventions embedded in this SMART design: (1) begin with B and then offer D; (2) begin with B and then offer E; (3) begin with C and then offer D; and (4) begin with C and then offer E.

Figure 2.

Sequential Multiple Assignment Randomized Trial with no embedded tailoring variables.

SMARTs in which re-randomization to different second-stage intervention options depends on an intermediate outcome

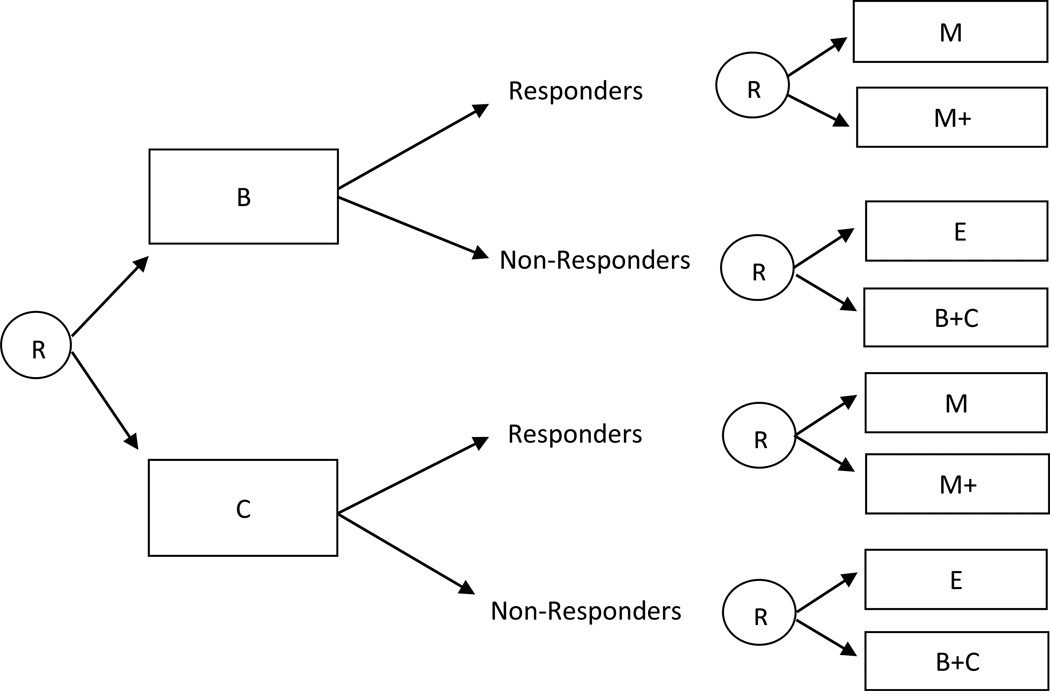
Consider a SMART design in which participants are first randomized to two different first-stage intervention options (e.g., B or C). Then (e.g., after 12 weeks), all participants are re-randomized to second-stage intervention options, but second-stage intervention options vary depending on an intermediate outcome (e.g., response/non-response to first-stage intervention options). More specifically, assume responders are re-randomized to one of two maintenance interventions, M or M+, whereas non-responders are re-randomized to either switch to a third intervention E, or to the combined intervention B+C. This design is illustrated in Figure 3.

Figure 3.

Sequential Multiple Assignment Randomized Trial design in which participants are re-randomized to different second-stage intervention options depending on an intermediate outcome (e.g., response/non-response).

There are eight adaptive interventions embedded in this design: (1) begin with B, and then offer E for non-responders and M for responders; (2) begin with B, and then offer E for non-responders and M+ for responders; (3) begin with B, and then offer B+C for non-responders and M for responders; (4) begin with B, and then offer B+C for non-responders and M+ for responders; (5) begin with C, and then offer E for non-responders and M for responders; (6) begin with C, and then offer E for non-responders and M+ for responders; (7) begin with C, and then offer B+C for non-responders and M for responders; (8) begin with C, and then offer B+C for non-responders and M+ for responders.

SMARTs in which whether to re-randomize or not depends on an intermediate outcome and prior treatment

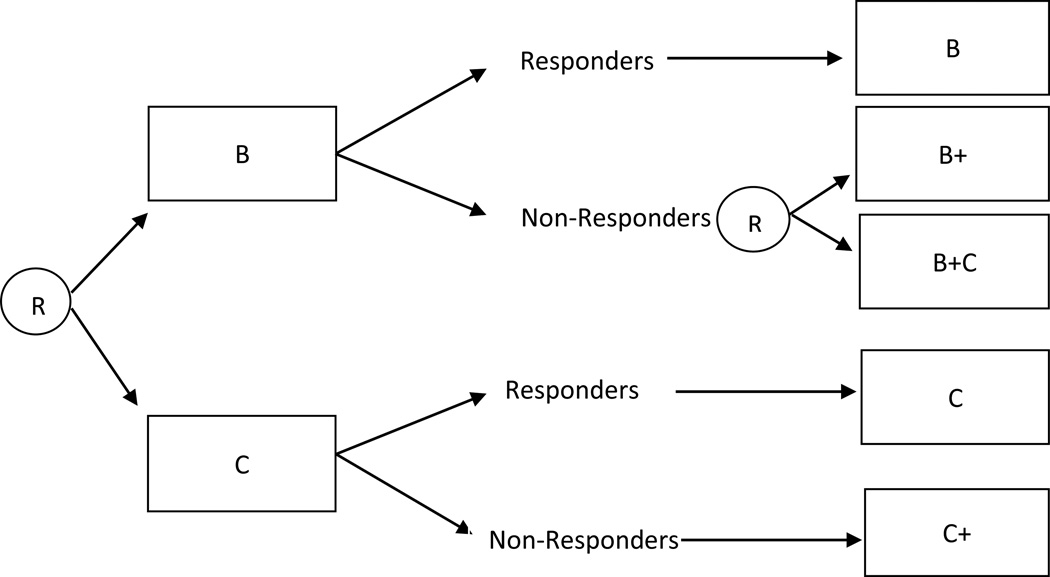
Assume for example that participants are first randomized to two different first-stage intervention options (e.g., B or C), and then (e.g., after 12 weeks) only non-responders to B are re-randomized to either intensify B (B+), or add the alternative intervention option (B+C). Responders to B are not re-randomized and remain on the same first-stage intervention option (B); responders to C are not re-randomized and remain on the same first-stage intervention option (C); and non-responders to C are not re-randomized and are offered an intensified version of C (C+). This design is illustrated in Figure 4. Notice that in this design, whether or not a participant is re-randomized to second-stage intervention option depends on both the observed intermediate outcome and the prior intervention option offered to the participant. There are three adaptive interventions embedded in this design: (1) begin with B and then offer B to responders and B+ to non-responders; (2) begin with B and then offer B to responders and B+C to non-responders; and (3) begin with C and then offer C to responders and C+ to non-responders.

Figure 4.

Sequential Multiple Assignment Randomized Trial design in which whether to re-randomize depends on an intermediate outcome and prior treatment.

To better understand the SMART design and its advantages, in the following we compare the SMART with other common experimental designs.

SMART Relative to Other Experimental Approaches

Factorial design

A classic 2X2 factorial is an experimental design with two factors, each with two levels that are crossed, resulting in 4 experimental conditions (Collins, Dziak & Lee, 2009). The SMART design in Figure 2 might seem like a 2X2 factorial design in which the first factor corresponds to the first-stage intervention options (with two levels: B and C) and the second factor corresponds to the second-stage intervention option (with two levels: D and E). However, in the SMART design, the second factor is provided after the provision of the first factor (e.g., 12 weeks). Furthermore, in many SMART designs, intermediate outcomes are used to determine whether an experimental unit will be re-randomized (e.g., the design in Figure 1) or the levels of the second factor to which an experimental unit will be re-randomized (e.g., the design in Figure 3). Hence, data analysis methods for addressing primary research questions might differ from those typically used in a classic 2X2 factorial design (as we later discuss in the analysis methods section).

Just as some factorial designs are unbalanced (e.g., some of the factors are not completely crossed; see Collins et al., 2009; Dziak, Nahum-Shani & Collins, in press), SMART designs can be unbalanced as well. In particular the SMART design will be unbalanced when the prior intervention option determines whether or not an experimental unit will be re-randomized (e.g., the designs in Figure 4) and/or the second stage intervention options depend on the prior intervention option (e.g., the design in Figure 1). To clarify this, consider the ADHD SMART (in Figure 1), in which the intervention option offered to the child at the first-stage (i.e., the first factor) was used to decide the set of second stage intervention options if the child did not respond in the first stage. That is, the second stage interventions for children who do not respond to low intensity behavioral modification are different from the second stage options for children who do not respond to low dose medication.

Randomized trial with multiple groups

Sometimes the SMART is equivalent to a randomized trial with multiple groups, each corresponding to a different adaptive intervention. For example, in the ADHD example (in Figure 1), instead of randomizing to two first-stage intervention options and then re-randomizing non-responders at the time of nonresponse, an investigator might conduct both randomizations prior to the first-stage intervention. In this case the second randomization will only be used if the participant does not adequately respond to the first-stage intervention. This approach is equivalent to randomizing children up-front to the four adaptive interventions in Table 1 with randomization probability .25 each. However, performing all randomizations prior to the first-stage intervention (e.g., randomizing to four adaptive interventions) is disadvantageous if there are important first-stage intermediate outcomes (e.g., adherence to the first-stage intervention or side effects experienced during the first-stage intervention) that might be strongly predictive of second-stage primary outcomes. Such first-stage intermediate outcomes are prognostic factors for the second-stage primary outcome. In this case, the second-stage intervention groups might, by chance, differ in the distribution of the prognostic factor, leading to spurious differences between the second-stage intervention groups in terms of the primary outcome.

To clarify this, suppose that in planning the ADHD (in Figure 1) study we believed that some families/children are less adherent to any intervention option and thus will generally exhibit poorer school performance. In this case a natural prognostic factor for the second-stage primary outcome is adherence to the first-stage intervention. In general, stratification or blocking is used to achieve distributional balance of a prognostic factor between intervention groups within each level of a stratum (Efron, 1971; Simon, 1979). In stratification we partition participants into mutually-exclusive subsets defined by the prognostic factor. Within these strata, we then randomize between intervention groups. The purpose of stratified randomization is to provide increased confidence that the compared groups are similar with respect to known prognostic factors (e.g., adherence to first-stage intervention) and thus reduce the suspicion that differences in the primary outcome are simply due to chance differences in the composition of the prognostic factors between intervention groups (Hedden, Woolson & Malcolm, 2006; Kernan, Viscoli, Makuch, Brass, & Horwitz, 1999).

Accordingly, if we believe adherence to the first-stage intervention is a prognostic factor for the second-stage primary outcome, we might stratify randomization to the second-stage intervention options by the level of adherence to the first-stage intervention. Because information concerning adherence to the first-stage intervention is not available prior to the first-stage intervention, we would not be able to randomize a priori to the four adaptive interventions in Table 1. Instead, we would delay the re-randomization for non-responders until the time of nonresponse (at which time we will also know the child’s level of adherence to the first-stage intervention). This is one advantage of multi-stage randomizations over conducting a trial which randomizes participants up-front to the different adaptive interventions.

A standard RCT

The traditional approach to intervention development involves constructing an intervention a priori and then evaluating it in an RCT. For example, Connell and colleagues (Connell, 2009; Connell & Dishion, 2008; Connell, Dishion, Yasui, & Kavanagh, 2007) conducted an RCT to evaluate an adaptive family-centered intervention (described in details in Dishion & Kavanagh, 2003) for reducing adolescent problem behaviors in public schools. High-risk adolescents were randomly assigned at the individual level to either control (school as usual) classrooms (498 youths) or adaptive intervention classrooms (500 youths) in the seventh grade. Typically, the adaptive intervention is constructed using theory, real-world experience, surveys of the literature and expert opinion.

In RCTs, the goal is to assess whether the intervention results in better primary outcomes than the control condition (e.g., placebo control, attention control or treatment as usual). Further development of the intervention is most frequently informed by nonrandomized comparisons. For example, a common secondary analysis uses lack of fidelity to intervention assignment (e.g., variation in intervention adherence by staff and participants) to inform which intervention options are best for which participants and to inform whether the intervention should vary in response to how the participant is progressing. These analyses, due to their dependence on nonrandomized comparisons, provide a lower quality of evidence than analyses based on randomized comparisons (Cook & Campbell, 1979; Shadish, 2002; Shadish, Cook & Campbell, 2002). Thus, although RCTs are well suited for evaluating an adaptive intervention (i.e., assessing its effectiveness compared to control), they are not as well suited for developing adaptive interventions (i.e., for revising or constructing adaptive interventions). On the other hand, as we demonstrate below and in the companion paper (Nahum-Shani et al., 2011), SMART designs enable the data analyst to conduct randomized comparisons in order to investigate which intervention options are best for which participants and to investigate whether the intervention should vary in response to how the participant is progressing.

Single-stage-at-a-time experimental approach

This is a natural alternative to SMART, particularly when randomized trials involving initial treatments have already been conducted. In this approach, a separate randomized trial is conducted for each stage, and each randomized trial involves a new group of participants. Then, the results from each separate randomized trial are pieced together to infer what the best adaptive intervention ought to be. Essentially, the single-stage at a time approach focuses separately on each individual intervention stage in the sequence, as opposed to considering the entire sequence as a whole. To ascertain the best adaptive intervention, this approach compares available intervention options at each stage based on a randomized trial for that stage alone and/or based on historical trials and the available literature. For example, Moore and Blackburn (1997) recruited outpatients with recurrent major depression who failed to respond to acute treatment with antidepressant medication, aiming to determine whether cognitive therapy is a better follow-up treatment than medication. Walsh et al., (2000) recruited patients with eating disorders who had not responded to, or had relapsed following, a course of cognitive behavior therapy or interpersonal psychotherapy, aiming to determine the utility of a pharmacological intervention for patients whose response to psychological treatment was not satisfactory. In these two examples, investigators conducted randomized trials in order to compare second-stage intervention options among non-responders, while explicitly or implicitly making conclusions concerning the best initial intervention option based on the available scientific literature.

To further clarify this point, assume that instead of the ADHD SMART study discussed earlier (in Figure 1), an investigator decides to first review the literature on childhood ADHD in order to choose whether to begin with low-dose medication or low-intensity behavioral intervention. Then, the researcher conducts a randomized trial for non-responders in which non-responding children are recruited and then randomized to one of the two second-stage intervention options (i.e., increase the dose of the first-stage intervention option, or augment the first-stage intervention option with the alternative type of intervention). While conceptually simpler than a SMART design, this approach has at least three disadvantages.

First, this approach might fail to detect possible delayed effects in which an early-stage intervention option has an effect that is less likely to occur unless it is followed by a particular subsequent intervention option. This might occur when subsequent intervention options intensify, facilitate or weaken the impact of initial intervention options. To clarify this concept, consider research in the area of experimental psychology which suggests that there might be a delayed effect when attention-control training is provided for improving individuals’ ability to cope with tasks that require dividing attention (e.g., driving a car). Gopher and colleagues (see Gopher, 1993; Shani, 2007) have shown that the knowledge and abilities acquired through attention-control training influence and benefit performance beyond the specific situation in which these skills were acquired (e.g., when a new concurrent task was introduced or when no feedback was provided). In fact, such training appears to contribute to the development of attention management skills that transfer beyond the specific situation in which the individual was originally trained, such that the individual continues to improve as he/she experiences other types of tasks that require the allocation of attention. In other words, subsequent training/experience that involves different types of tasks than those used during the initial training provides an opportunity for the individual to internalize the specialized knowledge acquired during the initial training and hence facilitates the development of attention management skills. Accordingly, the advantages of the initial training cannot be fully detected without exposing the participant to subsequent training or experiences.

Overall, when using the single-stage experimental approach, conclusions concerning the best initial intervention options are based on studies in which participants were not necessarily exposed to subsequent intervention options. This might reduce the ability of the researcher to detect these types of delayed effects, and hence might lead to the wrong conclusion as to the most effective sequence of intervention options.

Second, the SMART approach enables the researcher to detect prescriptive information that the initial intervention elicits. The investigator can use this information to better match the subsequent intervention to each participant, and thus improve the primary outcome. This is not possible by piecing together the results of single-stage specific randomized trials. For example, in the context of the ADHD study, results of secondary data analysis (reported in the companion paper, Nahum-Shani et al., 2011) indicate that the child’s adherence to the first-stage intervention might be a promising tailoring variable for the second-stage intervention. Non-responders (to either medication or behavioral intervention) with low adherence to the first-stage intervention performed better when the first-stage intervention was augmented with the other type of intervention, relative to when the dose of the first-stage intervention was increased. Assume the investigator had chosen to take the single-stage-at-a-time approach and conducted a non-responder trial in which children who did not respond to medication are randomized to two intervention options (increase the dose of medication or augment with behavioral intervention). In this more limited study the investigator would not obtain information concerning the second-stage intervention option for non-responders who do not adhere to behavioral intervention.

Third, subjects who enroll and remain in studies in which there are no options for non-responders (or responders) might be different than those who enroll and remain in a SMART trial. For example, previous studies might not offer subsequent intervention options to children who are not improving, and hence children in these studies might exhibit differing patterns of adherence and/or might be more prone to drop out relative to children in a SMART study who know that their intervention can be altered. Thus the choice of first-stage intervention option based on the single-stage approach might be based on poorer quality data (due to non-adherence) relative to the SMART. Moreover, in the single-stage approach, the investigator usually selects the first-stage and second-stage intervention options based on data from different samples of participants. Because the samples might differ due to changing schooling practices, changing diagnostic criteria, and so on, bias can be introduced into the results (see Murphy et al., 2007 for a detailed discussion of these cohort effects). In a SMART, on the other hand, conclusions concerning the best first and second-stage intervention options can be made in a synergetic manner using the same sample of participants throughout the stages of the decision process.

Analysis Methods

Denote the observable data for a subject in a two-stage SMART by (O₁, A₁, O₂, A₂, Y), where O₁ and O₂ are vectors of pretreatment information and intermediate outcomes, respectively, A₁ and A₂ are the randomly assigned first and second-stage intervention options, and Y is the primary outcome of an individual. For example, in the adaptive ADHD study (see Figure 1), O₁ might include severity of ADHD symptoms, whether the child received medication during the previous school year, or other baseline measures; O₂ might include the subject’s response status and adherence to the first-stage intervention; and Y might be the teacher’s evaluation of the child’s school performance at the end of the school year. Let A₁ denote the indicator for the first-stage intervention (1=low-intensity behavioral intervention; −1=low-dose medication) and A_2NR denote the indicator for the second-stage intervention for non-responders to the first-stage intervention (1=increase the initial intervention; −1= augment the initial intervention with the other type of intervention).

The multiple randomizations in the SMART allow the investigator to estimate a large variety of causal effects important in the development of adaptive interventions. Here we consider three primary research questions: (a) concerning the difference between first-stage intervention options; (b) concerning the difference between second-stage intervention options; and (c) concerning the comparison of adaptive interventions that are embedded within the SMART design.

Comparing First-Stage Intervention Options

Consider, for example, the following question concerning the difference between low-dose medication vs. low-intensity behavioral intervention: “In the context of the specified second-stage intervention options, does starting with low-intensity behavioral intervention result in a better long-term outcome relative to starting with low-dose medication?” This question is addressed by pooling Y from subgroups 1 through 3, and comparing the resulting average to the pooled Y from subgroups 4 through 6 (in Figure 1). This is the main effect of the first-stage intervention; that is, the difference between the two first-stage intervention options, averaging over the second-stage intervention options. Notice that responders to the first-stage intervention are included in this comparison because a particular first-stage intervention might lead to good initial response but the performance of responders might deteriorate over time (see Oetting, et al., 2007 for more details).

Comparing Second-Stage Intervention Options

Consider, for example, the following question concerning the difference between the two second-stage intervention options: “Among those who do not respond to their initial intervention, is there a difference between intensifying the initial intervention versus augmenting the initial intervention?” This question is addressed by pooling Y from subgroups 2 and 5 and comparing the resulting average to the pooled Y from subgroups 3 and 6 (in Figure 1). This is the main effect of the second-stage intervention options for non-responding children; that is, the difference between the two second-stage intervention options, averaging over the first-stage intervention options.

Comparing Adaptive Interventions that are embedded within the SMART design

To understand how to compare adaptive interventions that are embedded in the SMART design, consider first estimating the mean outcome of only one of the four adaptive interventions, say (1, 1). In adaptive intervention (1, 1) children are initially provided low-intensity behavioral intervention and then the intensity of the behavioral intervention is increased only if the child does not respond. To estimate the mean outcome under this adaptive intervention, a natural (yet incorrect) approach might be to average the outcomes of all children in the study who are consistent with this adaptive intervention (subgroups 4 and 5 in Figure 1). Observe that the outcomes of all children who responded to the low-intensity behavioral intervention are included in this sample average, whereas the outcomes of only half of all children who did not respond to low-intensity behavioral intervention are included in this sample average. It turns out that this sample average is a biased estimator for the mean outcome that would occur if all children in the population were provided the adaptive intervention (1, 1). This bias occurs because, by design, non-responding children are re-randomized and thus split into two subgroups (5 and 6 in Figure 1), whereas the responding children are not re-randomized and thus not split into two subgroups. Therefore, due to the restricted randomization scheme, the above sample average contains an over-representation of outcomes from responding children and an under-representation of outcomes from non-responding children. To accommodate this over-/under-representation, weights can be used. Since this over-/under-representation occur by design, we know the value of the weights to use in order to counteract this over-/under-representation. In particular, the weights are the inverse of the randomization probability, that is, W = 2 is the weight for responders and W = 4 is the weight for non-responders.¹ Informally, each participant receives a weight that is inversely proportional to his/her probability of receiving his/her own adaptive intervention. This is similar to the inverse-probability-of-treatment weights used in the estimation of marginal structural models (MSM) for making causal inferences concerning the effects of time varying treatments (see Hernán, Brumback, & Robins, 2000; Cole & Hernán, 2008).

In this estimation procedure, the weight assigned to each child depended on whether the child was a responder or a non-responder to the first-stage intervention. Therefore, the distribution of the weights depends on the observed response rate in the sample, a statistic that varies from one sample to the next. In order to account for the sample-to-sample variance in the distribution of the weights, robust (sandwich) standard errors can be used to make appropriate inferences (e.g., confidence intervals, p-values) with the weighted averages (see Hernán, et al., 2000 for more details).

Following the estimation procedure described above, one can obtain the average weighted outcome, separately, for each of the four adaptive interventions that are embedded in the SMART study. As indicated above, for each adaptive intervention, the investigator will need to restrict the dataset and estimate the average weighted outcome only for those participants who are consistent with that adaptive intervention. However, investigators are typically interested in carrying out one data analysis (i.e., using one fitted regression model) that enables them to (a) estimate the mean outcome under all four adaptive interventions simultaneously; (b) estimate all possible mean-comparisons between the four adaptive interventions simultaneously, while (c) providing appropriate inferences (e.g., confidence intervals, p-values) for these estimates. Apart from convenience, doing this has the added advantage of allowing investigators to control for baseline measures that may be highly correlated with the outcome. This has the potential to improve effect estimates by reducing error variance (i.e., leading to smaller standard errors and therefore increased statistical power).

To utilize the entire sample using standard software, the data set needs to be restructured. This is because some participants’ observations are consistent with more than one of the embedded adaptive interventions. In the ADHD study these are the responding participants. A participant who responds, say to low-intensity behavioral intervention has outcomes that are consistent with two adaptive interventions: Begin with low-intensity behavioral intervention and then add medication only if the child does not respond (1, −1); and begin with low-intensity behavioral intervention and then increase the intensity of the behavioral intervention only if the child does not respond (1, 1). Thus, in order to simultaneously estimate the mean outcome under adaptive intervention (1,-1) and (1,1) using the ADHD SMART data, each responder’s outcome would have to be used twice. This point was first made by Robins and colleagues (Robins, Orellana & Rotnitzky, 2008; Orellana, Rotnitzky & Robins, 2010) in their approach for use in observational studies to compare adaptive interventions. In this manuscript, we generalize their approach for use with SMART study data, as follows.

In the ADHD study we restructure the data set such that instead of one observation per responder, the new dataset includes two identical observations per responder. Then, for each responder, we set A_2NR to 1 in one of the two replicated observations and A_2NR to−1 in the other replicated observation. For example, if the original dataset included 58 responders with no value for the indicator A_2NR (in the original data set this happens because there is no variation in second-stage intervention options among responders since they were not re-randomized), the new dataset includes 116 responders, half in which A_2NR = 1 and half in which A_2NR = −1. The number of observations for non-responders (who were re-randomized with probability .5) remains the same. Such replication of observations enables investigators to conveniently “reuse” the observed primary outcome from each responding child in estimating the average outcome of two adaptive interventions using one fitted regression model. As before, the new dataset should contain a variable providing the weights for each observation that is the value 2 for observations that belong to responders and 4 for observations that belong to non-responders.

Note that the replication of observations and the use of weights discussed above serve different purposes. The weights are used to accommodate for over/under-representation of outcomes resulting from the randomization scheme. This can occur when (a) the number of randomizations vary across participants (e.g., some participants are re-randomized while others are not), and/or (b) randomization probabilities are not equal (e.g., at the first stage, participants are randomized with probability .6/.4 to medication vs. behavioral intervention respectively); and/or (c) participants are randomized to differing numbers of intervention options (e.g., responding children are randomized to two second-stage intervention options, while non-responders are re-randomized to three intervention options). The replication of observations on the other hand, is done in order to enable investigators utilize standard software to conduct simultaneous estimation and comparison of the effects of all four adaptive interventions. Such replication is required whenever there are participants whose observations are consistent with more than one embedded adaptive intervention. A technical explanation of this approach (including weighting and replication) as well as a justification for the validity of the robust standard errors is provided in Appendix 1.

Using the new dataset, the following model can be estimated

$$E[Y|A_1,A_{2NR},O_1]={\beta }_0+{\beta }_1{A}_1+{\beta }_2{A}_{2NR}+{\beta }_3{A}_1{A}_{2NR}+{\mathit{\gamma }}^T{O}_1,$$ (1)

where Y is the school performance at the end of the school year; O₁ is a vector of baseline measures (obtained prior to the first-stage intervention, and included in the regression model as mean-centered covariates); β₀ is the intercept; β₁ − β₃ are the regression coefficients expressing the effects of the first-stage intervention, the effects of the second-stage intervention offered to non-responders, and the interaction between them (respectively); and γ is the vector of regression coefficients expressing the effects of the baseline measures O₁. Accordingly, (1) models the average school performance for each adaptive intervention, such that E[Y| 1, −1] = β₀ + β₁ − β₂ − β₃ is the average school performance for children following adaptive intervention (1, −1); E[Y|−1, −1] = β₀ − β₁ − β₂ + β₃ is the average school performance for children following adaptive intervention (−1, −1); E[Y| 1, 1] = β₀ + β₁ + β₂ + β₃ is the average school performance for children following adaptive intervention (1, 1); and E[Y|−1, 1] = β₀ − β₁ + β₂ − β₃ is the average school performance for children following adaptive intervention (−1, 1).

Notice that because the aim of this analysis is to compare the four adaptive interventions embedded in the SMART design, equation 1 does not include an interaction between the intervention options (A₁, A_2NR) and the baseline measures, or intermediate outcomes (O₁, O₂). O₁ is included in equation 1 only to reduce error variance. However, interactions between the baseline measures and the intervention options could be included in this analysis to explore whether these intervention options should be more deeply tailored. Unfortunately the inclusion of intermediate outcomes in this analysis either by themselves or as interactions with intervention options can lead to bias; see the companion paper (Nahum-Shani et al., 2011), for discussion and for a method that can be used to jointly consider tailoring with baseline measures and with intermediate outcomes (e.g., whether and how the first-stage intervention should be adapted to the child’s baseline severity measures O₁; and whether and how the second-stage intervention for non-responders should be adapted to the child’s intermediate outcomes O₂).

In order to estimate the model in Equation 1 we use weighted regression with the SAS GENMOD procedure (SAS Institute, 2008); this procedure minimizes

$${\sum }_{j=1}^M{W}_j{(Y-{\beta }_0-{\beta }_1{A}_{1j}-{\beta }_2{A}_{2j}-{\beta }_3{A}_{1j}{A}_{2NRj}-{\mathit{\gamma }}^T{O}_{1_j})}^2$$ (2)

to estimate the regression coefficients. The summation is over the observations in the new dataset, M is the number of observations (i.e., rows) in the new dataset, and W is the weight assigned to each observation in the new dataset. Because the weights (depending on response/non-response) are random and observations are replicated, it is not immediately obvious that the estimator of the mean of the primary outcome for each adaptive intervention is consistent (unbiased in large samples). In Appendix 1 we provide an intuitive demonstration of how estimating this model with the SAS GENMOD procedure based on the new dataset results in consistent estimators of the population averages for the regression coefficients. To estimate the standard errors, we use the robust (sandwich) standard errors provided by the SAS GENMOD procedure (SAS Institute, 2008). Justification for the use of the robust standard errors is also included in Appendix 1. In Appendix 2 we provide the syntax for estimating the regression coefficients and robust standard errors, using SAS GENMOD procedure. SAS code for comparing adaptive interventions that are embedded this this SMART design (including generating the weights and replicating observations) is available at the following website: http://methodology.psu.edu/ra/adap-treat-strat/smartcodeex.

Data Analysis Methods for Other Forms of SMART Designs

Above, we discussed data analysis methods for addressing primary research questions using data from a SMART design in which response/non-response determines whether a participant is re-randomized (e.g., in the ADHD study only non-responders were re-randomized to second-stage intervention options). Here, we illustrate how the ideas discussed above can be used to compare the embedded adaptive interventions when data is obtained from other common types of SMART designs. More specifically, we focus on SMART designs with no embedded tailoring (e.g., the design in Figure 2); a SMART design in which participants are re-randomized to different second-stage intervention options, depending on an intermediate outcome (e.g., the design in Figure 3), and a SMART design in which whether a participant is re-randomized depends on both an intermediate outcome and the prior treatment (e.g., the design in Figure 4). To address questions concerning the main effects of the first-stage or second-stage intervention option using data from these SMART designs, one can use the same analysis methods discussed with respect to the ADHD SMART study. However, to compare adaptive interventions that are embedded in the SMART design, the primary difference between the analysis methods for the ADHD design and these designs concern the form of the weights and which, if any, participant observations need to be replicated. Also, the model used to compare the embedded adaptive interventions might differ.

Data analysis for SMART designs with no embedded tailoring variables

Consider the SMART design illustrated in Figure 2 and assume that at the first stage, participants were randomized with probability .5 to two intervention options: B or C. After 12 weeks, all participants were re-randomized with probability .5 to two second-stage intervention options: D or E, regardless of any information observed prior to the second-stage. Let A₁ denote the indicator for the first-stage intervention options (coded −1 for B, and 1 for C). Let A₂ denote the indicator for the second-stage intervention options (coded −1 for D, and 1 for E). Note that because there are no embedded tailoring variables, the embedded intervention sequences are non-adaptive unlike those in the ADHD study. There are 4 embedded non-adaptive intervention sequences (see below).

Weights are not required in this setting because all participants are randomized twice, each with equal probability, and all participants were randomized to the same number of intervention options (i.e., two). Furthermore because each participant’s observations are consistent with only one embedded non-adaptive intervention sequence there is no need to replicate participant observations in order to use common statistical software such as the SAS GENMOD procedure. Because no observations are replicated and weights are not assigned, traditional estimates of the standard errors can be used to conduct inference.

A model that can be used to compare the 4 embedded non-adaptive interventions is the usual ANOVA model:

$$E[Y|A_1,A_2,O_1]={\beta }_0+{\beta }_1{A}_1+{\beta }_2{A}_2+{\beta }_3{A}_1{A}_2+{\mathit{\gamma }}^T{O}_1.$$

where Y is the primary outcome; O₁ is a vector of baseline measures (obtained prior to the first-stage intervention, and included in the regression model as mean-centered covariates); β₀ is the intercept, β₁ − β₃ are the regression coefficients expressing the effects of the first-stage intervention, the effects of the second-stage intervention, and the interaction between them, respectively. γ is the vector of regression coefficients expressing the effects of the baseline measures O₁. Accordingly, E[Y| 1, −1] = β₀ + β₁ − β₂ − β₃ is the average outcome for participants following a non-adaptive intervention that begins with C and then offers E (1, −1); E[Y|−1,−1] = β₀ − β₁ − β₂ + β₃ is the average outcome for participants following a non-adaptive intervention that deigns with B and then offers E (−1, −1); E[Y| 1, 1] = β₀ + β₁ + β₂ + β₃ is the average outcome for participants following a non-adaptive intervention that begins with C and then offers D (1, 1); and E[Y|−1, 1] = β₀ − β₁ + β₂ − β₃ is the average outcome for participants following a non-adaptive intervention that begins with B and then offers E (−1, 1).

Data analysis for SMARTs in which re-randomization to different second-stage intervention options depends on an intermediate outcome

Consider the SMART design illustrated in Figure 3 and assume that at the first stage, participants were randomized with probability .5 to either B or C. After 12 weeks, responders were re-randomized with probability ½ to one of two maintenance interventions, M or M+. Non responders, on the other hand, were re-randomized with probability .5 to either switch to a third intervention E or to the combined intervention B+C. Let A₁ denote the indicator for the first-stage intervention options (coded −1 for B, and 1 for C); let A_2R denote the indicator for the second-stage intervention options for responders (coded −1 for M, and 1 for M+); and let A_2NR denote the indicator for the second-stage intervention options for non-responders (coded −1 for E, and 1 for B+C). There are 8 embedded adaptive interventions in this study (see below).

Weights are not required in this setting because all participants are randomized twice, each with equal probability, and all participants were randomized to the same number of intervention options (i.e., two). Next each participant’s observations are consistent with two adaptive interventions; hence the new dataset should contain two replicates of each participant’s observations. As written above, the replication enables the reuse of the observed outcome from each participant in estimating the mean outcome of the two adaptive interventions that are consistent with this participant’s observations. In particular for each participant who responded set A_2NR (i.e., the indicator for the second-stage intervention options for non-responders) to −1 in one of the two replicated observations and A_2NR to 1 in the other replicated observation; and for each participant who did not respond set A_2R (i.e., the indicator for the second-stage intervention options for responders) to −1 in one of the two replicated observations and A_2R to 1 in the other replicated observation.

Finally, using the new dataset, standard regression can be applied using a model such as

$$E[Y|A_1,A_{2R},A_{2NR},O_1]={\beta }_0+{\beta }_1{A}_1+{\beta }_2{A}_{2R}+{\beta }_3{A}_{2NR}+{\beta }_4{A}_1{A}_{2R}+{\beta }_5{A}_1{A}_{2NR}+{\beta }_6{A}_{2R}{A}_{2NR}+{\beta }_7{A}_1{A}_{2R}{A}_{2NR}+{\mathit{\gamma }}^T{O}_1,$$

where Y is the primary outcome; O₁ is a vector of baseline measures (obtained prior to the first-stage intervention, and included in the regression models as mean-centered covariates); β₀ is the intercept, β₁ − β₇ are the regression coefficients expressing the effect of the first-stage intervention option, the effects of the second-stage intervention options (offered to responders and non-responders, respectively), and the interactions between them, respectively. γ is the vector of regression coefficients expressing the effects of the baseline measures O₁. Accordingly, E[Y|−1,−1,−1] = β₀ − β₁ − β₂ − β₃ + β₄ + β₅ + β₆ − β₇ is the average outcome for participants following the adaptive intervention (−1, −1, −1); E[Y|−1,−1,1] = β₀ − β₁ − β₂ + β₃ + β₄ − β₅ − β₆ + β₇ is the average outcome for participants following the adaptive intervention (−1, −1, 1); E[Y|−1, 1,−1] = β₀ − β₁ + β₂ − β₃ − β₄ + β₅ − β₆ + β₇ is the average outcome for participants following the adaptive intervention (−1, 1, −1); E[Y|−1, 1, 1] = β₀ − β₁ + β₂ + β₃ − β₄ − β₅ + β₆ − β₇ is the average outcome for participants following the adaptive intervention (−1, 1, 1); E[Y|1,−1,−1] = β₀ + β₁ − β₂ − β₃ − β₄ − β₅ + β₆ + β₇ is the average outcome for participants following the adaptive intervention (1, −1, −1); E[Y|1, −1, 1] = β₀ + β₁ − β₂ + β₃ − β₄ + β₅ − β₆ − β₇ is the average outcome for participants following the adaptive intervention (1, −1, 1); E[Y|1, 1, −1] = β₀ + β₁ + β₂ − β₃ + β₄ − β₅ − β₆ − β₇ is the average outcome for participants following the adaptive intervention (1, 1, −1); and E[Y|1, 1, 1, O₁] = β₀ + β₁ + β₂ + β₃ + β₄ + β₅ + β₆ + β₇ is the average outcome for participants following the adaptive intervention (1, 1, 1).

Data analysis for SMARTs in which whether to re-randomize or not depends on an intermediate outcome and prior treatment

Consider the SMART design illustrated in Figure 4 and assume that at the first stage, participants were randomized with probability .5 to either B or C. After 12 weeks, only non-responders to first-stage intervention option B were re-randomized with probability .5 to either B+ or B+C. Let A₁ denote the indicator for the first-stage intervention options (coded −1 for B, and 1 for C). Let A_2NRB denote the indicator for the second-stage intervention options for non-responders to B (coded −1 for B+, and 1 for B+C). There are 4 embedded adaptive interventions (see below for a list).

In this study only a subset of participants are randomized twice: the participants who do not respond to first-stage intervention B. As a result, weights are needed. Specifically, W = 4 is the weight for non-responders to B because these participants are randomized twice, each randomization with probability .5. W = 2 is the weight for responders to B, as well as for responders and non-responders to C because these participants are randomized only once with probability .5. In terms of replicating observations, only the participants who responded to first-stage intervention B have observations that are consistent with more than one adaptive intervention. In particular responders to intervention B have observations consistent with the two adaptive interventions: begin with intervention B and then intensify to B+ only if the participant does not respond; and begin with intervention B and then augment to B+C only if the participant does not respond. In other words, replicating observations for responders to B enables the reuse of the observed outcome from each responder to B in estimating the average outcome of two adaptive interventions (−1, 1) and (−1, −1). Accordingly, for each participant who responded to intervention B, set A_2NRB to −1 in one of the two replicated observations and A_2NRB to −1 in the other replicated observation.

Next, to form a model note that because only participants who are initially randomized to intervention B (A₁ = −1), might potentially be re-randomized, A_2NRB is nested within A₁ = −1. To represent this nested structure, create a new indicator, Z, that equals 0 when A₁ = 1 (the first-stage intervention option is C) and equals 1 when A₁ = −1 (the first-stage intervention option is B). Finally, using the new dataset, standard weighted regression can be applied based on a model of the form

$$E[Y|A_1,A_{2}Z,O_1]={\beta }_0+{\beta }_1{A}_1+{\beta }_2{A}_{2NRB}Z+{\mathit{\gamma }}^T{O}_1$$

where Y is the primary outcome; O₁ is a vector of baseline measures (obtained prior to the first-stage intervention, and included in the regression models as mean-centered covariates); β₀ is the intercept; β₁ is the regression coefficient expressing the effect of the first-stage intervention options; and β₂ is the regression coefficient that expresses the effect of the second-stage intervention options offered to non-responders to B. Notice that because A_2NRB is nested within A₁ = −1 (or equivalently Z=1), A_2NRB only occurs in the product with Z in this model. γ is the vector of regression coefficients expressing the effects of the baseline measures O₁. Accordingly, E[Y| 1, 0] = β₀ + β₁ is the average outcome for participants following the adaptive intervention that begins with C, and then offers C for responders and C+ for non-responders; E[Y|−1, −1] = β₀ − β₁ − β₂ is the average outcome for participants following the adaptive intervention that begins with B and then offers B for responders and B+ for non-responders; and E[Y|−1, 1] = β₀ − β₁ + β₂ is the average outcome for participants following the adaptive intervention that begins with B and then offers B for responders and B+C for non-responders. The model above can be estimated with SAS GENMOD procedure, using a robust SE for inference.

Data Analysis Results Based On the Adaptive ADHD Data

Sample

149 children (75% boys) between the ages of 5 and 12 (mean 8.6 years) participated in the study. Due to dropout and missing data², the effective sample used in the current analysis was 139. At the first stage (A₁), 71 children were randomized to receive low-dose medication, and 68 were randomized to receive low-intensity behavioral intervention. By the end of the school year, 81 children were classified as non-responders and re-randomized to one of the two second-stage intervention options, with 40 children assigned to increasing the dose of the first-stage intervention, and 41 children assigned to augmenting the first-stage intervention with the other type of intervention. Overall, 46 children were consistent with adaptive intervention (1, −1; starting with low-intensity behavioral intervention and then adding low-dose medication to non-responders and offering the same intensity of behavioral intervention to responders), 53 children were consistent with adaptive intervention (−1, −1; starting with low dose of medication and then adding low-intensity behavioral intervention to non-responders and offering the same dose of medication to responders), 44 children were consistent with adaptive intervention (1, 1; starting with low-intensity behavioral intervention and then enhancing the intensity of the behavioral intervention to non-responders and offering the same intensity of behavioral intervention to responders), and 54 children were consistent with adaptive intervention (−1, 1; starting with low-dose medication and then enhancing the dose of medication to non-responders and offering the same dose of medication to responders).

Measures

Primary outcome (γ)

We consider a measure of children’s school performance based on the Impairment Rating Scale (IRS, Fabiano et al., 2006) after an 8-month period as our primary outcome. This primary outcome ranges from 1 to 5, with higher values reflecting better school performance. Because the current analysis is for illustrative, rather than for substantive purposes, we use this measure as a primary outcome despite limitations relating to its distribution and reliability.

Baseline measures

(1) Medication prior to first-stage intervention, reflecting whether the child did (coded as 1) or did not (coded as 0) receive medication at home during the previous school year (i.e., prior to the first-stage intervention); (2) ADHD symptoms at the end of the previous school year, which is the mean of teacher’s evaluation on 14 ADHD symptoms (the Disruptive Behavior Disorders, Rating Scale; Pelham et al., 1992), each ranging from 0 to 3. We reverse-coded this measure such that larger values reflect fewer symptoms (i.e., better school performance); (3) ODD diagnosis, reflecting whether the child was (coded as 1) or was not (coded as 0) diagnosed with ODD (oppositional defiant disorder) before the first-stage intervention.

Results

Table 2 presents parameter estimates for Model 1 (obtained using the SAS GENMOD procedure described in Appendix 2), Table 3 presents the estimated means and robust standard error for each adaptive intervention based on the estimated coefficients in Model 1 (as well as the sample size and the sample mean for each adaptive intervention), and Table 4 presents the estimated differences and the associated robust standard error for each possible comparison of the four adaptive interventions.

Table 2.

Results (Parameter Estimates) for Model 1.

Parameter	Estimate	Robust SE	95% Confidence limits		Z	Pr > |Z|
Intercept	3.43	0.23	2.97	3.89	14.63	<.0001
Baseline: ODD diagnosis	0.37	0.18	0.02	0.72	2.07	0.0384
Baseline: ADHD symptoms	0.57	0.14	0.29	0.85	3.95	<.0001
Baseline: medication before stage 1	−0.61	0.25	−1.10	−0.13	−2.47	0.0134
A1	0.07	0.09	−0.11	0.24	0.75	0.4555
A2	0.02	0.08	−0.13	0.18	0.26	0.7924
A1*A2	−0.12	0.08	−0.27	0.04	−1.46	0.1436

Table 3.

Estimated Mean and SE for Each Adaptive Intervention

Adaptive intervention			Responders		Non-Responders		Estimated weighted mean	Robust SE
	Stage 1	Stage 2	Sample size	Sample mean	Sample size	Sample mean
(1, −1)	BMOD	AUGMENT	22	4.64	24	4.08	4.36	0.15
(−1, −1)	MED	AUGMENT	36	4.39	17	3.47	4.00	0.15
(1, 1)	BMOD	INTENSIFY	22	4.64	22	3.96	4.17	0.22
(−1, 1)	MED	INTENSIFY	36	4.39	18	4.22	4.27	0.13

Table 4.

Estimated Differences Between the 4 Adaptive Interventions Based on the Estimated Regression Coefficients in Table 2.

Label	Estimate	95% Confidence limits		Robust SE	Chi- Square	Significance
Difference between (1, −1) and (−1, −1)	0.36	−0.06	0.79	0.22	2.82	0.0932
Difference between (1, 1) and (−1, 1)	−0.10	−0.60	0.40	0.26	0.16	0.6920
Difference between (1, −1) and (1, 1)	0.19	−0.32	0.70	0.26	0.55	0.4600
Difference between (1, −1) and (−1, 1)	0.09	−0.31	0.49	0.20	0.20	0.6563
Difference between (−1, −1) and (1, 1)	−0.17	−0.70	0.35	0.27	0.42	0.5161
Difference between (−1, −1) and (−1, 1)	0.27	−0.08	0.63	0.18	2.26	0.1328

As shown in Tables 3 and 4, school performance was higher for those children following adaptive intervention (1, −1; estimated mean=4.36, SE=0.15) relative to those following adaptive intervention (−1, −1; estimated mean=4.00, SE=0.15). The difference between adaptive interventions (1, −1) and (−1, −1) was found to be marginally significant (estimated difference=0.36, SE=0.22, P<.10). No other significant differences were found between the four adaptive interventions.

Accordingly, this analysis indicates that starting with low-intensity behavioral intervention and then adding medication to non-responders and offering the same intensity behavioral intervention to responders is better than starting with low-dose medication and then adding low-intensity behavioral intervention to non-responders and offering the same dose of medication to responders.

Discussion

Adaptive interventions are both conceptually and scientifically appealing. Here, we reviewed the ways in which decision rules can be used to operationalize adaptation and individualization of interventions in the social and behavioral sciences. We also reviewed SMART studies, emphasizing their advantages and arguing for an increase in their use for informing the construction of high-quality adaptive interventions. Finally, we presented a data analysis method for addressing primary research questions concerning the comparison of intervention options at different stages of the adaptive intervention, as well as the comparison of adaptive interventions that are embedded in the SMART design. An adaptive intervention for children with ADHD SMART study was used to illustrate this method.

SMART designs have the potential to advance research in many areas in the behavioral and social sciences. For example, in the area of goal setting, although goal-setting theorists assert that a goal will result in higher performance if it is difficult, attainable, and specific (Locke & Latham, 1990), more recent approaches to goal setting (see Barlas & Yasarcan, 2006; Fried & Slowik, 2004) suggest that the contribution of goal-setting theory has not been fully realized because of the failure to systematically capture its dynamic and sequential nature. For example, with respect to the difficulty of the goal, individuals might pursue sequential goals, which differ in their level of difficulty: they might function well with less challenging goals if they perceive the accomplishment of these goals as the basis for pursuing more difficult and challenging goals in the future (Fried & Slowik, 2004). Another example relates to the concept of floating goals (see Barlas & Yasarcan, 2006), a more sophisticated and realistic goal-related structure in which the difficulty of the goal is adjusted depending on current conditions (e.g., if the performance of an individual is persistently poor in approaching the original goal, then he/she lowers the goal, but if he/she exhibits surprisingly good performance, then the goal is pushed higher). These new approaches raise questions concerning the optimal sequence of goals, and the way in which the goals should be adjusted over time in order to maximize long-term performance. A SMART design in which each participant can be sequentially randomized multiple times might be appropriate for addressing such research questions by allowing within-individual variation in the extent to which the goal is difficult, attainable, and specific over time. However, capturing the dynamic and sequential nature of goal setting (in which both self-set goals and environmental feedback are incorporated into a system that monitors performance relative to the desired state and repeatedly adjusts subsequent goals; Campion & Lord, 1982), might require a SMART design with a high number of randomizations per participant. Accordingly, an important direction for future research would be developing methods for analyzing data from such designs.

Several other issues warrant further discussion in future research. First, the outcome of interest in the current paper was a single measurement that expresses long-term school performance. However, researchers might be interested in other types of outcomes, such as non-continuous outcomes (e.g., binary or count measures reflecting the severity of ADHD symptoms); multiple outcomes (e.g., a set of outcome measures reflecting different dimensions of school performance, such as peer relations, academic performance, and classroom performance); or longitudinal outcomes (e.g., improvement in children’s classroom performance over the school year). The model used in the current study can be easily generalized via a generalized linear model to estimate the difference between adaptive interventions with respect to binary, categorical or count outcomes. The SAS GENMOD procedure discussed in the current manuscript allows the specification of various types of distributions and link functions. Still, additional research attention should be given to developing data analysis methods for the comparison of adaptive interventions with respect to other types of outcome measures. It is especially important to generalize our approach to estimate the difference between adaptive interventions with respect to time-varying outcomes by utilizing random effects as in growth-curve modeling (Hu, Goldberg, Hedeker, Flay, & Pentz, 1998).

Second, in a SMART, like other trials (Montgomery, Peters & Little, 2003) there is concern about the loss of balance and subsequent loss of power due to study dropout and item missigness. Modern-day missing-data techniques will be needed in the analysis of data from SMART designs as in the case of any randomized trial. Like any other trials, these techniques will lead to unbiased results when the data is missing at random (MAR); that is, the probability that an observation is missing depends on information that is observed (i.e., characteristics of the child or baseline severity of ADHD symptoms). If data is missing not at random (MNAR), that is the probability that an observation is missing depends on information that is not observed, valuable information is lost from the data, and there is no universal method of handling the missing data properly (see Donders, van der Heijden, Stijnen, & Moon, 2006 for review).

Finally, in the current study we discussed primary research questions relating to the construction of adaptive interventions, but investigators often collect information concerning other potential moderators of the intervention options, aiming to use these measures to address secondary research questions concerning the best adaptive sequence of intervention options. For example, researchers might be interested in assessing whether both the first-stage intervention and the second-stage intervention should be more deeply tailored to the individual (perhaps the choice of the first-stage intervention option should depend on baseline severity, whereas the choice of the second-stage intervention option should depend on the participant’s willingness to adhere to the first-stage intervention option). In this sense, additional information concerning potential moderators can be used to explore ways to more deeply tailor the adaptive intervention while using the advantages of the multiple randomizations in the SMART to eliminate confounding. In the companion paper (Nahum-Shani et al., 2011), we provide a secondary data analysis method that can be used to find the best sequence of decision rules while evaluating potential tailoring variables at each intervention stage. This data analysis method takes a holistic approach--one that considers future intervention stages when assessing the best way to tailor the intervention at each specific stage.

Appendix 1

In Equation (1) we provided a method for estimating the mean of the primary outcome, conditional on baseline measures, for each adaptive intervention (a₁, a₂). This method employs random weights (e.g., the weight depends on response/non-response) and also replicates the data of the responders. Thus it is not immediately obvious that the estimator of the mean of the primary outcome for each adaptive intervention is consistent (unbiased in large samples). To demonstrate that this is indeed the case we define the mean of primary outcome, conditional on baseline measures for each adaptive intervention (a₁, a₂) using the language of potential outcomes. Subsequently we demonstrate that this conditional mean can be consistently estimated by minimizing the total mean squared error given in Equation (2). Last, we verify that the robust standard errors provided by SAS GENMOD are indeed unbiased (consistent) in large samples.

Recall that (O₁, A₁, O₂, A₂, Y) denotes a participant’s data in a SMART study. Here and following, uppercase letters represent random variables, and lowercase letters represent particular values, or realizations, of random variables. Recall that O₁ denotes a vector of baseline measures, (A₁, A₂) denotes the randomized intervention options and O₂ is a vector of intermediate outcomes. One intermediate outcome is R, the indicator for response (other intermediate outcomes might be measures of adherence to first-stage intervention, other measures of severity, etc.). Only non-responding participants have an A₂. A particular adaptive intervention is denoted by (A₁, A₂) = (a₁, a₂) (in the ADHD example both a₁ and a₂ are either 1 or −1). We write that a participant in a SMART study “follows” adaptive intervention (a₁, a₂) if this participant’s first-stage intervention is a₁ and either this participant responds throughout the study (R=1) or, if the participant does not respond, then the participant’s second-stage intervention is a₂. Thus, for example, in the ADHD study, participants who respond to first-stage intervention a₁ follow both adaptive interventions (a₁, 1) and (a₁, −1).

In the potential outcomes framework (Neyman, 1923; Rubin, 1978; Robins, 1986) and for each fixed sequence of interventions (a₁, a₂), we conceptualize potential outcomes denoted by O₂(a₁) and Y(a₁, a₂). O₂ (a₁) is the vector of intermediate observations that a participant would have had at the second stage if he/she had followed a₁ at the first-stage intervention; O₂(a₁) includes the indicator of response R(a₁). Y(a₁, a₂) is the primary outcome that would have been observed had the participant followed the sequence (a₁, a₂). In the ADHD study responding participants do not enter the second-stage intervention, thus we have that when R(a₁) = 1, Y(a₁, 1) = Y(a₁, −1). O₂(a₁) and Y(a₁, a₂) are called potential outcomes because they describe an individual outcome value that would have been observed under a potential exposure to the intervention that the individual might or might not have actually experienced. The assumption is that each intervention option has the potential to be observed until assignment to intervention options is made (for a more detailed definition of potential outcomes, see Rubin, 1974, as well as Hernán, 2004). The set of all potential outcomes is

$$𝒪=\left\{\right(O_2(a_1),Y(a_1,a_2)):a_1\in \{-1,1\},a_2\in \{-1,1\}\}.$$

By definition, the multivariate distribution of (O₁, O₂(a₁), Y(a₁, a₂)) is the multivariate distribution of (O₁, O₂, Y) when all individuals follow adaptive intervention (a₁, a₂). Denote E[Y(a₁, a₂)|O₁] by μ(a₁, a₂|O₁); we know that μ(a₁, a₂|O₁) minimizes the total mean squared error for the four adaptive interventions:

$$\begin{gathered} E\left[{(Y(-1,-1)-\mu (-1,-1|O_1))}^2\right]+E\left[{(Y(-1,1)-\mu (-1,1|O_1))}^2\right]+E\left[{(Y(1,1)-\mu (1,1|O_1))}^2\right] \\ +E\left[{(Y(1,-1)-\mu (1,-1|O_1))}^2\right]. \end{gathered}$$

Assume that μ(a₁, a₂|O₁) = β₀ + β₁a₁ + β₂a₂ + β₃a₁a₂ + γ^TO₁. The above can be rewritten as

$$E[{(Y(-1,-1)-{\beta }_0+{\beta }_1+{\beta }_2-{\beta }_3-{\gamma }^T{O}_1)}^2]+E[{(Y(-1,1)-{\beta }_0+{\beta }_1-{\beta }_2+{\beta }_3-{\gamma }^T{O}_1)}^2]+E[{(Y(1,1)-{\beta }_0-{\beta }_1-{\beta }_2-{\beta }_3-{\gamma }^T{O}_1)}^2]+E[{(Y(1,-1)-{\beta }_0-{\beta }_1+{\beta }_2+{\beta }_3-{\gamma }^T{O}_1)}^2].$$ (3)

Our goal is to show that the weighted least squares estimator obtained by minimizing Equation (2), (β̂₀, β̂₁, β̂₂, β̂₃, $\widehat{{\gamma }^T}$), is a consistent (unbiased in large samples) estimator of (β₀, β₁, β₂, β₃, γ^T). We do this by showing that Equation (3) is the large-sample version of Equation (2).

Since Y(a₁, a₂) = R(a₁)Y(a₁, a₂) + (1 − R(a₁))Y(a₁, a₂), (3) can be rewritten as

$$\sum _{a_1\in \{1,-1\}}\sum _{a_2\in \{1,-1\}}E\left[{(R(a_1)Y(a_1,a_2)+(1-R(a_1))Y(a_1,a_2)-{\beta }_0-{\beta }_1{a}_1-{\beta }_2{a}_2-{\beta }_3{a}_1{a}_2-{\gamma }^T{O}_1)}^2\right].$$

Splitting the squared terms by the indicators, R(a₁) and 1 − R(a₁), we obtain that Equation (3) is equal to

$$\begin{gathered} \sum _{a_1\in \{1,-1\}}\sum _{a_2\in \{1,-1\}}E[R(a_1){(Y(a_1,a_2)-{\beta }_0-{\beta }_1{a}_1-{\beta }_2{a}_2-{\beta }_3{a}_1{a}_2-{\gamma }^T{O}_1)}^2] \\ +\sum _{a_1\in \{1,-1\}}\sum _{a_2\in \{1,-1\}}E[(1-R(a_1)){(Y(a_1,a_2)-{\beta }_0-{\beta }_1{a}_1-{\beta }_2{a}_2-{\beta }_3{a}_1{a}_2-{\gamma }^T{O}_1)}^2]. \end{gathered}$$ (4)

Since A₁, A₂ are randomized independently of the potential outcomes, Equation (4) can be expressed as

$$\begin{gathered} \sum _{a_2\in \{1,-1\}}E[2R(A_1){(Y(A_1,a_2)-{\beta }_0-{\beta }_1{A}_1-{\beta }_2{a}_2-{\beta }_3{A}_1{a}_2-{\gamma }^T{O}_1)}^2] \\ +E[4(1-R(A_1)){(Y(A_1,A_2)-{\beta }_0-{\beta }_1{A}_1-{\beta }_2{A}_2-{\beta }_3{A}_1{A}_2-{\gamma }^T{O}_1)}^2]. \end{gathered}$$

(To see this, note that if we average out over A₁ in the first two terms, the weight 2 cancels out the randomization probability .5 and we get an additional sum over a₁; next if we average out over both A₁, A₂ in the last term, the weight 4 cancels out the product of the randomization probabilities .5*.5 and we get a double sum over a₁, a₂.)

Next we express Equation (4) and hence Equation (3) in terms of the observed data (O₁, A₁, O₂, A₂, Y) (recall that O₂ includes the response indicator R). We assume that Robins’ consistency assumption holds, namely that the observed outcome for a participant equals the participant’s potential outcome, when the intervention is set to the observed intervention option (see Robins and Wasserman, 1997). Accordingly, the potential outcomes are connected to the SMART data by R = R(A₁) and = Y(A₁, A₂); because responders are not provided a second-stage intervention, A₂, R(A₁)Y(A₁, 1) = R(A₁)Y(A₁, −1). The consistency assumption implies that Equation (4) is equal to

$$E[2R{(Y-{\beta }_0-{\beta }_1{A}_1-{\beta }_2-{\beta }_3{A}_1-{\gamma }^T{O}_1)}^2]+E[2R{(Y-{\beta }_0-{\beta }_1{A}_1+{\beta }_2+{\beta }_3{A}_1-{\gamma }^T{O}_1)}^2]+E[4(1-R){(Y-{\beta }_0-{\beta }_1{A}_1-{\beta }_2{A}_2-{\beta }_3{A}_1{A}_2-{\gamma }^T{O}_1)}^2].$$

However, the above display is the large-sample version of Equation (2). The number 2 in the first two terms is the weight given to responders and the number 4 in the third term is the weight given to non-responders in Equation (2). Thus under mild regularity conditions,(β̂₀, β̂₁, β̂₂, β̂₃, $\widehat{{\gamma }^T}$) is a consistent estimator (unbiased in large samples) of the regression coefficients in [Y(a₁, a₂)|O₁].

That is, (β̂₀, β̂₁, β̂₂, β̂₃, $\widehat{{\gamma }^T}$) is a consistent estimator of (β₀, β₁, β₂, β₃, γ^T).

Last, we provide a sketch of the proof that the robust standard error (sandwich standard error) provided by the SAS GENMOD procedure is a consistent estimator of the variance-covariance of the asymptotic normal distribution of (β̂₀, β̂₁, β̂₂, β̂₃, $\widehat{{\gamma }^T}$). Note that Equation (2) is equal to

$${\sum }_{i=1}^N[2R_i{(Y_i-{\beta }_0-{\beta }_1{A}_{1i}-{\beta }_2-{\beta }_3{A}_{1i}-{\gamma }^T{O}_{1i})}^2]+{\sum }_{i=1}^N[2R_i{(Y_i-{\beta }_0-{\beta }_1{A}_{1i}+{\beta }_2+{\beta }_3{A}_{1i}-{\gamma }^T{O}_{1i})}^2]+{\sum }_{i=1}^N[4(1-R_i){(Y_i-{\beta }_0-{\beta }_1{A}_{1i}-{\beta }_2{A}_{2i}-{\beta }_3{A}_{1i}{A}_{2i}-{\gamma }^T{O}_{1i})}^2]\mathrm{,}$$

where N is the number of subjects in the data.

Since (β̂₀, β̂₁, β̂₂, β̂₃, $\widehat{{\gamma }^T}$) minimizes Equation (2), the derivative of Equation (2) evaluated at (β̂₀, β̂₁, β̂₂, β̂₃, $\widehat{{\gamma }^T}$) is zero. That is, ${\sum }_{i=1}^N{U}_i({\widehat{\beta }}_0,{\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3,\widehat{{\gamma }^T})=0$, where

$$U_i({\widehat{\beta }}_0,{\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3,\widehat{{\gamma }^T})=4R_i(Y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{A}_{1i}-{\widehat{\beta }}_2-{\widehat{\beta }}_3{A}_{1i}-\widehat{{\gamma }^T}{O}_{1i}){(1,A_{1i},1,A_{1i},O_{1i}^T)}^T+4R_i(Y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{A}_{1i}+{\widehat{\beta }}_2+{\widehat{\beta }}_3{A}_{1i}-\widehat{{\gamma }^T}{O}_{1i}){(1,A_{1i},-1,-A_{1i},O_{1i}^T)}^T+8(1-R_i)(Y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{A}_{1i}-{\widehat{\beta }}_2{A}_{2i}-{\widehat{\beta }}_3{A}_{1i}{A}_{2i}-\widehat{{\gamma }^T}{O}_{1i}){(1,A_{1i},A_{2i},A_{1i}{A}_{2i},O_{1i}^T)}^T$$

for i = 1, …, N.

Recall that responders are replicated and get a weight of 2, and non-responders get a weight of 4. The sum of the weights is ${\sum }_{i=1}^N[2R_i+2R_i+4(1-R_i)]=4N$. Define $Z_N=\sqrt{4N}{({\widehat{\beta }}_0-{\beta }_0,{\widehat{\beta }}_1-{\beta }_1,{\widehat{\beta }}_2-{\beta }_2,{\widehat{\beta }}_3-{\beta }_3,\widehat{{\gamma }^T}-{\gamma }^T)}^T$. A Taylor series for $0={\sum }_{i=1}^N{U}_i({\widehat{\beta }}_0,{\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3,\widehat{{\gamma }^T})$ in $({\widehat{\beta }}_0,{\widehat{\beta }}_1,{\widehat{\beta }}_2,{\widehat{\beta }}_3,\widehat{{\gamma }^T})$ around (β₀, β₁, β₂, β₃, γ^T) results in $0=\frac{1}{\sqrt{4N}}{\sum }_{i=1}^N{U}_i({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }^T)+\frac{1}{4N}{\sum }_{i=1}^N\frac{\partial U_i({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }^T)}{\partial ({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }^T)}{Z}_N$. Solve for Z_N to obtain $Z_N={(-\frac{1}{4N}{\sum }_{i=1}^N\frac{\partial U_i({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }^T)}{\partial ({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }^T)})}^{-1}\frac{1}{\sqrt{4N}}{\sum }_{i=1}^N{U}_i({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }^T)$. Thus, the large-sample variance-covariance matrix of Z_N is given by $I_0^{-1}{I}_1{I}_0^{-1}$ where

$$\begin{gathered} I_0=4E\left[R{(1,A_1,1,A_1,{O_1}^T)}^T\right(1,A_1,1,A_1,{O_1}^T)+R{(1,A_1,-1,-A_1,{O_1}^T)}^T(1,A_1,-1,-A_1,{O_1}^T) \\ +(1-R){(1,A_1,A_2,A_1{A}_2,{O_1}^T)}^T(1,A_1,A_2,A_1{A}_2,{O_1}^T\left)\right] \end{gathered}$$

$(I_0=-E[\frac{\partial U_i({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }^T)}{\partial ({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\gamma }^T)}\left]\right)$ and

$$I_1=16E\left[R{(Y-{\beta }_0-{\beta }_1{A}_1-{\beta }_2-{\beta }_3{A}_1-{\gamma }^T{O}_1)}^2{(1,A_1,1,A_1,{O_1}^T)}^T\right(1,A_1,1,A_1,{O_1}^T)+R{(Y-{\beta }_0-{\beta }_1{A}_1+{\beta }_2+{\beta }_3{A}_1-{\gamma }^T{O}_1)}^2{(1,A_1,-1,-A_1,{O_1}^T)}^T(1,A_1,-1,-A_1,{O_1}^T)+R(Y-{\beta }_0-{\beta }_1{A}_1-{\beta }_2-{\beta }_3{A}_1-{\gamma }^T{O}_1)(Y-{\beta }_0-{\beta }_1{A}_1+{\beta }_2+{\beta }_3{A}_1-{\gamma }^T{O}_1)\times [{(1,A_1,1,A_1,{O_1}^T)}^T(1,A_1,-1,-A_1,{O_1}^T)+{(1,A_1,-1,-A_1,{O_1}^T)}^T(1,A_1,1,A_1,{O_1}^T)]+4(1-R){(Y-{\beta }_0-{\beta }_1{A}_1-{\beta }_2{A}_2-{\beta }_3{A}_1{A}_2-{\gamma }^T{O}_1)}^2\times {(1,A_1,A_2,A_1{A}_2,{O_1}^T)}^T(1,A_1,A_2,A_1{A}_2,{O_1}^T\left)\right],$$

where I₁ is the variance-covariance matrix of U_i(β₀, β₁, β₂, β₃, γ^T). Replacing the expectation with the weighted sample average (i.e. replacing E with $\frac{1}{4N}{\sum }_{i=1}^N$.) and plugging in the weighted least squares estimator, we obtain an estimator of the variance-covariance matrix of (β̂₀, β̂₁, β̂₂, β̂₃, $\widehat{{\gamma }^T}$), namely, ${\widehat{I}}_0^{-1}{\widehat{I}}_1{\widehat{I}}_0^{-1}$, where

$${\widehat{I}}_0=\frac{1}{4N}{\sum }_{i=1}^N[R_i{(1,A_{1i},1,A_{1i},{O_1}_i^T)}^T(1,A_{1i},1,A_{1i},O_{1i}^T)+R_i{(1,A_{1i},-1,-A_{1i},{O_1}_i^T)}^T(1,A_{1i},-1,-A_{1i},O_{1i}^T)+2(1-R_i){(1,A_{1i},A_{2i},A_{1i}{A}_{2i},{O_1}_i^T)}^T(1,A_{1i},A_{2i},A_{1i}{A}_{2i},O_{1i}^T)]$$

and

$${\widehat{I}}_1=\frac{1}{4N}{\sum }_{i=1}^N\left[R_i{(Y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{A}_{1i}-{\widehat{\beta }}_2-{\widehat{\beta }}_3{A}_{1i}-\widehat{{\gamma }^T}{O}_{1i})}^2{(1,A_{1i},1,A_{1i},O_{1i}^T)}^T\right(1,A_{1,i},1,A_{1i},O_{1i}^T)+R_i{(Y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{A}_{1i}+{\widehat{\beta }}_2+{\widehat{\beta }}_3{A}_{1i}-\widehat{{\gamma }^T}{O}_{1i})}^2{(1,A_{1i},-1,-A_{1i},O_{1i}^T)}^T(1,A_{1i},-1,-A_{1i},O_{1i}^T)+R_i(Y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{A}_{1i}-{\widehat{\beta }}_2-{\widehat{\beta }}_3{A}_{1i}-\widehat{{\gamma }^T}{O}_{1i}\left)\right(Y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{A}_{1i}+{\widehat{\beta }}_2+{\widehat{\beta }}_3{A}_{1i}-\widehat{{\gamma }^T}{O}_{1i})\times [{(1,A_{1i},1,A_{1i},O_{1i}^T)}^T(1,A_{1i},-1,-A_{1i},O_{1i}^T)+{(1,A_{1i},-1,-A_{1i},O_{1i}^T)}^T(1,A_{1i},1,A_{1i},O_{1i}^T)]+4(1-R_i){(Y_i-{\widehat{\beta }}_0-{\widehat{\beta }}_1{A}_{1i}-{\widehat{\beta }}_2{A}_{2i}-{\widehat{\beta }}_3{A}_{1i}{A}_{2i}-\widehat{{\gamma }^T}{O}_{1i})}^2\times {(1,A_{1i},A_{2i},A_{1i}{A}_{2i},O_{1i}^T)}^T(1,A_{1i},A_{2i},A_{1i}{A}_{2i},O_{1i}^T)].$$

Appendix 2

The following SAS syntax can be used to estimate the weighted regression in (1) (Hernan, Brumback and Robins, 2000; 2002):

• PROC GENMOD data=new;

• CLASS id;

• MODEL outcome = a1 a2 a1*a2 o1;

• SCWGT weights;

• REPEATED SUBJECT=id / TYPE=ind;

• ESTIMATE 'difference 1, −1 and −1, −1' a1 2 a2 0 a1*a2 −2;

• ESTIMATE 'difference 1, 1 and −1, 1' a1 2 a2 0 a1*a2 2;

• ESTIMATE 'difference 1, −1 and 1, 1' a1 0 a2 −2 a1*a2 −2;

• ESTIMATE 'difference 1, −1 and −1, 1' a1 2 a2 −2 a1*a2 0;

• ESTIMATE 'difference −1, −1 and 1, 1' a1 −2 a2 −2 a1*a2 0;

• ESTIMATE 'difference −1, 1 and −1, −1' a1 0 a2 −2 a1*a2 2;

• RUN;

The first line calls the GENMOD procedure and specifies the working dataset. The second line specifies the child’s identification number (id) as a categorical variable. The third line specifies the model to be estimated, identifying the outcome and the independent variables. The fourth line specifies the variable weights in the dataset as the variable that contains the weight for each observation, using the SCWGT statement. The program will provide robust standard errors for the model parameters when the option REPEATED is included, with the child’s identification number (SUBJECT=id) and the independent working correlation matrix (TYPE=ind) being specified (see Liang & Zeger, 1986). The ESTIMATE statements specify the comparisons between the adaptive interventions based on the estimated coefficients.