Abstract
Purpose
To assess bony trabecular changes potentially caused by loading stress around dental implants using fractal dimension analysis.
Methods
Fractal dimensions were measured in 48 subjects by comparing radiographs taken immediately after prosthesis delivery with those taken 1 year after functional loading. Regions of interest were isolated, and fractal analysis was performed using the box-counting method with Image J 1.42 software. Wilcoxon signed-rank test was used to analyze the difference in fractal dimension before and after implant loading.
Results
The mean fractal dimension before loading (1.4213±0.0525) increased significantly to 1.4329±0.0479 at 12 months after loading (P<0.05).
Conclusions
Fractal dimension analysis might be helpful in detecting changes in peri-implant alveolar trabecular bone patterns in clinical situations.
Keywords: Bone remodeling, Dental implants, Fractals
INTRODUCTION
Dental implants are osseointegrated into surrounding bone without the periodontal ligament. Trabecular bone around an implant thus plays major roles in supporting the functional pressure exerted by the implant and in dispersing stress by forming a load transfer path [1]. The key factor for successful implant treatment is the manner in which stresses are transferred to the surrounding bone [2]. Bone tissue undergoes continuous cycles of resorption and formation, and the associated combination of modeling and remodeling is critical to the ability to maintain the stability of the bone-implant interface after loading [3]. Such loading force interferes with local bone healing and predisposes the implant to a fibrous tissue interface instead of osseointergration [4,5]. Others suggest that when loading forces are appropriately controlled, it can stimulate bone remodeling around implants and help to maintain implant stability [6,7]. Thus, it has become crucial to monitor the bone surrounding an implant during maintenance.
Periapical radiographs, which are frequently taken during routine dental examination, are traditionally interpreted by measuring peri-implant marginal bone loss. Unfortunately, this most commonly used method has low sensitivity [8] and has been shown to be of limited diagnostic value for the early detection of changes in bone [9]. As a result, there has been a search for available, reliable, and sensitive methods of assessment, offering affordable and more accessible ways to measure early trabecular changes. Recent studies have suggested that fractal dimension analysis is a noninvasive tool that can be used to describe biological systems in clinical studies and is a method of identifying scale-invariant structure that is not affected by exposure or minor alignment variations on radiographs [10,11]. It is thus well suited to the analysis of three-dimensional trabecular bone patterns on plain radiographs.
Several studies have found a strong correlation between the demineralization of alveolar bone and decreasing fractal dimension [12-15]. This method has been employed to quantify trabecular bony structure under various conditions, not only those associated with dental diseases like root canal treatment [16] and periodontitis [17,18], but also the changes in osteoporosis and hyperparathyroidism patients [12,19]. When it comes to comparing the biomechanical competence of an implant, there are only two in vivo studies focusing on the correlation between fractal dimensions and parameters, finding a correlation between fractal dimensions and the implant stability quotient values [20], and with insertion torque [21].
Changes in the magnitude of habitual mechanical stimulation should be accompanied by corresponding changes in osseous structure and the orientation of bony trabeculae [22-24]. Therefore, the aim of this study was to assess bony trabecular changes caused by loading stress around dental implants using fractal dimension analysis.
MATERIALS AND METHODS
Patient selection
This retrospective study was approved by the Institutional Review Board of Yonsei University. All of the patients were informed in detail about the study procedures and provided written informed consent. Forty-eight subjects (23 men, 25 women; age range, 33 to 77 years; mean age, 58 years) were selected from among patients who received dental implants to replace missing teeth at the Department of Periodontology, Gangnam Severance Dental Hospital, between January 2007 and December 2010.
All of the patients selected for this study had functional prostheses for >12 months. Exclusion criteria were untreated active periodontitis, bruxism/parafunctional habits, poor oral hygiene (modified plaque index [mPI], >2 [25]), bone grafting in conjunction with implant placement, and uncontrolled compromised systemic disease.
Implants
Seventy-two internal hex implants (Astra Tech OsseoSpeed, Astra Tech Dental Implant System; Astra Tech AB, Mölndal, Sweden) were used to replace missing teeth. The implant lengths ranged from 8 to 13 mm and diameters ranged from 3.5 to 5.0 mm (Tables 1 and 2).
Table 1.
Distribution of analyzed implant length.
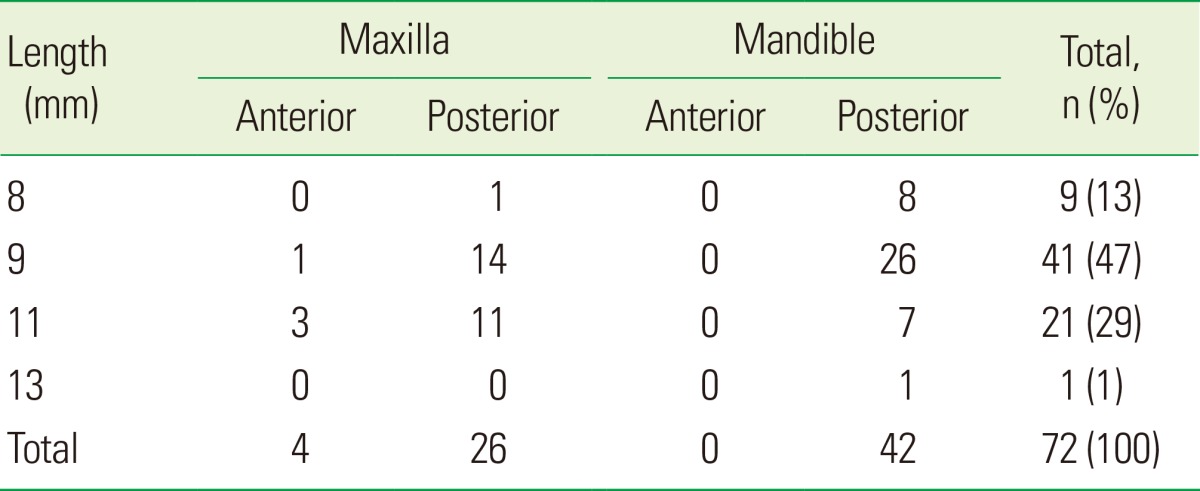
Table 2.
Distribution of analyzed implant diameter.
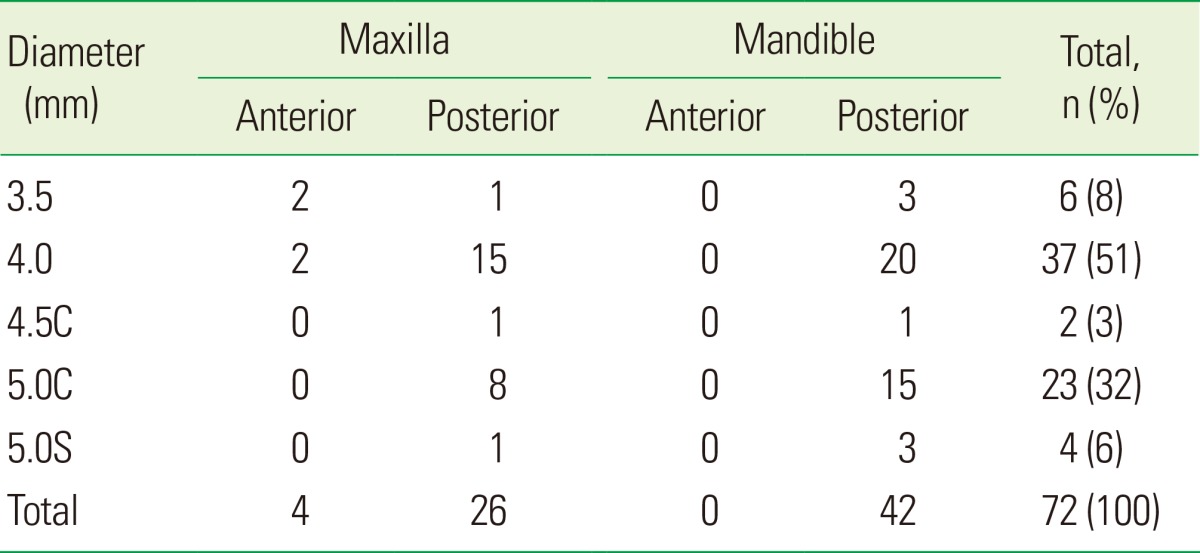
C: conical neck design, S: straight neck design.
Treatment procedure
A two-stage surgical protocol was used. Second-stage surgeries were performed 6 and 3 months after the first stage for maxillary and mandibular implants, respectively. The prostheses were delivered 3 weeks after the second-stage surgery. The patients were recalled every 6 months for professional plaque control and oral hygiene evaluation.
Radiographic examination and evaluation
Radiographs were taken with an extension cone paralleling device (Rinn, Elgin, IL, USA) using the parallel cone technique (70 kV, 8 mA, 0.250 second). A 5.5-mm spherical metal bearing was placed to aid length measurement. All of the films were developed using the same automatic processor (Periomat, Durr Dental, Bietigheim-Bissingen, Germany) according to the manufacturer's instructions. The radiographs were digitized using a digital scanner (GT-12000, EPSON, Nagano, Japan) at an input resolution of 2,400 dpi with a grayscale spectrum of 256 shades. Periapical radiographs (Kodak Insight, F speed film; Eastman Kodak Co., Rochester, NY, USA) were taken 1 day after implant placement, immediately before the second-stage surgery, immediately after prosthesis delivery, and 1 year after functional loading.
Selection of regions of interest and fractal analysis
The region of interest (ROI) was set to a width of 100 pixels and height of 200 pixels (1.0 mm×2.0 mm) at the first macrothread around the mesial and distal aspects of each implant. The ROIs avoided crestal bone, neighboring tooth roots and lamina dura, the sinus floor, and other structural entities. Because remodeling is pronounced in bone within 1 mm of an implant [26], the ROI was set to a width of 1.0 mm adjacent to the implant-bone interface.
Image processing was performed according to the method described in a previous study [27]. Briefly, the ROI was blurred using a Gaussian filter (sigma, 35 pixels; kernel size, 33×33). The heavily blurred image was then subtracted from the original, and 128 was added to the result at each pixel location. This generated an image with a mean grayscale value of 128, regardless of its initial intensity. The image was then made binary with a threshold brightness value of 128, and eroded and dilated once to reduce noise. The image of the trabeculae was then inverted and skeletonized. Fractal analysis was performed using the box-counting method. Using imaging software (Image J 1.43u; Wayne Rasband, National Institutes of Health, Bethesda, MD, USA), calibration was performed using the known distance of the spherical metal bearing (5.5 mm). Fractal dimensions were compared by using radiographs taken immediately after prosthesis delivery and those taken 1 year after functional loading (Fig. 1). Intraobserver agreement on ROI placement was assessed by re-evaluation of all of the images twice, with a 3-week interval between viewings.
Figure 1.
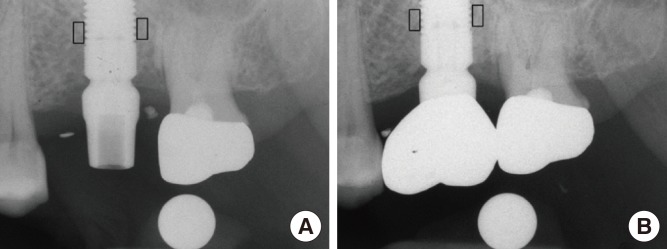
Regions of interest were selected on radiographs taken immediately after prosthesis delivery (A) and 1 year after loading (B).
Statistical analysis
The null hypothesis was that there would be no difference in the fractal dimension before and after implant loading. The D'Agostino-Pearson test was used to test the normality of distribution, which was rejected. Thus, the Wilcoxon signed-rank test was used to analyze differences in the fractal dimension before and after implant delivery. Computer software MedCalc ver. 11.2.1.0 (MedCalc, Ostend, Belgium) was used to process the data. The values were deemed statistically significant when P<0.05. The intraobserver agreement reliability was evaluated by calculating Cronbach alpha coefficients.
RESULTS
Clinical examination
All of the implants functioned normally, and no specific complication was found during the observation period. No subject complained of pain or implant mobility, and no inflammation was observed in any implant. The peri-implant soft tissues were found to be clinically healthy.
Fractal dimensions before and after occlusal loading
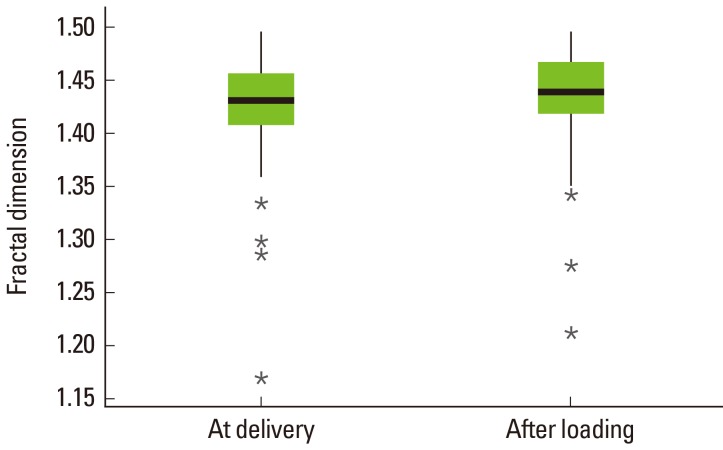
The Cronbach alpha value for inter-observer reliability was 0.8780. The mean fractal dimension was 1.4213±0.0525 before loading, and increased significantly to 1.4329±0.0479 at 12 months after loading (P<0.05) (Table 3, Fig. 2).
Table 3.
Fractal dimensions at the time of implant delivery and 12 months after loading.
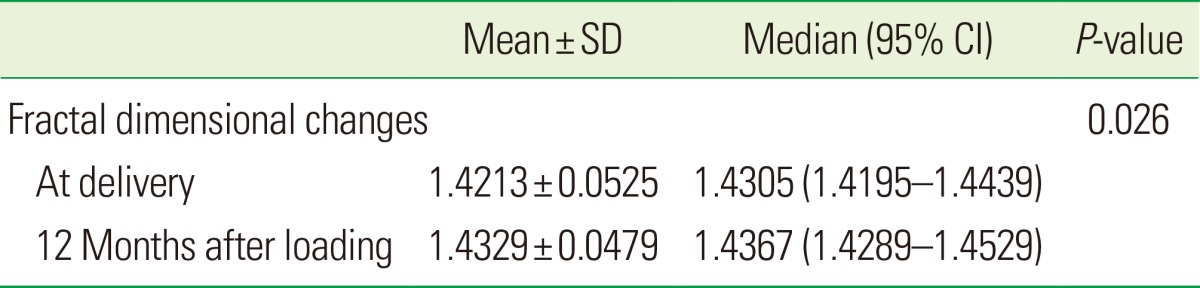
SD: standard deviation, CI: confidence interval.
Figure 2.
Change in fractal dimension.
DISCUSSION
Implants exposed to functional loading exhibit signs of bone remodeling, including the presence of bone multicellular units and a higher degree of bone-implant contact [7,28-30]. Mechanical loading also increases the bone volume fraction and trabecular thickness and content, and alters trabecular morphology [23]. The removal and addition of bone matrix by osteoclasts and osteoblasts may transform the trabecular architecture, which has been shown to be an important factor affecting the mechanical properties of bone and is highly correlated with bone strength [31,32].
Several studies have assessed the reliability of fractal dimension calculations from radiographs [15,33], finding that they are not sensitive to small alignment variations or over- or subexposure. Furthermore, ROI placement has been found to be more critical than ROI size [34]. In our study, we used standardized periapical radiographs and carefully placed ROIs to minimize the potential unknown effects of these factors.
The fractal dimension had increased significantly after 12 months of loading (P<0.05), suggesting an increase in the amount of bony microstructure around the implant [35]. Our findings are consistent with those of a similar study [13], which found an increased fractal dimension at 2 years after implant placement.
Jung [36] found no significant fractal dimension change in the first 6 months after implantation. However, that study used panoramic radiographs, which have a much lower resolution than periapical radiographs, which prevents the visualization of finer bony structures [37]. Moreover, the author provided no information about loading time because the study was focused on the healing process after implantation.
Not all of our data indicated that loading stress increased the fractal dimension. Three major factors affect the bony response around loaded dental implants: mechanical influence, implant design, and implant surface [38]. All of the implant fixtures (Astra Tech OsseoSpeed, Astra Tech Dental Implant System) used in the present study had the same surface treatment, implant-abutment interface (conical seal design; Astra Tech AB), and thread characteristics. Thus, external loading stress was the major factor influencing fractal dimensional change. Frost [39] hypothesized that bone modeling and remodeling would be initiated at a critical strain level; peak load magnitudes exceeding 2,500-3,500 microstrain led to new bone formation until the increased bone mass reduced strain, whereas disuse atrophy was proposed to occur at peak load magnitudes below 50-200 microstrain. Other investigators have reported similar findings but have proposed different thresholds. Melsen and Lang [24] found that loading significantly influenced the turnover and density of alveolar bone at magnitudes of 3,400-6,600 microstrain. In other words, the same amount of stress can result in different amounts of strain in bones with different mechanical properties. These factors may explain why some of our data showed decreased fractal dimensional values after loading. To date, the magnitude of force necessary to maintain a balance between disuse atrophy and overload resorption in a normal clinical environment has not been established.
Our study demonstrated that fractal analysis of alveolar bone can quantify the response of trabecular bone to functional loading. To achieve the common use of fractal analysis in routine clinical practice, a consensus must be reached about the most appropriate method of calculating fractal dimensions [40]. The limitation of this study was the short follow-up period, as the amount of peri-implant trabecular bone increases over a period longer than 12 months [13]. Further long-term studies are needed to evaluate the relationship between fractal dimension changes and functional loading.
In conclusion, the increased fractal dimension around implants after functional loading indicates an adaptive remodeling response of the surrounding bone. Fractal dimension analysis could be helpful in detecting changes in peri-implant alveolar trabecular bone patterns in clinical situations.
ACKNOWLEDGEMENTS
This study was supported by a faculty research grant from Yonsei University College of Dentistry (No. 6-2012-0071).
Footnotes
No potential conflict of interest relevant to this article was reported.
References
- 1.Matsunaga S, Shirakura Y, Ohashi T, Nakahara K, Tamatsu Y, Takano N, et al. Biomechanical role of peri-implant cancellous bone architecture. Int J Prosthodont. 2010;23:333–338. [PubMed] [Google Scholar]
- 2.Van Staden RC, Guan H, Loo YC. Application of the finite element method in dental implant research. Comput Methods Biomech Biomed Engin. 2006;9:257–270. doi: 10.1080/10255840600837074. [DOI] [PubMed] [Google Scholar]
- 3.Stanford CM, Brand RA. Toward an understanding of implant occlusion and strain adaptive bone modeling and remodeling. J Prosthet Dent. 1999;81:553–561. doi: 10.1016/s0022-3913(99)70209-x. [DOI] [PubMed] [Google Scholar]
- 4.Hoshaw SJ, Brunski JB, Cochran GV. Mechanical loading of Branemark implants affects interfacial bone modeling and remodeling. Int J Oral Maxillofac Implants. 1994;9:345–360. [Google Scholar]
- 5.Holmes DC, Loftus JT. Influence of bone quality on stress distribution for endosseous implants. J Oral Implantol. 1997;23:104–111. [PubMed] [Google Scholar]
- 6.Heitz-Mayfield LJ, Schmid B, Weigel C, Gerber S, Bosshardt DD, Jonsson J, et al. Does excessive occlusal load affect osseointegration? An experimental study in the dog. Clin Oral Implants Res. 2004;15:259–268. doi: 10.1111/j.1600-0501.2004.01019.x. [DOI] [PubMed] [Google Scholar]
- 7.Berglundh T, Abrahamsson I, Lindhe J. Bone reactions to longstanding functional load at implants: an experimental study in dogs. J Clin Periodontol. 2005;32:925–932. doi: 10.1111/j.1600-051X.2005.00747.x. [DOI] [PubMed] [Google Scholar]
- 8.Akesson L, Hakansson J, Rohlin M. Comparison of panoramic and intraoral radiography and pocket probing for the measurement of the marginal bone level. J Clin Periodontol. 1992;19:326–332. doi: 10.1111/j.1600-051x.1992.tb00654.x. [DOI] [PubMed] [Google Scholar]
- 9.Lang NP, Hill RW. Radiographs in periodontics. J Clin Periodontol. 1977;4:16–28. doi: 10.1111/j.1600-051x.1977.tb01879.x. [DOI] [PubMed] [Google Scholar]
- 10.Buckland-Wright JC, Lynch JA, Rymer J, Fogelman I. Fractal signature analysis of macroradiographs measures trabecular organization in lumbar vertebrae of postmenopausal women. Calcif Tissue Int. 1994;54:106–112. doi: 10.1007/BF00296060. [DOI] [PubMed] [Google Scholar]
- 11.Fazzalari NL, Parkinson IH. Fractal properties of cancellous bone of the iliac crest in vertebral crush fracture. Bone. 1998;23:53–57. doi: 10.1016/s8756-3282(98)00063-5. [DOI] [PubMed] [Google Scholar]
- 12.Caligiuri P, Giger ML, Favus M. Multifractal radiographic analysis of osteoporosis. Med Phys. 1994;21:503–508. doi: 10.1118/1.597390. [DOI] [PubMed] [Google Scholar]
- 13.Wilding RJ, Slabbert JC, Kathree H, Owen CP, Crombie K, Delport P. The use of fractal analysis to reveal remodelling in human alveolar bone following the placement of dental implants. Arch Oral Biol. 1995;40:61–72. doi: 10.1016/0003-9969(94)00138-2. [DOI] [PubMed] [Google Scholar]
- 14.Southard TE, Southard KA, Jakobsen JR, Hillis SL, Najim CA. Fractal dimension in radiographic analysis of alveolar process bone. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 1996;82:569–576. doi: 10.1016/s1079-2104(96)80205-8. [DOI] [PubMed] [Google Scholar]
- 15.Southard TE, Southard KA. Detection of simulated osteoporosis in maxillae using radiographic texture analysis. IEEE Trans Biomed Eng. 1996;43:123–132. doi: 10.1109/10.481981. [DOI] [PubMed] [Google Scholar]
- 16.Chen SK, Oviir T, Lin CH, Leu LJ, Cho BH, Hollender L. Digital imaging analysis with mathematical morphology and fractal dimension for evaluation of periapical lesions following endodontic treatment. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2005;100:467–472. doi: 10.1016/j.tripleo.2005.05.075. [DOI] [PubMed] [Google Scholar]
- 17.Shrout MK, Roberson B, Potter BJ, Mailhot JM, Hildebolt CF. A comparison of 2 patient populations using fractal analysis. J Periodontol. 1998;69:9–13. doi: 10.1902/jop.1998.69.1.9. [DOI] [PubMed] [Google Scholar]
- 18.Updike SX, Nowzari H. Fractal analysis of dental radiographs to detect periodontitis-induced trabecular changes. J Periodontal Res. 2008;43:658–664. doi: 10.1111/j.1600-0765.2007.01056.x. [DOI] [PubMed] [Google Scholar]
- 19.Law AN, Bollen AM, Chen SK. Detecting osteoporosis using dental radiographs: a comparison of four methods. J Am Dent Assoc. 1996;127:1734–1742. doi: 10.14219/jada.archive.1996.0134. [DOI] [PubMed] [Google Scholar]
- 20.Lee DH, Ku Y, Rhyu IC, Hong JU, Lee CW, Heo MS, et al. A clinical study of alveolar bone quality using the fractal dimension and the implant stability quotient. J Periodontal Implant Sci. 2010;40:19–24. doi: 10.5051/jpis.2010.40.1.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Veltri M, Ferrari M, Balleri P. Correlation of radiographic fractal analysis with implant insertion torque in a rabbit trabecular bone model. Int J Oral Maxillofac Implants. 2011;26:108–114. [PubMed] [Google Scholar]
- 22.Pauwels F. Biomechanics of the locomotor apparatus: contributions on the functional anatomy of the locomotor apparatus. New York: Springer-Verlag; 1980. [Google Scholar]
- 23.Roberts WE, Smith RK, Zilberman Y, Mozsary PG, Smith RS. Osseous adaptation to continuous loading of rigid endosseous implants. Am J Orthod. 1984;86:95–111. doi: 10.1016/0002-9416(84)90301-4. [DOI] [PubMed] [Google Scholar]
- 24.Melsen B, Lang NP. Biological reactions of alveolar bone to orthodontic loading of oral implants. Clin Oral Implants Res. 2001;12:144–152. doi: 10.1034/j.1600-0501.2001.012002144.x. [DOI] [PubMed] [Google Scholar]
- 25.Mombelli A, van Oosten MA, Schurch E, Jr, Land NP. The microbiota associated with successful or failing osseointegrated titanium implants. Oral Microbiol Immunol. 1987;2:145–151. doi: 10.1111/j.1399-302x.1987.tb00298.x. [DOI] [PubMed] [Google Scholar]
- 26.Garetto LP, Chen J, Parr JA, Roberts WE. Remodeling dynamics of bone supporting rigidly fixed titanium implants: a histomorphometric comparison in four species including humans. Implant Dent. 1995;4:235–243. doi: 10.1097/00008505-199500440-00002. [DOI] [PubMed] [Google Scholar]
- 27.White SC, Rudolph DJ. Alterations of the trabecular pattern of the jaws in patients with osteoporosis. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 1999;88:628–635. doi: 10.1016/s1079-2104(99)70097-1. [DOI] [PubMed] [Google Scholar]
- 28.Ogiso M, Tabata T, Kuo PT, Borgese D. A histologic comparison of the functional loading capacity of an occluded dense apatite implant and the natural dentition. J Prosthet Dent. 1994;71:581–588. doi: 10.1016/0022-3913(94)90441-3. [DOI] [PubMed] [Google Scholar]
- 29.Piattelli A, Corigliano M, Scarano A, Costigliola G, Paolantonio M. Immediate loading of titanium plasma-sprayed implants: an histologic analysis in monkeys. J Periodontol. 1998;69:321–327. doi: 10.1902/jop.1998.69.3.321. [DOI] [PubMed] [Google Scholar]
- 30.Gotfredsen K, Berglundh T, Lindhe J. Bone reactions adjacent to titanium implants subjected to static load. A study in the dog (I) Clin Oral Implants Res. 2001;12:1–8. doi: 10.1034/j.1600-0501.2001.012001001.x. [DOI] [PubMed] [Google Scholar]
- 31.Kinney JH, Ladd AJ. The relationship between three-dimensional connectivity and the elastic properties of trabecular bone. J Bone Miner Res. 1998;13:839–845. doi: 10.1359/jbmr.1998.13.5.839. [DOI] [PubMed] [Google Scholar]
- 32.Majumdar S, Kothari M, Augat P, Newitt DC, Link TM, Lin JC, et al. High-resolution magnetic resonance imaging: three-dimensional trabecular bone architecture and biomechanical properties. Bone. 1998;22:445–454. doi: 10.1016/s8756-3282(98)00030-1. [DOI] [PubMed] [Google Scholar]
- 33.Chen SK, Chen CM. The effects of projection geometry and trabecular texture on estimated fractal dimensions in two alveolar bone models. Dentomaxillofac Radiol. 1998;27:270–274. doi: 10.1038/sj/dmfr/4600361. [DOI] [PubMed] [Google Scholar]
- 34.Jolley L, Majumdar S, Kapila S. Technical factors in fractal analysis of periapical radiographs. Dentomaxillofac Radiol. 2006;35:393–397. doi: 10.1259/dmfr/30969642. [DOI] [PubMed] [Google Scholar]
- 35.Southard TE, Southard KA, Lee A. Alveolar process fractal dimension and postcranial bone density. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 2001;91:486–491. doi: 10.1067/moe.2001.112598. [DOI] [PubMed] [Google Scholar]
- 36.Jung YH. Evaluation of peri-implant bone using fractal analysis. Korean J Oral Maxillofac Radiol. 2005;35:121–125. [Google Scholar]
- 37.Bollen AM, Taguchi A, Hujoel PP, Hollender LG. Fractal dimension on dental radiographs. Dentomaxillofac Radiol. 2001;30:270–275. doi: 10.1038/sj/dmfr/4600630. [DOI] [PubMed] [Google Scholar]
- 38.Bianchi AE, Dolci G, Jr, Sberna MT, Sanfilippo S. Factors affecting bone response around loaded titanium dental implants: a literature review. J Appl Biomater Biomech. 2005;3:135–140. [PubMed] [Google Scholar]
- 39.Frost HM. Bone "mass" and the "mechanostat": a proposal. Anat Rec. 1987;219:1–9. doi: 10.1002/ar.1092190104. [DOI] [PubMed] [Google Scholar]
- 40.Geraets WG, van der Stelt PF. Fractal properties of bone. Dentomaxillofac Radiol. 2000;29:144–153. doi: 10.1038/sj/dmfr/4600524. [DOI] [PubMed] [Google Scholar]