Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Nov 13;3:3206. doi: 10.1038/srep03206

Ultrafast biexciton spectroscopy in semiconductor quantum dots: evidence for early emergence of multiple-exciton generation

Younghwan Choi 1, Sangwan Sim 1, Seong Chu Lim 2,3, Young Hee Lee 2,3,a, Hyunyong Choi 1,b
PMCID: PMC3826098  PMID: 24220495

Abstract

Understanding multiple-exciton generation (MEG) in quantum dots (QDs) requires in-depth measurements of transient exciton dynamics. Because MEG typically faces competing ultrafast energy-loss intra-band relaxation, it is of central importance to investigate the emerging time-scale of the MEG kinetics. Here, we present ultrafast spectroscopic measurements of the MEG in PbS QDs via probing the ground-state biexciton transients. Specifically, we directly compare the biexciton spectra with the single-exciton ones before and after the intra-band relaxation. Early emergence of MEG is evidenced by observing transient Stark shift and quasi-instantaneous linewidth broadening, both of which take place before the intra-band relaxation. Photon-density-dependent study shows that the broadened biexciton linewidth strongly depends on the MEG-induced extra-exciton generation. Long after the intra-band relaxation, the biexciton broadening is small and the single-exciton state filling is dominant.

The limiting factor for improving solar-cell efficiency lies in the simple physics that single-photon absorption generates one electron-hole pair1. The possibility of generating multiple charge carriers per photon, known as carrier multiplication (CM) or multiple exciton generation (MEG), is of crucial importance for developing efficient solar-cell devices2,3,4,5,6,7,8. Semiconductor quantum dots (QDs) represent well-defined structures to explore the quantum limit of harnessing solar-conversion efficiency9,10,11,12,13. By engineering the sizes of QD composites, it has been demonstrated that not only the optical properties14,15, but also the MEG efficiency in QDs can be modified16. MEG in a photo-excited QD system is a prominent route for enhancing the conversion efficiency because carriers confined in spatial dimensions that are smaller than the bulk exciton Bohr radius lead to the formation of discrete excitonic states such that efficient MEG is possible either by suppressing the ultrafast electron-phonon relaxation4,17,18 or by enhancing the Coulomb interactions via reduced dielectric screening at the QD surface19.

Numerous investigations have shown that the kinetic origin of MEG dynamics in QDs is intrinsically complex because the photo-generated single exciton initially suffers from extremely fast intra-band relaxation20,21,22, whose interaction time-scale is typically in the range of a few ps6. To enhance the MEG efficiency, it is desirable to circumvent the ultrafast energy-loss intra-band process23,24. Recent studies suggest that the MEG is an instantaneous phenomenon occurring before the intra-band energy relaxation25 via virtual single excitonic26 or biexcitonic optical transition27 or coherent superposition among multi-exciton states12. Other investigation suggests that the intra-band relaxation rate competes with the MEG formation rate6.

The above mentioned photo-physical complexity of MEG is largely due to the nature of intrinsic multi-particle (or multi-exciton) interaction28. When more than two excitons are created under high-energy excitation condition, the lowest lying energy state is not the single exciton; the mutual interaction between two excitons results in the formation of a Coulomb-correlated two excitonic state, called biexciton29,30,31,32,33. The biexciton is energetically more stable than the single exciton such that it exists below the single-exciton state32,34. Recent studies have reported that the final biexciton density strongly influences the solar-conversion efficiency25,26,35. Although it is important to study the impact of the MEG on the transient biexciton spectra, no experimental investigations have been provided to compare the MEG-induced biexciton dynamics with the intra-band relaxation dynamics.

The key experimental observation in this study is that the optically-induced MEG is an extremely fast process, arising before the intra-band relaxation. By exploring the lowest observable biexciton dynamics, we directly measure that the biexciton bleaching comes from early emergence of the photo-induced MEG, in which the effect of extra-exciton generation is manifested by the increased broadening of the biexciton linewidth via multi-exciton interaction. Note that, in contrast to the conventional single-exciton MEG spectroscopy11,36,37,38,39, our ultrafast time-resolved experiments were performed both in the MEG and in the non-MEG regimes via photon-energy and density-controlled measurements on the single- and biexciton spectra.

Results

Single-exciton MEG dynamics

Figure 1a shows data for the broadband optical absorption of the colloidal semiconductor PbS QDs and Fig. 1b shows a schematic for the ultrafast pump-probe measurements (See method for the detailed description of sample preparation and ultrafast spectroscopy). The lowest single-exciton bandgap energy Ex is identified as 0.93 ± 0.01 eV, and the ground-state biexciton energy Exx is estimated to be 0.87 ± 0.03 eV30,31,32,33.

Figure 1. QD absorption spectra and experimental setup.

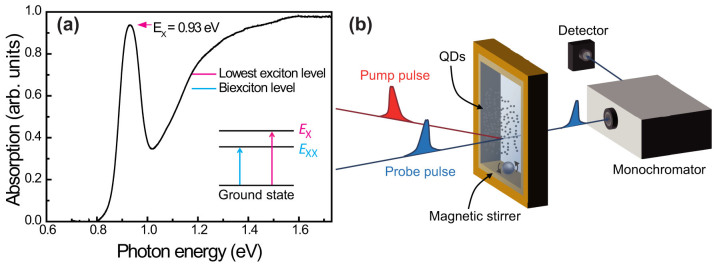
Figure 1

Open in a new tab

(a) Linear absorption spectra of the colloidal PbS QDs used in the study. Inset: schematic energy levels for the single-exciton Ex and the ground-state biexciton Exx, respectively. (b) Schematic for the ultrafast pump-probe measurements. For the spectrally-resolved measurements, the probe pulse is scanned through a monochromator (Newport 74125 Oriel Cornerstone 260 1/4 m) at each Δt. The measured FWHM of the pump and probe beam are 150 μm and 100 μm, respectively. All measurements are performed at room temperature.

Before the discussion on the biexciton dynamic, it is instructive to present detailed measurements on the intra-band relaxation dynamics because the linewidth broadening of single excitons and biexcitons is necessary related to the competing relaxation rate between the MEG and the intra-band dynamics, in which the time scale of the intra-band relaxation is typically a few ps16,40,41, comparable with the MEG time scale. In the experiment, the colloidal semiconductor PbS QD sample was pumped by two different pump-photon energy Epump with 1.55 eV and 3.10 eV, and the average number of initially photo-generated excitons per QD 〈N0〉, or initial exciton occupancy, was controlled from 0.1 to 2.2 to investigate the photon density-dependent Ex dynamics.

In order to determine the intra-band relaxation rate, we measured the Ex dynamics in a short Δt range between −1 ps and 7 ps as shown in Figs. 2a and b. By examining the rising edge of the Ex peak, we show that the relaxation process is completed at pump-probe delay Δt = 1 ps for 1.66Ex excitation (non-MEG regime) and Δt = 2 ps for 3.3Ex excitation (MEG regime). This 2 ps time constant is consistent with prior experimental studies of hot-carrier MEG dynamics in PbS quantum dots, where the reported value of intra-band relaxation is in the range of 2–2.5 ps16,40,41.

Figure 2. Single-exciton MEG dynamics.

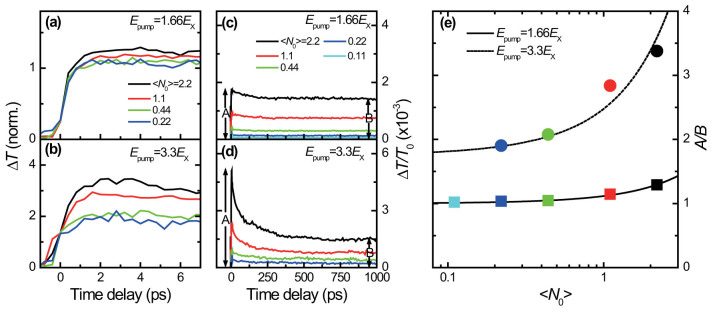
Figure 2

Open in a new tab

Single-exciton dynamics in a short pump-probe range between −1 and 7 ps for 1.66Ex (a) and 3.3Ex excitations (b). The differential transmission signals probed at Ex with the 1.66Ex pump (c) and the 3.3Ex pump (d) are displayed with 〈N0〉 ranging from 0.11 to 2.2. Here, 〈N0〉 is estimated via 〈N0〉 = jpσa, where jp is the pump fluence in unit of photons per cm2 and σa is the absorption cross-section in unit of cm2 14. (c) The experimentally measured A/B ratio is shown for the 1.66Ex pump (filled circle) and for the 3.3Ex pump (filled square). The calculated A/B ratio is obtained via Poisson distribution of the QD occupancies for the 1.66Ex pump (solid line) and for the 3.3Ex pump (dashed line).

Figure 2c shows the Ex transients excited by low Epump ( = 1.66Ex). The observed step-like signals with a small A/B ratio (amplitude ratio of the early to late pump-probe delay Δt) are not attributed to the MEG transients, because the MEG typically requires Epump greater than a few Ex. When the QDs are excited by high Epump ( = 3.3Ex), we observed fast (90 ps) and slow decay (~100 ns) components with a large A/B ratio, as depicted in Fig. 2d. The experimentally determined A/B ratio of the QD occupancy was modelled via Poisson statistics (Fig. 2e)42. Since multiple excitons generated by the MEG decay via Auger recombination, the amplitude at long Δt (denoted by B in Fig. 2c and d) provides a scaling factor for calculating the exciton multiplicity 〈Nx〉 = A/B, where A is the amplitude of single-exciton population immediately after pump excitation (denoted by A in Fig. 2c and d). By comparing the measured A/B ratios in the limit of 〈N0〉 → 0, a strong indication of the MEG for the 3.3Ex pump was identified43. As reported previously16,36,38,40,44, these observations confirm that the typical MEG dynamics are observable via probing the Ex dynamics.

Transient Stark shift and biexciton linewidth broadening

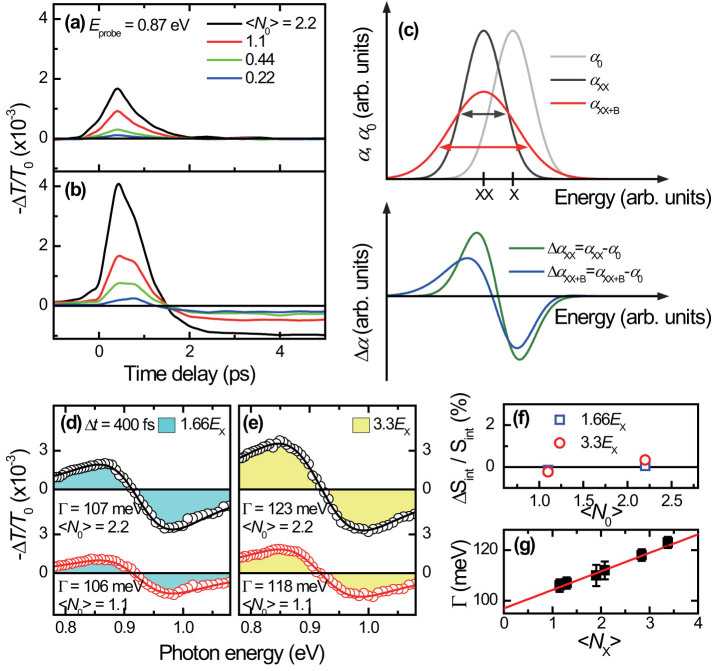
The central issue to address in this paper is to investigate how the biexciton dynamics is influenced by the early formation of MEG. Figures 3a and b display the biexciton transients for the 1.66Ex pump and 3.3Ex pump as a function of Δt with controlled excitations from 〈N0〉 = 0.22 to 〈N0〉 = 2.2. Immediately after pump excitation, the photo-induced absorption (PA) exhibits rapid bleaching at Exx within the first Δt = 400 fs with a much larger PA peak for the 3.3Ex pump than the 1.66Ex pump. While both signals decay non-exponentially, the signals pumped by 1.66Ex decay to zero after a few ps, and the transients pumped by 3.3Ex change their signs from positive to negative near Δt = 2 ps.

Figure 3. Ultrafast MEG-induced biexciton transients before the intra-band relaxation.

Figure 3

Open in a new tab

Transient Exx dynamics are shown as a function of Δt for the 1.66Ex pump (a) and for the 3.3Ex pump (b) with various 〈N0〉. (c) Schematic illustration of the PA caused by the transient Stark shift of the single-exciton absorption (black line) and the corresponding photo-induced biexciton broadening (red line). The gray line indicates the single-exciton absorption without the pump. The differential PA spectra exhibit an energy-shifted broader feature (blue line) due to the MEG-induced exciton scattering compared to the case of no MEG (green line). The spectrally-resolved PA spectra with the probe range from 0.78 to 1.08 eV measured at Δt = 400 fs are shown for the 1.66Ex pump (d) and for the 3.3Ex pump (e) with two different 〈N0〉. Solid lines represent numerical fits using equation (1). The obtained biexciton Γ for the 1.66Ex pump with 〈N0〉 = 1.1 and 2.2 are 106 meV and 107 meV, respectively, and those for the 3.3Ex pump with 〈N0〉 = 1.1 and 2.2 are 118 meV and 123 meV, respectively. (f) Spectrally integrated areas of the broadened biexciton absorption. (g) The biexciton Γ broadening linearly increases with increasing the total number of excitons. The experimentally determined Γ (black filled squares) from the Figs. 3d and e are compared to the equation (2).

In a strong quantum-confinement regime, the pump-created local electric field induces a large transient shift of absorption, a phenomenon known as transient Stark shift42,45. This effect is more considerable with increasing photo-generated carriers, which in turn produces a stronger local field and complicates the ultrafast PA spectra as schematically shown in Fig. 3c. Note that the increased carrier density is reflected both by the carrier-induced Stark shift and by the absorption linewidth Γ that leads to a broader feature46,47. As discussed later, this broadened Γ directly determines the effect of MEG on the biexciton dynamics through extra-exciton generation.

It is expected that high Epump excitation, larger than Ex, enhances the Γ broadening due to the extra-exciton generation. Immediately after the pump (Δt = 400 fs), we clearly observe that the biexciton Γ is broader for the 3.3Ex excitation case than for the 1.66Ex one, as shown in Figs. 3d and e with two different excitations of 〈N0〉 for each Epump excitation. Thus, the observed transient PA dynamics can be understood by combined effects of both the carrier-induced transient Stark shift and the MEG-induced biexciton Γ broadening. We additionally notice that the spectrally-integrated areas of the broadened biexciton absorption remain the same regardless of 〈N0〉 as shown Fig. 3f. This constraint indicates that the broadening is determined by the number of excitons, and it ensures that the biexciton PA peak is reduced by the exciton-exciton collision-induced broadening rather than the phase-space filling argument46.

Quantitative analysis of the MEG-induced biexciton broadening and the early emergence of MEG

The entire pump-induced changes of the absorption spectra can be faithfully fit via the following third-order susceptibility function31,33,

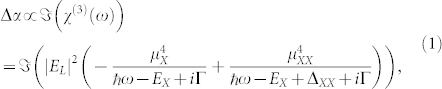graphic file with name srep03206-m1.jpg

where EL is the electric field of the pump, ΔXX is the biexciton binding energy, and μX and μXX are the transition dipole moments from the ground state to Ex and to Exx, respectively. The first term represents the bleaching at Ex and the second term represents the PA at ground-state Exx. For the PA dynamics measured at Δt = 400 fs (Figs. 3d and e), because the intra-band relaxation time (2 ps) is longer than Δt of 400 fs, the absorption change measured at Ex was not induced by the single-exciton state filling. In addition, Auger recombination and impact ionization (Auger processes) can be neglected because the time-scale of Auger processes is much slower (100 ~ 200 ps) than the intra-band relaxation. On the other hand, the difference in Γ, obtained from a fit of equation (1) to the measured PA spectra, shows that the broadening is associated with the MEG-induced biexciton broadening.

For quantitative analysis, the biexciton Γ is plotted as a function of the average number of total excitons per QD 〈Nx〉, and the results are displayed in Fig. 3g. Here, we note that the definition of 〈Nx〉 (obtained from the measured A/B ratios in Fig. 2c) differs from that of 〈N0〉 in a sense that 〈Nx〉 includes both the average number of initially photo-generated excitons and the MEG-induced excitons per QD; 〈N0〉 is the average number of photo-generated exciton per QD11. In other words, the biexciton broadening is directly related to the total number of excitons 〈Nx〉, not by the initial exciton occupancy 〈N0〉. By plotting the Γ as a function of 〈Nx〉, we obtain a linear relationship of

graphic file with name srep03206-m2.jpg

where γ ( = 6.8 meV per exciton) is the Γ broadening parameter per exciton. Because Γ(0) represents the linewidth broadening in the absence of photo-generated excitons, the value should corresponds to the Ex broadening in Fig. 1a. A simple Gaussian fit shows that the Ex broadening in Fig. 1a is 100 ± 5 meV, well corroborated with the fitted Γ(0) = 98 meV of the biexciton broadening. The characteristic broadening of Γ with increasing 〈Nx〉 entails the effect of MEG, i.e. as more excitons are injected, more broaden feature of biexciton Γ is expected.

Discussion

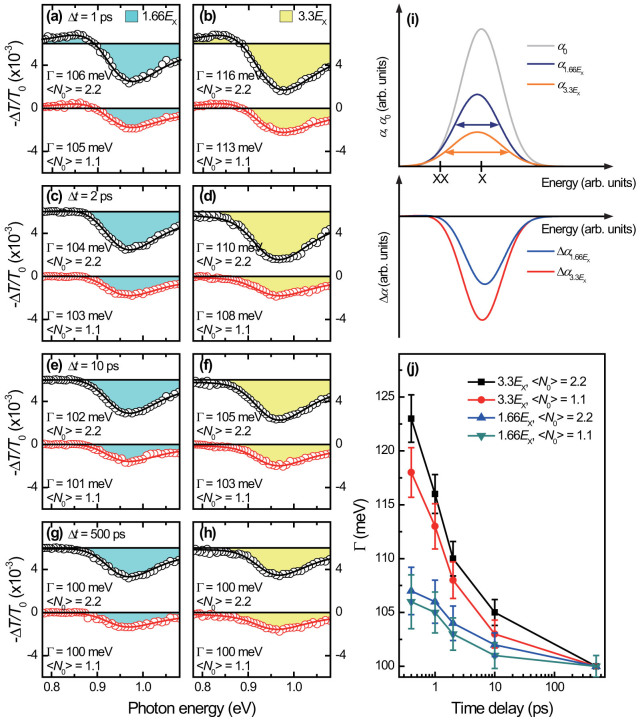
The early emergence of the MEG is substantiated by measuring the single- and biexciton spectra before/after the intra-band relaxation of 2 ps. It is expected that Γ should be large if Δt is shorter than the intra-band relaxation time, i.e. if the MEG-induces exciton-exciton scattering occurs earlier than the intra-band relaxation, Γ before the intra-band relaxation is larger than Γ after intra-band relaxation. Figures 4 (a) and (b) show the PA signals at Δt = 1 ps. As expected, the Γ broadening at Δt = 1 ps is smaller than at Δt = 400 fs, but larger than at Δt = 2 ps. Figures 4c and d show the spectra at Δt = 2 ps for the 1.66Ex pump and for the 3.3Ex pump, respectively. The Γ at 2 ps for 3.3Ex with 〈N0〉 = 2.2 is 110 meV while the Γ at Δt = 400 fs with same condition is 123 meV. Indeed, we clearly see that Γ at Δt = 2 ps is smaller than that of before intra-band relaxation both for the two 〈N0〉 excitations (see Fig. 3e and Figs. 4b and d).

Figure 4. Biexciton broadening at longer delays than 400 fs.

Figure 4

Open in a new tab

The single- and biexciton absorption change spectra at Δt of 1 ps (a,b), 2 ps (c,d), 10 ps (e,f) and 500 ps (g,h) with two Epump. (i) Schematic illustration of the PA bleaching dynamics at longer Δt > 2 ps for the 1.66Ex pump (blue line) and for the 3.3Ex pump (orange line). (j) Transient Γ broadening is shown as function of Δt.

Long after the intra-band relaxation finishes, the carrier-induced Stark shift becomes weak, and the single-exciton state filling is dominant (Figs. 4e–h). As schematically shown in Fig. 4i, the weak Stark shift is rendered as the absence of PA signals at 0.85 eV, but the effect is not completely vanished; negative PA peaks appear at 0.97 eV instead of the single-exciton energy of 0.93 eV in Fig. 1a. Because the PA peak is proportional to the generated exciton numbers, the magnitude of bleaching is larger for the case of 3.3Ex pump than the 1.66Ex pump case. We note that the chosen two Epump (1.66Ex and 3.3Ex) set the below and upper limit on the occurrence of MEG such that the observed two dynamics (before and after the intra-band relaxation) are distinguishable in comparing the MEG-induced biexciton lineshape and the single-exciton-dominated one. There is a possibility that significant re-shaping of single-exciton spectra can be observed at longer Δt, which may occur when as many as 50% of QDs are occupied by multiple electron-hole pairs (i.e. 〈N0〉 < 1). This scenario can be excluded in our investigation because the PA peaks at Δt = 2 ps show negligible energy shifts48 even when 〈N0〉 > 1.

To investigate the effect of Auger and single-exciton recombination on Γ, we compare the PA spectra at Δt of 10 ps and 500 ps. We noted that the single-exciton decay dynamics consists of two relaxation components (see Figs. 2c and d): one is “fast” Auger recombination (known as biexcitonic relaxation component6) and another is “slow” single-exciton recombination (referred to as excitonic background6). Figures 4e and f display the PA spectra at Δt = 10 ps. Because the Auger recombination is not completed, Γ at Δt = 10 ps is smaller than Γ at Δt = 2 ps. After the Auger recombination is finished, 〈Nx〉 at Δt = 500 ps approaches one both for the 1.66Ex and 3.3Ex pump cases. Because nearly one exciton is left at Δt = 500 ps, Γ for both Epump (Figs. 4g and h) is identical with Γ of 100 meV, representing negligible effect of single-exciton recombination on Γ.

The measured data are summarized in Fig. 4j. Two main aspects are addressed. First, Γ at Δt = 400 fs is the largest compared to the Γ at Δt > 400 fs, providing an evidence for the large biexciton Γ broadening in early Δt. Second, by observing the fact that the decreasing slope of Γ with Δt for 3.33Ex excitation is steeper than the 1.66Ex excitation up to Δt = 2 ps, we can find that the effect of MEG on Γ is strongly influenced by extra-exciton generation before the intra-band relaxation.

To conclude, we have investigated the transient dynamics of biexciton, located below the single-exciton energy, and have explored the impact of MEG on the biexciton spectra. Our ultrafast spectroscopy shows that the linewidth broadening of the biexciton spectra provides direct evidence on the early emergence of the MEG compared to the intra-band relaxation time. We additionally have presented quantitative analysis that the broadening parameter Γ per exciton increases linearly with increasing the total number of excitons. For detailed time-resolved spectral analysis, the PA spectra are compared with single-exciton ones at Δt = 400 fs and longer delays. The comparison underscores that Γ broadening before Δt = 2 ps is larger than the Γ after Δt = 2 ps, corroborating that the MEG indeed occurs before the intra-band relaxation.

Methods

Synthesis of PbS quantum dots

Our PbS colloidal quantum dots are capped using eleic acid and dispersed in toluene. The synthesis of the sample followed a procedure that used standard air-free solution based technique49. In a typical synthesis, 2.0 mmol of PbO (0.445 g), 8.0 mmol (2.25 g) of oleic acid (OA), and 9.9 mmol (2.5 g) of 1-octadecene (ODE) are placed in a flask and heated to 100°C under vacuum, and then nitrogen was introduced. The temperature was controlled to the appropriate injection temperature (100 to 150°C) to obtain the desired particle size. The sulfur precursor was prepared by mixing bis(trimethylsilyl)sulfide with ODE. Removal of excess ligand was completed by repeated the followings: precipitation in acetone, centrifugation of the particles, and dispersion in toluene.

PbS QDs and ultrafast spectroscopy

The sample used in this experiment is semiconductor colloidal PbS QDs dispersed in toluene with an average diameter of approximately 5.1 nm. The broadband optical absorption is measured by a Fourier transform infrared (FTIR) spectrometer (Bomem DA8). For the ultrafast pump-probe spectroscopy, the colloidal PbS QDs are maintained in a 3-mm cell contained in the toluene liquid with two optically-transparent MgO windows, and the samples are actively stirred using a magnetic stirrer to ensure that photo-charging does not occur during the measurements (Fig. 1b)50. Using a 250 kHz Ti-sapphire regenerative amplifier (Coherent RegA 9050), the samples are excited by 50 fs pulses with a pump-photon energy Epump of 1.55 eV and its second harmonic Epump of 3.10 eV for investigating the MEG photo-dynamics. A fraction of the amplifier output is used as a probe pulse with photon energy Eprobe of 0.93 eV for the lowest Ex and 0.87 eV for the Exx. Both probe pulses are delivered from wavelength-tunable optical parametric amplifier (Coherent OPA 9850).

Author Contributions

H.C. and Y.H.L. developed the original experimental ideas. Y.C. and S.S. performed the ultrafast pump-probe measurements. Y.C. and S.C.L. prepared the colloidal QD samples and analyzed the data. The manuscript was written through contributions of all authors.

Acknowledgments

The work at Yonsei was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (NRF-2011-0013255, NRF-2011-220-D00052, NRF-2011-0028594, NRF-2009-0083512, NRF-2012R1A1A2043180) and the LG Display Academic Industrial Cooperation Program. S. C. Lim and Y. H. Lee at SKKU are grateful for the support by Institute for Basic Science (grant number EM 1304).

References

  1. Shockley W. & Queisser H. J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 32, 510–519 (1961). [Google Scholar]
  2. Yu G., Gao J., Hummelen J. C., Wudl F. & Heeger A. J. Polymer Photovoltaic Cells: Enhanced Efficiencies via a Network of Internal Donor-Acceptor Heterojunctions. Science 270, 1789–1791 (1995). [Google Scholar]
  3. Semonin O. E. et al. Peak external photocurrent quantum efficiency exceeding 100% via MEG in a quantum dot solar cell. Science 334, 1530–1533 (2011). [DOI] [PubMed] [Google Scholar]
  4. Trinh M. T. et al. Direct generation of multiple excitons in adjacent silicon nanocrystals revealed by induced absorption. Nat. Photonics 6, 316–321 (2012). [Google Scholar]
  5. Timmerman D., Valenta J., Dohnalová K., de Boer W. D. A. M. & Gregorkiewicz T. Step-like enhancement of luminescence quantum yield of silicon nanocrystals. Nat. Nanotechnol. 6, 710–713 (2011). [DOI] [PubMed] [Google Scholar]
  6. Schaller R. D. & Klimov V. I. High Efficiency Carrier Multiplication in PbSe Nanocrystals: Implications for Solar Energy Conversion. Phys. Rev. Lett. 92, 186601 (2004). [DOI] [PubMed] [Google Scholar]
  7. Nozik A. J. Multiple exciton generation in semiconductor quantum dots. Chem. Phys. Lett. 457, 3–11 (2008). [DOI] [PubMed] [Google Scholar]
  8. Wolf M., Brendel R., Werner J. H. & Queisser H. J. Solar cell efficiency and carrier multiplication in Si1-xGex alloys. J. Appl. Phys. 83, 4213–4221 (1998). [Google Scholar]
  9. De Boer W. D. A. M. et al. Red spectral shift and enhanced quantum efficiency in phonon-free photoluminescence from silicon nanocrystals. Nat. Nanotechnol. 5, 878–884 (2010). [DOI] [PubMed] [Google Scholar]
  10. Unold T., Mueller K., Lienau C., Elsaesser T. & Wieck A. Optical Control of Excitons in a Pair of Quantum Dots Coupled by the Dipole-Dipole Interaction. Phys. Rev. Lett. 94, 137404 (2005). [DOI] [PubMed] [Google Scholar]
  11. Schaller R. D., Sykora M., Pietryga J. M. & Klimov V. I. Seven excitons at a cost of one: redefining the limits for conversion efficiency of photons into charge carriers. Nano Lett. 6, 424–429 (2006). [DOI] [PubMed] [Google Scholar]
  12. Ellingson R. J. et al. Highly efficient multiple exciton generation in colloidal PbSe and PbS quantum dots. Nano Lett. 5, 865–871 (2005). [DOI] [PubMed] [Google Scholar]
  13. Nozik A. J. Exciton multiplication and relaxation dynamics in quantum dots: applications to ultrahigh-efficiency solar photon conversion. Inorg. Chem. 44, 6893–6899 (2005). [DOI] [PubMed] [Google Scholar]
  14. Moreels I. et al. Size-dependent optical properties of colloidal PbS quantum dots. ACS Nano 3, 3023–3030 (2009). [DOI] [PubMed] [Google Scholar]
  15. Korkusinski M., Voznyy O. & Hawrylak P. Fine structure and size dependence of exciton and biexciton optical spectra in CdSe nanocrystals. Phys. Rev. B 82, 245304 (2010). [Google Scholar]
  16. Nootz G. et al. Size dependence of carrier dynamics and carrier multiplication in PbS quantum dots. Phys. Rev. B 83, 155302 (2011). [Google Scholar]
  17. Timmerman D., Izeddin I., Stallinga P., Yassievich I. N. & Gregorkiewicz T. Space-separated quantum cutting with silicon nanocrystals for photovoltaic applications. Nat. Photonics 2, 105–109 (2008). [Google Scholar]
  18. Nozik A. J. Nanoscience and nanostructures for photovoltaics and solar fuels. Nano Lett. 10, 2735–2741 (2010). [DOI] [PubMed] [Google Scholar]
  19. Klimov V. I. Spectral and dynamical properties of multiexcitons in semiconductor nanocrystals. Annu. Rev. Phys. Chem. 58, 635–73 (2007). [DOI] [PubMed] [Google Scholar]
  20. Sosnowski T. S. et al. Rapid carrier relaxation in In0.4Ga0.6As/GaAs quantum dots characterized by differential transmission spectroscopy. Phys. Rev. B 57, R9423–R9426 (1998). [Google Scholar]
  21. Nair G., Chang L.-Y., Geyer S. M. & Bawendi M. G. Perspective on the prospects of a carrier multiplication nanocrystal solar cell. Nano Lett. 11, 2145–2151 (2011). [DOI] [PubMed] [Google Scholar]
  22. Kambhampati P. Hot Exciton Relaxation Dynamics in Semiconductor Quantum Dots: Radiationless Transitions on the Nanoscale. J. Phys. Chem. C 115, 22089–22109 (2011). [Google Scholar]
  23. Urayama J., Norris T., Singh J. & Bhattacharya P. Observation of Phonon Bottleneck in Quantum Dot Electronic Relaxation. Phys. Rev. Lett. 86, 4930–4933 (2001). [DOI] [PubMed] [Google Scholar]
  24. Miaja-Avila L. et al. Direct mapping of hot-electron relaxation and multiplication dynamics in PbSe quantum dots. Nano Lett. 12, 1588–1591 (2012). [DOI] [PubMed] [Google Scholar]
  25. Franceschetti A., An J. M. & Zunger A. Impact ionization can explain carrier multiplication in PbSe quantum dots. Nano Lett. 6, 2191–2195 (2006). [DOI] [PubMed] [Google Scholar]
  26. Schaller R. D., Agranovich V. M. & Klimov V. I. High-efficiency carrier multiplication through direct photogeneration of multi-excitons via virtual single-exciton states. Nat. Phys. 1, 189–194 (2005). [Google Scholar]
  27. Rupasov V. & Klimov V. I. Carrier multiplication in semiconductor nanocrystals via intraband optical transitions involving virtual biexciton states. Phys. Rev. B 76, 125321 (2007). [Google Scholar]
  28. Klimov V., Hunsche S. & Kurz H. Biexciton effects in femtosecond nonlinear transmission of semiconductor quantum dots. Phys. Rev. B 50, 8110–8113 (1994). [DOI] [PubMed] [Google Scholar]
  29. Kim K., Norris T. B. & Hohenester U. Redshift of the excited state due to a nondegenerate biexciton in self-organized quantum dots. J. Appl. Phys. 103, 113702 (2008). [Google Scholar]
  30. Hu Y., Koch S. & Lindberg M. Biexcitons in semiconductor quantum dots. Phys. Rev. Lett. 64, 1805–1807 (1990). [DOI] [PubMed] [Google Scholar]
  31. Banyai L., Hu Y., Lindberg M. & Koch S. Third-order optical nonlinearities in semiconductor microstructures. Phys. Rev. B 38, 8142–8153 (1988). [DOI] [PubMed] [Google Scholar]
  32. Banyai L. Asymptotic biexciton “binding energy” in quantum dots. Phys. Rev. B 39, 8022–8024 (1989). [DOI] [PubMed] [Google Scholar]
  33. Hu Y., Lindberg M. & Koch S. Theory of optically excited intrinsic semiconductor quantum dots. Phys. Rev. B 42, 1713–1723 (1990). [DOI] [PubMed] [Google Scholar]
  34. Sewall S., Franceschetti A., Cooney R., Zunger A. & Kambhampati P. Direct observation of the structure of band-edge biexcitons in colloidal semiconductor CdSe quantum dots. Phys. Rev. B 80, 081310 (2009). [Google Scholar]
  35. Shabaev A., Efros A. L. & Nozik A. J. Multiexciton generation by a single photon in nanocrystals. Nano Lett. 6, 2856–63 (2006). [DOI] [PubMed] [Google Scholar]
  36. Stewart J. T. et al. Comparison of carrier multiplication yields in PbS and PbSe nanocrystals: the role of competing energy-loss processes. Nano Lett. 12, 622–628 (2012). [DOI] [PubMed] [Google Scholar]
  37. Nair G., Geyer S., Chang L.-Y. & Bawendi M. Carrier multiplication yields in PbS and PbSe nanocrystals measured by transient photoluminescence. Phys. Rev. B 78, 125325 (2008). [Google Scholar]
  38. Beard M. C. et al. Multiple exciton generation in colloidal silicon nanocrystals. Nano Lett. 7, 2506–2512 (2007). [DOI] [PubMed] [Google Scholar]
  39. Schaller R. D., Pietryga J. M. & Klimov V. I. Carrier multiplication in InAs nanocrystal quantum dots with an onset defined by the energy conservation limit. Nano Lett. 7, 3469–3476 (2007). [DOI] [PubMed] [Google Scholar]
  40. Gesuele F. et al. Ultrafast Supercontinuum Spectroscopy of Carrier Multiplication and Biexcitonic Effects in Excited States of PbS Quantum Dots. Nano Lett. 12, 2658–2664 (2012). [DOI] [PubMed] [Google Scholar]
  41. Istrate E. et al. Carrier relaxation dynamics in lead sulfide colloidal quantum dots. J. Phys. Chem. B 112, 2757–2560 (2008). [DOI] [PubMed] [Google Scholar]
  42. Klimov V. I. Optical nonlinearities and ultrafast carrier dynamics in semiconductor nanocrystals. J. Phys. Chem. B 104, 6112–6123 (2000). [Google Scholar]
  43. Schaller R. & Klimov V. Non-Poissonian Exciton Populations in Semiconductor Nanocrystals via Carrier Multiplication. Phys. Rev. Lett. 96, 097402 (2006). [DOI] [PubMed] [Google Scholar]
  44. McGuire J. A., Joo J., Pietryga J. M., Schaller R. D. & Klimov V. I. New aspects of carrier multiplication in semiconductor nanocrystals. Acc. Chem. Res. 41, 1810–1819 (2008). [DOI] [PubMed] [Google Scholar]
  45. Cho B., Peters W. K., Hill R. J., Courtney T. L. & Jonas D. M. Bulklike hot carrier dynamics in lead sulfide quantum dots. Nano Lett. 10, 2498–2505 (2010). [DOI] [PubMed] [Google Scholar]
  46. Wake D., Yoon H., Wolfe J. & Morkoc H. Response of excitonic absorption spectra to photoexcited carriers in GaAs quantum wells. Phys. Rev. B 46, 13452–13460 (1992). [DOI] [PubMed] [Google Scholar]
  47. Honold A., Schultheis L., Kuhl J. & Tu C. W. Collision broadening of two-dimensional excitons in a GaAs single quantum well. Phys. Rev. B 40, 6442–6445 (1989). [DOI] [PubMed] [Google Scholar]
  48. Malko A. V., Mikhailovsky A. A., Petruska M. A., Hollingsworth J. A. & Klimov V. I. Interplay between Optical Gain and Photoinduced Absorption in CdSe Nanocrystals. J. Phys. Chem. B 108, 5250–5255 (2004). [Google Scholar]
  49. Hines M. A. & Scholes G. D. Colloidal PbS Nanocrystals with Size-Tunable Near-Infrared Emission: Observation of Post-Synthesis Self-Narrowing of the Particle Size Distribution. Adv. Mater. 15, 1844–1849 (2003). [Google Scholar]
  50. McGuire J. A., Sykora M., Joo J., Pietryga J. M. & Klimov V. I. Apparent versus true carrier multiplication yields in semiconductor nanocrystals. Nano Lett. 10, 2049–2057 (2010). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES