Structure of the vortex wake in hovering Anna's hummingbirds (Calypte anna)

Abstract

Hummingbirds are specialized hoverers for which the vortex wake has been described as a series of single vortex rings shed primarily during the downstroke. Recent findings in bats and birds, as well as in a recent study on Anna's hummingbirds, suggest that each wing may shed a discrete vortex ring, yielding a bilaterally paired wake. Here, we describe the presence of two discrete rings in the wake of hovering Anna's hummingbirds, and also infer force production through a wingbeat with contributions to weight support. Using flow visualization, we found separate vortices at the tip and root of each wing, with 15% stronger circulation at the wingtip than at the root during the downstroke. The upstroke wake is more complex, with near-continuous shedding of vorticity, and circulation of approximately equal magnitude at tip and root. Force estimates suggest that the downstroke contributes 66% of required weight support, whereas the upstroke generates 35%. We also identified a secondary vortex structure yielding 8–26% of weight support. Lift production in Anna's hummingbirds is more evenly distributed between the stroke phases than previously estimated for Rufous hummingbirds, in accordance with the generally symmetric down- and upstrokes that characterize hovering in these birds.

1. Introduction

Flapping wings produce trailing vortices which are shed behind a flying animal, and these structures contain information about the forces generated by the wings over the course of a wingbeat [1–7]. Earlier studies of bird flight suggested that slow flight yields a single vortex loop wake for both of the wings which is shed at each wingstroke, but also that, as flight speed increases, the wake becomes more continuous and ladder-shaped [1]. Studies of flying bats, by contrast, indicate a bilaterally symmetric wake, with one vortex ring produced by each wing [8]. Examination of the vortex wake of flying blackcaps (Sylvia atricapilla L.) revealed a novel structure that included wing root vortices not previously identified in flying birds [9]. However, the wake of slow-flying pied flycatchers (Ficedula hypoleuca) contains a single vortex loop generated during the downstroke [7]. In aggregate, these results suggest that vortex structures and the wakes of flying vertebrates might be more variable according to particular kinematics and morphological features of the taxon in question, and are thus far more complex than has been previously assumed.

Hovering flight presents an aerodynamically simplified system given the absence of a forward translational velocity, with net vertical forces equal to the body weight but also with no net thrust. Hummingbirds hover with their wings fully extended throughout the entire wingbeat cycle, producing lift during both downstroke and upstroke [10]. This so-called normal or symmetrical hovering has been hypothesized to yield single vortex rings during each wingstroke, which then convect downwards [11]. The wake of hovering Rufous hummingbirds (Selasphorus rufus) was studied empirically by Warrick et al. [2] using particle image velocimetry (PIV) in both parasagittal and transverse planes. This study suggested a strong and single momentum jet directed downwards, with the downstroke being much stronger than the upstroke and producing an estimated 75% of weight support. The wake also revealed the presence of a secondary vortex consistent with the shedding of leading-edge vortices created during the downstroke, subsequently estimated to provide, on average, 16% of total vertical force [12].

By contrast, Altshuler et al. [13] studied the function of the tail in hovering Anna's hummingbirds (Calypte anna), and described voids in the flow field beneath each wing that led them to suggest that the wings of Anna's hummingbirds generate individual ring structures with each stroke. More recently, Pournazeri et al. [14] visualized the wake of Anna's hummingbirds using plumes of smoke. They concluded that the flow observed could be explained either by a single loop model with an hourglass shape, or by a bilateral model, with the latter being more likely. Pournazeri et al. [14] also found no distinct stop or start vortices for the different strokes, indicating a vertically connected ladder wake. We accordingly seek here to quantitatively characterize the shedding and structure of the bilateral vortex rings produced by hovering Anna's hummingbirds, and also to investigate the associated patterns of vertical force production throughout the wingbeat, with concomitant contributions to weight support.

2. Material and methods

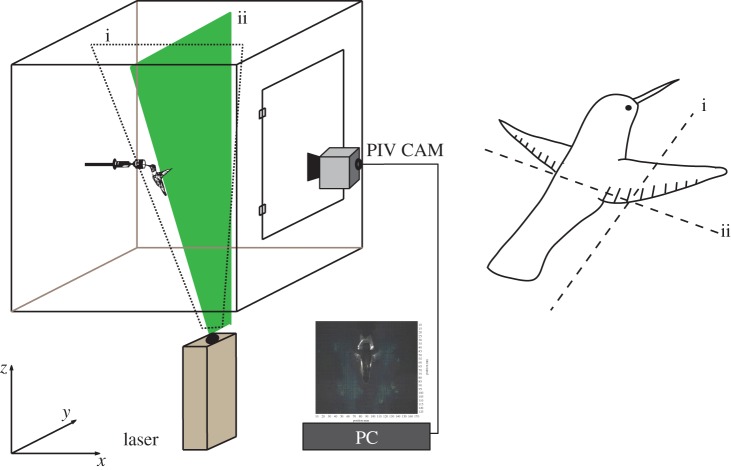
We used PIV to study the vortex wake of four adult male Anna's hummingbirds. Birds were captured on the campus of the University of California, Berkeley, and were kept separately in cages with unlimited access to Nektar-Plus solution (Nekton GmbH, Pforzheim, Germany). All hummingbird husbandry and research were conducted in compliance with UC-Berkeley's Animal Use Protocol R282-0310. Prior to experiments, birds were trained to hover at a feeder constructed from a 10 ml syringe, which was placed at a central position in a Plexiglas flight cube (figure 1). The cube measured approximately 0.9 × 0.9 × 0.9 m³, with distances from the hummingbird to walls exceeding five wing lengths, a distance sufficient to preclude possible boundary effects [15]. Between feeding bouts, the birds rested on a perch mounted at one side of the cube. Mean values of morphological data for the four birds are presented in table 1.

Figure 1.

Experimental arrangement for PIV with hummingbird hovering at a feeder inside the cube. Laser planes used for PIV were (i) parasagittal and (ii) transverse. (Online version in colour.)

Table 1.

Morphological data for four male Anna's hummingbirds (Calypte anna); mass (m), frequency (f), stroke amplitude (Φ), single wing length (b), wing chord (c), average wingtip speed (U_tip) and downstroke ratio (τ). Values are means ± s.e.

m (g)	f (Hz)	Φ (degree)	b (mm)	c (mm)	Utip (m s−1)	τ
4.52 ± 0.06	45.9 ± 1.2	112.7 ± 2.0	54.5 ± 0.5	13.1 ± 1.4	10.0 ± 0.2	0.5 ± 0.002

We sampled the vortex wake of hovering birds, using a LaVision system with a double-pulsed 50 mJ Nd:Yag laser running at a 15 Hz repetition rate (532 nm New Wave Research SoloPIV). We seeded the air in the cube with olive oil droplets for approximately 30 s before experiments, using a LaVision seeder that generated aerosol particles with a size of approximately 1 µm and at a production rate of 1.4×10¹⁰ particles per second. We illuminated the particles with a 2 mm-thick laser sheet in two different planes: (i) a parasagittal plane centred at the mid-wing, and (ii) a transverse plane within one chord length behind the trailing edge of the wing (figure 1). Pairwise images (dt = 100 µs) were captured using an ImageProX CCD camera (1600 × 1200 pixels), which filmed approximately 15 × 20 cm² in the vicinity of the bird (spanning from approx. two chord lengths above and eight chord lengths below the wing bases of the bird). The camera was equipped with a 52 mm f/1.8 D Nikon lens, with the aperture set at 1.8. Images were processed using DaVis software (LaVision, v. 7.2.1.76). Particle image displacements were calculated using a multipass cross-correlation at 64 × 64 pixels and 32 × 32 pixels, with a 50% overlap. Results were then post-processed with a peak ratio deletion (Q < 1.3) and a median vector filter removing vectors of magnitudes greater than the neighbouring RMS values. We also used a single 3 × 3 smoothing average for all derived vectors.

High-speed video films were also taken for all birds from both top and lateral views using two synchronized cameras (AOS Technologies, Baden Daettwil, Switzerland) recording at 1000 frames s⁻¹. For each bird, five consecutive wingbeats from each of three video sequences were digitized using ProAnalyst software (Xcitex Inc., Cambridge, MA, USA). A custom-written Matlab code was used for calculating the frequency (f, in Hz) and wingbeat amplitude in the stroke plane (Φ, in degrees) for each video frame, based on sequential positions of the left wingtip and the shoulder through the wingbeat. An example of the wingtip movement is presented in figure 2.

Figure 2.

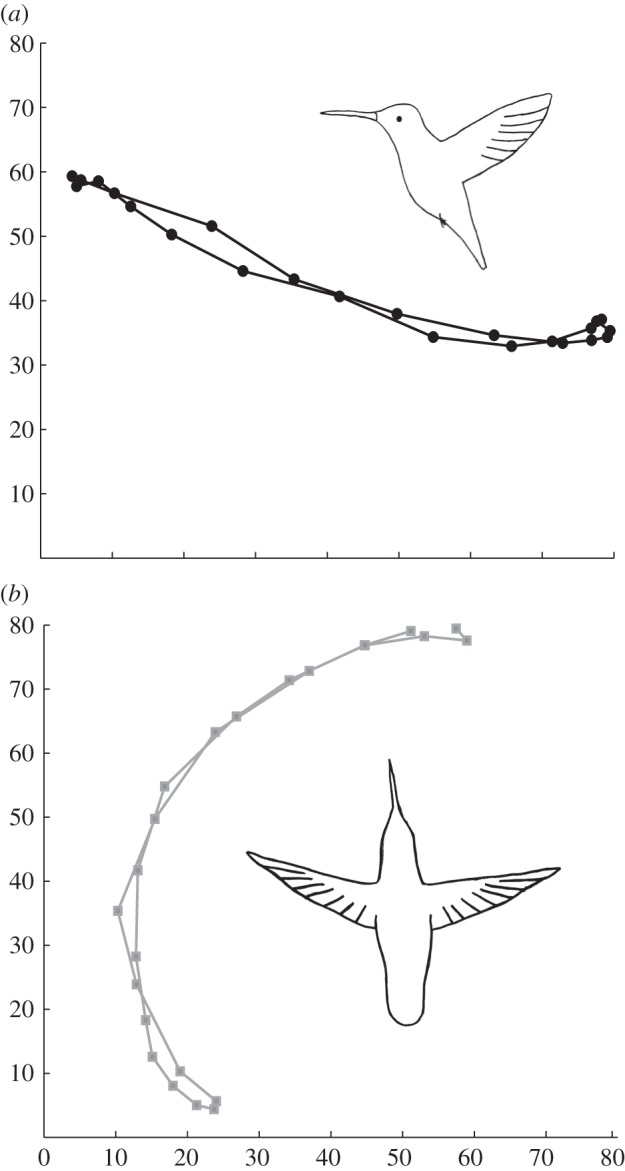
Representative wingtip movement kinematic for a hovering hummingbird, as seen from the side (a) and the top (b). Axes in millimetres.

For wake analysis of each hovering hummingbird, 100 derived velocity fields were chosen for each filming plane during the downstroke and the upstroke. The chosen images showed wakes with the bird maintaining a stable position at the feeder for a minimum of five wingbeats. An additional 50 derived velocity fields for each bird were used for the analysis of the leading-edge vortices. Vorticity was calculated from each velocity component of the streamwise (x) and vertical (z) for the i-plane and spanwise (y) and vertical (z) directions for the ii-plane (figure 1). Uncertainty in estimation of velocity is approximately ±1% and in vorticity ±10%. Circulation (Γ) for each frame was then calculated by integrating vorticity over the area of interest. All data were analysed using a custom-written Matlab code (courtesy of L. C. Johansson; Matlab v. 7.11.0 (R2010b)). In the transverse view, we measured circulation for each of the trailing wingtip vortices, for the wing root vortices, and the total same-sense circulation for the downstroke and upstroke. For the parasagittal plane, we measured the stop and start vortices characterizing a wingstroke, as well as the circulation of identifiable secondary vortices (see [2]). Circulation was measured according to Spedding et al. [1].

Weight support was estimated using the observed circulation and comparing it with the required circulation (Γ₀) calculated in accordance with previous studies (see [1]):

where W is the body weight (N), T is the wingbeat period (s), ρ is the air density (assumed to be 1.2 kg m⁻³) and S is the horizontally projected area swept out by the two wings (m²), as determined from high-speed video films. We compared circulation in the tip vortices for the downstroke and upstroke in the transverse view to evaluate relative contributions to weight support by the two stroke phases. We also examined stop vortices of the downstroke and start vortices of the upstroke for their contributions to weight support.

Data were analysed using two-way ANOVA with a Tukey post hoc test. Circulation of the different vortices and the extent of weight support were set as dependent variables, whereas individual identity, stroke phase and vortex position were set as independent factors, and were tested as main effects as well as two-way interactions. All statistical tests were carried out in JMP v. 10.0.2 (SAS Institute Inc., 2012).

3. Results

At the end of an upstroke, the hummingbird wing rapidly decelerates and then rotates to initiate acceleration at the beginning of the downstroke. The wing is rigid and the path of the wingtip is more or less equal for both half strokes (figure 2). The rapid changes in speed of the wing lead to shedding of a distinct start vortex from the wing (figure 3a, point 1), at the beginning of the downstroke. A trailing vortex is shed at the wingtip and another vortex of lower strength and of opposite sense is also shed at the wing root. As the downstroke progresses, these trailing vortices continue to be shed at both the wingtip and the wing root. At mid-downstroke, these two vortices can be clearly seen in the transverse plane (figure 3b, points 4 and 5).

Figure 3.

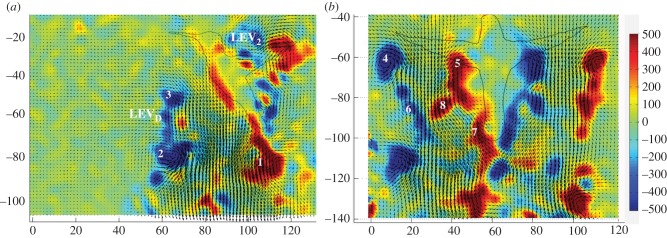
Sample images of hummingbird wake at the end of the upstroke for the (i) parasagittal and (ii) transverse planes. (a) Start vortex (1) and stop vortex (2) of the downstroke; LEV_D, the leading-edge vortex shed at the end of downstroke; LEV₂, the leading-edge vortex of the next downstroke and the start vortex for the upstroke (3). LEV refers here to the secondary vorticity tentatively identified as a leading-edge vortex from the wing (see text for details). (b) Tip vortex (4) and root vortex (5) for the downstroke, tip circulation (6) and root circulation (7,8) for the upstroke. The silhouette of the bird is included for clarity. Colour bar indicates vorticity (s⁻¹).

Wing root vortices were significantly weaker (i.e. 84 ± 14%) than tip vortices during the downstroke (F = 360.4, d.f. = 1, 792, p < 0.0001; figure 4b and table 2), with no significant differences among the four birds (F = 0.02, d.f. = 3, 792, p = 0.99). As the wing translates during the upstroke, the distance between the tip trailing vorticity and the wing root vorticity increases (figure 3b, points 6 and 7), but towards the end of the upstroke, the root vorticity shifts the position and is shed further out on the wing (figure 3b, point 8). This shift is not always visible, depending on the timing of data sampling. During the upstroke, the shedding of the vorticity is more continuous (figure 3b, points 6–8). There was a small difference between vorticity at the wingtip and root during the upstroke, with the root having slightly stronger circulation than the tip (F = 7.29, d.f. = 1, 792, p = 0.007; figure 4b and table 2), and with no differences among individuals (F = 0.09, d.f. = 3, 792, p = 0.97). Wingtip vortices were significantly stronger during the downstroke (F = 696, d.f. = 1, 792, p < 0.0001), with tip vorticity during the upstroke only about 57 ± 8% of that during the downstroke (figure 4a,b and table 2), and with no significant differences among the four birds (F = 0.02, d.f. = 3, 792, p = 0.92). Wing root vortices were also stronger during the downstroke (F = 288.7, d.f. = 1, 792, p < 0.0001), although the difference was smaller than that for the tip vortices (figure 4b and table 2). Root vorticity during the upstroke was approximately 68 ± 11% of that during the downstroke, with no significant difference among birds (F = 0.01, d.f. = 3, 792, p = 0.99). The presence of wing root vortices provides further evidence for the presence of a bilateral vortex wake, with each wing producing its own vortex loop during the downstroke.

Figure 4.

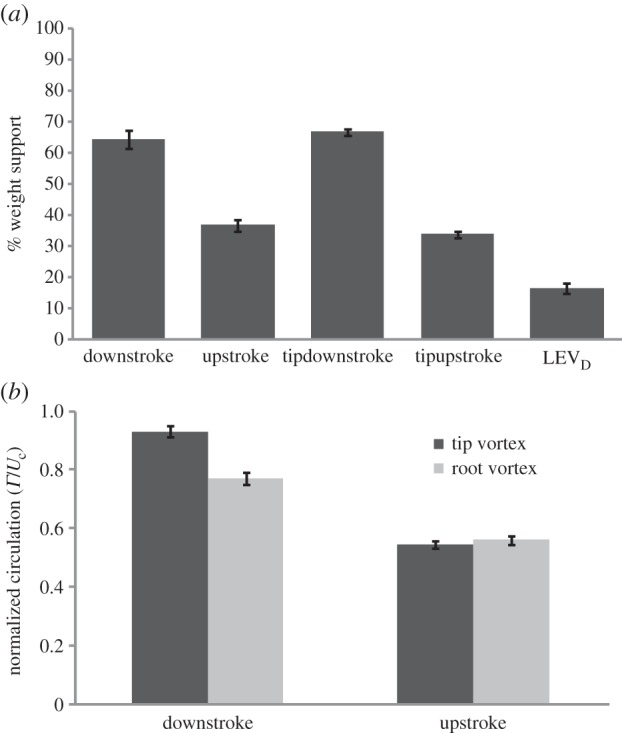
(a) Strength of the different vortices measured as the percentage of the required weight support calculated using downstroke stop vortex, upstroke start vortex and LEV_D (secondary vorticity tentatively identified as leading-edge vortex, see text for details) as measured in the parasagittal plane, and wingtip vortex at downstroke and wingtip vorticity during the upstroke, as measured in the transversal plane. (b) Normalized circulation (Γ/U_c) for the wingtip and wing root vortices of the two stroke phases, where U is the average wingtip velocity. Values are means ± s.e. (n = 4).

Table 2.

Measured circulation (Γ, m² s⁻¹) and calculated weight support (italicized text, %) values by bird for the start and stop vortices (Γ_Ds and Γ_up), the wingtip vorticity (Γ_{tip Ds} and Γ_{tip up}), the root vorticity (Γ_{root Ds} and Γ_{root up}) and secondary vorticity, tentatively identified as leading-edge vorticity (LEV_D); see text for details. All values but LEV_D are presented for the downstroke (Ds) and the upstroke (up). Values are means ± s.e.

bird	ΓDs	Γup	Γtip Ds	Γtip up	Γroot Ds	Γroot up	LEVD
1	0.115 ± 0.001 70.4 ± 1.0	0.058 ± 0.0007 35.6 ± 1.2	0.111 ± 0.001 67.7 ± 3.1	0.056 ± 0.0006 38.8 ± 1.4	0.094 ± 0.001	0.064 ± 0.0006	0.033 ± 0.001 20.2 ± 1.3
2	0.115 ± 0.001 64.0 ± 0.9	0.058 ± 0.0007 32.4 ± 0.9	0.111 ± 0.001 61.9 ± 2.4	0.063 ± 0.0005 35.1 ± 1.9	0.094 ± 0.001	0.064 ± 0.0006	0.036 ± 0.001 19.8 ± 1.6
3	0.115 ± 0.001 67.5 ± 0.9	0.058 ± 0.0007 34.2 ± 1.1	0.111 ± 0.001 65.0 ± 2.8	0.063 ± 0.0005 37.0 ± 1.6	0.094 ± 0.001	0.064 ± 0.0005	0.034 ± 0.001 20.0 ± 1.8
4	0.115 ± 0.002 65.1 ± 0.9	0.058 ± 0.0006 33.0 ± 1.2	0.111 ± 0.001 62.9 ± 3.2	0.063 ± 0.0004 35.7 ± 1.8	0.094 ± 0.0006	0.064 ± 0.0004	0.027 ± 0.001 16.0 ± 2.1

At the end of the downstroke, a stop vortex is shed at the wingtip (figure 3a, point 2). Simultaneous shedding at the wing root is more difficult to see and to interpret from the transverse plane. The wing root appears to shed a combined stop and start vortex (figure 3b, point 7), which would be consistent with fast rotational motion of the wing and the relatively short distance between the shed vortices.

Immediately following the shedding of the stop vortex at the end of the downstroke (figure 3a, point 2), a secondary vortex, which we tentatively identify as a leading-edge vortex, is shed (figure 3a, LEV_D), followed by initiation of the start vortex of the upstroke (figure 3a, point 3). At the transition between the upstroke and the downstroke, a patch of clockwise vorticity forms above the wing, indicating the presence of LEV (figure 3a, point LEV₂). This secondary vortex is approximately 28 ± 8% of the downstroke stop vortex, with significantly lower circulation (F = 694, 3, d.f. = 1, 792, p < 0.0001; figure 4a and table 2) and not significantly different among individuals (F = 0.002, d.f. = 3, 792, p = 1.0). This vortex of the downstroke corresponded to 8–26% (n = 400) of required weight support, with an average of 16 ± 5% (figure 4a). There was a statistically significant difference among birds (F = 7.6, d.f. = 3, 196, p < 0.0001), with bird no. 4 exhibiting significantly lower circulation at the leading edge (table 2). In comparison with the downstroke, the upstroke exhibits much more continuous shedding, particularly at the wing root (figure 3, point 7). Although each wing is producing its own vortex, the wake does not appear to be a clear linked loop. Circulation of the wingtip vortices over a wingbeat ranged between 80% and 122% (n = 400) of required weight support, with an average of 101 ± 3%. There was significant difference among the four birds, with birds no. 1 and no. 3 having higher total circulation than birds no. 2 and no. 4 (F = 30.0, d.f. = 3, 336, p < 0.001). Contributions to body weight support estimated from the downstroke stop vortex were approximately 67 ± 8%, and those from the start vortex of the upstroke were 34 ± 2% (n = 400, F = 714.2, d.f. = 1, 792, p < 0.0001; figure 4a and table 2). There was a significant difference among the four birds in this regard, with birds no. 1 and no. 3 producing more weight support than birds no. 2 and no. 4 (F = 20.3, d.f. = 7, 792, p < 0.0001). Weight support calculated using tip vortices from the transverse view yielded 64 ± 7% of body weight for the downstroke, and 37 ± 6% for the upstroke (n = 400, F = 706.0, d.f. = 1, 792, p < 0.0001; figure 4a). There was a small difference among birds, as birds no. 1 and no. 3 produced higher relative weight support throughout the wingbeat (F = 27.5, d.f. = 3, 792, p < 0.0001). The average weight support, as derived from both sampling planes, was 66 ± 8% for the downstroke and 35 ± 7% for the upstroke, with a small but significant difference among individual birds as birds no. 1 and no. 3 produced higher overall weight support (F = 6.2, d.f. = 3, 792, p = 0.02).

4. Discussion

The observed wake of hovering Anna's hummingbirds suggests more complex structures than previously envisioned. During both stroke phases, vorticity is shed at both wing root and tip. The presence of wing root vortices provides definitive evidence for the presence of a bilateral vortex wake, with each wing producing its own vortex structure during the downstroke. Altshuler et al. [13] visualized the flow field below hovering Anna's hummingbirds, and suggested that the wake consisted of separate vortex loops for each wing. In addition, they suggested that the vortex loops shed at the downstroke move ventrally, whereas the loops shed during the upstroke move dorsally. Although we clearly see evidence for a bilateral wake (figure 3b), there is no evidence for differences in the directionality of vortex loops between down- and upstroke, which would presumably be otherwise evident in displacement of the start and stop vortices in the parasagittal plane (figure 3a). Pournazeri et al. [14] also visualized the wake of hovering Anna's hummingbirds using smoke. Given the difficulty of precisely identifying vortex structures, however, they were not able to definitively conclude whether the wake of Anna's hummingbirds was a bilateral vortex loop, or an indented and merged vortex loop. Our study strongly indicates that hovering Anna's hummingbirds produce a bilateral vortex loop. Generating separate loops for each wing will decrease the projected area of the wake and thus lower lift production. The root vortices might also produce an upwash over the body and lead to a less efficient flight [16]. Muijres et al. [7] investigated the span efficiency of slow-flying flycatchers, and found that their efficiency was higher when compared with bats that also produced a bilateral wake. This observation suggests that hummingbirds should have a lower span efficiency than flycatchers given the presence of a bilateral vortex wake. A two-ring system, on the other hand, could provide greater aerodynamic possibilities as the two wings can potentially generate forces independent of each other. This would be highly useful for fast manoeuvres as well as for maintaining stable hovering when feeding; both are behaviours fundamental to hummingbirds and to nectar-feeding insects [17].

During the downstroke, the wake consists of two distinct vortices, one at the root and one at the tip of the wing. This pattern corresponds to the presumed shedding of broadly elliptical vortex loops by the wings in hummingbirds [2,13], slow-flying bats [8,18] and insects [17]. For hovering Anna's hummingbirds, the strength of the wing root vortex was approximately 85% of the circulation of the tip vortex, a value much higher than that found in slow-flying bats for which root circulation was only 42% of that at the tip [18]. Root vortices of similar size have also been found at forward flight speeds between 2 and 7 m s⁻¹ for another, larger species of nectar-feeding bat [6]. Johansson & Hedenström [9] observed the presence of root vortices in blackcaps, but they were much weaker and reversed their rotational directionality in the second half of the downstroke. The large difference in root circulation for hovering hummingbirds is likely to decrease as forward flight speed increases. Hummingbirds are also specialized hoverers with relatively rigid wings adapted to rapid rotation between the stroke phases [19], which may underlie such differences in observed circulation.

Although the downstroke produces two distinct vortices, at the tip and root of each wing, the upstroke displays a more complex wake, with more or less continuous shedding at both the tip and root of the wing. Pournazeri et al. [14] could identify neither stop nor start vortices in their visualization of the wake of Anna's hummingbirds. We found separate stop vortices for the downstroke and start vortices for the upstroke, but also a combined start/stop vortex at the end of downstroke and the beginning of upstroke, in agreement with what has previously been identified for Rufous hummingbirds [2]. Transitions between the stroke phases and the wing rotations occur quickly, which can lead to merging of individual vortex structures and result in complex wake configurations. Van der Berg & Ellington [20] studied the wake of a hawkmoth model flapping in a ‘hovering’ condition, and suggested that the strong and distinct downstroke vortex rings are connected by weaker upstroke vortex rings, thereby creating a chain of vortices. This might be the case for Anna's hummingbirds as well, to which end a three-dimensional PIV study would be necessary to unambiguously resolve wake structure. Variation in the strength of circulation in both planes was also higher during the upstroke (table 2), as was similarly noted in a previous study of hovering hummingbirds [2]. There is a notable shift in the position of the shedding of root vorticity towards the end of the upstroke. When the wing is outstretched at the end of upstroke, a gap is created between the innermost feathers of the wing and the body. The vorticity is plausibly shed at the tip of the feathers, just before the gap, and moves towards the body as the wake convects below the hummingbird (figure 3b). Shifts in the position of the shedding for root vorticity have been noted to occur in bats and insects [6,21], and a study of the wake of hummingbirds flying at different speeds is needed to further investigate the phenomenon. More continuous shedding of vorticity during the upstroke may also contribute to a less elliptical wake relative to the downstroke wake, rendering circulation estimates more sensitive to the exact position of the laser sheet used in imaging.

The strengths of root and tip vortices are more or less equal to each other during the upstroke, and normalized circulation of the root vortices differs less between the upstroke and the downstroke than does the circulation of the tip vortices (figure 4b). As circulation decreases, less lift is produced during the upstroke. Based on the kinematics of hummingbird hovering, it was once assumed that vertical force production should be approximately equal during the two halves of the wingbeat cycle [22]. Warrick et al. [2] investigated force production in hovering Rufous hummingbirds using flow visualization, and concluded that 75% of the weight support was produced by the downstroke. This contribution seems surprisingly high considering the specializations of hummingbirds for hovering, including rigid wings with efficient wing rotation [19] and the relatively symmetric kinematics of the downstroke and upstroke [5,23]. Warrick et al. [2], in fact, suggested that the small differences in kinematics between the stroke phases should result in the downstroke producing 64% of weight support. Indeed, we have found using measurements in both visualization planes that the downstroke generates, on average, 66% of weight support in Anna's hummingbirds.

We also found a patch of secondary vorticity, previously identified as a leading-edge vortex in the parasagittal view of the wake of hovering Anna's hummingbirds [2]. This vortex was always shed at the end of the downstroke, but varied considerably in strength. On average, this secondary vortex produced 16% of weight support, the same percentage as estimated for Rufous hummingbirds [12], but far less that estimated for the LEV of slow-flying birds and bats [7,18]. Similarly, values of relative weight support by the LEV in the hovering hawkmoth model range as high as 65% [20]. The relatively low value of the secondary circulation found here derives from the relatively large fraction of weight support produced during the upstroke, which is much lower in the aforementioned birds and bats [7,18]. Given the spatial resolution of the PIV system used here, we cannot unequivocally characterize wing vortex structures from the wake measurements alone, and can thus only tentatively identify this secondary vorticity as a LEV.

Because the filming speed of the PIV system used here was only 15 Hz (compared with a wingbeat frequency of about 45 Hz; table 1), our reconstruction of the vortex wake is necessarily confined to subsamples of a dynamically complex structure. Nonetheless, we obtained fairly consistent measurements across the four birds, which clearly show that hovering Anna's hummingbirds produce a bilateral vortex wake with comparatively strong root vortices. Wake measurements strongly indicate that vertical force production is more evenly distributed between the wing strokes than has been described for Rufous hummingbirds. Moreover, the wake has a more complex structure than simply elliptical rings produced during each stroke. Three-dimensional PIV would be helpful to resolve further details, particularly for visualization of vortex shedding during the upstroke and possible connections between the downstroke/upstroke wakes. Wake changes in hummingbirds at different flight speeds may also be predicted to differ dramatically from that in hovering flight. In nectar-feeding bats, some important features of the wake, for example, the location of the root vortices and their rotational directionality [6], change as flight speed increases. Because hovering is a specialized locomotor mode generally found only in dedicated nectarivores, it would be of interest to determine whether particular wake features used in hovering flight more broadly characterize forward flight performance as well.

Funding statement

This work was sponsored by grants from the Swedish Research Council and the US National Science Foundation. V.M.O. was supported by UC MEXUS-CONACYT.