Love, Hate and Murder: Commitment Devices in Violent Relationships

Abstract

Many violent relationships are characterized by a high degree of cyclicality: women who are the victims of domestic violence often leave and return multiple times. To explain this we develop a model of time inconsistent preferences in the context of domestic violence. This time inconsistency generates a demand for commitment. We present supporting evidence that women in violent relationships display time inconsistent preferences by examining their demand for commitment devices. We find that no-drop policies – which compel the prosecutor to continue with prosecution even if the victim expresses a desire to drop the charges – result in an increase in reporting. No-drop policies also result in a decrease in the number of men murdered by intimates suggesting that some women in violent relationships move away from an extreme type of commitment device when a less costly one is offered.

1. Introduction

Every day roughly 14 thousand women in the US are battered and 4 are killed by their intimate partners. An interesting and often puzzling aspect of violent relationships is its cyclical nature (Walker, 1979; Strube, 1988). Battered women who leave and seek the help of authorities in pressing criminal charges against their partners often return to the abuser and ask the authorities to drop the charges, despite the high probability of future victimization.² The well-documented fact that women repeatedly change their mind after leaving or reporting the batterer suggests that the idea of a rational agent with stable preferences weighing the benefits and costs of reporting abuse and leaving may not be the appropriate framework for studying domestic violence. Rather, a framework in which preferences change with battering may be more fitting.

In this paper we propose a model of time inconsistent preferences to study domestic violence. The victim’s preferences change with time from the battering incident. That is, right after a battering incident, while in shock and fear, a woman’s valuation of the relationship is low but increases as time passes. This is consistent with empirical evidence on how emotional states affect the desirability of different goods or actions (see Loewenstein, 1996; Read and van Leeuwen, 1998; Loewenstein et al, 2001; Gilbert et al. 2002; Wilson and Gilbert 2003). This model can explain how a woman might leave her partner after a battering incident with the intention of not returning, but after some time, her emotional attachment resurfaces and she returns.

In principle, models with changing but time consistent preferences (ie: traditional models of rational addiction or the cue theory of consumption) can also explain cyclical behavior.³ However, the key difference between time consistent and inconsistent agents is that the latter, if aware, will try to discipline their future behavior by committing themselves to a certain future action. In the case of smoking, for example, a person may wish to commit him or herself to quitting and therefore may welcome devices such as higher taxes (Gruber and Koszegi, 2001; Gruber and Mullanaithan, 2002). In the case of domestic violence, a woman may want to commit herself not to return to the batterer and thus welcomes policies that commit her to doing so.

In this paper we study the demand for such a commitment device: no-drop policy of prosecution. This policy stipulates that once a woman brings charges against a batterer, the prosecution will continue regardless of her stated wishes to drop the charges. In this way, no-drop policies offer a commitment device for women who want to terminate a violent relationship but fear that their intentions may change.⁴

We develop a model of time inconsistent preferences in the context of violent relationships that yields two predictions. First, if women are sufficiently time inconsistent, no-drop policies will increase reporting of battering incidents. That is, women will be more likely to report violent partners when they are offered a device that will enable them to commit to prosecuting them. Second, no-drop policies will reduce the number of men murdered by intimates as women in violent relationships will substitute an expensive private commitment device (murder of the batterer) for a cheaper public commitment device provided by the no-drop policy.

We follow this with empirical estimation of the impact of no-drop policies on reporting and intentional intimate partner homicide. The results provide evidence in favor of our theory of time inconsistent preferences in battering relationships. We find that no-drop policies lead to a 14 percent increase in 911 calls reporting domestic violence, and a 24 percent increase in the number of men arrested for domestic violence (a second measure of reporting). This is consistent with the model’s prediction that women in battering relationships demand commitment devices if they are sufficiently time inconsistent. We also find that no-drop policies lead to a 15–22 percent decline in the number of men intentionally murdered by intimates, a large fraction of whom have documented histories of battering. Our finding that no-drop policies reduce the number of men murdered by intimates provides evidence that battered women will move away from an extreme type of commitment device –murder– when a less costly one is offered in the form of no-drop prosecution. Finally, we find no evidence that no-drop policies lead to a reduction in domestic violence as measured by the number of women killed by intimate partners or the number of women admitted to the hospital for an assault. This suggests that the reduction in the number of men being murdered by intimates can not be explained by a reduction in domestic violence due to no-drop policies (as would be the case if the demand for commitment had a strategic foundation). Nor do we believe that the reduction can be due to underlying changes in the type or composition of violent relationships as the effect appears to be immediate.

The contribution of this paper is twofold. First, we explain the cyclical nature of battering relationships in the context of time inconsistent preferences. The economic literature on the subject of domestic violence is somewhat limited and explains violence under the assumption of time consistent rational agents engaged in a household bargaining problem.⁵ The main distinction between our work and previous work is our assumption of time inconsistent agents.

There exists an extensive literature on time inconsistency of time-preferences that can trace its roots to Strotz (1956) and Phelps and Pollak (1968). Yet most of the literature has focused on present biased preferences as in Ainslie (1991), Loewenstein and Prelec (1992), Laibson (1997) and O’Donoghue and Rabin (1999) among others. Our model differs in that the time inconsistency of preference is not in regards to discounting but in regards to the valuation of possible choices in a given period.

Our second contribution is that we provide new empirical evidence consistent with the theory of time inconsistent preferences, adding to the growing non-experimental empirical evidence of time inconsistency and the demand for commitments, see Angeletos et al. (2001), Madrian and Shea (2001), Gruber and Mullainathan (2002) and Della Vigna and Malmendier (2006).

The fact that the introduction of no-drop policies reduces the number of men murdered by intimates has interesting implications outside domestic violence. It implies that when agents are time inconsistent, the analysis of policies that incorporate a commitment element should consider the effect on the demand for alternative commitment devices. In this case, a public policy that offers a cheap commitment device results in a decrease in the demand for a costly private commitment device.

The rest of this paper is laid out as follows. In section 2 we provide background information on the prevalence and costs of domestic violence in the US. In section 3 we describe the cyclical nature of battering. In section 4 we describe no-drop policies and present anecdotal evidence in favor of the idea of time inconsistent preferences. In section 5 we present a model of domestic violence with time inconsistent preferences and examine the theoretical effect of no-drop policies on violence and reporting. In section 6 we present our empirical estimates of the impact of no-drop policies on domestic violence, reporting, and intimate partner homicide.

2. The problem of battering

Domestic violence is a problem of considerable social importance in the US given its prevalence and the severity of its impact on the health and well-being of those affected. In 2001, women in the US reported 590 thousand incidents of rape, sexual and other assault at the hands of intimate partners and on average 4 women are killed each day by a partner. Though the number of reported assaults is high – it is likely an underestimate. Survey data suggest that only one half to one fifth of such assaults are reported to the police.⁶ Data gathered through personal surveys and medical professional assessments suggest that between 8 and 14 percent of women have been assaulted in the past year by an intimate, with lifetime prevalence estimated at 25 – 30 percent (Jones et al., 1999). For women, intimate violence accounts for 33 percent of all homicides.

According to a report issued by the World Health Organization (WHO) in 2002, “intimate partner violence occurs in all countries, irrespective of social, economic, religious or cultural group.” Findings from population-based surveys of women from 35 countries around the world suggest that between 10 and 69 percent of women have been physically assaulted by an intimate male partner at some point in their lives, with 3 to 27 percent assaulted in the last year.

The costs associated with domestic violence are significant. Women who are victims of domestic violence suffer directly both physically and emotionally from the injury itself (Koss et al, 1991). One third of women injured by an intimate required medical attention and of those, 26 percent were hospitalized overnight for their injuries (Tjaden and Thoennes, 2000a). The CDC estimates that the direct medical costs associated with domestic violence amount to roughly 4 billion annually (CDC, 2003).

Domestic violence also diminishes a woman’s ability to work outside the home. The CDC estimates that in 1995, victims of physical assault lost on average 7.2 days of work outside the home as a direct result of their injuries and 8.4 days of household work, yielding total annual costs in terms of lost earnings in excess of $.7 billion. Women who have been victims of domestic violence are more likely to use welfare, have longer unemployment spells, and experience higher job turnover than those who have not (Lloyd and Taluc, 1999; Browne et al., 1999).

In addition, domestic violence generates significant negative externalities born primarily by children living in the household. Parker et al. (1994) study 1200 births to women in Boston and find that women who were the victims of intimate violence were at significant risk for low-birthweight, infections and anemia, controlling for a host of other potential confounders. Aizer (2007) employs instrumental variable methods to estimate the impact of violence against women on birth outcomes and finds that victimization while pregnant significantly increases the likelihood of a low birth weight birth. In addition, children who witness violence against their mothers (between 50 and 64 percent of all abused women report that their children routinely witnessed the abuse) are at increased risk for developmental problems including high levels of anxiety and depression, low self-esteem, and poor school performance - similar to those who have themselves been abused (WHO, 2002).

3. The cyclical nature of violent relationships

Despite the high costs of domestic violence in terms of physical and emotional injury, lost days of work and the negative impact on children, many victims refuse to leave their batters or seek the help of authorities. Among the reasons cited by battered women for why they remain are: love of their partners, financial dependence, lack of support by third parties and fear for their safety or the safety of their children (WHO, 2002; Sagot, 2000; Strube, 1988 and references therein). In a study of victims of domestic violence in Omaha, Nebraska, nearly 60 percent of women stated that one of the reasons they remain in relationships is their love for their abusers (Dunford et al, 1990). The decision to leave also depends on the severity and frequency of the beatings (Gelles,1976; Strube, 1988). Reasons for not reporting abuse to the authorities include considering the incident a private matter, not wanting the police or courts involved, fear of perpetrator, wanting to protect the perpetrator or the relationship and believing that the police could or would not do anything (Bureau of Justice Statistics, 1998; Tjaden and Thoennes, 2000). While these reasons are consistent with the idea of rational agents weighing the benefits and costs of leaving or reporting, a more complex picture appears once we consider the dynamics of battering.

While some women refuse to leave their batterers, perhaps just as common are women who leave their batterers multiple times only to return despite the high probability of future victimization. Past studies have found that between 25% and 75% of women seeking help in shelters return to their partners shortly after leaving the shelter (Strube, 1988). When women do leave, they typically do so only after years of abuse. Tjaden and Thoennes (2000) found that victims of physical assault suffered an average of 4.5 years of victimization by the same partner, with 26.6% of the women suffering more than five years. On average, women suffer seven assaults at the hands of the same partner.

Just as women leave and return to their batterers, it is also common for women who report their partners to the authorities to change their mind afterwards, dropping the charges and returning to their partners, only to be battered again in the future. Studies in the 1970s and 1980s found that among women whose husbands had been arrested for assault against them, between 50 and 90 percent requested that the charges be dropped by the prosecutor, despite evidence that women who drop charges are four times more likely to suffer future violence than those who do not.⁷

Studies by psychologists provide additional evidence of this cyclical pattern (see Walker, 1979). Reasons provided for dropping charges and returning include: a belief that the batterer wants to change, emotional attachment, economic needs, pressure from others and fear. Interestingly, women who seek help in shelters underestimate their probability of returning to the abuser (Griffing et al., 2002). Evidence suggests that after leaving, women may experience an increased emotional attachment to their batterers, making them more likely to return (Dutton, 1995; Griffing et al., 2002). Over time women seem to learn the importance of emotional attachment: Griffing et al (2002) find that women with past experience of leaving and returning assign more importance to emotional attachment as a reason to return.⁸

The well-documented fact that many women change their minds after leaving or reporting their partners suggests that the idea of a rational agent with stable preferences weighing the benefits and costs of leaving or reporting may not be appropriate. We argue that the dynamics of battering indicate that women’s preferences change as time from the battering incident elapses. Right after the incident, the costs of remaining in the relationship are clear to the woman and her valuation of the relationship will be low. As time passes her emotional attachment to the batterer may reappear as fear is replaced by other feelings such as loneliness. Our assumption that women value the relationship less when fearful is consistent with psychological evidence on how emotional states affect the desirability of different goods or actions (see Loewenstein 1996; Read and van Leeuwen, 1998; Loewenstein et al., 2001; Gilbert et al., 2002; Wilson and Gilbert, 2003). We propose to model women in battering relationships as having time inconsistent preferences.

The cyclical character of battering relationships could be explained without relying upon changing preferences. Women could leave and return in response to changes in the likelihood of violence. Women might also leave and report as a tool to improve their bargaining position in the relationship without intending to end the relationship.⁹ However, neither can explain the large number of women who initially report that they do want to end the relationship but finally return to their batterers. A third explanation may be that women have limited information about their outside opportunities and may return after they obtain better information. However, this is not completely consistent with the fact that battered women in shelters highly underestimate the likelihood of returning. Finally, cyclical behavior can in principle be explained with changing but time consistent preferences as in the rational theory of addiction (Becker and Murphy, 1988; Dockner and Feichtinger 1993; and Palacios-Huerta 2003) and the cue theory of consumption (Laibson, 1997).

A key difference between these alternative explanations of the cyclical nature of battering relationships and our theory of time inconsistent preferences concerns the demand for commitment devices. With time inconsistent preferences there is a tension between the intentions of a woman right after a battering incident and the same woman some time after. If a woman knows that her intentions will change in the future and she dislikes the decision that she will make in the future, she may desire to commit herself to a course of action now. In contrast, these alternative explanations do not generate a demand for commitment. In the rest of the paper we provide both anecdotal and quantitative evidence that is consistent with a model in which battered women do demand commitment devices by examining the effect of a policy that commits women to prosecute their batterer. This no-drop policy is described in the next section.

4. No-Drop policies

Over the past 30 years, local prosecutors and legislators have adopted a series of legal innovations with the objective of increasing prosecution of domestic violence. One of the most common and controversial is a no-drop policy which compels the prosecutor to continue with prosecution even if the victim expresses a desire to drop the charges and ceases to cooperate with the prosecution. In a survey of 50 of the largest US cities, in 1976 only one city (Omaha, Nebraska) had a no-drop policy and by 1996, all but six cities had a no-drop policy (Table 1.)

Table 1.

Year No-Drop Policy Adopted by City

			Intimate Partner Homicides in 1976
City	Year Adopted	2000 population	Male	Female
Albuquerque	1987	448,607	1	3
Atlanta	1993	416,474	22	20
Austin	1994	656,562	2	0
Boston	1992	589,141	3	4
Buffalo	1995	292,648	2	4
Charlotte	1993	540,828	3	2
Chicago		2,896,016	39	48
Cincinnati	1995	331,285	8	4
Cleveland	1992	478,403	14	11
Columbus		711,470	5	6
Dallas	1995	1,188,580	23	13
Denver	1986	554,636	9	2
Detroit	1994	951,270	26	30
El Paso	1989	563,662	4	1
Fort Worth	1991	534,694	0	1
Fresno	1996	922,516	6	4
Honolulu	1991	371,657	2	6
Houston	1994	1,953,631	40	17
Indianapolis	1989	791,926	3	3
Jacksonville	1992	735,617	6	7
Kansas City	1994	441,545	4	4
Long Beach	1991	461,522	2	3
Los Angeles	1986	3,694,820	23	39
Memphis	1995	650,100	10	10
Miami	1986	362,470	4	4
Milwaukee	1994	596,974	5	6
Minneapolis	1993	382,618	0	5
Nashville	1994	569,891	5	4
New Orleans	1996	484,674	4	17
New York	1990	8,008,278	12	31
Oakland	1994	399,484	5	8
Oklahoma City	1996	506,132	6	6
Omaha	1976	390,007	2	0
Philadelphia		1,517,550	15	26
Phoenix	1984	1,321,045	9	2
Pittsburgh		334,563	7	3
Portland	1987	529,121	2	1
Sacramento	1984	407,018	4	7
San Antonio	1990	1,144,646	7	7
San Diego	1984	1,223,400	1	1
San Francisco	1989	776,733	4	9
San Jose	1994	894,943	1	5
Seattle		563,374	4	0
St Louis		348,189	7	10
Toledo	1988	313,619	5	3
Tucson	1996	486,699	0	1
Tulsa	1996	393,049	7	3
Virginia Beach	1996	425,257	3	1
Washington	1996	572,059	15	7
Total 49 cities		44,129,403	391	409
Total US		281,421,906	1357	1600
Percent of total		16%	29%	26%

In this paper we offer a rationale for adopting no-drop policies that is based on the tension between the victim’s intentions at different points in time. Her preferences for prosecuting and ending the battering relationship are strongest right after a battering incident. Over time, her preferences change such that she no longer wishes to prosecute and she has often reconciled with the abuser. Hence, if at the time of the battering incident she knows that she will forgive her partner and drop charges in the future, she is less likely to report him at that time. But if her power to drop charges in the future is removed (because of a no-drop policy), she may be more willing to report him. In this way, the no-drop policy provides the victim with a commitment device to overcome the time inconsistency of her preferences.

Evidence from surveys of victims supports the idea of time inconsistency of preferences and the value of no-drop policies. Smith et al. (2001) presents the following comments by victims in cities with “no-drop” policies: “The prosecutor did not listen to me when I recanted my story. They continued to prosecute. In the long run, I am so glad. He got punished.” Another woman states “If it hadn’t been for the laws of arresting and prosecuting, I would have been back with him. I am glad they stuck with it and enforced the laws.”

To our knowledge, there is no scientific study of the effect of no-drop policies on violence or reporting.¹⁰ However, there is evidence that this policy did represent a significant change in policy and led to an increase in prosecutions and convictions (Smith et al., 2001).

5. The model

In this section we present a simple model of domestic violence in which the woman displays changing preferences regarding the value of the relationship and is aware of this. The objective of this model is to show how providing a commitment device in the form of no-drop policies would affect both a man’s behavior and a woman’s response to it. The model provides one surprising result: implementation of no-drop policies leads to a reduction in the number of batterers who are murdered. The reason is that murder is an extreme form of a commitment device. When the government provides a cheaper one, women who were willing to kill their partners to avoid returning to them, will now report them to the authorities instead. In addition the model shows that a no-drop policy results in an increase in reporting if the degree of time inconsistency is large enough and has an ambiguous effect on the amount of battering.

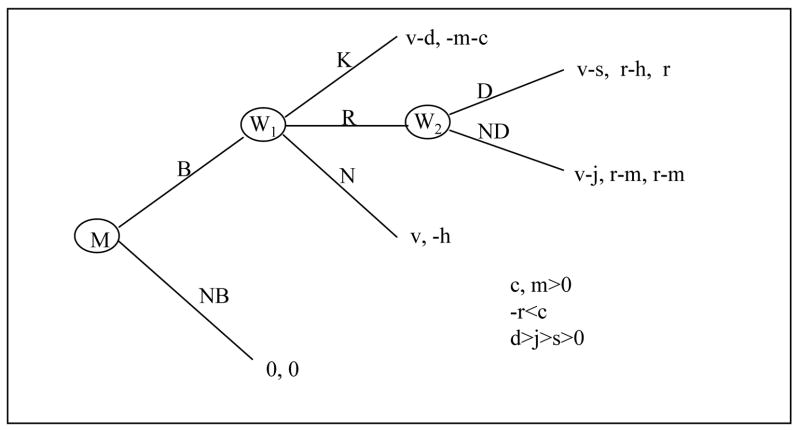
The model without a no-drop policy is depicted in Figure 1. First the man chooses between battering (B) or not (NB). Battering gives him a utility of v. We assume that this utility is randomly distributed in the real numbers –with c.d.f. G(v). This assumption captures the fact that some men really enjoy battering while others dislike it. If no battering occurs the game ends and the players receive a normalized payoff of zero. If battering occurs, the woman has three options: kill her partner (K), do nothing (N), or report him to the authorities (R). Note that reporting and prosecuting implies dissolution of the union.¹¹ If she kills him, he suffers a cost d for being dead,¹² and she faces the cost c of being prosecuted by the authorities and the loss m of the value she assigns to the relationship (this includes both the sentimental and economic value of the relationship). If she does nothing, the relationship continues. Since she has been battered her valuation of the relationship is diminished by the amount h. We assume that this utility is randomly distributed in the positive real numbers –with c.d.f. F(h). This assumption captures the fact that battering affects women’s valuation of the relationship differently. We assume that the man does not know the value of h when he makes his decision.

Figure 1.

Game Tree

We assume that reporting the battering partner to the authorities has a direct benefit (or cost) r to the woman. She benefits from reporting him to the authorities if the police scare him or remove him while he is still violent. Reporting him to the police may also have costs, resulting in a negative r. He may get upset and violent or there may be stigma costs associated with police intervention. Therefore, the parameter r may be positive or negative depending on whether the direct benefits or costs of reporting prevail (we assume that −r<c, that the cost of killing him is greater than the cost of reporting him).

If she reports him, the legal procedure starts and a new self of the woman (W₂) decides in period two whether to drop charges (D) or not (ND). Her new self (W₂) has a different valuation of the relationship than the valuation of the previous self (W₁). The payoffs of these two selves (W₁ and W₂) are written in the second and third place, respectively, in the payoff vectors for the actions D and ND. Both selves obtain the same utility level from ND and continuing with the legal procedures, −m in addition to r.¹³ The first self assigns a value of −h to dropping the charges and staying in the relationship, while the second self values it as if nothing had happened, 0. These payoffs are in addition to the direct benefit of reporting r. Note that the preferences between the woman’s selfs differs in h: the larger h, the greater the degree of time inconsistency displayed by the woman.

Finally, the man (whose payoff is indicated in the first place of the payoff vector) suffers a cost of s if the woman reports him and then drops the charges and suffers a cost of j if the woman does not drop the charges. This parameter represents the expected disutility of going to jail.

We assume that the parameters c, d, j, m and s are positive. In addition, we assume that the worst punishment is death, followed by jail and then arrest when it is not followed by prosecution (d>j>s).

If a no-drop policy is in place the game is the same with the exception that the second self does not have the option of dropping the charges. That is, once she reports him she is committed to prosecuting him.

We study next how a no-drop policy would affect the behavior of the players. First, we provide a description of equilibrium behavior with and without such a policy. We follow this with a comparison of the two situations in terms of battering, and the woman’s response to it.

5.1. Without a “no-drop” policy

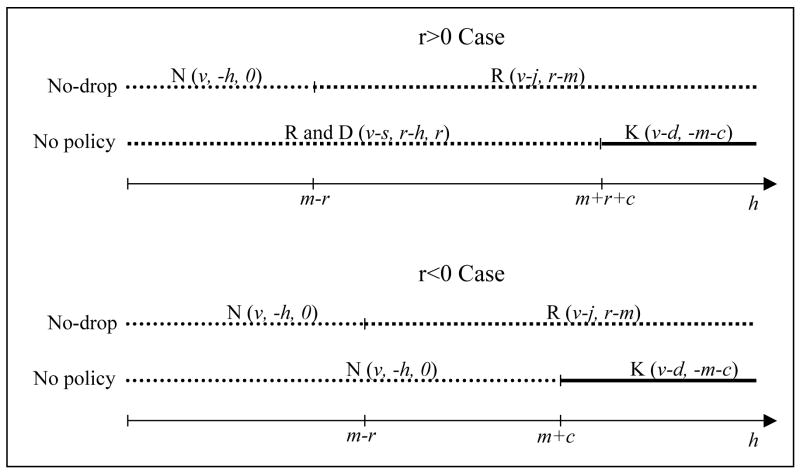
The subgame perfect equilibrium can be solved easily by backwards induction. W₂ always drops the charge since r−m is lower than r. Knowing this W₁ must choose among kill (K), report (R) and do nothing (N). Her decision will depend on the disutility of remaining in a battering relationship (h) and whether reporting him has direct benefits or costs regardless of what she does later (r positive or negative). If r is positive, reporting him when she will drop the charges later is always better than doing nothing. Thus she compares K and R. She will choose to report him if r−h>−m−c, (the utility from reporting exceeds that of killing him). Thus, the woman reports the batterer with probability F(r+m+c) and kills him with the complementary probability. If r is negative, reporting him when she will drop the charges later is always worse than doing nothing. Thus she compares K and N. She will choose to do nothing if −h>−m−c. Thus, the woman does nothing with probability F(m+c) and kills him with the complementary probability. Figure 2 shows the equilibrium response to battering for both positive and negative r and the corresponding vector of payoff for the players as a function of h.¹⁴

Figure 2.

Equilibrium Actions for the Woman

The decision of the man will depend on his expectation of the woman’s response to battering. Given the distribution of men’s taste for domestic violence, we have that a proportion 1−G((1−F(r+m+c))d+ F(r+m+c)s) will choose to batter if r is positive.

5.2. With a no-drop policy

The main difference between the case without a no-drop policy and with such a policy is under the latter, reporting is always better than killing. This follows from the fact that W₂ cannot drop the charges and reporting the man is less costly than killing him (−r<c). Thus she compares N and R. She will do nothing if −h>r−m. Thus, the woman does nothing with probability F(m−r) and reports him with the complementary probability. Note that the probability of reporting him is increasing in r and decreasing in m. Then, we have that a proportion 1−G((1−F(m−r))j) of men will choose to batter.

5.3. The effects of the “no-drop” policy

From the comparison of the ranges of h that result in a battering man being killed we obtain the following proposition. The result follows directly from Figure 2.

Proposition 1

A no-drop policy reduces the probability that a battering man is killed.

The intuition for this result is as follows. Without a no-drop policy the woman knows that she will drop the charges in the future, therefore reporting him to the authorities will not end the relationship. The only way she has to commit herself to ending the relationship is by killing him. She will do so if her valuation of her future life with the batterer (m−h) is low enough. If instead a “no-drop” policy is in place, reporting him to the authorities serves as a commitment device since she will not be able to drop charges.

From Figure 2 we can also study the effect of the “no-drop” policy on the reporting of battering.

Proposition 2

A no-drop policy increases the reporting if the degree of time inconsistency is large enough (h>m−r) but may decrease it otherwise.

If reporting a batterer to the police provides a short run cost to the woman but no benefit (r<0) the intuition is straight forward. The woman knows that withoug the policy she will drop the charges later and thus will not report him after the battering. If instead she cannot drop the charges later she may be willing to report him as a way to commit herself to ending the relationship. Moreover, a no-drop policy may increase reporting since some women (those with an extremely high h) will decide to report the batterer instead of killing him.

Contrary to what would be obtained under the assumption of stable preferences in this model, restricting the set of choices attached to reporting for a woman with unstable preferences may actually increase the reporting of battering incidents. However, when the degree of time inconsistency is sufficiently low (h<m−r) and there are short run benefits of reporting (r>0) no-drop policies actually decrease reporting. In this case, women are willing to report battering to obtain the short run benefit but are not willing to commit to prosecution, hence, they would report without a “no-drop” policy but not with such a policy in place.

Proposition 3

A no-drop policy has an ambiguous effect on the amount of battering.

The decision to batter depends on women’s response to battering. On the one hand, from proposition 1, we know that a “no-drop” policy will result in a lower probability of the batterer being killed. By reducing the probability of the harshest punishment possible, a “no-drop” policy can actually make battering more attractive. In addition, such a policy may result in fewer cases reported if the degree of time inconsistency is small, which would also make battering more attractive. On the other hand, there are cases in which a “no-drop” policy will increase the number of cases reported and prosecuted since charges cannot be dropped, and this would make battering less attractive. The total effect will depend on the relative strength of the different forces and can only be determined empirically.

While this simple model of domestic violence shows that the effect of no-drop policies on battering is theoretically ambiguous, its effect on the murder of batterers is not. When a woman displays time inconsistent preferences and exhibits some degree of sophistication regarding her inconsistency (eg, she can anticipate the inconsistency) she may be willing to commit herself to ending the relationship. If the government does not provide such a commitment option, she may prefer to kill her batterer rather than remain in the violent relationship. Hence, a non-ambiguous result of the model is that “no-drop” policies diminish the number of batterers murdered by their partners.

Moreover, if preferences display a large enough degree of time inconsistency, the effect of no-drop policies on reporting is positive since women may start reporting knowing that they will not be able to drop charges in the future.

6. Empirical Analysis

In this section we estimate the impact of no-drop policies on violence against women, reporting of battering, and intimate partner homicide. We proceed in two stages. First, we estimate the impact of no-drop policies on violence and reporting for the seven largest counties in California (population 20 million). For this analysis, violence is measured by the number of women admitted to the hospital for an assault. Reporting is measured by both 911 calls alleging domestic violence and arrests for domestic violence. Second, we estimate the impact of no-drop policies on intimate partner homicide using data on 49 of the 50 largest cities in the US for the period 1976–1996 (population 44 million).¹⁵ We rely on California data for the first analysis because of data availability.

6.1. Exogeneity of the timing of No-Drop Policies

Before we begin the analysis, we explore the exogeneity of the timing of no-drop policies. Specifically, we estimate a discrete time hazard model of time to adoption in each of the 49 cities in Table 1, following Allison (1982). The results are presented in Table 2. We include as covariates measures of previous violence (both intimate and non-intimate), demographic characteristics (education, racial composition, labor force participation and earnings), other domestic violence policies (mandatory arrest policies, police domestic violence unit), and the provision of services to victims of domestic violence (shelters and hotlines). We include all covariates simultaneously in regressions weighted by city population size and unweighted (columns 1 and 3, respectively). When we do so, two to three of the seventeen controls included (in addition to year and city fixed effects) significantly affect the timing of adoption in each specification. In order to rule out the possibility that the lack of significance is due to collinearilty of the covariates, we also run 17 individual regressions in which we include only one covariate at a time (columns 2 and 4). Again, even when entered separately, only two to three covariates are statistically significant (and they are not necessarily the same across the specifications). Moreover, the magnitude of the effects is always very small. For example, in the unweighted specifications, even though the lag of women killed by intimate partners is statistically significant, the coefficient estimate suggests that a one standard deviation increase in this variable leads to only a 2.3 percent decrease in the probability of adoption.¹⁶ While not conclusive, this evidence suggests that systematic variation in the timing of adoption of no-drop policies is unlikely to bias the results.

Table 2.

Predicting No-Drop Policies with Discrete Time Hazard Models, 49 Cities

	Weighted by City Size		Unweighted
	Entered together	Entered Separately	Entered together	Entered Separately
Share population black	0.003 [0.005]	0 [0.007]	0.001 [0.006]	0 [0.004]
Employment to population ratio	−0.214 [0.203]	−0.345 [0.188]	−0.196 [0.141]	−0.255 [0.071]
Average wage	−0.009 [0.024]	0.023 [0.010]	0.012 [0.021]	0.015 [0.009]
AFDC benefits	0.034 [0.031]	0.05 [0.026]	0.016 [0.023]	0.022 [0.017]
Male labor force participation	3.762 [2.074]	0.735 [1.119]	1.719 [1.404]	0.059 [0.947]
Female labor force participation	−1.362 [2.062]	−0.518 [1.162]	−1.882 [1.298]	−0.649 [0.856]
Male median earnings	0.021 [0.023]	0.018 [0.013]	0.035 [0.016]	0.015 [0.009]
Female median earnings	−0.001 [0.032]	0.028 [0.014]	−0.039 [0.026]	0.014 [0.012]
Share of men 25 + with at least 4 yrs college	−0.07 [0.025]	−0.016 [0.015]	−0.048 [0.019]	−0.011 [0.012]
Share of females 25 + with at least 4 yrs college	0.018 [0.028]	−0.011 [0.011]	0.024 [0.024]	−0.009 [0.011]
Lagged female IPH rate per 1000	−0.859 [0.752]	−0.934 [0.940]	−1.241 [0.530]	−1.379 [0.558]
Lagged male IPH rate per 1000	0.881 [0.968]	0.307 [0.862]	0.241 [0.635]	−0.005 [0.566]
Lagged nonintimate homicide rate per 1000	−0.03 [0.014]	−0.013 [0.014]	−0.017 [0.009]	−0.016 [0.009]
Policy of mandatory arrest for domestic violence	0.153 [0.140]	0.109 [0.126]	0.007 [0.061]	−0.008 [0.000]
Police domestic violence unit	−0.109 [0.100]	−0.009 [0.089]	−0.016 [0.085]	0.024 [0.000]
DV Beds per 1000 population	−0.006 [0.213]	−0.181 [0.140]	−0.281 [0.172]	−0.177 [0.135]
DV Hotlines per 1000 population	2.253 [5.460]	−3.623 [3.629]	5.289 [4.181]	−2.394 [3.538]
Observations	761		761
R-squared	0.3		0.28
Robust standard errors in brackets

6.2. Impact of no-drop policies on underlying violence and reporting

6.2.1. Data

For our analysis of the impact of no-drop policies on reporting and violence, we focus on the seven largest counties in California, representing 20 million residents (55 percent of the state) for the years 1990–2000.¹⁷ The seven counties vary in the timing of their adoption of no-drop policies. Four of the counties had a no-drop policy in place by 1990. Three of the counties adopted a no-drop policy during the study period: Santa Clara adopted in 1991 and Alameda and Fresno each adopted in 1994.

For this sample we have two measures of reporting - the number of men arrested for domestic violence and calls to 911 reporting domestic violence. The arrest data are available for all seven counties by race, county and year and the data on 911 calls are available by county and year (for all counties except San Francisco) but not by race.¹⁸

Our measure of domestic violence for this analysis is the number of women admitted to the hospital for an assault.¹⁹ This measure is imperfect but still very useful for three reasons: 1) it is the only local-area measure of violence available on a continual basis (and it is available by race and year); 2) it is devoid of any reporting bias as it does not depend on women admitting that they were battered by their partners and 3) since a high proportion of women (76–87 percent) who are assaulted are assaulted by an intimate, most hospital admissions for assault will likely have been caused by an intimate.²⁰

6.2.2. Results

In Table 3 we present estimates of the impact of no-drop policies on women admitted to the hospital for an assault and men arrested for domestic violence based on negative binomial regressions, following Grogger (1990).²¹ These data are available at the county-race-year level (three races, seven counties, 11 years, resulting in 231 observations). Controls include city fixed effects, per capita income, share black, share White Hispanic and share White non-Hispanic (omitted), non-intimate homicides, and race-specific linear time trends. We also control for whether the city has a mandatory arrest policy whereby police officers are required to arrest those they suspect of battery.²² All regressions are weighted by cell size. We find no significant impact of no-drop policies on violence as measured by women admitted to the hospital as a result of assaults (column 1). As a “falsification check” we also estimate the effect of no-drop policies on hospitalization for car crashes and non-intimate homicides and we find no effects (columns 2 and 3).

Table 3.

Impact of No-Drop Policies on Assaults Against Women and Arrests for Domestic Violence, 7 California Counties

Panel A: All Counties	Assaults vs Women	Car crashes	Non-intimate Homicide	DV Arrests	DV Arrests	DV Arrests
No drop policy	−0.13 [0.085]	−0.091 [0.052]	−0.038 [0.066]	0.203 [0.054]	0.131 [0.053]	0.186 [0.073]
Per capita income	−0.059 [0.014]	−0.023 [0.007]	−0.034 [0.011]	−0.022 [0.007]	−0.016 [0.007]	−0.017 [0.007]
employment to population ratio	4.552 [0.976]	5.821 [0.772]	−1.219 [0.732]	−0.629 [1.053]	−3.233 [0.973]	−3.023 [0.975]
Non-Intimate Homicide Rate	0.035 [0.003]	0.029 [0.001]	0.043 [0.005]	0.025 [0.002]	0.009 [0.003]	0.009 [0.003]
Female population in 1000s	0.002 [0.000]	0.002 [0.000]	0.002 [0.000]	0.002 [0.000]	0.001 [0.000]	0.001 [0.000]
Shelters for victims of DV	−0.046 [0.024]	0.018 [0.017]	0.001 [0.019]	−0.046 [0.030]	0.002 [0.032]	−0.005 [0.033]
White non-Hispanic	252.446 [43.500]	277.956 [24.573]	347.067 [61.641]	180.402 [39.500]	133.165 [26.658]	134.935 [26.771]
Hispanic	209.91 [28.733]	135.102 [28.146]	269.426 [34.646]	136.654 [29.285]	73.474 [25.515]	76.413 [25.600]
Assaults against women					0.003 [0.0004]	0.003 [0.0004]
Mandatory arrest for domestic violence						−0.092 [0.070]
Observations	231	231	231	231	231	231
Mean of dependent variable	128	4456	226	3333	3333	3333
Size of effect	−12%	−9%	−4%	23%	14%	20%
Panel B: Excluding LA County
No drop policy	−0.055 [0.082]	−0.059 [0.047]	0.044 [0.067]	0.195 [0.065]	0.131 [0.057]	0.153 [0.061]
Observations	198	198	198	198	198	198
Mean of dependent variable	43	2216	31	877	877	877
Size of effect	−5%	−6%	4%	22%	14%	17%
Panel C: Excluding LA and San Diego
No drop policy	0.049 [0.090]	0.04 [0.040]	−0.019 [0.073]	0.296 [0.064]	0.223 [0.059]	0.181 [0.057]
Observations	165	165	165	165	165	165
Mean of dependent variable	33	1376	24	661	661	661
Size of effect	5%	4%	−2%	34%	25%	20%
Robust standard errors (clustered on county) in brackets
All Regressions include county fixed effects and race specific linear time trends

Having established that no-drop policies do not appear to affect underlying violence, we turn to estimating their impact on arrest rates, our first proxy for reporting for which we have information for all seven counties broken down by race.

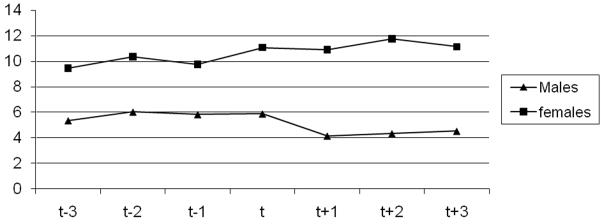
In Figure 3 we present the number of men arrested for domestic violence in the years immediately before and after a no-drop policy was adopted (t=0 in the year the policy is adopted, t= −1 in the year before and t=1 in the year after). There is a large increase in the years immediately after the adoption of a no-drop policy. Prior to the adoption of the policy, there does not appear to be much change in arrests, suggesting that the passage of the law does not coincide with underlying trends.

Figure 3.

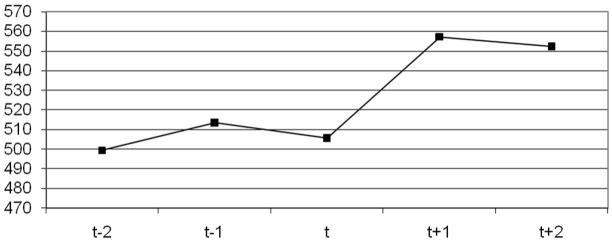
Impact of no-drop policies on arrests for domestic violence

To control for any other changes that might have been coincident with the adoption of no-drop policies and could influence arrests, we turn to regression analysis. In column 4 of Table 3 Panel A we present negative binomial estimates of the impact of no-drop policies on male arrests for domestic violence, including all controls mentioned above. We find that counties that adopt a no-drop policy witness a 23 percent increase in arrests for domestic violence relative to counties that do not adopt such a policy over this period. When we control for underlying violence (column 5) the impact declines to 14 percent and is still significant.²³ When we control for mandatory arrest (column 6), we find that a policy of mandatory arrests has a small and insignificant effect on arrests for domestic violence and the impact of no-drop policies on arrests increases to 20 percent.

Two of the seven counties (LA and San Diego) have more than one prosecutor’s office and our measure of no-drop policies refers to the largest city in each county, introducing measurement error if another city within either county should change its no-drop policies during this period.²⁴ To address this we exclude LA County from the sample in panel B and exclude LA and San Diego from the sample in panel C. The results with respect to arrests are significant and similar in magnitude to previous estimates, but the results with respect to assaults, car crashes and non-intimate homicides change considerably in magnitude with specification and never achieve significance.

However, it could be that the estimated effect on arrests does not just reflect changes in reporting but changes in arrests conditional on reporting. This might happen if police officers are more likely to arrest when prosecution is assured because of a no-drop policy. We show next that no-drop policies increase reporting as measured by calls to 911 reporting domestic violence by a similar amount.

In Table 4 we present regression estimates of the impact of no-drop policies on the rate of calls to 911 reporting domestic violence per woman age 18–64 in the county. Each observation is a county-year. There are only 66 observations for this analysis (6 counties, 11 years) and unlike for arrests, calls are not broken down by race. We include county fixed effects, per capita income, share black and Hispanic, non-intimate homicides, linear time trends and mandatory arrest policy as controls.

Table 4.

Impact of No-Drop Policy on Rate of Calls Reporting Domestic Violence, 6 California Counties

No-drop policy	0.005 [0.003]
Per capita income in 1000s	0.333 [0.517]
Employment to population ratio	−0.251 [0.062]
Non-intimate homicide rate	−0.021 [0.015]
Share black	0.231 [0.242]
Share hispanic	0.058 [0.133]
Mandatory arrest for domestic violence	0.001 [0.003]
Assaults against women per 1000 women	0.055 [0.018]
DV Shelters per 1000 women	0.061 [0.704]
Observations	66
R-squared	0.72
Mean of dependent variable	0.0358
Size of effect	14%
Robust standard errors (clustered on county) in brackets
Dependent variable is the number of calls per woman age 15–44 in the county (average =0.037)
Regressions include county fixed effects and linear time trend

The estimated impact of no-drop policy on calls to 911 reporting domestic violence is positive and significant at the 10 percent level. The effect is large in magnitude, suggesting that no drop policies result in a 14 percent increase in calls to 911 reporting domestic violence, which is similar to the impact on arrests for domestic violence (conditional on violence) reported in Table 3. The lack of significance is not surprising given the small sample size and inclusion of multiple controls which limit power. Due to data limitations, we regard these results as supportive of our previous results that no-drop policies increase reporting as measured by arrests for domestic violence, rather than conclusive.

In the next section we examine the impact of no drop policies on intimate partner homicide in 49 of the 50 largest cities in the US.

6.3. The impact of no-drop policies on intimate partner homicide

6.3.1. Data

Data on intentional intimate partner homicides come from the FBI Uniform Crime Reports Supplemental Homicide Reports (SHR) 1976–1996. Two cities are missing homicide data for one year each, yielding a final dataset of 1027. ²⁵ A homicide was considered an intimate partner homicide if the assailant was a husband (wife), ex-husband (ex-wife), common law husband (common-law wife), or boyfriend (girlfriend). Homicide by an ex-boyfriend (ex-girlfriend) is not recorded. The small number of intimate partner homicides in which the victim and assailant were of the same sex was dropped. These data exclude unintentional or negligent killings – all homicides included here were intentional. Intimate partner homicide figures were adjusted by the FBI for missing data on relationship assuming underreporting independent of sex, race and marital status of the victims. We keep all homicide victims between the ages of 20 and 55 (the age group for which intimate homicide is most prevalent).

Figures 4 and 5 display trends in intimate partner homicide for the nation as a whole and the 49 cities in our sample over time. The trends are similar. While the annual number of female intimate partner homicides nationally has declined from 1500 to 1250 over this 20 year period, the number of men killed by partners has declined much more dramatically from 1400 to less than 500 annually (Figure 4).²⁶ Intimate partner homicides of men and women fell equally until the early mid 1980s when they start to diverge with male rates falling more quickly. This divergence is slightly more pronounced in the 49 city data. We argue that these trends suggest that declines in intimate partner homicide of males cannot be explained entirely by the decline in the number of women in violent relationships as the former fall much more dramatically.

Figure 4.

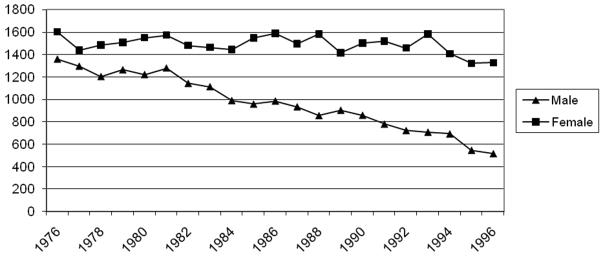
Intimate Homicide Victims by Sex: 1976–1996 National

Figure 5.

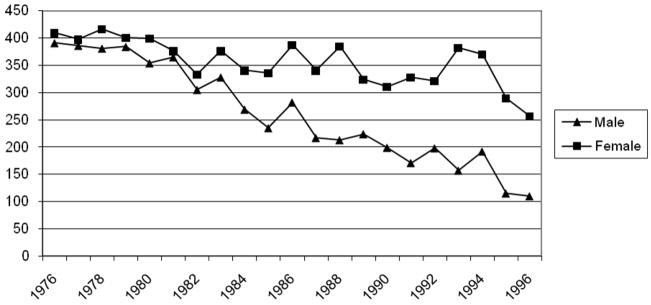
Intimate Partner Homicide by Sex: 1976–1996 49 Cities

The homicide data are merged with information on prosecutorial and police policies regarding domestic violence, and services for domestic violence victims in these cities.²⁷ We also include the following controls: AFDC benefit levels, county wages and the employment to population ratio from annual Bureau of Economic Analysis employer surveys, and population share black, male and female labor force participation and educational attainment from the decennial census (intercensal years are linear interpolations).

6.3.2. Results

In Figure 6 we present the average number of men and women killed by intimates over this period in the years immediately before and after a no-drop policy was adopted (t=0 in the year the policy is adopted, t= −1 in the year before and t=1 in the year after).²⁸ As is evident from the graph, there is a decline in the number of men killed by women in the years immediately after the adoption of a no-drop policy. In contrast, the number of women killed by their partners appears, if anything, to increase with the adoption of no-drop policies (though not significantly) and then decline. Prior to the adoption of the policy, there does not appear to be any downward trend in intimate homicides suggesting that adoption of the policy does not coincide with underlying trends.

Figure 6.

Average number of homicides per city before and after no-drop

In Table 5 we present negative binomial estimates of the impact of no-drop policies on male and female victims of intimate partner homicide. All regressions are weighted by city size. In column 1 are estimates of the impact of no-drop policies on men murdered by intimate partners controlling for city and year fixed effects, city-specific linear time trends, the natural log of the population of men age 20–55, the share black, and the rate of non-intimate homicides. The estimate of the impact of no-drop policy of −0.265 is statistically significant and implies a 23 percent decline in intimate partner homicide of males.²⁹ No-drop policies have a negative (−0.123) but insignificant impact on homicide of females by intimate partners (column 2). In columns 3–6, we present the results of regressions that include additional controls: average area wages, the employment to population ratio, AFDC benefits for a family of four, services for domestic violence victims, and the lag of the number of men (or women) killed by their partners to control for changes in underlying domestic violence. Services refer to the number of hotlines and shelter beds per 100,000 women in the city.³⁰ When we include all the additional controls, the estimate falls only slightly.

Table 5.

Impact of No-Drop Policies on Intimate Homicides, 49 Cities

	Male	Female	Male	Female	Male	Female	Non-Intimate Homicides
No-drop policy	−0.265 [0.137]	−0.123 [0.116]	−0.256 [0.134]	−0.127 [0.107]	−0.23 [0.138]	−0.116 [0.095]	−0.059 [0.068]	−0.042 [0.065]
Adult non-intimate homicides per 10000	0.105 [0.116]	0.088 [0.081]	0.102 [0.115]	0.085 [0.079]	0.099 [0.143]	0.088 [0.099]
Share population black	0.03 [0.061]	−0.004 [0.077]	0.034 [0.062]	−0.003 [0.072]	−0.103 [0.080]	−0.018 [0.127]	−0.157 [0.082]	−0.112 [0.105]
Average wage			0.022 [0.064]	−0.004 [0.048]	0.007 [0.078]	−0.026 [0.038]	−0.01 [0.031]	0.02 [0.043]
Employment to population ratio			0.423 [0.694]	0.212 [0.500]	0.096 [0.848]	0.2 [0.594]	0.842 [0.309]	0.749 [0.363]
AFDC benefits			0.001 [0.001]	0.001 [0.001]	0.001 [0.001]	0.001 [0.001]	0 [0.001]	0 [0.000]
DV hotlines per 100,000 women					−0.852 [0.300]	−0.203 [0.232]	−0.313 [0.159]	−0.254 [0.181]
DV shelter beds per 100,000 women					0.007 [0.009]	0.005 [0.007]	−0.002 [0.004]	−0.001 [0.005]
City and year fixed effects	Y	Y	Y	Y	Y	Y	Y	Y
City-specific linear time trends	Y	Y	Y	Y	Y	Y	Y	Y
Share black and non-intimate partner homicide	Y	Y	Y	Y	Y	Y	Y	Y
County wages, employment to popuation ratio and AFDC benefits			Y	Y	Y	Y	Y	Y
Domestic violence services (hotlines and shelter beds)			Y	Y	Y	Y	Y	Y
Lag dependent variable					Y	Y		Y
Observations	1027	1027	1027	1027	978	978	1027	978
Robust standard errors (clustered on city) in brackets
Mean of dependent variable	6.71	10.1	6.71	10.1	6.71	10.1	181	181
Size of effect	−23%	−12%	−23%	−12%	−21%	−11%	−6%	−4%

Finally in the last two columns we estimate the impact of no-drop policies on non-intimate partner homicides as a “falsification test.” The estimates in column 7 are based on regressions in which we include the full range of controls except for the lag of the dependent variable and in column 8 we include the lagged dependent variable as well. The estimated impacts are negative, small in magnitude (6 and 4 percent) and insignificant.

We also estimate the impact of no-drop policies on intimate partner homicide stratified by age of the victim (35–54 years of age and 20–34 years of age). If no-drop policies lead to a decline in male homicides because of substitution of commitment devices, then we argue that we should find greater effects among older men and women who would have time to learn of their difficulty committing. When we stratify (Table 6), we find that the impact of no-drop policies on intimate partner homicide is considerably stronger for older victims (−0.42, or 34 percent, for older males and −.23, or 21 percent, for younger males.) The estimates are still small and insignificant for women, regardless of age. These findings are consistent with the notion that women need time to learn of their difficulty to commit to leaving without any commitment device.

Table 6.

Impact of No-Drop Policies on Intimate Homicides Stratified by Age of the Victim, 49 Cities

	Older Victims		Younger Victims
	Male	Female	Male	Female
No-drop policy	−0.42 [0.209]	−0.097 [0.150]	−0.23 [0.127]	−0.126 [0.099]
Adult non-intimate homicides per 10000	0.115 [0.132]	0.059 [0.080]	0.117 [0.139]	0.091 [0.065]
Share population black	−0.039 [0.049]	0.139 [0.071]	0.05 [0.092]	−0.117 [0.094]
Observations	1027	1027	1027	1027
Robust standard errors (clustered on city) in brackets
All regressions include city and year fixed effects and city-specific linear time trends
Mean of dependent variable	3.46	3.84	3.25	6.26
Size of effect	−34%	−9%	−21%	−12%

6.3.3 Robustness

In this section we perform a number of robustness checks. First, to assess whether the results are driven by one city, we estimate 49 separate regressions dropping one city from each. We find that they are not.

An additional concern is that the estimates of the effect of no-drop policies may be capturing downward trends in homicides which are not controlled by year fixed effects or the city specific linear time trends. As a second robustness check, we randomly generate no-drop policies and estimate the impact of these randomly generated laws on male and female intimate partner homicide. We repeat this exercise 1000 times. The randomly generated no-drop policy has no significant impact on either the number of men or women killed by intimates which suggests that the significant results that we obtain are not driven by downward trends in homicides unrelated to the adoption of no-drop policies.

Finally, it may be that the adoption of no-drop policies coincides with the adoption of other policies that address domestic violence, in which case our estimates of the impact of no-drop policies on intimate partner homicide may suffer from omitted variable bias. To address this issue we present results of negative binomial regressions that include controls for other domestic violence policies for the full male sample and stratified by age in Table 7. These policies include: whether the police have a separate domestic violence unit, whether there is a “pro-arrest” policy for violation of a protection order and whether the city has a mandatory arrest policy.³¹ Of these additional covariates, only the policy pro-arrest policy for parole violator has a negative and significant impact on homicides. The inclusion of the additional controls for other domestic violence policies does not diminish the negative and significant impact of no drop policies on male intimate partner homicides.

Table 7.

Impact of No-Drop Policies on Intimate Partner Homicide of Males Controlling for other Domestic Violence Policies, 49 Cities

	All	Old	Young
No-Drop policy	−0.245 [0.133]	−0.455 [0.197]	−0.173 [0.109]
Adult non-intimate homicides per 10000	0.103 [0.119]	0.12 [0.131]	0.112 [0.150]
Share population black	−0.006 [0.049]	−0.015 [0.065]	−0.022 [0.072]
Average wage	0.013 [0.062]	0.057 [0.081]	−0.013 [0.074]
Employment to population ratio	0.289 [0.669]	1.256 [1.030]	−0.359 [1.024]
AFDCbenefits	0.001 [0.001]	0.001 [0.001]	0.001 [0.001]
DV hotlines per 100,000 women	−0.65 [0.230]	−0.542 [0.356]	−0.75 [0.312]
DV shelter beds per 100,000 women	0.001 [0.007]	−0.004 [0.009]	0 [0.009]
Police pro-arrest policy for PO violation	−0.355 [0.153]	−0.473 [0.156]	−0.384 [0.248]
Mandatory arrest for domestic violence	0.126 [0.159]	0.168 [0.162]	0.122 [0.241]
Police domestic violence unit	−0.14 [0.145]	−0.493 [0.214]	0.101 [0.176]
Observations	1027	1027	1027
Robust standard errors in brackets
All regressions include city and year fixed effects and city-specific linear time trends
Mean of dependent variable	6.71	3.46	3.25
Size of effect	−22%	−37%	−16%

In sum, the data support the prediction of our model that the number of batterers who are murdered unambiguously declines with the adoption of no-drop policies. Our findings with respect to females are smaller and insignificant (recall that the model provides no prediction with respect to the effect of no-drop policies on violence against women). We argue that these findings provide evidence against an alternative theory by which women value commitment for strategic reasons to shield them from violence or threats intended to change their minds. If they did, violence against women measured by assaults and intimate partner homicides should also decline, which they do not.

7. Conclusions

Motivated by the cyclicality of violent relationships we present a theory of domestic violence that incorporates time inconsistent preferences. Our theory predicts that the adoption of no-drop policies would result in an increase in the reporting of battering to the authorities and, more surprisingly, a decrease in the murder of violent partners. The reason for the latter is that no-drop policies provide women in battering relationships a cheaper commitment to end the relationship than murder.

Consistent with our theory we provide evidence that the adoption of no-drop policies in the US have resulted in a reduction of male homicides by intimates and an increase in reporting of battering. Finally, we find that no-drop policies have had no significant effect on the prevalence of domestic violence as measured by female intimate homicide and female hospitalizations for assault.

Our results underscore the importance of considering the value of commitments when evaluating policies. In particular, we provide evidence that agents may substitute a cheaper public commitment device when one is offered for a more expensive private one.

Appendix Table 1.

Means for 49 City Sample

Number of Male Intimate Partner Homicides	6.8
Number of Female Intimate Partner Homicides	10.8
Rate of Male Intimate Partner Homicides per 100,000	1.3
Rate of Female Intimate Partner Homicides per100,000	1.8
Non-intimate Partner Homicides	244
Rate of Non-intimate Partner Homicides per 100,000	16.7
Share black	0.23
AFDC benefits family of 4	0.464
Male median earnings (in 1000s)	0.738
Female median earnings (in 1000s)	0.554
% of men 25 + with at least 4 yrs college	24
% of females 25 + with at least 4 yrs college	18
Shelter beds per 100,000 women	15.47
Domestic Violence hotlines per 100,000	0.641

Appendix Table 2.

Means for Seven Counties in California Sample

	All	White	Black	Hispanic
Number of Female Assauults	128	77	198	168
Rate of Female Assaults per 100,000 women	34.3	19.37	136.17	24.07
Number of Male Arrests for Domestic Violence	3333	1635	2443	5674
Rate of Male arrests for Domestic Violence per 1000 men	7.03	3.85	18.34	7.76
Number of Non-intimate Homicides	226	69	256	397
Rate of Non-Intimate Homicides per 100,000	16.32	4.43	51.96	20.88
Per capita income	$27,630
Employment to population ratio	0.484
Shelters per 100,000 women	1.9
Calls reporting domestic violence per 100,000 women	3584
Means weighted by number of women age 15–44
Calls excludes San Francisco