Abstract
We conducted field experiments at a bar to test whether blood alcohol concentration (BAC) correlates with violations of the generalized axiom of revealed preference (GARP) and the independence axiom. We found that individuals with BACs well above the legal limit for driving adhere to GARP and independence at rates similar to those who are sober. This finding led to the fielding of a third experiment to explore how risk preferences might vary as a function of BAC. We found gender-specific effects: Men did not exhibit variations in risk preferences across BACs. In contrast, women were more risk averse than men at low BACs but exhibited increasing tolerance towards risks as BAC increased. Based on our estimates, men and women’s risk preferences are predicted to be identical at BACs nearly twice the legal limit for driving. We discuss the implications for policy-makers.
Keywords: Rationality, Expected utility theory, Risk aversion, Field experiment, Alcohol
Many kinds of economically and personally impactful decisions are made by individuals under the influence of alcohol: choices about additional alcohol consumption; choices about gambling strategies;1 choices about sexual partners; choices about whether or not to get behind the wheel of a car. Consider, for example, some of the economic and personal consequences associated with drunk driving: In 1997 more than 1.4 million driving while intoxicated (DWI) citations were issued. It is also difficult to estimate the individual economic impact of DWI citations but some studies suggest that it is as high as $40,000.2 In 2004 39% of the 42,800 traffic fatalities involved alcohol.3 Or consider the raw economic impact of alcohol: In 2009 some 572 million gallons of (pure) ethanol were consumed in the U.S.,4 resulting in nearly $100 billion in real (off-premises) sales.5 And if our measurements are representative of blood alcohol levels experienced by most people making choices about alcohol consumption, Americans make at least $90 billion of alcohol consumption decisions at non-zero blood alcohol concentrations (BACs).6
The consequences with regard to health and safety costs relating to alcohol consumption, to examine another domain, are serious enough that they have led to the development of numerous public policies intended to shape the behavior of individuals intoxicated by alcohol: For example, all 50 U.S. states prohibit the sale of alcohol to intoxicated individuals. This suggests a conviction by some policy-makers that intoxicated individuals lie beyond the pale of rational incentive structures.7 Twenty-seven states have some form of time-dependent price-controls on the sale of alcohol at bars (i.e. the prohibition of “happy hours” or “ladies nights”), suggesting a conviction that intoxicated decision-makers are sensitive to incentives but in different ways at different levels of intoxication.8 But is there an economic rationale for these policies? Are policies which preclude drunk people from purchasing additional alcohol really based on the idea that intoxicated humans will not respond to incentives in a rational manner? Is there evidence that choice consistency is in fact dramatically compromised when blood alcohol levels are elevated? Are policies aimed at modifying the risky-behavior of individuals intoxicated by alcohol making the opposite assumption? For example, do additional sentencing penalties for drunk drivers with high blood alcohol concentrations suggest a conviction that risk-attitudes change when BACs are high? Economic analysis can model risky choices made under the influence and inform these policies if sufficient data are available. But in order to do so, economists must first empirically investigate some basic questions about how the choices of individuals can be affected by alcohol.
Over the course of the last several decades, economists have addressed these issues by developing a number of highly influential theoretical models that predict and explain these behaviors as well as specifying interventional strategies. Foremost among these is the Becker and Murphy (1988) model of rational addiction. In that model, consumers of addictive drugs are proposed to behave as traditional expected utility maximizers, but with an innovative notion of “addictive capital.” A number of both variants of the Becker and Murphy model and counter-proposals have been developed, but nearly all share the quality that choosers are viewed as normatively rational expected utility maximizers. All of these rational choice models make clear statements about interventional policies, but perhaps surprisingly very few of the behavioral assumptions of these models have been empirically validated. This paper is the first step towards testing this class of model with experimental tools in an ecologically valid field environment — an American bar.
The natural starting point toward any choice-based assessment of the behavior of drunk people with regard to existing models of intoxicant-related behavior is to determine whether choosers really do behave rationally while they are under the influence. So we begin our field study with tests of whether the choices of drunk people are consistent with utility maximization, a central assumption maintained by this class of model. We do this by assessing whether blood alcohol concentration (BAC) is related to violations of the generalized axiom of revealed preference (GARP). The generalized axiom is a necessary and sufficient condition for utility maximization. So systematic and widespread failures of GARP observed in drunk choosers would be enormously informative. In addition to suggesting that formal economic analyses of the behavior of drunk people would then be impossible, such a finding would lend significant economic credibility to bans on alcohol purchases by the intoxicated —bans challenged by rational choice models of these choosers. If drunk choosers are wildly inconsistent in their choice behavior, then incentive structures aimed at reducing everything from highway fatalities to teenage pregnancies must respect this fact. Our data, however, suggest that there is no meaningful relationship between measured BAC and choice consistency as measured by GARP, a finding which supports this general class of model.9
Next, given the prevalence of risky choices (and policies aimed at shaping the risky choices) made by intoxicated individuals, we turn our attention to the baseline economic model of choices over risk employed by these models: expected utility. We investigate whether the choices of drunk people can be consistent with the expected utility (EU) hypothesis by examining violations of the independence axiom, a critical representational condition for EU-maximization, and then explore how BAC changes risk preferences. Systematic violations of the independence axiom (IA) by drunken choosers would raise serious questions about applying the baseline EU model to the risky choices of drunk people and much more critically would raise the question of whether or not these choosers would respond to probabilistic incentives in a consistent manner. For the independence axiom our results are less clear-cut: Intoxicated individuals make more violations of independence in our experiment but the magnitude of this difference is quite small. An average agent in our sample who goes from a BAC of 0.000% (sober) to a BAC of 0.100% (a level well above the legal limit for driving in most U.S. states) would just be beginning to show an economically detectable increase in the frequency/likelihood of additional violations of independence. Thus, while even the sober participants in our experiments cannot be considered perfect EU-maximizers (an observation consistent with many previous reports), we conclude that for most commonly experienced BACs, alcohol does not significantly impair the applicability of the baseline EU model. This result is significant because it indicates, in broad strokes, that even subjects with high BACs are sensitive to risk and it is this kind of sensitivity that is required for many classes of incentive structures to be effective.
Finally, with the observation that drunk choosers can both be seen as consistent and sensitive to risk, we turn our attention to examining how risk preferences themselves might be affected by BAC (in our population). The critical insight here is that policies aimed at modifying the behavior of drunk people could have unintended consequences if the risk preferences of drunk individuals deviate significantly from those of sober agents. For example, consider the possibility that drunk people could be generally risk loving while the same people are risk averse when sober. In that case, policies aimed at changing the risk-profile of drunken decision making could, counterintuitively, result in increases in risky behavior. Thus, we conduct a third experiment intended to measure risk aversion. We calibrate random utility models with a systematically varying constant relative risk aversion (CRRA) utility (Bernoulli) function and we find evidence for gender-specific changes in risk preferences across BAC. On average, we found men to be more risk-tolerant than women (consistent with previous findings in the experimental literature; Eckel and Grossman (2008); Croson and Gneezy (2009)) and (perhaps surprisingly) we found that risk preferences in men showed little variation as a function of BAC. In contrast, we found that risk-aversion in women declined as a function of BAC in such a way that the risk preferences of intoxicated men and women are predicted to be identical at BACs of about 0.150%, nearly twice the legal limit for driving. These results suggest that policies aimed specifically at modifying the risky behavior of intoxicated individuals might be less effective for women than predicted with estimates based on their behavior while sober (or estimates based on the behavior of men) and this suggests, from a policy level, that traditional incentive structures may have more effect on male than on female drinkers.
To develop these points, this paper is divided into six sections. The next section explores the connections of our research to literatures in economics, psychology, and physiology. Section 2 details our sampling and measurement designs. The subsequent three sections discuss our experiments designed to assay adherence to (i) GARP and (ii) IA, and (iii) to measure risk preferences. The final section discusses our results and suggests some directions for future research.
1 Background
Our paper has two broad research foci. The first focus is whether BAC can compromise choice consistency. The second focus is whether either consistency with regard to risk and risk attitudes varies with BAC. These two foci have connections to several literatures. We begin first by discussing how these foci are related to some extant theoretical and empirical work in the economic literature, and then to the physiology and psychology literatures.
Both of our research foci have strong connections to the rational addiction literature pioneered by Becker and Murphy (1988). Becker and Murphy argued that drug users could be viewed as consistent, that they respond to traditional incentive mechanisms when they are under the influence. Recently, Bernheim and Rangel (2004) challenged this view, at least in part, by suggesting that while choosers may behave in a locally consistent fashion, meaningful differences in preferences might arise across states of intoxication. Gul and Pesendorfer (2007) have explored a related model intended to capture the features of a “harmful” addiction. Their work distinguishes between compulsive and non-compulsive consumption in a consistent framework and assesses both price sensitivity and welfare under these assumptions. The Bernheim and Rangel (2004) and Gul and Pesendorfer (2007) models and others like them in the literature (Benhabib and Bisin 2005; Fudenberg and Levine 2006), explicitly assume that within each of the possible states a chooser can experience, their choices are consistent (i.e. that choices adhere to GARP, when one can assume the existence of Walrasian budgets). Thus, for these classes of models choosers are 1) assumed to be rational and consistent at any given blood level of an addictive substance and 2) that the preferences of these agents are a function of addictive substance blood level.10 Oddly, despite wide discussion of these models, and the fact that meaningful policy implications are drawn from them, neither the sensitivity of state-specific rationality to drug consumption, nor whether preferences change across states in such a way that would induce apparent global inconsistencies, appears to have been the subject of any behavioral test whatsoever for any drug of abuse. Here we begin to contribute to this literature by offering empirical data bearing on the assumptions made in these models.
Our experiments and results can also inform the extensive literature that empirically investigates how policies can shape risky behaviors related to alcohol (e.g. drunk driving and demand for alcoholic beverages).11 A recent exemplar of work in this area that could be informed by our experiments is Jackson and Owens (2011) who find that for exogenous changes in Washington D.C. train schedules, DWI arrests and fatal traffic accidents decline in geographic areas that are within walking distance of transit stations. However, what is unclear from that report is whether this finding is principally due to drinkers using behavioral strategies for pre-commitment that are employed while sober (i.e. leaving the car at home before a night out drinking) or, whether individuals optimize over transportation choices once intoxicated. That we find intoxicated individuals are weakly consistent with the EU-maximization hypothesis indicates that the latter remains a plausible explanation. Of course for a policy-maker this leaves open the possibility that policies aimed specifically at the population of individuals acutely intoxicated by alcohol could be as efficient as policies aimed at encouraging pre-commitment if those policies respected empirically observed preference structures of intoxicated choosers.
That individuals intoxicated by alcohol remain rational in their choosing may also have some potential implications for law, particularly with regard to consequentialist approaches. In some states, high blood levels of alcohol can mitigate a defendant’s culpability for violent actions. Were high blood alcohol levels to be associated with decreased rationality, then one might argue that both the consequentialist and deontological legal approaches would support such a view. But if the intoxicated are both consistent and risk-sensitive, then consequentialist considerations (at the very least) would argue against the notion that high BACs should mitigate culpability and punishment.
Our experiments can also be informative for questions about whether economic experiments conducted in lab settings are consistent with results from the field (Levitt and List 2007; Camerer 2011) because, where possible, we adapted previously published and validated experimental designs to assess our hypotheses. The experiment we used to assay adherence to GARP is adapted from the design used by Harbaugh et al. (2001) to examine the relationship between age and violations of GARP.12 Our experiment to measure risk preferences was adapted from the design of Holt and Laury (2002) and Holt and Laury (2005). Our approach to the independence axiom was more novel (which is the result of institutional constraints and a desire to be consistent across probability and prize spaces between our two experiments with money lotteries) but respects the fact that it is often violated, even by trained economists (Allais 1953; Kahneman and Tversky 1979; Wu 1994; Wu and Gonzales 1998; Prelec 1998).13 Because we use previously published and validated laboratory experiments, this permits us the opportunity to place our findings from the field setting into the context of previously published, lab-based results. The results from our experiments, discussed in the respective experimental sections below, are quite similar with those found in lab settings which would be consistent with the view that findings from laboratory experiments can be representative of choices made in the field (Camerer 2011). This result seems especially striking given that our samples are principally comprised of individuals that have non-zero BACs, many of which are too drunk to legally drive.
While examining the acute effects that drugs of abuse have on choice behavior has been rare in the economics literature,14 the psychological and medical literatures have carefully explored how alcohol intoxication can affect behavior. But these literatures do not focus on economic concepts such as consistency and preferences which lie at the heart of every economic model. One example of this is the psychological hypothesis that elevated BACs induce what is called “alcohol myopia” (Steele and Josephs 1990). This theory posits that alcohol intoxication makes reactions to prominent stimuli more extreme. An example of risky choice data consistent with this psychological theory is discussed by MacDonald et al. (2000). MacDonald interprets this theory as accounting for intoxicated individuals’ stated intentions to engage in unprotected (risky) sex at a higher level. That there is a large body of evidence consistent with the theory of alcohol myopia suggests some potential cautions when interpreting our experimental results. It could certainly be the case that the particular presentation of stimuli in our experiments creates more or less consistency, or drives risk preferences in a specific direction, an issue that has been explored extensively in the decision-making literature for the risky choices of sober individuals (Moskowitz 1974; Keller 1985).
While most of the investigations in the physiology and psychology literatures tend to focus on behaviors relating to information processing, motor performance, aggression, and social interactions, several of these studies have explored how risky choices are influenced by alcohol, although with techniques that differ from those that would be undertaken by economists. An example of such a study is Lane et al. (2004). In that report, the number of times a subject selects a lottery that has a lower expected value than a degenerate, reference lottery increases with alcohol administration. While from an economic perspective the design and analysis of that study can make it difficult to disentangle learning and wealth effects from risk preferences, it is consistent with the picture painted by studies such as Fromme et al. (1997) and Lane et al. (2008)15 that implicate alcohol in lowering inhibitions, which is hypothesized to result in increases in risk taking.
Using this extensive work from psychology and physiology as motivation we pursue economic questions aimed both at theoretical implications and relevance to policy: We employ traditional economic tools to examine how the theoretical representation of choices is related to BAC. With evidence in hand that drunk individuals are (weakly) consistent with an EU representation, we proceed naturally toward assessing whether Arrow-Pratt risk aversion varies with BAC. While institutional constraints mandated that we employ a between-subjects approach to our questions, our data can speak clearly to the behavior of agents in economically significant settings.
2 Experimental methods
All experimental participants provided verbal informed consent after reading a consent document as approved by NYU’s Institutional Review Board. Our consent procedure did not permit signing of a consent form, so as to guarantee the anonymity of participants. Each participant was, however, required to correctly answer four out of five questions about the consent document before they could participate in the experiment.16
After obtaining consent, each participant went through a computerized (E-Prime 1.2; Psychology Software Tools Inc., Sharpsburg, PA) practice and instructional session (5–10 minutes) that detailed the objects of choice and the incentive-compatible payment mechanism. This instructional session was followed immediately by the computerized decision-making portion of the experiment.
Each of the choice-situations in the three experiments were presented one-at-a-time and in random order. At the conclusion of the experiment one choice-situation was selected randomly to be realized for payment. The experimental software randomly selected the choice-situation, and indicated the participant’s choice. If a non-degenerate lottery was selected the uncertainty was resolved using either a 100-sided die or a 10-sided die, as required. Participants then provided a breathalyzer reading, received their incentive-compatible payment, and signed a receipt.17
BAC was measured with an AlcoHawk PT500 (Q3 Innovations LLC, Independence, IA) which estimates BAC by measuring breath alcohol concentration.18 This meter provides U.S. Department of Transportation precision (±0.002% BAC) and is analytically identical to breath alcohol meters used by law enforcement agents.19 All participants were provided with a new, sterile breathalyzer mouthpiece that was discarded after use.
2.1 Sampling
All experimental participants were recruited between 8 p.m. and 1 a.m. (the following morning) on Tuesdays or Wednesdays from a population of customers at a bar in Manhattan’s Lower East Side neighborhood. These times were employed because (i) it was easier to explain the instructions to participants when the bar was less crowded and (ii) because the bar permitted us to recruit participants from among their patrons on these days.
2.2 Physiology, females, and blood alcohol concentration
A given level of ingested alcohol is known to result in different blood alcohol concentrations for different people and the factors that can affect this are numerous: body weight, proportion of lean body mass, hydration level, time since last meal, content of previous meal, genetic pre-disposition toward levels of alcohol dehydrogenase (the enzyme used to metabolize alcohol in vivo), and recent (48-hour) drinking history (Meyer and Quenzer 2005; Iversen et al. 2009). Table 1 details estimated blood alcohol concentrations for both men and women for a range of ingested alcohol and body weights and Table 2 details the physiological effects of various blood alcohol concentrations for both sexes.
Table 1.
Estimated blood alcohol concentrations (Male/Female;%)
| Standard drinks | Body weight in pounds
|
|||||||
|---|---|---|---|---|---|---|---|---|
| 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | |
| 1 | .04/.05 | .03/04 | .02/.03 | .02/.03 | .02/.03 | .02/.02 | .02/.02 | .02/.02 |
| 2 | .08/.09 | .06/.08 | .05/.07 | .05/.06 | .04/.05 | .04/.05 | .03/.04 | .03/.04 |
| 3 | .11/.14 | .09/.11 | .08/.10 | .07/.09 | .06/.08 | .06/.07 | .05/.06 | .05/.06 |
| 4 | .15/.18 | .12/.15 | .11/.13 | .09/.11 | .08/.10 | .08/.09 | .07/.08 | .06/.08 |
| 5 | .19/.23 | .16/.19 | .13/.16 | .12/.14 | .11/.13 | .09/.11 | .09/.10 | .08/.09 |
| 6 | .23/.27 | .19/.23 | .16/.19 | .14/.17 | .13/.15 | .11/.14 | .10/.12 | .09/.11 |
| 7 | .26/.32 | .22/.27 | .19/.23 | .16/.20 | .15/.18 | .13/.16 | .12/.14 | .11/.13 |
| 8 | .30/.36 | .25/.30 | .21/.26 | .19/.23 | .17/.20 | .15/.18 | .14/.17 | .13/.15 |
| 9 | .34/.41 | .28/.34 | .24/.29 | .21/.26 | .19/.23 | .17/.20 | .15/.19 | .14/.17 |
| 10 | .38/.45 | .31/.38 | .27/.32 | .23/.28 | .21/.25 | .19/.23 | .17/.21 | .16/.19 |
One standard drink is 1.25 oz. of 80 proof liquor, 12 oz. beer, or 5 oz. wine
This is a reproduction of Table 9.1 in Meyer and Quenzer (2005)
Table 2.
Blood alcohol concentration and effects on behavior
| BAC (%) | Behavior |
|---|---|
| .02 – .03 | Minimal effects; slight relaxation; mild mood elevation |
| .05 – .06 | Decreased alertness; relaxed inhibitions; mildly impaired judgement |
| .08 – .10 | Loss of motor coordination; slower reaction times; less caution |
| .14 – .16 | Major impairment of mental and physical control; slurred speech; exaggerated emotions; blurred vision; serious loss of judgement; large increases in reaction time |
| .20 – .25 | Staggering; inability to walk or dress without help; tears or rage with little provocation; mental confusion; double vision |
| .30 | Conscious but in a stupor; unaware of surroundings |
| .45 | Coma; lethal for 50% of the population |
This is a reproduction of Table 9.2 in Meyer and Quenzer (2005)
Close examination of Table 1 reveals that for the same body-weight and amount of ingested alcohol, women tend to exhibit higher BACs. The explanations for this phenomenon are (i) conditional on body weight, women tend to have less lean-body mass than men and alcohol is more readily absorbed by bodies with less lean-body mass (Meyer and Quenzer 2005). And (ii) women generally exhibit lower levels of alcohol dehydrogenase (Meyer and Quenzer 2005; Iversen et al. 2009).
Across all three of our experiments, female participants exhibited higher average blood alcohol concentrations than male participants. The explanation for this doubtless rests on the differences between female and male physiology detailed above (in addition to the observation that women tend to weigh less than men in samples like ours), combined with social norms related to drinking at bars: People tend to go to a bar in groups and to imbibe roughly the same total amount of alcohol. The resultant positive relationship between gender and BAC is an important consideration as we use statistical tools to assess potential relationships between BAC, GARP violations, independence axiom violations, and risk preferences: omitting a variable that is correlated with an included variable can result in biased parameter estimates. To address this concern we therefore included in all of our statistical estimations a binary variable indicating the gender of the participant.
3 GARP experiment
Does alcohol intoxication compromise individual responses to incentives? To assess whether intoxicated individuals will respond to incentives we employ traditional economic reasoning by testing whether the choices of drunk people adhere to the generalized axiom of revealed preference at rates similar to sober individuals. The generalized axiom provides a convenient way to examine this question because it generates testable conditions on economic observables (prices and demands). In addition, the sensitivity of GARP to alcohol intoxication has never previously been explored.
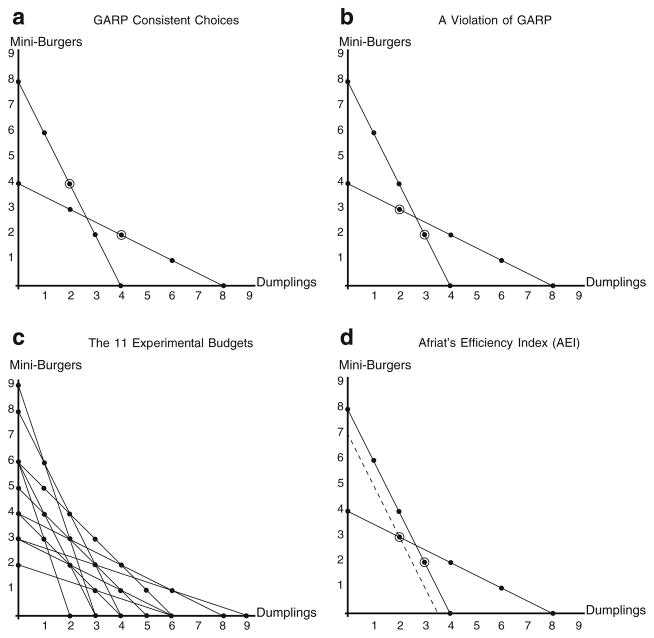
Our experiment designed to assay adherence to GARP consisted of 11 Walrasian budgets such as those depicted in Fig. 1a through d. Each of the choice-situations involved explicit tradeoffs between two types of food items served at the bar. Figure 2 displays two different screen shots from the experimental software. Figure 2a depicts the alternatives in the shallow budget in Fig. 1a and b, while Fig. 2b depicts the alternatives in the steep budget in Fig. 1a and b.
Fig. 1.
GARP violations, experimental design, and Afriat’s Efficiency Index
Fig. 2.
Two screen shots from the GARP experiment
The hollow circles in Fig. 1a depict a subject’s choices from those two budgets that do not involve a cycle. In contrast, the hollow circles in Fig. 1b depict a different set of choices which do involve a choice cycle, and thus violate GARP.
The full set of 11 Walrasian budgets is depicted in Fig. 1c. The choice options available appear as dots in the figure and include all the integer bundles of goods available from the 11 budgets. This set of budgets is identical to those used by Harbaugh et al. (2001) and Andreoni and Miller (2002) to assess the transitivity of children’s choices for food/drink items, and the transitivity of choices in the Dictator Game.20
3.1 Sample
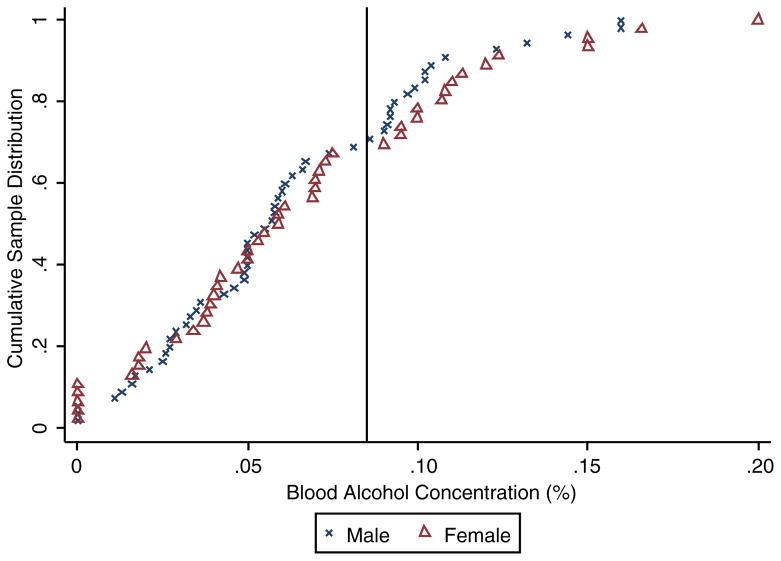
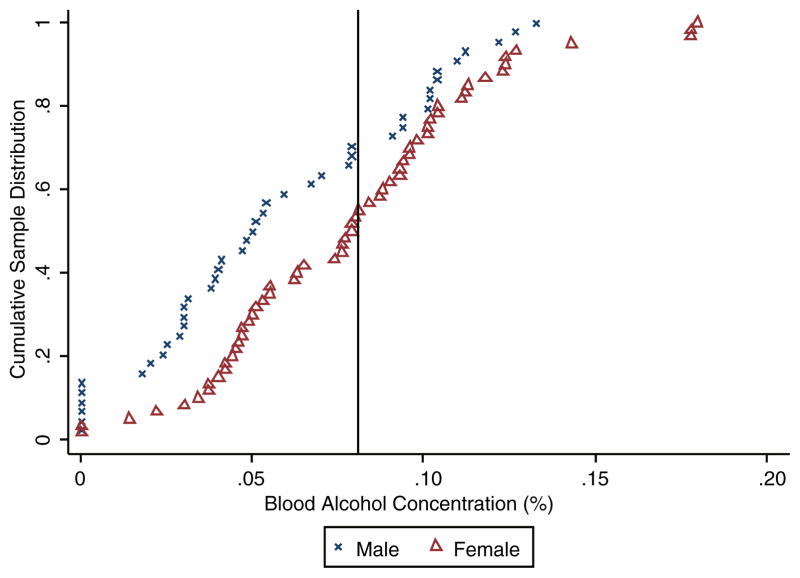
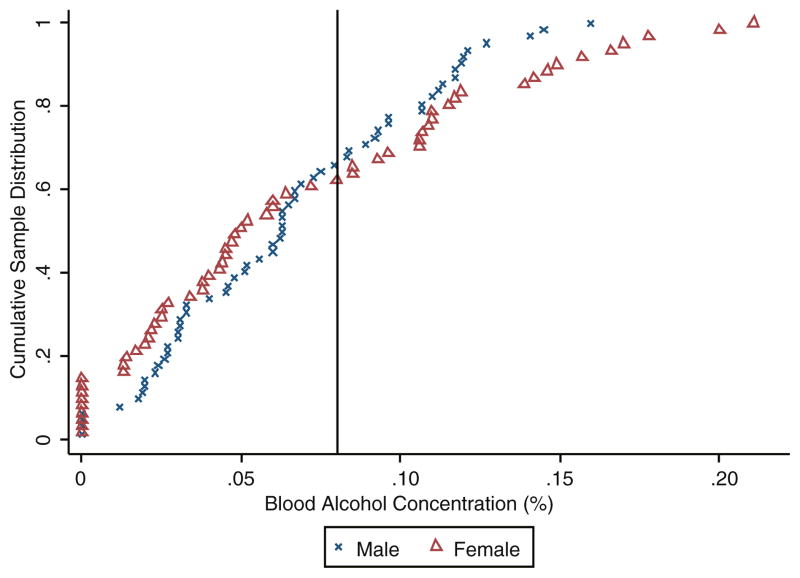
Table 3 reports summary statistics for participants in the GARP experiment. This sample is comprised of 101 individuals: 55 men and 46 women, at an average BAC of 0.062% and 0.066%, respectively. There is no statistically significant difference in average BACs observed between men and women in this sample. Figure 3 depicts the cumulative sample distributions of BAC for both men (crosses) and women (triangles). As manifested by the uniform slope of this cumulative sample distribution function between BACs of 0.020% and 0.125%, our GARP sample includes a fairly uniform distribution.
Table 3.
GARP sample BAC characteristics
| N | Mean | Std. Dev. | Min. | Max. | |
|---|---|---|---|---|---|
| Male | 55 | 0.062 | 0.039 | 0.000 | 0.16 |
| Female | 46 | 0.066 | 0.047 | 0.000 | 0.200 |
| Total | 101 | 0.064 | 0.043 | 0.000 | 0.200 |
All numbers (except sample sizes) are % BAC
Fig. 3.
GARP sample BAC cumulative distributions. The solid vertical line depicts 0.080% BAC, the legal driving limit in many U.S. states
3.2 Measures
Adherence to the Generalized Axiom is discrete: subjects either adhere to GARP or they do not. And, while it may be illustrative to consider how strict adherence to GARP is related to BAC, a more typical approach is to determine the “severity” of observed violations. When choices are made over Walrasian budgets, one classic measure of severity is Afriat’s Efficiency Index (Afriat 1967; Varian 1982). Afriat’s Efficiency Index (AEI) is the proportional distance that a Walrasian budget must be moved back toward the origin to absorb an observed transitivity violation. Figure 1d provides a graphical depiction: the choices (indicated by the hollow circles) violate GARP. The budget line would have to be shifted to the dashed line in (d) to completely absorb this violation. For Walrasian budgets, the value of (1 − AEI) can thus be interpreted as the proportion of a chooser’s wealth wasted through cycles.
An alternative measure of GARP violation severity is the Houtman-Maks (HM) index (Houtman and Maks 1985; Choi et al. 2007). HM is defined as the largest subset of all observed choices that do not include any cycles. HM has the benefit that it is more general than AEI: calculating HM does not require Walrasian budgets.
However, unlike the AEI, HM equally penalizes both “small” and “large” violations of GARP. For example, consider a set of 11 choices in which the AEI is 0.99 and the HM is 10. Only one of the choices represents a departure from adherence to GARP. However, the size of this violation is small because the chooser wastes only 1% of her wealth through this offending choice. In contrast, consider a set of 11 choices in which the AEI is 0.87 and the HM is again 10. As in the previous case only one choice violates GARP but the severity of that violation is quite large. For this reason we consider both the AEI and HM as dependent measures in our analyses although we relegate the analyses of HM to the online Appendix A, available from the author’s web site, for editorial brevity and because the qualitative findings are the same for both measures.
3.3 Analysis
3.3.1 Dependent variable: Afriat’s Efficiency Index
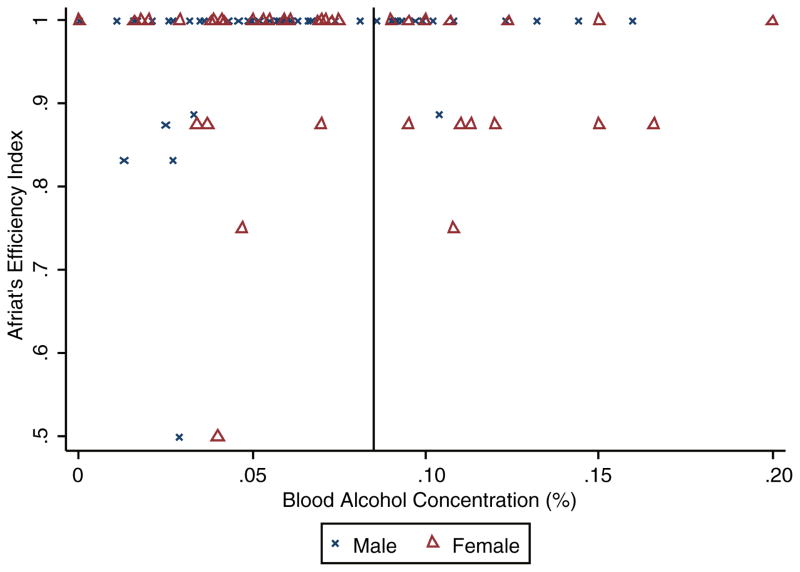
The scatter plot in Fig. 4a shows all of the AEI-BAC pairs of data for our sample which suggest little correlation even at surprisingly high BACs. Table 4 confirms this: of our 101 participants 82.2% have Afriat Indices of at least 0.999. The average AEI across all BAC levels is 0.967 which is similar to the average AEIs reported by Harbaugh et al. (2001) and Andreoni and Miller (2002).21 Our average AEIs also lie within the marginal distribution of AEIs reported by Choi et al. (2007) who use a different experimental design. Our average AEIs are also similar to the results reported by Sippel (1997).22
Fig. 4.
Afriat’s Efficiency Index and blood alcohol concentration. The solid vertical line depicts 0.080% BAC, the legal driving limit in many U.S. states
Table 4.
Afriat’s Efficiency Index and blood alcohol concentration
| Afriat’s Efficiency Index | N | Avg. BAC | Std. Dev. |
|---|---|---|---|
| 1.00 | 59 | .060 | .039 |
| 0.999 | 24 | .067 | .049 |
| 0.888 | 2 | .069 | .050 |
| 0.875 | 10 | .092 | .049 |
| 0.833 | 2 | .02 | .010 |
| 0.75 | 2 | .078 | .043 |
| 0.50 | 2 | .035 | .008 |
| 0.967a | 101 | .064a | .043a |
Sample averages
When we estimate models of the form,
| (1) |
where AEI is indexed by subject (i), BACi is measured blood alcohol concentration, and 1(Female)i is an indicator variable for sex, we do not find any statistically significant relationship between AEI and BAC across the range of BACs we measured. Also included in these models, but not reported in Table 5, are a set of control variables that capture which food-pairing, of the six possible combinations, the subject selected.
Table 5.
Regressions demonstrating no relationship between Afriat’s Efficiency Index (AEI) and Blood Alcohol Concentration (BAC)
| Variable | (1) | (2) | (3) | (4) | (5) |
|---|---|---|---|---|---|
| BAC | −0.118 (0.332) | 0.102 (0.320) | −0.290 (0.244) | −0.153 (0.232) | −0.077 (0.121) |
| Female | −0.086** (0.037) | −0.066** (0.031) | −0.065*** (0.024) | −0.053** (0.023) | −0.020* (0.011) |
| Constant | 1.101*** 0.037) | 1.134*** (0.049) | 1.084*** (0.027) | 1.103*** (0.036) | 1.005*** (0.011) |
| Est. type | Tobit | Tobit | Tobit | Tobit | OLS |
| Number Obs. | 101 | 101 | 99 | 99 | 99 |
| Censored Obs. | 59 | 59 | 59 | 59 | N.A. |
| Log likelihood | −12.0 | −7.4 | 4.7 | 6.7 | – |
| Pseudo R2/R2 | 0.197 | 0.508 | Not Def. | Not Def. | 0.114 |
| Food controls | No | Yes | No | Yes | Yes |
| Excl. Crit. | N.A. | N.A. | AEIi ≤ 0.675 | AEIi ≤ 0.675 | AEIi ≤ 0.675 |
Robust standard errors in parentheses. Significance at the 1% level is denoted ***, 5% as **, 10% as *
Models (1) through (4) in Table 5 report results from Tobit estimations with an upper limit of unity. The difference between models (1) and (2) (and models (3) and (4)) is the exclusion/inclusion of food-pairing controls in the estimating specification. The difference between models (1)/(2) and (3)/(4) are the exclusion of the two AEI outliers visible in the lower portion of panel (a) in Fig. 4: The two subjects with AEI s below the level of a simulated random chooser (AEI < 0.675; see Harbaugh et al. (2001)) are dropped from the estimating sample in models (3), (4), and (5).
The lack of variation in AEIi makes the Tobit results in Models (1) through (4) reported in Table 5 somewhat questionable: The positive, maximal log likelihood values suggest that our ability to identify parameter estimates is especially dubious. Model (5) employs ordinary least squares (OLS) as an identification mechanism and includes controls for food-pairings and excludes the two subjects with AEIi < 0.675 with no change in qualitative results: There thus does not appear to be a statistically significant relationship between BAC and AEI over the range of BACs and the choice sets we examined. In addition, the magnitude of these statistically insignificant parameter estimates is economically meaningless. Consider, for example, the parameter estimate for BAC in Model (5) of Table 5 and a representative Male subject who starts out sober (BAC = 0.000%) with an AEI of 1.00. Our data suggest that this representative subject would need to arrive at a BAC of 0.650% to reduce his AEI to 0.95 on our choice sets, a commonly-used threshold to declare a chooser as “irrational.” We note that this BAC would be lethal for the representative agent (see Table 2). The results that emerge from these regressions (and for analyses of the Houtman-Maks measure, reported in the online Appendix A) indicate that alcohol does not appear to statistically or economically compromise response to incentives in our population, for the BACs we observe.
4 Independence experiment
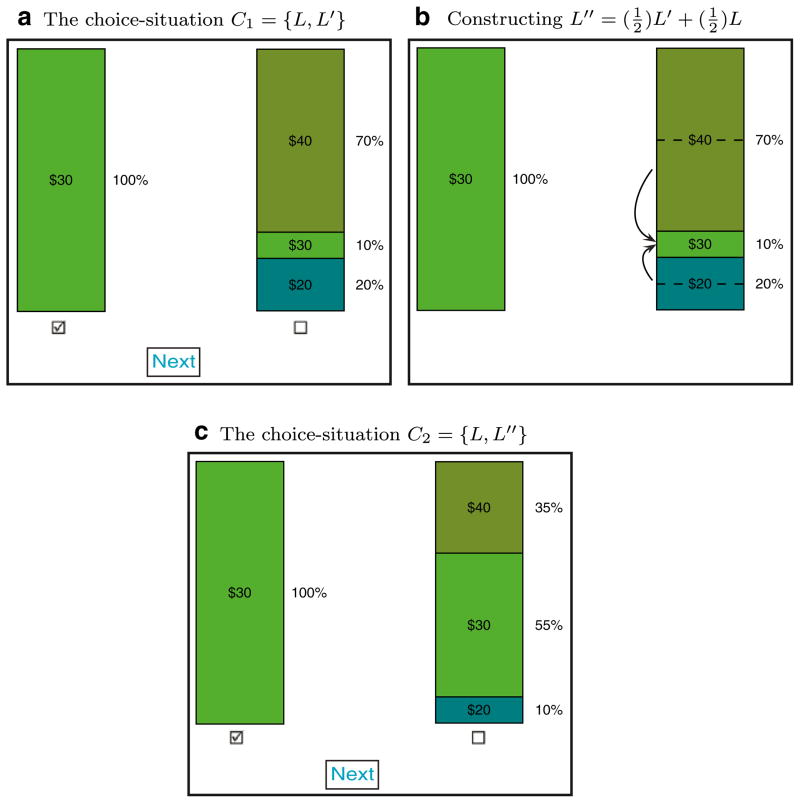
With the observation that choosers with extremely high BACs will, at a very basic level, respond to incentives, we turn our attention to assessing how alcohol might compromise response to incentives with an element of risk. We ask whether the risky choices made by drunk people can be consistent with the baseline economic model of choices that involve known probabilities: expected utility. The critical feature of choices that would respond in a manner consistent with EU would be adherence to the independence axiom at similar rates across a wide range of BACs. Thus, we fielded an experiment designed to assay adherence to the independence axiom.23 This experiment presented participants with 45 choice-situations in the form of visually displayed monetary lotteries. As shown in screen shots from our experimental software in Fig. 5a and c, each choice-situation involved a decision between a certain $30 and a “lottery” with three possible prizes.24 Each alternative in the experiment was presented graphically with probabilities proportional to the areas of a vertically oriented rectangle. The prizes were also represented by unique colors.25 In addition, all prize and probability information was presented numerically “on top” of these graphical displays.
Fig. 5.
Construction of choice-situation-pairs. The choice-situation-pair, {C1, C2}, can be used to test the independence axiom
Our experiment includes 30 choice-situations designed to assay adherence to the independence axiom and these 15 choice-situation-pairs (CSPs) were all designed in a similar way: each of these choice-situations include a lottery in which the three possible prizes are less than, equal to, and greater than $30. Adopting the notation that L is the certain $30 and L′ is the lottery, all of our choice-situation-pairs (C1, C2) take the following form:
Choice-situation C1: {L, L′}
Choice-situation C2: {L, L″} where
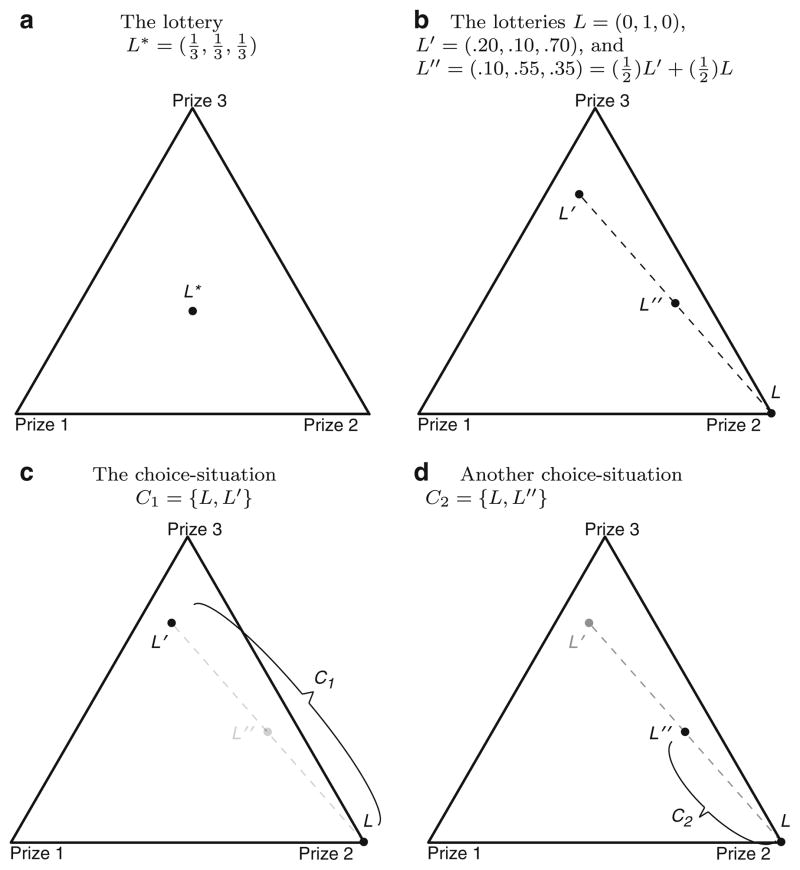
Graphically, there are two ways to depict the constructions of these CSPs. The first is through a “re-shuffling” of the probabilistic masses attached to each of the prizes. Consider Fig. 5a which represents a choice between $30 for sure and a lottery L′ = (0.70, 0.10, 0.20) over the prize space Z = {$40, $30, $20}. To produce a choice-situation that can be used to assay adherence to IA, we split in half the probabilistic masses associated with the $40 and $20 prizes and place them on the $30 prize: . The result is the choice-situation depicted in Fig. 5c. The choice-situation-pair in Fig. 5a and c can be used to test for violations of IA.
An alternative way to depict our choice-situation-pairs is with a unit simplex. As shown in panels (a) through (d) of Fig. 6 the unit simplex is a two-dimensional depiction of the plane x + y + z = 1 in , from the perspective along the ray (1, 1, 1). Any point in the simplex is a (two-dimensional) representation of a probability distribution over the three prizes at the vertices of the simplex. Figure 6a depicts the lottery which corresponds to the centroid of the unit-simplex. Depicted in Fig. 6b is a set of three lotteries, L, L′, and L″. Note that L″ is the convex combination of L and L′ with . As shown in Fig. 6c and d these lotteries can be organized as two choice-situations, C1, and C2 that can be used to test for violations of IA. Specifically, if L′ ≳* L, the independence axiom requires that L″ ≳* L. If, however, the lottery L was selected over L″ (when L′ was also selected over L) this would be a violation of IA.
Fig. 6.
Construction of choice-situation-pairs. The choice-situation-pair, {C1, C2}, can be used to test the independence axiom
Our experiment also includes a set of 15 ancillary choice-situations: five in which the lottery first-order stochastically dominates the certain $30, five in which the lottery is first-order stochastically dominated by the $30, and five in which the lottery is second-order stochastically dominated by the certain $30. These ancillary choice-situations are used primarily as a screening device in our analyses as described below.
A final experimental design criterion was to avoid sampling very low and very high probability prizes where violations of IA consistently arise even in sober individuals (Kahneman and Tversky 2000; Prelec 1998): All the lotteries in our experiment do not include probabilities that were lower than 10% or higher than 90%. We avoided lotteries near the edges of the simplex for two principal reasons: First, we wanted the probability spaces to be consistent between our independence and risk experiments. Second, because the maximum payout we could offer subjects was $100 and for such limited prize amounts the marginal changes in lottery EVs (within a CSP) for low probability events is relatively small. Consider, for example, a lottery L′ with a probability of winning $100 of 0.06. For the way we constructed our CSPs a lottery L″ would have an expected value that is decreased by at most $3 (it would be less than this given the construction of our lotteries). In the event we observed an independence axiom violation (IAV) in this CSP it could be difficult to interpret this as a “strict” IAV; indifference could be a reasonable alternative interpretation. On the other hand, consider a lottery that is consistent with our design criteria: L′ has a probability of winning $100 of 0.20 which would imply that L″ has that prize’s probability at 0.10. This implies that EV could change by at most $10. Interpreting any inconsistency in this CSP as a “strict” IAV seemed more justifiable than with lotteries that included small probabilities.
4.1 Sample
The sample for our independence experiment is comprised of 104 individuals, 44 of whom are male (42.3%) and 60 of whom are female (57.7%). As reported in Table 6 the average BAC of these sub-samples was 0.057% for men and 0.079% for women. This difference in average BACs is the largest amongst our three samples and represents a statistically significant difference when using a t-test (at 1% confidence). The male and female subsamples do, however, show uniformity between measured BAC levels of 0.020% and 0.125%, as depicted in the cumulative sample distribution functions in Fig. 7.
Table 6.
Independence sample characteristics
| N | Mean | Std. Dev. | Min. | Max. | |
|---|---|---|---|---|---|
| Male | 44 | 0.057 | 0.039 | 0.000 | 0.133 |
| Female | 60 | 0.079 | 0.040 | 0.000 | 0.180 |
| Total | 104 | 0.070 | 0.041 | 0.000 | 0.180 |
All numbers (except sample sizes) are % BAC
Fig. 7.
Independence sample BAC cumulative distributions. The solid vertical line depicts 0.080% BAC, the legal driving limit in many U.S. states
4.2 Measures
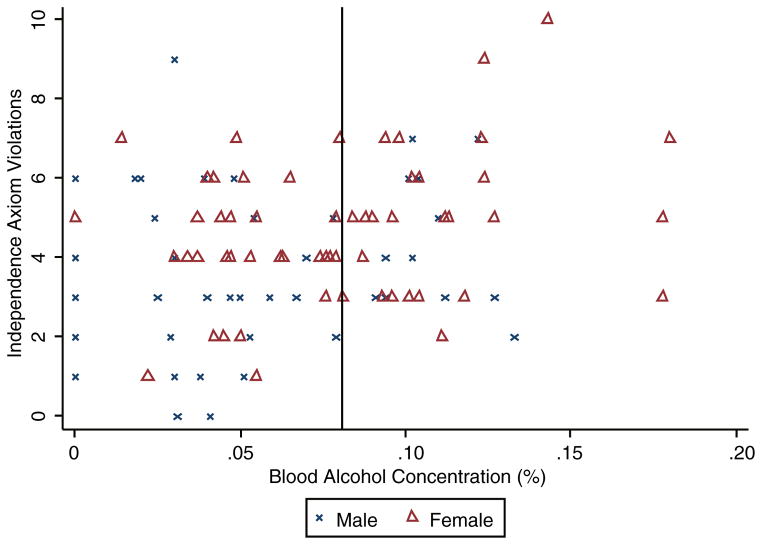
We use the number of independence axiom violations (IAVs) made in our experiment (out of a possible 15) as a principal measure in our analyses and we relate the number of IAVs made by a participant to their blood alcohol concentration (BAC). Figure 8 is a scatter plot of all the BAC-IAV pairs observed in the experiment. Table 7 details the mean and median BAC for each observed IAV count.
Fig. 8.
Independence axiom violations and blood alcohol concentration. The solid vertical line depicts 0.080% BAC, the legal driving limit in many U.S. states
Table 7.
Independence axiom violations and BAC
| Independence Axiom violations | Number of Observations | Average BAC | Median BAC |
|---|---|---|---|
| 0 | 2 | .036 | .036 |
| 1 | 6 | .033 | .034 |
| 2 | 11 | .056 | .042 |
| 3 | 21 | .083 | .093 |
| 4 | 18 | .059 | .026 |
| 5 | 19 | .075 | .044 |
| 6 | 15 | .064 | .039 |
| 7 | 9 | .096 | .047 |
| 8 | 0 | – | – |
| 9 | 2 | .077 | .066 |
| 10 | 1 | .143 | – |
| 4.22a | 104 | .070a | .041a |
Sample averages
In general, the frequency of IAVs (across all BACs) are consistent with a number of previous reports. Camerer and Ho (1994) provide an extensive summary of previous experimental results in their Fig. 4. While making direct comparisons between ours and those previous reports can be problematic,26 for our type of experiment27 the number of individuals who make at least one violation of independence in our experiment is potentially large.28 However, it is worth noting that our experiment provides subjects with many more opportunities to violate IA than the studies discussed there.
It is also important to note that the analyses presented in this section are not intended to show that our measured variable ‘IAV’ reveals systematic or non-systematic violations of independence. In fact several interpretations of any observed variation in IAVs with BAC are possible. Consider the case in which IAVs are increasing with BAC: It could be the case that there is an increase in the quasi-concavity/-convexity of indifference curves (ICs) in the simplex (i.e. variation in the probability weighting function for a prospect theory chooser). It could also be the case that as BAC increases choosers switch from possessing quasi-concave to quasi-convex ICs and that the extent of the curvature is different across the two states (so that for a prospect theory chooser their probability weighting function would be asymmetrically reflected across the 45-degree line as BAC increased). Alternatively, a plausible interpretation of any IAV in our experiment is that it is the result of an “EU + error” process, a viewpoint argued for by Hey (1995) and Harless and Camerer (1994). Given this view it could be the case that it is only the error component that is varying with BAC.29 Indeed, this latter interpretation is well supported by additional analyses performed in the online Appendix B in which we find no systematic changes in the “direction” or “severity” of IAVs across BAC.30 However, our focus here is not whether individuals have quasi-concave/-convex indifference curves versus just make errors (most subjects appear to demonstrate one and/or the other) but instead whether the severity of violations (as measured by the number of IAVs a specific subject makes in our experiment) is related to BAC: Dramatic changes in the frequency of violations of independence across BAC would raise serious doubts about applying any interpretation of the baseline EU model to the risky choices made by intoxicated individuals.
4.3 Analysis
While it is tempting to interpret the slightly increasing trend observed in Fig. 8 and Table 7 as evidence for a positive relationship between BAC and IAV, these reports do not give us any leverage to determine whether the higher blood alcohol concentrations observed in females could be inducing this apparent trend. To assess whether there is a statistically reliable relationship between BAC and IAVs we estimate regressions of the following form:
| (2) |
where the variable I AVi is the number of independence axiom violations (out of a possible 15) that were made by participant i, the variable BACi is their measured blood alcohol concentration, and 1(Female)i is an indicator variable that is equal to unity if the participant was female and zero if male. Model (1) in Table 8 reports parameter estimates and standard errors for our full sample of 104 participants. The parameter estimate for BAC is statistically different than zero at the 10% level when using a two-tailed test. This level of significance is also observed when we exclude those participants who made more violations than a random chooser would in our experiment (i.e. I AVi > 7.5, which corresponds to Model (2) in Table 8), or when we exclude those individuals who failed to correctly select the first order stochastically dominant alternative (i.e. F OSDi < 80%, Model (3) in the Table), or both (Model (4)).
Table 8.
Regressions demonstrating a weak relationship between the number of independence axiom violations (IAVs) and Blood Alcohol Concentration (BAC)
| Variable | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| BAC | 9.826* (5.006) | 7.582* (4.538) | 9.833* (5.442) | 8.249* (4.914) |
| Female | 0.727* (0.375) | 0.749** (0.359) | 0.664* (0.386) | 0.755** (0.369) |
| Constant | 3.118*** (0.444) | 3.118*** (0.396) | 2.994*** (0.467) | 2.928*** (0.414) |
| Est. type | OLS | OLS | OLS | OLS |
| Number Obs. | 104 | 101 | 92 | 90 |
| R2 | 0.096 | 0.091 | 0.094 | 0.104 |
| N.A. | I AVi > 7.5 | F OSDi < 80% | F OSDi < 80% | |
| Excl. Crit. | – | – | – | I AVi > 7.5 |
Robust standard errors in parentheses. Significance at the 1% level is denoted ***, 5% as **, 10% as *
None of the parameter estimates for BAC are significant at the traditional 5% threshold. It can also, however, be informative to explore the economic significance of these parameter estimates. Consider one of the large parameter estimates for BAC in our table; the one resulting from our full sample of participants (i.e. Model (1) in Table 8). A representative male subject who starts out sober, and at that BAC makes three violations of independence, would need to imbibe enough alcohol to arrive at a BAC of 0.102% to make one additional violation in our experiment. Although above the legal limit for driving in the United States of America, this BAC does lie within the bounds of our sample. At the other extreme, consider the relatively small parameter estimate from Model (2) in Table 8. Our representative sober male subject who made three violations of independence would need to imbibe enough alcohol to arrive at a BAC of 0.132% to make one more violation, again a level of intoxication that lies within our sample but is relatively high. Thus, while IAVs are rare, it is clear that independence is more fragile than GARP with respect to BAC in our sample. Still, one cannot help but see this glass as more than half full. Indeed, several full glasses only marginally compromise the independence axiom, for the average participant in our sample.
5 Risk preference experiment
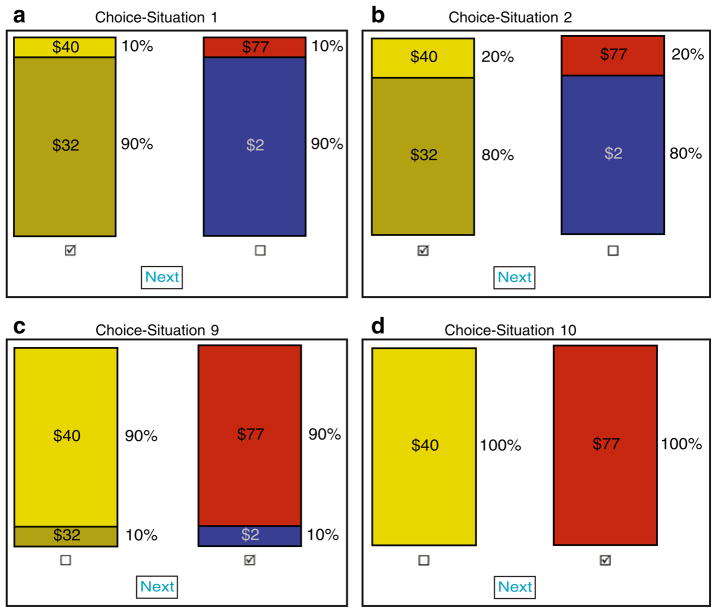
The results from our independence experiment indicate that intoxicated individuals will respond to risk-based incentives at a wide range of BACs. So how might preferences towards risks change as a function of blood alcohol? To address this question we use an experiment to measure risk aversion. The lotteries in our experiment are motivated by the design of Holt and Laury (2002, 2005) in their studies of risk aversion and incentive effects: we present subjects with a pair of lotteries that have two possible prizes and identical probability distributions. As depicted by the experimental screen-shots in Fig. 9a through d these choice-situations include a “safe” alternative (the lottery in which the prizes amounts are closer together) and a “risky” alternative (the lottery in which the two prize amounts are farther apart).
Fig. 9.
Screen shots from the risk preference experiment
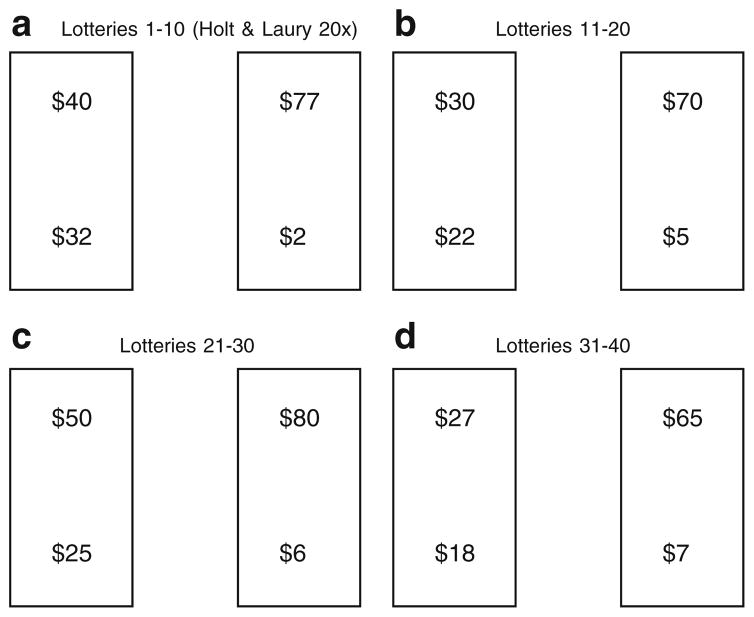
Each subject was presented with forty choice-situations. As displayed in Fig. 10a, the first ten choice-situations have a prize space of $32/$40 and $2/$77 which correspond to the “20x” lotteries used by Holt and Laury (2002). The other thirty choice-situations use the same ten probability distributions but with three different prize spaces. All of the prize spaces used in the experiment are depicted in Fig. 10a–d, and a detail of each of the 40 choice-situations can be found in the online Appendix C. We included the additional 30 lotteries to achieve finer parametric resolution on risk preferences.
Fig. 10.
The four prize spaces used to measure risk preferences
5.1 Sample
The sample for our risk-preference experiment is comprised of 114 individuals: 56 men and 58 women (49.1% and 50.9%, respectively). As can be seen in Table 9 the average BAC of these sub-samples were 0.061% for men and 0.062% for women. The cumulative sample distribution functions of BAC for both men and women are displayed in Fig. 11. While this sample has additional observations at 0.000% BAC, relative to our GARP and independence samples, the distribution of measured BACs is again fairly uniform between 0.020% and 0.125%.
Table 9.
Risk-Sample Characteristics
| N | Mean | Std. Dev. | Min. | Max. | |
|---|---|---|---|---|---|
| Male | 56 | 0.061 | 0.041 | 0.000 | 0.160 |
| Female | 58 | 0.062 | 0.056 | 0.000 | 0.211 |
| Total | 114 | 0.062 | 0.050 | 0.000 | 0.211 |
All numbers (except sample sizes) are % BAC
Fig. 11.
Risk sample BAC characteristics. The solid vertical line depicts 0.080% BAC, the legal driving limit in many U.S. states
5.2 Analysis
To identify how risk preferences vary with BAC we assume choosers possess a random utility representation and proceed by calibrating risk preferences with maximum likelihood methods. For the two lotteries (Lsaf e and Lrisky ) in each choice-situation we assign random utility levels:
| (3) |
| (4) |
where EU (·) is the systematic, expected utility of a given lottery, EU (L) = p1u(z1) + p2u(z2), and ε is an additive error component. We assume that choosers possess a utility (Bernoulli) function over monetary prizes of the constant relative risk aversion (CRRA) form,31
| (5) |
If we can assume that the additive error components for random utility are independently, identically distributed Type I extreme value then choice probabilities take on the standard logit form:
| (6) |
| (7) |
where we use the notation Lsaf e ≳* Lrisky to indicate that the safe lottery was selected over the risky one. To explore how risk preferences might vary with observable attributes, we permit the relative risk aversion parameter (θ), and the error dispersion parameter (κ) to vary as linear-in-parameters functions of BAC and sex.32 Mathematically, we express θ and κ as:
| (8) |
| (9) |
Table 10 reports estimation results from four different maximum likelihood estimates of a systematically varying CRRA specification. As commonly found in studies exploring risk preferences, women in our sample are more risk averse than men (Eckel and Grossman 2008; Croson and Gneezy 2009). We also find male- and female-specific blood alcohol effects. Consider the parameter estimates in Model (4): A representative male with a BAC of 0.000% has relative risk aversion of 0.551, which corresponds to what Holt and Laury label as “risk averse” (this is also the most frequent type of chooser for their “20x real” design). If our representative male imbibed enough alcohol to arrive at a BAC of 0.100% he would become more risk averse and have relative risk-aversion of 0.606 which also corresponds to Holt and Laury’s “risk averse” category.
Table 10.
Maximum likelihood estimates of CRRA utility with systematically varying θ and κ
| Variable | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Systematically varying CRRA parameters (θ) | ||||
| Constant (θ1) | 0.578*** (0.017) | 0.552*** (0.021) | 0.600*** (0.017) | 0.551*** (0.021) |
| BAC (θ2) | −0.132 (0.285) | 0.330 (0.373) | −0.138 (0.303) | 0.553 (0.368) |
| Female (θ3) | 0.092*** (0.030) | 0.146*** (0.041) | 0.116*** (0.030) | 0.207*** (0.041) |
| BAC*1(Female) (θ4) | – | −0.791*** (0.387) | – | −1.322 (0.392) |
| Systematically varying error dispersion parameters (κ) | ||||
| BAC (κ1) | 6.771*** (1.564) | 6.726*** (1.552) | 3.852*** (1.184) | 4.548*** (1.221) |
| Female (κ2) | 0.015 (0.119) | −0.039 (0.119) | −0.248*** (0.089) | −0.131*** (0.091) |
| Number Obs. | 114 | 114 | 106 | 106 |
| Log Likelihood | −2265.4 | −2263.3 | −1944.5 | −1938.8 |
| Excl. Crit. | N.A. | N.A. | F OSDi < 80% | F OSDi <80% |
| Riskyi ≠ 100% | Riskyi ≠ 100% | |||
Quantitative standard errors are in parentheses. See online Appendix C for details on how these are calculated. Significance at the 1% level is denoted ***, 5% as **, 10% as *
Referring again to the parameter estimates of Model (4) in Table 10, a representative female with a BAC of 0.000% has relative risk aversion of 0.758 which corresponds to Holt and Laury’s “very risk averse” category. If that representative female imbibed enough alcohol to arrive at a BAC of 0.100% her relative risk aversion would decline to 0.681 which is right on the border between Holt and Laury’s “risk averse” and “very risk averse” classifications. This representative female with a BAC of 0.100% has a relative risk aversion that is statistically indistinguishable from a representative male with a BAC of 0.100%. Moreover, for the parameter estimates in Model (4), men and women would have identical relative risk aversions at a BAC of 0.157%.
That drunk women become more open towards risks could have implications for policy. Consider a policy aimed at reducing risky behaviors in the population of drunk choosers. According to our results, predictions of changes in men’s risky behavior would be accurate if they were based on estimates of risk preferences collected from sober men. In contrast, changes in drunk women’s risky choices would be dramatically lower if estimates were used from sober women.33 Of course our samples are in no way representative of the population of drunk choosers (even in NYC). Thus drawing strong conclusions without additional research to determine whether our risk-preference findings are the result of sampling, pharmacology, or selection would be inappropriate.
6 Discussion and conclusion
The title of our paper raises the question of whether an expected utility maximizer who walks into a bar and has several alcoholic beverages is likely to walk out an EU-maximizer. While the results from our experiments indicate that almost no perfect EU-maximizers walk into bars, it appears that people walk out of bars not dramatically less EU-maximizing than when they walked in. Our data also suggest that choice consistency does not appreciably decline as blood alcohol levels increase. Even highly intoxicated subjects, who had difficulty walking, remained sensitive to incentive structures. While a huge body of evidence indicates that the profoundly intoxicated have slower reaction times and reduced coordination (Meyer and Quenzer 2005; Iversen et al. 2009) it was not the case that their choices in our experiments became disordered, irrational, or insensitive to costs. That is a novel observation that may have important implications for policy that are discussed below.
Our studies of risk attitudes as a function of blood alcohol level tell a similar story. As blood alcohol level increased in our pool of subjects they continued to broadly obey the independence axiom; their choices remained largely consistent with regard to risky lotteries, even at very high blood alcohol levels. Our measurements of actual risk attitudes, however, told a slightly different story. While we found that the specific risk attitudes of males showed little change as a function of blood alcohol level, females did show a change in risk-attitudes. In our samples, female risk attitudes converged towards those of males as blood alcohol levels increased; there do not appear to be appreciable differences between women and men’s risk preferences when they are intoxicated. This is also an observation of significance to policy-makers. Policy-makers might well consider the possibility that the intoxicated can consistently represent risks of penalties but should consider the possibility that the intoxicated (and particularly females) have a heightened tolerance for these risks.
Before using these data to draw broad conclusions about the consistency and risk attitudes of intoxicated Americans in general, however, a number of important issues must be considered. Foremost among these is the sampling technique we employ: We recruit participants from a single bar in a single New York neighborhood on Tuesdays and Wednesday nights during a single year. This seriously limits the generalizability of our study. Additional studies are required. Further, we should note that recruiting from the same bar led us to a relatively homogeneous sample in terms of age and ethnicity (over 85% of our participants are between 25 and 34 years of age; unfortunately, our Institutional Review Board required a sampling technique that guaranteed the strictest of anonymity which excluded collection of ethnicity information). This meant that we were unable to exploit exogenous variation in our subject pool to explain changes in preferences or adherence to revealed preference axioms across sub-populations.
Another problem with our study was that we identified our econometric estimates on between-subject variation in BAC when our research question would be better addressed using within-subject variation. A more controlled way of performing our measurements would be to experimentally control the BAC of our participants through either random assignment or with the use of treatment and placebo groups. However, this approach also has two principal disadvantages. First, our Institutional Review Board considered any such procedure unethical. Second, it would have driven us towards a finding more likely to reflect something about pharmacology than about the macroeconomy. Exploring the effects of variation in BAC that occurs in “the wild” was our primary goal because it is this variation that is relevant to economic outcomes. Indeed, List (2006) has argued that representativeness of environment may be the most important factor for generalizability of behavior in a large class of experiments and it was with this consideration in mind that we focused our efforts on a field-based approach.
A related criticism is that individuals likely to opt-into high levels of BAC might also be those less likely to violate GARP or IA at any BAC level. That is also an important point, although perhaps more for a biologist than for a policy-maker interested in the behavior of intoxicated New Yorkers. We note, however, that females in our sample tended to have lower Afriat Indices, Houtman-Maks measures, and were more likely to violate the independence axiom. And yet, females were also more likely (conditional on their being female) to experience higher BAC levels in our samples. The critical point here is that if there were a meaningful difference in rationality between sober and intoxicated states, a policy aimed at preventing people from becoming intoxicated would be more effective than one aimed at altering the behavior of individuals who are already intoxicated. But that is not what we observed in this study.
In terms of an algorithmic approach towards human decision-making, the weak relationship between BAC and adherence to GARP that we observed suggests that consistent choice behavior must be a relatively robust feature of human decision-making as was originally suggested by Becker and Murphy (1988). This robustness indicates that economists can, in principle, model choices by alcohol intoxicated individuals with the same suite of tools that are applied to more standard samples. Our observation that female preferences change as a function of BAC also suggests an important validation of the Bernheim and Rangel (2004) approach to modeling inconsistent choice in at least one intoxicated population. More generally, this apparent robustness also suggests a relatively wide purview for the application of economic models and ensuing policy analyses when intoxicated individuals are an object of consideration. We note, however, that our data cannot be used, indeed they must not be used, to argue that all drugs of abuse are like alcohol in this regard. Growing evidence indicates that subjects consuming drugs of abuse that specifically alter the activity of brain systems employing the neurotransmitter dopamine probably cannot be modeled as rational (Redish 2004; Caplin and Dean 2008). Were this same experiment to be conducted in cocaine users it is almost certain that a different result would have been obtained. It is critical to remember that each category of drug of abuse must be examined separately and that the results we present here pertain only to alcohol (Redish et al. 2008; Koob and Volkow 2010). That is a hugely important point of which policy-makers must be aware.
In summary, these data lead us to conclude that additional tests of the robustness of preference coherence in more varied populations of intoxicated individuals will vastly enhance economists’ understanding of the explicit boundaries of our modeling tool-kit. Our study validates, with regard to alcohol, both the Becker and Murphy (1988) approach and the Bernheim and Rangel (2004) approach and suggests that these models can and should be tested with regard to drugs of abuse. For example, understanding whether heroin addicts really are as consistent in their choices for opiods as non-addicts are in their choices for grocery store items could provide valuable insights into the boundaries of economic models. Furthermore, the idea that preference coherence could substantively change as intoxication changes leads naturally to other domains in which “cognitive impairment” might affect economists’ ability to model choices using standard methods. Indeed, recent neuro-biological evidence suggests that damage to regions of the brain typically implicated in value-based decision-making could compromise adherence to GARP (Camille et al. 2011). Certainly it would be important to understand the extent to which the choices of individuals with cognitively debilitating diseases like Multiple Sclerosis, Parkinson’s Disease, or Alzheimer’s Disease can, in principle, be modeled with standard economic tools.
Acknowledgments
All authors gratefully acknowledge valuable input from John Rotrosen, M.D., Bill Harbaugh, Mark Dean and Daniel Martin. Matthew Kelly and Michael Laba generously permitted us access to their bar and patrons. Begoña Fernandez Diaz, Eric DeWitt, Maggie Grantner, Dino Levy, and Linnaea Ostroff provided valuable assistance with participant queuing. This work was supported by the U.S. National Institutes of Health (5R01NS054775 and 5F32MH084431).
Footnotes
Casinos commonly provide complimentary alcohol to individuals seated at gaming tables.
Most recently available data from the Bureau of Justice Statistics: http://bjs.ojp.usdoj.gov/content.../pub/pdf/dwiocs.pdf
National Highway Traffic Safety Administration: http://www.nhtsa.gov/Research/Human+Factors/Alcohol+Impairment
National Institute for Alcohol Abuse and Alcoholism Statistical Tables: http://pubs.niaaa.nih.gov/publications/Surveillance92/CONS09.pdf
National Income and Product Accounts table 2.4: http://www.bea.gov/national/consumerspending.htm
This number is likely a dramatic underestimate of the total dollar value of risky choices made while intoxicated. For example, we cannot find data on the amount of alcohol sold each year at bars, a large proportion of which is sold to individuals with non-zero BACs. And these are but a limited class of risky decisions made by intoxicated individuals.
We should note, however, that these laws rarely appear to be enforced which may reflect any number of considerations with regard to this apparent conviction.
Both of these statistics come from the NHTSA 2005 research report titled “Preventing Over-consumption of Alcohol - Sales to the Intoxicated and “Happy Hour” (Drink Special) Laws.”
Although, as reported and discussed in the online Appendix A (available on the author’s web site http://www.decisionsrus.com/documents/Appendix_JRU.pdf), we find potential, but very weak, evidence for a minuscule female-specific effect on adherence to GARP at very high BACs.
Note that our empirical strategy is to measure BAC and use it as a continuously varying proxy for what these classes of models typically assume are discrete states.
Cook (2007) provides an excellent summary of this vast literature.
While the budgets we employ come from the Harbaugh et al. (2001) design, we use computer-based graphically presented bundles similar to the mechanism employed by Choi et al. (2007). At a more procedural level, we took extensive pains to limit stereotyped choice behaviors, like corner solving, which limit the power of some studies that use these approaches.
Three excellent reviews of this literature are Cox and Harrison (2008), chapters 10 and 11 in Glimcher et al. (2009), and Kahneman and Tversky (2000).
Two counter-examples are Kagel et al. (1980), which explores the relationship between work performance and marijuana consumption, and Krishnamurti et al. (2011) which explores the choices of drunk people in the ultimatum game.
This study administers a benzodiazepene agonist which shares the same principal pharmacological mechanism as alcohol.
Only two out of 321 potential participants failed this test.
Participants were informed during the instructional phase of the experiment that they would need to sign a receipt for their payment but that their signature did not need to be legible.
An amount constantly proportional to blood alcohol concentration (over a range of BAC up to 0.400%) is exhaled with each breath (O’Daire 2009)
The difference between our breathalyzer and ones used by law enforcement agents for evidentiary testing is that our breathalyzer has no memory nor can it be attached to a printer.
Table 14 in the online Appendix A (available on the author’s web site http://www.decisionsrus.com/documents/Appendix_JRU.pdf) describes all of the budget details (prices and wealth levels).
Harbaugh et al. (2001) report average AEIs of 0.93, 0.96, and 0.94 in their populations of students in second-grade, sixth-grade, and undergraduate classrooms. Andreoni and Miller (2002) report that only four of their 176 undergraduate subjects had AEIs less than unity which, based on our calculations from their Table II, gives an average AEI of 0.998.
Although Sippel (1997) reports the proportions of his two samples (1/12 and 3/30) above an AEI threshold of 0.950. As can be inferred from Table IV, we find a slightly smaller proportion of our sample to have AEIs above that threshold.
Technically our experiment tests for violations of a slightly weaker condition: Betweenness (Dekel 1986; Camerer and Ho 1994). However, because betweenness is a necessary condition for independence, to any extent that our empirical results suggest failures of betweenness, they also imply failures of independence although of course the reverse is not necessarily the case. However, because our experimental design employed three-state lotteries, any true test of independence (as opposed to betweenness) would greatly increase the complexity of the choice-situations: subjects would need to compare two three-state lotteries instead of one degenerate and one three-state lottery. For this reason we adopted the test of betweenness described here to examine the stability of the independence axiom.
Henceforth, we use the term “lottery” to refer to the non-certain option for brevity.
For a complete description of the unique colors and prize values used in this experiment see the online Appendix B, available on the author’s web site http://www.decisionsrus.com/documents/Appendix_JRU.pdf
These comparisons are problematic due to differences in the number of choice-situations, prize spaces, specific probabilities, and real vs. hypothetical choices.
Our experiment is an example of what Camerer and Ho (1994) label as “on-border” types of tests for independence because our choice-situations include lotteries on an edge of the simplex.
Most studies listed in the “Gain” column of Camerer and Ho’s Fig. 4 report that, generally, about 70% of individuals violate independence. We find that for our subjects (who made choices in 15 CSPs) nearly all of them make some form of IAV.
We would like to thank an anonymous referee for pointing out these lines of interpretation.
In fact we take the “increase in error rates” interpretation to a literal extreme in our modeling of risk preferences because we allow the error dispersion parameter (κ) in our logit model to vary systematically with BAC.
We have also calibrated models with a constant absolute risk aversion (CARA) Bernoulli but find significantly better fits with CRRA in this dataset.
When we constrain the error dispersion parameter (κ) to be constant across BAC and sex, we find significantly reduced maximized log-likelihood values. Moreover, based on the findings from our IA experiment, the dispersion-parameter estimate for BAC (κ1) bears the expected signs.
For a policy-maker, whether this apparent change in risk preferences is the result of selection, or is causally related to BAC, is less of an issue if less risk averse women are disproportionately opting into higher BACs. It would not change the fact that the population of drunk women is substantially less risk averse than their sober counter-parts.
JEL Classifications D01 · D81 · C93
Contributor Information
Daniel R. Burghart, Email: dan.burghart@econ.uzh.ch, Department of Economics, University of Zürich, Blümlisalpstrasse 10, 8006 Zürich, Switzerland
Paul W. Glimcher, Center for Neuroeconomics, New York University, 4 Washington Place, Room 809, New York, NY 10003, USA
Stephanie C. Lazzaro, Institute of Cognitive Neuroscience, University College London, 26 Bedford Way, London WC1H0AP, UK
References
- Afriat S. The construction of a utility function from expenditure data. International Economic Review. 1967;8:67–77. [Google Scholar]
- Allais M. Behavior of the rational man before risk - criticism of American school postulates and axioms. Econometrica. 1953;21(4):503–546. [Google Scholar]
- Andreoni J, Miller J. Giving according to GARP: an experimental test of the consistency of preferences for altruism. Econometrica. 2002;70(2):737–753. [Google Scholar]
- Becker G, Murphy K. A theory of rational addiction. Journal of Political Economy. 1988;96(4):675–700. [Google Scholar]
- Benhabib J, Bisin A. Modeling internal commitment mechanisms and self-control: a neuro-economic approach to consumption-saving decisions. Games and Economic Behavior. 2005;52(2):460–492. [Google Scholar]
- Bernheim D, Rangel A. Addiction and cue-triggered decision processes. American Economic Review. 2004;94(5):1558–1590. doi: 10.1257/0002828043052222. [DOI] [PubMed] [Google Scholar]
- Camerer C. The promise and success of lab-field generalizability in experimental economics: a critical reply to levitt and list. 2011;10(2139) Available at SSRN: http://ssrn.com/abstract=1977749. ssrn.1977749. [Google Scholar]
- Camerer C, Ho T. Violations of the betweenness axiom and nonlinearity in probabilities. Journal of Risk and Uncertainty. 1994;8(2):167–196. [Google Scholar]
- Camille N, Griffiths CA, Vo K, Fellows LK, Kable JW. Ventromedial frontal lobe damage disrupts value maximization in humans. The Journal of Neuroscience. 2011;31(20):7527–7532. doi: 10.1523/JNEUROSCI.6527-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caplin A, Dean M. Dopamine, reward prediction error, and economics. Quarterly Journal of Economics. 2008;123(2):663–701. [Google Scholar]
- Choi S, Gale D, Fisman R, Kariv S. Consistency and heterogeneity of individual behavior under uncertainty. American Economic Review. 2007;97(5):1921–1938. [Google Scholar]
- Cook PJ. Paying the tab: the costs and benefits of alcohol control. Princeton: Princeton University Press; 2007. [Google Scholar]
- Cox JC, Harrison GW. Risk Aversion in Experiments. Bingley: Emerald Group Publishing Limited; 2008. [Google Scholar]
- Croson R, Gneezy U. Gender differences in preferences. Journal of Economic Literature. 2009;47(2):1–27. [Google Scholar]
- Dekel E. An axiomatic characterization of preferences under uncertainty: weakening the independence axiom. Journal of Economic Theory. 1986;40(2):304–318. [Google Scholar]
- Eckel CC, Grossman PJ. Men, women and risk aversion: experimental evidence. In: Plott C, Smith V, editors. Handbook of experimental economics results. Vol. 1. New York: Elsevier; 2008. pp. 1061–1073. [Google Scholar]
- Fitzgerald EF, Hume DN. Intoxication test evidence: criminal and civil. San Francisco: Bancroft-Whitney; 1987. [Google Scholar]
- Fromme K, Katz E, D’Amico E. Effects of alcohol intoxication on the perceived consequences of risk taking. Experimental and Clinical Psychopharmacology. 1997;5(1):14–23. doi: 10.1037//1064-1297.5.1.14. [DOI] [PubMed] [Google Scholar]
- Fudenberg D, Levine D. A dual self model of impulse control. American Economic Review. 2006;96(5):1449–1476. doi: 10.1257/aer.96.5.1449. [DOI] [PubMed] [Google Scholar]
- Glimcher PW, Camerer CF, Fehr E, Poldrack RA. Neuroeconomics: decision making and the brain. London: Academic Press; 2009. [Google Scholar]
- Gul F, Pesendorfer W. Harmful addiction. Review of Economic Studies. 2007;74(1):147–172. [Google Scholar]
- Harbaugh WT, Krause K, Berry T. GARP for kids: on the development of rational choice behavior. American Economic Review. 2001;91(5):1539–1545. [Google Scholar]
- Harless DW, Camerer CF. The predictive utility of generalized expected utility theories. Econometrica. 1994;62(6):1251–1289. [Google Scholar]
- Hey JD. Experimental investigations of errors in decision-making under risk. European Economic Review. 1995;39(3–4):633–640. [Google Scholar]
- Holt CA, Laury SK. Risk aversion and incentive effects. American Economic Review. 2002;92(5):1644–1655. [Google Scholar]
- Holt CA, Laury SK. Risk aversion and incentive effects: new data without order effects. American Economic Review. 2005;95(3):902–904. [Google Scholar]
- Houtman M, Maks JAH. Determining all maximal data subsets consistent with revealed preference. Kwantitatieve Methoden. 1985;19:89–104. [Google Scholar]
- Iversen LL, Iversen SD, Bloom FE, Roth RH. Introduction to neuropsychopharmacology. New York: Oxford University Press; 2009. [Google Scholar]
- Jackson CK, Owens EG. One for the road: public transportation, alcohol consumption, and intoxicated driving. Journal of Public Economics. 2011;95(1–2):106–121. [Google Scholar]
- Kagel JH, Battalio RC, Miles CG. Marijuana and work performance: results from an experiment. Journal of Human Resources. 1980;15(3):372–395. [PubMed] [Google Scholar]
- Kahneman D, Tversky A. Prospect theory - analysis of decision under risk. Econometrica. 1979;47(2):263–291. [Google Scholar]
- Kahneman D, Tversky A. Choices, values, and frames. New York: Cambridge University Press; 2000. [Google Scholar]
- Keller LR. The effects of problem representation on the sure-thing and substitution principles. Management Science. 1985;31(6):738–751. [Google Scholar]
- Koob G, Volkow N. Neurocircuitry of addiction. Neuropsychopharmacology. 2010;35(1):217–238. doi: 10.1038/npp.2009.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnamurti T, Morewedge C, Ariely D. Mimeo. 2011. Focused on unfairness. [Google Scholar]
- Lane SD, Cherek DR, Peitras CJ, Tcheremissine OV. Alcohol effects on human risk taking. Psychopharmacology. 2004;172(1):68–77. doi: 10.1007/s00213-003-1628-2. [DOI] [PubMed] [Google Scholar]
- Lane SD, Cherek DR, Nouvion SO. Modulation of human risky decision making by flunitrazepam. Psychopharmacology. 2008;196(2):177–188. doi: 10.1007/s00213-007-0951-4. [DOI] [PubMed] [Google Scholar]
- Levitt S, List JA. Viewpoint: on the generalizability of lab behaviour to the field. Canadian Journal of Economics. 2007;40(2):47–370. [Google Scholar]
- List JA. Field experiments: a bridge between lab and naturally occurring data. The BE Journal of Economic Analysis and Policy. 2006;6(2):Article 8. Available at: http://www.bepress.com/bejeap/advances/vol6/iss2/art8. [Google Scholar]
- MacDonald TK, Fong GT, Zanna MP, Martineau AM. Alcohol myopia and condom use: can alcohol intoxication be associated with more prudent behavior? Journal of Personality and Social Psychology. 2000;78(4):605–619. doi: 10.1037//0022-3514.78.4.605. [DOI] [PubMed] [Google Scholar]
- Meyer J, Quenzer L. Psychopharmacology: drugs, the brain, and behavior. Sunderland: Sinauer; 2005. [Google Scholar]
- Moskowitz H. Effects of problem representation and feedback on rational behavior in allais and morlat-type problems. Decision Sciences. 1974;5(2):225–242. [Google Scholar]
- O’Daire A. Blood alcohol, breath alcohol, impairment and the law. AuthorHouse; Bloomington: 2009. [Google Scholar]
- Prelec D. The probability weighting function. Econometrica. 1998;66(3):497–527. [Google Scholar]
- Redish D. Addiction as a computational process gone awry. Science. 2004;306(5703):1944–1947. doi: 10.1126/science.1102384. [DOI] [PubMed] [Google Scholar]
- Redish D, Jensen S, Johnson A. A unified framework for addiction: vulnerabilities in the decision process. Behavioral and Brain Sciences. 2008;31(4):415–487. doi: 10.1017/S0140525X0800472X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sippel R. An experiment on the pure theory of consumer’s behavior. The Economic Journal. 1997;107(444):1431–1444. [Google Scholar]
- Steele C, Josephs R. Alcohol myopia: its prized and dangerous effects. American Psychologist. 1990;45(8):921–933. doi: 10.1037//0003-066x.45.8.921. [DOI] [PubMed] [Google Scholar]
- Varian HR. The nonparametric approach to demand analysis. Econometrica. 1982;50(4):4945–973. [Google Scholar]
- Wu G. An empirical test of ordinal independence. Journal of Risk and Uncertainty. 1994;9(1):39–60. [Google Scholar]
- Wu G, Gonzales R. Common consequence conditions in decision making under risk. Journal of Risk and Uncertainty. 1998;16(1):115–139. [Google Scholar]