Abstract
For high-velocity running or swimming, the relationship between velocity (v) and its sustainable duration (t) can be described by a hyperbolic relationship: (v - Vcrit)·t = D’, where Vcrit is termed critical velocity, and D’ is defined as a curvature constant of the hyperbolic curve. The purposes of this study were to examine whether the Vcrit could be applied to evaluate short-distance breaststroke swimming performance and to evaluate the relative contribution of D’ in short-distance swimming performance. Eleven male swimmers performed a series of time trials corresponding to 75, 100, and 150-m in an indoor 50-m swimming pool. The observed records were calculated into average velocities of each event to determine Vcrit and D’. After the determination of Vcrit and D’, all subjects performed 50-m time trial on another day. A maximal anaerobic power test using cycle ergometer was also performed in the laboratory. The average velocity of the 50-m time trial significantly correlated with the obtained Vcrit, but not with D’. D’ was significantly correlated with the residual error, calculated from the regression analysis for the relationship between Vcrit and the average velocities of 50-m time trial. A cluster analysis showed that most of the subjects were classified as Vcrit dependency when performing 50-m time trial. Those results indicated that Vcrit could be applied to evaluate short-distance swimming performance, and it determined around 80% of the short-distance breaststroke swimming performance.
Key Points.
For high-velocity running or swimming, the relationship between velocity (v) and its sustainable duration (t) can be described by a hyperbolic relationship: (v - Vcrit)·t = D’, where Vcrit is termed critical velocity, and D’ is defined as a curvature constant of the hyperbolic curve. The D’ contributed only around 20% of the breaststroke swimming performance even in a short-distance event.
Critical velocity determined around 80% of 50-m breaststroke swimming performance, and it could be a useful tool for evaluating short-distance swimming performance.
Most of the swimmers showed characteristics for critical velocity dependent physical fitness even in short-distance swimming event.
Key words: Critical swimming velocity, D’, hyperbolic curve, cluster analysis
Introduction
Monod and Scherrer, 1965 have found a linear relationship between total work done (kJ) at several work intensities and time to exhaustion during high-intensity cycle ergometer exercise. It means that a hyperbolic relationship exists between power output (watt) and time to exhaustion (sec) during high-intensity cycle ergometer exercise. Such a hyperbolic relationship possesses a curvature constant with an asymptote, which is termed “critical power”. Critical power has been utilized as a “fatigue threshold” in consideration of its practical application for high-intensity endurance sports, such as running (Florence and Weir, 1997; Hughson et al., 1984; Kolbe et al., 1995), swimming (Wakayoshi et al., 1992a; 1992b; 1992c; 1993), and cycling (Housh et al., 1989; Smith et al., 1997). However, the hyperbolic relationship between power output and time to exhaustion has been applied to endurance sports event, completed from, at least, several minutes to 1 hour (e.g., Hughson et al. , 1984).
Compared to treadmill running or cycling in the laboratory, it is inconvenient to measure blood lactate concentrations or gas exchange parameters in the swimming pool, so that the application of critical power or “critical velocity (Vcrit)” will give valuable information for swimmers to estimate swimming potential as a non-invasive and inexpensive method. To date, previous studies regarding critical velocity and swimming performance were quite limited (Dekerle et al., 2002; Martin and Whyte, 2000; Wakayoshi et al., 1992a; 1992b; 1992c; 1993). Almost all of the previous studies focused on middle- and/or long-distance free-style swimming. In other words, it has not been revealed whether the critical velocity can be applied to shorter swimming events with other swimming styles.
Fukuba et al., 1996 suggested that previously defined indices for evaluating physical fitness (e.g. maximal oxygen uptake) always have a physiological background, on the other hand, critical velocity is obtained from the actual performance done by the subject. The first purpose of this study was to examine whether the critical velocity could be applied to estimate short-distance swimming performance in a breaststroke style. It was hypothesized that critical velocity could be a useful predictor even in short-distance swimming events.
The curvature constant of the hyperbolic curve between power output and time to exhaustion during high-intensity cycle ergometer exercise has attracted a great deal of research attention (Fukuba et al., 2003; Miura et al., 1999, 2000, 2002). Indeed, the curvature constant of the hyperbolic curve can be expressed by the product of velocity and time above Vcrit, thus, it was suggested that the curvature constant related to a possible distance being performed by anaerobic working capacity. However, as far as we know, nothing has been discussed regarding curvature constant in swimming yet. If the curvature constant is solely reflecting anaerobic working capacity, then it will significantly contribute to the short- distance swimming performance. The second purpose of this study was to evaluate the relative contribution of the curvature constant of the hyperbolic curve in swimming. It was also hypothesized that the curvature constant of the hyperbolic curve could be explained by the anaerobic working capacity, and it would significantly relate to the short-distance swimming performance.
Methods
Subjects
Eleven male swimmers belonging to the varsity swimming team participated in this study. The physical characteristics and other observed variables of each subject were summarized in Table 1. The best record of 50- m breaststroke swimming of each subject was expressed in percentage of the current world record. Most of the subjects were ranked at a regional competition level. After being informed of the purpose and possible risks of this study, the subjects gave their written consent. An approval of the local Ethical Review Committee was obtained for all procedures.
Table 1.
Physical characteristics of the subjects and other observed variables.
| Subject | Age (yrs) |
Height (m) |
Mass (kg) |
Vcrit (m·s-1) |
D’ (m) |
MAnP (W·kg-1) |
V50 (m·s-1) |
50m Best (m·s-1) |
%WR (%) |
Sp |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 20 | 1.75 | 81.9 | 0.989 | 9.38 | 11.2 | 1.217 | 1.316 | 65.8 | Br |
| 2 | 21 | 1.54 | 60.7 | 0.771 | 6.14 | 12.7 | 0.878 | 1.020 | 51.0 | Bt |
| 3 | 20 | 1.70 | 67.1 | 0.670 | 18.88 | 9.1 | 0.946 | 1.010 | 50.5 | Fr |
| 4 | 20 | 1.72 | 60.7 | 0.800 | 9.70 | 10.1 | 0.992 | 1.042 | 52.1 | Fr |
| 5 | 19 | 1.69 | 64.6 | 0.978 | 4.96 | 10.1 | 1.087 | 1.136 | 56.8 | Br |
| 6 | 20 | 1.72 | 71.0 | 0.869 | 10.40 | 9.7 | 1.094 | 1.149 | 57.4 | Br |
| 7 | 19 | 1.78 | 83.0 | 0.943 | 12.56 | 10.3 | 1.232 | 1.250 | 62.5 | Br |
| 8 | 19 | 1.80 | 61.5 | 0.947 | 9.56 | 12.2 | 1.176 | 1.205 | 60.2 | Br |
| 9 | 19 | 1.73 | 63.5 | 0.858 | 12.98 | 9.2 | 1.151 | 1.235 | 61.7 | Br |
| 10 | 21 | 1.55 | 49.2 | 0.717 | 9.28 | 11.2 | 0.904 | 0.904 | 45.2 | Fr |
| 11 | 19 | 1.76 | 58.0 | 0.861 | 8.23 | 10.5 | 1.032 | 1.111 | 55.5 | Br |
| Mean | 19.7 | 1.70 | 65.6 | .855 | 10.19 | 10.6 | 1.064 | 1.125 | 56.2 | — |
| SD | 0.9 | 0.09 | 10.0 | 0.106 | 3.73 | 1.2 | 0.124 | 0.123 | 6.2 | — |
Vcrit, critical velocity; D’ curvature constant of the hyperbolic relationship between swimming velocity and its time to exhaustion; MAnP, maximal anaerobic power; V50, average velocity of 50-m time trial. 50m Best, average swimming speed calculated from the best record of 50m breaststroke swimming of each subject;%WR, percentage of the current world record; Sp, most favorite swimming style of each subject; Br, breaststroke; Bt, butterfly; Fr, free-style, respectively.
Protocols for Vcrit and D’ determination
A series of time trials for the determination of Vcrit and curvature constant (D’) of the hyperbolic relationship between swimming velocity and time to exhaustion took place in a 50- m indoor swimming pool. On all measurement days, water temperature was set at 28~29 degrees celsius. All data samplings were performed from late April to early May, just before the first competition of each individual’s annual race schedule.
Based on a previous study done by Wakayoshi et al., 1992a, each subject performed 75, 100, and 150-m time trials in breaststroke style to determine Vcrit and D’. The subjects sufficiently stretched and warmed up before the trials. The subjects were instructed to perform each predetermined distance as quickly as they could. Each time trial was performed with a sufficient resting period (~ 2hr). The order of each trial was randomized. At each time trial the same three timekeepers checked the performance time with a stopwatch. Each time measured by three timekeepers was averaged, and the averaged time was regarded as the time of the event. The obtained performance time of each event was further converted into average velocities of each event to calculate Vcrit and D’. Three days later, each subject performed 50-m time trial in breaststroke style in the same swimming pool, and then the observed time was converted into the average velocity of its event (V50).
The relationship between swimming velocity (v) and its time to exhaustion (t) is well characterized by the following equation:
where Vcrit is the critical velocity, t is time represented in seconds, and D’ is the curvature constant which represents the total amount of distance which can be performed above Vcrit (Figure 1a). If the relationship between v and t is hyperbolic, then the rearranged eq. 1 behaves linearly as shown in Figure 1b:
Figure 1.
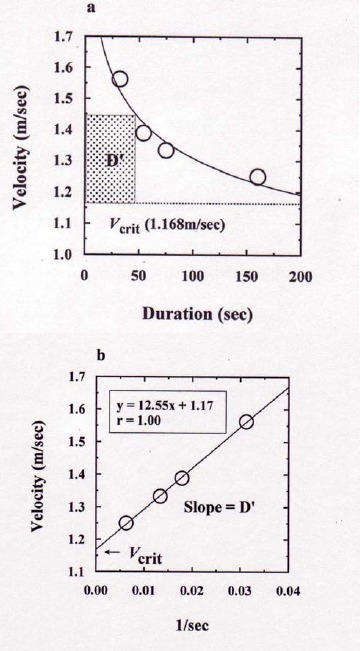
(a) An example of the calculation of critical velocity (Vcrit) and curvature constant (D’). The swimming velocity (m·sec-1) and time to exhaustion (sec). (b) The linear relationship between inverse of time (1/t) and swimming velocity.
Number of trials
Hill, 1993 proposed that four trials be recommended when obtaining critical power and curvature constant during high-intensity cycle ergometer exercise. Wakayoshi et al., 1993 obtained two data sets to determine Vcrit in highly trained competitive swimmers. The present study employed subjects who were well accustomed to swimming regardless of performance level, and the possible risks of repeatable maximal efforts were also considered for the subjects. For a confirmation of number of trials, an additional subject performed four repeatable measurements at maximal effort (Figure 1), even though this additional subject was not included in the group of subjects because the level of performance was much greater than that of other subjects. The result clearly showed that three time trials seemed to be sufficient to obtain Vcrit and D’, so the other remaining subjects performed three time trials.
Laboratory test
On the hypothesis that D’ represents anaerobic working capacity and it will mainly explain the short-distance swimming performance, each subject performed a maximal anaerobic power (MAnP) test using a cycle ergometer (PowerMax-VII, Combi, Tokyo) based on a standardized procedure (Bulburian et al., 1996; Nakamura et al., 1984). It was recognized that this MAnP test was not performed in the water, thus, the direct comparison between the results obtained from the laboratory test and those in the water might require some caution. However, it is known that this MAnP test has a reliable reproducibility (McCartney et al., 1983), so that it was assumed that the following procedure would have a validity to estimate MAnP in swimmers.
After warming-up at 50 W for 10 minutes, subjects were instructed to perform a pre-maximal trial at 1kp. When subjects were accustomed to cycle ergometer exercise, the first maximal trial started. The initial workload for determining maximal anaerobic power was determined based on the subjects’ body mass (less than 60 kg, 3 kp, n = 2; 61 to 80 kg, 4 kp, n = 7; above 81 kg, 5 kp, n = 2). The second work load was determined based on the rotations at the initial stage (less than 149 rpm, + 1 kp, n = 1; 150 to 179 rpm, + 2 kp, n = 8; above 180 rpm, + 3 kp, n = 2). The final workload was determined with the same criteria as the second stage. These maximal efforts were performed within 10 seconds at each stage with 120 seconds resting. Maximal anaerobic power (MAnP) was calculated based on the observed maximal rotations at each stage with Nakamura et al., 1984’s calculation.
Statistical analyses
The observed values were presented as mean and standard deviation (SD). The relationships between V50 and Vcrit and/or D’ as well as between Vcrit and MAnP were evaluated using a simple linear regression analysis. The residual error of V50 was obtained from the relationship between V50 and Vcrit. The relationship between D’ and its residual error was also evaluated by a simple linear regression analysis. Statistical significance was established at the 0.05 probability level. A cluster analysis, particularly in Ward method with a squared Euclidean distance, was further applied for the observed values of Vcrit and D’ to classify the characteristics of subjects’ physical fitness either Vcrit or D’ dependency. The result of the cluster analysis was described as a dendrogram.
Results
A high correlation was found in the relationship between 1/t and v in each subject when obtaining D’ and Vcrit using eq. 2. The correlation coefficient values between 1/t and v of each subject ranged from 0.97 to 1.00.
Table 1 shows the physical characteristics of the subjects and data obtained from the tests in the present study. The average Vcrit was 0.855 ± 0.106 m/sec, ranging from 0.670 to 0.989 m/sec. The average velocity of 50-m breaststroke swimming was 1.064 ± 0.124 m/sec, ranging from 0.878 to 1.232 m/sec. Linear regression analysis indicated that there was a strong relationship between Vcrit and V50 (r = 0.85, p < 0.05; Figure 2). Vcrit was not significantly correlated with MAnP. D’ widely ranged from 4.96 to 18.88 m, with an average value of 10.19 ± 3.73 m. D’ was significantly correlated with neither V50 nor MAnP. D’ was significantly correlated with the residual error, calculated from the regression analysis for the relationship between Vcrit and V50 (r = 0.84, p < 0.05; Figure 3).
Figure 2.
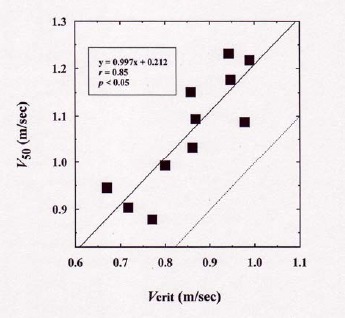
Relationship between critical velocity (Vcrit) and 50-m breaststroke swimming performance (V50). Dotted line represents identity line.
Figure 3.
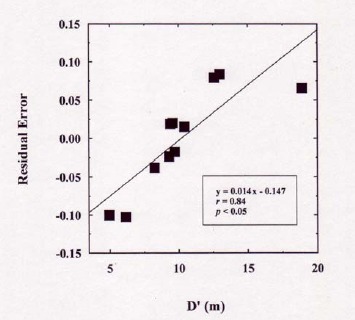
Relationship between D’ and residual error of V50, calculated from the regression analysis for the relationship between Vcrit and V50.
Figure 4 showed that only one subject was classified as D’ dependency, while the remaining ten subjects were classified as Vcrit dependency if the subjects were classified into two groups. Moreover, if the subjects were classified into three groups, two subjects were classified as “intermediate between Vcrit and D’”.
Figure 4.
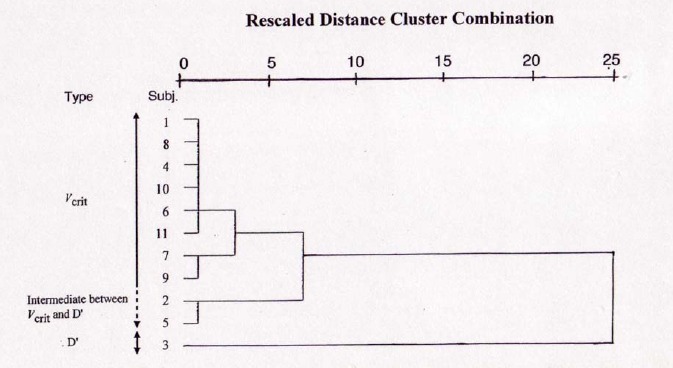
Rescaled distance cluster combination obtained from hierarchical cluster analysis.
Discussion
In support of our first hypothesis, the strictly new finding of the present study was that Vcrit was significantly correlated with the average V50 even though the average V50 was 24.4% faster than the observed Vcrit (Figure 2). This result simply proposed that Vcrit be of potential to estimate short-distance swimming event done in breaststroke style.
Many previous studies have employed various physical fitness relating indices to evaluate endurance sports performance. However, it has been pointed out that those previously defined indices cannot always explain the variation of endurance sports performance (Abe et al., 1998; 1999). It is assumed that those previously employed indices for evaluating physical fitness are solely defined under consideration of its physiological mechanism (Fukuba et al., 1996). In contrast, observed hyperbolic relationship between swimming velocity and its time to exhaustion in this study directly measured performance itself done by the athletes.
In relation to Vcrit, it was possible to estimate a predictable Vcrit from the time required to swim 50-m at the time trial (t50) and observed D’ with an average value of 10.19 ± 3.73 m. The equation for predictable Vcrit was calculated as follows:
yielding a very close value with the observed Vcrit (0.855 m, see Table 1). The difference between predictable Vcrit and observed Vcrit was less than 1%, meaning that the observed Vcrit from a series of time trials has a high reliability. It has been considered that the anaerobic contribution for 50-m or 100-m swimming event was 80% or more (Holmer, 1983), thus, it was quite surprising to note that D’ contributed only 20.4% to the 50-m breaststroke swimming performance in the present study, being consistent with 29.6% in 50-m free-style swimming performance (Dekerle et al., 2002). The swimming velocity associated with Vcrit was identical with that associated with onset of blood lactate accumulation (Wakayoshi et al., 1992c; 1993). Moreover, in cycle ergometer exercise, the curvature constant of the hyperbolic relationship between power output and its tolerable duration was significantly decreased under glycogen-depleted condition (Miura et al., 2000). Miura et al., 1999 also reported that the oral creatine supplementation increased the curvature constant by 25%. Those previous results and the current result that D’ was not significantly associated with MAnP might give a possible explanation that the curvature constant of such a hyperbolic relationship was consisted of both anaerobic glycolysis and ATP-PCr shuttle. It was also interesting to note that the relative contribution of D’ (20.4%) to the swimming performance might explain that the average V50 was 24.4% faster than the observed Vcrit. Figure 3 showed the relationship between D’ and the residual error of V50 calculated from the regression analysis for the relationship between Vcrit and V50. Those results indicated that V50 could be considerably explained by Vcrit (Figure 2), however, unexplained residual error could be explained by D’ (Figure 3).
As discussed above, little attention has been paid for the physiological implication of D’ in sports performance. This study found that D’ was not significantly correlated with neither V50 nor MAnP, although, as hypothesized above, the curvature constant of the hyperbolic relationship has been recognized as an anaerobic working capacity that can be performed above the critical power (Fukuba et al., 2003; Miura et al., 2002). Indeed, the result of the present study showed that D’ still contributed for the performance by 20%, suggesting that the appropriate training program to improve both critical velocity and D’ simultaneously could bring a better performance for breaststroke swimmers. In addition to investigations concerning energetics of swimming, some recent studies have examined the mechanics of the breaststroke swimming to improve the performance (Leblanc et al., 2005; Seifert and Chollet 2005; Takagi et al., 2004). This could be because a greater potential to improve the performance will be available in breaststroke swimming than in free-style swimming due to an existence of a large active drag during swimming. Future investigations considering both mechanics and energetics of swimming will bring a further understanding of swimming, resulting in a development of an efficient training program for swimmers.
The obtained MAnP consisted of three maximal pedalling at different workloads for, at most, 10 seconds each, meaning that the test must be too brief to utilize glycolytic ATP production system completely. This interpretation was in consistent with Bulburian et al. (1996). It means that MAnP observed in this study would reflect only breakdown of PCr (ATP-PCr shuttle), not anaerobic glycolysis (Figure 5). It was also hypothesized that the observed Vcrit in swimming was not necessary to reflect pure aerobic working capacity. Indeed, Fukuba et al., 1996 showed that respiratory responses did not reach the steady-state during cycle ergometer exercise at around the critical power, indicating that the exercise intensity associated with critical power exceeds the ‘lactate threshold’, which, in theory, represents the highest metabolic rate where a steady state response can be achieved during prolonged exercise. The results of the present study and those previous studies suggest that exercise intensity corresponding to Vcrit be sustained in part by the pure aerobic work capacity and anaerobic glycolysis (Figure 5), supporting an interpretation obtained from the model analysis (Toussaint et al., 1998).
Figure 5.
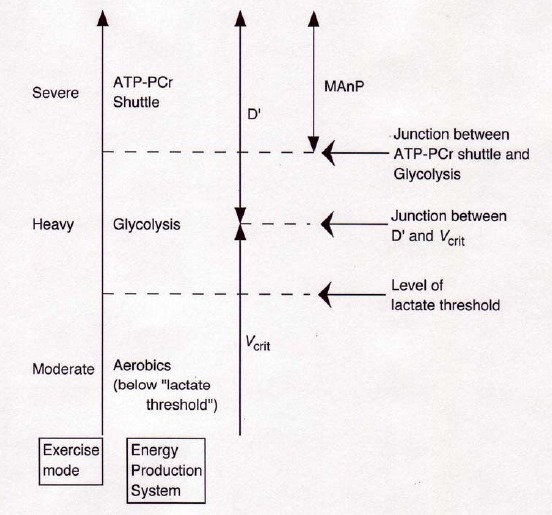
Illustration of the relationship among MAnP, D’, Vcrit, and energy production system as a function of exercise intensity.
The present study further performed cluster analysis to classify the subjects’ physical fitness for either D’ or Vcrit dependency. It was worth noting that ten of eleven subjects showed Vcrit dependency even in short-distance swimming event (Figure 4). If the cluster was divided into three groups, two subjects were classified as an intermediate situation between Vcrit and D’ dependency, meaning that most of the subjects were still classified as Vcrit dependency. The result of the present study clearly suggested that Vcrit, not D’, mainly determined athletes’ success even in short-distance breaststroke swimming. In other words, the higher the Vcrit, the better the performance in short-distance breaststroke swimming. Although Dekerle et al., 2002 suggested that D’ could not be employed by coaches to control an anaerobic swimming training program, we hereby pointed out that it might be relevant to the maximal swimming velocity, which would be performed at the end and/or start of the race.
Conclusion
In conclusion, Vcrit could be a potential index to evaluate short-distance swimming performance in breaststroke style. Vcrit, but not D’, determined most of 50-m breaststroke swimming performance.
Acknowledgements
This study was supported in part by Grant-in-Aid from The Japan Ministry of Education, Culture, Sports, Science and Technology (17770217 to D.A. and 16500407 to S.U.) and Athletic Performance Promotion in Kumamoto, Japan (to Y.F.).
Biographies

Daijiro ABE
Employment
Assistant Professor, Faculty of Integrated Cultures and Humanities, University of East Asia, Japan.
Degree
MSc, MEd
Research interests
Biomechanics, ergonomics and exercise physiology
E-mail: daijiro@toua-u.ac.jp

Hiroaki TOKUMARU
Employment
Undergraduate Student, Faculty of Integrated Cultures and Humanities, University of East Asia, Yamaguchi Japan.
Degree
BSc
Research interests
Sports science in swimming.

Shigemitsu NIIHATA
Employment
Professor, Faculty of Welfare and Health, Fukuyama Heisei University, Fukuyama, Hiroshima, Japan.
Degree
PhD
Research interests
Coaching science and sports medicine

Satoshi MURAKI
Employment
Associate Professor, Department of Human Living System Design, Faculty of Design, Kyushu University, Fukuoka, Japan.
Degree
PhD
Research interests
Ergonomics

Yoshiyuki FUKUOKA
Employment
Professor, Faculty of Environmental and Symbiotic Sciences, Prefectural Univ. of Kumamoto, Kumamoto, Japan.
Degree
PhD
Research interests
Respiration and circulation physiology

Sachio USUI
Employment
Associate Professor, Faculty of Integrated Arts and Sciences, Hiroshima University, Higashi-hiroshima, Hiroshima, Japan.
Degree
MEd
Research interests
Mathematical analysis for human movement

Takayoshi YOSHIDA
Employment
Professor, Department of Health and Sport Sciences, Graduate School of Medicine, Osaka University, Japan.
Degree
PhD
Research interests
Evaluation for sports performance
References
- Abe D., Yanagawa K., Yamanobe K., Tamura K. (1998) Assessment of middle-distance running performance in sub-elite young runners using energy cost of running. European Journal of Applied Physiology 77, 320-325 [DOI] [PubMed] [Google Scholar]
- Abe D., Sakaguchi Y., Tsuchimochi H., Endo M., Miyake K., Miyahiro S., Kanamaru K., Niihata S. (1999) Assessment of long-distance running performance in elite male runners using onset of blood lactate accumulation. Applied Human Science 18, 25-29 [DOI] [PubMed] [Google Scholar]
- Bulburian R., Jeong J.W., Murphy M. (1996) Comparison of anaerobic components of the Wingate and critical power tests in males and females. Medicine and Science in Sports and Exercise 28, 1336-1341 [DOI] [PubMed] [Google Scholar]
- Chollet D., Seifert L., Leblanc H., Boulesteix L., Carter M. (2004) Evaluation of arm-leg coordination in flat breaststroke. International Journal of Sports Medicine 25, 486-495 [DOI] [PubMed] [Google Scholar]
- Dekerle J., Sidney M., Hespel J.M., Pelayo P. (2002) Validity and reliability of critical speed, critical stroke rate, and anaerobic capacity in relation to front crawl swimming performances. International Journal of Sports Medicine 23, 93-98 [DOI] [PubMed] [Google Scholar]
- Florence S., Weir J.P. (1997) Relationship of critical velocity to marathon running performance. European Journal of Applied Physiology 75, 274-278 [DOI] [PubMed] [Google Scholar]
- Fukuba Y., Yanagawa K., Kan A., Usui S., Koga S., Fukuoka Y. (1996) Fatigue threshold (θF): its physiological implication as the index of endurance capacity. Bulletin of Physical Fitness and Research Institute 91, 89-100 [Google Scholar]
- Fukuba Y., Miura A., Endo E., Kan A., Yanagawa K., Whipp B.J. (2003) The curvature constant parameter of the power-duration curve for varied-power exercise. Medicine and Science in Sports and Exercise 35, 1413-1418 [DOI] [PubMed] [Google Scholar]
- Hill D.W. (1993) The critical power concept. Sports Medicine 16, 237-254 [DOI] [PubMed] [Google Scholar]
- Holmer I. (1983) Energetics and mechanical work in swimming. In: Biomechanics and medicine in swimming. : Hollander A.P., Huijing P.A., Groot G.D.Champaign III: Human Kinetics Publishers; 154-164 [Google Scholar]
- Housh D.J., Housh T.J., Bauge S.M. (1989) The accuracy of the critical power test for predicting time to exhaustion during cycle ergometry. Ergonomics 32, 997-1004 [DOI] [PubMed] [Google Scholar]
- Hughson R.L., Orok C.J., Staudt L E. (1984) A high velocity treadmill running test to assess endurance running potential. International Journal of Sports Medicine 5, 23-25 [DOI] [PubMed] [Google Scholar]
- Kolbe T., Dennis S.C., Selley E., Noakes T.D., Lambert M.I. (1995) The relationship between critical power and running performance. Journal of Sports Science 13, 265-269 [DOI] [PubMed] [Google Scholar]
- Leblanc H., Seifert L., Baudry L., Chollet D. (2005) Arm-leg coordination in flat breaststroke: a comparative study between elite and non-elite swimmers. International Journal of Sports Medicine 26, 787-797 [DOI] [PubMed] [Google Scholar]
- Martin L., Whyte G.P. (2000) Comparison of critical swimming velocity and velocity at lactate threshold in elite triathletes. International Journal of Sports Medicine 21, 366-368 [DOI] [PubMed] [Google Scholar]
- McCartney N., Heigenhauser G.J., Sargent A.J., Jones N.L. (1983) A constant-velocity cycle ergometer for the study of dynamic muscle function. Journal of Applied Physiology 55, 212-217 [DOI] [PubMed] [Google Scholar]
- Miura A., Kino F., Kajitani S., Sato H., Fukuba F. (1999) The effect of oral creatine supplementation on the curvature constant parameter of the power-duration curve for cycle ergometry in humans. Japanese Journal of Physiology 49, 169-174 [DOI] [PubMed] [Google Scholar]
- Miura A., Sato H., Sato H., Whipp B.J., Fukuba Y. (2000) The effect of glycogen depletion on the curvature constant parameter of the power-duration curve for cycle ergometry. Ergonomics 43, 133-141 [DOI] [PubMed] [Google Scholar]
- Miura A., Endo M., Sato H., Sato H., Barstow T.J., Fukuba Y. (2002) Relationship between the curvature constant parameter of the power-duration curve and muscle cross-sectional area of the thigh for cycle ergometry in humans. European Journal of Applied Physiology 87, 238-244 [DOI] [PubMed] [Google Scholar]
- Monod H., Scherrer J. (1965) The work capacity of synergic muscle group. Ergonomics 8, 329-338 [Google Scholar]
- Nakamura Y., Mutoh Y., Miyashita M. (1984) A method for determining maximal anaerobic power using a bicycle ergometer. Japanese Journal of Sports Science 4, 834-839 [Google Scholar]
- Seifert L., Chollet D. (2005) A new index of flat breaststroke propulsion: a comparison of elite men and women. Journal of Sports Science 23, 309-320 [DOI] [PubMed] [Google Scholar]
- Smith J.C., Dangelmaier B.S., Hill D.W. (1997) Critical power is related to cycling time trial performance. International Journal of Sports Medicine 20, 374-378 [DOI] [PubMed] [Google Scholar]
- Takagi H., Sugimoto S., Nishijima N., Wilson B. (2004) Differences in stroke phases, arm-leg coordination and velocity fluctuation due to event, gender and performance level in breaststroke. Sports Biomechanics 3, 15-27 [DOI] [PubMed] [Google Scholar]
- Toussaint H.M., Wakayoshi K., Hollander A.P., Ogita F. (1998) Simulated front crawl swimming performance related to critical speed and critical power. Medicine and Science in Sports and Exercise 30, 144-151 [DOI] [PubMed] [Google Scholar]
- Wakayoshi K., Yoshida T., Udo M., Kasai T., Moritani T., Mutoh Y., Miyashita M.(1992a) A simple method for determining critical speed as swimming fatigue threshold in competitive swimming. International Journal of Sports Medicine 13, 367-371 [DOI] [PubMed] [Google Scholar]
- Wakayoshi K., Yoshida T., Kasai T., Moritani T., Mutoh Y., Miyashita M.(1992b) Validity of critical velocity as swimming fatigue threshold in the competitive swimmer. Annals of Physiological Anthropology 11, 301-307 [DOI] [PubMed] [Google Scholar]
- Wakayoshi K., Ikuta K., Yoshida T., Udo M., Moritani T., Mutoh Y., Miyashita M.(1992c) Determination and validity of critical velocity as an index of swimming performance in the competitive swimmer. European Journal of Applied Physiology 64, 153-157 [DOI] [PubMed] [Google Scholar]
- Wakayoshi K., Yoshida T., Udo M., Harada T., Moritani T., Mutoh Y., Miyashita M. (1993) Does critical swimming velocity represent exercise intensity at maximal lactate steady state? European Journal of Applied Physiology 66, 90-95 [DOI] [PubMed] [Google Scholar]


