Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Nov 14;3:3223. doi: 10.1038/srep03223

Flexible high-repetition-rate ultrafast fiber laser

Dong Mao 1, Xueming Liu 1,a, Zhipei Sun 2,3, Hua Lu 1, Dongdong Han 1, Guoxi Wang 1, Fengqiu Wang 2
PMCID: PMC3827608  PMID: 24226153

Abstract

High-repetition-rate pulses have widespread applications in the fields of fiber communications, frequency comb, and optical sensing. Here, we have demonstrated high-repetition-rate ultrashort pulses in an all-fiber laser by exploiting an intracavity Mach-Zehnder interferometer (MZI) as a comb filter. The repetition rate of the laser can be tuned flexibly from about 7 to 1100 GHz by controlling the optical path difference between the two arms of the MZI. The pulse duration can be reduced continuously from about 10.1 to 0.55 ps with the spectral width tunable from about 0.35 to 5.7 nm by manipulating the intracavity polarization controller. Numerical simulations well confirm the experimental observations and show that filter-driven four-wave mixing effect, induced by the MZI, is the main mechanism that governs the formation of the high-repetition-rate pulses. This all-fiber-based laser is a simple and low-cost source for various applications where high-repetition-rate pulses are necessary.

Ultrafast lasers with repetition rates in the megahertz and gigahertz regimes and beyond have been investigated for their immense applications in the fields of fiber optic communications1,2,3,4, materials processing5,6, frequency comb7, and nonlinear optics8,9,10,11,12,13. In particular, ultrafast fiber lasers exhibit inherent advantages such as high gain coefficient, wide operating wavelength range, excellent heat dissipation, and robust mode confinement14,15,16,17,18,19,20, and offer an attractive platform for implementing high-repetition-rate (HRR) pulse sources. In the early demonstrations of achieving HRR pulse sources, an active mode-locking scheme was typically proposed, e.g., a fiber laser with repetition rate of 10 GHz was reported21. However, further enhancement of the repetition rate is limited by the available electrical bandwidth of the modulator and its driving electronics21,22. Currently, various approaches have been exploited to generate HRR pulses in passively mode-locked fiber lasers, which are simpler in construction and are free from electrical bandwidth limitation. Therefore, pulses with higher repetition rate could be achieved in passive mode-locking, compared with active mode-locking. For example: in fundamentally mode-locked fiber lasers, pulse repetition rates in the range 10–20 GHz have been obtained by minimizing cavity length and employing thin film absorbers based on nanotubes and graphene23,24. However, further scaling to higher repetition rate is limited by the physical length of the fiber-based cavity. For > 1000 GHz, the necessary cavity length L should be less than 100 μm, assuming a typical refractive index n = 1.46 for a typical single-mode-fiber based linear cavity. For such a short L, it is not easy to provide enough gain for lasing and also offering reasonable output power (e.g., > 1 mW). For harmonic mode-locking, where multiple pulses circulate simultaneously in the cavity per round-trip time4,25,26, repetition rate up to 10 GHz has been realized and such a laser can operate at as high as the 634th harmonic of the fundamental cavity frequency27. But the harmonic mode-locking operation of laser is hardly controllable in practice4,25.

Recently, HRR pulse trains (up to 200 GHz) were generated in a fiber laser incorporating an intracavity Mach-Zehnder interferometer (MZI)28. However, a semiconductor saturable absorber mirror (SESAM) was employed to achieve the mode-locking operation and the pulse duration appeared to be independent of the interferometer settings. It is worth noting that Yoshida et al. demonstrated a low-threshold 115-GHz pulse train in a long-cavity fiber laser without any saturable absorber29. This scheme was later reinterpreted in terms of dissipative four-wave mixing (DFWM) where only two frequencies experience positive gain and transmit their energy by four-wave mixing (FWM) to high-order harmonics that undergo linear loss owing to the bandpass nature of the filter30,31. Peccianti et al. have recently realized stable HRR pulses in a mode-locked fiber laser based on a high-Q factor microring resonator32. They term this new mode-locking scheme filter-driven four-wave mixing (F-D FWM) because the microring resonator works as both a nonlinear element and a Fabry-Perot filter32,33. Despite the elegance of the FWM-based methods, the repetition rates of lasers based on these schemes are typically fixed29,30,31,32,34, and even researchers have to overcome the difficulty of splicing the fiber and microcavity32,33. Therefore, it is of great significance to study and realize repetition-rate-tunable duration-controllable ultrafast fiber lasers with an all-fiber approach.

Here, we propose a compact all-fiber laser with HRR pulses, in which an intracavity MZI plays a crucial role in the realization of the mode locking. By adjusting the optical path difference between the two arms of the MZI, the repetition rate of the pulses can be flexibly tuned from ~ 7 to 1100 GHz. Meanwhile, the spacing between adjacent peaks of the spectrum increases from ~ 0.06 to 9.5 nm. Interestingly, the pulse duration can be adjusted continuously from ~ 10.1 to 0.55 ps. The simulation results closely reproduce experimental observations. Our study provides a simple and low-cost method for generating HRR pulses by utilizing an all-fiber MZI.

Results

Setup of the HRR fiber laser

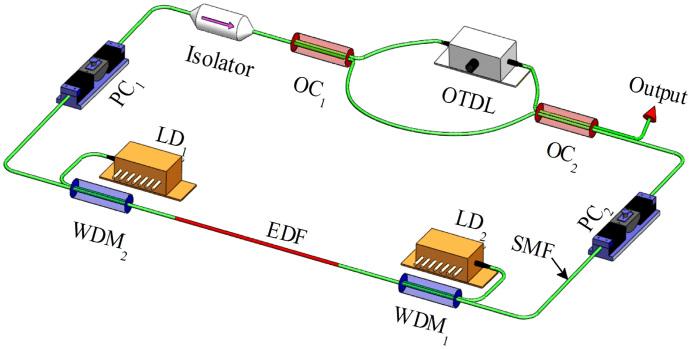
The schematic diagram of the laser setup is shown in Fig. 1. The resonator consists of a 17.6 m erbium-doped fiber (EDF: CoreActive C300) with a 3 dB/m absorption at 980 nm, an isolator, two polarization controllers (PCs), and a MZI. The other fibers are single-mode fibers (SMFs) with a total length of 9.4 m. The dispersion parameters D for EDF and SMF are about −9 ps/(nm·km) and 17 ps/(nm·km) at 1550 nm, respectively. The net dispersion of laser cavity is about −0.0018 ps2, which approaches zero, and then the Gaussian-profile pulse will be generated from the laser system. The MZI is constructed by splicing two identical 5:5 optical couplers (OCs). A tunable optical time delay line (OTDL) with a pigtail of 1.5 m is placed in one of the arms and the total length between two OCs is ~ 2 m. The MZI works as a spectral filter for wavelength selection, and the transmission spectrum can be precisely controlled by the OTDL. The output ratio of the OC is 50%. Two 980-nm laser diodes (LDs) and wavelength division multiplexers (WDMs) are used to provide bidirectional pumps. The total pump power is tunable from 0 to 1 W, which is sufficient to induce strong nonlinear effects in cavity. The isolator is used to ensure unidirectional operation in the oscillator. Note that HRR pulses can be generated by using either a polarization-sensitive isolator or a polarization-insensitive isolator in the experiment and output pulses are almost independent of the two different isolator settings.

Figure 1. Setup of the HRR fiber laser.

Figure 1

Open in a new tab

LD, laser diode; WDM, wavelength division multiplexer; EDF, erbium-doped fiber; SMF, single-mode fiber; PC, polarization controller; OC, optical coupler; OTDL, optical time delay line. The MZI is composed of two 5:5 OCs and an OTDL.

Experimental observations

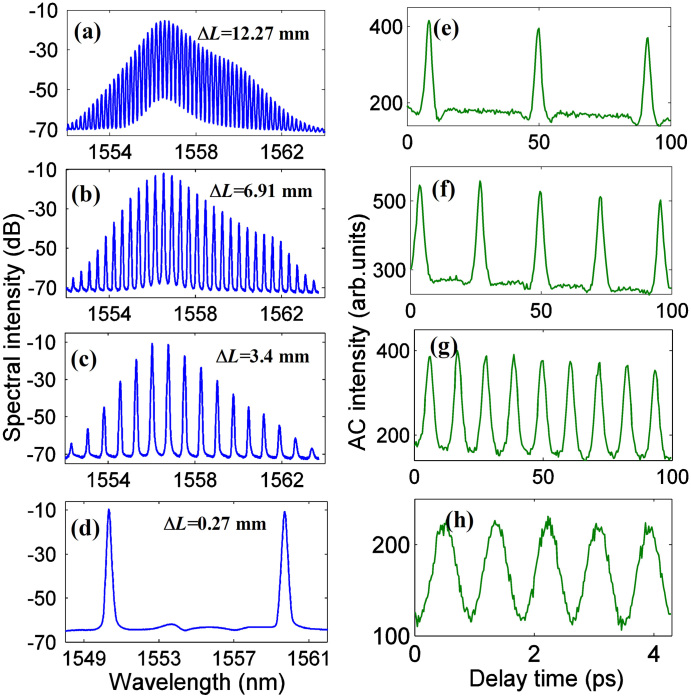
Self-starting HRR pulse trains can always be obtained in the fiber laser by precisely adjusting the settings of PCs and OTDL. When the forward and backward pumps are increased to 400 mW, the average output power is ~ 50 mW and is insensitive to the time delay of OTDL. Figures 2(a)–(d) show the output spectra for optical path differences of 12.27, 6.91, 3.4, and 0.27 mm, respectively. The optical spectra exhibit comb profiles with spectral separations of 0.193, 0.37, 0.75, and 9.5 nm, and the bandwidths of the spectral envelopes are estimated as 1.66, 1.6, 1.62, and 9.5 nm, respectively. The slight asymmetry of the spectra may be attributed to the uneven gain characteristics of the EDF. The relevant autocorrelation (AC) traces, as shown in Figs. 2(e)–(h), demonstrate that the laser produces equidistant pulse trains with temporal spacings of 41, 23, 11, and 0.9 ps, corresponding to pulse repetition rates of about 24, 43, 91, and 1100 GHz, respectively. If a Gaussian profile is assumed for fitting, the durations of the individual pulses in Figs. 2(e)–(h) are estimated as 2.20, 2.23, 2.21, and 0.37 ps. Then, the time bandwidth products (TBPs) of the pulses are calculated as 0.45, 0.44, 0.44, and 0.43, indicating that the output pulses are nearly chirp-free (i.e., transform-limited). Practically, the highest repetition rate of the pulses is limited by the available gain bandwidth of EDF. For example, only two spectrum peaks are generated within the gain bandwidth, as shown in Fig. 2(d). The HRR pulses with well-separated spectral peaks can be used for wavelength-division-multiplexed applications, an approach that may be economically advantageous over employing a large number of individually selected continuous-wave sources.

Figure 2.

Figure 2

Open in a new tab

(a)–(d) Optical spectra of the pulses and (e)–(h) corresponding AC traces at optical path differences ΔL of 12.27, 6.91, 3.4, and 0.27 mm, respectively.

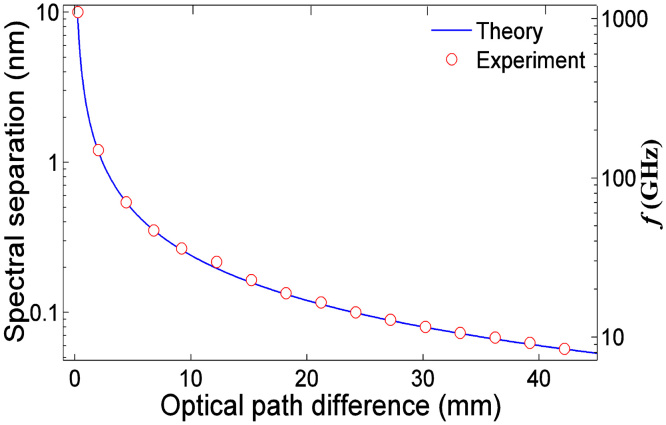
Figure 3 shows the spectral separation as a function of the optical path difference ΔL. Based on the transmission function of MZI, the spectral separation Δλ of adjacent peaks is given by Δλ = λ2/ΔL (see Methods for details), where λ is the operating wavelength. The repetition rate of the pulses is equal to the frequency difference of adjacent spectral peaks and is expressed as f = c·Δλ/λ2, where c is the speed of lightwave in vacuum. Experimental results show that the spectral separation increases from ~ 0.06 to ~ 9.5 nm by decreasing ΔL. Correspondingly, the repetition rate f of the pulses increases from ~ 7 to ~ 1100 GHz. It is evident that the wavelength spacing and repetition rate of the output pulses can be flexibly tuned over a large range with the OTDL in the MZI, which is a distinct advantage over the fiber laser mode locked with the micro-resonator32.

Figure 3. Spectral separation versus optical path difference ΔL.

Figure 3

Open in a new tab

The repetition rate f = c·Δλ/λ2. The theoretical curve of spectral separation is obtained from the equation Δλ = λ2/ΔL.

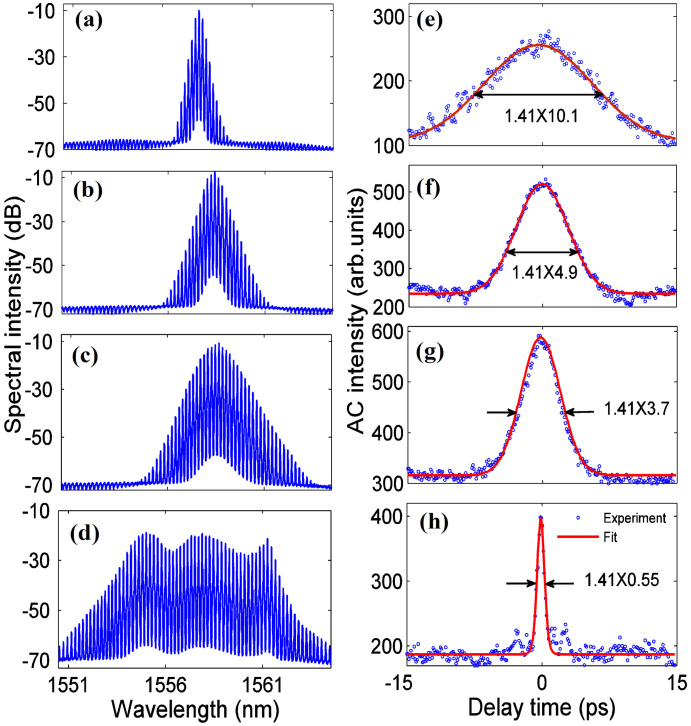
A notable feature of the laser is that the spectral width and pulse duration could be varied by adjusting the settings of the intracavity PCs if a polarization-sensitive isolator is used. Here, the optical path difference of the interferometer is fixed at 12.27 mm, and thus the spectral separation and pulse-pulse separation keep unchanged at 0.193 nm and 41 ps respectively in the following experiment. As shown in Figs. 4(a)–(h), the spectral widths of pulses are about 0.35, 0.74, 0.91, and 5.7 nm, and the corresponding pulse durations are about 10.1, 4.9, 3.7, and 0.55 ps, respectively. Although the pulses have different spectral widths and durations, they almost process the same TBP of about 0.44. The small periodic modulation on the spectral pedestal can be attributed to spectral filtering effect induced by the MZI. One can see from Fig. 4 that a broader optical spectrum corresponds to a narrower pulse, which coincides with the theory of soliton mode locking35. Furthermore, we find that the central wavelength of the spectrum can be adjusted from 1530 to 1570 nm by changing the polarization state. Here, the tuning range of the laser is practically limited by the available pump power and gain bandwidth of the EDF. The tuning feature of the pulse is possibly caused by the birefringence-induced spectral filtering effect. The PC-induced birefringence may introduce a wavelength-dependent polarization that, in conjunction with the polarization-sensitive isolator, will impose amplitude modulation on the optical spectrum. As a result, the transfer function of the cavity relies on the PC states, and mode locking tends to be realized at the wavelength with a higher transmission. This assumption can be further confirmed from Figs. 4(d) and 4(h), in which the optical spectrum exhibits modulation and the AC trace has small satellites. It is worth noting that the output spectrum in Fig. 4(d) is distinct from that of DFWM mode locking29,30,31 where the spectral intensity decreases from center to edges significantly. The results indicate that the dissipative process plays a less important role in the HRR pulse formation.

Figure 4.

Figure 4

Open in a new tab

(a)–(d) Optical spectra of pulses and (e)–(f) corresponding AC traces at different PC states. The optical path difference of the interferometer is fixed at 12.27 mm, and the spectral separation keeps unchanged at 0.193 nm. If a Gaussian profile is assumed for fitting, the pulse duration is the width of AC trace divided by a factor of ~ 1.41.

Numerical results

Figure 5 shows the numerical results of the HRR fiber laser. In the simulation, the initial signal is a weak light field. Due to the combined effects of spectral filtering, FWM, cavity dispersion, and fiber nonlinearity, the optical field evolves to a steady state and becomes symmetric after ~ 600 round trips. As shown in Fig. 5(a), multi-wavelength spectrum is gradually formed due to spectral filtering effect, and the central wavelengths transfer their energy to side wavelengths through FWM effect. Figure 5(b) shows that the light field is splitted into several sub-pulses and eventually evolves to a stable state with the increase of round-trip number. One can see that the output pulses are uniform and are equally spaced with a separation of 11 ps in the temporal domain.

Figure 5.

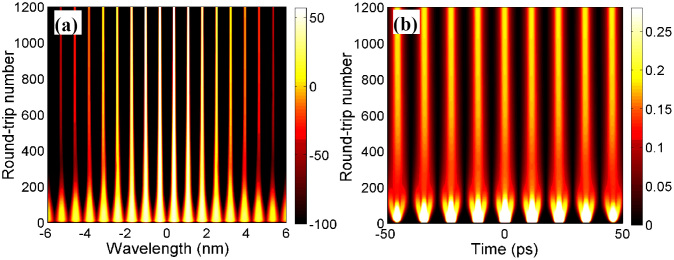
Figure 5

Open in a new tab

Evolution of (a) optical spectrum and (b) pulse profile with the round-trip number.

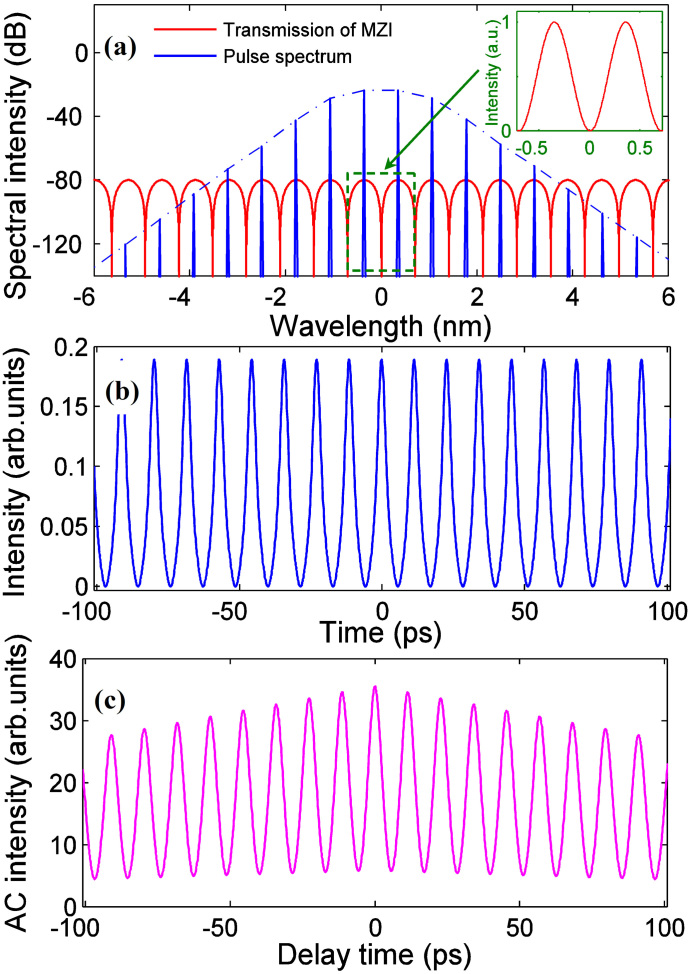
The red curve in Fig. 6(a) shows the transmission spectrum of the MZI, which is characterized by a series of equally spaced transmission peaks in the frequency domain. As shown in the inset of Fig. 6(a), the full width at half maximum (FWHM) of a single transmission peak is about 0.35 nm. The output spectrum at round trip of 1200 (the blue curve in Fig. 6(a)) exhibits a multi-channel structure with a wavelength spacing of 0.75 nm. We observe that lasing can only take place at the transmission peaks of the MZI, and the wavelength spacing of the comb-shape spectrum is equal to that of the transmission spectrum. The corresponding temporal profile and AC trace of the HRR pulses are shown in Figs. 6(b) and 6(c), respectively. The calculated AC trace is similar to that of the experimental results in which the intensity of AC peaks decreases slightly from center to edges. Our numerical results have fully confirmed experimental observations in Figs. 2(c) and 2(g), and demonstrated that the MZI-induced filtering effect dominates the pulse formation.

Figure 6.

Figure 6

Open in a new tab

(a) Transmission of the MZI and output spectrum of pulses, (b) pulse train, and (c) AC trace at round trip of 1200. The inset in Fig. 6(a) is the transmission spectrum in linear scale.

Discussion

In the experiments, the measured FWHM ΔλFWHM of a single spectral peak ranges from 0.015 to 0.025 nm, which is limited by the resolution of optical spectrum analyzer (0.015 nm). For example, the ΔλFWHM of a single peak in Fig. 2(c) is about 0.02 nm. The longitudinal mode spacing Δv is ~ 7.61 MHz, which corresponds to spectral separation ΔλLM of ~ 6.08 × 10−5 nm. Then there are about 300 modes in a single spectral peak. In comparison with a traditional mode-locking fiber laser that contains ~ 4 × 105 modes (ΔλFWHM ≈ 0.96 nm, Δv ≈ 0.29 MHz, ΔλLM ≈ 2.3 × 10−6 nm)16, the modes here are much less in a single spectral peak. As a result, the fewer modes (~300) in this experiment are more easily synchronized than the more modes (~4 × 105) in Ref. 16 from a theoretical point of view35.

Because every spectral peak is composed of many longitudinal modes, the intensity of the output pulses can be modulated with ~ 7.61 MHz, corresponding to ~ 131 ns. Due to the limited operating range of the autocorrelator (100 ps), the modulation period can not be directly obtained from the AC trace. We have theoretically investigated the modulation of pulse trains by summing the longitudinal modes in every spectral peak35. In the calculation, the mode separation and the optical path difference are assumed as 7.61 MHz and 3.4 mm, respectively, which are coincided with that of the experiment in Fig. 2(c). The phase of each mode is assumed to change randomly from 0 to 1. The theoretical results show that the HRR pulses are modulated with a period of ~ 131 ns. The calculated AC envelope decreases slightly from left to right, which is similar to that of Fig. 2(g).

We have replaced the polarization-sensitive isolator by a polarization-insensitive isolator in the cavity. HRR pulses with multi-wavelength spectrum are still achieved, and the repetition rate can be tuned over a wide range by the OTDL. The output spectrum and AC trace are similar to that of Fig. 2. However, the central wavelength and bandwidth of the spectrum are hard to be adjusted by PCs as other cavity components are polarization-insensitive. Our above experimental observations (i.e., successful demonstration of mode-locking using a polarization-insensitive or polarization-sensitive isolator) immediately demonstrate that the mode-locking is not achieved by nonlinear polarization rotation technique. This is further confirmed by that removing MZI from cavity cannot lead to mode-locking with the polarization-insensitive isolator. Compared with the laser in Ref. 28 that a SESAM is inserted in the cavity as a mode-locking element, only a MZI is used to generate HRR pulses in this scheme. Our results confirm that the F-D FWM induced by the MZI mainly contributes to the generation of pulses.

The formation of the HRR pulses may be understood as follows. During the pulse amplification process in EDF, the optical spectrum broadens strongly with the increase of pulse intensity due to the SPM and other nonlinear effects. With the help of the intracavity MZI, the optical spectrum of the pulses is modulated periodically. And then, the energy in the cavity is confined in several selective wavelengths. Due to the FWM and other nonlinear effects, the high-intensity central wavelengths distribute their energy to side wavelengths and form the comb-shape spectrum. Because each wavelength has the regular phase and position during the FWM process, they interfere and form the HRR pulses in the temporal domain. This process occurs at each circulation, and stable HRR pulses are formed when the optical field becomes self-consistent. Compared with methods in Refs. 29,30,31,32, only a fiber-based MZI is used as a spectral filter to achieve HRR pulses in our cavity. As the spectral filtering effect plays a key role in the FWM process, we attribute the pulse formation to F-D FWM effect.

Methods

Measurement method

An optical spectrum analyzer (Yokogawa AQ-6370) and a commercial autocorrelator (APE PulseCheck) are employed to characterize the laser output simultaneously. The repetition rate is deduced from the pulse-pulse separation measured by the autocorrelator.

Numerical simulation

To get an in-depth understanding of the experimental observations, we numerically simulate the dynamic evolution of HRR pulses based on the nonlinear Schrödinger equation (NLSE)35,36. We follow the propagation of the optical pulses in the laser cavity and consider functions of every cavity components on pulses. When pulses meet a cavity component, we then discretely multiply the light field by the relevant transformation matrix. After one round-trip circulation in the cavity, we use the obtained results as the input of the next round of calculation until the optical field becomes self-consistent. As the pulse duration is much larger than the delayed Raman response, the term related to Raman interaction can be neglected35,36,37,38. Pulse propagation within each fiber in laser cavity is modeled by36,38

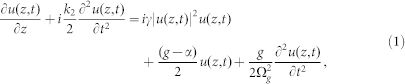graphic file with name srep03223-m1.jpg

where u(z,t) designates the slowly varying envelope of the optical field. The variables t and z represent the time and propagation distance, respectively. k2 is the second-order dispersion coefficient, and γ is the cubic refractive nonlinearity of the fiber. Ωg is the gain bandwidth of the laser. g is the saturable gain of the fiber, which is set as zero for SMF. For the EDF, the gain saturation is expressed as g = g0·exp(−Ep/Es)39, where g0, Ep and Es are the small-signal gain coefficient, pulse energy, and gain saturation energy, respectively. There is not any saturable absorber in the numerical model.

The filtering effect induced by the MZI is taken into account in our simulations. The transfer function of the interferometer can be expressed as35:

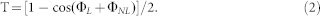graphic file with name srep03223-m2.jpg

And the linear and nonlinear parts of the relative phase shift are given by

graphic file with name srep03223-m3.jpg

where β0 is propagation constant, γ is the nonlinear coefficient, P0 is the pulse peak power, ΔL is the optical path difference between the two arms of the MZI, and λ is the lasing wavelength. As ΦNL << ΦL in this experiment, the simplified transfer function of interferometer can be described as

graphic file with name srep03223-m4.jpg

Since the linear phase shift is frequency-dependent, the transmission spectrum of the interferometer depends on the wavelength of light and the modulation frequency is mainly determined by ΔL. The modulation period corresponds to ΦL = 2π. The relation between modulation period and spectral separation Δλ is deduced as follows:

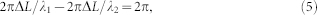graphic file with name srep03223-m5.jpg
graphic file with name srep03223-m6.jpg

Here, Δλ = λ2 − λ1. Because Δλ is very small, λ1λ2 approximately equals λ2. Then, the spectral separation between adjacent transmission peaks can be expressed as:

graphic file with name srep03223-m7.jpg

The NLSE is solved with a predictor–corrector split-step Fourier technique38,40. The gain spectrum of EDF is assumed to have a Gaussian profile with a 3-dB bandwidth of 18 nm. We use the following parameters to match the experimental conditions. c = 3 × 108 m/s, g0 = 3 dB/m, n = 1.46, ΔL = 3.4 mm, α = 0.2 dB/km, Ωg = 18 nm, Es = 15 pJ. γ = 3 W−1·km−1 and k2 = 11.47 ps2/km for EDF; γ = 1 W−1·km−1 and k2 = −21.67 ps2/km for SMF. The lengths of EDF and SMF are 17.6 and 9.4 m, respectively. The other parameters are the same as that of experiments.

Author Contributions

D.M. proposed the laser system, performed the main experimental and numerical results, and wrote the main manuscript text. X.L. improved the design of the system, instructed the experiments and simulations, and supervised the whole project. Z.S. considerably improved the manuscript presentation. H. L. carried out the data analysis and revised the manuscript. D.H. performed the part of the experimental results. G.W. provided technical support and prepared part figures. F. W. contributed to the scientific discussion and improved the manuscript presentation. All authors discussed the results and substantially contributed to the manuscript.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grants 10874239, 10604066, 61223007, and 11204368.

References

  1. Haus H. A. & Wong W. S. Solitons in optical communications. Rev. Mod. Phys. 68, 423–444 (1996). [Google Scholar]
  2. Keller U. Recent developments in compact ultrafast lasers. Nature 424, 831–838 (2003). [DOI] [PubMed] [Google Scholar]
  3. Zhang Z. Y. et al. 1.55 μm InAs/GaAs quantum dots and high repetition rate quantum dot SESAM mode-locked laser. Sci. Rep. 2, 477 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Liu X. et al. Passively harmonic mode-locked erbium-doped fiber soliton laser with a nonlinear polarization rotation. Laser Phys. 18, 1357–1361 (2008). [Google Scholar]
  5. Gattass R. R. & Mazur E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2, 219–225 (2008). [Google Scholar]
  6. Sun Z. et al. A compact, high power, ultrafast laser mode-locked by carbon nanotubes. Appl. Phys. Lett. 95, 253102 (2009). [Google Scholar]
  7. Diddams S. A., Hollberg L. & Mbele V. Molecular fingerprinting with the resolved modes of a femtosecond laser frequency comb. Nature 445, 627–630 (2007). [DOI] [PubMed] [Google Scholar]
  8. Liu X. M. Pulse evolution without wave breaking in a strongly dissipative-dispersive laser system. Phys. Rev. A 81, 053819 (2010). [Google Scholar]
  9. Grelu P. & Akhmediev N. Dissipative solitons for mode-locked lasers. Nat. Photonics 6, 84–92 (2012). [Google Scholar]
  10. Solli D. R., Ropers C., Koonath P. & Jalali B. Optical rogue waves. Nature 450, 1054–1057 (2007). [DOI] [PubMed] [Google Scholar]
  11. Krauss G. et al. Synthesis of a single cycle of light with compact erbium-doped fibre technology. Nat. Photonics 4, 33–36 (2009). [Google Scholar]
  12. Mao D., Liu X. & Lu H. Observation of pulse trapping in a near-zero dispersion regime. Opt. Lett. 37, 2619–2621 (2012). [DOI] [PubMed] [Google Scholar]
  13. Kobtsev S., Kukarin S., Smirnov S., Turitsyn S. & Latkin A. Generation of double-scale femto/pico-second optical lumps in mode-locked fiber lasers. Opt. Express 17, 20707–20713 (2009). [DOI] [PubMed] [Google Scholar]
  14. Lecaplain C., Grelu P., Soto-Crespo J. M. & Akhmediev N. Dissipative rogue waves generated by chaotic pulse bunching in a mode-locked laser. Phys. Rev. Lett. 108, 233901 (2012). [DOI] [PubMed] [Google Scholar]
  15. Turitsyn S. K. et al. Random distributed feedback fibre laser. Nat. Photonics 4, 231–235 (2010). [Google Scholar]
  16. Liu X. M. Soliton formation and evolution in passively mode-locked lasers with ultralong anomalous-dispersion fibers. Phys. Rev. A 84, 023835 (2011). [Google Scholar]
  17. Oktem B., Ülgüdür C. & Ilday F. Ö. Soliton-similariton fibre laser. Nat. Photonics 4, 307–311 (2010). [Google Scholar]
  18. Liu X. M. Dynamic evolution of temporal dissipative-soliton molecules in large normal path-averaged dispersion fiber lasers. Phys. Rev. A 82, 063834 (2010). [Google Scholar]
  19. Dudley J. M., Finot C., Richardson D. J. & Millot G. Self-similarity in ultrafast nonlinear optics. Nat. Physics 3, 597–603 (2007). [Google Scholar]
  20. Liu X. Hysteresis phenomena and multipulse formation of a dissipative system in a passively mode-locked fiber laser. Phys. Rev. A 81, 023811 (2010). [Google Scholar]
  21. Carruthers T. & Duling III I. 10-GHz, 1.3-ps erbium fiber laser employing soliton pulse shortening. Opt. Lett. 21, 1927–1929 (1996). [DOI] [PubMed] [Google Scholar]
  22. Haus H. A. Mode-locking of lasers. IEEE J. Select. Topics Quantum Electron. 6, 1173–1185 (2000). [Google Scholar]
  23. Martinez A. & Yamashita S. Multi-gigahertz repetition rate passively modelocked fiber lasers using carbon nanotubes. Opt. Express 19, 6155–6163 (2011). [DOI] [PubMed] [Google Scholar]
  24. Martinez A. & Yamashita S. 10 GHz fundamental mode fiber laser using a graphene saturable absorber. Appl. Phys. Lett. 101, 041118 (2012). [Google Scholar]
  25. Collings B. C., Bergman K. & Knox W. H. Stable multigigahertz pulse-train formation in a short-cavity passively harmonic mode-locked erbium/ytterbium fiber laser. Opt. Lett. 23, 123–125 (1998). [DOI] [PubMed] [Google Scholar]
  26. Amrani F. et al. Passively mode-locked erbium-doped double-clad fiber laser operating at the 322nd harmonic. Opt. Lett. 34, 2120–2122 (2009). [DOI] [PubMed] [Google Scholar]
  27. Sobon G., Krzempek K., Kaczmarek P., Abramski K. M. & Nikodem M. 10 GHz passive harmonic mode-locking in Er-Yb double-clad fiber laser. Opt. Communications 284, 4203–4206 (2011). [Google Scholar]
  28. Lhermite J. et al. Tunable high-repetition-rate fiber laser for the generation of pulse trains and packets. Opt. Lett. 32, 1734–1736 (2007). [DOI] [PubMed] [Google Scholar]
  29. Yoshida E. & Nakazawa M. Low-threshold 115-GHz continuous-wave modulational-instability erbium-doped fibre laser. Opt. Lett. 22, 1409–1411 (1997). [DOI] [PubMed] [Google Scholar]
  30. Sylvestre T., Coen S., Emplit P. & Haelterman M. Self-induced modulational instability laser revisited: normal dispersion and dark-pulse train generation. Opt. Lett. 27, 482–484 (2002). [DOI] [PubMed] [Google Scholar]
  31. Quiroga-Teixeiro M., Clausen C. B., Sørensen M. P., Christiansen P. L. & Andrekson P. A. Passive mode locking by dissipative four-wave mixing. J. Opt. Soc. Am. B 15, 1315–1321 (1998). [Google Scholar]
  32. Peccianti M. et al. Demonstration of a stable ultrafast laser based on a nonlinear microcavity. Nat. Communications 3, 765 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Razzari L. et al. CMOS-compatible integrated optical hyper-parametric oscillator. Nat. Photonics 4, 41–45 (2009). [Google Scholar]
  34. Schröder J., Coen S., Vanholsbeeck F. & Sylvestre T. Passively mode-locked Raman fiber laser with 100 GHz repetition rate. Opt. Lett. 31, 3489–3491 (2006). [DOI] [PubMed] [Google Scholar]
  35. Agrawal G. P. Applications of Nonlinear Fiber Optics. (Academic Press, San Diego, 2001). [Google Scholar]
  36. Ilday F. Ö., Buckley J. R., Clark W. G. & Wise F. W. Self-similar evolution of parabolic pulses in a laser. Phys. Rev. Lett. 92, 213902 (2004). [DOI] [PubMed] [Google Scholar]
  37. Tang D. Y., Zhang H., Zhao L. M. & Wu X. Observation of high-order polarization-locked vector solitons in a fiber laser. Phys. Rev. Lett. 101, 153904 (2008). [DOI] [PubMed] [Google Scholar]
  38. Liu X. et al. Versatile multi-wavelength ultrafast fiber laser mode-locked by carbon nanotubes. Sci. Rep. 3, 2718 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Agrawal G. P. Amplification of ultrashort solitons in erbium-doped fiber amplifiers. IEEE Photon. Technol. Lett. 2, 875–877 (1990). [Google Scholar]
  40. Liu X. & Lee B. A fast method for nonlinear Schrödinger equation. IEEE Photon. Technol. Lett. 15, 1549–1551 (2003). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES