Abstract
First order latent growth curve models (FGMs) estimate change based on a single observed variable and are widely used in longitudinal research. Despite significant advantages, second order latent growth curve models (SGMs), which use multiple indicators, are rarely used in practice, and not all aspects of these models are widely understood. In this article, our goal is to contribute to a deeper understanding of theoretical and practical differences between FGMs and SGMs. We define the latent variables in FGMs and SGMs explicitly on the basis of latent state-trait (LST) theory and discuss insights that arise from this approach. We show that FGMs imply a strict trait-like conception of the construct under study, whereas SGMs allow for both trait and state components. Based on a simulation study and empirical applications to the CES-D depression scale (Radloff, 1977) we illustrate that, as an important practical consequence, FGMs yield biased reliability estimates whenever constructs contain state components, whereas reliability estimates based on SGMs were found to be accurate. Implications of the state-trait distinction for the measurement of change via latent growth curve models are discussed.
Keywords: Latent growth curve models, latent state-trait theory, reliability estimation, longitudinal modeling, latent change, CES-D
Generally it is certainly the case that most psychological attributes will neither be, strictly speaking, traits or states. That is, attributes can have both trait and state components.
(Hertzog & Nesselroade, 1987, p. 95)
Latent growth curve models (LGCMs; McArdle & Epstein, 1987; Meredith & Tisak, 1990) are currently among the most widely used statistical approaches for analyzing change over time in the social and behavioral sciences. To date, most methodological work and applications in the area of LGCMs have focused on models that analyze change based on a single repeatedly measured observed (manifest) variable (e.g., a single depression scale score measured at four time points). These models are often referred to as first order latent growth curve models (FGMs; e.g., Hancock, Kuo, & Lawrence, 2001).
Recently, several authors (e.g., Chan, 1998; Ferrer, Balluerka, & Widaman, 2008; Leite, 2007; Mayer, Steyer, & Mueller, 2011; Murphy, Beretvas, & Pituch, 2011; Sayer & Cumsille, 2001; von Oerzen, Hertzog, Lindenberger, & Ghisletta, 2010) have emphasized the limitations of FGMs and recommended the use of second order latent growth curve models (SGMs) that are based on multiple repeatedly measured observed variables. The most important strengths of SGMs can be summarized as follows:
SGMs properly separate measurement error from true change and reliable time-specific variance (Sayer & Cumsille, 2001)
SGMs allow testing the assumption of measurement invariance across time (Chan, 1998; Ferrer et al., 2008)
SGMs have greater statistical power to detect individual differences in change (von Oerzen et al., 2011).
SGMs use multiple indicators and thus allow isolating indicator-specific (or method) effects from shared construct variance.
Despite these advantages, the vast majority of applications of LGCMs use FGMs (Leite, 2007), and there have been only a few applications of SGMs (e.g., Duncan & Duncan, 1996). One reason for the dominance of FGMs may be that the advantages of SGMs (and the limitations of FGMs) still are not widely known among both methodological and substantive researchers. As Ferrer et al. (2008) point out, “much remains to be done to understand all aspects of the fitting and the interpretation of these models” (p. 24).
In this article, we want to contribute to a better understanding of the theoretical differences between FGMs and SGMs (and advocate the use of SGMs) by looking at these models from the perspective of latent state-trait (LST) theory (Steyer, Ferring & Schmitt, 1992; Steyer & Schmitt, 1990; Steyer, Schmitt, & Eid, 1999)—and demonstrate some practical implications of these differences for empirical applications. In particular, we show that according to LST theory, FGMs are only appropriate when the construct under study is a pure trait, that is, when there are no systematic occasion-specific influences. As has been stated by numerous authors (e.g., Anastasi, 1983; Steyer et al., 1992), however, measurement rarely takes place in a situational vacuum, and the assessment of most psychological constructs has to deal with both trait and state components (Hertzog & Nesselroade, 1987; Tisak & Tisak, 2000). This is true even when scales are constructed to reflect stable traits (Deinzer et al., 1995).
Ignoring occasion-specific effects in FGMs is unsatisfactory both from a theoretical and a practical point of view. Theoretically, it is desirable to estimate all relevant sources of variance properly. From a practical point of view, neglecting specific sources of variation can lead to bias in parameter estimates and hence to incorrect conclusions. In particular, as shown in this article, applying FGMs to constructs that have both trait and state components leads to a systematic bias in the estimates of indicator reliabilities that can cause confusion and lead to erroneous conclusions as to the psychometric properties of indicators chosen for measuring change.
LST theory (Steyer et al., 1992; 1999; Steyer & Schmitt, 1990) was originally developed to address the problem of variability of psychological scores around a fixed set-point or trait value, and LST models are widely used in psychological research to determine to which extent measurements reflect individual differences due to stable, occasion-specific, and measurement error components (Geiser & Lockhart, in press). Although LST models are mainly used for studying variability processes rather than for measuring change, LST theory is flexible and allows formulating various models of change as well (Eid & Hoffmann, 1998; Mayer et al., 2011; Steyer, 2005; Steyer, Eid, & Schwenkmezger, 1997; Steyer, Krambeer, & Hannöver, 2004). As has been shown by Tisak and Tisak (2000), the advantages of models for measuring variability and models for measuring change can be combined into a single modeling framework.
In this article, we apply the fundamental concepts of LST theory to the study of latent growth curves and show that the well-defined concepts of LST theory can be used to explicitly define each latent variable in both FGMs and SGMs. To our knowledge, the link between the fundamental concepts of LST theory, FGMs, and SGMs has not yet been explicitly addressed in the literature. The advantage of the LST approach to formulating FGMs and SGMs is that the meaning of the latent variables is clear in both models (for a slightly different approach to formulating LGCMs see Mayer et al., 2011). Specifically, it makes clear that FGMs implicitly assume that the construct under study is a pure trait, that is, that there are no occasion-specific influences on the measurements. As an important practical consequence, FGMs lead to an underestimation of indicator reliabilities whenever occasion-specific variance is present. We show that the patterns of bias in FGMs can be diverse and confusing depending on whether and how occasion-specific variance varies over time. This bias can lead to incorrect conclusions about (1) the amount of measurement error at a given point in time and (2) changes in the reliabilities of the indicators over time.
The organization of this article is as follows. We first provide an informal introduction to FGMs and SGMs. We then discuss the key concepts of LST theory and show how both FGMs and SGMs can be formally derived based on LST theory. We conclude that from the point of view of LST theory, FGMs imply a trait-like conception of the construct under study that is unlikely to hold true in many (if not most) social science applications, whereas SGMs do not share this limitation. Based on a small simulation study as well as an empirical application to a widely used depression measure, we show that the presence of occasion-specific variance leads to various forms of reliability biases in FGMs. Finally, we provide recommendations for the application of LGCMs in practice.
FGMs Versus SGMs
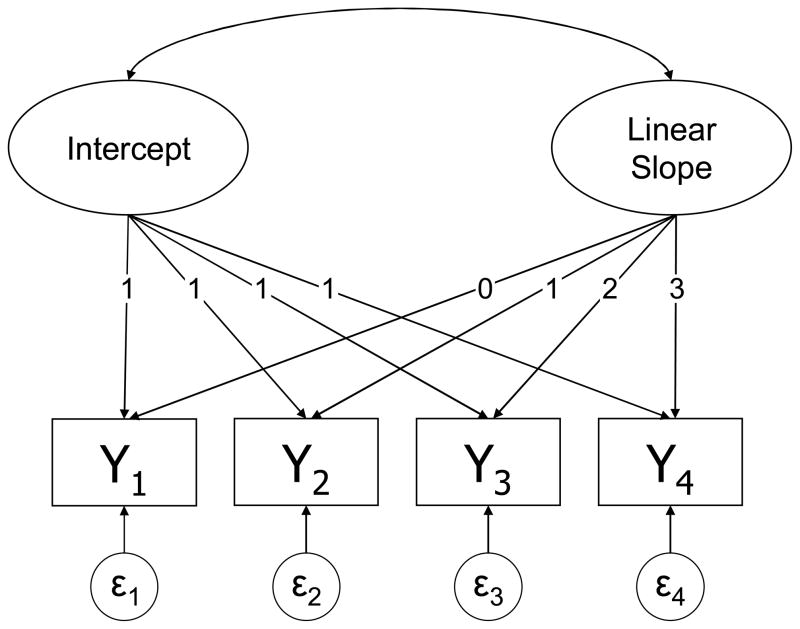
A path diagram of a linear FGM for four time points is shown in Figure 1A. In the FGM, the construct is assessed by a single observed variable (e.g., a global test or questionnaire sum score) that is measured at each time point. The observed variables are influenced by a first order intercept factor, a first order slope factor, and an error term. The intercept factor represents the initial status, whereas the slope factor reflects the rate of linear change over time. Below we present exact mathematical definitions of these factors based on LST theory.
Figure 1.
Linear FGM for four measurement occasions. Yt denotes an observed variable (indicator) measured at time t.
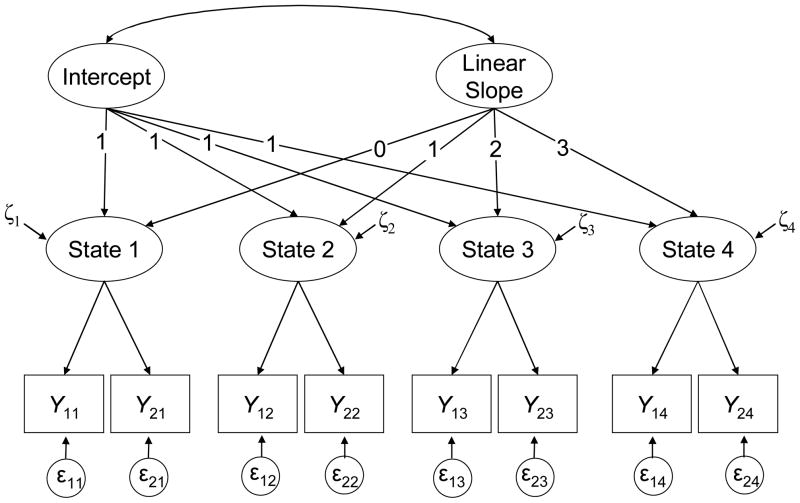
SGMs were originally introduced by McArdle (1988) as “curve-of-factors” models. In SGMs, the construct is assessed by multiple (at least two) observed variables at each time point (see Figure 1B). It is assumed that indicators assessed at the same measurement occasion measure a common time-specific factor. The time-specific factors themselves are indicators of a second order intercept and slope factor. The growth process is thus modeled at the level of latent rather than observed variables in SGMs and hence the alternative terminology “curve-of-factors” model. As a consequence, time-specific residual variability (as reflected in the latent residual variables) can be separated from random error in SGMs (Sayer & Cumsille, 2001).
In the following, we introduce the fundamental concepts of LST theory, provide an explicit definition of each latent factor in both FGMs and SGMs based on these concepts, and show that these definitions lead to a better understanding of what the latent variables in these models actually mean and in which way FGMs differ from SGMs. Furthermore, this approach has the advantage that it allows us to make the assumptions that lead to the formulation of a specific model more explicit than in conventional approaches to formulating LGCMs.
LST Theory
LST theory was developed by Steyer and colleagues (Steyer & Schmitt, 1990; Steyer et al., 1992; 1999) to provide a formal mathematical framework for measuring persons in situations. LST models are widely used in social science research to study variability processes as well as the impact of situations on psychological measurements (Geiser & Lockhart, in press). Although methodological approaches that integrate models for measuring change with models for analyzing variability as provided by LST theory have already been presented (e.g., Cole, Martin, & Steiger, 2005; Eid & Hoffmann, 1998; Steyer et al., 2004; Tisak & Tisak, 2000), to our knowledge the formal link between the fundamental concepts of LST theory and LGCMs has not yet been explicitly established.1
Random experiment
The starting point for defining the fundamental concepts of LST theory is the consideration of the random experiment (RE) that formally describes the empirical phenomenon considered in LST theory (i.e., the measurement of persons in situations). This RE is not an experiment in the classical sense, because it does not involve any kind of experimental manipulation of independent variables. The RE simply summarizes the empirical phenomenon studied in LST theory in a formal way, namely that we measure an attribute of the same person across different situations using multiple measurements (e.g., multiple indicators, raters, observations, or methods) at each time point (e.g., Eid, 1996; Steyer et al., 1992). Let Ω denote the set of possible outcomes of this RE. Then,
| (1) |
In Equation 1, ΩU is the set of observational units u (persons), ΩSitt is the set of situations at time t, t = 1, …, n, ΩMeat is the set comprising all measurements at time t, and × is the Cartesian set product operator. Because we assume multiple measurements (multiple indicators) at each time point, each set ΩMeat itself consists of the Cartesian product of subsets ΩMeat:
| (2) |
where the subsets ΩMeat contain the values on the observed indicators i (e.g., item or scale scores), i = 1, …, m at time t.
As an example, consider the case of two indicators (i = 1, 2), each of which is measured on two time points (t = 1, 2). For this example, Ω can be written as:
| (3) |
Further, an element of Ω can be written as ω = (u, sit1, mea11, mea21, sit2, mea12, mea22), where u indicates the specific person drawn from the set of persons ΩU, sit1 indicates the specific situation drawn from the set of situations ΩSit1 on the first time point, mea11 indicates the specific score observed for the first indicator on the first time point, mea21 indicates the specific score observed for the second indicator on the first time point, sit2 indicates the specific situation drawn from the set of situations ΩSit2 on the second time point, mea12 indicates the specific score observed for the first indicator on the second time point, and mea22 indicates the specific score observed for the second indicator on the second time point. It is important to note that (1) the situations depend on both inner and outer influences and (2) they do not have to be known. Moreover, they need not be the same for all persons (Steyer, 1988).
Let Yit denote a random variable that represents the observed scores obtained for indicator i at time t. The values of the mapping pu : Ω → ΩU are the persons u. The values of the mapping pSitt : Ω → ΩSitt are the situations in which the persons are measured at a particular measurement occasion t. Hence, pu and pSitt are qualitative random variables. The values of (pu, pSitt) are the persons in situations at time t.
Basic latent variables
On the basis of the random variables introduced above, latent variables can be defined that have a clear meaning, because they are based on clearly defined quantities (Steyer et al., 1992). The latent state variables Sit are defined as the conditional expected value of the observed variable given the person and the situation variables:
| (4) |
The measurement error variables εit are defined as the difference between the observed variable and the conditional expectation of Yit given the person and the situation:
| (5) |
Algebraic manipulation of Equation 5 leads to the basic decomposition of observed variables in LST theory:
| (6) |
where εit by definition has an expected value of zero and is uncorrelated with the regressor Sit (Steyer, 1989; Zimmerman, 1975). The following simple manipulation of E(Yit | pu, pSitt) is the basis for defining latent trait and latent state residual variables in LST theory (Steyer et al., 1992):
| (7) |
The latent trait variables are defined as the conditional expectation of an observed variable given the person:
| (8) |
Equation 8 shows that the trait variable represents that part of the observed variable that is determined by the person only. Hence, it represents stable, person-specific individual differences only. (As we will show below, this definition does not imply that the trait could not change over time; it only implies that the trait does not depend on influences of the situation.)
The latent state residual variables are defined as the conditional expectation given the person and the situation minus the conditional expectation of an observed variable given the person:
| (9) |
Equation 9 shows that individual values on the variable SRit represent the differences between latent state and latent trait scores. Consequently, Sit= Tit + SRit. Combining this equation with Equation 6 yields the extended decomposition of observed variables in LST theory:
| (10) |
The latent state residual represents that part of the latent state that is determined by the situation and/or person-situation interactions (Steyer et al., 1992; 1999). Equations 1 through 10 only describe the basic concepts considered in LST theory. These equations are just definitions; they do not imply any restrictive assumptions (other than the rather trivial assumption that the variances of the Yit variables are positive and finite), and they do not define specific testable statistical models. Testable models of LST theory can be derived by making assumptions about the homogeneity of state, trait, and/or state residual variables. Various testable LST models and their assumptions have been described in detail in the literature, for example, by Steyer et al. (1992; 1999), Eid, Schneider, and Schwenkmezger (1999), and Geiser and Lockhart (in press). Here, we only consider the assumptions that allow defining FGMs and SGMs based on the latent variables introduced above.
Formulating LGCMs on the Basis of LST Theory
FGMs
FGMs imply a design with a single observed variable at each measurement occasion. Hence, we can drop the index i from the observed variable, such that the basic decomposition reduces to:
| (11) |
Further, note that with only a single indicator measured at several time points individual differences with regard to occasion-specific influences cannot be isolated from individual differences regarding random measurement error. In other words, SRt cannot be isolated from εt, unless there are least two indicators measured on at least two time points (Steyer et al., 1992). As a logical consequence, we have to make the rather restrictive assumption that Var(SRt) = 0 for all t, such that the latent state variables are identical to the latent trait variables:
It follows that the decomposition of observed variables reduces to:
| (12) |
implying that an observed score consists of trait and measurement error influences only.
In terms of LST theory, the initial status (or “intercept”) is represented by the first latent state variable, S1, which according to the (necessary) assumption made above is identical to the latent trait variable pertaining to the first time point, T1. To define a slope factor, consider the following unrestrictive decomposition that is always true (Steyer, Eid, & Schwenkmezger, 1997; Pohl, Steyer, & Krauss, 2008):
| (13) |
We can now define an intercept and slope factor as follows, using the well-defined latent variables of LST theory:
| (14) |
| (15) |
Assuming equal spacing between time points for simplicity, a linear growth model is obtained by postulating the following relationship among trait variables:2
| (16) |
In contrast to Equation 13, Equation 16 does introduce a restrictive assumption, namely that trait change is linear for all individuals. Equation 16 implies the following model for the observed variables:
| (17) |
Equation 17 makes clear that in a linear FGM, each indicator is decomposed into the latent trait variable pertaining to the first time point plus (t − 1) times the latent difference score between the latent trait variable pertaining to the second time point and the latent trait variable pertaining to the first time point. Hence, this definition shows that what we are actually considering in FGMs is a latent (trait) difference score model (McArdle & Hamagami, 2001) with restrictions on how the latent trait variables are decomposed into initial trait value plus trait change (Mayer et al., 2011; Nachtigall, Kraus, & Steyer, 2000). According to LST theory, an intercept factor in a growth model is identical to the trait variable pertaining to the first time point, whereas a slope factor is a latent trait difference variable. Note that occasion-specific (state residual) influences are not explicitly represented in the model (they are confounded with time-specific random error). Hence, FGMs imply a trait-like conception of the construct under study that may not be realistic in many social science applications.
SGMs
In SGMs, multiple indicators Yit are used at each time point. According to Equation 10, each observed variable Yit has its own associated latent state and error variable, where the state variable can be further decomposed into a latent trait and a latent state residual component. In order to define an SGM based on Equation 10, we make the assumption of occasion-specific congenerity of the latent state variables. This assumption means that we assume all latent state variables measured at the same time point to be linear functions of each other:
| (18) |
Equation 18 shows that under this assumption all latent state variables measured at the same time point differ from one another only by an additive and a multiplicative constant. In other words, we assume that all latent state variables measured on the same time point are unidimensional. This assumption is equivalent to postulating the existence of a single common latent factor for each time point (for a formal proof, see, Steyer, 1989, p. 59), such that Equation 18 is equivalent to:
| (19) |
where St denotes the common latent state factor at time t. 3 The coefficients αit and λit can be interpreted as measurement intercepts and factor loadings, respectively.
In the next step, we consider the decomposition of the common latent state factors St. According to Equation 9, each latent state variable can be decomposed into a latent trait and a latent state residual component. This holds also for the common state factors St, because these latent variables are linear functions of the indicator-specific state variables Sit according to Equation 19:
| (20) |
We can again introduce the following unrestrictive decomposition of the latent trait variables that is always true to define intercept and slope factors:
| (21) |
| (22) |
| (23) |
A linear growth model can again be formulated by assuming the following relationship among trait variables:
| (24) |
Again, whereas Equation 21 is completely unrestrictive, Equation 24 introduces the restrictive assumption that trait change is linear for all individuals. By combining Equations 6, 19, 20, and 24, we obtain the following model for the observed variables:
| (25) |
A comparison of Equation 17 and 25 makes clear that in contrast to FGMs, SGMs explicitly account for potential situation-specific (state residual) effects of a construct by including an occasion-specific latent residual factor SRt. This factor is clearly defined as the difference between a latent state variable and the corresponding latent trait variable (see Equation 9). In contrast, FGMs assume that although a trait may change over time, constructs are not affected by systematic situation-specific influences.
Reliability Estimation in FGMs and SGMs
In classical test theory (CTT; Novick, 1966), reliability is defined as the ratio of true score variance to total observed score variance. LST theory can be viewed as a generalization of CTT to the measurement of persons in situations. In LST theory, the variables that correspond to the true score variables in CTT are the latent state variables Sit. Consequently, reliability in LST theory is defined as the ratio of the variance of the latent state variable to the total observed variance (Steyer et al., 1992):
| (26) |
According to Equation 25, LST theory allows decomposing the latent state variables into trait, trait change, and state residual components. Therefore, all three components are relevant for the proper estimation of the reliability of an indicator. FGMs and SGMs allow a researcher to quantify the reliability of each indicator in terms of the proportion of variance in the indicator that is accounted for by these components, although FGMs do not take into account the state residual component. Tisak and Tisak (1996) have defined reliability in FGMs as the ratio of variance accounted for by the growth factors to total observed score variance. Using our notation, we can write the reliability coefficient as follows:
| (27) |
In SGMs, reliability can be defined in a more inclusive way, since reliable variability due to occasion-specific state residual effects is taken into account:4
| (28) |
A comparison of Equation 27 and 28 makes clear that reliability will be underestimated in FGMs whenever the variance of the occasion-specific state residual variable is non-zero, because this component is ignored in FGMs. As a consequence, FGMs confound reliable occasion-specific variance and error variance (Sayer & Cumsille, 2001). This means that for constructs that are influenced by effects of the situation or occasion of measurement, reliability estimates in FGMs will generally be too small. Raykov (2000) noted that longitudinal researchers are often interested in changes in reliabilities over time. As we will show below, FGM may obscure patterns of change in reliabilities if occasion-specific variance is present.
SGMs are more flexible and allow for more accurate estimates of indicator reliabilities, because they separate out reliable occasion-specific variance from random measurement error variance. SGMs therefore allow defining two additional coefficients that summarize different reliable sources of variance. The consistency and trait change (CC) coefficient reflects the proportion of observed variance that is accounted for by trait and trait change effects: 5
| (29) |
Note that effects of the initial trait and trait change cannot be separated from each other because T1 and (T2 − T1) can be correlated. The occasion-specificity (OS) coefficient (Steyer et al., 1992; 1999) reflects the proportion of observed variance that is due to occasion-specific effects:
| (30) |
The occasion-specificity coefficient defined in Equation 30 is a classical measure in LST theory to quantify the degree to which measurements are influenced by momentary states. CC(Yit) and OS(Yit) sum up to Rel(Yit), illustrating once again that in SGMs, occasion-specific influences are considered as part of the reliable variance of an indicator, whereas in FGMs, those influences are implicitly combined with random error and therefore not included in the estimation of reliability.
We now present a small simulation study to illustrate the problem of systematic underestimation of reliabilities in FGMs. Our simulation shows that underestimation of reliabilities in FGMs is not the only concern. Depending on the kind of occasion-specific influences, the absence of an occasion-specific factor in FGMs can also lead to incorrect and confusing conclusions as to the stability of, or changes in, indicator reliabilities over time. Further below, we present two applications to actual psychological data to demonstrate that these problems actually occur in real data sets.
Simulation Study
Method
The goals of the simulation study were (1) to illustrate the extent to which reliability estimates are underestimated in FGMs for varying amounts of occasion-specificity and (2) to demonstrate that the presence of occasion-specific effects can lead to erroneous conclusions as to whether the reliabilities of the indicators change or remain stable over time. Data were generated based on SGMs as population models with different parameter values corresponding to zero, small to medium [.10 ≤ OS(Yit) ≤ .24], medium to large [.26 ≤ OS(Yit) ≤ .40], and large occasion-specific variance [.38 ≤ OS(Yit) ≤ .52]. In Conditions 1–4, occasion-specific variance was specified as decreasing over time, so as to offset the increase in the variance of the latent state variables due to the increasing influence of the slope factor over time. This was done to hold the state variances, measurement error variances, and indicator reliabilities constant across occasions in the population model. To simplify the calculation (and comparison) of reliabilities, all indicators were assumed to be tau-parallel, that is, they had equal loadings, equal intercepts, and equal residual variances within each time point. Intercept and slope factors were assumed to be uncorrelated to simplify the manipulation of the key parameter values of interest. The full set of population parameter values chosen for each of the conditions of the simulation study is given in Appendix A. 1,000 Monte Carlo samples of size N = 1,000 were drawn from each condition using Mplus 6.1 (Muthen & Muthen, 1998–2010). A large sample size of N = 1,000 was chosen to ensure the stability of the results. All data sets were analyzed with (1) the data-generating SGMs and (2) FGMs using maximum likelihood (ML) estimation.
For the purpose of analyzing the data with FGMs, the indicators pertaining to the same measurement occasion were aggregated by calculating the arithmetic average of the two indicators, respectively. This method of aggregation is appropriate when indicators are at least tau-equivalent (Leite, 2007), as was assumed in the present study. Aggregating the two indicators allowed us to simulate the procedure of analyzing a single sum score with FGMs—as is widely done in practice (instead of analyzing multiple indicators using SGMs). Reliability estimates in FGMs were calculated for each indicator and each condition using Equation 27. True reliabilities for each indicator in the SGM population model were calculated based on the true population parameters using Equation 28. True reliabilities of the sum score (true composite reliabilities) were calculated using the Spearman-Brown formula. The Spearman-Brown formula is appropriate to calculate the composite reliability of the sum or mean of tau-parallel indicators (Li, Rosenthal, & Rubin, 1996). True composite reliabilities were compared to the reliabilities estimated for the actual sum of the indicators in the FGMS. Bias was calculated as
and averaged across replications.
Results
Table 1 shows the true population composite reliabilities as well as the mean estimated reliabilities in the FGMs and SGMs for all conditions. It can be seen that reliabilities were accurately reproduced by SGMs across all conditions, whereas FGMs yielded unbiased reliability estimates only in Condition 1 with zero occasion-specific variance. As the amount of occasion-specific variance increased, reliabilities were increasingly underestimated for the FGMs. This bias amounted to up to −65 % in Condition 4 (with the highest level of occasion-specific variance). Reliability estimates in FGMs also systematically increased across time (due to the decrease in OS in the population model), although the actual population reliabilities were stable at .89.
Table 1.
Estimated Reliabilities and Parameter Bias for the Composite Scores in the Simulation Study
| True reliability | Model
|
||||
|---|---|---|---|---|---|
| SGM
|
FGM
|
||||
| Mean Rel (SD) | Mean Bias | Mean Rel (SD) | Mean Bias | ||
| Condition 1: No occasion-specific variance [OS(Yit) = 0] | |||||
| Y1 (time 1) | .8649 | .8651 (.0093) | 0.03 % | .8651 (.0132) | 0.03 % |
| Y2 (time 2) | .8677 | .8677 (.0080) | −0.01 % | .8679 (.0088) | 0.02 % |
| Y3 (time 3) | .8756 | .8753 (.0074) | −0.03 % | .8756 (.0085) | 0.00 % |
| Y4 (time 4) | .8869 | .8863 (.0079) | −0.07 % | .8864 (.0117) | −0.05 % |
|
| |||||
| Condition 2: Low to medium occasion-specific variance [.10 ≤ OS(Yit) ≤.24] | |||||
| Y1 (time 1) | .8889 | .8888 (.0098) | −0.01 % | .6229 (.0279) | −29.92 % |
| Y2 (time 2) | .8889 | .8884 (.0089) | −0.05 % | .6409 (.0183) | −27.90 % |
| Y3 (time 3) | .8889 | .8884 (.0087) | −0.05 % | .6932 (.0161) | −22.02 % |
| Y4 (time 4) | .8889 | .8883 (.0092) | −0.07 % | .7812 (.0237) | −12.12 % |
|
| |||||
| Condition 3: Medium to high occasion-specific variance [.26 ≤ OS(Yit) ≤.40] | |||||
| Y1 (time 1) | .8889 | .8887 (.0107) | −0.02 % | .4453 (.0360) | −49.90 % |
| Y2 (time 2) | .8889 | .8883 (.0097) | −0.07 % | .4635 (.0220) | −47.86 % |
| Y3 (time 3) | .8889 | .8884 (.0097) | −0.06 % | .5152 (.0200) | −42.04 % |
| Y4 (time 4) | .8889 | .8883 (.0102) | −0.07 % | .6026 (.0341) | −32.20 % |
|
| |||||
| Condition 4: High occasion-specific variance [.38 ≤ OS(Yit) ≤.52] | |||||
| Y1 (time 1) | .8889 | .8887 (.0112) | −0.02 % | .3120 (.0403) | −64.91 % |
| Y2 (time 2) | .8889 | .8881 (.0103) | −0.09 % | .3302 (.0226) | −62.85 % |
| Y3 (time 3) | .8889 | .8883 (.0104) | −0.06 % | .3817 (.0209) | −57.06 % |
| Y4 (time 4) | .8889 | .8883 (.0108) | −0.07 % | .4689 (.0400) | −47.25 % |
|
| |||||
| Condition 5:Truly increasing reliability over time and increasing occasion-specific variance [.08 ≤ OS(Yit) ≤.24] | |||||
| Y1 (time 1) | .7805 | .7795 (.0156) | −0.12 % | .6831 (.0260) | −12.48 % |
| Y2 (time 2) | .8341 | .8343 (.0125) | 0.02 % | .6823 (.0171) | −18.20 % |
| Y3 (time 3) | .8904 | .8900 (.0086) | −0.05 % | .6836 (.0171) | −23.23 % |
| Y4 (time 4) | .9412 | .9412 (.0062) | 0.00 % | .6899 (.0243) | −26.70 % |
Note. Rel = reliability; OS = occasion-specificity. Results are based on 1000 replications and samples size of N = 1000 for each condition, respectively. Bias was calculated relative to the true population reliability of the composite given in the second column of the table.
To demonstrate that FGMs can also lead to the erroneous conclusion that indicator reliabilities remain stable over time, when in fact they are changing, we simulated an additional condition. In Condition 5, the true composite reliabilities in the population model were now specified to increase over time from .78 to .94. At the same time, occasion-specific variance was specified to increase in such a way as to exactly offset the decrease in random error variance over time [.08 ≤ OS(Yit) ≤ .24]. As shown in Table 1, SGMs showed unbiased results and clearly indicated that reliabilities were increasing over time. In contrast, FGMs again substantially underestimated the reliabilities. Moreover, the reliabilities in the FGMs were estimated to be stable at a level of roughly .68.
Discussion
Our simulation study illustrated that reliability estimates in FGMs represent underestimates whenever occasion-specific variance is present in the data. For high amounts of occasion-specific variance, bias in reliability estimates was dramatic (up to −65 %). In addition, the simulation study showed that underestimation of reliabilities is not the only concern when analyzing FGMs. In addition to generally providing estimates of indicator reliabilities that are too low, FGMs can obscure patterns of change in indicator reliabilities: Changes in the reliabilities of indicators can either be spurious (when the true change occurs in the occasion-specific component and not in the error variances of the indicators) or can be masked in FGMs (this is the case when actual increases or decreases in error variance are compensated for by increasing or decreasing occasion-specific variance). These issues are of even greater concern than the general underestimation of reliabilities in FGMs, because a researcher will have no way of knowing whether the pattern of change or stability he or she observes in indicator reliabilities based on FGMs is valid or not, because FGMs do not allow estimating the amount of occasion-specific variance. In the following, we show that bias in the estimation of reliability is a concern not only in simulations, but also occurs in actual data applications.
Application
Method
We used data from Proyecto: La Familia (The Family Project; Roosa, Torres, Gonzales, Knight, & Saenz, 2008), which assessed the health and adjustment of Mexican American children and their parents every two years, beginning in the 5th grade for the target children. In this application, we fit FGMs and SGMs to mothers’ (N = 591 complete cases) and fathers’ (N = 323 complete cases) ratings of their own depressive symptoms using the widely used, 20-item Center for Epidemiological Studies Depression Scale (CES-D; Radloff, 1977). Sample items include “You felt depressed” and “You felt that everything you did was an effort”. Items were answered on a 4-point scale ranging from “Rarely or none of the time” to “Most or all of the time”. Of importance to the present study, the CES-D has shown high internal consistency reliability in previous studies (Cronbach’s alpha = .85 to .90; Radloff, 1977). For the current study, we dropped the 4 positively worded items from this scale to minimize method effects due to item wording (see, e.g., Geiser, Eid, & Nussbeck, 2008). In order to analyze FGMs, an overall sum score was created based on the remaining 16 negatively worded items by calculating the average across those items for each time point. This “calculating and analyzing a single overall sum score” procedure is typically used by researchers who use FGMs to study change over time.
For the analysis of SGMs, at least two indicators per time point are required to properly separate measurement error from reliable occasion-specific variance. We therefore created test halves for each time point by assigning the 16 items to two parcels that were calculated as the mean of 8 of the items, respectively. Homogeneity of the test halves was maximized by distributing the items based on the strength of their loadings in a single factor item factor analysis. This procedure helps to minimize test half-specific method effects, although these may not be completely eliminated (see below). The composition of the test halves was identical for each of the three time points. ML estimation in Mplus 6.1 (Muthen & Muthen, 1998–2010) was used to estimate the parameters of FGMs and SGMs for each type of rater separately. The Mplus input files are in Appendix B.
Results
Table 2 displays the means, standard deviations, and correlations of the observed variables for each type of rater. The FGMs fit the overall depression scores well [mothers: χ2(1, N = 591) = 4.53, p = .03; CFI = .990; RMSEA = .08; SRMR = .02; fathers: χ2(1, N = 323) = 1.24, p = .26; CFI = .999; RMSEA = .03; SRMR = .02]. Only the RMSEA for mother report was above the common threshold of .05 for good fit. Likewise, the SGMs fit the depression test halves well. Preliminary analyses revealed that for mothers, a model with equal loadings and equal intercepts both within and across time points as well as equal error variances within each time point fit the data well, χ2(15, N = 591) = 24.63, p = .06; CFI = .997; RMSEA = .03; SRMR = .04. In addition, it was necessary to include a method factor for the second test half due to a slight deviation of the second test half from the first one. Such method effects are not uncommon even when test halves are constructed to be homogenous (Geiser, Eid, Nussbeck, Courvoisier, & Cole, 2010). In fact, the possibility of separating out method effects through the inclusion of method factors is another advantage of SGMs. Using one residual method factor to contrast two test halves against one another has been recommended by Eid et al. (1999) who discuss this approach in detail.
Table 2.
Means, Standard Deviations, Correlations, and Proportions of Variance Accounted For of CES-D Sum Scores and Test Halves Used in the Empirical FGM and SGM Applications
| Type of Reporter
|
||||||
|---|---|---|---|---|---|---|
| Mother Reports (N = 591) | Father Reports (N = 323) | |||||
|
| ||||||
| Sum Scores | ||||||
| 1 | 2 | 3 | 1 | 2 | 3 | |
| 1. Sum score, time 1 | — | — | ||||
| 2. Sum score, time 2 | .49 | — | .51 | — | ||
| 3. Sum score, time 3 | .43 | .45 | — | .49 | .53 | — |
| M | 1.72 | 1.68 | 1.73 | 1.47 | 1.52 | 1.52 |
| SD | 0.55 | 0.57 | 0.60 | 0.41 | 0.44 | 0.43 |
| FGM reliability estimates | .56 | .47 | .46 | .57 | .49 | .63 |
| Test Halves | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 1. Test half 1, time 1 | — | — | ||||||||||
| 2. Test half 2, time 1 | .84 | — | .79 | — | ||||||||
| 3. Test half 1, time 2 | .48 | .45 | — | .49 | .45 | — | ||||||
| 4. Test half 2, time 2 | .44 | .46 | .87 | — | .44 | .45 | .83 | — | ||||
| 5. Test half 1, time 3 | .40 | .40 | .42 | .40 | — | .46 | .41 | .53 | .49 | — | ||
| 6. Test half 2, time 3 | .38 | .42 | .41 | .44 | .89 | — | .44 | .45 | .45 | .46 | .82 | — |
| M | 1.71 | 1.73 | 1.69 | 1.68 | 1.74 | 1.72 | 1.58 | 1.35 | 1.64 | 1.39 | 1.63 | 1.40 |
| SD | 0.58 | 0.56 | 0.60 | 0.59 | 0.62 | 0.62 | 0.49 | 0.38 | 0.51 | 0.41 | 0.49 | 0.41 |
| SGM reliability estimates | .86 | .87 | .89 | .89 | .90 | .91 | .85 | .76 | .86 | .79 | .85 | .78 |
| CC | .52 | .50 | .44 | .42 | .43 | .42 | .54 | .49 | .47 | .43 | .60 | .54 |
| OS | .34 | .33 | .45 | .43 | .47 | .45 | .30 | .27 | .39 | .36 | .26 | .23 |
| IS | —a | .04 | —a | .04 | —a | .04 | —b | —b | —b | —b | —b | —b |
Note. FGM = first order growth model; SGM = second order growth model; CC = consistency and trait change coefficient; OS = occasion-specificity coefficient. IS = indicator-specificity coefficient. The CC, OS, and IS coefficients were estimated based on the SGMs.
In line with Eid et al.’s (1999) approach to modeling indicator-specific effects, no indicator-specific factor was included for the first indicator in this model.
No indicator-specific factor was needed in the SGMs for father reports.
For fathers, we chose a model with unequal (but time-invariant) loadings and intercepts as well as equal error variances, χ2(16, N = 323) = 26.28, p = .05; CFI = .992; RMSEA = .05; SRMR = .04. No method factor was required in this model. Whereas mothers showed no mean growth in depression (slope factor mean = 0.004, p = .75), father reports indicated a slight increase in depression over time (slope factor mean = .03, p = .05). There was no significant variability in the rate of change for either mother (slope factor variance = 0.01, p = .31) or father reports (slope factor variance = 0.01, p = .22). (These growth estimates are based on the SGMs; identical or very similar estimates were obtained from the FGMs.)
Table 2 also contains the estimated indicator reliabilities for each model as well as the CC and OS coefficients estimated in the SGMs. For the SGMs of mother ratings, the proportion of variance accounted for by the indicator-specific factor (IS coefficient) is also included. It can be seen that reliability estimates were significantly lower in the FGMs than in the SGMs for both reporters. This can be explained by the fact that both mother and father reports showed a substantial amount of occasion-specific variability as uncovered by the SGMs. Between 40 and 52 % of the variance in mother report latent state scores and 30 to 45 % of the variance in father report latent state scores was accounted for by occasion-specific effects. Hence, father ratings of depression were somewhat less prone to occasion-specific influences. This difference explains why FGM reliability estimates for mothers were even more attenuated than the corresponding estimates for fathers.
Discussion
Our application of FGMs and SGMs to actual data showed that the problem of underestimated reliabilities is not an artificial effect that only occurs in simulation studies. Instead, this problem is real and in the experience of the authors of this article, it does occur in nearly every application of LGCMs to social science data. Although both FGMs and SGMs fit the depression data quite well, indicator reliabilities were strongly underestimated in FGMs compared to SGMs, showing that FGMS did not appropriately represent the data. The underestimation of reliabilities in FGMs is also confirmed through comparison with internal consistency reliabilities reported in Radloff’s (1977) original work, which also were significantly higher than the reliabilities estimated in the FGMs.
Note that depression is a construct for which a substantial amount of occasion-specific variance has also been found in other studies (e.g., Dumenci & Windle, 1996; Schmitt & Maes, 2000). Other psychological constructs may be less prone to occasion-specific influences and may thus show less dramatic bias in reliability estimates. Nonetheless, researchers interested in studying changes in depression (for example, over the course of an intervention) have to face this issue. Furthermore, the problem holds in general, as most measurements are at least to some extent dependent on the occasion of measurement.
General Discussion
LGCMs are powerful and widely used statistical models for analyzing longitudinal data. There appears to be strong agreement among methodological researchers that SGMs offer important advantages over FGMs (Chan, 1998; Ferrer et al., 2008; Leite, 2007; Sayer & Cumsille, 2001; von Oerzen et al., 2010; Murphy et al., 2011). SGMs allow researchers to properly separate variance components due to trait and trait change, occasion-specific effects, indicator-specific effects, and random measurement error. Furthermore, SGMs allow for tests of important assumptions that are implicitly made in FGMs, namely the assumption that indicators are unidimensional at each time point and that measurement invariance holds over time (Sayer and Cumsille, 2001; Ferrer et al., 2008). SGMs also have greater statistical power than FGMs to detect variability in change over time (von Oerzen et al., 2011), and they allow identification and modeling of method effects.
In the present study, we examined FGMs and SGMs from a slightly different angle than previous studies comparing the two approaches. By formulating both FGMs and SGMs on the basis of well-defined latent variables derived from LST theory, we showed that FGMs make the implicit assumption that the construct under study is a pure trait. More than two decades of research in the area of LST theory and modeling have shown, however, that this assumption is not realistic for most constructs in psychology (e.g., Deinzer et al., 1995). Instead of conceiving of psychological constructs as pure traits, it must be assumed that most constructs contain both trait and state components (Hertzog & Nesselroade, 1987). The comparison of FGMs and SGMs based on LST theory shows that SGMs, but not FGMs, support this conclusion. Hence, from a theoretical point of view, SGMs are more appropriate to model change in general and should therefore be preferred unless the construct under study is clearly trait-like (e.g., intelligence scores).
As we have demonstrated in this paper using empirical and simulated data, one practical consequence is that the estimation of indicator reliabilities in FGMs is compromised whenever occasion-specific variance is present. This can have the confusing consequence that indicator reliabilities may be underestimated or that changes in the reliabilities of the indicators may be masked or spurious “changes” may occur. Hence, researchers using growth modeling and estimating reliabilities of the indicators based on FGMs should be cautious about statements as to the size, stability, and change of indicator reliabilities, as these reliability estimates are likely biased.
One strategy to find out whether indicator reliabilities are biased is to compare the FGMs based on reliability estimates to other reliability estimates available from the literature or from previous studies (e.g., reliability estimates based on Cronbach’s alpha or correlation of parallel forms). If the reliability estimates obtained from an FGM are theoretically implausible and/or substantially lower than previous reliability estimates, this can be a sign that occasion-specific effects are present and should be taken into account. Note that reliability estimates that are based on test-retest correlations should only be used with caution for this type of comparison, because these reliability estimates may also be attenuated if a construct is prone to occasion-specific influences. Furthermore, as has been pointed out by Tisak and Tisak (1996), a test-retest correlation provides an appropriate estimate of reliability only if (1) error variances are time-invariant and (2) there is no differential change between individuals. Another indicator of unmodeled occasion-specific variance in FGMs is a theoretically unexpected pattern of change (or stability) of reliabilities over time.
Promoting the Use of SGMs
Despite the fact that SGMs have been presented in the literature more than 20 years ago (McArdle, 1988) and despite their undisputed advantages over FGMs, SGMs are less frequently used in practice than FGMs. One reason may be that applied researchers do not always have multiple repeatedly measured scales at their disposal, as is required for the use of SGMs. However, constructs are often measured by scales that consist of multiple items (e.g., multiple-item questionnaires or test batteries). Therefore, instead of using a single sum score created on the basis of the entire set of items, researchers can create two or more item parcels (“test halves”; Mayer et al., 2011) and use these parcels as indicators at each time point as illustrated in our application to the CES-D data. 6 An alternative strategy is to conduct the analysis at the item level using appropriate factor models for dichotomous or ordinal variables (e.g., Crayen, Geiser, Scheithauer, & Eid, in press), if necessary based on a subset of items that are in line with a unidimensional model.
Another way to deal with occasion-specific variance is to use single indicators and to constrain the error variances to known values so that occasion-specific variance can be properly estimated (Leite, 2007). However, this strategy requires that appropriate reliability estimates be available for each indicator at each time point so that the error variances can be fixed to proper values and occasion-specific variances are correctly estimated.
Complexities Arising From the Use of Multiple Indicators
As shown in our application, the use of multiple indicators may lead to shared method effects of the same indicators over time that must be adequately modeled. This problem can occur when indicators are not strictly parallel and is a ubiquitous phenomenon in longitudinal studies that use multiple indicators (Marsh & Grayson, 1994; Raffalovich & Bornstedt, 1987). To our knowledge, the question of how method effects should best be modeled has not yet been studied for SGMs, although research on this topic in the context of classical LST models may to some extent apply to SGMs as well. Based on a simulation study, Geiser and Lockhart (in press) recommend the use of M − 1 method factors (as illustrated in this article) as well as models with indicator-specific trait factors (e.g., Eid, Courvoisier, & Lischetzke, 2011). In summary, the question of how to most appropriately model shared method effects in SGMs remains an interesting topic for future research.
Some researchers may wonder whether one should even care about reliability estimates in the context of LGCMs. After all, the main purpose of these models is usually not the estimation of reliability or occasion-specificity, but to investigate (trait) change. It seems indeed true that growth parameters are little affected by ignoring occasion-specific variance. At least this was found in the simulation conditions and applications studied here. Therefore, researchers who are only interested in studying trait change (and do not care about reliability estimates derived from their growth model), may be fine with FGMs. However, we believe that in most cases researchers will be interested in applying the type of model that is (1) most appropriate from a theoretical point of view and (2) provides the most (and the most accurate) information possible based on their data. SGMs are more theoretically sound than FGMs, as they make more realistic assumptions (among others that constructs have both trait and state components). Furthermore, SGMs allow defining different coefficients for quantifying variance components due to trait and trait change, occasion-specificity, and reliability.
Conclusion
Most psychological attributes are not characterized by perfect stability over time or a continuous change pattern. Instead, most constructs have both trait and state components. Therefore, statistical models for analyzing change should take occasion-specific effects into account to more adequately describe variability and change in a construct and to properly estimate the reliabilities of its indicators. SGMs are powerful tools in this regard and we recommend that they be chosen as an alternative to FGMs for analyzing change in social science research whenever possible.
Figure 2.
Linear SGM for four measurement occasions. Yit denotes the ith observed variable (indicator) measured at time t.
Acknowledgments
The authors wish to thank Mark Roosa for supplying the data set used for the empirical application of the models. These data were collected under NIMH grant number RO1 MH68920 awarded to Mark Roosa.
Appendix A. Population Parameters Used in the Simulation Study
Table A1.
True Population Parameter Values Used to Generate Data in the Simulation Study
| Condition
|
|||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Intercept factor variance Var(Intercept) |
0.8 | 0.7 | 0.5 | 0.35 | 0.7 |
| State residual variances Var(SR1)–Var(SR4) |
0 for all t | 0.30, 0.28, 0.22, 0.12 | 0.50, 0.48, 0.42, 0.32 | 0.65, 0.63, 0.57, 0.47 | 0.10, 0.16, 0.236, 0.32 |
| Error variances Var (ε11)–Var(ε42) |
0.25 for all i and t | 0.25 for all i and t | 0.25 for all i and t | 0.25 for all i and t | 0.45, 0.45, 0.35, 0.35, 0.25, 0.25, 0.15, 0.15 |
Note. The intercept and slope factor means were set to 0.0 and 0.25 in all conditions, respectively. The slope factor variance was set to 0.02 in all conditions. The covariance between intercept and slope factor was set to 0.0 in all conditions. The intercepts and loadings of all observed variables were set to 0.0 and 1.0 in all conditions, respectively. The intercepts of all latent state factors were set to 0.0 in all conditions.
Appendix B. Mplus Input Files For Estimating SGMs
Mother Report
title: SGM depression mother report
This syntax also produces the CC, OS, IS, and REL coefficients
data: File = Depression_Mom.dat;
variable: names = depmom1 depmom2 depmom3
depmom11 depmom21 depmom12 depmom22 depmom13 depmom23;
usevar = depmom11 depmom21 depmom12 depmom22 depmom13 depmom23;
model: ! Latent state factors
dep1 by depmom11@1
depmom21@1; ! tau-equivalence assumed
dep2 by depmom12@1
depmom22@1;
dep3 by depmom13@1
depmom23@1;
! Set the intercepts of all observed variables to zero (tau equivalence assumed)
[depmom11@0 depmom21@0 depmom12@0 depmom22@0 depmom13@0 depmom23@0];
! Set observed variable error variances (ev) equal within each time point
epmom11 (ev1);
depmom21 (ev1);
depmom12 (ev2);
depmom22 (ev2);
depmom13 (ev3);
depmom23 (ev3);
! 2nd order growth factors
interc linear | dep1@0 dep2@1 dep3@2;
! Intercept and slope variances
interc (intv);
linear (slov);
! Intercept and slope covariance
interc with linear (inlicov);
! Estimate the means of the intercept and slope factors
[interc linear];
! Indicator-specific factor for the second test half (equal loadings assumed)
is2 by depmom21@1 depmom22@1 depmom23@1;
! Non-admissible covariances are set to zero
is2 with dep1-dep3@0 interc@0 linear@0;
! Indicator-specific factor variance
is2 (isv);
! State residual variances
dep1 (sr1);
dep2 (sr2);
dep3 (sr3);
! Calculation of CC, OS, IS, and REL coefficients
model constraint:
! Calculate model-implied variances of each observed variable
new(v11 v21 v12 v22 v13 v23);
v11 = intv + sr1 + ev1;
v21 = intv + sr1 + isv + ev1;
v12 = intv + slov + 2*inlicov + sr2 + ev2;
v22 = intv + slov + 2*inlicov + sr2 + isv + ev2;
v13 = intv + 4*slov + 4*inlicov + sr3 + ev3;
v23 = intv + 4*slov + 4*inlicov + sr3 + isv + ev3;
! Calculate consistency and trait change (CC) coefficients
new(CC11 CC21 CC12 CC22 CC13 CC23);
CC11 = intv/v11;
CC21 = intv/v21;
CC12 = (intv + slov + 2*inlicov)/v12;
CC22 = (intv + slov + 2*inlicov)/v22;
CC13 = (intv + 4*slov + 4*inlicov)/v13;
CC23 = (intv + 4*slov + 4*inlicov)/v23;
! Calculate occasion-specificity (OS) coefficients
new(OS11 OS21 OS12 OS22 OS13 OS23);
OS11 = sr1/v11;
OS21 = sr1/v21;
OS12 = sr2/v12;
OS22 = sr2/v22;
OS13 = sr3/v13;
OS23 = sr3/v23;
! Calculate indicator-specificity (IS) coefficients (2nd test half only)
new(IS21 IS22 IS23);
IS21 = isv/v21;
IS22 = isv/v22;
IS23 = isv/v23;
! Calculate reliability (REL) coefficients
new(REL11 REL21 REL12 REL22 REL13 REL23);
REL11 = CC11 + OS11;
REL21 = CC21 + OS21 + IS21;
REL12 = CC12 + OS12;
REL22 = CC22 + OS22 + IS22;
REL13 = CC13 + OS13;
REL23 = CC23 + OS23 + IS23;
output: sampstat stdyx;
Father Report
title: SGM depression father report
This syntax also produces the CC, OS, and Rel coefficients
data: File = Depression_Dad.dat;
variable: names = depdad1 depdad2 depdad3
depdad11 depdad21 depdad12 depdad22 depdad13 depdad23;
usevar = depdad11 depdad21 depdad12 depdad22 depdad13 depdad23;
model: ! Latent state factors; loadings set equal across time
dep1 by depdad11@1
depdad21 (l2);
dep2 by depdad12@1
depdad22 (l2);
dep3 by depdad13@1
depdad23 (l2);
! Intercepts set to zero for the marker indicator
! and set equal across time for the 2nd indicator
[depdad11@0 depdad12@0 depdad13@0];
[depdad21 depdad22 depdad23] (2);
! Error variances (ev) set equal for all indicators
depdad11 (ev);
depdad21 (ev);
depdad12 (ev);
depdad22 (ev);
depdad13 (ev);
depdad23 (ev);
! 2nd order growth factors
interc linear | dep1@0 dep2@1 dep3@2;
! Intercept and slope variances
interc (intv);
linear (slov);
! Intercept and slope covariance
interc with linear (inlicov);
! Estimate the means of the intercept and slope factors
[interc linear];
! State residual variances
dep1 (sr1);
dep2 (sr2);
dep3 (sr3);
! Calculate CC, OS, and REL coefficients
model constraint:
! Calculate the model implied variance of each observed variable
new(v11 v21 v12 v22 v13 v23);
v11 = intv + sr1 + ev;
v21 = (l2**2)*intv + (l2**2)*sr1 + ev;
v12 = intv + slov + 2*inlicov + sr2 + ev;
v22 = (l2**2)*intv + (l2**2)*slov + 2*(l2**2)*inlicov + (l2**2)*sr2 + ev;
v13 = intv + 4*slov + 4*inlicov + sr3 + ev;
v23 = (l2**2)*intv + 4*(l2**2)*slov + 4*(l2**2)*inlicov + (l2**2)*sr3 + ev;
! Calculate the consistency and trait change (CC) coefficients
new(CC11 CC21 CC12 CC22 CC13 CC23);
CC11 = intv/v11;
CC21 = (l2**2)*intv/v21;
CC12 = (intv + slov + 2*inlicov)/v12;
CC22 = ((l2**2)*intv + (l2**2)*slov + 2*(l2**2)*inlicov)/v22;
CC13 = (intv + 4*slov + 4*inlicov)/v13;
CC23 = ((l2**2)*intv + 4*(l2**2)*slov + 4*(l2**2)*inlicov)/v23;
! Calculate the occasion-specificity (OS) coefficients
new(OS11 OS21 OS12 OS22 OS13 OS23);
OS11 = sr1/v11;
OS21 = (l2**2)*sr1/v21;
OS12 = sr2/v12;
OS22 = (l2**2)*sr2/v22;
OS13 = sr3/v13;
OS23 = (l2**2)*sr3/v23;
! Calculate the reliability (REL) coefficients
new(REL11 REL21 REL12 REL22 REL13 REL23);
REL11 = CC11 + OS11;
REL21 = CC21 + OS21;
REL12 = CC12 + OS12;
REL22 = CC22 + OS22;
REL13 = CC13 + OS13;
REL23 = CC23 + OS23;
output: sampstat stdyx;
Footnotes
Although Tisak and Tisak (2000) referred to LST models in their article, they did not define their growth models based on the fundamental concepts of LST theory. Mayer et al. (2011) show how to construct growth components based on latent state variables defined in LST theory. However, in their approach to defining LGMs, they do not explicitly distinguish between state and trait components, as is done in the present work.
For the sake of simplicity, we only consider linear growth models in this paper. Note that other forms of growth models can also be formulated based on LST theory by postulating a different loading structure on the slope factor [e.g., (t − 1)2 for quadratic growth].
Note that every one of the latent state variables Sit could play the role of the common latent state factor. For example, if we set αlt = 0 and λ1t = 1, this would imply that S1t plays the role of the common latent state factor. Hence, the common latent state factors in this model are uniquely defined only up to positive linear transformations (Steyer, 1988).
Note that Tisak & Tisak (2000) discuss different types of reliability coefficients in the context of SGMS. Here, we only consider the most inclusive version that is defined as the total portion of systematic variance to observed variance and is referred to as “systematic reliability” in Tisak & Tisak’s (2000) work.
This coefficient corresponds closely to Tisak and Tisak’s (2000) “dynamic reliability” coefficient.
It should be noted that item parceling is controversial (e.g., Bandalos, 2002), mainly because the basic assumption underlying the creation of item parcels is that the items are unidimensional, an assumption that may not hold true for many social sciences scales. However, if this assumption is violated, FGMs do not solve the problem, because the creation of a single sum score across multidimensional items would be similarly problematic.
Contributor Information
Christian Geiser, Department of Psychology, Utah State University.
Brian Keller, Department of Psychology, Arizona State University.
Ginger Lockhart, Department of Psychology, Utah State University.
References
- Anastasi A. Traits, states, and situations: A comprehensive view. In: Wainer H, Messick S, editors. Principals of modern psychological measurement. Hillsdale, NJ: Erlbaum; 1983. pp. 345–356. [Google Scholar]
- Bandalos DL. The effects of item parceling on goodness-of-fit and parameter estimate bias in structural equation modeling. Structural Equation Modeling. 2002;9:78–102. [Google Scholar]
- Chan D. The conceptualization and analysis of change over time: An integrative approach incorporating longitudinal mean and covariance structures analysis (LMACS) and multiple indicator latent growth modeling (MLGM) Organizational Research Methods. 1998;1:421–483. [Google Scholar]
- Cole DA, Martin NM, Steiger JH. Empirical and conceptual problems with longitudinal trait-state models: Introducing a trait-state-occasion model. Psychological Methods. 2005;10:3–20. doi: 10.1037/1082-989X.10.1.3. [DOI] [PubMed] [Google Scholar]
- Crayen C, Geiser C, Scheithauer H, Eid M. Evaluating interventions with multimethod data: A structural equation modeling approach. Structural Equation Modeling in press. [Google Scholar]
- Deinzer R, Steyer R, Eid M, Notz P, Schwenkmezger P, Ostendorf F, Neubauer A. Situational effects in trait assessment: The FPI, NEOFFI and EPI questionnaires. European Journal of Personality. 1995;9:1–23. [Google Scholar]
- Dumenci L, Windle M. A latent trait-state model of adolescent depression using the Center for Epidemiologic Studies-Depression Scale. Multivariate Behavioral Research. 1996;31:313–330. doi: 10.1207/s15327906mbr3103_3. [DOI] [PubMed] [Google Scholar]
- Duncan SC, Duncan TE. A multivariate latent growth curve analysis of adolescent substance use. Structural Equation Modeling. 1996;3:323–347. [Google Scholar]
- Eid M, Courvoisier DS, Lischetzke T. Structural equation modeling of ambulatory assessment data. In: Mehl MR, Connor TS, editors. Handbook of research methods for studying daily life. New York: Guilford; 2011. pp. 384–406. [Google Scholar]
- Eid M, Hoffmann L. Measuring variability and change with an item response model for polytomous variables. Journal of Educational and Behavioral Statistics. 1998;23:193–215. [Google Scholar]
- Eid M, Schneider C, Schwenkmezger P. Do you feel better or worse? The validity of perceived deviations of mood states from mood traits. European Journal of Personality. 1999;13:283–306. [Google Scholar]
- Geiser C, Lockhart G. A comparison of four approaches to account for method effects in latent state trait analyses. Psychological Methods. doi: 10.1037/a0026977. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiser C, Eid M, Nussbeck FW. On the meaning of the latent variables in the CT-C(M−1) model: A comment on Maydeu-Olivares and Coffman (2006) Psychological Methods. 2008;13:49–57. doi: 10.1037/1082-989X.13.1.49. [DOI] [PubMed] [Google Scholar]
- Geiser C, Eid M, Nussbeck FW, Courvoisier DS, Cole DA. Analyzing true change in longitudinal multitrait-multimethod studies: Application of a multimethod change model to depression and anxiety in children. Developmental Psychology. 2010;46:29–45. doi: 10.1037/a0017888. [DOI] [PubMed] [Google Scholar]
- Ferrer E, Balluerka N, Widaman KF. Factorial invariance and the specification of second-order growth models. Methodology. 2008;4:22–36. doi: 10.1027/1614-2241.4.1.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock GR, Kuo W, Lawrence FR. An illustration of second-order latent growth models. Structural Equation Modeling. 2001;8:470–489. [Google Scholar]
- Hertzog C, Nesselroade JR. Beyond autoregressive models: Some implications of the trait-state distinction for the structural modeling of developmental change. Child Development. 1987;58:93–109. [PubMed] [Google Scholar]
- Leite WL. A comparison of latent growth models for constructs measured by multiple items. Structural Equation Modeling. 2007;14:581–610. [Google Scholar]
- Li H, Rosenthal R, Rubin DB. Reliability of measurement in psychology: From Spearman-Brown to maximal reliability. Psychological Methods. 1996;1:98–107. [Google Scholar]
- Marsh HW, Grayson D. Longitudinal confirmatory factor analysis: Common, time-specific, item-specific, and residual-error components of variance. Structural equation modeling. 1994;1:116–145. [Google Scholar]
- Mayer A, Steyer R, Mueller H. A general approach to defining latent growth components. Structural Equation Modeling in press. [Google Scholar]
- McArdle JJ. Dynamic but structural equation modeling of repeated measures data. In: Cattell RB, Nesselroade J, editors. Handbook of multivariate experimental psychology. 2. New York: Plenum Press; 1988. pp. 561–614. [Google Scholar]
- McArdle JJ, Epstein D. Latent growth curves within developmental structural equation models. Child Development. 1987;58:110–133. [PubMed] [Google Scholar]
- Meredith W, Tisak J. Latent curve analysis. Psychometrika. 1990;55:107–122. [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide. 6. Los Angeles, CA: Muthén & Muthén; 1998–2010. [Google Scholar]
- Murphy DL, Beretvas SN, Pituch KA. The effects of autocorrelation on the curve-of-factors growth model. Structural Equation Modeling. 2011;18:430–448. [Google Scholar]
- Nachtigall C, Kraus K, Steyer R. The analysis of change: True change models and growth curves. In: Blasius J, Hox J, de Leeuw E, Schmidt P, editors. Social Science Methodology in the New Millenium; Proceedings of the 5th International Conference on Social Science Methodology.2000. [Google Scholar]
- Novick MR. The axioms and principal results of classical test theory. Journal of Mathematical Psychology. 1966;3:1–18. [Google Scholar]
- Pohl S, Steyer R, Kraus K. Modelling method effects as individual causal effects. Journal of the Royal Statistical Society Series A. 2008;171:41–63. [Google Scholar]
- Radloff LS. The CES-D Scale: A self-report depression scale for research in the general population. Applied Psychological Measurement. 1977;1:385–401. [Google Scholar]
- Raffalovich LE, Bohrnstedt GW. Common, specific, and error variance components of factor models: Estimation with longitudinal data. Sociological Methods & Research. 1987;15:385–405. [Google Scholar]
- Raykov T. A method for examining stability in reliability. Multivariate Behavioral Research. 2000;35:289–305. doi: 10.1207/S15327906MBR3503_01. [DOI] [PubMed] [Google Scholar]
- Roosa MW, Liu F, Torres M, Gonzales N, Knight G, Saenz D. Sampling and recruitment in studies of cultural influences on adjustment: A case study with Mexican Americans. Journal of Family Psychology. 2008;22:293–302. doi: 10.1037/0893-3200.22.2.293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sayer AG, Cumsille PE. Second-order latent growth models. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, D. C: APA; 2001. pp. 177–200. [Google Scholar]
- Schmitt M, Maes J. Simplification of the Beck-Depression-Inventory (BDI) Diagnostica. 2000;46:38–46. [Google Scholar]
- Steyer R. Unpublished habilitation thesis. University of Trier; Trier, Germany: 1988. Experiment, Regression und Kausalität. Die logische Struktur kausaler Regressions modelle. Experiment, regression, and causality. The logical structure of causal regression models. [Google Scholar]
- Steyer R. Models of classical psychometric test theory as stochastic measurement models: Representation, uniqueness, meaningfulness, identifiability, and testability. Methodika. 1989;3:25–60. [Google Scholar]
- Steyer R. Analyzing individual and average causal effects via structural equation models. Methodology. 2005;1:39–54. [Google Scholar]
- Steyer R, Ferring D, Schmitt MJ. States and traits in psychological assessment. European Journal of Psychological Assessment. 1992;8:79–98. [Google Scholar]
- Steyer R, Krambeer S, Hannöver W. Modeling Latent Trait-Change. In: Van Montfort K, Oud H, Satorra A, editors. Recent developments on structural equation modeling: theory and applications. Amsterdam: Kluwer Academic Press; 2004. pp. 337–357. [Google Scholar]
- Steyer R, Schmitt M. The effects of aggregation across and within occasions on consistency, specificity, and reliability. Methodika. 1990;4:58–94. [Google Scholar]
- Steyer R, Schmitt M, Eid M. Latent state-trait theory and research in personality and individual differences. European Journal of Personality. 1999;13:389–408. [Google Scholar]
- Tisak J, Tisak MS. Longitudinal models of reliability and validity: A latent curve approach. Applied Psychological Measurement. 1996;20:275–288. [Google Scholar]
- Tisak J, Tisak MS. Permanency and ephemerality of psychological measures with application to organizational commitment. Psychological Methods. 2000;5:175–198. doi: 10.1037/1082-989x.5.2.175. [DOI] [PubMed] [Google Scholar]
- von Oerzen T, Hertzog C, Lindenberger U, Ghisletta P. The effect of multiple indicators on the power to detect inter-individual differences in change. British Journal of Mathematical and Statistical Psychology. 2010;63:627–646. doi: 10.1348/000711010X486633. [DOI] [PubMed] [Google Scholar]