Skip to main content
PMC home page
CPT: Pharmacometrics & Systems Pharmacology logoLink to CPT: Pharmacometrics & Systems Pharmacology
. 2013 Aug 14;2(8):e65. doi: 10.1038/psp.2013.40

A Generic Integrated Physiologically based Whole-body Model of the Glucose-Insulin-Glucagon Regulatory System

S Schaller 1,2,*, S Willmann 1, J Lippert 1, L Schaupp 3, T R Pieber 3, A Schuppert 1,2, T Eissing 1
PMCID: PMC3828004  PMID: 23945606

Abstract

Models of glucose metabolism are a valuable tool for fundamental and applied medical research in diabetes. Use cases range from pharmaceutical target selection to automatic blood glucose control. Standard compartmental models represent little biological detail, which hampers the integration of multiscale data and confines predictive capabilities. We developed a detailed, generic physiologically based whole-body model of the glucose-insulin-glucagon regulatory system, reflecting detailed physiological properties of healthy populations and type 1 diabetes individuals expressed in the respective parameterizations. The model features a detailed representation of absorption models for oral glucose, subcutaneous insulin and glucagon, and an insulin receptor model relating pharmacokinetic properties to pharmacodynamic effects. Model development and validation is based on literature data. The quality of predictions is high and captures relevant observed inter- and intra-individual variability. In the generic form, the model can be applied to the development and validation of novel diabetes treatment strategies.

Diabetes affects a continuously growing population of already over 350 million patients worldwide. The disease causes close to five million deaths per year and accounted for global healthcare expenditures of 465 billion USD in 2011 alone.1 To improve both preventive measures and economic disease management options, more research efforts are required that cover all relevant aspects of the glucose insulin metabolism (GIM). These can range from disease prevention to management by identification of novel targets for type 1 diabetes mellitus (T1DM) and type 2 diabetes mellitus pharmacotherapies and automation of blood glucose control, that is, developing artificial pancreas systems.2,3,4,5

The complex system of interacting hormonal and metabolic signaling networks on the molecular level regulating whole-body blood glucose homeostasis, however, remains challenging. Model-based research is a standard approach for gaining a deeper understanding of diabetes for over half a century now and has since become the state-of-the-art approach. Mathematical models of the GIM are developed mainly for two reasons: as a tool for fundamental research to analyze the underlying mechanistics of the GIM in healthy individuals and individuals with diabetes, or as a model kernel for automatic blood glucose control in T1DM.

Structures of early mathematical models of the GIM6,7 give only an abstract reflection of the underlying physiological properties and mechanisms involved in hormonal glycemic control. However, detailed mechanistic representations of physiology are useful for research, for example, identification of drug targets and pharmaceutical intervention strategies, and modern model-based glucose control algorithms can benefit from model kernels with increased accuracy and predictive power.4,5,8

In recent years, semi-mechanistic modeling approaches with an increased level of detail have gained in popularity. The UVa/Padova simulator, based on a model by Dalla Man et al.,9 accepted by the Food and Drug Administration to replace animal testing of glucose controllers,10 and the Cambridge Model, developed by Hovorka et al.11 for closed-loop glucose control contain physiological aspects and represent the current state-of-the-art in glucose modeling used for model-based glucose control. However, to date, no system for automatic glucose control has been brought to market.12

Current state-of-the-art models contain semi-mechanistic aspects, but are not physiologically based, e.g., do not explicitly consider blood flows or organ volumes. A state-of-the-art model developed more than 25 years ago by Sorensen13 already included such details for the distribution, metabolization and excretion dynamics of glucose, insulin, and even glucagon, which is neglected in most other models. Drawbacks of Sorensen's approach are missing detail on the organ level, and a missing framework for model individualization, making model adjustments to interindividual variability (IIV) cumbersome, if not impossible. This may be the reason why on the one hand this model was used only for in silico studies in closed-loop control,14 but has never been used as a kernel for automated closed-loop control in a clinical trial, and why on the other hand current state-of-the-art models rely on a more parsimonious but easy to individualize model structure.

Over the years, the availability of highly informative but complex physiological data over multiple scales has steadily increased, paving the way for detailed modeling approaches. Current models only partly accommodate to this trend with augmented model structures or by only analyzing subsystems leaving the following issues: (i) the lumped design of semi-mechanistic models results in a coarse mechanistic structure, which makes the integration of multiscale data and related translation steps required for fundamental research difficult. However, integration of multiscale data can strengthen the extrapolative properties of the simulation models, which is also a critical aspect in automatic glucose control. (ii) Analysis of subsystems in isolation neglects the effect of interacting subsystems. (iii) The abstract relation between important physiology and its mathematical representation, that is, model structure and parameterization, hinders the identification and direct quantification of detailed (metabolic) processes to distinguish physiologic differences in healthy and diabetic populations. Abstraction also (iv) masks the lag-times of distribution processes and (v) does not allow the integration of an individualization framework based on patient physiology.

Models of increasing complexity require an extensive database. Otherwise, they require additional assumptions which can introduce error. Physiologically based pharmacokinetic (PBPK) models are based to a large extend on prior information, taken from extensive databases of anatomical and physiological data, dependent on the organism and its changes associated with age, weight, height, gender and race and data calculated from drug-dependent properties. These properties are directly reflected in the parameterization of the model, for example, through organ volumes or blood flows, or drug-property dependent membrane permeability. PBPK models thus provide the structural (and spatial) detail as well as the mechanistic and structural framework to address the above raised issues. These models can then be used to simulate drug concentration profiles in all relevant organs and tissues.15 Once a reference PBPK model has been established, it can be used to extrapolate between species or individuals outside the selected cohort16 and allows a straightforward extension to additional mechanistic details such as target-side pharmacokinetic/pharmacodynamic (PK/PD) interaction.

We developed an integrated physiologically based whole-body model of the glucose-insulin-glucagon regulatory system consisting of three PBPK models for glucose, insulin, and glucagon. The integrated PBPK/PD approach presented here will address above raised issues with a generic widely applicable physiological model providing (i) the necessary structural detail for the integration of multiscale data, and (ii) detailed mathematical descriptions of physiologic processes and properties. (iii) It combines subcellular systems in one single model, (iv) including distribution and action processes associated with lag-times and (v) it provides a generic framework for a priori model individualization. The generic mechanistic approach of PBPK models is therefore well suited to mechanistically link PK and PD at an organ and molecular level.

Results

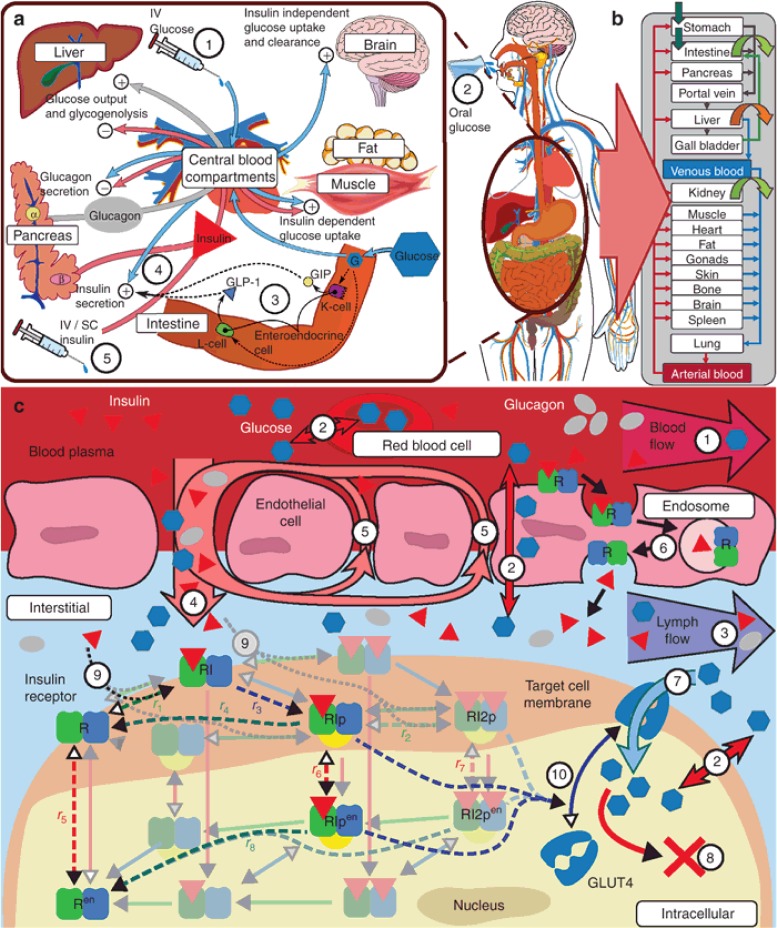
The concept of translating whole-body GIM physiology into a PBPK model structure is depicted in Figure 1a,b and, on an organ and molecular level regarding mechanistic modeling, in Figure 1c. The glucose PK model features a detailed compartmental oral absorption model17 reflecting gastrointestinal physiology such as anatomical dimensions and mucosal blood flow with explicit representations of facilitating- and sodium dependent glucose transporters 2 and 1 (GLUT2 and SGLT1). To reflect known glucose distribution physiology the model features tissue specific facilitating transporters (Figure 1c; 7). The PBPK model for insulin was extended by an adapted version of a published subcutaneous (s.c.) absorption model18,19 to account for s.c. administrations. For insulin PK, we implemented receptor-mediated transcytosis as model simulations and literature data20 suggest that extravasation is an insulin receptor mediated process21 (Figure 1c; 6). The PBPK description of glucagon, a generally omitted7,11,22 or lumped13,23 component in state-of-the-art models, was also extended by a s.c. absorption model.

Figure 1.

Figure 1

Open in a new tab

GIM structure overview. (a) Overview on PD interactions: Glucose has self-regulating effects consisting of suppression of endogenous glucose production, insulin-independent glucose uptake, renal glucose clearance, and stimulation of pancreatic insulin secretion (4), as well as, during episodes of low glucose concentrations, the stimulation of pancreatic glucagon secretion. Insulin, as a glucoregulatory hormone, maintains glucose homeostasis by insulin dependent glucose uptake in muscle and adipose tissue and suppression of endogenous (hepatic) glucose production as well as activation of hepatic glucose uptake. Glucagon, released at low glucose levels, counter-regulates low blood glucose levels, that is, hypoglycemia, through stimulation of hepatic glucose production. Interactions of glucose, insulin, and glucagon vary depending on the type of glucose challenge and pathological conditions. In contrast to intravenous (i.v.) glucose (1), oral glucose (2) additionally triggers the incretin effect (3), which affects insulin secretion (4) via the secretion of gastric hormones (e.g., GLP-1) prior to glucose appearance in the blood. In T1DM insulin secretion (4) is no longer functional, necessitating the infusion of exogenous insulin (5) via the i.v. or subcutaneous (s.c.) route. (b) Organ-level structure of whole-body model: each physiological organ translates to a compartment with several sub-compartments interconnected with convection and diffusion flows (see c). (c) Sub-organ-level and molecular details (1–10): organs are divided into five sub-compartments (blood plasma and cells, endothelial endosomes, interstitial, and intracellular). All compartments are interconnected via passive convection and diffusion flows (1–5) and facilitative transports (7). Distribution of compounds is ultimately dependent on for example, concentration gradients, flow rates, permeability, partition coefficients, transporter properties, and target protein binding properties.24 Both insulin distribution and its glucoregulatory PD effects are influenced or mediated at the molecular level. Bound to insulin receptors (IR) insulin is eliminated from the plasma by trans-endothelial transport (6), and in the interstitial space (9) triggering molecular signaling in target tissues inherently coupling its PK and PD (9, 10). Two receptor models from literature (Quon et al.,25 dashed lines; Koschorreck et al.,26 solid shaded lines) were evaluated. Adapted to the same organism and tissues (human fat, muscle, and liver), both models display similar dynamic properties (data not shown). Therefore, the less complex model by Quon et al. was implemented in the PBPK model, curated and adapted to human physiology (un-shaded receptor-states, see Supplementary Information online). At the molecular level, downstream signaling of the insulin receptor model in fat and muscle triggers translocation of insulin sensitive glucose transporter GLUT4, increasing peripheral glucose uptake (7, 10).

The PBPK models are interlinked via detailed molecular PD mechanisms (Figure 1a,c). As in Sorensen,13 the mathematical representation of the PD interactions is based on sigmoidal transfer-functions. Key PD components are a model representing the incretin mediated effects following oral absorption of carbohydrates and an insulin receptor model in the insulin sensitive tissues, fat, muscle, and liver. The insulin receptor acts as the key driver for insulin action but also clearance. It thereby couples PK with PD and reflects in a natural physiological way the observation that insulin action in insulin sensitive tissues correlates with degradation better than with delivery.27,28 Standard compartmental GIMs do not explicitly represent this dependency.

Model development was based on datasets from standard tolerance tests (glucose and insulin)13 and a published clinical-trial dataset by El-Khatib et al.29 The respective simulation results are presented in the following. First, we describe the performance of mean models for healthy volunteers and T1DM patients. In a second part, evaluation results for individualized models based on the clinical-trial data are presented. Here, data from the first visit was used for parameter identification, and data from the second visit was used for model evaluation. For more details on model development see the “Methods” section and Supplementary Texts S1 and S2 online.

Dynamics of the glucose metabolism model

The parameterization of a mean model for healthy subjects and subjects with T1DM was initialized with boundary conditions and parameter values over multiple scales extracted from literature. Values included tissue clearance fractions,28 tissue concentration gradients,20 protein properties (i.e., Km-values),30 and expression levels.26 The PK model basis and the PD functions were then continuously refined using experimental data. Based on their IIV the parameters were divided into three sets: (i) a global set displaying the lowest variability and assumed equal for all subjects, (ii) a set of parameters distinguishing healthy volunteers and T1DM patients, and (iii) a set of parameters for patient individualization (see Supplementary Tables S1–3 online). All model parameters are time-invariant.

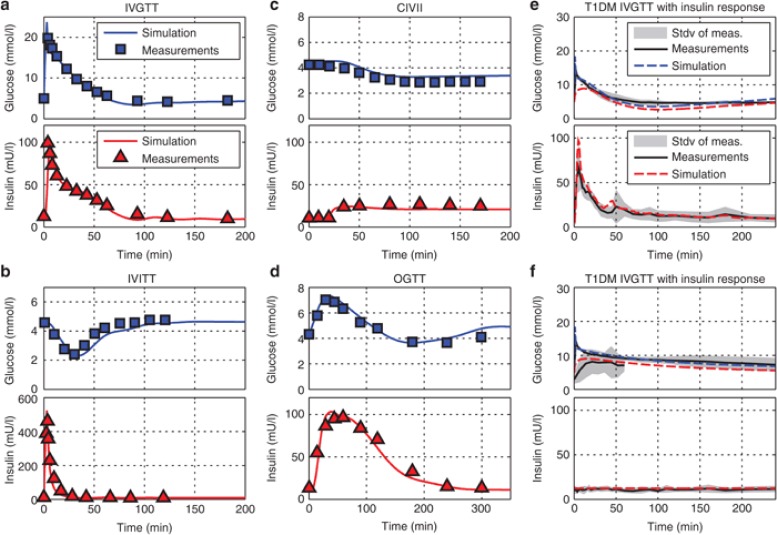
For parameterization of the mean models, we used datasets from intravenous (i.v.) glucose (healthy and T1DM) and insulin tolerance tests (IVGTT, IVITT), oral glucose tolerance tests as well as continuous i.v. insulin infusion as displayed in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Model development steps including fits to different tolerance test data sets in healthy individuals (a–d)13 and individuals with T1DM (e–f).31 (a) IVGTT: 3 min intravenous (i.v.) glucose infusion of 0.5 g/kg glucose in 110 normal adult males. The datasets were used to identify the systemic distribution behavior of glucose and for validation of the adapted insulin secretion model. (b) IVITT: 15 subjects received a 3-min infusion of 0.04 U/kg i.v. insulin, used to identify the systemic distribution behavior of insulin and the PD effect of insulin, especially the response times to and recovery times from insulin. (c) CIVII: At t = 20 min an infusion of 0.25 mU/min/kg was started in six normal subjects. This test evaluates the shift in steady state behavior during a forced prolonged hypoglycemic state. (d) Oral glucose tolerance test (OGTT): data was obtained from 145 normal adult males who received a 100g oral glucose challenge. This dataset was used for the identification of the oral glucose absorption and the incretin effect model. (e,f) IVGTT of 250 mg/kg glucose in six T1DM subjects; once with an imitated physiological insulin response using the biostator algorithm (e) and once without insulin response (f). The dataset triggered the reevaluation of glucose effectiveness and was necessary for the identification of the vascular and cellular insulin receptor parameterization in T1DM (Supplementary Table S2 online).

The identified mean models for healthy subjects and subjects with T1DM agree well with the experimental datasets with only a minor delay in the recovery of glucose levels after an IVITT.

The key result here is the distinguishing parameterization for healthy subjects and subjects with T1DM. Dynamics in healthy individuals, especially with respect to insulin action, are faster as compared with subjects with T1DM. This is reflected in the difference in receptor recycling and internalization rates but also insulin receptor expression levels (Supplementary Table S2 online). For T1DM, model fits showed a 50% increase in liver receptor concentrations with minor changes in concentrations in muscle and adipose tissue. Moreover, receptor recycling- and internalization rates were reduced by 20–30% in T1DM.

Post hoc evaluation of T1DM model predictions

We parameterized and validated the PBPK/PD model for T1DM in a post hoc in silico study using the published dataset by El-Khatib.29 The cohort investigated in this study covers a broad range of individual PK/PD properties for validation of the model. Although, the individuals in the study were sedated, the dataset is challenging, as the time between the two visits spanned up to several months. For each subject, the dataset obtained in the first visit was used for model individualization. This individualized model was then used to predict the outcome (i.e., dataset) of the second visit of the same subject. Differences between the two visits in their experimental setup (i.e., time-course and amount of injection rates) were considered. Without a treatment plan for each subject in between visits, estimates on long-term intra-individual changes in patients cannot be obtained and were neglected in the following.

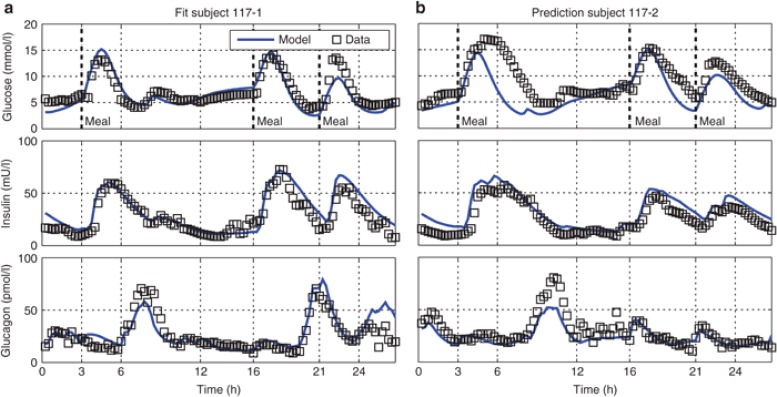
We present model results for a single representative patient (Subject 117; ref. 13, Figure 3), as well as the summarized results for the whole cohort (Figure 4). The fitted individualized PBPK/PD model of the single subject accurately captures the measurement data of all three compounds, glucose, insulin, and glucagon (Figure 3a).

Figure 3.

Figure 3

Open in a new tab

Simulated fitted (a) and predicted (b) trajectories of Subject 117 (ref. 13) from the first (a) and second (b) visit, respectively. Simulated trajectories are displayed as blue lines; data for comparison is displayed as black squares. Displayed are peripheral venous blood plasma concentrations of glucose (top), insulin (center), and glucagon (bottom).

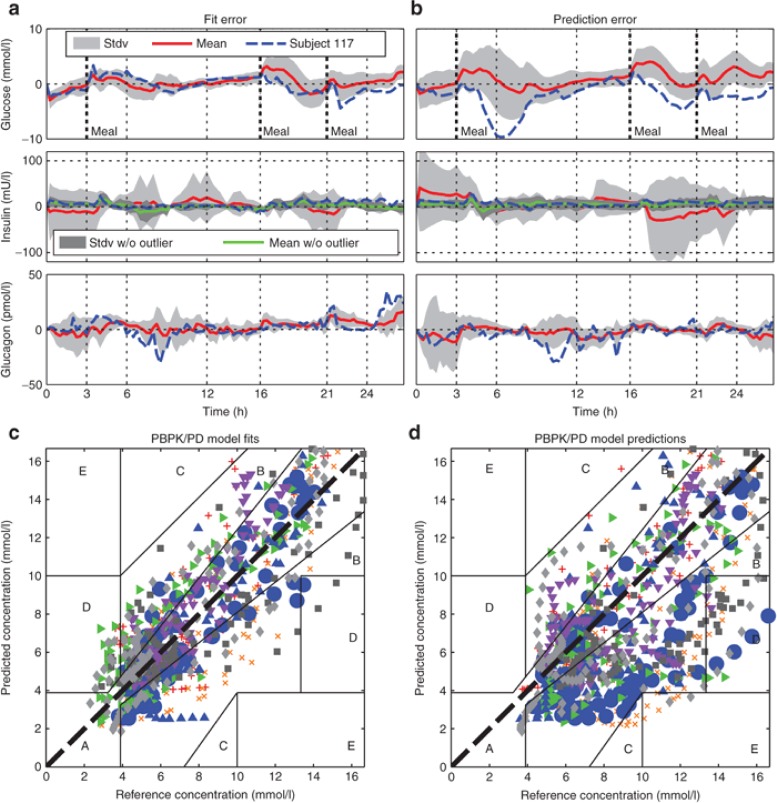
Figure 4.

Figure 4

Open in a new tab

Mean error residuals of simulated fitted (a,c) and predicted (b,d) trajectories of peripheral venous blood plasma concentrations of glucose (top), insulin (center), and glucagon (bottom) from all eight subjects from the first (a) and second (b) visit, respectively, displayed in comparison to the exemplary residual error from Subject 117. Visualized as time-concentration-error curves (a,b, for glucose (top), insulin (center), and glucagon (bottom) concentrations) and in a Clarkes Error Grid Analysis styled visual predictive check (c,d, only glucose concentrations). Displayed are for the eight subjects the mean error residuals (red solid lines, a,b), standard deviation of mean error residuals (light grey shaded area, a,b), all individual residual errors of glucose (c,d) as well as the single residual error from Subject 117 (blue dashed line, a,b, and large blue dots, c,d). For insulin concentration curves (a,b, center), the dark shaded area represents the mean error residuals without the outlier Subject 122.

Starting with the resulting model fits, the residual error over time of the fitted trajectories throughout the cohort (visit 1, Figure 4a) is comparable with Subject 117 (11% absolute normalized fit error, cohort: 12%). In Figure 4c, the quality of model fits for glucose is displayed as a summarized visual predictive check. For the visual predictive check plot, we used the Clarkes Error Grid, although it is commonly used to evaluate glucose monitoring devices rather than models, to give an idea of model accuracy for dosing decisions in clinical practice. The visual predictive check shows that the average absolute value of the fit error is evenly distributed around the line of identity indicating no systematic bias and a suitable description along the whole concentration range.

The residual error of the model fits, although small, shows minor systematic characteristics. In some cases subjects, including Subject 117, received large infusions of glucagon (Figure 3a, bottom, t = 6–8 h; 3B, bottom, t = 8–10 h) following postprandial hypoglycemia (Figure 3a, top, t = 6–7 h; Figure 3b, top, t = 8–9 h). Measured glucose then quickly rise to normo-glycemic levels (Figure 3a, top, t = 8 h; Figure 3b, top, t = 10 h). The corresponding simulated effect of glucagon in this situation is too small indicating that the modeled effect of glucagon in this situation is too low. A second point is that postprandial rise of measured glucose levels is slightly delayed and absorption is in some cases prolonged when compared with simulations. Outside these observations, however, the dynamics of glucose levels (Figure 4a, top) show no systematic error suggesting no further structural shortcomings of the glucose PBPK/PD model.

For insulin (Figure 4a, center) the residual error of fits show a minor overshoot (Figure 4a, center, i.e., t = 4 h) at times of steep increases in insulin infusion rate (following a meal). During these occasions, simulated insulin levels rise too quickly. The insulin error peaks in Figure 4a,b (center, t = ~4, 17, and 22 h) suggest that this behavior seems systematic for the whole cohort and likely associated with the s.c. absorption model. Overall, the fitted trajectories of insulin are very accurate.

For glucagon, only one systematic error, the overestimation of glucagon levels after the last meal, was observed. Establishing a physiological interpretation for this observation remains challenging. Moreover, this behavior was not observed during model predictions. Otherwise, the residual mean error of glucagon fits and predictions is nonsystematic (Figure 4a,b, both bottom plots) but with a larger absolute error during high infusion rates likely reflecting inter-occasional variability (IOV) of s.c. absorption. Overall, the residual error shows a noise-like behavior with faster changes in measured than in simulated concentration values and thus may be attributable to measurement noise, but otherwise shows no large deviations for both Subject 117 and the whole cohort.

For a single subject (Subject 122; ref. 13) the total plasma insulin was ~20-times higher than for all other individuals and the Subject can be considered as an outlier in that respect. Although quality of fit for Subject 122 with respect to the relative error is comparable with the other subjects, the resulting absolute error distorts the average results (compare light and dark shadings Figure 4a,b, center).

During model predictions, all parameters, including meal parameters, were left at their fit values. The second half of the glucose prediction (i.e., second visit) of Subject 117 corresponds well with the measurement data (Figure 3b, top), whereas the first half is characterized by a large error during absorption of the first meal (average error: Individual 117: 25% absolute normalized prediction error, cohort: 29%). In average, the variations in meal absorption become apparent for the prediction of the second visit (Figure 4b, top). Although the patients received the exactly same meals with respect to carbohydrate, fat and protein content, the qualitative shape of the measured glucose curves during a meal were strikingly different, reflecting IOV of glucose absorption from meals. In the Clarkes Error Grid, by contrast to the model fits, the predictions show a larger absolute error in the hyperglycemic range than in the normo-glycemic range. This indicates that the predictions during meal absorption are less reliable as compared with predictions in the fasted state.

Prediction of glucagon and insulin profiles are equally good as the model fit, indicating a reduced long-term IOV of PK properties but also underlining the very good long term predictive power of the model when taking into consideration that the two visits were months apart.

Discussion

This study describes the development of a physiologically based PK/PD model for glucose, insulin, and glucagon. Application to clinical data showed that the model is able to predict the time-courses of these three substances with one consistent time-invariant parameter set with an overall good accuracy. Whereas this clearly demonstrates the power of the PBPK/PD modeling approach, a full quantification of the quality of fit and predictions of the model presented here in comparison to state-of-the-art model implementations of the GIM is difficult as no validations of individual model predictions of full-day trials are published, but only pure predictions without data22 or only fitted trajectories.32 In summary, our modeling approach distinguishes itself from state-of-the-art models by its generic concept separating compound and organism properties, the detailed whole-body physiological compartmental structure, the a priori individualization framework, and the integration of detailed cellular mechanistic processes. Although the resulting models are computationally demanding, they were solved on standard laptop computers within a minute and the steady increase in computational power makes this a minor drawback.

Given the individualization framework and the detailed model structure, the developed model captures IIV and IOV. With respect to the numbers of parameters, the lion's share of IIV is captured by a priori parameterization of the individual physiology, which is mapped by the modeling platform based on the individual's anthropology. With over 600 unique parameters in the whole model, only 38 for the global mean and 26 distinctive parameters for healthy and T1DM mean population models were fitted. Ultimately, only ten parameters were used for model individualization. As the results clearly show, each of the patients was fitted successfully.

Whereas the development of a global generic integrated GIM model with parameters representing explicit physiological detail, for example, transporter expression and parameterization, is new, a key result is the distinguishing parameterization for healthy and T1DM individuals. Current state-of-the-art models of glucose metabolism merely change basal hepatic glucose production to distinguish these groups.13,33 However, considering subjects with T1DM, where insulin secretion and the incretin effect are lacking, a key difference to healthy subjects is from a modeling perspective the distinctive route by which insulin is provided to the body. In healthy subjects large amounts of endogenous insulin first pass the liver before being distributed to other tissues, whereas in subjects with T1DM, where insulin is exogenous, the liver is exposed only downstream to a lower level of insulin and insulin may exert only a fraction of its regulatory (e.g., glucose lowering) effect on the liver.

It is known that stimulation with insulin reduces receptor expression but increases receptor recycling rates.34,35,36 The detailed description of the human physiology and distributive fluid flows within the PBPK/PD model result in the naturally expected change in insulin concentration levels at the target tissue following a shift from endogenous to exogenous insulin supply. Model fits show that the reduced hepatic insulin levels in T1DM result in an increased receptor expression but reduced recycling rate, in-line with the experimental observations.

To predict concentration levels or even to fit data over a longer time-scale, the model also needs to capture IOV, that is, dynamics on a separate time-scale than plasma glucose or insulin levels, for example, insulin receptor dynamics or vascular endosomal transit of insulin. In current state-of-the-art models IOV is captured by time-variant parameter-sets.22,37 However, to improve the predictive power of the model, a mechanistic, preferably also physiologic description of IOV is paramount. The here integrated insulin receptor model is a first step in this direction, as it directly couples insulin clearance with insulin action as a dynamic system with long-term changes in surface receptor levels dependent on long-term cellular insulin load due to the slow receptor recycling rates. However, long-term changes in postreceptor signaling may also be a yet unresolved issue. The rationale for the distinguishing parameter set for T1DM and healthy individuals is a self-regulating feedback-loop of insulin receptor transcription and recycling rates.38 As insulin levels were predicted with high accuracy, the lion's share of the residual error of glucose predictions in Figure 4b probably arises at the postreceptor level. indeed, the observed average drift, caused by a major deviation of fasting glucose levels in only one single subject out of eight, can be compensated by a change in the single parameter insulin sensitivity (data not shown).

In general, model components, which self-adapt on a long time-scale, for example, insulin signal transduction or transcription and degradation dynamics of insulin receptors adjusting to average cellular insulin load,39 and on a short time-scale, for example, an exercise model with metabolic and regulatory networks,40,41 to exogenous influences would be beneficial. Here, however, the subjects were sedated, experiencing only little change in physical activity and variation in metabolic rate.

One of the largest sources of IOV is probably the absorption of carbohydrates of a meal as already outlined in the “Results” section. The most likely explanation for the changes observed in meal absorption is the high variability in the characteristic properties of meal absorption, depending on nutrient content. Different types of carbohydrates, with varying glycemic indexes define how quickly glucose is available for absorption,42 that is, in the “dissolved” state. The effects of amount and types of fat and proteins, meal texture as well as fiber content influence stomach emptying rates as well as intestine transit rates.43 Due to a lack of information, only total carbohydrates, caloric content, meal texture (fraction solid) and total meal volume is considered. Detailed a priori food characterization, with respect to covariates influencing gastric emptying (i.e., through the incretin effect itself), intestinal transit and absorption, integrated within a reliable mechanistic model describing effects of nutrition could likely improve predictions of meal absorption.

Another source of IOV (mainly glucagon) but also IIV is subcutaneous absorption. The reduced-order adaptation for continuous infusion of the s.c. absorption model also reduces the effect on the time delay of insulin appearance by local distribution at the injection site. However, implementation of the full model, adapted to continuous infusions seemed excessive as the time delay is only minor and shows high variability. Possibly, variability could be reduced if a better understanding of insulin distribution and degradation at the s.c. injection site is obtained.44 For s.c. glucagon absorption this could be due to changing s.c. properties over time or changing injection sites with different s.c. diffusion/absorption properties and/or additional subcutaneous degradation.45

Not only insulin absorption, but also action and/or secretion in healthy subjects are reported to be subjected to a circadian rhythm leading to additional variation.46 However, our results within this post hoc study including only individuals with T1DM do not further support this observation. A plausible explanation could be that these circadian properties are a property of insulin secretion or are otherwise disturbed in T1DM.47 Another unresolved issue is the effect on hepatic glucose production of high hepatic glucagon levels in the presence of increased insulin levels (Figure 3a, top). This strongly indicates that insulin inhibition of glucagon action is too strong or too prolonged. This indicates a necessity for stronger dynamic decoupling either at the interstitial or intracellular level. Solutions for dynamic decoupling of insulin and glucagon could be decoupling of plasma and interstitial dynamics in general or the inclusion of an intracellular cAMP pool affected by both hormones,48,49 instead of the direct multiplicative inhibition as adapted from Sorensen.13

Lastly, for the outlier Subject 122, a consistent explanation has to be validated with respect to the abnormally high insulin levels. Possible reasons could be differences in insulin receptor levels or insulin antibodies, both strongly affecting the distribution and clearance. During model development, both hypotheses were tested, latter being carried forward as it both resulted in better predictions and was supported in discussions with El-Khatib (data not shown; personal communication). A fraction unbound of 1% was necessary for Subject 122 to achieve the observed 20-fold increase in total plasma insulin levels. Plausibility of the low fraction unbound for insulin in Subject 122 remains to be confirmed and requires trials where antibody levels are measured.

With all the remaining issues considered, overall, the GIM model presented here agrees well with the datasets used for model validation. The model was developed in such a way that its purpose of use is versatile. The generic modeling concept provides a rigorous framework for individualization (even across organisms), data integration and model extension. It can be used for (i) fundamental research to uncover physiological properties and the relevance of biological mechanistics in whole-body physiology, that is integration of sub-models for exercise, (ii) prediction and automatic control of blood glucose in T1DM and (iii) due to the high level of detail including for example, proteins like SGLT1 and GLP-1 which are currently under investigation as drug targets and analogs in the R&D community, the model would also provide an ideal framework for fundamental research on diabetes related drug targets and corresponding pharmaceutical intervention strategies.

Our work thus provides a powerful model to the medical scientific, pharmaceutical and device R&D community for the development and validation of novel diabetes treatment strategies.

Methods

Physiologically based PK/PD modeling. The coupled PBPK/PD model of glucose metabolism was developed using Computational Systems Biology Software Suite® 5.1.3 (PK-Sim 5.1.3 and MoBi 3.1.3), commercial software packages for PBPK and molecular biology modeling.15,24,50 For details on the model structure, the reader is referred to Supplementary Texts 1 and 2 online.

PK-Sim provides a framework to efficiently implement all-important absorption, distribution, metabolization and excretion processes with a number of different basic model structures available for choice.

MoBi is a tool for mechanistic and dynamic modeling of biological processes. It is fully compatible with PK-Sim. Models that were created in PK-Sim can be exported to MoBi to be modified, extended, and/or coupled. By connecting PK-Sim models in MoBi it is possible to develop complex PBPK/PD models of models with interacting compounds such as glucose, insulin and glucagon in the glucose-insulin-glucagon regulatory system.15 In this work, all models created with PK-Sim were exported to MoBi for coupling via the known PD interactions, integration of an insulin receptor and secretion model and the addition of the s.c. absorption model of insulin and glucagon.

Patient data and model individualization. Iterative model improvement and individualization (i.e., parameter identification) have been conducted using the MoBi Toolbox for MATLAB in combination with MATLAB (optimization toolbox). The different parameter-sets used for model parameterization evolved from experience, ranking the parameters depending on their sensitivity and IIV (data not shown). The range of distribution of parameter values were adjusted manually, guided by experience and literature data (see Supplementary Tables 1–3 online). For the initial conditions of each patient, we simulated the steady state with two-thirds of the total daily insulin dose (see Supplementary Table S4 online) given s.c. over 24 h.

Author contributions

S.S and T.E. wrote the manuscript. S.S., S.W., J.L., A.S., and T.E. designed the research. S.S. performed the research. S.S analyzed the data. S.W., J.L., L.S., T.P., and T.E. contributed new reagents/analytical tools.

Conflict of interest

S.S., J.L., S.W., A.S., and T.E. are employees of Bayer Technology Services GmbH, the company developing PK-Sim and MoBi, the software used for model development.

Study Highlights

graphic file with name psp201340i1.jpg

Acknowledgments

We thank M. Krauss for fruitful discussion and proofreading of the manuscript and T. Gaub, J. Solodenko, C. Niederalt, K. Thelen, and K. Coboeken for the strong technical support. We also thank Firas H. El-Khatib and especially Steven J. Russell for fruitful personal discussions on their work. We also thank W. Regittnig for the provision of additional data information. The authors acknowledge financial support by the European Commission under Grant Agreement 248590 (FP7 Integrated Project Reaction; Remote Accessibility to Diabetes Management and Therapy in Operational Healthcare Networks).

Supplementary Material

Supplementary Table S1
Click here for additional data file. (588KB, doc)
Supplementary Table S2
Click here for additional data file. (223.5KB, doc)
Supplementary Table S3
Click here for additional data file. (167.5KB, doc)
Supplementary Table S4
Click here for additional data file. (173KB, doc)
Supplementary Text
Click here for additional data file. (550.2KB, zip)
Supplementary Information
Click here for additional data file. (13.5MB, doc)

References

  1. International-Diabetes-Federation. IDF Diabetes Atlas. International Diabetes Federation, Brussels, Belgium; 2011. [Google Scholar]
  2. Ban K., Hui S., Drucker D.J., Husain M. Cardiovascular consequences of drugs used for the treatment of diabetes: potential promise of incretin-based therapies. J. Am. Soc. Hypertens. 2009;3:245–259. doi: 10.1016/j.jash.2009.04.001. [DOI] [PubMed] [Google Scholar]
  3. Charbonnel B., Cariou B. Pharmacological management of type 2 diabetes: the potential of incretin-based therapies. Diabetes. Obes. Metab. 2011;13:99–117. doi: 10.1111/j.1463-1326.2010.01317.x. [DOI] [PubMed] [Google Scholar]
  4. El Youssef, J., Castle, J., Ward, W.K. A review of closed-loop algorithms for glycemic control in the treatment of type 1 diabetes. Algorithms. 2009;2 1:518–532. [Google Scholar]
  5. Hovorka R. Closed-loop insulin delivery: from bench to clinical practice. Nat. Rev. Endocrinol. 2011;7:385–395. doi: 10.1038/nrendo.2011.32. [DOI] [PubMed] [Google Scholar]
  6. BOLIE V.W. Coefficients of normal blood glucose regulation. J. Appl. Physiol. 1961;16:783–788. doi: 10.1152/jappl.1961.16.5.783. [DOI] [PubMed] [Google Scholar]
  7. Bergman R.N., Ider Y.Z., Bowden C.R., Cobelli C. Quantitative estimation of insulin sensitivity. Am. J. Physiol. 1979;236:E667–E677. doi: 10.1152/ajpendo.1979.236.6.E667. [DOI] [PubMed] [Google Scholar]
  8. Renard E. Closed-loop insulin delivery: is the Holy Grail near. Lancet. 2010;375:702–703. doi: 10.1016/S0140-6736(09)62165-6. [DOI] [PubMed] [Google Scholar]
  9. Dalla Man C., Rizza R.A., Cobelli C. Meal simulation model of the glucose-insulin system. IEEE Trans. Biomed. Eng. 2007;54:1740–1749. doi: 10.1109/TBME.2007.893506. [DOI] [PubMed] [Google Scholar]
  10. Kovatchev B.P., Breton M., Man C.D., Cobelli C. In silico preclinical trials: a proof of concept in closed-loop control of type 1 diabetes. J. Diabetes Sci. Technol. 2009;3:44–55. doi: 10.1177/193229680900300106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hovorka R., Chassin L.J., Ellmerer M., Plank J., Wilinska M.E. A simulation model of glucose regulation in the critically ill. Physiol. Meas. 2008;29:959–978. doi: 10.1088/0967-3334/29/8/008. [DOI] [PubMed] [Google Scholar]
  12. Dassau E., Atlas E., Phillip M. Closing the loop. Int. J. Clin. Pract. Suppl. 2010;65:20–25. doi: 10.1111/j.1742-1241.2009.02274.x. [DOI] [PubMed] [Google Scholar]
  13. Sorensen, J.T. A Physiologic Model of Glucose Metabolism in Man and its Use to Design and Assess Improved Insulin Therapies for Diabetes. PhD thesis, MIT. 1985.
  14. Parker R.S., Doyle F.J., 3rd, Peppas N.A. A model-based algorithm for blood glucose control in type I diabetic patients. IEEE Trans. Biomed. Eng. 1999;46:148–157. doi: 10.1109/10.740877. [DOI] [PubMed] [Google Scholar]
  15. Eissing T., et al. A computational systems biology software platform for multiscale modeling and simulation: integrating whole-body physiology, disease biology, and molecular reaction networks. Front. Physiol. 2011;2:4. doi: 10.3389/fphys.2011.00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Strougo A., Eissing T., Yassen A., Willmann S., Danhof M., Freijer J. First dose in children: physiological insights into pharmacokinetic scaling approaches and their implications in paediatric drug development. J. Pharmacokinet. Pharmacodyn. 2012;39:195–203. doi: 10.1007/s10928-012-9241-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Thelen K., Coboeken K., Willmann S., Burghaus R., Dressman J.B., Lippert J. Evolution of a detailed physiological model to simulate the gastrointestinal transit and absorption process in humans, part 1: oral solutions. J. Pharm. Sci. 2011;100:5324–5345. doi: 10.1002/jps.22726. [DOI] [PubMed] [Google Scholar]
  18. Mosekilde E., Jensen K.S., Binder C., Pramming S., Thorsteinsson B. Modeling absorption kinetics of subcutaneous injected soluble insulin. J. Pharmacokinet. Biopharm. 1989;17:67–87. doi: 10.1007/BF01059088. [DOI] [PubMed] [Google Scholar]
  19. Tarín C., Teufel E., Picó J., Bondia J., Pfleiderer H.J. Comprehensive pharmacokinetic model of insulin Glargine and other insulin formulations. IEEE Trans. Biomed. Eng. 2005;52:1994–2005. doi: 10.1109/TBME.2005.857681. [DOI] [PubMed] [Google Scholar]
  20. Bodenlenz M., et al. Measurement of interstitial insulin in human adipose and muscle tissue under moderate hyperinsulinemia by means of direct interstitial access. Am. J. Physiol. Endocrinol. Metab. 2005;289:E296–E300. doi: 10.1152/ajpendo.00431.2004. [DOI] [PubMed] [Google Scholar]
  21. Barrett E.J., Wang H., Upchurch C.T., Liu Z. Insulin regulates its own delivery to skeletal muscle by feed-forward actions on the vasculature. Am. J. Physiol. Endocrinol. Metab. 2011;301:E252–E263. doi: 10.1152/ajpendo.00186.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Dalla Man C., Rizza R.A., Cobelli C. Mixed meal simulation model of glucose-insulin system. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2006;1:307–310. doi: 10.1109/IEMBS.2006.260810. [DOI] [PubMed] [Google Scholar]
  23. Markakis M.G., Mitsis G.D., Marmarelis V.Z. Computational study of an augmented minimal model for glycaemia control. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2008;2008:5445–5448. doi: 10.1109/IEMBS.2008.4650446. [DOI] [PubMed] [Google Scholar]
  24. Willmann, S., et al. PK-Sim®: a physiologically based pharmacokinetic ‘whole-body' model. Biosilico. 2003;1:121–124. [Google Scholar]
  25. Quon M.J., Campfield L.A. A mathematical model and computer simulation study of insulin receptor regulation. J. Theor. Biol. 1991;150:59–72. doi: 10.1016/s0022-5193(05)80475-8. [DOI] [PubMed] [Google Scholar]
  26. Koschorreck M., Gilles E.D. Mathematical modeling and analysis of insulin clearance in vivio. BMC Syst. Biol. 2008;2:43. doi: 10.1186/1752-0509-2-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Huber C.T., Solomon S.S., Duckworth W.C. Time-course of insulin degradation in perifused isolated rat adipose cells. J. Clin. Invest. 1980;65:461–468. doi: 10.1172/JCI109689. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Duckworth W.C., Bennett R.G., Hamel F.G. Insulin degradation: progress and potential. Endocr. Rev. 1998;19:608–624. doi: 10.1210/edrv.19.5.0349. [DOI] [PubMed] [Google Scholar]
  29. El-Khatib F.H., Russell S.J., Nathan D.M., Sutherlin R.G., Damiano E.R. A bihormonal closed-loop artificial pancreas for type 1 diabetes. Sci. Transl. Med. 2010;2:27ra27. doi: 10.1126/scitranslmed.3000619. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Zierler K. Whole body glucose metabolism. Am. J. Physiol. 1999;276:E409–E426. doi: 10.1152/ajpendo.1999.276.3.E409. [DOI] [PubMed] [Google Scholar]
  31. Regittnig W., et al. Plasma and interstitial glucose dynamics after intravenous glucose injection: evaluation of the single-compartment glucose distribution assumption in the minimal models. Diabetes. 1999;48:1070–1081. doi: 10.2337/diabetes.48.5.1070. [DOI] [PubMed] [Google Scholar]
  32. Chen C.L., Tsai H.W., Wong S.S. Modeling the physiological glucose-insulin dynamic system on diabetics. J. Theor. Biol. 2010;265:314–322. doi: 10.1016/j.jtbi.2010.05.002. [DOI] [PubMed] [Google Scholar]
  33. Magni L., et al. Model predictive control of type 1 diabetes: an in silico trial. J. Diabetes Sci. Technol. 2007;1:804–812. doi: 10.1177/193229680700100603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Di Guglielmo G.M., Drake P.G., Baass P.C., Authier F., Posner B.I., Bergeron J.J. Insulin receptor internalization and signalling. Mol. Cell. Biochem. 1998;182:59–63. [PubMed] [Google Scholar]
  35. Bottaro D.P., Bonner-Weir S., King G.L. Insulin receptor recycling in vascular endothelial cells. Regulation by insulin and phorbol ester. J. Biol. Chem. 1989;264:5916–5923. [PubMed] [Google Scholar]
  36. Gorden P., Arakaki R., Collier E., Carpentier J.L. Biosynthesis and regulation of the insulin receptor. Yale J. Biol. Med. 1989;62:521–531. [PMC free article] [PubMed] [Google Scholar]
  37. Hovorka R., et al. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol. Meas. 2004;25:905–920. doi: 10.1088/0967-3334/25/4/010. [DOI] [PubMed] [Google Scholar]
  38. Puig O., Tjian R. Transcriptional feedback control of insulin receptor by dFOXO/FOXO1. Genes Dev. 2005;19:2435–2446. doi: 10.1101/gad.1340505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Tolic I.M., Mosekilde E., Sturis J. Modeling the insulin-glucose feedback system: the significance of pulsatile insulin secretion. J. Theor. Biol. 2000;207:361–375. doi: 10.1006/jtbi.2000.2180. [DOI] [PubMed] [Google Scholar]
  40. Richter E.A., Nielsen J.N., Jørgensen S.B., Frøsig C., Birk J.B., Wojtaszewski J.F. Exercise signalling to glucose transport in skeletal muscle. Proc. Nutr. Soc. 2004;63:211–216. doi: 10.1079/PNS2004343. [DOI] [PubMed] [Google Scholar]
  41. Chalhoub E., Xie L., Balasubramanian V., Kim J., Belovich J. A distributed model of carbohydrate transport and metabolism in the liver during rest and high-intensity exercise. Ann. Biomed. Eng. 2007;35:474–491. doi: 10.1007/s10439-006-9217-2. [DOI] [PubMed] [Google Scholar]
  42. Galgani J., Aguirre C., Díaz E. Acute effect of meal glycemic index and glycemic load on blood glucose and insulin responses in humans. Nutr. J. 2006;5:22. doi: 10.1186/1475-2891-5-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Fleisher D., Li C., Zhou Y., Pao L.H., Karim A. Drug, meal and formulation interactions influencing drug absorption after oral administration. Clinical implications. Clin. Pharmacokinet. 1999;36:233–254. doi: 10.2165/00003088-199936030-00004. [DOI] [PubMed] [Google Scholar]
  44. Jockel J.P., Roebrock P., Shergold O.A. Insulin depot formation in subcutaneoue tissue. J. Diabetes Sci. Technol. 2013;7:227–237. doi: 10.1177/193229681300700128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Schade D.S., Duckworth W.C. In search of the subcutaneous-insulin-resistance syndrome. N. Engl. J. Med. 1986;315:147–153. doi: 10.1056/NEJM198607173150302. [DOI] [PubMed] [Google Scholar]
  46. Saad, A., et al. Diurnal pattern to insulin secretion and insulin action in healthy individuals. Diabetes. 2012;61(11):2691–2700. doi: 10.2337/db11-1478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Hagström-Toft E., Bolinder J., Ungerstedt U., Arner P. A circadian rhythm in lipid mobilization which is altered in IDDM. Diabetologia. 1997;40:1070–1078. doi: 10.1007/s001250050789. [DOI] [PubMed] [Google Scholar]
  48. Bollen M., Keppens S., Stalmans W. Specific features of glycogen metabolism in the liver. Biochem. J. 1998;336 (Pt 1):19–31. doi: 10.1042/bj3360019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Hetherington J., et al. A composite computational model of liver glucose homeostasis. I. Building the composite model. J. R. Soc. Interface. 2012;9:689–700. doi: 10.1098/rsif.2011.0141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Services BT. SB Model Suite 5.1.4 – users manual. 2012.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table S1
Click here for additional data file. (588KB, doc)
Supplementary Table S2
Click here for additional data file. (223.5KB, doc)
Supplementary Table S3
Click here for additional data file. (167.5KB, doc)
Supplementary Table S4
Click here for additional data file. (173KB, doc)
Supplementary Text
Click here for additional data file. (550.2KB, zip)
Supplementary Information
Click here for additional data file. (13.5MB, doc)

Articles from CPT: Pharmacometrics & Systems Pharmacology are provided here courtesy of Wiley

RESOURCES