Comparison of observer reliability of three-dimensional cephalometric landmark identification on subject images from Galileos and i-CAT cone beam CT

Abstract

Objectives:

Recently, there has been increasing interest in the use of cone beam CT (CBCT) for three-dimensional cephalometric analysis and craniofacial reconstruction in orthodontic and orthognathic surgical treatment planning. However, there is a need to redefine the cephalometric landmarks in three dimensional cephalometric analysis and to demonstrate the reproducibility of landmark identification on the type of CBCT machine being used.

Methods:

CBCT images of 20 subjects aged 15–25 years were selected, ten each from Galileos^® (Sirona Dental Systems Inc., Bensheim, Germany) and Next Generation i-CAT^® (Imaging Sciences International, Hatfield, PA). 2 observers located 18 landmarks on each subject twice using Dolphin-3D v. 11 software (Dolphin Imaging and Management Systems, Chatsworth, CA). Inter- and intraobserver reliability was assessed using Euclidean distances and linear mixed models.

Results:

Overall, the intra- and interobserver reliability was excellent for both machines. The landmarks Gonion, Nasion, Orbitale and Anterior Nasal Spine (ANS) showed the greatest median Euclidean distances for both intra- and interobserver measurements. There were significant observer effects in the unified models for Sella, Menton and all six dental landmarks. For Sella, the distances between the measures were significantly smaller (more closely spaced) on the i-CAT machine than on the Galileos in both intra- and interobserver measurements.

Conclusions:

The intra- and interobserver reliability was excellent for both machines. Some of the landmarks were not as reproducible as others. Which machine produced the highest reliability depended on the landmark considered.

Introduction and literature review

Two-dimensional (2D) cephalometric analysis has been successfully used for several decades and is still an integral part of orthodontic diagnosis and treatment planning. Measurements based on 2D radiography frequently involve projection and magnification errors as well as overlap of adjacent structures on the region of interest. With increasing availability of maxillofacial cone beam CT (CBCT), three-dimensional (3D) assessment of skeletal and dental relationships is now feasible.¹ CBCT-generated panoramic and cephalometric images are increasingly being used as substitutes for conventional panoramic and cephalometric images for orthodontic treatment planning.^2–7 Several studies have established the precision and accuracy of linear measurements of different CBCT systems using the reconstructed 2D tomographic slices and lateral cephalometric images. The diagnostic reliability is found to be comparable to or even better than that of conventional lateral cephalographs.⁸ CBCT offers potential for 3D cephalometrics in the orthodontic assessment of bony landmarks. In many straightforward orthodontic and simple orthognathic cases, 3D vs 2D cephalometrics will not likely alter the treatment decision or the outcome. However, reliability in 3D landmark position has many implications not only for 3D cephalometrics, which has important applications in the diagnostic and treatment planning and other aspects of craniofacial reconstruction on patients with craniofacial anomalies, severe trauma or cancer, but also for more sophisticated 3D landmark shape methods, such as geomorphometric (GM) methods, which rely heavily on landmark location. GM methods are utilized in studies of normal and pathological facial shape variation and in the evaluation of shape outcomes post treatment.^9–11

Observer reliability (reproducibility) of landmark location for 3D cephalometric analysis has been studied in the past on images from different CBCT machines.^12–15 However, CBCT units available in the market differ from each other in many aspects, including, but not limited to, image acquisition, reconstruction, field of view (FOV) and resolution. Thus, study results from one type of machine may not be applicable to images from another type. 3D cephalometric analysis requires defining the landmarks on complex curving structures in a 3D space and redefining some landmarks used in 2D analysis that are the results of superimposition of points in different planes. However, there is a paucity of literature addressing suitable working definitions for landmarks for 3D cephalometric analysis.

A review of the literature failed to identify studies on observer reliability for the identification of 3D cephalometric landmarks on Galileos® (Sirona Dental Systems Inc., Bensheim, Germany) images or any study comparing observer reliability for the identification of 3D cephalometric landmarks on images acquired from two different machines in vivo. The aim of our study was to assess the intra- and interobserver reliability for anatomical landmark identification on subject images from Galileos and Next Generation i-CAT® (Imaging Sciences International, Hatfield, PA) and to compare their performance. In addition, in this study, the landmarks were defined in a systematic way, guiding the examiner to navigate through the slices and locate the landmark.

Materials and methods

Existing CBCT images of 20 subjects aged 15–25 years were selected—10 each from Galileos® and Next Generation i-CAT® data sets. Images from both machines had been acquired and reconstructed with isotropic voxels of size 0.3 × 0.3 × 0.3 mm. The FOV was 15 cm (H) × 15 cm (D) for Galileos and 17 cm (H) × 23 cm (D) for i-CAT. Other imaging parameters were 85 kV/42 mAs for Galileos and 120 kV/19 mAs for i-CAT.

Images were selected using the following inclusion and exclusion criteria:

Inclusion criteria:

1. acceptable quality images

2. sufficient FOV to include temporomandibular joints, Sella turcica and the tip of chin.

Exclusion criteria:

1. motion artefacts

2. large number of metallic attenuation artefacts

3. prior orthognathic surgery or trauma to head and neck region causing gross changes in the osseous structures

4. missing permanent incisors or first molars

5. unerupted or supernumerary teeth overlapping the incisor apices.

The study was approved by The University of Iowa Institutional Review Board, Iowa City, IA. A research database was created in axiUm (Exan group, Las Vegas, NV) on the collegiate server. The images were anonymized and imported into Dolphin-3D v. 11 (Dolphin Imaging and Management Systems, Chatsworth, CA) for viewing.

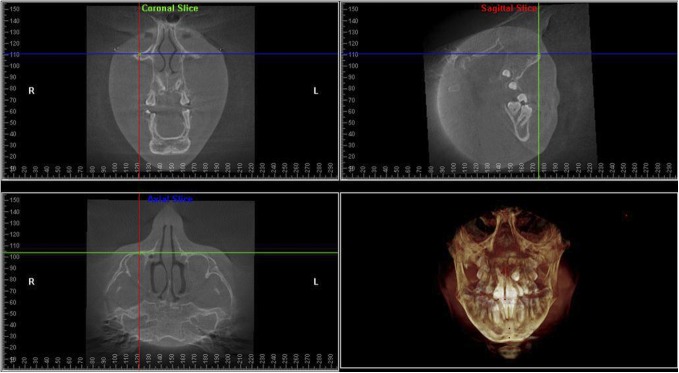
Two observers, Observer 1 (resident) and Observer 2 (faculty member) in oral and maxillofacial radiology, reviewed the images. Observer 1 had 2 years of experience examining CBCT and conventional cephalometric images and Observer 2 had 5 years of experience examining CBCT images and over 40 years of experience examining conventional cephalometric radiographs. However, this was the first time either of the observers had examined orthodontic landmarks on CBCT. The landmarks were defined, and the way to localize them using the 2D planes of space—axial, sagittal and coronal—was decided by discussion among the two observers and an orthodontist on the research committee (Table 1). Figure 1 shows the location of the Orbitale landmark. Not all three planes were required to locate all the landmarks. Interobserver calibration on the landmark locations was obtained prior to initiating the study. The observers were allowed to use any of the software's image enhancing features to better visualize structures.

Table 1.

Landmark definitions

Landmark name	Definition
Upper molar	Most inferior point of the mesiobuccal cusp of the upper right first molar. When going medially on the sagittal, followed by going posteriorly on the coronal
Lower molar	Most superior point of the mesiobuccal cusp of the lower right first molar. When going medially on the sagittal, followed by going posteriorly on the coronal
Mx1 tip	Midpoint of the incisal edge of the upper right central incisor. When going inferiorly on the axial, followed by going posteriorly on the coronal, followed by going medially on the sagittal
Mx1 root	Root apex of the upper right central incisor. When going inferiorly on the axial, followed by going posteriorly on the coronal, followed by going medially on the sagittal
Md1 tip	Midpoint of the incisal edge of the lower right central incisor. When going superiorly on the axial, followed by going posteriorly on the coronal, followed by going medially on the sagittal
Md1 root	Root apex of the lower right central incisor. When going superiorly on the axial, followed by going posteriorly on the coronal, followed by going medially on the sagittal
A point	Point of maximum concavity in the midline of the alveolar process of the maxilla. When going posteriorly on the coronal, followed by going medially on the sagittal, followed by going inferiorly on the axial
ANS	Most anterior midpoint of the nasal spine of the maxilla. When going posteriorly on the coronal, followed by going medially on the sagittal, followed by going inferiorly on the axial
PNS	Most posterior midpoint of the nasal spine of the maxilla. When going anteriorly on the coronal, followed by going medially on the sagittal, followed by going inferiorly on the axial
Nasion	Point of maximum concavity in the midline in the region of the frontonasal suture. When going posteriorly on the coronal, followed by going medially on the sagittal, followed by going inferiorly on the axial
B point	Point of maximum concavity in the midline of the alveolar process of the mandible. When going posteriorly on the coronal, followed by going medially on the sagittal, followed by going inferiorly on the axial
Menton	Most inferior midpoint of the chin on the outline of the mandibular symphysis. When going posteriorly on the coronal, followed by going medially on the sagittal, followed by going inferiorly on the axial
Pogonion	Most anterior midpoint of the chin on the outline within one centimeter from the inferior border. When going posteriorly on the coronal, followed by going medially on the sagittal, followed by going inferiorly on the axial
Gonion	Most posteroinferior point on the curvature of the right angle of the mandible in the sagittal slice where the posterior border of the ramus is first continuous, and the most lateral point in the coronal plane that cuts through the first position of the point. Sagittal → coronal
Condylion	Most posterosuperior point of the right mandibular condyle in the sagittal plane, where the sagittal plane corresponds to the most posterior point on the coronal plane. Coronal → sagittal
Orbitale	Most inferior point of right infraorbital rim midway on the cortex of the bone on the sagittal plane, which corresponds to the first axial plane showing complete rim when going inferiorly. Axial → sagittal → coronal
Sella	Geometric centre of the pituitary fossa. When going inferiorly on the axial, followed by going medially on the sagittal
Sigmoid notch	Most inferior point along the superior border of right ramus of the mandible, which corresponds to the first axial plane that shows a complete border when going inferiorly, followed by going medially on the sagittal.

Figure 1.

Location of the Orbitale landmark on the multiplanar reconstruction slices and three-dimensional surface-rendered image

The volumes were oriented using the 3D hard tissue surface representation, such that the midsagittal plane was vertical, the transorbital plane was horizontal and the Frankfort horizontal plane was horizontal. The orientation was saved and kept the same, so that every image of each subject had the same reference planes. This allowed constant references to which x-(mediolateral), y-(craniocaudal) and z-(anteroposterior) coordinates were derived for each landmark identified by an observer. The images were evaluated in the same order by both observers—Galileos images first and i-CAT images second. The landmarks were localized using the axial, sagittal and coronal sections as needed. The landmarks were then digitized, i.e. were assigned x-, y- and z-coordinates, and exported into a Microsoft Excel^® (2007; Microsoft Corporation, Redmond, WA) worksheet by the Dolphin software. All digitized landmark identification sessions took place in a dimly lit room without interruption for as long as each observer needed to finish. A notebook computer—HP Pavilion DV7 (Hewlett-Packard Company, Palo Alto, CA)—with an NVIDIA (NVIDIA Corporation, Santa Clara, CA) GeForce GT 230M graphics card was used. The computer had a 32-bit colour monitor. The display screen resolution was 1600 × 900 pixels. Each observer localized each landmark on each subject twice, with a gap of at least 7 days between the first and the second measurements.

Statistical analysis

The Euclidean distance, which is the square root of the sum of squared coordinate differences between the two selected landmark positions, was calculated for each pair of observations (either the duplicate measures made by a single observer or the measures of the same landmark by two different observers). Descriptive statistics were calculated for these Euclidean differences, and the differences in the distribution of Euclidean differences between the two machines were evaluated using the Wilcoxon rank-sum test. Linear mixed models (LMMs) were also used to assess reliability between machines. Because the subjects evaluated were different for each machine, a unified LMM was used to model the Euclidean distances for each landmark, treating the observer and the machine as fixed effects and modelling variability among subjects within machines using a random effect approach. The residuals from each model were examined for normality using the Shapiro–Wilk test. LMM residuals were examined for validation of assumptions including normality; data transformations, including square root and natural logarithm, of the dependent variable were explored and implemented where required. No adjustment was made for multiple comparisons. Analysis was carried out using SAS^® Enterprise Guide^® 4.2 (SAS Institute Inc., Cary, NC) and R statistical software, and a significance level of 0.05 was specified.

Results

Intraobserver agreement

Intraobserver Euclidean distance analysis

The Euclidean distance between first and second landmark coordinates were calculated between the two points in 3D space. Although there is no uniform standard for acceptable levels of error for landmark location, available literature in 2D cephalometrics and 3D reconstructions for the application of geometrics morphometric methods have reported acceptable measurement errors of ≤1 mm.^16,17 In the current study, for Observer 1, the landmarks with the greatest median Euclidean distances were Gonion (Galileos: 0.96 mm, i-CAT: 1.45 mm), Pogonion (Galileos: 0.70 mm, i-CAT: 1.01 mm), Condylion (Galileos: 0.93 mm, i-CAT: 0.88 mm) and Nasion (Galileos: 0.85 mm, i-CAT: 0.73 mm). The distances for each landmark were tested for significance between the i-CAT and Galileos images using the Wilcoxon rank-sum test. For Observer 1, the landmarks Sella (p = 0.0046), Md1 tip (p = 0.0312) and upper molar (p = 0.0126) were significantly different, with the distances significantly smaller on the Galileos machine than on the i-CAT machine for the Md1 tip and upper molar landmark and on the i-CAT for Sella (Table 2).

Table 2.

Summary of Euclidean distances between the first and second measures of Observer 1

Landmarka	Galileos® (n = 10)						Next Generation i-CAT® (n = 10)						Wilcoxon rank-sum p-valueb
	Mean	Standard deviation	Median	Minimum	Maximum	Range	Mean	Standard deviation	Median	Minimum	Maximum	Range
A	0.62	0.4183	0.51	0.20	1.55	1.35	0.86	0.6321	0.76	0.00	2.40	2.40	0.2730
ANS	0.73	0.4347	0.65	0.20	1.45	1.25	0.82	0.5450	0.61	0.30	1.95	1.65	0.7337
B point	1.07	0.8733	0.65	0.22	2.91	2.68	0.83	0.5303	0.69	0.00	1.73	1.73	0.6776
Condylion	0.97	0.3461	0.93	0.28	1.62	1.34	1.07	0.4428	0.88	0.70	2.18	1.48	0.9097
Gonion	1.53	1.4081	0.96	0.00	4.19	4.19	1.87	1.5721	1.45	0.40	5.80	5.40	0.4725
Sella	0.55	0.1644	0.62	0.22	0.73	0.50	0.32	0.0871	0.30	0.20	0.45	0.25	0.0046
Sigmoid notch	0.38	0.1870	0.35	0.10	0.75	0.65	0.60	0.2950	0.68	0.00	1.08	1.08	0.0640
Lower molar	0.63	0.5811	0.48	0.20	2.17	1.97	0.62	0.3809	0.51	0.20	1.49	1.29	0.8798
Md1 root	0.52	0.4821	0.45	0.00	1.72	1.72	0.68	0.7453	0.44	0.20	2.75	2.55	0.6232
Md1 tip	0.33	0.1694	0.30	0.10	0.57	0.47	0.91	1.1746	0.53	0.28	4.20	3.92	0.0312
Me	0.56	0.4809	0.38	0.20	1.73	1.53	0.60	0.3590	0.52	0.00	1.21	1.21	0.2413
Mx1 root	0.54	0.1381	0.50	0.36	0.81	0.45	0.70	0.3234	0.63	0.20	1.21	1.01	0.1735
Mx1 tip	0.51	0.1213	0.52	0.30	0.71	0.41	0.49	0.2903	0.48	0.00	1.03	1.03	0.7913
Nasion	1.30	1.4980	0.85	0.49	5.49	5.00	0.68	0.3615	0.73	0.10	1.46	1.36	0.3073
Orbitale	1.23	1.2955	0.75	0.32	4.58	4.26	0.85	0.2513	0.81	0.42	1.27	0.84	0.9097
PNS	1.17	1.3345	0.80	0.30	4.77	4.47	0.69	0.4624	0.68	0.00	1.65	1.65	0.6230
Pog	1.52	1.7100	0.70	0.30	5.75	5.45	1.05	0.6758	1.01	0.00	2.43	2.43	1.0000
Upper molar	0.41	0.1435	0.39	0.22	0.71	0.48	0.76	0.3162	0.79	0.28	1.28	1.00	0.0126

^aSee Table 1 for definitions of the landmarks.

^bSignificance probability associated with the Wilcoxon rank-sum test to assess whether the distributions for the Euclidean distances differed between machines. Highlighting in bold indicates the significance value of <0.05.

Galileos is manufactured by Sirona Dental Systems Inc., Bensheim, Germany and Next Generation i-CAT by Imaging Sciences International, Hatfield, PA.

For Observer 2, the landmarks with the greatest median Euclidean distances were PNS (Galileos: 0.83 mm, i-CAT: 1.13 mm), Gonion (Galileos: 2.01 mm, i-CAT: 1.11 mm), Pogonion (Galileos: 1.23 mm, i-CAT: 0.98 mm), Orbitale (Galileos: 1.35 mm, i-CAT: 0.53 mm), A point (Galileos: 1.34 mm, i-CAT: 0.69 mm), ANS (Galileos: 1.24 mm, i-CAT: 0.76 mm), Mx1 root (Galileos: 1.25 mm, i-CAT: 0.91 mm) and Me (Galileos: 1.24 mm, i-CAT: 0.81 mm). There were significant differences, using the Wilcoxon rank-sum test, in the Euclidean distances between the two landmark selections for Sella (p = 0.0140) and Me (p = 0.0140) for Observer 2. In both cases, the i-CAT machine had significantly smaller distances between landmark selections than did the Galileos machine (Table 3).

Table 3.

Summary of Euclidean distances between the first and second measures of Observer 2

Landmarka	Galileos® (n = 10)						Next Generation i-CAT® (n = 10)						Wilcoxon rank-sum p-valueb
	Mean	Standard deviation	Median	Minimum	Maximum	Range	Mean	Standard deviation	Median	Minimum	Maximum	Range
A	1.33	0.7441	1.34	0.22	2.30	2.08	0.87	0.6807	0.69	0.14	2.56	2.42	0.1403
ANS	1.21	0.5489	1.24	0.36	2.01	1.65	0.81	0.3232	0.76	0.30	1.50	1.20	0.1041
B point	1.10	1.1314	0.78	0.00	3.96	3.96	1.11	0.9531	0.65	0.33	3.08	2.75	0.9097
Condylion	0.88	0.4143	0.81	0.36	1.66	1.30	1.29	0.8352	0.99	0.28	2.94	2.66	0.2730
Gonion	2.22	1.4223	2.01	0.97	5.97	5.00	2.17	2.6125	1.11	0.54	9.21	8.67	0.3447
Sella	1.14	0.3651	1.07	0.79	2.05	1.26	0.70	0.3329	0.76	0.28	1.22	0.94	0.0140
Sigmoid notch	0.66	0.3765	0.65	0.00	1.18	1.18	0.72	0.3189	0.66	0.22	1.35	1.13	0.8501
Lower molar	1.62	2.8720	0.71	0.50	9.78	9.28	0.78	0.3043	0.75	0.37	1.24	0.87	0.9698
Md1 root	1.06	0.4718	1.03	0.36	2.00	1.64	1.35	1.2494	0.86	0.44	4.53	4.10	0.9698
Md1 tip	0.76	0.2303	0.78	0.41	1.12	0.71	1.14	1.4264	0.79	0.32	5.12	4.81	0.9097
Me	1.74	0.9794	1.24	0.94	3.58	2.64	0.94	0.6970	0.81	0.28	2.65	2.36	0.0140
Mx1 root	1.13	0.5506	1.25	0.10	1.82	1.72	1.07	0.4657	0.91	0.51	1.67	1.16	0.8501
Mx1 tip	0.74	0.3515	0.75	0.28	1.32	1.03	0.75	0.3799	0.63	0.30	1.48	1.18	0.9698
Nasion	1.06	0.7877	0.78	0.22	2.71	2.49	1.58	1.5303	0.80	0.28	4.71	4.43	0.5706
Orbitale	1.55	1.3124	1.35	0.10	4.46	4.36	0.63	0.4805	0.53	0.00	1.67	1.67	0.0757
PNS	1.44	1.3110	0.83	0.20	4.04	3.84	1.53	1.5306	1.13	0.37	5.40	5.02	0.7913
Pog	1.83	1.8577	1.23	0.35	5.91	5.56	1.35	1.2704	0.98	0.37	4.51	4.14	0.7337
Upper molar	0.79	0.2704	0.83	0.36	1.22	0.86	0.99	0.4659	0.82	0.45	1.98	1.53	0.4274

^aSee Table 1 for definitions of the landmarks.

^bSignificance probability associated with the Wilcoxon rank-sum test to assess whether the distributions for the Euclidean distances differed between machines. Highlighting in bold indicates the significance value of <0.05.

Galileos is manufactured by Sirona Dental Systems Inc., Bensheim, Germany and Next Generation i-CAT by Imaging Sciences International, Hatfield, PA.

Intraobserver Euclidean distance linear mixed models

An LMM was used to model the Euclidean distances for each landmark and each observer with a fixed machine effect and a random subject within machine effect. The results of the LMM validated all significant machine differences in Euclidean distance measures detected with the Wilcoxon rank-sum test. However, in addition to these, a significant machine difference (p = 0.0023) was also found for Gonion for Observer 2 (Table 4). The variance of this landmark was much greater than that of the other landmarks (Table 3), particularly on the i-CAT CBCT. Whereas the Wilcoxon test is excellent at detecting differences in location, the model may be more sensitive to the magnitude of variance that exists in the data.

Table 4.

Results of the linear mixed model predicting the Euclidean distance between dual landmarks with fixed machine and random subject effects (Observer 2)

Landmarka	Machine effect (Type-III tests of fixed effects)			Covariance parameter estimates		Shapiro–Wilk p-valuec	Data transformation
	F	p-valueb	Degrees of freedom	Intercept and subject	Residual
A	2.14	0.1608	18	0.1714	0.3371	0.3911
ANS	3.96	0.0620	18	0.0342	0.1686	0.9436
B point	0.09	0.7736	18	0.0395	0.1800	0.2283	Square root
Condylion	2.01	0.1733	18	0.1316	0.3029	0.2640
Gonion	12.60	0.0023	18	7.3123	0.8913	0.8641
Sella	7.89	0.0116	18	0.0133	0.1088	0.0659
Sigmoid notch	0.14	0.7092	18	0.0132	0.1085	0.9038
Lower molar	0.71	0.4101	18	0.0615	0.2191	0.0001	Subject nine outliers
Md1 root	0.06	0.8127	18	0.1022	0.2727	0.5955	Natural log
Md1 tip	0.09	0.7735	18	0.0951	0.2645	0.0072	Natural log
Me	7.18	0.0153	18	0.0873	0.2551	0.8707	Natural log
Mx1 root	0.08	0.7834	18	0.0537	0.2063	0.1213
Mx1 tip	0.01	0.9443	18	0.0158	0.1181	0.1843
Nasion	0.49	0.4926	18	0.3119	0.4239	0.4269	Natural log
Orbitale	4.20	0.0552	18	0.0339	0.1679	0.9820	Square root
PNS	0.06	0.8048	18	0.3203	0.4280	0.6150	Natural log
Pog	0.27	0.6076	18	0.3309	0.4331	0.3496	Natural log
Upper molar	1.28	0.2726	18	0.0184	0.1267	0.2198

^aSee Table 1 for definitions of the landmarks.

^bSignificance probability associated with the F-test of significance of the machine effect in the mixed model. Highlighting in bold indicates the significance value of <0.05.

^cSignificance probability associated with the Shapiro–Wilk test of normality of model residuals following data transformation if required.

Interobserver agreement

Interobserver Euclidean distance analysis

For the first measures, the landmarks with the greatest median Euclidean distances were Nasion (Galileos: 2.94 mm, i-CAT: 0.96 mm), Gonion (Galileos: 2.81 mm, i-CAT: 4.89 mm), Orbitale (Galileos: 1.49 mm, i-CAT: 0.93 mm) and B point (Galileos: 1.23 mm, i-CAT: 0.99 mm). The distances for each landmark were tested for significance between the i-CAT and Galileos images using the Wilcoxon rank-sum test. For the first measures, the landmarks Sella (p = 0.0140) and Mx1 root (p = 0.0140) were significantly different, with the distances significantly smaller on the i-CAT machine for Sella and on the Galileos machine for the Mx1 root landmark (Table 5).

Table 5.

Summary of Euclidean distances between the first measures of Observers 1 and 2

Landmarka	Galileos® (n = 10)						Next Generation i-CAT® (n = 10)						Wilcoxon rank-sum p-valueb
	Mean	Standard deviation	Median	Minimum	Maximum	Range	Mean	Standard deviation	Median	Minimum	Maximum	Range
A	1.79	2.4005	1.05	0.41	8.44	8.02	1.13	0.5269	1.03	0.35	2.22	1.87	0.9698
ANS	1.01	0.4367	0.93	0.54	1.86	1.32	1.17	0.5372	1.08	0.51	2.24	1.73	0.6232
B point	1.38	0.9940	1.23	0.30	3.54	3.24	1.11	0.4904	0.99	0.75	2.44	1.69	0.2730
Condylion	1.13	0.4728	1.16	0.22	1.87	1.64	1.38	0.9421	1.02	0.61	3.70	3.09	0.9097
Gonion	3.94	3.0397	2.81	0.75	9.17	8.42	4.75	2.1534	4.89	0.83	7.57	6.74	0.4727
Sella	0.91	0.4006	0.84	0.30	1.70	1.40	0.49	0.2574	0.54	0.10	0.91	0.81	0.0140
Sigmoid notch	0.73	0.3154	0.61	0.41	1.32	0.91	0.90	0.2972	0.83	0.54	1.35	0.81	0.2730
Lower molar	1.84	2.7831	1.03	0.45	9.72	9.27	1.34	0.5469	1.16	0.81	2.21	1.40	0.5205
Md1 Root	1.08	0.6041	1.10	0.28	2.20	1.91	1.75	1.5752	1.30	0.47	5.80	5.33	0.3075
Md1 tip	0.72	0.3300	0.72	0.24	1.14	0.90	1.07	0.5402	1.07	0.36	2.22	1.86	0.1212
Me	1.18	0.5517	1.17	0.28	2.06	1.78	1.25	0.9003	1.00	0.24	3.44	3.20	0.8501
Mx1 Root	0.77	0.3022	0.66	0.50	1.28	0.78	1.30	0.5030	1.22	0.58	2.30	1.72	0.0140
Mx1 tip	0.86	0.2665	0.88	0.35	1.22	0.88	0.77	0.3189	0.82	0.30	1.26	0.96	0.5708
Nasion	3.30	2.7001	2.94	0.36	7.75	7.39	1.45	1.1741	0.96	0.14	3.75	3.61	0.2413
Orbitale	1.74	1.3346	1.49	0.41	4.86	4.45	0.89	0.3419	0.93	0.44	1.39	0.96	0.1041
PNS	0.95	0.5875	0.74	0.41	2.01	1.60	1.76	1.7282	1.36	0.22	6.37	6.14	0.2123
Pog	1.27	1.1684	0.87	0.36	4.25	3.89	1.07	0.6003	0.83	0.54	2.16	1.62	0.8501
Upper molar	0.88	0.4471	0.82	0.40	1.90	1.50	0.84	0.5635	0.66	0.22	2.03	1.81	0.6232

^aSee Table 1 for definitions of the landmarks.

^bSignificance probability associated with the Wilcoxon rank-sum test of whether the distributions of the Euclidean distance between dual measures were equal. Highlighting in bold indicates the significance value of <0.05.

Galileos is manufactured by Sirona Dental Systems Inc., Bensheim, Germany, and Next Generation i-CAT by Imaging Sciences International, Hatfield, PA.

For the second measures, the landmarks with the greatest median Euclidean distances were Gonion (Galileos: 5.54 mm, i-CAT: 4.79 mm), Nasion (Galileos: 2.13 mm, i-CAT: 0.85 mm), ANS (Galileos: 1.07 mm, i-CAT: 1.39 mm) and Orbitale (Galileos: 1.42 mm, i-CAT: 0.80 mm). There were significant differences, using the Wilcoxon rank-sum test, in the Euclidean distances between the 2 s landmark selections for Nasion (p = 0.0073) and Orbitale (p = 0.0073). In both cases, the i-CAT machine had significantly smaller distances between landmark selections than did the Galileos machine (Table 6).

Table 6.

Summary of Euclidean distances between the second measures of Observers 1 and 2

Landmarka	Galileos® (n = 10)						Next Generation i-CAT® (n = 10)						Wilcoxon rank-sum p-valueb
	Mean	Standard deviation	Median	Minimum	Maximum	Range	Mean	Standard deviation	Median	Minimum	Maximum	Range
A	1.82	2.0946	1.03	0.30	7.18	6.88	1.07	0.5954	0.86	0.36	2.00	1.64	0.6232
ANS	1.07	0.3473	1.07	0.57	1.71	1.14	1.31	0.4274	1.39	0.59	1.91	1.32	0.1620
B point	1.57	1.2072	1.31	0.28	4.73	4.44	1.12	0.4558	1.11	0.62	1.77	1.16	0.4723
Condylion	0.98	0.2973	0.96	0.60	1.64	1.04	0.87	0.4691	0.80	0.17	1.71	1.54	0.3447
Gonion	5.67	3.2599	5.54	0.55	11.48	10.94	5.90	2.5034	4.79	2.56	9.90	7.34	0.9698
Sella	0.91	0.6333	0.64	0.30	2.28	1.98	0.76	0.2662	0.78	0.30	1.12	0.82	0.7337
Sigmoid notch	0.77	0.4186	0.80	0.22	1.61	1.39	0.81	0.3583	0.79	0.22	1.41	1.18	0.7913
Lower molar	1.14	0.4174	1.15	0.57	2.04	1.47	0.81	0.2695	0.77	0.42	1.14	0.72	0.0640
Md1 Root	1.21	0.7345	0.87	0.36	2.27	1.91	1.48	0.7425	1.58	0.50	2.85	2.35	0.5205
Md1 tip	0.77	0.2905	0.80	0.36	1.16	0.80	1.57	1.7454	0.88	0.47	4.93	4.46	0.6232
Me	1.09	0.7998	0.92	0.20	2.91	2.71	0.79	0.4811	0.80	0.17	1.53	1.35	0.5205
Mx1 Root	1.06	0.4346	0.94	0.59	1.94	1.35	1.15	0.4014	1.15	0.41	1.85	1.43	0.5205
Mx1 tip	0.73	0.3170	0.67	0.14	1.24	1.10	0.88	0.4717	0.69	0.22	1.67	1.44	0.6232
Nasion	2.91	1.9704	2.13	0.90	6.76	5.86	1.14	1.1828	0.85	0.22	4.27	4.04	0.0073
Orbitale	1.86	1.3491	1.42	0.73	5.47	4.74	0.94	0.5225	0.80	0.37	2.22	1.84	0.0073
PNS	1.19	0.6863	1.01	0.30	2.26	1.96	1.21	0.6705	0.97	0.32	2.28	1.97	0.9698
Pog	2.10	2.0765	0.99	0.30	6.05	5.75	1.40	1.1435	1.13	0.30	4.22	3.92	0.6776
Upper molar	0.86	0.2824	0.79	0.52	1.32	0.80	0.83	0.3922	0.90	0.00	1.45	1.45	0.8501

^aSee Table 1 for definitions of the landmarks.

^bSignificance probability associated with the Wilcoxon rank-sum test to determine whether the distributions of the Euclidean distance between dual measures were equal. Highlighting in bold indicates the significance value of <0.05.

Galileos is manufactured by Sirona Dental Systems Inc., Bensheim, Germany, and Next Generation i-CAT by Imaging Sciences International, Hatfield, PA.

Interobserver Euclidean distance linear mixed models

An LMM was used to model the Euclidean distances for each landmark separately for the first and second measures with a fixed machine effect and a random subject within machine effect, separately considering the first and second measures. Again, the results of the LMM validated all significant machine differences in the Euclidean distance measures detected with the Wilcoxon rank-sum test. For the first measures, the models for Sella (p = 0.0122) and Mx1 root (p = 0.0062) had significant machine effects. For the second ratings, there was a significant machine effect in the models for Nasion (p = 0.0064) and Orbitale (p = 0.0129).

Thus, overall, the landmarks Gonion, Nasion, Orbitale and ANS showed the greatest median Euclidean distances for both intra- and interobserver measurements. There were significant machine differences in both intra- and interobserver measurements for the landmark Sella.

The unified model is described in Table 7.

Table 7.

Results of the linear mixed model predicting the Euclidean distance between dual landmarks with fixed machine and observer, and random subject within machine, effects

Landmarka	Machine effect (Type-III tests of fixed effects)			Observer effect			Covariance parameter estimates		Shapiro–Wilk p-valuec	Data transformation
	F	p-valueb	Degrees of freedom	F	p-value	Degrees of freedom	Intercept and subject	Residual
A	0.35	0.5602	18	3.17	0.0911	19	0.0000	0.1170	0.9807	Square root
ANS	0.36	0.5547	18	3.30	0.0850	19	0.0000	0.3361	0.6003	Natural log
B point	0.05	0.8341	18	0.19	0.6657	19	0.0614	0.1214	0.3513	Square root
Condylion	1.29	0.2718	18	0.07	0.7948	19	0.0279	0.2261	0.2694	Natural log
Gonion	0.04	0.8476	18	1.23	0.2812	19	0.0000	0.3191	0.0324	Square root
Sella	19.72	0.0003	18	39.24	<0.0001	19	0.0068	0.1319	0.1076	Natural log
Sigmoid notch	2.22	0.1537	18	4.22	0.0539	19	0.0000	0.0907	0.5152
Lower molar	0.15	0.6998	18	5.12	0.0355	19	0.0000	0.4252	0.0006	Natural log
Md1 root	0.76	0.3942	18	9.91	0.0053	19	0.0000	0.1196	0.0043	Square root
Md1 tip	3.87	0.0649	18	7.57	0.0127	19	0.0163	0.4233	0.0046	Natural log
Me	2.03	0.1718	18	23.01	0.0001	19	0.0393	0.0660	0.7453	Square root
Mx1 root	0.13	0.7272	18	21.08	0.0002	19	0.0510	0.1105	0.6495
Mx1 tip	0.00	1.0000	18	6.67	0.0183	19	0.0000	0.0893	0.2746
Nasion	0.19	0.6674	18	1.10	0.3080	19	0.1852	0.4615	0.0795	Natural log
Orbitale	2.78	0.1125	18	0.08	0.7804	19	0.0625	0.1061	0.0614	Square root
PNS	0.30	0.5920	18	3.53	0.0758	19	0.0520	0.1704	0.0845	Square root
Pog	0.71	0.4090	18	0.97	0.3382	19	1.1316	0.9534	0.0735
Upper molar	5.83	0.0266	18	11.88	0.0027	19	0.0231	0.0791	0.0835

^aSee Table 1 for definitions of the landmarks.

^bSignificance probability associated with the F-test of significance of the machine effect in the mixed model. Highlighting in bold indicates the significance value of <0.05.

^cSignificance probability associated with the Shapiro–Wilk test of normality of model residuals following data transformation if required.

Further modelling used a unified approach to assess machine effects after adjusting for the effect of observer. There were significant machine effects for Sella (p = 0.0003) and upper molar (p = 0.0266) after adjusting for observer effect. There were also significant observer effects in the models for the following landmarks: Sella (p < 0.0001), Lower molar (p = 0.0355), Md1 root (p = 0.0053), Md1 tip (p = 0.0127), Me (p = 0.0001), Mx1 root (p = 0.0002), Mx1 tip (p = 0.0183) and Upper molar (p = 0.0027).

Table 8 provides a summary of the analyses undertaken to determine whether the reliability of landmarking CBCT images differed by machine.

Table 8.

Summary of the machine differences in observer reliability

Landmarka	Galileos® and Next Generation iCAT® machine differences
	Intraobserver differences				Interobserver differences
	Euclidean		Mixed model		Euclidean		Mixed model
	Observer 1	Observer 2	Observer 1	Observer 2	First measures	Second measures	First measures	Second measures
	A
ANS
B point
Condylion
Gonion
Sella	+ (I)	*(I)	+(I)	*(I)	*(I)		*(I)
Sigmoid notch
Lower molar
Md1 root
Md1 tip	*(G)		*(G)
Me		*(I)		*(I)
Mx1 root					*(G)		+(G)
Mx1 tip
Nasion						+(I)		+(I)
Orbitale						+(I)		*(I)
PNS
Pog
Upper molar	*(I)		*(I)

*, significant at the 0.05 level; +, significant at the 0.01 level. (G) indicates that Galileos machine was more accurate, (I) indicates that i-CAT machine was more accurate.

^aSee Table 1 for the landmark definitions.

Galileos is manufactured by Sirona Dental Systems Inc., Bensheim, Germany, and Next Generation i-CAT by Imaging Sciences International, Hatfield, PA.

Discussion

It is known that in 2D cephalometry, the magnitude of error varies from landmark to landmark and each landmark has its own characteristic and usually non-circular envelope of error.¹⁸ In addition, the reliability of each landmark depends on numerous factors, such as the clarity of the definition used to describe the landmark, the quality of the image, the geometry of the object to be identified (curved vs straight, centre of object vs edge of object) and the image contrast between adjacent objects.¹⁸

The present study compares the Galileos and the i-CAT CBCT machines for observer reliability of 3D cephalometric landmark identification on subjects in the 15–25 years age group. With proper definition of landmarks and adequate examiner training, the localization of landmarks in 3D can become precise and efficient. In this study, the landmarks were defined in a systematic way, guiding the examiner to navigate through the slices and locate the landmark. It was decided that not all the landmarks needed to be visualized on all the planes if it did not add any value in further locating the landmarks on the remaining planes. Fuyamada et al¹⁹ compared the reproducibility of nine landmarks on a single phantom using traditional 2D definitions and proposed definitions using X, Y and Z planes. They concluded that the reliability was higher using the latter method. However, all the landmarks were initially determined on the sagittal plane and it was suggested that it might be better to initially plot them on other planes for higher reproducibility. Intra- and interobserver reliability was not calculated in this study.

The Euclidean distance between the first and second landmark coordinates was calculated between the two points in 3D space. Assessment of reliability via the intraclass correlation coefficient (ICC) was not carried out in this study. The use of retrospective images taken with different machines, with different subsets of subjects evaluated for each machine, rendered required standardization problematic. This implies that ICC methods might have resulted in artificially high evaluations of reliability owing to underestimation of the error in landmark location relative to an inflated level of total variability induced by lack of standardization of positioning. By contrast, the Euclidean distance is not affected by these concerns and may therefore be more clinically relevant.²⁰

Little information was available for power analyses in this pilot effort; certainly no a priori estimates of Euclidean distances were available. The study members were guided in part by their experience with other 3D imaging studies, where ICCs were above 0.8 in most cases, indicating that the sample sizes used in this study were reasonable. In an article by Donner and Eliasziw²¹ on sample size requirements for reliability studies, figure 1 gives a nice representation of the sample size needed and the 0.8 line corresponds to this study. Although the ICC approach was not used in this study, it was felt that these considerations could be used to guide the sample size choice in this initial effort.

Overall, the greatest median Euclidean distances were observed for Gonion for both intra- and interobserver measures (the highest being 5.54). For interobserver measures, the next largest Euclidean distance was observed for Nasion (2.94) followed by Md1 root (2.81). All the other Euclidean distances were smaller than 1.50.

Some of the landmarks viz. Gonion, Orbitale, Condylion, A point, ANS and Pogonion were mentioned as the most variable landmarks in previously reported studies.^12,14,22 These studies used ICC analysis for 3D CBCT cephalometric landmark identification in vivo. In a study by Chien et al,¹⁴ the landmarks that were significantly further from the best estimate in 3D were Gonion, U1 and L1 tip, and Sella in the Y direction and Orbitale and Condylion in the X direction. Ludlow et al²² found greater variation in the craniocaudal (Y) direction for A point and Pogonion and in the anteroposterior (Z) direction for ANS. In a study by de Oliveira et al¹² poor reliability was found for the Z coordinate of Condylion.

Medelnik et al²³ studied accuracy of landmark identification on a cadaver head using four different CBCT machines and one multislice CT (MSCT) scanner. They concluded that these CBCT and MSCT devices are suitable for taking exact 3D measurements of anatomical structures and meet all requirements for 3D cephalometric analysis. They identified 11 landmarks using 3D surface-rendered images as well as the X, Y and Z planes. They, however, used the traditional 2D definitions for landmark identification. This might be the reason for higher standard deviations for certain landmarks, such as Pogonion and Gnathion in the X-axis.

All the dental landmarks used in this study showed significant observer effects when a unified model was used (Table 7). This might suggest that skeletal landmarks are more reproducible than dental landmarks.

It is interesting to note that for Sella, both intra- and interobserver Euclidean distance analyses showed that the distances between the measures were significantly smaller (more closely spaced) on the i-CAT machine than the Galileos. One possible cause for this could be that the FOV of the Galileos machine was smaller than that of the i-CAT machine. Although complete visualization of Sella turcica was one of the inclusion criteria in this study, it was closer to the edge of the volume on the Galileos machine.

Although machine differences were significant for several landmarks examined in this analysis, quality of reproducibility depended on the landmark considered. PNS was the only landmark in which no machine differences were found in any of the analyses.

In the observers' opinions, some of the landmarks, including Gonion, PNS and Condylion, were challenging to locate. These landmarks are variable in different subjects and not easy to define in 3D. They lie on a broad curved anatomical structure and therefore could be more subject to identification errors. The high Euclidean distances observed for Gonion in this study could be explained by this. Many of the popular landmarks used in 2D analysis can no longer be used in 3D because they were created by the superimposition of structures from different planes in the patient. Thus, there is a need to define new landmarks that are applicable and easy to identify in 3D. The landmark Porion was the most imprecise to locate in some of the previous studies and was not included in this study because of the difficulty in defining and identifying it in 3D.^22,24

For Gonion, it would be better to rotate the volume such that the long axis would be parallel to the posterior part of the body and angle of the mandible. Because of the curvature of the angle of the mandible and its variability in different subjects, it is difficult to find a definition for Gonion that suits all the possible variations. It might be better defined using the 3D surface-rendered or maximum intensity projection image instead of multiplanar reconstruction (MPR) slices. In a recent study, the precision of identification of Gonion was found to be reduced when the MPR slices were analysed in addition to the 3D surface-rendered models when compared with the latter alone.²⁴ In the same study, however, locating the landmarks on MPR slices in addition to 3D surface-rendered models improved the tracing precision in 15 of 22 landmarks and was statistically significantly more precise in tracing 6 of 22 landmarks than locating on 3D surface-rendered models alone. In our study, we did not use the 3D surface-rendered models to locate the landmarks. The quality of 3D surface-rendered models from CBCT depends on several factors, including the type of scanner and detector used for FOV selection, segmentation threshold and image artefacts.^25–27 After locating the landmarks on MPR slices as per our definitions, using the surface-rendered models would have increased the total evaluation time without adding to the precision of identification.

In 2D cephalometry, identification errors below 1 mm are considered precise according to several reliability studies as defined by Richardson and others.^28,29 Whether this measure is applicable in 3D cephalometry is questionable, given that in 3D, a third axis is introduced, which may add to the overall error.²⁴ In a recent study comparing reliability in 2D cephalometry with 3D CBCT landmark location, the suggestion was made that up to 2 mm of measurement error could be deemed acceptable given the difficulties in landmark definitions in 3D.¹⁶ Further research is needed to define precision for 3D cephalometry in terms of clinical significance.

A possible limitation of the present study might be that blinding was not possible, i.e. the observers knew from the image characteristics which machine each image was obtained from. However, as the observers located the landmarks using the step-by-step definitions, the possibility of bias was very minimal if it existed at all.

In conclusion, overall, the intra- and interobserver reliability for identification of 3D cephalometric landmarks was excellent for both the machines. This is based on the fact that the median Euclidean distances were less than 1.5 mm for all the landmarks, which is clinically acceptable except for Gonion, Nasion and Md1 root. There were, however, significant observer effects in the unified models for Sella, Me and all the dental landmarks used in this study.

Although machine differences were significant for almost all landmarks for one of the indicators examined in this analysis, which machine produced the highest reliability depended on the landmark considered. The Euclidean distance between two different landmarkings was significantly smaller (closely spaced) on images using the i-CAT machine for Sella, Me, Nasion and Orbitale and the Galileos machine for Md1 tip, upper molar and Mx1 root landmarks. For Sella, both intra- and interobserver Euclidean distance analyses showed that the distances between the measures were significantly smaller on the i-CAT machine than on the Galileos.