Longitudinal Growth Curves of Brain Function Underlying Inhibitory Control through Adolescence

Abstract

Neuroimaging studies suggest that developmental improvements in inhibitory control are primarily supported by changes in prefrontal executive function. However, studies are contradictory with respect to how activation in prefrontal regions changes with age, and they have yet to analyze longitudinal data using growth curve modeling, which allows characterization of dynamic processes of developmental change, individual differences in growth trajectories, and variables that predict any interindividual variability in trajectories. In this study, we present growth curves modeled from longitudinal fMRI data collected over 302 visits (across ages 9 to 26 years) from 123 human participants. Brain regions within circuits known to support motor response control, executive control, and error processing (i.e., aspects of inhibitory control) were investigated. Findings revealed distinct developmental trajectories for regions within each circuit and indicated that a hierarchical pattern of maturation of brain activation supports the gradual emergence of adult-like inhibitory control. Mean growth curves of activation in motor response control regions revealed no changes with age, although interindividual variability decreased with development, indicating equifinality with maturity. Activation in certain executive control regions decreased with age until adolescence, and variability was stable across development. Error-processing activation in the dorsal anterior cingulate cortex showed continued increases into adulthood and no significant interindividual variability across development, and was uniquely associated with task performance. These findings provide evidence that continued maturation of error-processing abilities supports the protracted development of inhibitory control over adolescence, while motor response control regions provide early-maturing foundational capacities and suggest that some executive control regions may buttress immature networks as error processing continues to mature.

Introduction

Inhibitory control, the ability to voluntarily suppress task-irrelevant, prepotent responses in favor of goal-directed responses, continues to mature through adolescence, concurrent with changes in brain function (Luna et al., 2010). Three circuits, sets of interconnected regions that facilitate a common functional goal, are known to support inhibitory control. The motor response control circuit prepares and guides an appropriately timed, goal-directed response, and includes the supplementary motor area (SMA) and pre-SMA, posterior parietal cortex (pPC), and putamen (Everling et al., 1999; Rubia et al., 2003). The executive control circuit coordinates and plans adaptive, goal-directed behavior, and includes the dorsolateral prefrontal cortex (dlPFC) and ventrolateral prefrontal cortex (vlPFC; Aron et al., 2004). The error-processing circuit, guided primarily by the dorsal anterior cingulate (dACC), monitors performance and, upon detection of errors, signals the executive control circuit to adjust activation, leading to improved performance (Carter et al., 1998; Ridderinkhof et al., 2004; Kerns, 2006).

Neuroimaging studies examining developmental changes in inhibitory control have predominantly highlighted changes within the executive control circuit, reporting both increases (Bunge et al., 2002; Rubia et al., 2006, 2007) and decreases (Durston et al., 2002; Durston and Casey, 2006; Velanova et al., 2008) in activation from childhood to adulthood. Whole-brain studies suggest that brain function in motor response control regions may be mature by childhood, while brain function associated with error processing may continue to mature throughout adolescence (Rubia et al., 2007; Velanova et al., 2008). Though most prior studies have been cross-sectional, longitudinal studies have increased power to detect age-related change (Singer and Willett, 2003; Durston and Casey, 2006). Further, large longitudinal studies with multiple time points per person can extend our understanding of development by producing growth curves that characterize the shape and rate of development, and also individual differences in trajectories. This type of research can indicate how change occurs and can identify sensitive periods of accelerated growth, which can reveal relative timing of maturation across regions. Examining interindividual variability can reveal whether individual trajectories diverge, converge, or maintain rank-order stability.

Using data from a large, multi-time point longitudinal fMRI study of inhibitory control in youth, we applied hierarchical linear modeling (HLM) to characterize the shape and slope of growth curves of brain function in motor response control, executive control, and error-processing regions; interindividual variability in growth curves; and the contribution of sex and IQ to variability. Inhibitory control was assessed using an oculomotor paradigm with well delineated neural correlates (Munoz and Everling, 2004). Based on cross-sectional studies that also account for developmental change in performance (Rubia et al., 2007; Velanova et al., 2008, 2009), we hypothesized nonlinear growth across all regions and a later maturation of executive control and error-processing function relative to motor control function (Luna et al., 2010). Given evidence for interindividual variability in growth curves of structural brain maturation that are partially accounted for by sex and IQ (Shaw et al., 2006; Lenroot et al., 2007), we predicted that interindividual variability would also be evident in growth curves of brain function supporting inhibitory control, and this would be partially explained by sex and IQ.

Materials and Methods

Participants.

Volunteers were native English speakers screened by phone to ensure no neurological, psychiatric, or eye movement problems, a negative history of medications known to affect brain function or eye movements, and no first degree relatives with schizophrenia or bipolar disorder. In addition, volunteers were screened for non-removable metal on the body, claustrophobia, and weight >300 pounds to ensure scanner eligibility. The study complied with Institutional Review Board guidelines, and participants were compensated for their participation.

An accelerated cohort longitudinal study design, whereby a wide age span of individuals is followed over time, was used to enable growth to be characterized over an extended age range with minimal cohort effects. Cross-sectional data from the first time point have previously been published (Velanova et al., 2008, 2009; Hwang et al., 2010). Visits occurred at ∼12 month intervals, and participants contributed between one and six time points (Table 1); this study design including single visits is effective for characterizing longitudinal trajectories using the statistical analyses described below (Bryk and Raudenbush, 2002). A total of 139 participants (75 females) completed a total of 356 visits (177 females). Over the course of the study, 24 individuals (14 females) did not return for follow-up due to (in order of frequency) obtaining braces, difficulty rescheduling or contacting, loss of interest, and change of residence.

Table 1.

Number of individuals per frequency of study visit after accounting for excluded visits, but before excluding participants outside the age range of 9 to 26 years, entailing a total of 312 visits (163 female visits)

Visits	Individuals (no. of females)
1	47 (28)
2	23 (10)
3	30 (14)
4	17 (8)
5	11 (7)
6	1 (1)
Total	129 (68)

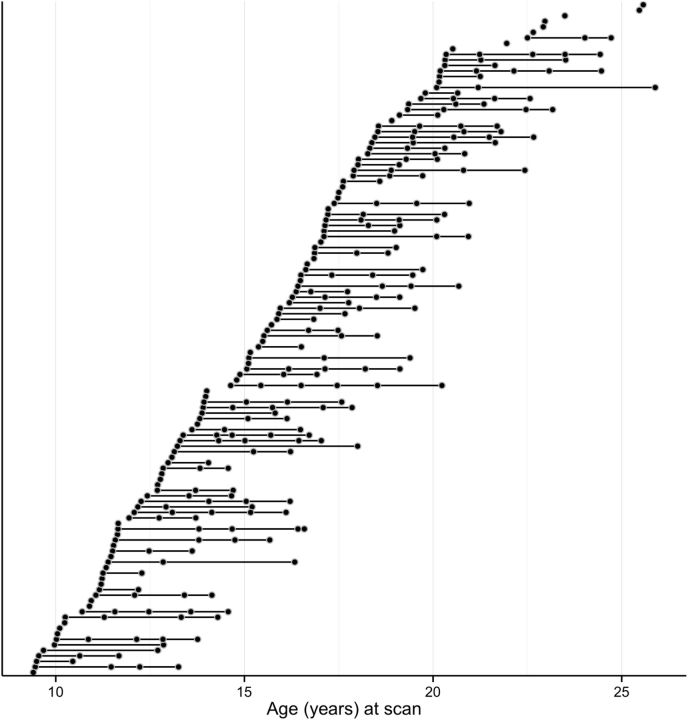
A total of 21 visits (8 females) were not included in subsequent data analyses due to technical errors (n = 11), participant sleepiness (n = 4), participant requests to stop the scan (n = 5), or the discovery of a brain abnormality (n = 1). Following preprocessing, additional visits were excluded due to lack of integrity in structural MRI images (n = 4), lack of at least three runs inclusive of both usable functional and eye movement data (n = 3), poor quality of eye tracking (n = 1), and scanner inhomogeneities (n = 1). Twenty visits (9 females) were excluded due to movement (described below). Thus, a total of 312 visits from 129 individuals spanning ages 8.1 to 28.9 years were included in initial statistical analyses. Final statistical models were limited to visits from participants between the ages 9.0 and 26.0 years (mean, 16.65 years; SD, 3.69 years) to ensure that estimates were based on an equal distribution of data across the age range, resulting in analyses of 302 visits from 123 individuals (64 females). The age distribution of scans included in the final analyses is depicted in Figure 1. The racial distribution of participants represented the demographics of the Pittsburgh region (80% white, 10% black, 5% biracial, 2% Latino, 2% Asian and/or Native American/Pacific Islander, 2% not reported).

Figure 1.

Age distribution of the data reveals consistent sampling throughout the age range represented in final statistical models. Each black circle denotes a scan acquisition that was included in the final analyses, and multiple scans for a single participant are denoted by a line interconnecting multiple black circles. For each participant, the leftmost circle denotes the age at the first scan.

IQ scores.

The four-subtest Wechsler Abbreviated Scale of Intelligence was used to estimate Full-Scale IQ at first visit. Full-Scale IQ scores are conceptualized to be stable with age but were administered at years 1, 3, and 5. Participants varied in the number of test administrations, so the score obtained at the first testing was selected for use a priori to ensure comparability of the construct being measured. Mean IQ was 110.68 (SD, 11.10; range, 85–134) and did not differ between the sexes (t₍₁₂₁₎ = 1.326, p = 0.187).

Neuroimaging data acquisition.

Data were acquired using a Siemens 3 tesla MAGNETOM Allegra fitted with a standard circularity-polarized head coil. Head movement was minimized through prior acclimation in an MR simulator and use of pillows during scanning to immobilize the head. Earplugs dampened scanner noise. A PC (Dell Dimension 8200, Pentium 4, 2 GHz, Windows XP) running E-Prime (Psychology Software Tools) controlled stimulus display. Stimuli were projected onto a screen at the head of the scanner bore viewable via a mirror attached to the head coil. Structural images were acquired using a sagittal magnetization-prepared rapid gradient-echo T1-weighted sequence (TR, 1570 ms; echo time [TE] = 3.04 ms; flip angle, 8°; inversion time [TI] = 800 ms, voxel size = 0.78125 × 0.78125 × 1 mm) and used for alignment of functional images. Functional images were acquired using an echoplanar sequence sensitive to blood oxygen level-dependent contrast [T2*] (TR, 1500 ms; TE, 25 ms; flip angle, 70°; voxel size, 3.125 × 3.125 mm in-plane resolution), with 29 contiguous 4-mm-thick axial images acquired parallel to the anterior–posterior commissure plane during each TR. Participants performed four functional runs (each, 6 min 15 s), followed by three runs of an unrelated experiment. The first six images in each run were discarded to allow stabilization of longitudinal magnetization.

Antisaccade paradigm.

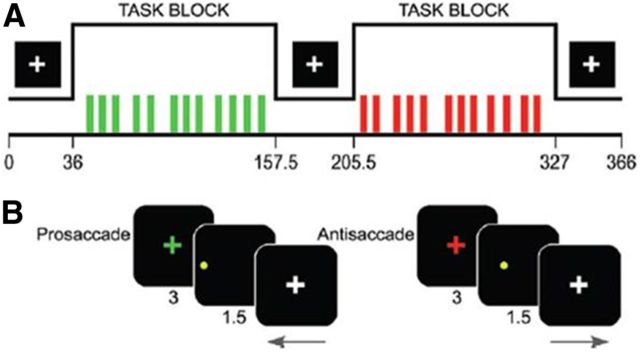
Full details of the experimental paradigm (Fig. 2) are described by Velanova et al. (2008). Each run consisted of three blocked periods of fixation interspersed by a block of the antisaccade (AS) task and a block of the visually guided saccade (VGS) task. The VGS task is a reflexive task that served to enhance the inhibitory demands during AS trials. As described further in the fMRI data analyses section, the fixation trials rather than VGS trials were used as a baseline comparison to maximize data reliability and also to explore any potential findings in motor response control regions, which are present to some degree in both tasks. Task order was counterbalanced across runs and participants. Twelve AS or VGS trials were presented in each task block, for a total of 48 of each trial type. Intertrial intervals (3–9 s) were “jittered” to permit estimation of trial-related activation (Dale, 1999). Each trial began as participants fixated on a colored cross-hair for 3 s instructing them to make a VGS (green) or an AS (red). Next, the saccade target stimulus, a yellow circle, appeared at one of six horizontal eccentricities for 1.5 s. For AS trials, participants were instructed to inhibit the reflexive saccade toward the target and to look instead to its horizontal mirror location. Target location order was randomized within each task block. No “gap” was interposed between the instruction cue and saccade target stimulus to increase the probability of accurate performance in younger participants (Fischer et al., 1997).

Figure 2.

A, B, Depiction of experimental run structures (A) and task trial structures (B). From Velanova et al. (2008), used with permission.

Eye movement measurements were obtained during scanning using a long-range optics eye-tracking system (Model R-LRO6, Applied Science Laboratories) with a sampling rate of 60 Hz. Nine-point calibrations were performed at the beginning of the session and between runs as necessary. Real-time monitoring also permitted immediate identification of head movement or gross inattention to the task, and experimenters redirected subjects immediately following the run.

Eye-tracking data.

Eye-movement data were analyzed and scored off-line by trained raters using ILAB (Gitelman et al., 1999) in conjunction with an in-house scoring suite written in MATLAB (MathWorks). Saccades were identified using a velocity algorithm using a 20°/s criterion, and were presented graphically and numerically so that each could be inspected for measurements and blink artifacts could be identified. Each eye movement trial was scored for performance accuracy (correct, corrected error, uncorrected error, or dropped due to blinks or signal loss). Errors were typically followed by a saccade to the correct location, indicating that participants understood the instruction but were unable to inhibit the automatic response toward the cue. Error rates were calculated as the number of corrected error trials divided by the total number of retained (i.e., not dropped) trials.

fMRI data preprocessing.

Neuroimaging data were preprocessed using an in-house script incorporating tools from FSL (Jenkinson et al., 2012) to remove noise and motion artifacts, and to align functional images to structural images (Jenkinson and Smith, 2001; Jenkinson et al., 2002). Functional data were slice time corrected, and motion was corrected within and across runs using a rigid-body rotation and translation algorithm. Functional files from each visit were registered to the 3 mm MNI standardized atlas using a series of affine and nonlinear transforms. Data were then smoothed using a weighted 5 mm full-width at half-maximum Gaussian kernel, a 0.025 Hz high-pass temporal filter was applied, and the voxel time series was normalized and scaled to have a mean intensity of 100 so that regression coefficients could be interpreted as the percentage signal change. Structural and functional data were visually inspected to ensure data integrity, including ghosting and magnetic field inhomogeneities.

Movement analyses.

Measures of head movement during functional sequences were obtained using a rigid-body rotation and translation algorithm. Translations and rotations in the x, y, and z dimensions were averaged across frames, and total root mean square (RMS) linear and angular precision measures were calculated for each run. Runs in which total RMS movement exceeded 1 mm (translations) or 1° (rotations) were excluded from further analysis. Excluded visits encompassed individuals ranging in age from 8.5 to 18.4 years (mean, 13.2 years; SD, 2.9 years; conducted before limiting the sample to 9 to 26 year olds). The mean age for excluded visits did not differ by sex (t₍₁₈₎ = −0.98, p = 0.923).

HLM regressions appropriate for longitudinal data (see description in Statistical analyses) were run to examine whether age was associated with the amount of average RMS motion. Average RMS translational and rotational movement was analyzed for the average of all runs included within visits included in the final analyses (i.e., limited to 9 to 26 year olds). Using the best-fitting model, the inverse age model, revealed developmental declines in both average RMS translational motion (β₁₀ = 2.4431, t₍₁₂₂₎ = 3.496, p = 0.001) and average RMS rotational motion (β₁₀ = 2.3379, t₍₁₂₂₎ = 4.561, p = 0.000), as is consistent with the developmental literature. There were sex differences in translational motion (β₁₀ = 0.0665, t₍₁₂₁₎ = 3.483, p = 0.001), with males demonstrating more motion, but sex did not moderate age-related change (β₁₁ = −0.2015, t₍₁₂₁₎ = −0.143, p = 0.887). In contrast, there were no main effects of sex in rotational motion (β₁₀ = 0.0173, t₍₁₂₁₎ = 1.149, p = 0.253), but sex did moderate age-related change, with males revealing steeper rates of change (β₁₁ = −1.949, t₍₁₂₁₎ = −1.985, p = 0.049). It is, however, important to consider that we later covaried for these motion regressors. These analyses also overestimate motion, as they still include motion from TR values that were subsequently censored when estimating the hemodynamic response for each visit (see below).

fMRI data analyses.

Our goal was to maximize data reliability while also examining theoretically meaningful and valid metrics of inhibitory control. Reliability, specifically test–retest reliability of a given individual's data, is essential for minimizing developmental confounds when estimating growth curves, and particularly when testing interindividual variability in growth. On the basis of prior research that was specifically designed to examine test–retest reliability of fMRI data by testing subjects across short time intervals (Bennett and Miller, 2010), we selected the following data analytic approach. First, we analyzed regions of interest (ROIs) rather than estimating growth curves on a voxelwise basis, though the latter were also estimated to evaluate regions that may merit further analyses. Second, we used a fixation baseline comparison rather than a VGS (control task) baseline, because the AS versus fixation contrast has been empirically demonstrated in an independent sample to have a higher test–retest reliability than the AS versus VGS comparison (Raemaekers et al., 2007). Another study designed to examine test–retest reliability similarly reported higher reliabilities when using a fixation baseline versus a task baseline (Sheu et al., 2012). After following the analytic procedures described below, we confirmed the reliability of data in our sample to the extent possible, as outlined in Reliability of fMRI data section.

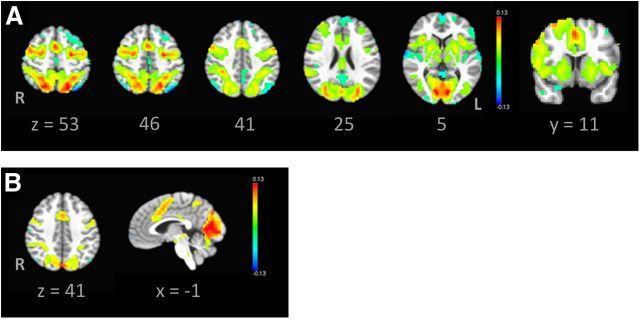
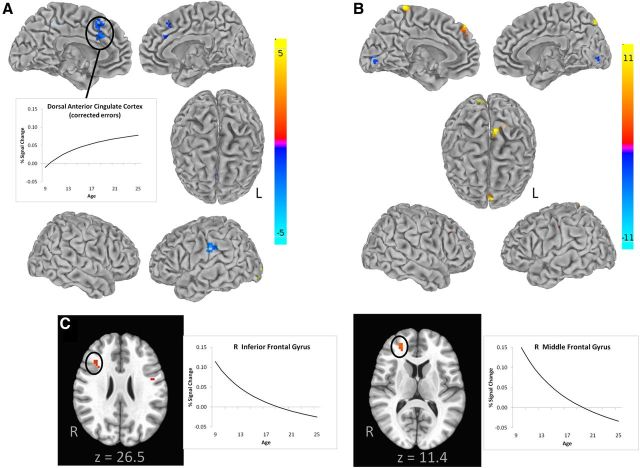
For each voxel, a general linear model that estimates the average hemodynamic response was generated using Analysis of Functional Neuro-Images (AFNI; Cox, 1996). Correct, corrected error, and uncorrected error/dropped trials were modeled using the SPM gamma function, with baseline signal drift plus six motion parameters entered as covariates. In addition, spikes in motion were addressed by censoring TR values with significant motion (if a derivative value of a TR had a Euclidean norm above 0.9) while estimating the hemodynamic response. These steps to address motion were informed by evidence that addressing both can minimize confounds in developmental functional neuroimaging results (Fair et al., 2012; Power et al., 2012; Van Dijk et al., 2012; Satterthwaite et al., 2013). Hemodynamic responses during correct trials were estimated (separately) and were contrasted with responses during the fixation baseline. Given the role of dACC in error processing, activation in dACC was also examined through the comparison of corrected error trials versus baseline. The voxelwise main effect of time maps from this sample are depicted in Figure 3 and indicate robust activation in ROIs selected a priori because of their known association with AS performance.

Figure 3.

Main effect of time maps from all participants in this sample, shown in radiological view and thresholded at p < 0.001, indicate robust activation in regions known to be associated with AS performance. To avoid overestimating activation, only one randomly selected visit per participant is depicted. A, Axial images of the AS correct with a fixation baseline comparison indicate engagement of motor response control and the executive control system, with an additional coronal image highlighting right dlPFC activation. B, Axial and mid-sagittal images of AS-corrected errors with a fixation baseline comparison corroborate expected activation in the dorsal anterior cingulate cortex. R, Right.

Our analyses focused on a priori ROIs associated with inhibitory control but generally not specific to the AS task, including regions associated with motor response control [supplementary eye field (SEF), pre-SMA, and bilateral pPC, putamen, and frontal eye field (FEF)], executive control (bilateral dlPFC and vlPFC), and error monitoring (dACC; Munoz and Everling, 2004; Kenner et al., 2010; Swick et al., 2011). These are inclusive of regions activated in children and adolescents completing the AS task as revealed by using prior fMRI studies using voxelwise analyses (Luna et al., 2008; Geier et al., 2010; Padmanabhan et al., 2011); this includes a study from a cross-sectional subsample of this sample data (Velanova et al., 2008). To generate unbiased ROIs based on the large extant literature, central coordinates were identified using the Neurosynth platform and database (www.Neurosynth.org, accessed March, 2012), a meta-analytic program that generates voxelwise statistical maps for a given term or topic (Yarkoni et al., 2011). Terms and topics were selected based on their having been implicated in inhibitory control. As topic maps are factor maps that summarize results from a larger set of studies associated with a related set of terms, topic maps were used when possible. We examined the list of studies that were included in the Neurosynth meta-analysis for potential topics/terms to ensure that they included multiple studies with child and/or adolescent participants. Reverse, rather than forward, inference maps were used because these depict the probability of each topic/term given activation observed at each voxel (assuming 50% probabilities of “term” and “no term”), and these provide a statistical measure of the specificity of activation to each topic/term at each coordinate across the hundreds of studies in the Neurosynth database associated with each topic/term. Small corrections to central coordinates were made using anatomical references to ensure that final spheres overlapped with canonical eye movement regions reliably elicited by the AS task (Munoz and Everling, 2004). ROIs were defined as voxels within a given radius of each identified peak; a 10 mm radius was used for most ROIs, but exceptions were made to avoid overlap (SEF, SMA) and to accommodate differing anatomical sizes (putamen, dlPFC). Table 2 summarizes the central coordinates and size of each ROI, which are also depicted visually as part of Figure 5. Beta values reflecting response magnitudes for all voxels within each ROI were averaged to produce a mean percentage signal change metric for each ROI per visit.

Table 2.

Mean coordinates and cluster sizes for all ROIs

	Center voxel coordinates			Radius (mm)	Voxels (no.)
	x	y	z
SEF	0.0	−4.6	62.0	7	37
Pre-SMA	0.0	5.0	52.1	7	37
FEF
Left	−25.5	−1.5	56.0	10	107
Right	26.5	−1.5	58.0	10	107
Putamen
Left	−26.0	4.0	6.0	7	37
Right	26.0	2.0	4.0	7	37
pPC
Left	−32.0	−48.0	50.0	10	107
Right	32.0	−54.0	48.0	10	107
dlPFC
Left	−41.0	19.0	41.0	12	185
Right	42.0	18.0	42.0	12	183
vlPFC
Left	−46.5	10.5	24.0	10	107
Right	49.5	12.0	22.0	10	107
dACC	0.0	19.5	40.5	10	107

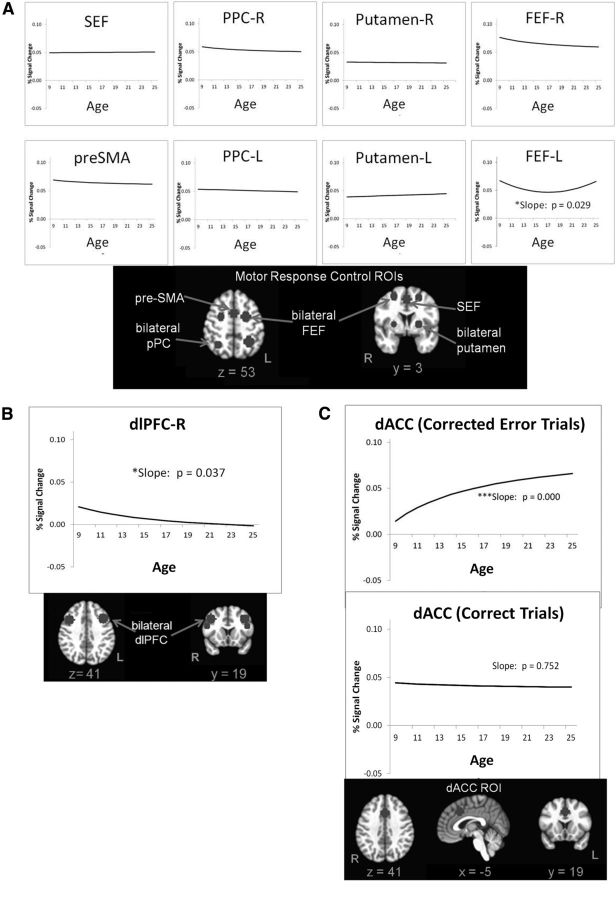
Figure 5.

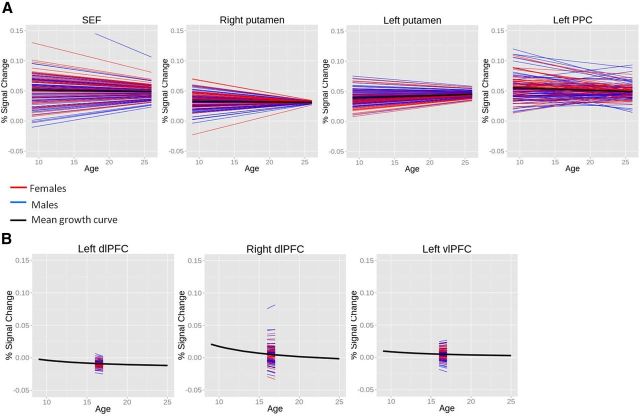
A, Mean growth curves for motor response control ROIs (shown below graphs in radiological view) consistently indicate no developmental change in activation, with one exception noted. B, Mean growth curves for executive control regions indicate that only the right dlPFC demonstrates developmental changes in activation, as illustrated below. C, Mean growth curve for error processing (dACC during corrected error trials) indicates increases in the percentage of signal change with age. This effect is specific to error-related activation, as indicated by a lack of significant age-related change in the dACC during correct trials.

The voxelwise main effect of time maps across all participants for both the correct trials and for corrected error trials were visually inspected to ensure that the task elicited activation in canonical AS task regions (Fig. 3). Indeed, the activation elicited by this task in this sample comported with the a priori selected ROIs from Neurosynth for both activation associated with AS correct (with fixation baseline) and with AS-corrected errors (with fixation baseline). In addition, to confirm that these two main effects of time maps were indeed specific to an inhibitory control process, they were compared with voxelwise maps that used a VGS correct baseline comparison and to the Neurosynth-based ROI maps. A VGS correct baseline for AS-corrected error activation theoretically isolates activation associated with monitoring and correcting the initial, erroneous reflexive VGS. Both of the main effects of time maps using the VGS baseline revealed activation within similar overlapping areas, including the ROIs selected. Together, this affirms the validity of the sample-independent ROI selection we used, while also highlighting the robust nature of the patterns of activation as they persist, regardless of the baseline chosen for contrasts.

Reliability of fMRI data.

The analytic approach, including the use of a fixation baseline and the emphasis on using ROIs, was selected to maximize the reliability of our outcome metrics, as described previously. The following steps were taken to ensure that the outcome metric of the percentage signal change was indeed reliable over time in our sample.

First, test–retest reliability of fMRI measurements across sessions was established by examining change within subjects who provided two scans after the age of 20 years (n = 14), as change over time in this subsample should be most reliable and least related to developmental factors. Correlations between percentage of signal change estimates at the first and second scan were calculated for each ROI for each participant. As these adult participants demonstrated few error trials (see Results), only reliabilities for brain activation during correct trials are reported. Mean test–retest reliabilities for each ROI (Table 3) are in the moderate range, consistent with reliabilities seen in adults during executive control tasks (Bennett and Miller, 2010) and specifically during AS performance (Raemaekers et al., 2007).

Table 3.

Test-retest reliabilities, ICCs, and AIC values from model-fitting for both behavioral and fMRI data included in final analyses

	Test–retest reliability	ICCa	AIC value from unconditional growth modelb			Pseudo-R2, age term in unconditional model
			Inverse age	Linear age	Quadratic age
ROI
SEF	0.475	0.359	−1004.27	−1004.96	−1008.18	0.019
Pre-SMA	0.556	0.382	−1000.41	−998.49	−1000.77	0.072
FEF
Left	0.784	0.383	−1254.19	−1250.68	−1264.20	0.182
Right	0.624	0.273	−1123.06	−1119.10	−1128.13	0.104
Putamen
Left	0.163	0.209	−1214.23	−1214.85	−1217.84	0.000
Right	0.160	0.228	−1258.72	−1258.91	−1260.88	0.039
pPC
Left	0.553	0.406	−1222.03	−1222.46	−1230.78	0.043
Right	0.765	0.355	−1142.69	−1137.84	−1146.84	0.103
dlPFC
Left	0.504	0.169	−1277.61	−1276.11	−1272.42	0.029
Right	0.484	0.428	−1236.27	−1234.63	−1231.18	0.031
vlPFC
Left	0.548	0.170	−1222.83	−1219.95	−1231.04	0.034
Right	0.302	0.291	−1185.97	−1185.16	−1189.69	0.033
dACC
Correct trials	0.693	0.290	−1061.05	−1057.20	−1060.86	0.076
Error trials		0.151	−860.43	−859.24	−860.21	0.070
Behavioral variables
AS percent errors	0.763	0.650	−249.79	−236.37	−245.52	0.202
AS latency (correct)	0.533	0.606	3198.73	3204.29	3201.75	0.140

^aAll ICC values were statistically significant (2 SDs of CIs did not overlap with 0).

^bLower (more negative) AIC values indicate improved model fit. If AIC indicated the quadratic model fit best, this model was only chosen if the quadratic term was also significant. AIC values for selected models are bolded.

Second, to index a sufficient amount of homogeneity of data collected from the same individual over multiple time points, intraclass correlations (ICCs; ρ̂) were calculated via ρ̂ = $\frac{{\widehat{\tau }}_{00}}{{\widehat{\tau }}_{00}+{\widehat{\sigma }}^2}$, the proportion of intersubject variability to total variability using restricted maximum likelihood (REML) estimates. ICCs for each ROI are reported in Table 3 and are all >0.10, suggesting proper within-subject dependency, or nesting of observations within individuals, needed for subsequent HLM analyses (Lee, 2000). These values are consistent with reliability measurements for other fMRI studies including youth and adults (Koolschijn et al., 2011). Additionally, the significance of the ICC value was statistically tested using a Wald test, H₀ : ρ̂ = 0. Results indicated significant clustering effects, validating the need to use hierarchical linear modeling to model dependency within individuals. In all ROIs for correct trial performance, ICCs were significantly different from zero. The ICC estimate for the single region of interest (dACC) for corrected error trials was not different from zero (Z = 1.804, p = 0.071). Visual inspection indicated outliers, and after removing points outside of 3 SDs of the mean percentage signal change (n = 4), the ICC for the dACC was significant (Z = 2.102, p = 0.036). These visits were excluded from subsequent analyses of activation on corrected error trials. As three of the four data points were from individuals with at least three visits, removal of these data points was unlikely to alter findings of individual variability.

Due to developmental changes in the total number of correct (β₁₀ = 1.363, t₍₁₂₂₎ = 7.080, p = 0.000) and corrected error trials (β₁₀ = −1.070, t₍₁₂₂₎ = −7.759, p = 0.000), the reliability of signal estimates from single-subject general linear models changed over development. To address this concern, a weighted average β estimate was calculated for each ROI that incorporated the SEs of each voxel estimate as a weight. However, this minimally changed ICCs (mean, 0.244, SD, 0.086; range, 0.112–0.335), so HLM analyses proceeded with unweighted average betas.

Third, unequal sampling across the age range can produce variable data reliability across development, so we visually inspected the data to determine (1) whether spline models were superior to combining all individuals into a single model and (2) whether limiting the age range could minimize unequal sampling across the age range. Spline models were not superior, but the age range was limited to 9.0 to 26.0 years.

Statistical analyses.

Growth curve modeling extends multiple regression for use with repeated-measures data and involves statistical model-building procedures to (1) model general patterns of developmental change, (2) test for significant individual differences in intercepts and slopes of individual growth models, and (3) test predictors of the intercept and the slope that may explain individual differences (Singer and Willett, 2003). Growth curve modeling was accomplished in the present study using HLM analyses (also termed “random effects,” “mixed effects,” or “multilevel modeling”). HLM utilizes multilevel fixed and random-effects analyses to account for the nesting of data within individuals. Further, HLM uniquely permits flexible modeling of time, so that data collected at uneven intervals and from individuals with varying numbers of time points can be included in the model (Bryk and Raudenbush, 2002; Raudenbush and Bryk, 2002). HLM models provide estimates of both (1) a grand-mean trajectory that captures the mean developmental pathway of the full sample, and (2) an individual trajectory for each individual that enables one to test individual differences in intercepts and slopes of trajectories and predictors of such variability, should it exist. HLM requires model estimation and model-building procedures to be used to remove most nonsignificant terms in the model, according to convention. Models were estimated using the eponymous program HLM version 6 (Scientific Software International).

Consistent with the latest developmental research methodology (Kail and Ferrer, 2007), the following model-building procedure was followed for each outcome variable (i.e., AS-corrected error rates, AS latencies, and percentage signal change for each ROI). First, linear, quadratic, and inverse unconditional growth curves were modeled. The optimally fitting model was selected as the unconditional growth model on the basis of the Akaike Information Criterion (AIC) fit index. AIC is a standardized model-fit metric that permits comparison of models that are not nested (i.e., linear and inverse age models have an equivalent number of parameters, so they are not nested) and offers standardized comparison of models with differing numbers of parameters (i.e., linear and quadratic age models). More negative AIC values reflect a better model fit to the data. To ensure validity of the AIC-informed selection of model shape, note that the final model (age, inverse age, or quadratic age) was only selected if the relevant age term was also statistically significant. Thus, if AIC values indicated that the quadratic model was best fitting, this model was only selected if the quadratic term was also significant.

The unconditional growth model is a base from which to begin model-building procedures. In all cases, the age term was centered to facilitate meaningful interpretation of the intercept as the estimated value of the dependent variable at the mean age of the sample (16.7 years). An unconditional model using the inverse of age (centered) to predict AS-corrected error rates would be denoted as follows for Level 1:

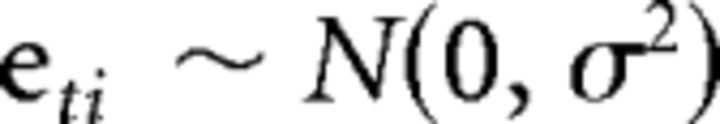and for Level 2:

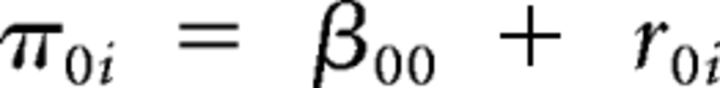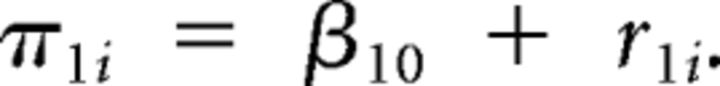In such a model, β₀₀ reflects the grand mean AS-corrected error rate at the mean age of the sample, and β₁₀ reflects the grand mean slope of the trajectory. The random-effect term for the intercept and slope are r_0i and r_1i, respectively, with a unique estimate of both terms generated for each individual. Significant variability in the r_0i term (τ₀₀) indicates individual differences in AS-corrected error rates at the mean age of the sample, and significant r_1i variability (τ₁₁) indicates individual differences in slopes of AS-corrected error rates.

Second, model-building procedures were used to determine whether the random terms were indeed significant and, if so, whether adding the time-invariant predictors of sex and IQ can explain the individual variability in the intercept and/or slope. The significance of the random terms was determined via χ² tests for improvement in model fit over a model without each random term. If random intercept and/or slope terms were significant, indicating that variability exists, then centered sex and IQ terms were added as Level 2 predictors to determine whether they predicted some or all of the individual variability. Finally, any insignificant terms were removed to produce a final model. Models were fit using (1) full information maximum likelihood estimates for the purposes of calculating deviance, degrees of freedom, and model comparison tests (AIC); and (2) REML estimates for reporting of fixed effect and variance component estimates as well as their significance tests.

Given that this is the initial study to examine growth curves in brain activity and variability of such trajectories, we also sought to minimize false-negative findings. We therefore report results from ROI-based growth curve analyses both before and after correction for multiple comparisons, consistent with published research (Galliano et al., 2013). The inclusion of uncorrected results is consistent with the other known developmental study using growth curve modeling (Shaw et al., 2012) and merited due to: (1) the use of a limited number of hypothesis-driven a priori ROIs informed by a large body of animal and human (adults and youth) research examining brain function supporting AS and inhibitory control, and (2) evidence that multilevel models that yield more reliable estimates (Gelman et al., 2012). However, to explore how robust the mean growth curve findings were, we also used a more conservative approach by correcting for multiple comparisons as per Benjamini and Hochberg (1995). Specifically, this was applied to tests of significance for intercept and slope terms, random intercept and slope terms (i.e., tests of variability), and sex differences where applicable.

Planned post hoc analyses using a dummy-coded variable with females or males coded as the reference group were used to test the significance of intercepts and slopes for trajectories for each sex. In addition, sex differences in outcomes at ages other than the mean age of the sample were tested by running models with age centered at ages 11 and 23 years, and then testing the significance of the sex term coefficient. These ages were chosen because they reflect ages at the relative extremes of the ages sampled, but still had a high number of sample points to ensure reliability of estimates.

Voxelwise HLM analyses.

To ensure that our selection of ROIs did not bias our patterns of findings or obscure findings of age-related change in other regions, we also conducted voxelwise HLM analyses. These were conducted by applying the nlme function in R (R Core Team, 2012) to each voxel and then reconstructing model outputs into a three-dimensional statistical map. As with the ROI analyses, we followed a standard model-fitting procedure for each voxel. First, inverse, linear age, and quadratic unconditional growth models were estimated with the intercept and slopes as random effects. AIC values for each model were compared. A quadratic model was only selected for a given voxel if the coefficient of the quadratic term in the regression model was significant and the AIC value indicated this to be the best-fitting model. Second, significant clusters of voxels were identified only after correcting the map for multiple comparisons using a combination of cluster size and individual voxel probabilities, and parameters determined following a Monte Carlo simulation using the AFNI AlphaSim program. This analysis specified that 14 contiguous voxels along with a single-voxel threshold of p < 0.005 was required to achieve a cluster threshold of α = 0.050.

Results

Trajectories of behavioral performance

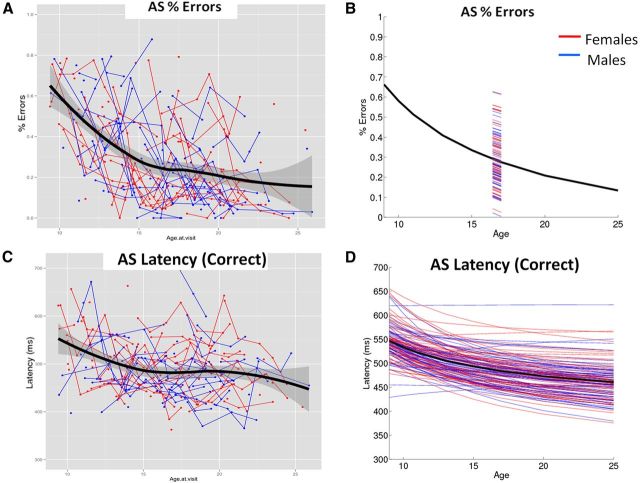
AIC values for the inverse, linear, or quadratic unconditional model are listed in Table 3 and were used to guide which of the three models was selected to characterize the shape of growth. The proportion of variance explained by age in the unconditional model is also listed in Table 3.

Inverse models provided the most optimal fit for growth curves of AS-corrected error rates and AS latencies on correct trials, indicating that improvements in performance decelerated with age but persisted into early adulthood (Fig. 4; Table 4,). For AS-corrected error rates, variability existed in the intercept random-effects term but not the slope random-effects term. As interindividual variability in inhibitory errors was only manifested in intercepts, this reveals a pattern whereby individuals show parallel trajectories over development. Individual variability existed for both the intercept and the slope for AS latency, but no clear pattern of heteroscedasticity emerged—that is, variability did not decline with age to indicate convergence of trajectories, nor did it increase with age to indicate divergence of trajectories. Sex and IQ did not predict any variability.

Figure 4.

A, C, Raw behavioral data with superimposed loess lines corroborate selection of inverse functions to model mean growth curves (right; black). B, Since results indicated significant variance in intercepts but not slopes for AS-corrected error rates, the mean growth curve is plotted along with a portion of each individual's estimated regression line. D, For AS latencies, results indicated significant variability in both intercepts and slopes, so each individual's full estimated regression line is plotted.

Table 4.

HLM model-fitting results for behavioral data

	Final model for AS percentage errors	Final model for AS latency (correct)
Fixed-effects (robust SE)
Model for intercept, π0i
INTRCPT, β00	0.283*** (0.016)	485.237 (4.795)***
SEX,a β01
IQ,a β02
Model for age slope, π1i	Inverse age	Inverse age
INTRCPT, β10	7.437*** (0.752)	1206.411 (271.808)***
SEX,a β11
IQ,a β12
Random-effects (variance components)
Variance in individual means	0.02***	1792.79**
Variance in slopes	1.148+	1765740.456*
Variance within individuals	0.013	1215.272
AIC	−249.792	3198.729

Values for each term included in the final model and their significance are noted below. These include fixed-effect terms (regression coefficients and their standard errors) and random-effect terms (intercept variance and slope variance). Model-fitting procedures are described in Materials and Methods.

***Significant at p < 0.001,

**significant at p < 0.01,

*significant at p < 0.05,

⁺Trend, significant at p < 0.10.

^aPredictor centered so that 0 reflects the grand mean; in the case of sex, a weight was created for each sex so that the sum of sex codes across all participants was 0.

Mean growth curves for brain function

Table 3 lists the AIC values used to guide the selection of unconditional models characterizing the shape of growth and also lists the proportion of variance explained by age in the unconditional model. Model-fitting procedures resulted in a final growth curve model for the percentage signal change for each ROI. Final β values, variances, their significance, and whether significance tests survive correction for multiple comparisons are presented in Tables 5, 6, and 7, and mean growth curves are depicted in Figure 5. The following analyses account for developmental differences in performance because they are limited to brain activation during trials associated with only one type of performance (either correct or corrected errors). Unless otherwise noted, findings described below also survived correction for multiple comparisons.

Table 5.

HLM model-fitting results for each a priori ROI values for each term included in the final model and their significance

	dlPFC		vlPFC		dACC
	Left	Right	Left	Right	Errors	Correct
Fixed effects (robust SE)
Model for intercept, π0i
INTRCPT, β00	−0.0083 (0.0018)***	0.0048 (0.0027)+	0.0048 (0.0024)*	0.0285 (0.0024)***	0.0517 (0.0041)***	0.0411 (0.0032)***
SEX,a β01				0.0030 (0.0048)
IQ,a β02					0.0005 (0.0003)+
Model for age term slope, π1i	Inverse age	Inverse age	Inverse age	Inverse age	Inverse age	Inverse age
INTRCPT, β10	0.0502 (0.1395)	0.3154 (0.1495)*,b	0.0980 (0.1220)	0.1935 (0.1557)	−0.7274 (0.1883)***	0.0644 (0.2036)
SEX,b β11				−0.8186 (0.3113)*
IQ,b β12
Model for age2 slope, π2i
INTRCPT, β20
Random effects (variance components)
Variance in individual means, var(r0) = τ00	0.00008*	0.00044***	0.00023***	0.00027**	0.00059+	0.00050***
Variance in slopes, var(r1) = τ11	0.26576	0.46675	0.22957+	0.13754*	0.44370	1.070*
Variance in Age2 slopes, var(r2) = τ22
Variance within individuals, var(et) = σ−2	0.00068	0.00062	0.00085	0.00090b	0.00251	0.00121
AIC	−1280.426	−1236.269	−1210.828	−1174.973	−848.987	−1056.761

Results include fixed effect terms (regression coefficients and their standard errors) and random effect terms (intercept variance and slope variance). Significance was set as follows:

***Significant at p < 0.001,

**significant at p < 0.01,

*significant at p < 0.05,

⁺Trend, significant at p < 0.10.

^aPredictor centered so that 0 reflects the grand mean; in the case of sex, a weight was created for each sex so that the sum of all codes across all participants was 0.

^bDoes not survive correction for multiple comparisons.

Table 6.

HLM model-fitting results for each a priori ROI values for each term included in the final model and their significance

	SEF	Pre-SMA	FEF
			Left	Right
Fixed effects (robust SE)
Model for intercept, π0i
INTRCPT, β00	0.0501 (0.0034)***	0.0636 (0.0035)***	0.0467 (0.0032)***	0.0642 (0.0027)***
SEX,a β01	−0.0052 (0.0068)	0.0078 (0.0071)		0.0001 (0.0055)
IQ,a β02
Model for age slope, π1i	Age	Inverse age	Age	Inverse age
INTRCPT, β10	0.0001 (0.0008)	0.1034 (0.2456)	−0.0002 (0.0006)	0.2389 (0.1937)
SEX,a β11	0.0043 (0.0015)**	−1.0896 (0.4913)*		−1.011 (0.3875)*
IQ,a β12
Model for age2 slope, π2i
INTRCPT, β20			0.0003 (0.0001)*
Random effects (variance components)
Variance in individual means	0.00074***	0.00064***	0.00055***	0.00030**
Variance in slopes	0.00000*,b	1.57311**	0.00001	0.94294*,b
Variance in Age2 slopes			0.00000
Variance within individuals	0.00152	0.00143	0.00054	0.00103
AIC	−997.671	−991.677	−1244.205	−1116.213

These include fixed-effects terms (regression coefficients and their SEs) and random-effects terms (intercept variance and slope variance). Significance was set as follows:

***Significant at p < 0.001,

**significant at p < 0.01,

*significant at p < 0.05,

⁺Trend, significant at p < 0.10.

^aPredictor centered so that 0 reflects the grand mean; in the case of sex, a weight was created for each sex so that the sum of all codes across all participants was 0.

^bDoes not survive correction for multiple comparisons.

Table 7.

HLM model-fitting results for each a priori ROI values for each term included in the final model and their significance

	Putamen		pPC
	Left	Right	Left	Right
Fixed effects (robust SE)
Model for Intercept, π0i
INTRCPT, β00	0.0417 (0.0022)***	0.0321 (0.0021)***	0.0516 (0.0027)***	0.0533 (0.0031)***
SEX,a β01
IQ,a β02
Model for age slope, π1i	Age	Age	Age	Inverse age
INTRCPT, β10	0.0004 (0.0005)	−0.0001 (0.0005)	−0.0003 (0.0007)	0.1137 (0.1889)
SEX,a β11
IQ,a β12
Model for age2 slope, π2i
INTRCPT, β20
Random effects (variance components)
Variance in individual means	0.00023*	0.00020*	0.00044***	0.00057***
Variance in slopes	0.00000*,b	0.00000+	0.00001**	0.89928***
Variance in Age2 slopes
Variance within individuals	0.00086	0.00074	0.00068	0.00086
AIC	−1202.854	−1246.914	−1210.630	−1133.884

These include fixed-effects terms (regression coefficients and their standard errors) and random-effects terms (intercept variance and slope variance). Significance was set as follows:

***Significant at p < 0.001,

**significant at p < 0.01,

*significant at p < 0.05,

⁺Trend, significant at p < 0.10.

^aPredictor centered so that 0 reflects the grand mean; in the case of sex, a weight was created for each sex so that the sum of all codes across all participants was 0.

^bDoes not survive correction for multiple comparisons.

When examining activation in motor response control ROIs (bilateral putamen, bilateral pPC, bilateral FEF, SEF, pre-SMA) during correct performance, slope terms of mean growth curves (β₁₀) did not show significant age-related change in magnitudes of brain activation, with the exception of the left FEF, which was fit by a quadratic function indicating lowest magnitudes in adolescence. For all ROIs, the intercept at mean age of the sample was significant and positive. Together, these findings indicate that the activation (percentage signal change) was positive, yet unchanged with age in all but one of the eight motor response control regions (Fig. 5A).

Among executive control ROIs during correct performance, the right dlPFC showed a significant positive slope of inverse age, indicating declining activation levels with development. Activation at age 11 years (based on the intercept of a model centered at age 11 years) was greater than zero (β_{00 age11} = 0.015, t₍₁₂₂₎ = 3.346, p = 0.001), only a trend at the mean age of the sample (16.7 years; Tables 5, 6, 7), and was not significant at age 23 years (β_{00 age23} = −0.000, t₍₁₂₂₎ = −0.074, p = 0.942), suggesting that magnitudes of activation in the right dlPFC approached zero by early adulthood. However, the finding of age-related change in the right dlPFC did not survive correction for multiple comparisons. Left dlPFC and bilateral vlPFC activation did not change with age, but a significant intercept term for these all executive control ROIs indicates these regions were activated throughout the course of development, albeit at levels much lower than in the motor response control ROIs.

Brain function associated with error processing (dACC activation during corrected error trials) was best fit by a negatively sloped inverse function, indicating increasing levels of activation with age that are different from zero even at age 11 years (β_{00 age11} = 0.029, t₍₁₁₉₎ = 5.817, p = 0.000). This was specific to corrected error trials, as dACC activation during correct trials revealed no significant developmental change despite positive levels of activation at the mean age of the sample.

Variability in growth curves for brain function

In all motor response control regions except the right pPC, both intercepts and slopes varied with age (Tables 6, 7), though some slopes (as noted in Tables 6, 7) did not survive correction for multiple comparisons. The left and right putamen, left pPC, and SEF showed a pattern of equifinality, whereby trajectories tend to converge over time (Fig. 6A). Statistically, this was evidenced by a decline in variance in intercept values for equations centered at ages 11, 16.7, and 23 years, respectively, in combination with negative correlations between intercept and slope for regions modeled by linear age (left putamen, r = −0.937; right putamen, r = −0.982; left pPC, r = −0.295) and positive correlations for regions modeled by an inverse function (SEF, r = 0.913). Neither IQ nor sex predicted variability in either intercept or slope in the putamen or left pPC, indicating that other, yet to be identified factors contribute to the decline in variability.

Figure 6.

A, Variability declines with age in a subset of motor response control regions, including the SEF, bilateral putamen, and left pPC. B, Parallel trajectories in executive control regions. Dashed lines indicate significant variability in intercepts, but not in slopes, and convey the range of interindividual variability in brain activation at all ages.

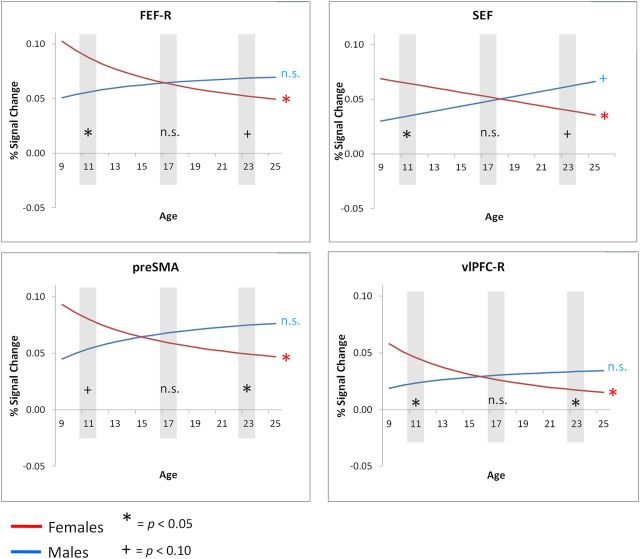
In the right FEF, SEF, and pre-SMA, sex but not IQ predicted slope variability, and neither predicted intercept variability (Tables 6, 7). Figure 7 illustrates that activation in these motor control regions declined in females during childhood to reach male levels in adolescence. Planned follow-up simple-effects analyses were conducted to examine (1) the significance of age-related change in female and male trajectories, and (2) whether differences in activation between the sexes in childhood (age 11 years) and adulthood (age 23 years) were significant. In all of these regions, the same pattern emerged, whereby magnitudes of activation declined with age in females (right FEF: β_{10 FemaleRef} = 0.745, t₍₁₂₁₎ = 3.223, p = 0.002; SEF: β_{10 FemaleRef} = −0.002, t₍₁₂₁₎ = −2.027, p = 0.045; pre-SMA: β_{10 FemaleRef} = 0.648, t₍₁₂₁₎ = 2.114, p = 0.036), but there was no age-related change or only a trend in males (right FEF: β_{10 MaleRef} = −0.267, t₍₁₂₁₎ = −0.858, p = 0.393; SEF: β_{10 MaleRef} = 0.002, t₍₁₂₁₎ = 1.934, p = 0.055; pre-SMA: β_{10 MaleRef} = −0.441, t₍₁₂₁₎ = −1.150, p = 0.253). Second, sex differences were present in childhood (age 11 years) and adulthood (age 23 years). In childhood, females showed higher levels of activation in the SEF (β_{00 age11} = −0.030, t₍₁₂₁₎ = −2.513, p = 0.014) and right FEF (β_{00 age11} = −0.031, t₍₁₂₁₎ = −2.556, p = 0.012), and a trend for higher activation in the pre-SMA (β_{00 age11} = −0.026, t₍₁₂₁₎ = −1.666, p = 0.098). In adulthood (age 23 years), males showed trend levels of higher activation in the SEF (β_{00 age23} = 0.022, t₍₁₂₁₎ = 1.976, p = 0.050) and right FEF (β_{00 age23} = 0.017, t₍₁₂₁₎ = 1.824, p = 0.070), and significantly higher activation in the pre-SMA (β_{00 age23} = 0.026, t₍₁₂₁₎ = 2.207, p = 0.029). Therefore, these results indicate that in these three motor response control regions, female trajectories of activation decline with age, intersecting with stable male trajectories in adolescence. The sex difference switches with development, proceeding from greater female activation at age 11, to no sex differences in adolescence, and less (or a trend for less) female activation by age 23 years.

Figure 7.

Sex effects in trajectories exist predominantly in motor response control regions. Red and blue symbols denote whether there is significant age-related change for each sex. Black symbols indicate the significance of sex differences at ages 11, 16.7, and 23 years, ages selected a priori to reflect different stages of development.

In the executive control regions of the bilateral dlPFC and left vlPFC, models revealed variance at the intercept but not the slope (Table 5), indicating variability across individuals is manifested as parallel trajectories with equivalent slopes (Fig. 6B). The intercept-based variability was not explained by IQ, sex, or trait-like behavioral variability in performance (see Variability in growth curves for brain function section).

In the right vlPFC, significant intercept and slope variability was explained in part by sex differences in trajectories (Table 5). Sex differences in the right vlPFC were consistent with those seen in the other ROIs where trajectories differed by sex. That is, females showed significant age-related declines (β_{10 FemaleRef} = 0.603, t₍₁₂₁₎ = 2.985, p = 0.004), while males did not (β_{10 MaleRef} = −0.216, t₍₁₂₁₎ = −0.911, p = 0.364), and right vlPFC activation was significantly greater in females in childhood (β_{01 age11} = −0.022, t₍₁₂₁₎ = −2.079, p = 0.039), whereas the males showed greater activation in adulthood (β_{01 age23} = 0.016, t₍₁₂₁₎ = 2.256, p = 0.026).

For dACC activation during corrected error trials, there was no significant intercept (trend level) or slope variability (Table 5). This was unique to error processing, as dACC during correct trials evidenced both significant intercept and slope variability.

Except for where noted above, all results for variability in intercept and slope terms survived correction for multiple comparisons.

Associations between brain function and behavioral performance

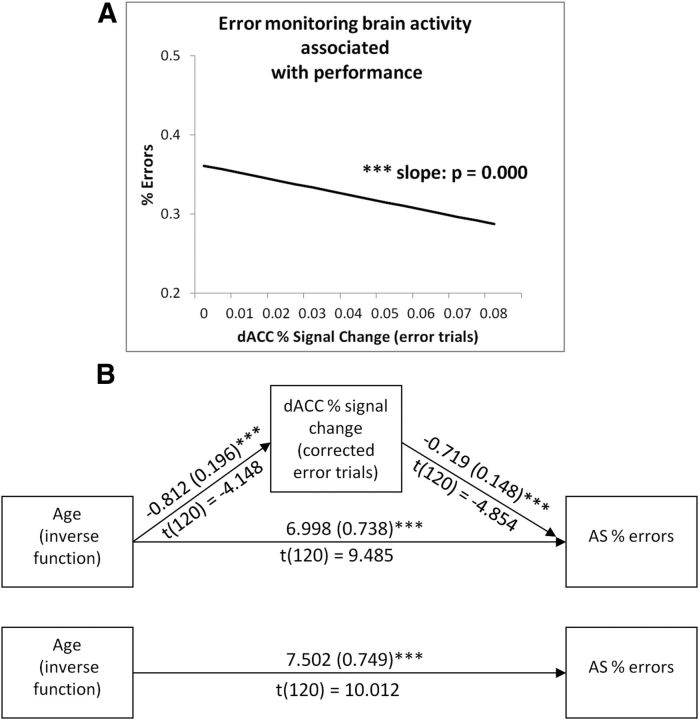
To explore whether brain activation was associated with behavioral performance, AS performance was regressed on magnitudes of brain activation for each region that showed developmental change in brain function: right dlPFC and left FEF during correct trials, and dACC during corrected error trials. After controlling for age (modeled as an inverse function), AS-corrected error rates were not associated with activation in either right dlPFC (β₁₀ = −0.354, t₍₁₂₂₎ = −1.276, p = 0.205) or left FEF (β₁₀ = −0.014, t₍₁₂₂₎ = −0.041, p = 0.967). However, increased dACC activation during corrected error trials was associated with decreased AS-corrected error rates (β₁₀ = −0.674, t₍₁₂₀₎ = −4.735, p = 0.000), after controlling for age (Fig. 8A). A test of mediation using MacKinnon's Product of Coefficients Test (MacKinnon et al., 2002) revealed that the effect of age (modeled as inverse age) on AS-corrected error rates was mediated by dACC activation during corrected error trials (αβ = 0.583, SE_αβ = 0.185, CI = 0.177–0.896; Fig. 8B). AS latencies on correct trials were not associated with activation in any region that showed age-related change in performance (dACC: β = −43.801, t₍₁₂₀₎ = −0.999, p = 0.320; right dlPFC: β = −33.305, t₍₁₂₂₎ = −0.396, p = 0.692; left FEF: β = 35.731, t₍₁₂₂₎ = 0.376, p = 0.707), and therefore mediation was not tested.

Figure 8.

A, Increased activation in the dACC during corrected error trials is associated with better overall task performance, as indicated by lower AS error rates. B, Percentage of signal change in the dACC during corrected error trials mediates the effect of age (modeled as an inverse function) on AS error rates, as indicated by the product of coefficients test (MacKinnon et al., 2002).

Voxelwise HLM analyses

For activation associated with AS correct trials and AS-corrected error trials, the quadratic model was not best fitting for any voxel that also fell within a significant cluster of age-related activation. Model comparison between the inverse age and linear age models revealed the inverse age model to be best fitting for all voxels characterized by significant age-related change. For correct trials, clusters characterized by significant age-related change as modeled by an inverse function are depicted in Figure 9, B and C, and Table 8. For corrected errors, significant age-related change was evident in various regions of the lateral prefrontal cortex, including areas of the right middle and inferior frontal gyrus, and the left superior medial frontal gyrus. Notably, age-related change was not evident within the a priori right dlPFC ROI used in prior analyses.

Figure 9.

Results from voxelwise HLM analyses. All maps are based on the inverse age model, which was the best-fitting regression for all voxels during both correct trials and corrected error trials. A–C, Statistical maps for activation associated with AS-corrected error trials (A) and AS correct trials (B, C) illustrate regression coefficients for the slope term, in voxels that surpassed a thresholded t value and after cluster correction. Axial slices in C serve to highlight areas not readily evident from AS correct trials cortical surface maps. These illustrate activation in the right inferior frontal gyrus (z = 26.5, left image) and right middle frontal gyrus (z = 11.4, right image). In the dACC (A) and selected prefrontal clusters (C), trajectories determined by the average intercept and slope values for a given cluster are displayed.

Table 8.

Voxelwise HLM analyses reveal clusters showing significant age-related change in activation associated with correct or corrected error trials

Area	Voxels (n)	Peak voxels x, y, z (mm; in LPI)	Slope of inverse age at peak	Mean slope of inverse age
Correct trials
L precentral and postcentral gyri	48	−46.5, −16.5, 31.5	0.799	0.615
L lingual gyrus and L visual association area	34	−1.5, −82.5, −1.5	−3.001	−2.359
R inferior frontal gyrus (pars triangularis)	34	40.5, 19.5, 28.5	2.740	1.957
L superior medial gyrus	29	−1.5, 49.5, 49.5	18.453	6.208
L paracentral lobule	29	−4.5, −40.5, 76.5	14.365	8.713
R middle frontal gyrus	20	28.5, 37.5, 16.5	3.600	2.972
Bilateral precuneus	15	−1.5, −76.5, 52.5	26.919	20.111
Corrected error trials
L dorsal anterior cingulate cortex	75	−1.5, 25.5, 31.5	−2.301	−1.238
L postcentral gyrus	39	−70.5, −22.5, 22.5	−3.872	−1.984
L precuneus	23	−13.5, −37.5, 46.5	−3.680	−2.787
L lingual gyrus	22	−34.5, −91.5, 13.5	11.308	6.100

L, Left; R, right.

Few voxels, let alone clusters of voxels, revealed significant age-related change in activation associated with corrected error AS trials (Fig. 9A; Table 8). The largest cluster was the dACC (cluster size = 75), and 48% of this cluster fit within the a priori dACC ROI used in the prior analyses. A negative slope fit by an inverse function indicated that activation increased at a declining rate with age.

Discussion

The ability to voluntarily suppress a reflexive response in favor of a planned goal-directed response is central to cognitive control of behavior. This study sought to characterize the normative growth curves of underlying brain activation, examine the relationship of brain activation to performance, explore variability in trajectories, and probe contributions of sex and IQ to any such variability. Growth curves were modeled using statistical model-building approaches typically used in developmental studies, but which are novel to functional neuroimaging studies of youth (but see Shaw et al., 2012). Behavioral results accord with the extant cross-sectional literature indicating asymptotic growth that is protracted through adolescence (Klein and Foerster, 2001; Luna et al., 2004; Ordaz et al., 2010), and neither sex (Ross et al., 1994; Luna et al., 2004) nor IQ (Michel and Anderson, 2009) explained variability. Mean growth curves for brain activation in a priori regions of interest revealed little developmental change in motor response control regions and increased activation in an error-processing region. Post hoc voxelwise growth curve analyses underscored the significance of developmental changes in activation related to error processing. There was equivocal evidence for age-related declines within the identified a priori right dorsolateral prefrontal executive control region, though post hoc voxelwise analyses revealed similar patterns of age-related decline in other regions of the right lateral prefrontal cortex also involved in executive control, highlighting a common pattern of decelerating rates of activation as children proceed into adolescence. Together, these findings fit with our hypothesis that executive control and error-processing regions matured later than motor response control regions, and results also clarified that error-processing function was the latest to mature. Only error-processing activation was associated with performance, and this was shown to mediate the relationship between age and inhibitory error rates. Variability patterns were unique to each functional network, suggesting that similar mechanisms may support development within different circuitries. Contrary to hypotheses based on growth curves of structural brain maturation, IQ did not explain any variability in brain activation; however, sex did explain variability in some regions, predominantly those involved in motor response control. Importantly, activation associated with error processing was unique in that there was no significant interindividual variability in growth curves, underscoring its centrality in facilitating developmental improvements in behavior.

Unlike activation in all motor response control and executive control ROIs, dACC activation during corrected error trials was associated with AS performance. Importantly, this relationship did not exist for dACC activation during correct trials, suggesting that dACC-supported error processing specifically underlies the developmental improvements in performance on an inhibitory control task. Indeed, dACC-supported error processing statistically mediated the relationship between age and AS performance. The dACC is known to monitor performance, detect incorrect responses, and adjust subsequent responses, which enhance overall performance (Gehring et al., 1993; Menon et al., 2001; Polli et al., 2005). Though it is unclear whether the dACC detects responses to be corrected via error detection (Garavan et al., 2003) or monitoring of conflicting/incompatible responses (Carter et al., 1998; Braver et al., 2001), the dACC seems to adjust performance by signaling the right dlPFC to increase activation on the next trial, which subsequently improves performance (Kerns, 2006; Cavanagh et al., 2009). Our finding of developmental increases in error processing-related activation fits with cross-sectional fMRI and event-related potential studies reporting greater such activation in adults than youth (Davies et al., 2004; Ladouceur et al., 2007; Rubia et al., 2007; Velanova et al., 2008). It also aligns with results from a large, cross-sectional, developmental structural neuroimaging study that revealed that the dACC is unique among all cortical areas in that its cortical surface area explains significant variability in performance on another inhibitory control task, even after accounting for age (Fjell et al., 2012). Our characterization of a growth curve with decelerating rates of change reveals that the developmental change is characterized by continued subtle refinements in activation that occur throughout adolescence. These results extend previous research focused on traditional prefrontal executive regions to provide a novel understanding of the primary role of performance monitoring for facilitating the development of mature inhibitory control over behavior.

In contrast to the dACC during corrected errors, activation in the right dlPFC ROI, a key executive control region, decreased with age and reached adult levels by adolescence. This finding, however, did not survive correction for multiple comparisons, and voxels corresponding to this ROI did not evidence developmental change in voxelwise growth curve analyses. Nonetheless, the voxelwise investigation revealed significant clusters of voxels in other areas of the right lateral prefrontal cortex (middle and inferior frontal gyri)—areas that also followed a pattern of steeper declines in childhood followed by a decelerating rate of activation levels in adolescence. The lack of voxels showing developmental change within the predefined right dlPFC ROI in voxelwise analyses may be attributable to the lesser test–retest reliabilities of voxelwise versus ROI-based metrics or they may underscore the small effect size of the ROI-based dlPFC finding over the large age range sampled in this study. For this reason, future research seeking to clarify age-related changes in lateral prefrontal cortex ought to examine a targeted age group limited to older children and young adolescents. What is consistent across any of these ROI-based and voxelwise findings is the pattern that areas of the lateral prefrontal cortex are recruited most by children and used at a decelerating rate over development. That activation in the right lateral prefrontal cortex reaches maturity before dACC is consistent with evidence from functional connectivity studies indicating that prefrontal executive circuits are functionally integrated into distributed inhibitory control circuits by adolescence (Hwang et al., 2010) and from Diffusion Tensor Imaging studies, indicating that white matter tracts that link to dlPFC (superior longitudinal fasciculus) are mature by adolescence, whereas those linking to dACC (cingulum) mature into adulthood (Lebel et al., 2012). Right dlPFC activation was not correlated with performance, which may suggest that the right dlPFC may not be directly involved with trial-level performance but may reflect overall effort (Braver et al., 1997). Indeed, experimental manipulations indicate that this region supports determining which task features require attention and which processes should be prioritized—once this is determined, right dlPFC activation diminishes (Rypma et al., 2002; Chein and Schneider, 2005; Lee et al., 2012). Other areas of the executive control network did not show age-related change, suggesting that only portions of this network are involved in facilitating the maturation of performance.

Our data, the first to examine variability in growth curves of inhibitory control, indicate that patterns of variability are consistent within functional circuitries, which may reflect different developmental processes across different brain regions. dACC activation was the most developmentally invariant, as it did not demonstrate significant variability in either intercepts or slopes, suggesting a central role of error processing in supporting the emergence of mature inhibitory control. In contrast, variability was present in the trajectories of activation in executive control regions, but rank-order between individuals was preserved across development, suggesting this type of activation is a trait-like characteristic. Variability in multiple motor response control regions was heteroscedastic. This variability was relatively high in childhood and diminished with age, and activation increased over development in some individuals but decreased in others. Together, this indicates that maturation reflects a stabilizing process of convergence, and the observed variability may reflect a dynamic tuning of optimal motor control engagement as error processing matures.

Despite comparable task performance across sexes at all ages, this study revealed sex-specific patterns of developmental change in brain function in a subset of motor response control regions (SEF, pre-SMA, and right FEF) and an executive control region (right vlPFC). Whereas males did not show differential recruitment with age, females showed declines indicating a greater reliance on these regions early in development. Given that both sexes show the same developmental patterns in dACC and dlPFC activation, the female-specific change in predominantly motor response control recruitment may reflect sex differences in compensatory approaches. Females' white matter matures earlier than that of males and at a time when dACC continues to mature (Asato et al., 2010; Bava et al., 2011), so females may take advantage of earlier access to speeded connections by relying upon motor control regions during early adolescence. Indeed, developmental changes in white matter microstructure are associated with magnitudes of brain function supporting executive function (Olesen et al., 2003) via their effects on network integration (Stevens et al., 2009). Importantly, the lack of sex differences in dACC and dlPFC further underscores that these areas of the inhibitory control network are foundational.

In sum, our longitudinal approach enabled us to discern the contributions of different brain systems to the development of inhibitory control, revealing that error processing/performance monitoring is the primary process supporting the maturation of inhibitory control. Importantly, executive processes are engaged in childhood to support inhibitory control but do not underlie the transition to adult-level inhibitory control of behavior. In this initial study, we examined regions known to be functionally interconnected within circuits, and future studies could extend this work by examining growth curves of functional connectivity. This could reveal how strengths of connections between regions change with age and whether the strength of such associations varies across individuals. Analyses examining the connectivity of error-processing activation to activation in regions to which the dACC is anatomically and functionally interconnected could reveal the process by which error processing-related activation facilitates age-related improvements in inhibitory control.