Minimal Clinically Important Difference (MCID)—Adding Meaning to Statistical Inference

In an earlier issue of the American Journal of Public Health, Vaughan published an article, “The Importance of Meaning,” in the Statistically Speaking section.¹ This article continues the conversation by explicitly demonstrating what “meaning” is in statistical inference.

Let us begin with an example of a clinical trial to test the effectiveness of a new drug to lower one’s systolic blood pressure. Let us assume that the new drug could reduce one’s systolic blood pressure by 2 millimeters of mercury for everyone and this was measured very precisely. One could imagine that the P value on even a moderately sized randomized controlled trial for the new drug would be extremely small, making the point estimate extremely statistically significant; this new drug has a very precise effect of −2 millimeters of mercury. Should this new drug be considered a game changer? No. For most individuals, a reduction of 2 millimeters of mercury is not big enough to make much of a clinical difference. It is the amount of reduction of systolic blood pressure that is big enough to make such a clinical difference that is the topic of discussion here. The term commonly used in clinical settings is the “minimal clinically important difference” (MCID). Continuing with this example, suppose that the consensus with the experts for this new drug was that a reduction of at least 20 millimeters of mercury would be considered clinically significant. Here the MCID is 20 millimeters of mercury.

In general, an MCID of an outcome indicator, be it expressed as an absolute difference or a rate, or any relative statistic, such as an odds ratio, is essential in the interpretation of the results after the experiment has been executed and the data analyzed. We need to determine the significance of the difference between 2 treatments and answer 1 of the following questions: Is treatment A equivalent to treatment B? Is treatment A more superior than treatment B? Is treatment B more superior than treatment A?

Very often an investigator calculates the P value between the means of the 2 treatments and declares that there is no difference between the 2 treatments because P > .05. As we all know, the P value is highly dependent on the sample size, or the power of the study. Biostatisticians and epidemiologists have long been advocating the use of confidence intervals (CIs) in place of or in addition to P values.^2,3 The common simple statements “P < .05” and “P > .05” are not helpful and can lead to erroneous conclusions. CIs provide information about a range in which the true value lies with a certain degree of probability, as well as about the direction and strength of the demonstrated effect. This information enables conclusions to be drawn about the statistical plausibility and clinical relevance of the study findings.

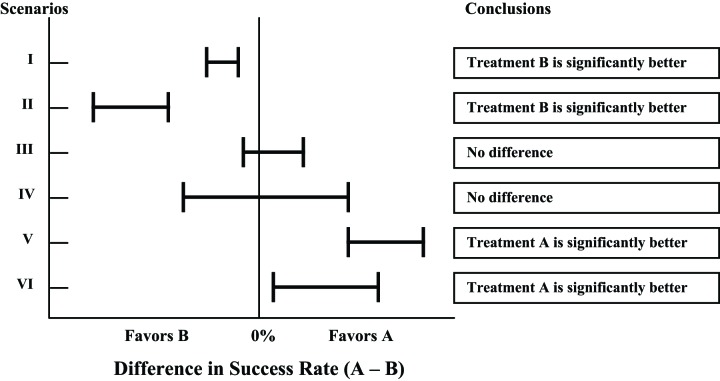
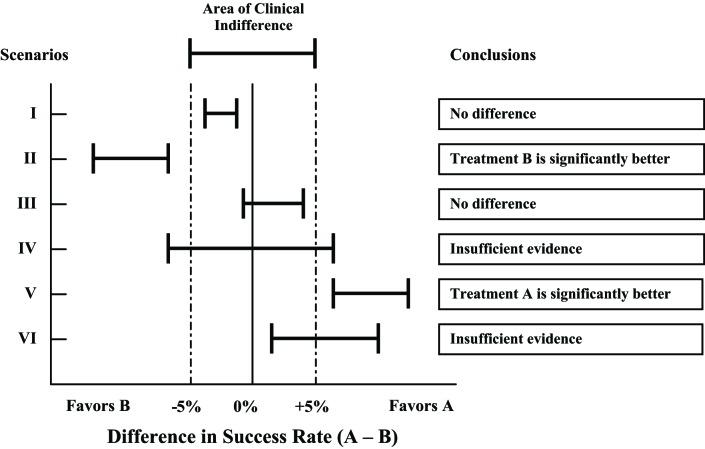
Two figures demonstrate the conclusions that can be drawn depending on the width and location of the 95% CI in relation to a specified MCID. Figure 1 illustrates the conclusions that can be reached for different scenarios when no MCID is used, and Figure 2 illustrates the conclusions for the same scenarios when MCID is used.

FIGURE 1—

Statistical inferences with confidence intervals without using minimal clinically important difference.

FIGURE 2—

Statistical inferences with confidence intervals using minimal clinically important difference.

Scenarios I and II favor treatment B. Without using MCID, one would conclude that treatment B is significantly better than treatment A for both scenarios. However, the 95% CI for scenario I lies within the area of clinical indifference defined by MCID; thus, the difference between the 2 treatments is not clinically significant, a conclusion that is different when MCID is not taken into consideration. For scenario II, because the 95% CI lies to the left of the area of clinical indifference, one can conclude that treatment B is significantly better than treatment A both statistically and clinically.

Scenarios III and IV do not favor either treatment. Without using MCID, both scenarios would conclude no difference between the 2 treatments. However, in scenario IV the 95% CI crosses the limits defined by MCID; thus, one cannot make a conclusion until more data are obtained. Here one would conclude that the evidence to draw a conclusion is insufficient. For scenario III, because the 95% CI lies within the area of clinical indifference, one can conclude that the difference between the 2 treatments is not significant both statistically and clinically.

Scenarios V and VI favor treatment A. Without using MCID, both scenarios would conclude that treatment A is significantly better than treatment B. The 95% CI in scenario V lies to the right of the area of clinical indifference defined by MCID, thus allowing the conclusion that no difference exists between the 2 treatments. However, the 95% CI in scenario VI crosses into the area of clinical indifference defined by MCID; thus, a conclusion cannot be made until more data are obtained. Here one would conclude that the evidence is insufficient to draw a conclusion.

In summary, CIs falling within the area defined by MCID are considered to establish evidence of no difference, and confidence intervals outside the area are considered to establish difference. If the confidence intervals cross into the area of clinical indifference defined by MCID, an effect (positive or negative) of the treatment option on the outcome cannot be established.

As illustrated, one should not make a conclusion on the basis of P value or 95% CI alone. Clinical significance must be taken into consideration to reach valid conclusions. One major advantage in adding MCID to the interpretation is the opportunity to identify when the evidence to draw a conclusion is insufficient. This concept is especially useful in systematic reviews when data are pooled from different experimental studies. It allows one to assess whether the evidence is sufficient to draw a conclusion.

The preceding illustration is used to demonstrate the use of MCID and CIs in decision-making. However, one should not and could not ignore the size and location of the CIs. For example, in Figure 2, both scenarios IV and VI show insufficient evidence, scenario IV is leaning toward no clinical difference, and scenario VI is leaning toward favoring treatment A. If the sample size were larger, the width of the CI would be narrower. Therefore, the width of the confidence interval and its location with respect to the MCID are important considerations in making clinical conclusions.

Last, establishing an MCID for a specific area of research has been challenging. Efforts have been made to identify an appropriate MCID in many clinical and health care disciplines using empirical studies.