Molecular Mechanisms, Thermodynamics, and Dissociation Kinetics of Knob-Hole Interactions in Fibrin

Background: Knob-hole interactions underlie formation and properties of fibrin polymer, the scaffold of blood clots and thrombi.

Results: The structural mechanisms, dissociation kinetics, and thermodynamic parameters of the A:a and B:b knob-hole interactions have been determined.

Conclusion: The knob-hole bonds are inherently variable and sensitive to pH and temperature.

Significance: The emerging molecular picture offers mechanistic insights into fibrin polymerization.

Abstract

Polymerization of fibrin, the primary structural protein of blood clots and thrombi, occurs through binding of knobs ‘A’ and ‘B’ in the central nodule of fibrin monomer to complementary holes ‘a’ and ‘b’ in the γ- and β-nodules, respectively, of another monomer. We characterized the A:a and B:b knob-hole interactions under varying solution conditions using molecular dynamics simulations of the structural models of fibrin(ogen) fragment D complexed with synthetic peptides GPRP (knob ‘A’ mimetic) and GHRP (knob ‘B’ mimetic). The strength of A:a and B:b knob-hole complexes was roughly equal, decreasing with pulling force; however, the dissociation kinetics were sensitive to variations in acidity (pH 5–7) and temperature (T = 25–37 °C). There were similar structural changes in holes ‘a’ and ‘b’ during forced dissociation of the knob-hole complexes: elongation of loop I, stretching of the interior region, and translocation of the moveable flap. The disruption of the knob-hole interactions was not an “all-or-none” transition as it occurred through distinct two-step or single step pathways with or without intermediate states. The knob-hole bonds were stronger, tighter, and more brittle at pH 7 than at pH 5. The B:b knob-hole bonds were weaker, looser, and more compliant than the A:a knob-hole bonds at pH 7 but stronger, tighter, and less compliant at pH 5. Surprisingly, the knob-hole bonds were stronger, not weaker, at elevated temperature (T = 37 °C) compared with T = 25 °C due to the helix-to-coil transition in loop I that helps stabilize the bonds. These results provide detailed qualitative and quantitative characteristics underlying the most significant non-covalent interactions involved in fibrin polymerization.

Introduction

Formation and decomposition of fibrin clots are essential for hemostasis, thrombosis, and wound healing (1–3). Fibrin network formation is initiated by limited proteolysis of fibrinogen by thrombin, resulting in polymerization of fibrin in two major steps: self-assembly of fibrin monomers into two-stranded half-staggered rodlike protofibrils and lateral aggregation of protofibrils into thicker fibrils that form the branched three-dimensional network (4–7). Building of fibrin protofibrils is driven by the intermolecular A:a knob-hole interactions, whereas B:b knob-hole bonds are involved in the lateral aggregation of protofibrils. Roughly, the length and diameter of fibrin fibers are determined by the relative rates of longitudinal oligomerization versus lateral aggregation of fibrin oligomers reaching a critical length (8). During and after formation, the stability of blood clots in response to mechanical forces imposed by the blood flow, wound stretching, and other dynamic environmental conditions is regulated by the kinetics of dissociation of the knob-hole bonds until the clot is cross-linked by Factor XIIIa bonds (9). Consequently, the binding and unbinding kinetics of knob-hole interactions determine the formation of fibrin fibers and influence the final structure and stability of clots and thrombi, including the potential for clot remodeling, embolization, contraction, and other (patho)physiological processes related to blood clotting and thrombosis. Impaired knob-hole interactions result in loose, weak, unstable clots and are associated with the tendency to bleed. Dense fibrin networks originating from enhanced knob-hole interactions show increased stiffness, a higher fibrinolytic resistance, and mechanical resilience, which may predispose individuals to cardiovascular diseases, such as heart attack and stroke (10–12).

Fibrinogen, the soluble fibrin precursor, consists of three pairs of polypeptide chains, Aα, Bβ, and γ, linked together by 29 disulfide bonds (13). Thrombin splits off two pairs of fibrinopeptides A and B from the N termini of the Aα and Bβ chains, respectively, in the central nodule. This results in the exposure of binding sites ‘A’ and ‘B’ that interact, respectively, with constitutively accessible sites ‘a’ and ‘b’ in the γ- and β-nodules of the lateral D regions of another fibrin molecule (see Fig. 1) (14–16). The polymerization sites have also been called knobs ‘A’ and ‘B’ and holes ‘a’ and ‘b’ (14) because x-ray crystallographic studies of fibrinogen fragments revealed binding pockets (holes) complementary to the peptides, GPRP and GHRP, corresponding to the newly exposed N-terminal ends (knobs) of the α and β chains of fibrin (17). Because the structure of the actual complexes that form in fibrin polymerization have not been observed, it is not yet known whether the binding sites consist only of the peptides fitting into the holes or whether the association processes are more complex, involving other surface amino acids of the two interacting species.

FIGURE 1.

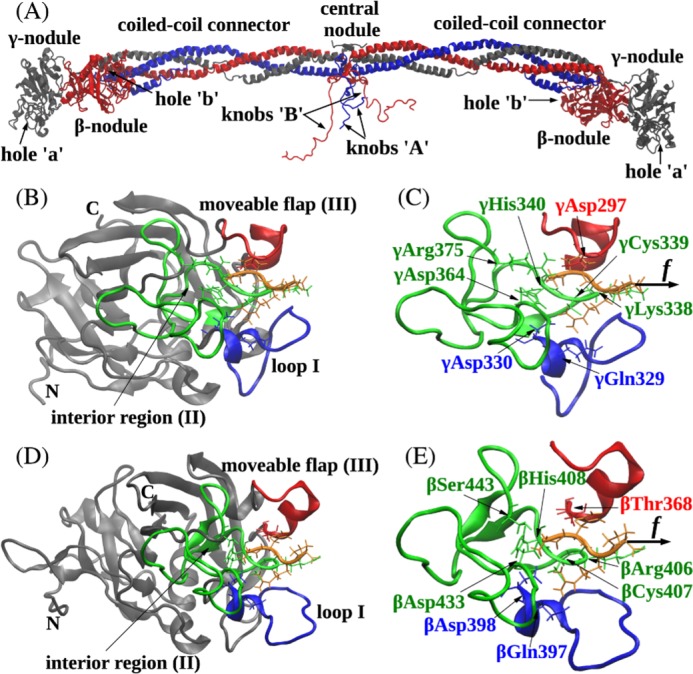
Ribbon structures of fibrin(ogen) (A), the A:a knob-hole bond (B and C), and the B:b knob-hole bond (D and E). The structures correspond to the A:a knob-hole complex (model system Aa1) and B:b knob-hole complex (system Bb1), respectively, at pH 7 and T = 25 °C. B and D, the interface of the A:a knob-hole complex (B) and B:b knob-hole complex (D) in which the binding determinants, loop I (region I shown in blue), interior region (region II shown in green), and moveable flap (region III shown in red), interact with peptides GPRP and GHRP (shown in orange), respectively. C and E, simulation setup. Holes ‘a’ and ‘b’ are constrained through fixing the C termini of the γ chain (residue γGly¹⁶⁰) and β chain (residue βVal²⁰⁵), respectively (see “Experimental Procedures”). A constant pulling force f (represented by the black arrow) is applied to the Pro⁴ residue of GPRP peptide and Pro⁴ residue of GHRP peptide in the direction perpendicular to the binding interface to dissociate the knob-hole bond. Also shown are structural details of A:a and B:b knob-hole bonds in which residues in binding regions I–III in holes ‘a’ and ‘b’ establish binding contacts with peptides GPRP and GHRP.

The N-terminal α chain motif GPR, the main functional sequence in the knob ‘A’, is complementary to hole ‘a’ located in the γ-nodule. The N-terminal β chain motif GHRP is a major part of knob ‘B’ that binds to hole ‘b’ located in the β-nodule. Analysis of the structures of fragment D (containing the γ-nodule) co-crystallized with GPRP peptide (synthetic knob ‘A’ mimetic) has revealed that binding hole ‘a’ is localized to residues γ337–379 of the γ-nodule: γAsp³⁶⁴, γArg³⁷⁵, γHis³⁴⁰, and γGln³²⁹ accommodate binding of the GPRP peptide, and γLys³³⁸ and γGlu³²³ shift slightly to allow γLys³³⁸ to interact with the C terminus of the peptide (see Fig. 1) (18). Due to homology of the amino acid sequences forming hole ‘a’ (in the γ-nodule) and hole ‘b’ (in the β-nodule) and structural similarity of their binding pockets (see Fig. 1), hole ‘b’ involves similar binding regions βAsp³⁸³–Asp³⁹⁸, βTyr⁴⁰⁴–Gly⁴³⁴, and βGln³⁵⁹–Ile³⁶⁹, which accommodate formation of binding contacts with and subsequent association of the peptide GHRP (synthetic knob ‘B’ mimetic).

Although the x-ray crystallographic studies have provided valuable structural data about the binding sites mediating the knob-hole associations, this information is limited to a static molecular image of the A:a and B:b knob-hole complexes. Optical trap-based force spectroscopy and atomic force microscopy have been used to probe directly the strength of knob-hole interactions via dissociation of knob-hole bonds at the single molecule level (6, 19, 20). However, these experiments have limited spatial resolution and do not reveal the molecular mechanisms of the knob-hole interactions. To address these limitations, here we have embarked on the computational exploration of the knob-hole interactions in fibrin using molecular dynamics (MD)³ simulations, which in conjunction with atomic structural models help to advance our understanding of protein function and dynamics (21). In computer-based modeling of the force-induced dissociation of protein-protein complexes, conditions of force application are similar to force protocols used in dynamic force spectroscopy (22, 23). To approach physiologically relevant conditions, tensile forces and temperature can be varied, ionic strength can be modeled by including an appropriate number of ions in the solvation box, and solvent acidity (pH) can be modeled by taking into account the degree of protonation of amino acid residues.

In this work, we performed MD simulations of forced dissociation of non-covalent A:a and B:b bonds to explore and compare the dynamic behavior of the A:a and B:b knob-hole complexes subject to tension. Here, we report the results of our studies of the kinetics (time scales and reaction pathways), thermodynamics (energy landscapes), and molecular mechanisms of the forced dissociation of the A:a and B:b knob-hole complexes performed under different virtual ambient conditions (pH and temperature). We used the atomic resolution inherent to MD simulation approaches to assess the importance of particular amino acid residues and clusters of residues for the binding affinity and strength of the knob-hole interactions. We probed the dynamic network of residues in holes ‘a’ and ‘b’ forming electrostatic contacts with the peptides GPRP and GHRP, respectively. Taken together, the results obtained provide a broad foundation for understanding the key interactions in fibrin polymerization. The kinetic and thermodynamic characteristics can also be used to formulate new drug design strategies to attenuate the knob-hole interactions in fibrin, to modify the fibrin clot structure and properties, and to reduce the danger of thromboembolic complications.

EXPERIMENTAL PROCEDURES

Model Systems for A:a and B:b Knob-Hole Complexes

Structural models for the A:a and B:b knob-hole complexes were obtained using the x-ray structure of the double-D fragment from human fibrin containing both holes ‘a’ and ‘b’ co-complexed with the Gly-Pro-Arg-Pro-amide peptide and Gly-His-Arg-Pro-amide peptides (Protein Data Bank code 1FZC) (24). In these structures, holes ‘a’ and ‘b’ contain residues γ143–392 and β197–458, respectively. We used the synthetic knob ‘A’ (GPRP) and knob ‘B’ (GHRP), which mimic the N-terminal portions of knobs ‘A’ and ‘B’ binding with holes ‘a’ and ‘b’, respectively (18). Hole ‘a’ is localized to clusters of residues γTrp³¹⁵–Trp³³⁰, γTrp³³⁵–Asn³⁶⁵, and γPhe²⁹⁵–Thr³⁰⁵ in the γ-nodule. Hole ‘b’ in the β-nodule involves binding regions βAsp³⁸³–Asp³⁹⁸, βTyr⁴⁰⁴–Gly⁴³⁴, and βGln³⁵⁹–Ile³⁶⁹ (see Fig. 1). The summarized description for the preparation of each model system, Aa1 (pH 7, T = 37 °C), Aa2 (pH 7, T = 25 °C), Aa3 (pH 5, T = 37 °C), and Aa4 (pH 5, T = 25 °C) for the A:a knob-hole bond and Bb1 (pH 7, T = 37 °C), Bb2 (pH 7, T = 25 °C), Bb3 (pH 5, T = 37 °C), and Bb4 (pH 5, T = 25 °C) for the B:b knob-hole bond, is given in supplemental Tables S1 and S2.

To model the pH dependence of forced dissociation of knob-hole bonds, we considered the degree of protonation of amino acids. Because at pH 5 only His residues are protonated compared with pH 7 (pK_a ≈ 6), we replaced neutral His residues with positively charged His residues. Ion concentration translates to including an appropriate number of ions Na⁺ and Cl⁻ in the water box. We used the relevant physiological 150 mm concentration of NaCl. Details regarding the system preparation are given in supplemental Tables S1 and S2. Each system was solvated in a water box; the number of water molecules and size of the solvation box are given in supplemental Table S2. In umbrella sampling calculations, we increased the volume of the water box to 47.6 Å × 49.1 Å × 98.7 Å (for systems Aa1–Aa4) and to 50.1 Å × 50.9 Å ×103.6 Å (for systems Bb1–Bb4). Each model system was first minimized for 5000 steps using the steepest descent algorithm. After initial minimization, each system was heated to T = 25 or 37 °C and equilibrated for 0.3 ns. The simulations were carried out at constant temperature. The water density was maintained at 1 g/cm³, and periodic boundary conditions were applied to the water molecules. Non-bonded interactions were switched off at 12-Å distance and had a switching function from 10 to 12 Å. The long range electrostatics were described using the particle mesh Ewald method. We used a Langevin thermostat to maintain the conditions of constant temperature. The damping coefficient was set to γ = 6πηa/m = 50 ps⁻¹, which corresponds to the water viscosity η = 0.01 poise and size and mass of amino acid a = 5 × 10⁻⁸ cm and m = 2 × 10⁻²² g, respectively.

MD Simulations of the A:a and B:b Knob-Hole Complexes

To carry out computational modeling of systems Aa1–Aa4 and Bb1–Bb4, we used the NAMD 2.7 software package (25) and the CHARMM22 force field (26). Each initial protein structure was solvated with at least 15 Å of TIP3P water (27) using the VMD solvate plug-in (28). We carried out 10-ns equilibrium simulations of the D region of the fibrinogen molecule, which includes the γ-nodule (with hole ‘a’) and the β-nodule (with hole ‘b’) co-complexed with the peptide GPRP (knob ‘A’ mimetic) and GHRP (knob ‘B’ mimetic), respectively (see Fig. 1). The forced dissociation of GPRP peptide from the γ-nodule (A:a knob-hole complex) and of GHRP peptide from the β-nodule (B:b knob-hole complex) was performed using steered molecular dynamics implemented in the NAMD package. To mimic the experimental force clamp measurements, we constrained hole ‘a’ (hole ‘b’) by fixing the C-terminal part of one γ chain (β chain), residue γGly¹⁶⁰ (βVal²⁰⁵); constant tensile force f = f·n was applied to the C^α carbon of Pro⁴ residue in peptide GPRP (GHRP) in the direction n perpendicular to the binding interface to dissociate the A:a (B:b) knob-hole bond. We used force f = 150, 200, 250, 300, 350, and 400 pN. To obtain statistically meaningful information, we performed multiple pulling runs: 15 trajectories of forced unbinding were generated for each force value (a total of 90 trajectories for each model system).

Analysis of Simulation Output

Analysis of Structures

To probe conformational flexibility of the protein domains forming hole ‘a’ and hole ‘b,’ we computed the root mean square deviations: r.m.s.d.(i) = (1/t_totΣ_tj(x_i(t_j) − x̃_i))^1/2 where x_i(t_j) and x̃_i are positions of the C^α atom i (ith residue) in the current state and in the reference state, respectively, and t_tot is the length of the simulation run. To remove rotational and translational contributions, we used a “running average” structure for each 150-ps time interval as a reference state. To probe the global conformational transitions, we analyzed transient structures for each model system and visualized them using the VMD plug-in (28).

Analysis of Kinetics

We analyzed the average bond lifetimes and standard deviations. A pair of amino acids i and j is said to form a binary contact if the distance between the center of mass of their side chains r_ij < 6.5 Å exists for more than 0.1 ns. The time-dependent maps of interacting residues were constructed, and the total number of binding contacts Q(t) was used to monitor the dissociation progress. The bond lifetime τ was defined as the time at which Q = 0.

Molecular Mechanism

We utilized essential dynamics (29, 30) to capture collective displacements of amino acid residues Δx(t) = x(t) − x₀ from their equilibrium positions x₀ along the unbinding reaction coordinate X (see the supplemental data for details). We performed numerical diagonalization of the covariance matrix C(t) = M^1/2Δx(t)(M^1/2Δx(t))^T = T^TLT to compute the matrix of eigenvalues L and the matrix of eigenvectors T (M is the matrix of masses of amino acids). These were used to calculate the root mean square deviations for each residue I along the eigenmode k; i.e. r.m.s.d._I^k = (C_II/M_II)^1/2 = (1/M_IIΣ_kl(T^T_IkL_klT_lI))^1/2 = (L_kIT_kI²/M_II)^1/2, in the center-of-mass representation. The native structure of the knob-hole complex was superposed with the structure corresponding to the maximum displacement along the first (principal) mode, k = 1.

Analysis of Thermodynamics

To resolve the unbinding free energy landscape G(X), we used the umbrella sampling method (31, 32), which is described in detail in the supplemental data, to compute the potential of mean force and to quantify the interaction energy.

RESULTS

Native Properties of A:a and B:b Knob-Hole Complexes at Various Ambient Conditions

To identify the residues in holes ‘a’ and ‘b’ principally involved in dynamic interactions with GPRP and GHRP and assess the plasticity of the knob-hole bonds in response to varying environmental conditions, we explored the A:a and B:b knob-hole complexes in their native state. Because the knob-hole interactions are mainly electrostatic, it should be expected that the strength of knob-hole bonds is susceptible to variation in proton concentration (pH) and temperature, both of which can change at a wound site in vivo. It is known that at the sites of inflammation and tumor growth the microenvironment is acidified, e.g. as a result of local metabolic acidosis due to hypoxia (33). Therefore, we performed equilibrium simulations of the A:a and B:b knob-hole complexes at pH 5 and 7 and at T = 25 and 37 °C (body temperature). By varying pH and temperature, we generated four model systems to study the A:a knob-hole complexes (Aa1–Aa4) and four model systems for the B:b knob-hole complexes (Bb1–Bb4) as described under “Experimental Procedures” and in supplemental Tables S1 and S2.

For each of the eight model systems (Aa1–Aa4 and Bb1–Bb4), we analyzed the r.m.s.d. quantifying fluctuations for each amino acid residue in holes ‘a’ and ‘b’ in the bound state with the corresponding ligand peptide, GPRP and GHRP, respectively. It should be expected that amino acids in holes ‘a’ and ‘b’ involved in binding of the peptides would be more flexible to accommodate small amplitude thermal peptide motion in the binding pocket. Hence, these residues would show larger r.m.s.d. values. We found that in all four model systems (Aa1–Aa4 for the A:a knob-hole complexes) the largest fluctuations (r.m.s.d. > 1.5 Å) correspond to the same structural regions in hole ‘a’ localized to residues γTrp³¹⁵–Trp³³⁰, γTrp³³⁵–Asn³⁶⁵, and γPhe²⁹⁵–Thr³⁰⁵ (supplemental Fig. S1, A and B). Specifically, residues γGlu³²³, γPro³⁶⁰, and γPro²⁹⁹ were found to have the highest r.m.s.d. values. These same stretches of residues have been found in earlier studies of the x-ray structures of fragment D co-crystallized with the peptide GPRP to participate in the binding interactions (14, 34). These binding determinants were termed loop I or region I (γTrp³¹⁵–Trp³³⁰), interior region or region II (γTrp³³⁵–Asn³⁶⁵), and moveable flap or region III (γPhe²⁹⁵–Thr³⁰⁵) (Fig. 1, B and C). There were smaller changes in r.m.s.d. values for amino acid residues in loop I and the moveable flap observed at the higher temperature (T = 37 °C) as compared with the lower temperature (T = 25 °C) and for the neutral environment (pH 7) as compared with an acidic environment (pH 5). The only significant difference was detected for amino acids in the interior region for which r.m.s.d. values increased from 1.7–1.8 to 2.0–2.2 Å upon decreasing pH from 7 to 5 (e.g. see peak at residue γPro³⁶⁰ in supplemental Fig. S1, A and B). We obtained similar results for the model systems Bb1–Bb4 for the B:b knob-hole complexes (supplemental Fig. S1, C and D). The largest fluctuations detected (r.m.s.d. > 2.0 Å) correspond to the regions of hole ‘b’ localized to residues βAsp³⁸³–Asp³⁹⁸, βTyr⁴⁰⁴–Gly⁴³⁴, and βGln³⁵⁹–Ile³⁶⁹. The residues βGly³⁶², βSer³⁸⁸, and βHis⁴²⁹ were found to have the highest r.m.s.d. values. Consistent with the previous crystallographic studies (14, 24), the three binding regions in hole ‘b’ had secondary structure similar to that for loop I (region I), the interior region (region II), and the moveable flap (region III) forming the binding interface in hole ‘a’ (e.g. Fig. 1, compare B and C with D and E). For this reason, we used these same notations to denote the binding structures in hole ‘b’: loop I (βAsp³⁸³–Asp³⁹⁸), interior region (βTyr⁴⁰⁴–Gly⁴³⁴), and moveable flap (βGln³⁵⁹–Ile³⁶⁹) (Fig. 1E). We also found that the mobility of amino acids forming these binding determinants in hole ‘b’ does not change much upon changing temperature and pH (supplemental Fig. S1, C and D).

To summarize, our results of equilibrium simulations are in full agreement with published x-ray crystallographic data in terms of identifying the binding determinants for the A:a and B:b knob-hole complexes, validating our MD simulation protocol. The results indicate that the binding structures and near-native ensemble of the A:a and B:b knob-hole bonds are fairly similar. There is a minor difference in mobility of the binding determinants, which are generally more flexible at pH 7 in hole ‘b’ than in hole ‘a’. Varying temperature and pH within the studied ranges does not much affect the binding structures that stabilize the A:a and B:b knob-hole bonds except for the binding residues γTrp³³⁵–Asn³⁶⁵ (region II) in hole ‘a’ that become more mobile in an acidic environment.

Forced Dissociation Kinetics of A:a and B:b Knob-Hole Complexes

We used a 150–400-pN range of constant pulling force to model the influence of varying stress due to blood flow on the knob-hole bond lifetimes. These forces were chosen as physiologically relevant. The range of hydrodynamic forces of the blood flow acting on knob-hole bonds in fibrin can be obtained using the relationship f = 6πηCRhr, which links the shear rate (r) and the tensile force (f). Here, C ≈ 1–2 is the dimensionless constant, η is blood viscosity (∼10 poise), R is clot size, and h is the average distance between the clot and vessel walls (∼0.1–1 μm). Our estimates show that under (patho)physiological conditions of blood circulation the knob-hole bonds in fibrin polymers forming R ≈ 10¹–10²-μm clots are subjected to tensile forces from a few tens of piconewtons (normal arterial blood flow with r ≈ 10² s⁻¹) to a few nanonewtons (stenotic blood flow with r ≈ 10⁴ s⁻¹).

We mechanically tested the strength of the A:a and B:b knob-hole bonds under varying conditions, i.e. for different temperature (25 and 37 °C) and acidity (pH 5 and 7), using pulling simulations (see “Experimental Procedures”). Lowering the pH from 7 to 5 results in the protonation of six His residues (pK_a ≈ 6) in hole ‘a’, four His residues in hole ‘b’, and one His residue in the GHRP peptide (see supplemental Table S1). These additional positive charges could alter the pattern of electrostatic interactions.

The strength of non-covalent bonds usually decreases with increased pulling force, meaning that protein-ligand complexes dissociate faster at higher forces (34–36). We found that as the pulling force (f) increased, the average bond lifetime (τ) decreased, and the dependence of τ on f was monotonic for all model systems Aa1–Aa4 and Bb1–Bb4 (Fig. 2). For equivalent ambient conditions, the A:a and B:b knob-hole bonds were found to be roughly equally strong in the entire force range of 150–400 pN (Fig. 2). However, both A:a and B:b knob-hole bonds were stronger and had longer lifetimes in neutral solution (pH 7) as compared with acidic solution (pH 5). Also, the A:a knob-hole bonds were found to be stronger at T = 37 °C as compared with T = 25 °C for both pH 5 and 7, whereas the B:b knob-hole bonds were weaker at T = 37 °C for pH 7 and almost equally strong at T = 37 and 25 °C for pH 5 (Fig. 2). Hence, increasing proton concentration has a more profound effect on the A:a and B:b knob-hole bonds as compared with varying temperature.

FIGURE 2.

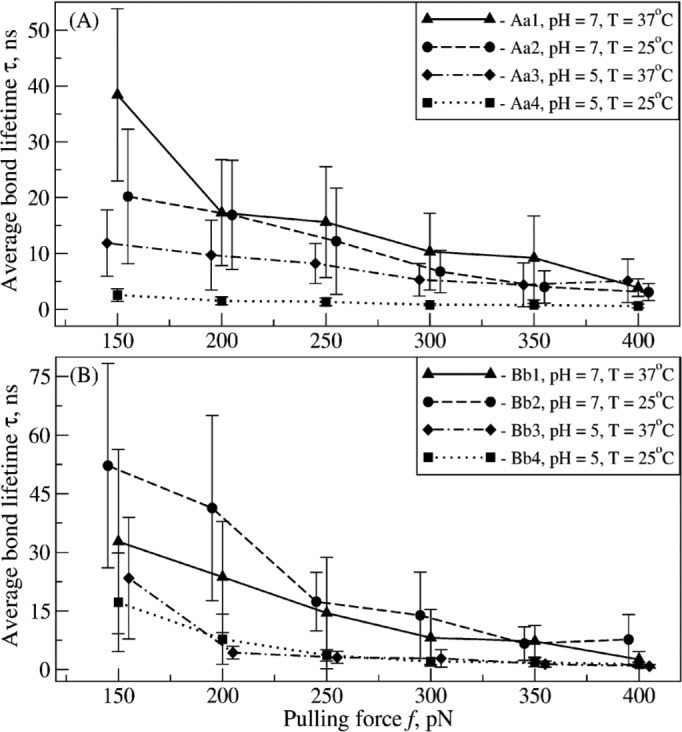
Kinetics of the forced dissociation of the A:a and B:b knob-hole complexes. The average bond lifetimes (τ) with standard deviations (error bars) for the A:a knob-hole complex (model systems Aa1–Aa4; A) and for the B:b knob-hole complex (model systems Bb1–Bb4; B) as a function of pulling force (f) are compared for different ambient conditions (at pH 5 and 7 and T = 25 and 37 °C; see supplemental Tables S1 and S2).

Single and Two-step Dissociation of A:a and B:b Knob-Hole Complexes

Statistics of bond lifetimes indicate that the force-driven dissociation of the A:a and B:b knob-hole bonds is intrinsically stochastic and quite variable. This can be seen, e.g. from the large standard deviations of the average bond lifetimes, especially at lower 150–250-pN force (Fig. 2). To understand the origin of large fluctuations in the bond lifetimes, we analyzed the dynamics of forced disruption of the binding contacts. In the studies of the near-native ensemble, we have identified 16 most important amino acid residues in the binding interface in holes ‘a’ and ‘b’ that formed ∼90% of all stable contacts with the residues in the GPRP and GHRP peptides, respectively. These are residues γPhe²⁹⁵, γAsp²⁹⁷, γAsp²⁹⁸, γAsp³⁰¹, γPhe³⁰⁴, γThr³⁰⁵, γPhe³²², γCys³²⁶, γGln³²⁹, γAsp³³⁰, γLys³³⁸, γCys³³⁹, γHis³⁴⁰, γTyr³⁶³, γAsp³⁶⁴, and γArg³⁷⁵ in hole ‘a’ and residues βGln³⁵⁹, βLeu³⁶⁰, βAsn³⁶⁴, βThr³⁶⁸, βTrp³⁸⁵, βLys³⁹², βCys³⁹⁴, βGlu³⁹⁷, βAsp³⁹⁸, βArg⁴⁰⁶, βCys⁴⁰⁷, βHis⁴⁰⁸, βThr⁴³¹, βAsp⁴³², βMet⁴³⁸, and βSer⁴⁴³ in hole ‘b’.

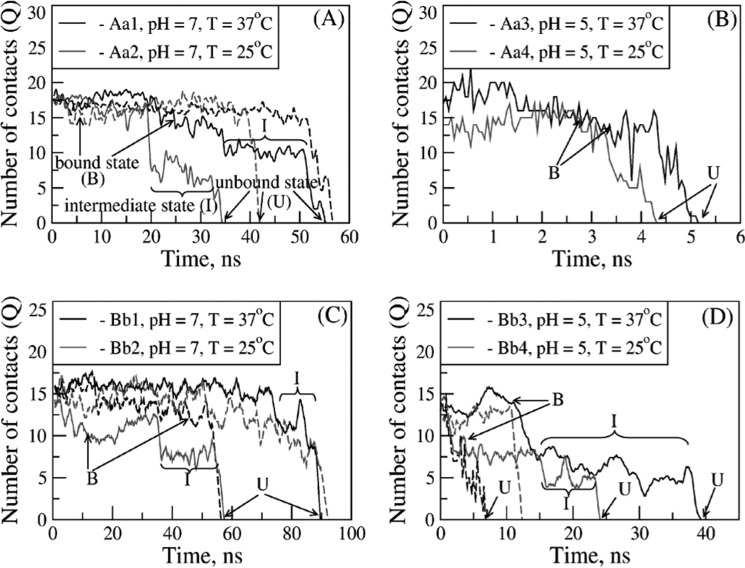
Next, we performed extensive analyses of the simulation output generated at the lowest attainable pulling force, f = 150 pN. To study the dissociation dynamics, we monitored the total number of stable contacts at the knob-hole interface as a function of time Q(t) (see “Experimental Procedures”), which reflects the instantaneous changes in the strength of the bond during forced unbinding. The time-dependent profiles of Q obtained from the most representative knob-hole unbinding trajectories for the model systems Aa1–Aa4 and Bb1–Bb4 show that Q(t) starts off from ∼15–18 contacts for the A:a knob-hole complexes (Fig. 3, A and B) and from ∼15–17 contacts for the B:b knob-hole complexes (Fig. 3, C and D), which correspond to the native bound state (B), but decays to zero along the unbinding pathway. The moment of time τ at which all the binding contacts have been disrupted and hence Q(t) = 0 signifies a complete dissociation of the complex and formation of the unbound (dissociated) state (U). A closer analysis revealed that in some simulation runs the forced dissociation occurred in a single step, B → U, whereas in other runs, the dissociation occurred by populating the intermediate state (I), i.e. B → I → U. This is reflected in the profiles of Q(t) (Fig. 3), some of which show a one-step transition, i.e. initial plateau followed by a sharp decay to zero, whereas other profiles exhibit two-step transitions. The former pathway (P1) corresponds to the single step transition (B → U), whereas the latter pathway (P2) represents the two-step unbinding transition (B → I → U). We have estimated the extent of this kinetic partitioning. In the case of the A:a and B:b knob-hole bonds at pH 7, the two-step unbinding pathway P2 was observed in only ∼10% of simulated trajectories (Fig. 3, A and C); in the acidic environment (pH 5), the share of this minor pathway increased to ∼30% (Fig. 3, B and D). In summary, our results indicate that dissociation of the A:a and B:b knob-hole bonds occurs through multiple competing kinetic pathways with or without intermediate (partially dissociated) states, which can underlie the remarkable variability of bond lifetimes.

FIGURE 3.

Dependence of kinetic pathways for forced dissociation of the A:a and B:b knob-hole bonds on pH and temperature. Shown are the time-dependent profiles of the total number of binary contacts (Q) stabilizing the A:a knob-hole complex for model systems Aa1 and Aa2 (A) and Aa3 and Aa4 (B) and the B:b knob-hole complex for model systems Bb1 and Bb2 (C) and Bb3 and Bb4 (D). The profiles of Q indicate two distinct dissociation pathways: the one-step pathway of unbinding (B → U) from the bound state (B) to the unbound state (U) and the two-step pathway of unbinding (B → I → U) in which formation of the intermediate state (I) occurs. The time-dependent maps of binary contacts for A:a and B:b knob-hole bond complexes for different pH values and temperature are presented in supplemental Figs. S2 and S3, respectively.

Dynamic Maps of Binding Contacts Forming A:a and B:b Knob-Hole Bonds

To obtain insight into structural details of the knob-hole formation and dissociation, we constructed and analyzed the time-dependent molecular maps of amino acid residues in holes ‘a’ and ‘b’ coupled to the residues in GPRP and GHRP peptides, respectively, during their forced unbinding. Supplemental Figs. S2 and S3 show the maps of stable binary contacts and how they change over time for model systems Aa1–Aa4 and Bb1–Bb4. For all systems Aa1–Aa4 and Bb1–Bb4, stable binary contacts formed between residues in hole ‘a’ and knob ‘A’ and between residues in hole ‘b’ and knob ‘B’ are summarized in Table 1.

TABLE 1.

Stable binary contacts between amino acid residues in hole ‘a’ and knob ‘A’ and between residues in hole ‘b’ and knob ‘B’ that stabilize the non-covalent A:a and B:b knob-hole bonds in fibrin

Model systems	Residues involved in A:a and B:b knob-hole interactions
	Holes ‘a’ and ‘b’	Knobs ‘A’ and ‘B’
Aa1 and Aa2 (pH 7)	γPhe295, γAsp330, γCys339, γHis340, γArg375	Gly1 in GPRP
	γPhe295, γAsp297, γAsp298, γThr305, γAsp364, γArg375	Pro2 in GPRP
	γPhe322, γCys326, γGln329, γAsp330, γCys339, γTyr363	Arg3 in GPRP
Aa3 and Aa4 (pH 5)	γPhe295, γAsp297, γThr305, γAsp364, γArg375	Gly1 in GPRP
	γPhe295, γAsp297, γAsp298, γAsp301, γThr305	Pro2 in GPRP
	γPhe322, γCys326, γGln329, γAsp330, γCys339, γTyr363, γAsp364	Arg3 in GPRP
Bb1 and Bb2 (pH 7)	βAsp398, βCys407, βHis408, βAsp432, βMet438, βSer443	Gly1 in GHRP
	βLeu360, βAsn364, βThr308, βMet438, βSer443	His2 in GHRP
	βCys394, βGlu397, βAsp398, βCys407, βThr431	Arg3 in GHRP
Bb3 and Bb4 (pH 5)	βAsp398, βCys407, βHis408, βAsp432, βMet438, βSer443	Gly1 in GHRP
	βLeu360, βAsn364	His2 in GHRP
	βCys394, βGlu397, βAsp398, βCys407	Arg3 in GHRP

The results obtained indicate that for the A:a knob-hole bonds at pH 7, the strongest contacts are formed between amino acid residues in loop I and residues Gly¹ and Arg³ in GPRP; between residues in the interior region and residues Gly¹, Pro², and Arg³ in GPRP; and between residues in the moveable flap and residues Pro² and Pro⁴ in GPRP (Fig. 1). The pH lowering results in weakening of interactions between residues in the interior region and residues Gly¹ and Pro² in GPRP and between residues in loop I and residue Gly¹ in GPRP but also results in formation of stable contacts between Gly¹ and Pro² in GPRP and residues in the moveable flap. At pH 5, there is a preference for association with the moveable flap, which is opposite to what is observed at pH 7 where binding to the interior region and loop I is more favorable. Redistribution of binding contacts leads to weakening of the A:a knob-hole bonds, also reflected by the decrease of the average bond lifetime for systems Aa3 and Aa4 (Fig. 3A). This finding implies that molecular interactions of hole ‘a’ with residues Gly¹ and Pro² in GPRP play a crucial role. For the B:b knob-hole bonds, the strongest contacts are between residues in loop I and the interior region and residues Gly¹ and Arg³ of GHRP (Fig. 1). At pH 7, additional contacts form between His² of GHRP and residues in the interior region and moveable flap. The pH lowering results in weakening of the interactions between residues in the interior region and the moveable flap with His² of GHRP but preserves contacts between residues in loop I and the interior region with residues Gly¹ and Arg³ in GHRP.

Structural Transitions Underlying Forced Dissociation of A:a and B:b Knob-Hole Complexes

We used the essential dynamics approach (see “Experimental Procedures” and the description of the method in the supplemental data) to single out the most important types of motion showing the largest contribution in the direction of the global transition (dissociation). Using the positions of amino acid residues as a function of time, x(t) = {x₁(t), x₂(t), … , x_N(t)}, we numerically diagonalized the covariance matrix of their mass-weighted displacements Δx(t) from the reference (native) structure x₀ = {x₁(0), x₂(0), … , x_N(0)} (bound state) to obtain the matrix of eigenvalues L and the matrix of eigenvectors T. The eigenvalues L_I provide information about the amplitude of the Ith eigenvector t_I along the displacement Δx(t). We calculated the r.m.s.d. for each Ith residue along mode k, r.m.s.d._I^k = (L_kIT_kI²/M_II)^1/2, where M_II is the element of M, the matrix of masses of amino acids. The r.m.s.d. profiles for the first three modes (k = 1, 2, and 3) capturing ∼85% of the dissociation dynamics for model systems Aa1–Aa4 and Bb1–Bb4 were determined (supplemental Figs. S4 and S5).

The peaks of r.m.s.d._I^k correspond to residues forming the main binding determinants, loop I, interior region, and moveable flap, described in Fig. 1 (see also supplemental Fig. S1). For these regions, the r.m.s.d._I^k values are in the 2–4-Å range for the A:a knob-hole bonds (supplemental Fig. S4) and in the 2–5-Å range for the B:b knob-hole bonds (supplemental Fig. S5). The r.m.s.d._I^k values for the A:a and B:b knob-hole bonds are close, implying similar flexibility of their binding interface. At pH 7, the interfaces in the A:a and B:b knob-hole complexes show more flexibility at the higher temperature (T = 37 °C) (supplemental Figs. S4, A and B , and S5), but when the pH is lowered to 5, the amplitude of motions is roughly the same at T = 25 and 37 °C (supplemental Figs. S4, C and D, and S5). For the A:a knob-hole bond, r.m.s.d._I^k = 3–5 Å for the interior region and moveable flap at pH 7 (both at T = 25 and 37 °C), and r.m.s.d._I^k = 2 Å for loop I. For the A:a knob-hole bonds, lowering the pH resulted in smaller values of r.m.s.d._I^k for all three regions: at T = 37 °C, motions of binding residues in loop I are quenched (supplemental Fig. S4). For the B:b knob-hole bonds, changing the pH from 7 to 5 leads to an increase (r.m.s.d._I^k = 5 Å) for residues in the moveable flap (supplemental Fig. S5).

For each system, the most essential structural changes associated with the first (principal) mode (k = 1) are summarized in supplemental Fig. S6. Both for the A:a and B:b knob-hole complexes, dissociation is associated with partial opening of the binding interface, which is accompanied by the simultaneous stretching of all binding regions, the extent of which is determined by ambient conditions. The binding interface in the B:b knob-hole complex is slightly more flexible. The binding determinants in hole ‘b’ maintain their secondary structure (supplemental Fig. S6, E–H); however, there are minor changes in the secondary structure propensities for regions I and III in hole ‘a’ (supplemental Fig. S6, A–D). For both the A:a and B:b knob-hole complexes, there is a displacement of loop I and translocation of the moveable flap from the periphery to the center of the interface. The latter transition is coupled to partial stretching of the interior region. Both temperature and pH variation bring about rather small changes to the molecular arrangement.

Thermodynamics of Forced Dissociation of A:a and B:b Knob-Hole Bonds

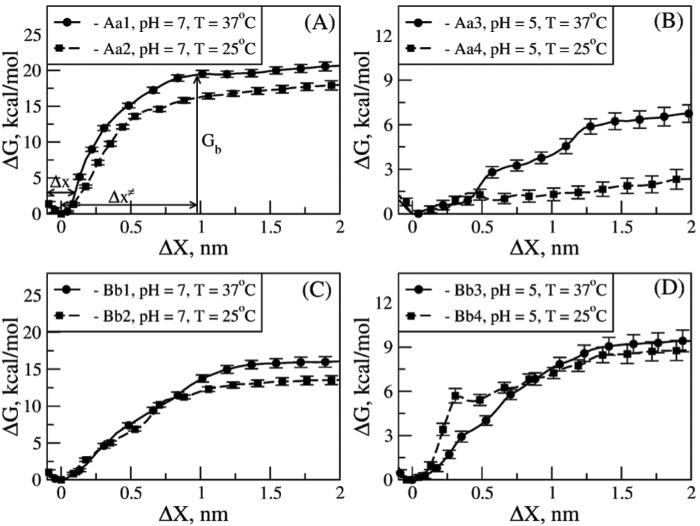
We resolved the profile of the Gibbs free energy change for forced unbinding, ΔG, as a function of the “receptor-ligand distance,” X, for various solution conditions (see “Experimental Procedures” and the supplemental data) (31, 32). For the A:a knob-hole complex, X was taken to be the distance between the residue γGly¹⁶⁰ in hole ‘a’ and the C-terminal Pro⁴ residue in GPRP. For the B:b knob-hole complex, X was taken to be the distance between the residue βVal²⁰⁵ in hole ‘b’ and the C-terminal Pro⁴ residue in GHRP. Residues γGly¹⁶⁰ and βVal²⁰⁵ were chosen because they are in the core of the binding pockets in holes ‘a’ and ‘b’, respectively. The results are presented in Fig. 4 where we have compared the profiles of the average ΔG as a function of the distance change ΔX for systems Aa1–Aa4 and Bb1–Bb4. We also estimated the “bond width” Δx and the “transition state position” Δx^≠ directly from the curves of ΔG. These characteristics (Δx and Δx^≠) are difficult if not impossible to obtain experimentally. The average width of the bond Δx, which we have defined as half of the width of the energy well for the bound state (B) corresponding to the energy change greater than thermal fluctuations (ΔG > 3k_BT ≈ 1.8 kcal/mol at T = 25 °C and 1.9 kcal/mol at T = 37 °C), shows how tightly coupled the protein and ligand molecules are. For example, a steeper growth in ΔG and hence narrower Δx are indicative of a stronger and tighter coupling. The position of the transition state Δx^≠ (or the critical bond extension at which ΔG reaches the energy plateau (bond dissociation)) is a measure of the conformational tolerance of the bimolecular complex under tension. Smaller (larger) values of Δx^≠ correspond to more brittle (more flexible) bonds. The values of these parameters (Δx and Δx^≠) and the bond dissociation energy G_b, defined as the plateau of ΔG at large ΔX (see Fig. 4A), for all model systems Aa1–Aa4 and Bb1–Bb4 are summarized in Table 2.

FIGURE 4.

Free energy landscape underlying the thermodynamics of A:a and B:b knob-hole interactions in fibrin. The Gibbs free energy for unbinding, ΔG, for model systems Aa1 and Aa2 (A) and Aa3 and Aa4 (B) and for model systems Bb1 and Bb2 (C) and Bb3 and Bb4 (D) as a function of knob-hole interaction range X are compared for different ambient conditions (at pH 7 and 5 and T = 25 and 37 °C; see supplemental Tables S1 and S2). The standard deviations (error bars) of ΔG are shown. The values of the equilibrium binding energy G_b, the width of the bound state Δx, and the distance between the bound state and transition state Δx^≠ shown in A are given in Table 2.

TABLE 2.

Average thermodynamic parameters (binding energy G_b, width of the bound state Δx, and transition state position Δx^≠) with the standard deviations for the A:a and B:b knob-hole interactions obtained for different model systems using the umbrella sampling calculations

For the umbrella sampling calculations, see “Experimental Procedures” and the description in the supplemental data and Tables S1 and S2).

Model system	Gb	Δx	Δx≠
	kcal/mol	nm	nm
Aa1	19.3 ± 0.5	0.15 ± 0.01	0.98 ± 0.03
Aa2	16.2 ± 0.4	0.19 ± 0.01	0.99 ± 0.04
Aa3	6.1 ± 0.6	0.55 ± 0.02	1.45 ± 0.05
Aa4	1.7 ± 0.5	0.41 ± 0.07	1.51 ± 0.05
Bb1	15.3 ± 0.6	0.29 ± 0.01	1.31 ± 0.06
Bb2	12.6 ± 0.4	0.22 ± 0.01	1.21 ± 0.02
Bb3	9.2 ± 0.5	0.45 ± 0.02	1.25 ± 0.06
Bb4	8.4 ± 0.5	0.30 ± 0.01	1.37 ± 0.05

For all the systems studied, the curves of ΔG show a well around the minimum at a zero bond extension (ΔX = 0), but ΔG rapidly increases, reaching an energy plateau at larger values of ΔX = 1–2 nm. The smooth curves of ΔG for the A:a and B:b knob-hole complexes obtained in the neutral environment (pH 7) correspond to the single step transition (B → U), which is the dominant pathway of dissociation P1 described earlier (Fig. 4). However, the curves of ΔG obtained in the acidic environment (pH 5) show several shallow energy wells separated by regions of energy increase. This is because ΔG represents an ensemble average picture, and hence, it also contains the contribution from the two-step transition (B → I → U), the alternative minor pathway of dissociation P2 (Fig. 4). Both the A:a and B:b knob-hole bonds are characterized by more narrow Δx (Δx = 0.15–0.19 nm for A:a knob-hole bond and Δx = 0.22–0.29 nm for the B:b knob-hole bond) and shorter Δx^≠ (Δx^≠ = 0.98–0.99 nm for A:a knob-hole bond and Δx^≠ = 1.21–1.31 nm for the B:b knob-hole bond) at pH 7 as compared with the same quantities at pH 5 (i.e. Δx = 0.41–0.55 nm and Δx^≠ = 1.45–1.51 nm for the A:a knob-hole bond and Δx = 0.30–0.45 nm and Δx^≠ = 1.25–1.37 nm for the B:b knob-hole bond) (Table 2). Also, the A:a knob-hole bonds are characterized by smaller Δx and shorter Δx^≠ than the B:b knob-hole bonds at pH 7 but larger Δx and longer Δx^≠ at pH 5 (Table 2). The temperature variation does not seem to much affect the values of Δx and Δx^≠.

To summarize, our results reveal that both the A:a and B:b knob-hole bonds are stronger in the neutral solution (pH 7) compared with the acidic environment (pH 5). The A:a knob-hole bonds are stronger than the B:b knob-hole bonds at pH 7 but weaker at pH 5 (Fig. 4). These conclusions become evident when comparing the values of bond dissociation energy G_b for all model systems (Table 2). Quite unexpectedly, the A:a and B:b knob-hole bonds become stronger, not weaker, upon the temperature increase from 25 to 37 °C both in acidic and neutral solutions. The A:a and B:b knob-hole bonds tend to form tighter and more brittle complexes at pH 7 than at pH 5. The B:b knob-hole bonds are looser and more compliant than the A:a knob-hole bonds at pH 7 but tighter and more brittle at pH 5.

DISCUSSION AND CONCLUSIONS

Fibrin polymerization driven by knob-hole interactions is a highly dynamic, kinetically controlled process (37). From the previous x-ray crystallographic studies, knowledge about the molecular interactions mediating formation of the A:a and B:b knob-hole complexes has been limited to the structure of fragment D co-crystallized with synthetic peptides GPRP and GHRP mimicking knobs ‘A’ and ‘B’, respectively (17, 18, 38). On the other hand, state-of-the-art experimental instrumentation, such as optical trap-based force spectroscopy, has made it possible to directly quantify the strength of the A:a and B:b knob-hole bonds at the single molecule level (6, 19). However, these experiments cannot access the full dynamics of molecular transitions and resolve the molecular structural details of coupling of knobs ‘A’ and ‘B’ to holes ‘a’ and ‘b’, respectively. The heterogeneity of experimental force signals, partial elongation of fibrin molecules, and presence of nonspecific interactions all make interpretation of experimental data difficult. Despite the critical biological and clinical significance of blood clotting, there have been no theoretical studies of the kinetics (time scales and pathways) and thermodynamics (energy landscapes) of the knob-hole interactions aiming at a fundamental understanding of their mechanism(s) at the molecular and submolecular level. Here, we showed that these goals can be achieved by using MD simulations, which in combination with experimental results continue to play an important role in advancing our understanding of protein-protein interactions (39). In recent years, dynamic force measurements in silico in which tensile forces are used to unfold proteins and to dissociate protein-protein complexes have become a powerful tool to interpret and clarify the results of nanomechanical experiments in vitro (22, 39, 40).

Here, for the first time, using a combination of MD simulations and theoretical methods, we explored the kinetics and thermodynamics and resolved the structural mechanisms of the knob-hole interactions in fibrin that initiate and drive fibrin polymerization. These approaches have enabled us to describe in atomic detail the native properties of the A:a and B:b knob-hole complexes and their force-induced dissociation. We also probed the influence of varying important ambient conditions, pH and temperature, on the A:a and B:b knob-hole coupling. The rationale for varying these parameters is that the knob-hole interactions are mainly electrostatic and hence are susceptible to a change in temperature and acidity, both of which have (patho)physiological significance. Our knowledge regarding the mechanism of knob-hole interactions in fibrin would be incomplete had we not understood the dynamic mosaic of binding residues stabilizing the A:a and B:b knob-hole bonds. For this reason, we constructed and analyzed the entire molecular maps of amino acid residues in holes ‘a’ and ‘b’ that establish strong persistent binding contacts with residues in the peptides GPRP (knob ‘A’ mimetic) and GHRP (knob ‘B’ mimetic), respectively. This has helped us identify the residues critical for binding and assess the relative importance of specific amino acid residues, clusters of residues, and even whole binding determinants. These comprehensive efforts have enabled us to extract qualitative and quantitative characteristics of fibrin polymerization.

Profiling the dependence of the knob-hole bond lifetimes on tensile force revealed that the A:a and B:b knob-hole bonds are roughly equally strong when probed mechanically; albeit the dissociation kinetics are sensitive to pH and temperature variation (Fig. 3). The finding that the strength of the A:a and B:b knob-hole bonds is similar is at odds with the recently reported experimental data according to which the A:a knob-hole bond is about 6-fold stronger than the B:b knob-hole bond (6, 19). To shed light on the origin of this disagreement, we performed pilot MD simulations by reproducing formation of the A:a knob-hole bonds using not just a GPRP-hole a construct but a short double-stranded fibrin oligomer formed by three fibrin monomers. In short, the oligomer was first built by superposing the structures of the double-D fragment (Protein Data Bank code 1FZC (24)) and fibrin monomer (Protein Data Bank code 3GHG (41)); the unresolved portions of the α chain and β chain with knobs ‘A’ and ‘B’ were reconstructed manually (Fig. 5A). Next, we ran long 250-ns simulations for the oligomer. We found that binding of the N-terminal end of the α chain (knob ‘A’) to the pocket in the γ-nodule (hole ‘a’) is accompanied by electrostatic coupling between residues γGlu³²³, γLys³⁵⁶, and γAsp²⁹⁷ in the γ-nodule and residues βLys⁵⁸, βAsp⁶¹, and βHis⁶⁷ in the central nodule of the adjacent fibrin monomers (Fig. 5, A and B). Hence, our preliminary data seem to indicate that the binding interface might extend beyond the GPR motif exposed upon thrombin cleavage at the N termini of the α chains that is traditionally named knob ‘A’; however, more simulations are needed to verify this result. In fact, secondary involvement of the N-terminal portion of the β chain in the A:a knob-hole binding is consistent with transient interactions between fibrin molecules mediated by the N terminus of the β chain revealed at the single molecule level (42). Furthermore, this finding supports an idea that the A:a knob-hole interactions in fibrin might have a much broader interface than just the peptide-in-pocket complex. The difference in the binding interfaces between natural protein complexes and peptide-based constructs is the most likely source of disagreement between the published experimental data and our results regarding the relative strength of the A:a and B:b knob-hole bonds. To the best of our knowledge, this is the first substantial evidence for interactions mediated by “the full knob,” which extends beyond the N-terminal GPR sequence.

FIGURE 5.

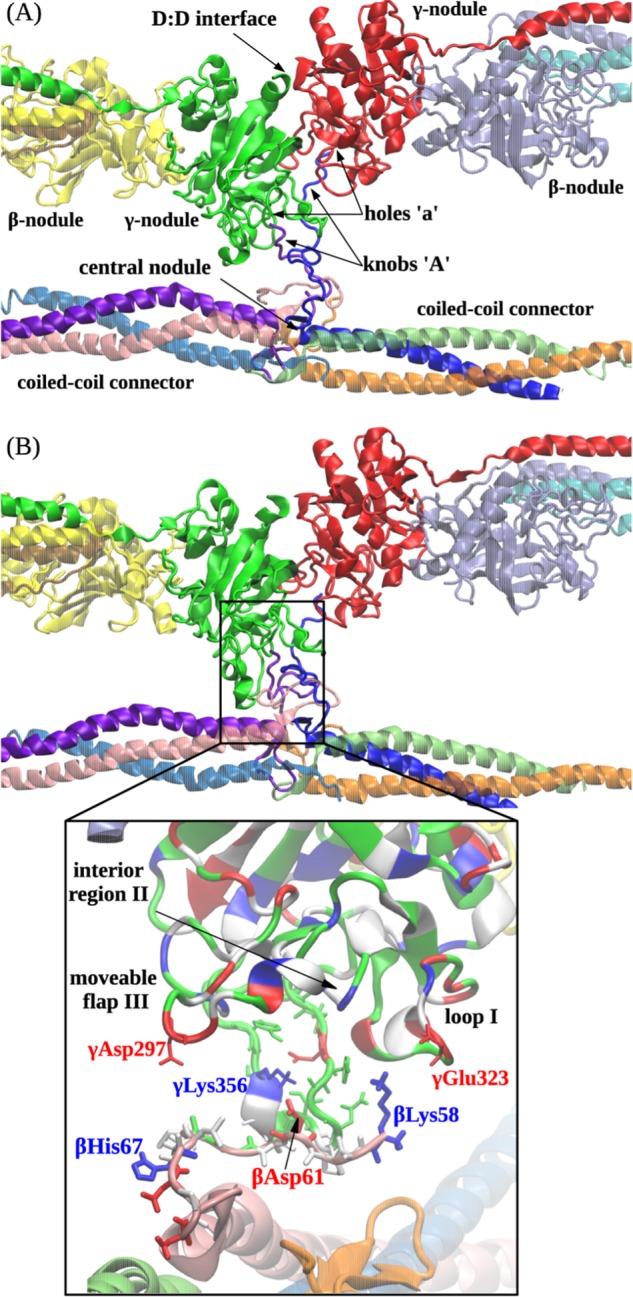
Computational reconstruction of the non-covalent coupling of the central nodule (bearing sites ‘A’) and the γ-nodules (bearing sites ‘a’). A, ribbon representation of the initial structure (before equilibration) of the double-D fragment of abutted fibrin molecules containing two γ- and two β-nodules. The residues in site ‘a’ form binding contacts with the residues of site ‘A’ emanating from the central nodule of the third fibrin monomer between the coiled coil connectors. B shows the translocation of the central nodule following formation of the A:a knob-hole bonds observed at the end of the simulation run. Also shown is the magnified view of electrostatic contacts between residues γGlu³²³ in loop I, γLys³⁵⁶ in the interior region, and γAsp²⁹⁷ in the moveable flap (all residues belong to site ‘a’ in the γ-nodule) and residues βLys⁵⁸, βAsp⁶¹, and βHis⁶⁷ in the N-terminal portion of the β chain in the central nodule (the GPR motif has been suppressed for clarity). In the central nodule, the residues colored in red represent negatively charged amino acids, whereas the residues colored in blue represent positively charged amino acids.

Although the A:a (and perhaps B:b) knob-hole interactions are very likely not limited to the GPR (or GHRP) motifs, the corresponding peptides have been widely used as “synthetic knobs” and as effective competitive inhibitors of the knob-hole interactions (6, 9, 19, 42–45). Thus, the core of the knob-hole binding characterized using x-ray crystallography is represented by the complexes formed with the GPRP and GHRP peptides, which have been successfully used to study the most basic aspects of the A:a and B:b knob-hole interactions (45, 46).

Another important finding is that the A:a and B:b knob-hole interactions in fibrin are not the end product of “all-or-none” transitions because they might occur through distinct pathways via formation of intermediate states (Fig. 3, pathway P2). An immediate consequence of this finding in the context of fibrin polymerization is that this might lead to the formation of A:a and B:b knob-hole bonds of varying strength. This should be expected because the knob-hole interactions occur in an environment where the contact duration and tensile force change due to the varying blood shear. There is a question whether the knob-hole bonds in fibrin exhibit a so-called “catch-slip” behavior (34, 35, 47, 48), i.e. when the strength of the bond, quantified by the average lifetime, first increases with increasing tensile force and then decreases at higher forces. This unusual type of protein-ligand interaction has been demonstrated for a number of interacting pairs, such as such as P-selectin/PSGL-1 (34), GP1bα/von Willebrand factor (49), bacterial adhesin FimH/mannose (50), integrin α5β1/fibronectin (51), and integrin LFA-1/ICAM-1 (52). Our results show that the A:a and the B:b knob-hole bonds behave as typical “slip” bonds in the 150–400-pN range of tensile forces, but we do not rule out the possibility that the knob-hole bonds might behave as “catch” bonds at lower forces (<150 pN). Because pulling simulations become prohibitively more expensive computationally at lower pulling forces, we were unable to probe the force dependence of the strength of the A:a and B:b knob-hole bonds below 150 pN.

Our results indicate that despite some differences in the kinetics depending on the magnitude of applied force and variation in temperature and pH there are similar structural transitions in holes ‘a’ and ‘b’ that accompany the force-induced dissociation of the A:a and B:b knob-hole bonds. We singled out the most important modes of motion in the direction of the “reaction coordinate,” receptor-ligand distance, both type and amplitude, which contribute the most to the forced dissociation reaction. We found that for the A:a (B:b) knob-hole bonds these structural changes are as follows: 1–4 Å (2–4 Å) elongation of loop I, stretching of the interior region by 3.5–4.5 Å (1–4 Å), and 2.5–7-Å (2–6.5-Å) translocation of the moveable flap. The extent of these changes depends on the degree of protonation and temperature (supplemental Fig. S6), and the amplitude of motions is larger at higher temperature.

Because in the simulations we have maintained the conditions of constant pressure and temperature, we used the Gibbs free energy to describe the thermodynamics of the A:a and B:b knob-hole interactions in fibrin. The profiles of the Gibbs free energy change, ΔG, as a function of the change in the interaction distance, ΔX, indicate rather strongly that in both the neutral solution and acidic solution the A:a and B:b knob-hole bonds become stronger at higher temperature (T = 37 °C) compared with the lower temperature (T = 25 °C). For the A:a knob-hole bonds at pH 7, G_b = 19.3 kcal/mol at 37 °C and 16.2 kcal/mol at 25 °C, and for pH 5, G_b = 6.1 kcal/mol at 37 °C and 1.7 kcal/mol at 25 °C. For the B:b knob-hole bonds at pH 7, G_b = 15.3 kcal/mol at 37 °C and 12.6 kcal/mol at 25 °C, and for pH 5, G_b = 9.2 kcal/mol at 37 °C and 8.4 kcal/mol at 25 °C (see Table 2). This is counterintuitive given that in general thermal fluctuations tend to destabilize and weaken non-covalent bonds. To find a structural basis for these unusual findings, we have compared the output from umbrella sampling calculations at T = 37 and 25 °C and found that in both hole ‘a’ and hole ‘b’ in neutral and acidic solutions there is an α-helix-to-random-coil transition in loop I that occurs at a higher temperature (T = 37 °C). The “melting transition” is displayed for the A:a knob-hole bond in Fig. 6 where we have compared the structures of the A:a knob-hole complex at 37 and 25 °C (pH 7; model systems Aa1 and Aa2). We see that residues γ327–330 in loop I form an α-helical pitch at 25 °C that melts into a more flexible random coil structure at 37 °C. As a result, residues γGlu³²⁸, γGln³²⁹, and γAsp³³⁰ come closer and bind more strongly with Arg³ in GPRP, which provides an additional ∼2.5–4.5 kcal/mol stabilization to the A:a knob-hole bond. This combined entropic (order-disorder transition) and enthalpic effect (formation of stronger contacts) compensates for the thermal destabilization of the knob-hole interfaces and accounts for the increased stability of the A:a knob-hole bond at T = 37 °C as compared with T = 25 °C. We found a similar transition in loop I in hole ‘b’ (data not shown).

FIGURE 6.

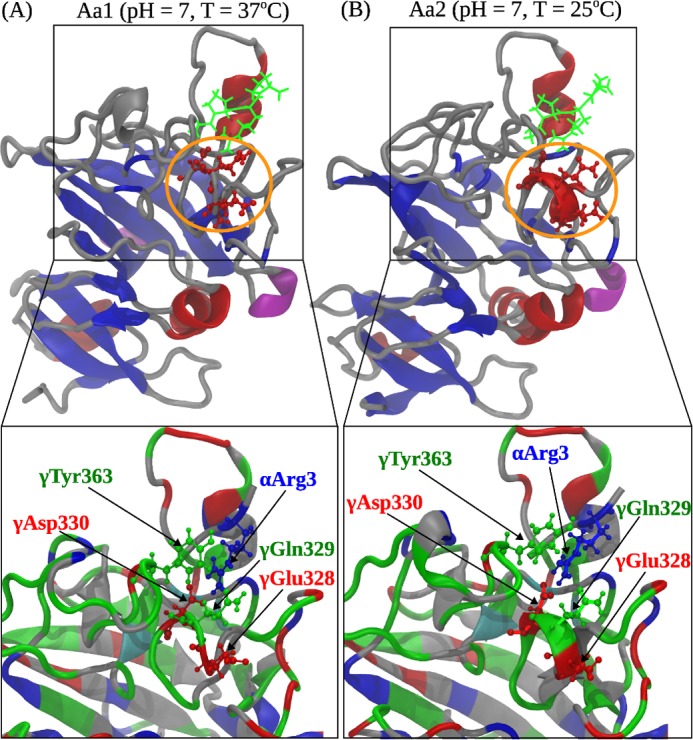
Comparison of the A:a knob-hole interactions in neutral solution (pH 7) at T = 37 °C (model system Aa1; A) and T = 25 °C (model system Aa2; B). Shown are the ribbon structures of binding site ‘a’ interacting with knob ‘A’. Color denotation is as follows: in hole ‘a’, α-helices are shown in red color, β-strands are in blue color, and coils and turns are shown in gray color; knob ‘A’ is displayed in green color. Residues γ327–330 in loop I form an α-helix at 25 °C but transition to a random coil structure at 37 °C. Interacting residues in loop I and GPRP are magnified below. The electrostatic coupling among residue γTyr³⁶³; residues γGlu³²⁸, γGln³²⁹, and γAsp³³⁰ in loop I; and residue Arg³ in the GPRP peptide is indicated.

In conclusion, we have performed a comprehensive study of the molecular mechanisms, thermodynamics, and kinetics of the knob-hole interactions in fibrin using theory and simulations. The results obtained provide a broad theoretical foundation for the key interactions in the fibrin polymerization process and offer physiologically relevant structural mechanistic insights into this biologically important process at the molecular and submolecular level. The results of these studies can be potentially helpful in translational research aiming at the computer-based design of fibrin-specific compounds (53) that could attenuate the knob-hole interactions in a desired fashion or modify the final clot structure to reduce the risk of thromboembolic complications.