Application of quantitative second-harmonic generation microscopy to dynamic conditions

Abstract

We present a quantitative second-harmonic generation (SHG) imaging technique that quantifies the 2D spatial organization of collagen fiber samples under dynamic conditions, as an image is acquired. The technique is demonstrated for both a well-aligned tendon sample and a randomly aligned, sparsely distributed collagen scaffold sample. For a fixed signal-to-noise ratio, we confirm the applicability of this method for various window sizes (pixel areas) as well as with using a gridded overlay map that allows for correlations of fiber orientations within a given image. This work has direct impact to in vivo biological studies by incorporating simultaneous SHG image acquisition and analysis.

1. Introduction

The first demonstration of second-harmonic generation (SHG), a second-order process wherein a noncentrosymmetric material (i.e., one with no center of inversion symmetry) converts a portion of incident light (with an efficiency of 10⁻⁸ ~ 10⁻⁹) to scattered light at exactly twice the incident frequency, dates back to the seminal work of Franken et al. in the early sixties [1, 2]. Its adaptation to an imaging modality was then demonstrated in inorganic structures in the next decade [3, 4]. The work of Freund and Deutsch subsequently extended SHG microscopy to image rat tail tendon—marking the first time the technique had been applied to a biological sample [5]. Since that time SHG microscopy has become increasingly recognized in bio-imaging studies for its unique imaging features, namely, high 3D spatial resolution and high contrast and specificity to some biological structures such as myosin and fibrillar collagen [6–8]. Further, the push to identify useful quantitative metrics for this imaging modality has resulted in several approaches [9–14]. For example, in recent years, Fourier transform-second harmonic generation imaging (FT-SHG) has been developed, whereby either 2D or 3D spatial-frequency analysis is used to quantify the spatial organization of structures at cellular scales (300 nm-100 µm), particularly type I collagen fibers [15–21]. Indeed, using measures such as preferred orientation (of collagen fibers) and orientation anisotropy, FT-SHG has been utilized to differentiate between healthy and injured tendon [17], assess age-related changes in cortical bone [18], quantify dissimilarities in stromal collagen fiber organization in human breast biopsies at different pathological stages [19], and to quantify the 3D spatial arrangement of collagen fibers, in general, and especially in the cervix [20, 21]. Notwithstanding these developments, full applicability of such quantitative SHG techniques to biological problems will necessitate their extension to dynamic situations. That is, although there has been some progress using SHG imaging for in vivo studies [22–24], to our knowledge, none have attempted real-time quantitative SHG imaging, i.e., computing some quantitative parameter(s) of interest simultaneously with image acquisition. Simultaneous image acquisition and image processing under dynamic conditions would inform the image acquisition process itself. It would permit an end user to update or change the imaging parameters (based on, for example, looking for fibers that are highly aligned along a particular direction) during image acquisition. This could greatly enhance imaging and would especially be significant for in vivo studies. In addition, simultaneous image acquisition and processing could potentially translate into added efficiency in disease diagnosis by reducing the feedback time between primary diagnosis and further action.

In an effort to adapt quantitative SHG imaging to eventual in vivo biological studies, this paper examines the experimental conditions that permit quantitative SHG imaging under dynamic conditions. We look at two extremes of test samples: stained tendon with well-aligned, highly organized collagen fibers and unstained, synthesized collagen scaffold. Using these samples, we apply quantitative SHG imaging to two dynamic situations. The first determines fiber-orientation information as the samples are spatially scanned in a plane. The second situation computes the same information for a collagen gel sample as it dries to form a 2D collagen scaffold assembly. To facilitate computation, a straightforward 2D gradient method (which is applied to the intensity of the images in real-space) is employed. Furthermore, we apply our approach to an example application to image and quantitatively analyze stromal collagen fibers belonging to individual cores in a standard breast tissue microarray (TMA) sample as they are progressively stage scanned, and where each core has been clinically classified as either benign or malignant. The paper is organized in the following way: section 2 describes the sample preparation, experimental setup, and quantitative measures used. Section 3 presents the results and discussion, while section 4 gives the conclusion.

2. Sample preparation and experimental setup

2.1 Sample preparation

Tendon, collagen scaffold, and tissue microarray samples were used in this study. Porcine tendon tissues were obtained from a local abattoir and embedded and preserved in OCT compound at −80° C. Next, the samples were brought to −20° C and 4-μm thick sections were cut using a cryostat (Leica CM3050S). They were then thawed and stained with a hematoxylene and eosin (H&E) stain. Finally, each tissue section was mounted with a permanent mounting media (Permount) onto a microscope coverslip (No 1.5).

The procedure for synthesizing the collagen scaffold follows closely to that described in the literature [25]. High concentration type I collagen solution (BD Biosciences) was extracted from rat tail tendon. A solution of 50 μL of 10x PBS was added to 426 μL of ultra-pure H₂O, followed by 0.5 μL of 1 N NaOH and 23.5 μL of collagen solution. The components were mixed in an eppendorf tube, sealed and refrigerated at 4° C for 24 hours. During experimentation, 10 μl volumes were transferred onto a coverslip for imaging.

A breast tissue microarray sample (US Biomax BR1003) was obtained from formalin-fixed, paraffin-embedded tissue. The sample comprised 1-mm diameter, 5-μm thick, cores of histologically variant classes of tissues (e.g., normal, dysplastic, and malignant). The samples were stained with H&E and mounted with xylene mounting medium onto a microscope coverslip (No 1.5).

2.2 Experimental setup & image analysis

Figure 1(a) shows the schematic of the experimental setup used for the purpose of this study. All experiments were carried out with a spectrally tunable, Ti:sapphire pulsed laser (Spectra-Physics Mai-Tai HP DeepSee), producing 100-fs duration pulses with 80-MHz repetition rate. The excitation wavelength used in this study is spectrally centered at 780 nm, and a combination of half-wave plate and polarizer are used to control the input power. A pair of galvanometer-based scanning mirrors (GVS012, Thorlabs) is used to scan the beam over a desired rectangular area. Scanning incorporates two triangular patterns of the same amplitude but with frequencies that are not harmonically related. This ensures fast and uniform illumination over the entire scanned area. Next, the scanned beam is reflected by a short pass, 670-nm dichroic beam splitter, and subsequently focused onto the sample using a 1.4 NA oil-immersion objective lens (Olympus U Plan S Apo 100x). The backward emitted SHG signal is collected by the same illumination objective followed by a laser-blocking filter (Semrock FF01-680/sp-25) and an SHG filter (Semrock FF01-390/18-25). The signal is captured using an EMCCD camera (Hamamatsu EM-CCD C9100-13) with a total pixel area of 512 x 512 with a constant EM gain of 100x for all images.

Fig. 1.

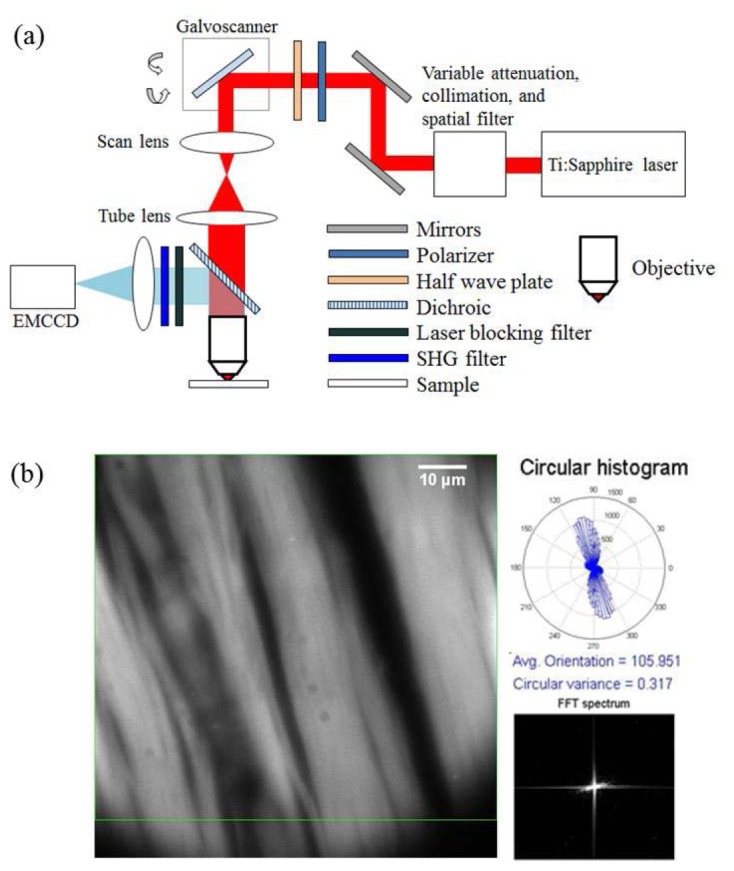
(a) Schematic of the experimental setup used and (b) an example SHG image of stained tendon sample with associated circular histogram (top right) and FFT spectrum (bottom right). See text for details.

Figure 1(b) displays the interface used for the real-time quantitative SHG analysis. Continuous frames of 512 x 512 pixel images are captured by the EMCCD camera and displayed on the screen. A customized MATLAB code permits simultaneous data analysis with image capture. A 2D gradient method [26, 27] is employed to determine the fiber orientation. First, a region of interest (ROI) is identified (outlined by the green rectangle). Next, the preferred fiber orientation at each pixel within the ROI is obtained by calculating the local intensity gradient and the result is subsequently depicted in the form of a circular histogram [Fig. 1(b), top right corner]. The associated circular variance, which varies from 0 to 1, renders a quantitative measurement of orientation isotropy, and information about it can be found elsewhere [28, 29]. An FFT spectrum of the ROI is also displayed [Fig. 1(b), bottom right corner], which can be used to directly determine preferred fiber orientation [15].

3. Results and discussion

In order to determine the capabilities of our approach under dynamic conditions, we first examine the application of quantitative SHG for two sample types for various imaging areas. Specifically, we estimate the acquisition time and processing time as a function of input power, sample type, scan area, fiber density, and desired signal-to-noise ratio (SNR). Figure 2 summarizes the results of this experiment, where (a) corresponds to images of tendon and (b) images of collagen scaffold for window sizes (green box) referring to (i) 120 x 120 (ii) 240 x 240 (iii) 360 x 360 and (iv) 512 x 512 pixels. As mentioned earlier, these two sample types are representative of two of the more extreme conditions: well-aligned, highly organized, dense (stained) collagen fibers, and randomly aligned, fairly disorganized, more sparse (unstained) collagen fibers. To make any comparison between the two image types feasible, an SNR of 7 is maintained for both samples by using an input power of ~3 mW and 40 mW for the tendon and scaffold samples, respectively. In terms of the fiber orientation analysis that is typical for quantitative SHG, it is clear from Figs. 2(a) and 2(b) that a change in the window size does not bring about any significant changes in the preferred orientation results (indicated at the bottom of each image). Indeed, we observe across all window sizes, the circular variance is lower for tendon than scaffold, consistent with the fact that the latter is a more randomly aligned sample. Figure 2(c) depicts the acquisition time per window size for each sample, ranging from ~400 ms to 6 sec. Note that although the EMCCD camera can capture a frame in ~32 ms, we use much longer image acquisition times to account for the low conversion efficiency of second-harmonic generation. In addition, we confirm that the acquisition time scales with window size for the first three pixel areas; however, for 512 x 512 pixels, more than 4x the base window size (120 x 120), the corresponding acquisition time is ~12x longer. This comes from the fact that the average power is distributed over a larger area, and thus, the corresponding laser dwell time per point needs to increase in order to generate SHG. Therefore, it is expected that for increased window sizes and fixed input power, the acquisition time will increase in order to maintain the same SNR between various window sizes. Finally, Table 1 presents the processing time required for each image size for each sample. The time is observed to scale with both the image size and the distribution of fibers on the image, as can be observed for tendon and scaffold images of the same size; hence, for the same pixel area, tendon sample requires a longer processing time compared to the sparsely distributed scaffold sample. It should be noted that the three parameters considered, namely, imaging window size, SNR, and acquisition time, are all interdependent. For our purposes, we have chosen the SNR to be the fixed parameter since we believe it to be the more pragmatic choice to a microscopist.

Fig. 2.

SHG images of (a) tendon and (b) collagen scaffold fibers for various pixel areas and a fixed SNR of 7. The corresponding pixel areas are: (i) 120 x 120 (ii) 240 x 240 (iii) 360 x 360 and (iv) 512 x 512 pixels. The same scale applies to all images. (c) The acquisition time for each image area is plotted against the pixel area.

Table 1. Image processing time for various image sizes.

Image Area	Image Processing time (ms)
(Square pixels)	Tendon	Scaffold
120 x 120	420	280
240 x 240	570	430
360 x 360	680	570
512 x 512	950	750

Using the information summarized in Fig. 2 and Table 1, we next consider two dynamic situations. A video of the first case is provided (Media 1 ^{(2.1MB, MP4)} ) along with select frames shown in Fig. 3(a) . Here, the tendon sample is scanned by moving the stage laterally in 5-μm steps [relative to the initial position (0, 0)] in arbitrary directions, the lateral coordinates (x, y) of which are shown in the bottom, right-hand corner of each image. The window size used here is 240 x 240 pixels, with an acquisition time of 1.2 s per location and a fixed input power. The preferred orientation and circular variance are computed simultaneously as the sample is scanned. The same procedure is repeated and captured in a video (Media 2 ^{(1.7MB, MP4)} ) for the collagen scaffold sample, select frames from which are shown in Fig. 3(b). A 1.2 s acquisition time per location is also used here, with an adjusted input power of 40 mW. Overall, we observe that ~2 s is required for image acquisition and processing; therefore, dynamic processes that are of the order of 2 s or longer can be simultaneously captured and analyzed (using our metrics) without any tradeoffs. Again, we observe that for the case of collagen scaffold, the circular variance is almost twice that of tendon.

Fig. 3.

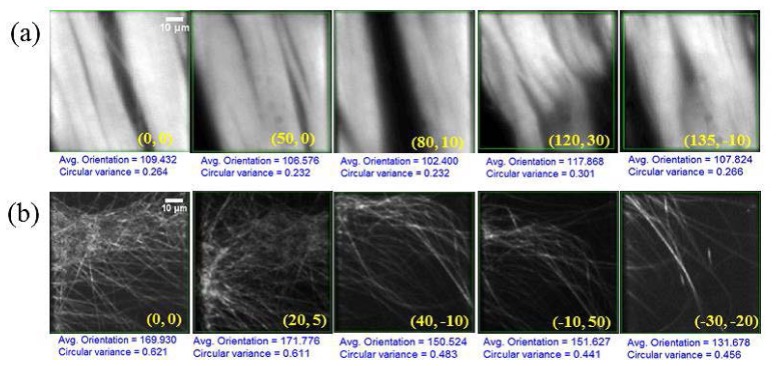
SHG images of stage-scanned (a) tendon (Media 1 ^{(2.1MB, MP4)} ) and (b) collagen scaffold fibers (Media 2 ^{(1.7MB, MP4)} ) at different locations shown in top left corner. The lateral coordinates for each image, relative to the initial (0, 0), are provided in the bottom right hand corner for each frame. The same scale applies to all images. See text for additional details.

For the second dynamic situation, we attempt to carry out quantitative-SHG imaging of a collagen gel solution in real time, as it dries at room temperature (~23° C) over a period of 30 min. In this case, 10 μL of solution dries to form a 2D collagen fiber layer on a microscope coverslip. To visualize this process, the objective lens is focused on to the bottom of the coverslip. A video (Media 3 ^{(1.6MB, MP4)} ) is captured and select frames are shown in Fig. 4 . Initially, blurred images are observed, consistent with the fact that collagen fibers occupy a 3D volume, causing SHG signals to be generated and scattered from various layers within that volume. As the fibers begin to settle down, the SNR increases [see Fig. 4 (ii)-(iv)]. In addition, we confirm that the preferred orientation and circular variance, our metrics of interest, can easily be computed during drying; note that the circular variance decreases with time as more defined fiber structures become visible. It is worth mentioning here, that collagen scaffolds are extremely important to many areas of tissue and bioengineering, especially for bone repair applications. An approach that noninvasively monitors the drying and assembly of such fibers in situ, while simultaneously quantifying fiber organization, would be attractive to these fields and could ultimately facilitate new strategies in fiber scaffold design.

Fig. 4.

SHG images of collagen scaffold fiber formation (Media 3 ^{(1.6MB, MP4)} ) at different times in (i)10 (ii)11.4 (iii)11.6 (iv)12.2 minutes. The same scale applies to all images.

It is interesting to consider how our approach may be useful in a clinical setting. Let us consider a scenario where a pathologist would be interested in analyzing several tissue biopsies (e.g., breast or skin samples) for malignancy. It would be tremendously useful to be able to simultaneously image and analyze each sample in order to promptly make an initial recommendation. To simulate such a scenario, we next apply quantitative SHG to stromal collagen fibers from breast tissue biopsies from various cores in a TMA as the cores are continuously stage scanned; such TMA slides offer clinical compatibility and are used for gold-standard histopathological diagnosis of cancer. FT-SHG has previously been applied to such tissue cores, where it was found that there exists clear differences in regularity of fiber orientation between healthy and malignant tissues. Specifically, malignant tissues generally have well-directed, organized fibers, and healthy tissues exhibit significantly more random organization [19]. In an effort to adapt our simultaneous imaging and quantitative analysis method to capture this difference in fiber orientation, we have applied a gridded overlay map for each image as we moved from one core to another of a TMA, to allow for potential correlation analysis between fibers from different spatial regions within the same image. A video (Media 4 ^{(2.3MB, MP4)} ) is captured and two representative frames are shown in Fig. 5 . Here we use 10 mW of average power, 1.2 s acquisition time, and 512 x 512 pixel area comprising an 8 x 8 grid (and thus each grid contains 64 pixels). Details on 2D quantitative-SHG analysis to calculate localized fiber orientation can be found elsewhere [15]. The processing times varied from 300 to 800 ms depending on the density of fibers. We confirm in Fig. 5 (and the accompanying video) that malignant tissues generally have well-directed, organized fibers, and healthy tissues exhibit significantly more random organization [19].

Fig. 5.

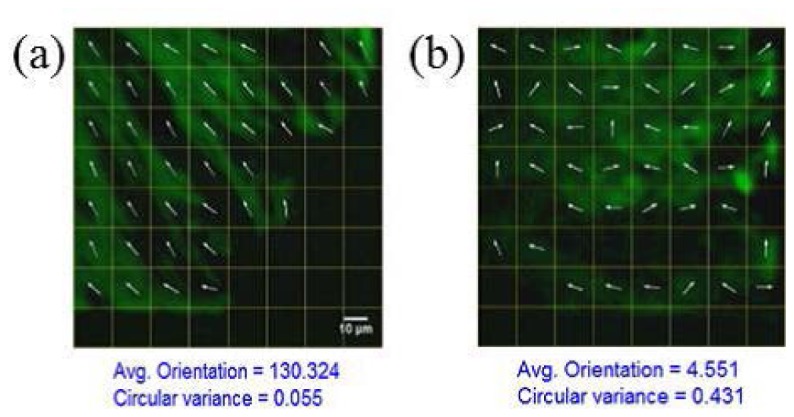
SHG images of breast tissue samples (Media 4 ^{(2.3MB, MP4)} ) at different cores corresponding to (a) malignant (b) healthy tissues. The same scale applies to all images.

Conclusion

In an effort to move quantitative-SHG imaging to eventual in vivo studies, we demonstrated its application to several dynamic situations and calculated the quantitative metrics. Primarily we have considered two extremes of collagen sample types: well-aligned, dense (stained) tendon samples and sparsely distributed, randomly aligned (unstained) collagen scaffolds. We first established the minimum acquisition time for a fixed input power and SNR of 7, and for various window sizes (pixel areas) ranging from 120 x 120 to 512 x 512 pixels (the maximum pixel area for our EMCCD camera). We found that the acquisition time scales with window size for small to moderate pixel areas, and increases nonlinearly for the maximum pixel area—a direct result of the increased laser dwell time necessary to generate an SHG signal. We then showed that quantitative metrics such as preferred fiber orientation and circular variance can be computed simultaneously for each sample as an SHG image is acquired. In one case, we computed the aforementioned metrics for each sample during lateral stage scanning. Here, we established that for a window size of 240 x 240 pixels, average input powers of 3 mW and 40 mW were required for the tendon and collagen scaffold samples, respectively, with a corresponding minimum acquisition time of 1.2 s per frame and a processing time from ~500 to 700 ms depending on the density of fiber distribution. For the second dynamic condition we again determined the desired quantitative metrics during a collagen gel drying process. We observed a progressively smaller degree of circular variance as the fibers dried and assembled on the coverslip. Our approach was also applied to a simulated clinical scenario by demonstrating quantitative SHG imaging on regularly, stage-scanned breast tissue cores in a tissue microarray sample. By analyzing localized fiber orientations for each imaged area, we showed that it was possible for our approach to discern between healthy and malignant tissues under this dynamic condition. We believe that our approach has potential application to real-time imaging of other noncentrosymmetric biological structures such as axons for neuroimaging studies [30], and collagen fibers during cervical remodeling for studies of premature birth [21]. Additionally, our basic approach can also be applied to other nonlinear imaging methods [31]. We are currently investigating extending our method to video rates using a combination of a detector with higher quantum efficiency and GPU-based parallel processing algorithm.