Abstract
Rodent models are increasingly used to study refractive eye development and development of refractive errors; however, there is still some uncertainty regarding the accuracy of the optical models of the rat and mouse eye primarily due to high variability in reported ocular parameters. In this work, we have systematically evaluated the contribution of various ocular parameters, such as radii of curvature of ocular surfaces, thicknesses of ocular components, and refractive indices of ocular refractive media, using variational analysis and a computational model of the rodent eye. Variational analysis revealed that not all variation in ocular parameters has critical impact on the refractive status of the eye. Variation in the depth of the vitreous chamber, thickness of the lens, radius of the anterior surface of the cornea, radius of the anterior surface of the lens, as well as refractive indices for the lens and vitreous, appears to have the largest impact on the refractive error. The radii of the posterior surfaces of the cornea and lens have much smaller contributions to the refractive state. These data provide the framework for further refinement of the optical models of the rat and mouse eye and suggest that extra efforts should be directed towards increasing the linear resolution of the rodent eye biometry and obtaining more accurate data for the refractive indices of the lens and vitreous.
OCIS codes: (080.0080) Geometric optics; (170.0170) Medical optics and biotechnology; (330.0330) Vision, color, and visual optics; (000.1430) Biology and medicine; (080.1753) Computation methods; (170.3660) Light propagation in tissues; (170.4460) Ophthalmic optics and devices; (170.4470) Ophthalmology; (330.7326) Visual optics, modeling
1. Introduction
Mouse and rat animal models have been increasingly used for the studies of normal eye development and various pathological conditions, affecting visual system. These models are used because of high similarity of the rodent physiology and genome organization to those of humans and availability of well-established techniques for targeted genome manipulation in mice and rats. Mice also recently have been introduced as a promising model for the studies of refractive eye development. Although extensive efforts have been directed towards elucidation of the rodent eye anatomy and physiology, much less is known about mouse eye optics and refractive properties.
Several studies analyzed the biometry and schematics of the mouse and rat eyes using frozen sections and refractive indices obtained from ray tracing experiments. Hughes [1], Campbell and Hughes [2], and Chaudhuri et al. [3] have measured basic ocular parameters of the rat eye and proposed a schematic eye model for the rat eye. Similar studies were conducted in mice by Remtulla and Hallett [4] and Schmucker and Schaeffel [5], who proposed schematic eye models for the mouse. These studies reported average radii of curvature and thickness of the ocular components and refractive indices at different wavelengths for both mouse and rat and calculated average refractive errors predicted by the schematic eye models at different wavelengths. Remtulla and Hallett [4] also compared the mouse and rat eyes in terms of linear scale, magnification factor and refractive indices. High resolution imaging of the rodent eyes using adaptive optics is complicated by the high optical power of the eye and relatively high amounts of spherical aberration and coma [6, 7]; however, Geng et al. found that the optical quality of the mouse eye for retinal imaging is remarkably good because mouse eye has larger numerical aperture and a similar amount of root mean square (RMS) higher order aberrations compared to the human eye [8].
Although these studies provided baseline information about optical properties of the rodent eye, including average schematics of the eye, there is a great degree of uncertainty regarding the contribution of various optical parameters to the calculated refractive error of the eye. This is particularly important due to high variability in the reported biometrical parameters and refractive errors among different inbred mouse strains, as well as significant differences in ocular parameters and refractive errors even for the same strain of mice [9–11]. For example, significant differences in the corneal radius of curvature, crystalline lens thickness, vitreous chamber depth, and refractive error were reported between C57BL/6J, C57L/J and CZECHII/EiJ mouse strains [10]. There are also significant differences in the reported refractive errors for the most commonly used C57BL/6 mice. Although several studies found that refractive errors in C57BL/6 mice are close to zero diopters [12–19], other studies reported either 4.1-6.4 D of hyperopia or 5.6-9.2 D of myopia in the same strain of mice [5, 8, 20–22]. The source of these differences is currently unknown and the extent to which errors in the measurements of different ocular parameters affect the calculated refractive errors is unclear.
In this paper, we used a custom-built paraxial ray tracing model of the rodent eye to analyze the impact of variations in individual ocular parameters (i.e., curvatures of the ocular surfaces, thicknesses of the ocular components, and depths of the chambers of the eye) on the refractive state of the rodent eye and the resulting refractive error. This “variational analysis” allowed us to identify ocular parameters, which have the largest impact on the refractive state and the value of the refractive error in the mouse and rat eye, as well as those parameters, which have relatively minor influence.
2. Methods
2.1. Mouse and rat schematic eye parameters
The rat schematic eye used in this study was developed using ocular parameters reported by Hughes [1], Campbell and Hughes [2], and Chaudhuri et al. [3]. The mouse schematic eye was based on the parameters obtained from Remtulla and Hallett [4] and Schmucker and Schaeffel [5]. Ocular parameters used for modeling of the rat and mouse eyes are summarized in Table 1 and Table 2 respectively.
Table 1. Summary of the ocular parameters used for the optical model of the rat eye*.
| Parameters | Anterior Cornea | Posterior Cornea | Anterior Lens | Posterior Lens | Anterior Retina | Posterior Retina | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Radius (r, µm) | 3051 (rac) | 2959 (rpc) | 2535(rpc) | -2441(rpl) | -3543(rar) | -3706 (rpr) | ||||||
| ︸ | ︸ | ︸ | ︸ | ︸ | ||||||||
| Thickness (tt, µm) | 156 (ttc) | 708(ttacd) | 3814 (ttl) | 1409 (ttvcd) | 217 (ttr) | |||||||
| Refractive index (n) at wavelength (nm) | nc | nacd | nl | nvcd | nr | |||||||
| λ = 475 | 1.3882 | 1.3381 | 1.6974 | 1.3379 | 1.3379 | |||||||
| λ = 500 | 1.3864 | 1.3366 | 1.6925 | 1.3367 | 1.3367 | |||||||
| λ = 525 | 1.3848 | 1.3355 | 1.6888 | 1.3358 | 1.3358 | |||||||
| λ = 550 | 1.3838 | 1.3346 | 1.6854 | 1.3349 | 1.3349 | |||||||
| λ = 575 | 1.3829 | 1.3336 | 1.6825 | 1.3341 | 1.3341 | |||||||
| λ = 600 | 1.3821 | 1.3329 | 1.6798 | 1.3332 | 1.3332 | |||||||
| λ = 625 | 1.3812 | 1.3321 | 1.6777 | 1.3322 | 1.3322 | |||||||
| λ = 650 | 1.3804 | 1.3315 | 1.6761 | 1.3319 | 1.3319 | |||||||
Table 2. Summary of the ocular parameters used for the optical model of the mouse eye*.
| Parameters | Anterior Cornea | Posterior Cornea | Anterior Lens | Posterior Lens | Anterior Retina | Posterior Retina | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Radius (r, µm) | 1517 (rac) | 1463 (rpc) | 1248 (ral) | -1155 (rpl) | -1643 (rar) | -1666 (rpr) | |||||
| ︸ | ︸ | ︸ | ︸ | ︸ | |||||||
| Thickness (tt, µm) | 93 (ttc) | 452(ttacd) | 2032 (ttl) | 558 (ttvcd) | 237 (ttr) | ||||||
| Refractive index (n) at wavelength (nm) | nc | nacd | nl | nvcd | nr | ||||||
| λ = 488 | 1.4102 | 1.3390 | 1.6952 | 1.3390 | 1.3390 | ||||||
| λ = 544 | 1.4060 | 1.3376 | 1.6778 | 1.3365 | 1.3365 | ||||||
| λ = 596 | 1.4030 | 1.3353 | 1.6665 | 1.3343 | 1.3343 | ||||||
| λ = 655 | 1.4015 | 1.3336 | 1.6590 | 1.3329 | 1.3329 |
2.2. Optical modeling and ray tracing
Ray tracing for both rat and mouse eyes has been performed using the laws and principles of paraxial optics [23] and a custom computer program written and run in MATLAB® (The MathWorks, Inc., Natick, MA). Snell’s law [24, 25] was applied to calculate ray paths and the optical geometry of the eye. The ray tracing model described below relies on exact formulas for Snell’s law applied at each interface, and thus it is applicable for wide-angle ray tracing. In this paper, the subject of the study is limited to the analysis of paraxial eye parameters using homogeneous lens model. Specifically, we analyzed the ametropia and its dependence on the radii of curvature, relative distances, and refractive indices of the eye components. In the particular numerical implementation, the input ray approaching the eye is parallel to the optical axis and the distance between this ray and optical axis, yp, is set to be much smaller than all the linear dimensions of the eye components. We found that with yp < 25µm, our ray tracing model generates the values for ametropia, as well as locations of all cardinal points, consistent with the models reported in [3–5].
The parameters used for ray tracing are radii of curvatures, thicknesses of ocular components and refractive indices of the ocular refractive media. Figure 1 shows main refracting surfaces, ocular components and paraxial schematic model of the emmetropic rodent eye. For the emmetropic eye, which has zero refractive error (ametropia, A), paraxial rays of light traveling parallel to the optical axis will converge at the focal point located at the photoreceptor layer of the retina. In the case of the myopic eye (A < 0), the focal point will be located in front of the retina, whereas in the case of the hyperopic eye (A > 0), the focal point will be located behind the retina.
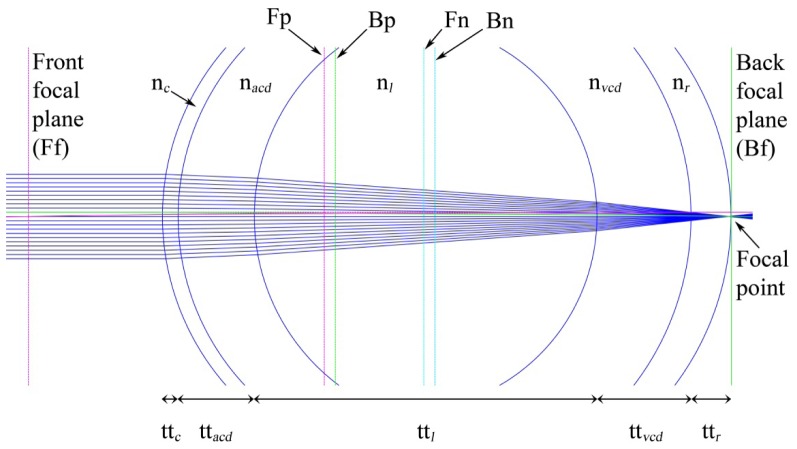
Fig. 1.
Paraxial schematic model of the emmetropic rodent eye. Paraxial rays meet at the focal point located at the level of photoreceptors. The eye consists of six main refracting surfaces, i.e., anterior cornea, posterior cornea, anterior lens, posterior lens, anterior retina, and posterior retina. The main volume of a rodent eye is occupied by the crystalline lens, followed by the vitreous chamber, anterior chamber, and retina respectively. Fp: front principal plane; Bp: back principal plane; Ff: front focal plane; Bf: back focal plane; Fn: front nodal point; Bn: back nodal point; nc: refractive index of cornea; nacd: refractive index of the aqueous; nl: refractive index of the lens; nvcd: refractive index of the vitreous; nr: refractive index of the retina; ttc: thickness of the cornea; ttacd: anterior chamber depth; ttl: thickness of the lens; ttvcd: vitreous chamber depth; ttr: thickness of the retina.
Paraxial rays emanate from the source (x = -∞) and after refraction through different surfaces converge at a specific point, which is called the back focal point. The plane corresponding to the back focal point is called the back focal plane (Bf). If the source is at x = + ∞ and paraxial rays meet at a point in front of surfaces after number of refractions through surfaces, this point is called front focal point and the plane corresponding to it is called front focal plane (Ff). If the rays from front and back focal points are back-traced and the incident rays travel without changing their angles, the incident rays and focal point rays will intersect at specific points. These points of intersection are called front principal and back principal points respectively. The planes corresponding to the front and back principal points are called front principal plane (Fp) and back principal plane (Bp). Figure 1 shows all layers and planes with the proper notations.
We used all these ocular parameters, i.e., radii of curvature (r), thicknesses of ocular components (tt), and refractive indices of ocular media (n), to perform ray tracing: where s denotes the points in which layers intersect the x plane or, thus, denoting the location of the layers on the x-axis. Elements of s can be written as:
For forward ray tracing, paraxial rays are coming from infinite source. Thus, x0 = -∞ and the height of paraxial rays (yp) is y0 = yp. Slope is given as t0 = - (y0/x0); Xmin = 0 and Xmax = length of surfaces (s). Thus, the equation of the line at first surface is given as:
| (1) |
| (2) |
If we have N surfaces, the equations of ray tracing are given as:
| (3) |
where
| (4) |
| (5) |
| (6) |
| (7) |
By following the same approach as in forward ray tracing, we had derived the formulae for calculation of Xb, Yb and slope tb for backward ray tracing as shown in Eq. (8), Eq. (11) and Eq. (12) respectively:
| (8) |
where
| (9) |
| (10) |
| (11) |
| (12) |
After forward and backward ray tracing was done, we had obtained equations for the principal planes, focal planes and nodal planes which are shown below:
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
2.3. Refractive error and variational analysis
All necessary information required for the calculation of refractive error was extracted from the ray tracing models. By incorporating known values for the optical parameters r, t, s and n in Eqs. (1) through (12), we were able to calculate X, Y and slope t. Further substituting these values in Eqs. (13) through (18), we had obtained principal planes and focal planes, which are required for the calculation of the refractive error. Finally, the refractive error of an eye was calculated using Eq. (19):
| (19) |
In order to study the effects of minor changes in optical parameters on refractive error, we performed variational analysis. In the variational analysis, only one optical parameter out of the possible 16 parameters is changed and its effect on the refractive error is observed. We have 6 refractive layers in the eye and other ocular parameters, which are shown in Fig. 1. Radius r is a set of 6 values and is expressed by Eq. (20):
| (20) |
Similarly, thicknesses tt and refractive indices n of the refracting surfaces contain 5 elements each. These are represented by Eq. (21) and Eq. (22) respectively:
| (21) |
| (22) |
To estimate the effects of r, tt and n on the refractive error, each parameter is incremented by a small variable value. This incremented variable is denoted by “d” for r and tt, and “dd” for n. While performing variational analysis, we have set the values of d to 1µm and dd to 0.001. For example, if we would like to estimate the effect of the radius of the anterior cornea, the radius of the anterior cornea (rac) will be incremented by d = 1 µm and the rest of the parameters will remain unchanged. The new set of r, tt and n are expressed by Eq. (23), Eq. (24), and Eq. (25):
| (23) |
| (24) |
| (25) |
If the new calculated value of the refractive error due to change “d” in the radius of the anterior cornea rac is A1, then the change in the value of the refractive error due to the change in a single optical parameter rac is called the derivative for the radius of anterior cornea and represented by Eq. (26):
| (26) |
The same approach was used to calculate the derivatives for all ocular parameters and estimate the impact of changes in these parameters on the refractive error.
3. Results
All derivatives for the radii of curvature (r), thickness (tt) and refractive indices (n) of various ocular components for the rat and mouse eye at different wavelengths are shown in Table 3 and Table 4 respectively. The wavelength-specific refractive error values for the rat and mouse eyes calculated using ocular parameters from Tables 1 and 2 match data reported by Chaudhuri et al. [3] and Remtulla and Hallett [4] (Tables 3 and 4). We found that a change of 14.4 µm in the axial position of the rat retina would cause a shift in refraction of 1 D, which is close to 14.8 µm per diopter reported by Chaudhuri et al. for an age-matched P120 rat [3]. Our data suggest that the axial position of the retina would have to change by 4.1 µm to cause a shift in refraction of 1 D in the mouse, which is close to 4 µm per diopter reported by Remtulla and Hallett [4] and slightly less than 7 µm suggested by the age-matched P140 schematic mouse eye model proposed by Schmucker and Schaeffel [5]. Variational analysis revealed that different ocular parameters have different effects on the refractive state of the eye. The refractive indices of the lens and vitreous, as well as vitreous chamber depth and lens thickness would have the largest effect on the refractive state of the eye in both rats and mice. The radii of the anterior surfaces of the cornea and lens also have significant impact on the refractive state, while radii of the posterior surfaces of the cornea and lens have much smaller contributions to the refractive state. The radii of the anterior and posterior surfaces of the retina have no effect on refractive error.
Table 3. Variational analysis of optical parameters for the rat eye*.
| Wavelength (nm) | 475 | 500 | 525 | 550 | 575 | 600 | 625 | 650 | |
|
Refractive error (D)
Chaudhuri et al. [ 3 ] |
+ 6.3 | + 7.7 | + 8.7 | + 9.7 | + 10.5 | + 11.2 | + 11.7 | + 12.2 | |
|
Calculated
Refractive error (D) |
+ 6.3 | + 7.7 | + 8.7 | + 9.7 | + 10.5 | + 11.2 | + 11.7 | + 12.2 | |
|
D
E R I V A T I V E S |
drac | 0.0427 | 0.0428 | 0.0427 | 0.0428 | 0.0428 | 0.0428 | 0.0428 | 0.0428 |
| drpc | −0.0057 | −0.0057 | −0.0056 | −0.0057 | −0.0057 | −0.0057 | −0.0057 | −0.0057 | |
| dral | 0.0488 | 0.0485 | 0.0483 | 0.0481 | 0.0480 | 0.0478 | 0.0477 | 0.0476 | |
| drpl | −0.0083 | −0.0082 | −0.0081 | −0.0081 | −0.0080 | −0.0080 | −0.0079 | −0.0079 | |
| drar | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | −3.55e−15 | 0.0000 | 1.78e−15 | |
| drpr | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| dttc | −0.0131 | −0.0134 | −0.0135 | −0.0137 | −0.0138 | −0.0139 | −0.0140 | −0.0141 | |
| dttacd | −0.0104 | −0.0106 | −0.0108 | −0.0109 | −0.0111 | −0.0112 | −0.0112 | −0.0113 | |
| dttl | −0.0370 | −0.0372 | −0.0373 | −0.0374 | −0.0374 | −0.0375 | −0.0376 | −0.0376 | |
| dttvcd | −0.0697 | −0.0695 | −0.0694 | −0.0693 | −0.0692 | −0.0692 | −0.0691 | −0.0691 | |
| dttr | −0.0697 | −0.0695 | −0.0694 | −0.0693 | −0.0692 | −0.0692 | −0.0691 | −0.0691 | |
| dnc | 0.0016 | 0.0016 | 0.0015 | 0.0015 | 0.0015 | 0.0014 | 0.0014 | 0.0014 | |
| dnacd | 0.0140 | 0.0137 | 0.0136 | 0.0134 | 0.0132 | 0.0131 | 0.0130 | 0.0130 | |
| dnl | −0.3176 | −0.3182 | −0.3186 | −0.3190 | −0.3194 | −0.3197 | −0.3201 | −0.3202 | |
| dnvcd | 0.1290 | 0.1289 | 0.1288 | 0.1287 | 0.1286 | 0.1286 | 0.1286 | 0.1285 | |
| dnr | 0.0119 | 0.0118 | 0.0117 | 0.0116 | 0.0116 | 0.0115 | 0.0115 | 0.0114 | |
*Derivatives indicate the change in the value of the refractive error due to change in the value of the respective optical parameter. Critical parameters for the rat are enclosed in red boxes. drac: derivative for the radius of the anterior surface of the cornea; drpc: derivative for the radius of the posterior surface of the cornea; dral: derivative for the radius of the anterior surface of the lens; drpl: derivative for the radius of the posterior surface of the lens; drar: derivative for the radius of the anterior surface of the retina; drpr: derivative for the radius of the posterior surface of the retina; dttc: derivative for the thickness of the cornea; dttacd: derivative for the depth of the anterior chamber; dttl: derivative for the thickness of the lens; dttvcd: derivative for the depth of the vitreous chamber; dttr: derivative for the thickness of the retina; dnc: derivative for the refractive index of the cornea; dnacd: derivative for the refractive index of the aqueous; dnl: derivative for the refractive index of the lens; dnvcd: derivative for the refractive index of the vitreous; dnr: derivative for the refractive index of the retina. Derivatives are calculated for 1 µm change in the radius (r) and thickness (tt), and for 0.001 units change in the refractive index (n).
Table 4. Variational analysis of optical parameters for the mouse eye*.
| Wavelength (nm) | 488 | 544 | 596 | 655 | |
|
Refractive error (D)
Remtulla & Hallett [ 4 ] |
−9.4 | + 0.4 | + 6.6 | + 10.8 | |
|
Calculated
Refractive error (D) |
−9.4 | + 0.4 | + 6.6 | + 10.8 | |
|
D
E R I V A T I V E S |
drac | 0.1748 | 0.1765 | 0.1775 | 0.1783 |
| drpc | −0.0315 | −0.0308 | −0.0309 | −0.0312 | |
| dral | 0.1860 | 0.1798 | 0.1765 | 0.1744 | |
| drpl | −0.0310 | −0.0294 | −0.0285 | −0.0279 | |
| drar | 3.5e−15 | 5.5e−17 | 0.0000 | 0.0000 | |
| drpr | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| dttc | −0.0473 | −0.0511 | −0.0535 | −0.0552 | |
| dttacd | −0.0332 | −0.0369 | −0.0390 | −0.0404 | |
| dttl | −0.1294 | −0.1314 | −0.1326 | −0.1334 | |
| dttvcd | −0.2455 | −0.2428 | −0.2412 | −0.2401 | |
| dttr | −0.2455 | −0.2428 | −0.2412 | −0.2401 | |
| dnc | 0.0041 | 0.0037 | 0.0034 | 0.0032 | |
| dnacd | 0.0156 | 0.0124 | 0.0106 | 0.0093 | |
| dnl | −0.5971 | −0.6004 | −0.6027 | −0.6042 | |
| dnvcd | 0.1964 | 0.1946 | 0.1936 | 0.1929 | |
| dnr | 0.0496 | 0.0493 | 0.0489 | 0.0486 | |
*Derivatives indicate the change in the value of the refractive error due to change in the value of the respective optical parameter. Critical parameters for the mouse are enclosed in red boxes. See footnote to Table 3 for the definition of each derivative. Derivatives are calculated for 1 µm change in the radius (r) and thickness (tt), and for 0.001 units change in the refractive index (n).
In the rat, the relative contribution of ocular components to the refractive state of the eye varied from 0.0697 D per 1 µm for ttr and ttvcd to 0 D per 1 µm for rar and rpr: ttr = ttvcd > ral > rac > ttl > ttc > ttacd > rpl > rpc > rpr = rar. The relative contribution of refractive indices inthe rat varied from 0.3176 D per 0.001 units for nl to 0.0016 D per 0.001 units for nc: nl > nvcd > nacd > nr > nc.
In the mouse, the relative contribution of ocular components to the refractive state of the eye varied from 0.2455 D per 1 µm for ttr and ttvcd to 0 D for rpr: ttr = ttvcd > ral > rac > ttl > ttc > ttacd > rpc > rpl > rar > rpr. The relative contribution of refractive indices in the mouse varied from 0.5971 D per 0.001 units for nl to 0.0041 D per 0.001 units for nc: nl > nvcd > nr > nacd > nc.
4. Discussion
There is a moderate degree of uncertainty regarding the available optical models of the rodent eye primarily due to substantial variability in the reported biometrical parameters even for the same strain of mice [11]. There are also considerable differences in the reported adult refractive error values for the most frequently used mouse strain C57BL/6 [11], which makes it difficult to reconcile existing optical models of the rodent eye with the reported experimental data. The small size and high power of the rodent eyes, as well as still insufficient resolution of available methodologies for measuring both refractive errors and biometrical parameters in rodents, makes optical modeling of the eye in rodents to suffer from greater errors. The question, which we posed in this study, was how much the variability in each specific ocular parameter affects the refractive state of the eye and the calculated refractive error. Our data suggest that different parameters have different impact on the refractive state of the eye.
Infrared high-resolution photorefraction and high-resolution small animal MRI provide the best currently achievable resolution for the rodent eye biometry [16, 18, 20]. The smallest difference in refractive error, which can be identified using high-resolution photorefraction, is approximately 1.2 D [26]. The smallest difference in the thicknessof an ocular component, which can be detected by the high-resolution MRI, is approximately 23 µm and the smallest identifiable difference in the radius is approximately 26 µm [26]. The variability of the reported refractive indicesis approximately 0.02. These data can be used to calculate the critical thresholds and identify ocular parameters most affected by the biometrical errors. The critical threshold for the thickness/length of ocular components can be calculated using Eq. (27):
| (27) |
where is the ratio of and the incremented thickness (d) of an ocular parameter and is described by Eq. (28):
| (28) |
Substituting values for = 23 µm and d = 1 µm in Eq. (28), gives as shown in Eq. (29):
| (29) |
Substituting values for = 1.2 D, and = 23 in Eq. (27), gives the critical threshold for the thickness as shown in Eq. (30):
| (30) |
Thus, the values of dtt above 0.0522 D will identify ocular parameters critically affected by the biometrical errors.
Critical thresholds for the radii of curvature and refractive indices can be calculated following similar algorithms and are described by Eq. (31) and Eq. (32) respectively:
| (31) |
| (32) |
As shown in Tables 3 and 4, experimental errors in ocular biometry and differences in refractive indices for the crystalline lens and vitreous would have the largest impact on the calculated refractive error, whereas errors and differences in refractive indices for the cornea, aqueous and retina would have less significant impact on the refractive error in both mice and rats. Variation in the thickness/length of the retina and vitreous chamber, as well as in the radius of the anterior surface of the lens, would also significantly affect refractive error in both mice and rats. However, the impact of the differences in the thickness of the lens and radius of the anterior surface of the cornea would be critical only in mice, while the effect on refraction in the rat would be less critical. Changes in other parameters, such as thickness of the cornea, depth of the anterior chamber, radii of the posterior surfaces of the cornea and lens, as well as radii of the anterior and posterior surfaces of the retina, have very small impact on refractive error. Variational analysis also revealed that the impact of changes in ocular parameters is substantially higher in the mouse eye compared to the rat eye.
Analysis of the mathematical model of the chicken eye also suggests that the impact of variations in ocular parameters on the refractive error in rodents is substantially higher than in the species with larger eyes [27]. For example, a change of 1mm in the corneal radius of curvature would cause a shift in refraction of ~22 D in the chicken, whereas the same change in the rat would result in a shift in refraction of ~30 D, and in a shift of ~100 D in the mouse. A 1 mm change in the axial position of the chicken retina would cause a shift in refraction of 15 D. The same change in the position of the rat retina would cause a shift in refraction of ~55 D, while this would result in a shift of ~170 D in the mouse.
5. Conclusion
Rat and mouse models are increasingly used to study refractive eye development and the development of refractive errors such as myopia. In the small and optically powerful rodent eyes, the precision of biometrical measurements and refraction plays crucial role for optical modeling and obtaining accurate data for the refractive state of the eye. Our data suggest that not all ocular parameters are critical. Depth of the vitreous chamber, thickness of the lens, radius of the anterior surface of the cornea, radius of the anterior surface of the lens, as well as refractive indices for the lens and vitreous, appear to have the most significant impact on the refractive state of the rodent eye. Our data suggest that measurement errors in these ocular parameters can lead to substantial differences in the reported refractive errors in mice and rats. Developing new methodologies with higher linear resolution for rodent eye biometry and obtaining more accurate data for the refractive indices of the lens and vitreous will help to generate better optical models of the rodent eye.
References and links
- 1.Hughes A., “A schematic eye for the rat,” Vision Res. 19(5), 569–588 (1979). 10.1016/0042-6989(79)90143-3 [DOI] [PubMed] [Google Scholar]
- 2.Campbell M. C., Hughes A., “An analytic, gradient index schematic lens and eye for the rat which predicts aberrations for finite pupils,” Vision Res. 21(7), 1129–1148 (1981). 10.1016/0042-6989(81)90016-X [DOI] [PubMed] [Google Scholar]
- 3.Chaudhuri A., Hallett P. E., Parker J. A., “Aspheric curvatures, refractive indices and chromatic aberration for the rat eye,” Vision Res. 23(12), 1351–1363 (1983). 10.1016/0042-6989(83)90146-3 [DOI] [PubMed] [Google Scholar]
- 4.Remtulla S., Hallett P. E., “A schematic eye for the mouse, and comparisons with the rat,” Vision Res. 25(1), 21–31 (1985). 10.1016/0042-6989(85)90076-8 [DOI] [PubMed] [Google Scholar]
- 5.Schmucker C., Schaeffel F., “A paraxial schematic eye model for the growing C57BL/6 mouse,” Vision Res. 44(16), 1857–1867 (2004). 10.1016/j.visres.2004.03.011 [DOI] [PubMed] [Google Scholar]
- 6.Zhou X., Bedggood P., Metha A., “Limitations to adaptive optics image quality in rodent eyes,” Biomed. Opt. Express 3(8), 1811–1824 (2012). 10.1364/BOE.3.001811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.de la Cera E. G., Rodríguez G., Llorente L., Schaeffel F., Marcos S., “Optical aberrations in the mouse eye,” Vision Res. 46(16), 2546–2553 (2006). 10.1016/j.visres.2006.01.011 [DOI] [PubMed] [Google Scholar]
- 8.Geng Y., Schery L. A., Sharma R., Dubra A., Ahmad K., Libby R. T., Williams D. R., “Optical properties of the mouse eye,” Biomed. Opt. Express 2(4), 717–738 (2011). 10.1364/BOE.2.000717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhou G., Williams R. W., “Mouse models for the analysis of myopia: an analysis of variation in eye size of adult mice,” Optom. Vis. Sci. 76(6), 408–418 (1999). 10.1097/00006324-199906000-00021 [DOI] [PubMed] [Google Scholar]
- 10.Tkatchenko A. V., Shen Y., Tkatchenko T. V., “Genetic background modulates refractive eye development and susceptibility to myopia in the mouse,” Invest. Ophthalmol. Vis. Sci. 53, E-Abstract 3465 (2012).
- 11.Pardue M. T., Stone R. A., Iuvone P. M., “Investigating mechanisms of myopia in mice,” Exp. Eye Res. 114, 96–105 (2013). 10.1016/j.exer.2012.12.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhou X., Shen M., Xie J., Wang J., Jiang L., Pan M., Qu J., Lu F., “The development of the refractive status and ocular growth in C57BL/6 mice,” Invest. Ophthalmol. Vis. Sci. 49(12), 5208–5214 (2008). 10.1167/iovs.07-1545 [DOI] [PubMed] [Google Scholar]
- 13.Zhou X., An J., Wu X., Lu R., Huang Q., Xie R., Jiang L., Qu J., “Relative axial myopia induced by prolonged light exposure in C57BL/6 mice,” Photochem. Photobiol. 86(1), 131–137 (2010). 10.1111/j.1751-1097.2009.00637.x [DOI] [PubMed] [Google Scholar]
- 14.Zhou X., Huang Q., An J., Lu R., Qin X., Jiang L., Li Y., Wang J., Chen J., Qu J., “Genetic deletion of the adenosine A2A receptor confers postnatal development of relative myopia in mice,” Invest. Ophthalmol. Vis. Sci. 51(9), 4362–4370 (2010). 10.1167/iovs.09-3998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yu Y., Chen H., Tuo J., Zhu Y., “Effects of flickering light on refraction and changes in eye axial length of C57BL/6 mice,” Ophthalmic Res. 46(2), 80–87 (2011). 10.1159/000323179 [DOI] [PubMed] [Google Scholar]
- 16.Tkatchenko T. V., Shen Y., Tkatchenko A. V., “Analysis of postnatal eye development in the mouse with high-resolution small animal magnetic resonance imaging,” Invest. Ophthalmol. Vis. Sci. 51(1), 21–27 (2010). 10.1167/iovs.08-2767 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tkatchenko T. V., Shen Y., Tkatchenko A. V., “Mouse experimental myopia has features of primate myopia,” Invest. Ophthalmol. Vis. Sci. 51(3), 1297–1303 (2010). 10.1167/iovs.09-4153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tkatchenko T. V., Tkatchenko A. V., “Ketamine-xylazine anesthesia causes hyperopic refractive shift in mice,” J. Neurosci. Methods 193(1), 67–71 (2010). 10.1016/j.jneumeth.2010.07.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schmucker C., Schaeffel F., “Contrast sensitivity of wildtype mice wearing diffusers or spectacle lenses, and the effect of atropine,” Vision Res. 46(5), 678–687 (2006). 10.1016/j.visres.2005.04.015 [DOI] [PubMed] [Google Scholar]
- 20.Schaeffel F., Burkhardt E., Howland H. C., Williams R. W., “Measurement of refractive state and deprivation myopia in two strains of mice,” Optom. Vis. Sci. 81(2), 99–110 (2004). 10.1097/00006324-200402000-00008 [DOI] [PubMed] [Google Scholar]
- 21.Pardue M. T., Faulkner A. E., Fernandes A., Yin H., Schaeffel F., Williams R. W., Pozdeyev N., Iuvone P. M., “High susceptibility to experimental myopia in a mouse model with a retinal on pathway defect,” Invest. Ophthalmol. Vis. Sci. 49(2), 706–712 (2008). 10.1167/iovs.07-0643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wisard J., Faulkner A., Chrenek M. A., Waxweiler T., Waxweiler W., Donmoyer C., Liou G. I., Craft C. M., Schmid G. F., Boatright J. H., Pardue M. T., Nickerson J. M., “Exaggerated eye growth in IRBP-deficient mice in early development,” Invest. Ophthalmol. Vis. Sci. 52(8), 5804–5811 (2011). 10.1167/iovs.10-7129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.J. Alda and J. Arasa, “Paraxial ray tracing,” in Encyclopedia of optical engineering (Marcel Dekker, New York, NY, 2004). [Google Scholar]
- 24.Schechter R. J., “Snell’s Law: optimum pathway analysis,” Surv. Ophthalmol. 21(6), 464–466 (1977). 10.1016/S0039-6257(77)80002-7 [DOI] [PubMed] [Google Scholar]
- 25.J. E. Greivenkamp, Field guide to geometrical optics (SPIE Press, Bellingham, Wash., 2004). [Google Scholar]
- 26.Tkatchenko T. V., Shen Y., Braun R. D., Bawa G., Kumar P., Avrutsky I., Tkatchenko A. V., “Photopic visual input is necessary for emmetropization in mice,” Exp. Eye Res. 115, 87–95 (2013). 10.1016/j.exer.2013.06.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schaeffel F., Howland H. C., “Mathematical model of emmetropization in the chicken,” J. Opt. Soc. Am. A 5(12), 2080–2086 (1988). 10.1364/JOSAA.5.002080 [DOI] [PubMed] [Google Scholar]