Automated lamina cribrosa microstructural segmentation in optical coherence tomography scans of healthy and glaucomatous eyes

Abstract

We demonstrate an automated segmentation method for in-vivo 3D optical coherence tomography (OCT) imaging of the lamina cribrosa (LC). Manual segmentations of coronal slices of the LC were used as a gold standard in parameter selection and evaluation of the automated technique. The method was validated using two prototype OCT devices; each had a subject cohort including both healthy and glaucomatous eyes. Automated segmentation of in-vivo 3D LC OCT microstructure performed comparably to manual segmentation and is useful for investigative research and in clinical quantification of the LC.

1. Introduction

Glaucoma is an optic neuropathy marked by irreversible loss of the retinal ganglion cells resulting in functional visual field (VF) deficits and is the second leading cause of blindness worldwide [1]. Early detection is essential to retard disease progression and retain maximal vision. Optical coherence tomography (OCT) is an imaging technology implemented in clinical eye care for examining tissue structure, and is used for early glaucoma detection. Traditionally this is accomplished by measuring retinal nerve fiber layer thickness [2–4], as well as the thickness of other retinal layers [5–8]. More recently, the lamina cribrosa (LC) has been investigated as another potential location to identify glaucomatous damage [9–11].

The LC is a meshwork structure composed primarily of collagen fibers located deep within the optic nerve head, and is the supportive tissue surrounding retinal nerve fibers as they exit the eye. The LC is regarded as a primary target of glaucomatous insult [12]. Finite element modeling of the LC has shown it susceptible to biomechanical stress caused by elevated intraocular pressure (IOP) associated with glaucoma [13,14]. Until recently, full three-dimensional (3D) in-vivo imaging of the LC has been impossible. Fast scanning spectral-domain (SD-) OCT and swept-source (SS-) OCT systems permit such imaging, and consequently several new studies evaluated the LC in healthy and glaucomatous eyes, primarily by examining the anterior and posterior boundaries along with lamina insertion points using manual delineation methods on two-dimensional cross sectional slices [10,11,15]. However, signal attenuation and shadowing from vasculature and other reflective structures make measurements involving the posterior lamina and insertion points difficult.

In-vivo investigations of LC microstructure to date have only described local irregularities in the anterior surface of the lamina and LC thickness [16,17]. Individual pores have been imaged but not quantified in 3D [18,19]. The only studies to investigate laminar pore shape and size are those using fundus photography and en face confocal scanning laser ophthalmoscopy (CSLO) images [20,21]. More recently, adaptive optics has augmented studies targeting pore geometry by improving contrast and transverse resolution [22,23]. While CSLO is capable of imaging pore and beam structure at various depths, poor axial resolution restricts the ability to attain detailed 3D tissue structure [24]. In OCT, the 3D nature of the microstructure has only been partially explored; specifically, previous studies haven’t considered the LC beams and pores with depth. Because the axons pass through the entire depth of the LC on their way to the brain, a comprehensive evaluation should consider this structure in its 3D entirety. The purpose of this study was to develop and validate an automated segmentation method for microstructure in 3D OCT scans of the LC. To assess the robustness of the proposed segmentation method, images acquired by two iterations of OCT technology were used.

2. Methods

3D LC images acquired by two OCT systems were analyzed using an automated microstructure segmentation analysis and compared with manual segmentation. The study was approved by the University of Pittsburgh’s Institutional Review Board and adhered to the tenets of the Declaration of Helsinki. All subjects provided informed consent prior to enrollment in the study. The cohort used in this study included both healthy and glaucoma subjects, enrolled to Pittsburgh imaging technology trial (PITT) at the University of Pittsburgh medical center (UPMC) Eye Center. Study participants underwent a comprehensive ocular examination of the anterior and posterior segments, intraocular pressure measurement and visual field testing. Subjects were divided into healthy and glaucomatous groups according to conventional clinical criteria based on typical glaucomatous features observed in clinical examination and VF findings.

Two prototype OCT systems that allow thorough sampling of the optic nerve head region were used for data acquisition: A SS-OCT and a multimodal retinal imaging system with adaptive optics (MAO-OCT), whose imaging channels include SD-OCT, confocal scanning laser ophthalmoscopy, and a line scanning ophthalmoscope. Both devices have been previously described in detail [25,26]. Both devices operate with a light source centered at a wavelength of 1050nm, enabling greater tissue penetration than conventional SD-OCT, ideal for imaging deeper ocular structures such as the LC. The SS-OCT system is equipped with automated registration software utilizing orthogonal scans of horizontal and vertical fast-scanning directions [27]. With the MAO-OCT, the additional imaging channels are used for precise spatial registration of individual SD-OCT B-scan frames. Scanning with the SS-OCT device lasted approximately 2 seconds, and acquired a 12° × 12° (400 × 400 pixel) data cube centered on the LC where each A-scan had a depth of 900 pixels. The theoretical transverse and axial resolutions for SS-OCT were 18μm and 5μm, respectively. Acquisition with the MAO-OCT device required dilation using phenylephrine and tropicamide (for optimal AO performance) and each scan took nearly 7 seconds. MAO-OCT scans were collected from a 6° × 6° (1024 × 200 pixel) data volume centered on the LC, where each A-scan had a depth of 512 pixels. The transverse and axial resolutions for MAO-OCT were 5μm and 4.5μm, respectively. MAO-OCT scans were digitally resampled post-hoc using bilinear interpolation to an isotropic 1024 × 1024 × 512 pixels data volume. Resampling was performed because local contrast enhancement and local thresholding (of the automated segmentation) operated isotropically in 2D.

Each data volume was resampled in a coronal plane and visualized as C-scan slices. The automated segmentation operates on 2D frames but was implemented on each slice in the volume rendering a full 3D segmentation. A typical 3D OCT scan of the LC includes a large number of frames, and manual segmentation of the LC microstructure in each individual frame is unrealistic. Therefore, performance validation in comparison with manual segmentation was only performed on a single randomly selected 2D frame (Fig. 1 ). Within the slice, the portion containing the LC was manually selected.

Fig. 1.

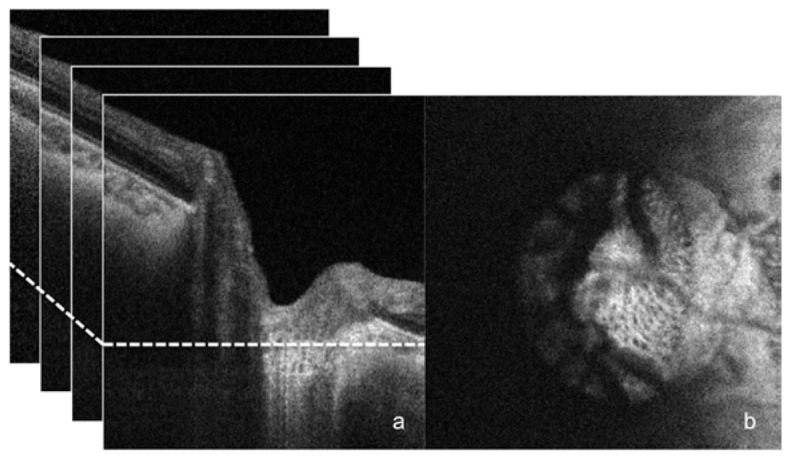
SS-OCT scan of healthy eye. B-scan frames are stacked (a) into a 3D data cube from which an individual C-mode slice is selected at random (at the location of the dotted line on the left) to undergo manual and automated segmentation analysis (b).

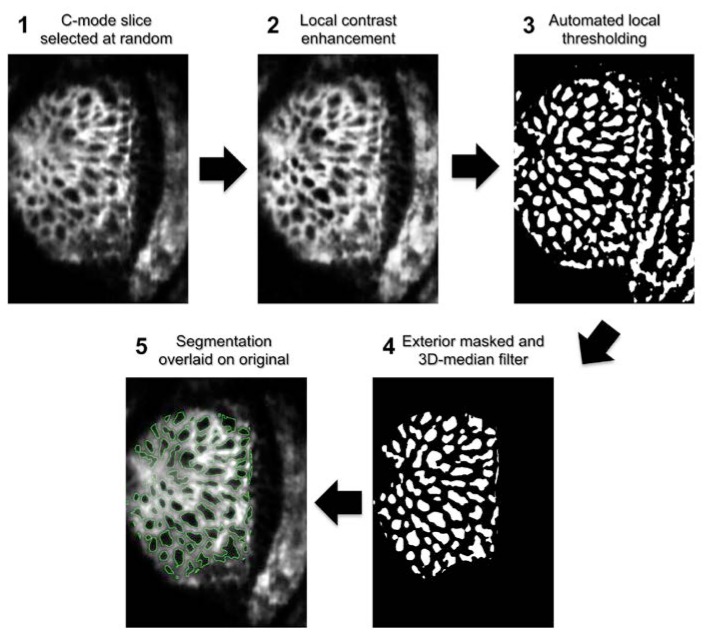
The automated segmentation algorithm included the following steps, all performed using the open source FIJI software package (ImageJ version 1.47c) [28] (Fig. 2 ):

Fig. 2.

Automated pore segmentation process for MAO-OCT scan. Following a 3D-Gaussian filter, a C-mode slice is randomly selected from the stack (1). A local contrast enhancement highlights local features of the structure (2), which are then thresholded (3). A 3D median filter removes pores unconnected in depth and the regions exterior to the visible lamina are masked (4). Finally, the segmentation is overlaid on the original image for subjective evaluation (5). The outline for automated segmentation is shown in green.

• 1. Image smoothing using 3D Gaussian filter with a three-pixel σ_z and a one-pixel σ_x,y to reduce high frequency noise (Fig. 2.1).
• 2. Contrast limited adaptive histogram equalization to equalize local differences in pixel intensity [28] (Fig. 2.2).
• 3. An automated local thresholding technique developed by Niblack [28] was used to binarize the image, differentiating pores in the C-mode slice from the surrounding LC structure (Fig. 2.3). The local thresholding algorithm required a few input parameters detailed in the appendix. Because two devices were used in this study, and each sampled the tissue at slightly different pixel resolution, these parameters were adjusted in accordance with the device (the method of parameter selection is detailed in the appendix). However, once set, the parameters were not adjusted for each individual image when applied to the full patient data sets.
• 4. A 3D median filter was passed over the segmented volume with 1 × 1 × 3 kernel size (Fig. 2.4). The z filtering removes segmented pixels due to intensity drops in a single C-mode. This allows the automated algorithm to account for 3D continuity. Because this operation could result in pixels with a grey value of 127, the resulting images were then re-thresholded.
• 5. A manually defined mask was applied to the region peripheral to the LC, restricting the segmented components to those within the region of interest (Fig. 2.4). Full processing took ~2 seconds per image.

Segmentation was also manually performed by two experienced observers masked to one another, clinical information, and the outcome of automated segmentation. Frames for manual segmentations underwent the same smoothing (step 1) and local contrast enhancement (2) as performed for the automated segmentation to ensure comparable conditions for analysis. After this preprocessing, the human observers manually demarcated regions of the image considered as pores using the TrakEM2 [29] feature of the FIJI image analysis software. When necessary, adjacent C-mode slices were consulted to discriminate pores from noise, by observing the continuity of local regions of low pixel intensity through the stack. The same peripheral mask used in the automated segmentation was applied to the manual segmentations. Manual delineation took on average approximately 18 minutes per image, which equates to nearly 6 hours for an entire volume.

The pore segmentation was compared between the automated and manual methods, first qualitatively and then quantitatively by calculating sensitivity and specificity using pixels classified as pores on a per-pixel basis. The gold standard pore segmentations were taken as the pixels both observers agreed upon within the boundary of a pore. In addition, the following parameters were measured, using FIJI, and compared using a measurement error model: pore number, average pore area, average pore aspect ratio, average pore thickness, average beam thickness, and connective tissue volume fraction (CTVF). Pore area, and aspect ratio were calculated by considering each segmented pore as a particle and averaging over all particles in the frame. Aspect ratio refers to the ratio of the major axis to minor axis of an ellipse fitted to each pore. Beam thickness is taken as the average thickness of the region inverse to the pores within the boundaries of the laminar surface while pore thickness is a radial thickness measurement of segmented pores. Thicknesses were computed by expanding circles from each point within the segmented region until the boundary is first reached. Each point is assigned a value corresponding to the radius of the largest circle containing that point, from which a global mean ‘thickness’ can be calculated [30]. The manually defined peripheral mask determined external beam edges. The CTVF is a ratio of the segmented laminar beams to total LC area within a slice.

The measurement error model estimated the latent ‘true’ value for each parameter within a subject and calculated the bias (systematic error) and imprecision (random error) component for each observer and the automated technique based on the set of values within the population. In order to allow for comparison between imprecisions, the computed values were adjusted for the scale bias. R Language and Environment for Statistical Computing program, was used for the statistical analysis (version 2.15.1; R Foundation for Statistical Computing, Vienna, Austria; http://www.R-project.org) [31–34]. The performance between devices was not compared because they scanned different study populations. Also, such analysis would be confounded by distinct physical differences in imaging modalities, for example improved speed for SS-OCT or increased lateral resolution for MAO-OCT, which are not the subject of the present study.

3. Results

The study population imaged with SS-OCT included 14 healthy and 16 glaucoma subjects with an average age of 55.2 ± 18.6 yrs, and an average visual field mean deviation (MD) of −6.39 ± 5.95 dB for glaucoma subjects. The cohort imaged with MAO-OCT had 6 healthy and 24 glaucoma subjects with an average age of 53.4 ± 20.0 yrs. The average MD for glaucoma subjects in the later population was −6.41 ± 7.20 dB.

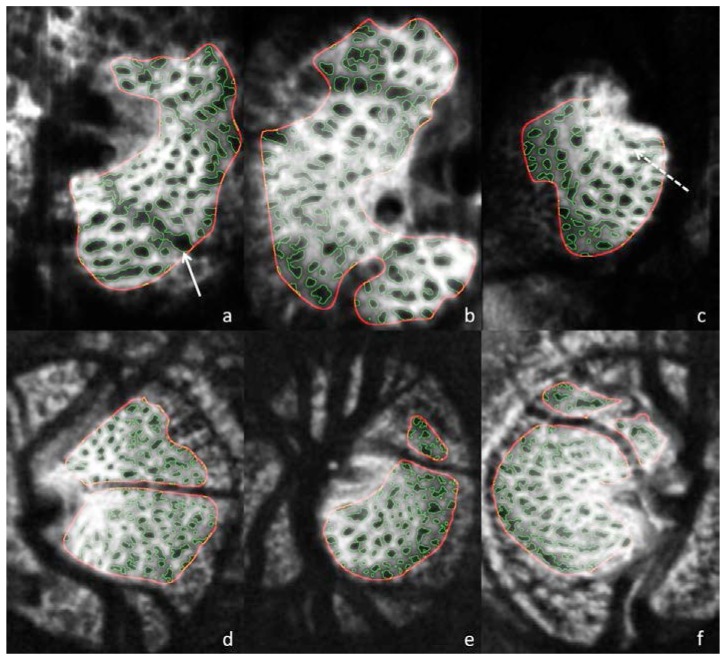
Subjective evaluation of the automated segmentation method, determined that there were no pores that were obviously misclassified (Fig. 3 ). Subjective comparison of pore segmentation showed strong agreement between segmentation methods in regions of the lamina with good signal strength (Fig. 4 and 5 ). Segments of the image with poorer signal highlighted the regions of disparity between the segmentation methods (Fig. 5). However, disagreement between observers seemed to appear as much as between observer and automated segmentation.

Fig. 3.

Automated segmentation results for MAO-OCT (a-c) and SS-OCT (d-f). Solid arrow (a) points to a region where blood vessel shadow is unmasked, and as a result the pore boundaries exhibit irregular boarders within the shadow. Dotted arrow (c) shows region where small adjacent pores are combined into a single pore.

Fig. 4.

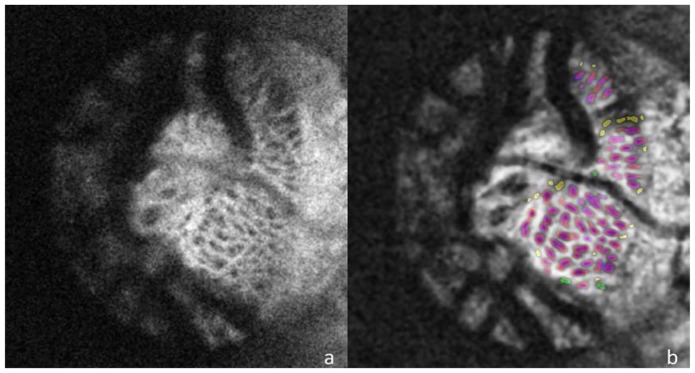
The unprocessed C-mode slice (a) and corresponding segmentation (b) for a scan of a healthy eye taken with the SS-OCT device. For pores identified by both automated and manual segmentations the automated pores are colored red and manual are colored blue so that overlapping segmentation appears as purple. Pores identified only by the automated method are colored yellow and those seen solely in the manual segmentation are colored green.

Fig. 5.

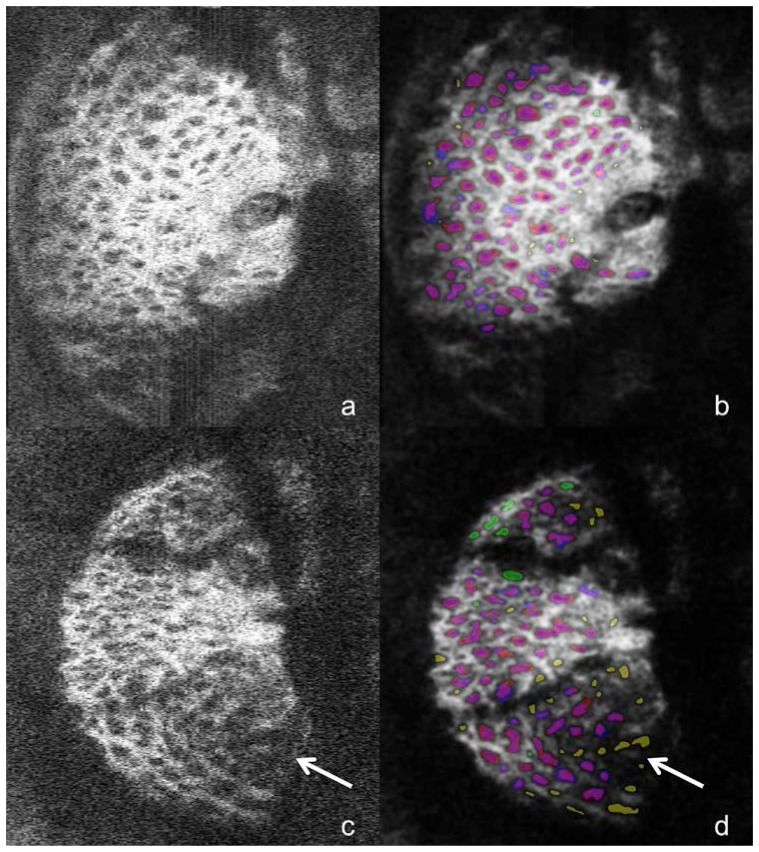
The unprocessed C-mode slice (a,c) and corresponding segmentation (b,d) for scans of one glaucomatous (top) and one healthy eye (bottom) taken with the MAO-OCT system. Segmentations are colored according the scheme outlined in Fig. 4. The top image shows relatively good agreement between manual and automated methods, while the bottom images exhibit regions of segmentation disagreement; the arrow points to pores identified in the automated method but not manually. These locations exhibits low signal-to-noise ratio in the original image (c), which explains the discrepancy.

Pore areas varied greatly within eyes, throughout the population, and between devices: some pores were as small as 10 pixels² while others stretched as large as several thousand pixels². The largest observed pore for SS-OCT was 2441 pixels² and for MAO-OCT the largest was 3588 pixels². The standard deviation of mean pore area through the population was 67.2 pixels² for SS-OCT and 71.4 pixels² for MAO-OCT.

Using manual segmentation as gold standard, average sensitivity and specificity of the automated segmentation was 82.3% and 91.0% for SS-OCT, and 80.1% and 88.0% for MAO-OCT, respectively. The inter-observer agreement constituted 85.5% of segmented pixels for SS-OCT and 87.0% for MAO-OCT. Tables 1 and 2 summarize the measurements values, and imprecision for the two graders and the automated segmentation. For both imaging modalities the estimated imprecisions, when accounting for scale bias of the parameters, are similar when comparing between manual segmentations and when comparing between manual and automated segmentations. None of the parameter averages or imprecision values showed statistically significant differences between the manual and automated methods.

Table 1. Average measurement and imprecision estimate for each segmentation method using SS-OCT.

Parameter	Average			Imprecision
	Auto	Obs. 1	Obs. 2	Auto	Obs. 1	Obs. 2
Pore number	99.7	94.1	87.8	19.04	20.40	21.59
Pore area (pixels2)	201.2	211.4	268.9	42.0	29.3	42.9
Pore aspect ratio	2.05	1.77	1.71	0.096	0.118	0.100
Pore Thickness	11.19	12.81	15.36	0.61	0.45	0.00
Beam Thickness	20.29	22.53	22.62	1.51	0.54	0.53
CTVF	0.748	0.748	0.693	0.02	0.03	0.02

Obs – Observer. CTVF – Connective Tissue Volume Fraction.

Table 2. Average measurement and imprecision estimate for each segmentation method using MAO-OCT.

Parameter	Average			Imprecision
	Auto	Obs. 1	Obs. 2	Auto	Obs. 1	Obs. 2
Pore number	71.3	82.4	90.2	9.63	8.59	7.49
Pore area (pixels2)	475.8	356.0	379.1	45.3	57.6	54.19
Pore aspect ratio	2.27	1.76	1.67	0.23	0.00	0.43
Pore Thickness	16.73	17.40	19.57	0.47	0.46	0.80
Beam Thickness	23.16	26.28	23.99	0.80	0.65	0.87
CTVF	0.667	0.643	0.591	0.01	0.02	0.03

Obs – Observer. CTVF – Connective Tissue Volume Fraction.

4. Discussion and conclusion

Using two prototype OCT devices, 3D LC scans were acquired and automatically segmented using a customized algorithm. Single C-mode slices were selected at random from each scanning volume and two observers manually delineated pores. Their outcome was compared with an automated algorithm for identifying porous features. The automated algorithm performed comparably to the observers.

The performance of the software was tested in this study on 2D images. Yet, it should be emphasized that this segmentation method is fully operational on 3D scans providing a novel method for microstructural segmentation of 3D OCT scans of the LC. The method is also applicable in other imaging modalities visualizing LC microstructure, although differences in image size, contrast, and noise characteristics should be considered in order to attain good segmentation performance.

The automated LC segmentation analysis we propose includes multiple steps. A local contrast enhancement was chosen because the average image intensity varied through individual B-scans in the 3D volume. Nevertheless, our primary interest was in quantifying pores, which have local drops in intensity. The local enhancement provides better pixel-scale contrast that aids visualization of pore edges without substantially changing the appearance of global features. The Gaussian filter adequately removed noise, improving the overall image quality. The 3D median filter with a large Z radius, discriminated local intensity drops in isolated C-mode slices from those present in multiple sequential slices and more likely to be classified as pores by a human observer. Taken together, the performance of the automated segmentation was subjectively judged to adequately delineate the lamina microstructure using both OCT systems.

The study was performed using images acquired by 2 prototype clinical OCT devices. These devices were selected due to their ability to produce detailed images of the LC. Moreover, these devices provided access to the raw images before further processing; while all commercial devices provide only post-processed images. Finally, to test the robustness of the segmentation method we used two independent OCT devices that employ different methodologies and physical properties.

Varying disagreement between observers for manual segmentation reveals the difficulty with subjective assessment as a gold standard for LC segmentation. Nevertheless, acceptable sensitivity and specificity of the automated method was noted with both devices. For each modality the automated analysis tends to provide lower pore thickness values and an overall more elliptical shape of the pores (higher aspect ratio) than manual segmentations. The difference in aspect ratio may be due to the automated method connecting adjacent pores separated by low contrast connective tissue. This may also contribute to the relatively low pore thickness values since connections tend to be thinner than the pores they connect. Because thickness is computed by expanding circles from each point within the segmented region until the boundary is first reached, having a narrow connection limits the maximal size of the circle leading to lower pore thickness. Merging pores would also decrease pore number while increasing pore area: all of which are seen with MAO-OCT. The discordance in number and area observed with SS-OCT might be explained by higher sensitivity of the automated method to local signal intensity drops than either observer. These small pores would interrupt beam structure, decreasing beam thickness, pore thickness, and average pore area while increasing pore number.

Two of the tuned parameters in the automated algorithm address local contrast enhancement, but depending on the size of segmented features some local intensity drops are not detected. Also, pore segmentations are filtered in the Z-direction to remove noise due to intensity drops in single slices. This may result in the merging or splitting of pores, which bifurcate with depth as they pass through the lamina. The depth position of a split or merge varies subjectively and the decision of observers sometimes disagreed with the outcome of the automated method. The most robust parameter appeared to be CTVF. Pore number, size, and aspect ratio were sensitive to the splitting and merging of pores, and to a lesser degree so were beam and pore thickness. Ratio measurements provide a macroscopic look at the fine structure without over-weighing pixels with indefinite classifications. Nevertheless, measurement imprecision, or variability, was similar for manual and automated analysis: within 4.0% of one another (compared to 3.7% between observers). When combined with the favorable outcome of subjective evaluation, the similarity in imprecision and lack of statistically significant difference in any of the parameters indicated that the automated method described in this paper is an effective tool for LC segmentation.

Some discrepancies between manual and automated segmentation methods arise in regions of blood vessel shadow and other areas of low signal-to-noise ratio (SNR) (Fig. 3, 5). While pores seem present, the lack of clear pore boundaries makes manual delineation difficult, and as a result inter-observer agreement is low. The automated algorithm processes these regions the same as regions of high SNR, but because local pixel intensities exhibit different characteristics, segmentation will fail without adaptive parameter values. Finding appropriate parameter values is impossible without robust manual segmentation, and therefore regions of low SNR should be masked. Future work may incorporate compensation techniques to improve contrast in regions of low SNR.

A limitation of this study is the relatively small number of scans that were analyzed. The heavily labor-intensive procedure of manually delineating numerous pores in each scan restricts the feasibility of a larger cohort. As a result, confidence intervals on imprecision values could not be reliably established. In fact, this limitation highlights the necessity of such an automated technique, particularly when used on a dense 3D volume routinely and rapidly acquired by OCT.

In conclusion, an automated method for segmenting 3D LC structure within in-vivo OCT scans of the human optic nerve head performed similarly to manual segmentation but did so over 100 times faster. The automated algorithm permits rapid 3D segmentation for use in broader population studies of the LC structure.

7. Appendix

Parameter selection for the contrast limited adaptive histogram equalization (CLAHE) and auto local thresholding steps of the segmentation process were performed for each device using a 15 scan training set of randomly selected eyes. The parameters input into the CLAHE filter were block-size—the size of the local region on which the histogram adjustment is applied—and the slope—the degree of contrast stretching occurring in a local window. For the thresholding step the adjustable parameters appear in the local thresholding algorithm [35]

$$I_{segmented}=\{\begin{array}{l}background,If{I}_{original}>\mu +k\times \sigma +c;\\ object,else\end{array}$$ (1)

where I is the pixel intensity, μ is the mean pixel value for the local region, σ is the standard deviation within this region, and k and c are adjustable constants. The size of the local region also has an adjustable radius. The complexity of relationships between the five tunable parameters presented a technical challenge for parameter selection.

Using the training set, each parameter value was iterated over regularly spaced values centered on values assessed to produce acceptable results. The total number of permutations of parameter values was 2500. Each permutation’s automated segmentation was then compared with the manual segmentation, and specificity and sensitivity was calculated, which were then averaged over the training set. The standard deviation of sensitivity and specificity was also calculated throughout the training set to provide a measure of the consistency of a set of parameters. The parameter values producing the twenty highest sensitivity and specificity averages (all were within 0.1% of the maximum sensitivity-specificity average) were subjectively evaluated by overlaying their segmentations on the original images, and the set of parameters producing the best segmentation was subjectively selected (Table 3

Table 3. Final parameter values selected for segmentation for SS-OCT and MAO-OCT.

	CLAHE Filter Radius (pixels)	CLAHE Filter Slope	Local Block Size (pixels)	Parameter 1 (k)	Parameter 2 (c)
SS-OCT	61	2.0	20	−0.1	20
MAO-OCT	111	2.0	20	−0.1	10

).