Re-scan confocal microscopy: scanning twice for better resolution

Abstract

We present a new super-resolution technique, Re-scan Confocal Microscopy (RCM), based on standard confocal microscopy extended with an optical (re-scanning) unit that projects the image directly on a CCD-camera. This new microscope has improved lateral resolution and strongly improved sensitivity while maintaining the sectioning capability of a standard confocal microscope. This simple technology is typically useful for biological applications where the combination high-resolution and high-sensitivity is required.

1. Introduction

Due to the stormy developments in the field of super-resolution microscopy [1], it is often forgotten that confocal microscopy was the first super-resolution technique giving improvement of lateral resolution by a factor of √2 compared to wide-field fluorescence microscopy [2]. Remarkably, the historical success of the confocal microscope was not caused by its improved lateral resolution but by its sectioning properties (axial resolution). The reason why is clear: lateral resolution can only be reduced by minimizing the pinhole diameter (in theory down to zero). This, however, would reduce the detection efficiency dramatically and result in images with a very low signal-to-noise ratio. Therefore, in practice most microscopists adjust the pinhole radius to one Airy unit (equal to 1.2λ/NA); thus sacrificing lateral resolution for the sake of signal-to-noise ratio.

More than 20 years ago Sheppard [3] proposed to solve this problem by removing the pinhole and using a camera instead at the original position of the pinhole. In this technique, named Image Scanning Microscopy (ISM) in ref [4], the camera takes an image of the distribution of emitted light for every position of the excitation focus in the sample. Subsequently, an image reconstruction algorithm calculates the final image with enhanced lateral resolution; a time consuming image acquisition and processing procedure. Throughout the years, several groups worked on the implementation of ISM for both scanning with a single focus [4–7] and scanning with multiple foci at the same time [8]. ISM allows imaging with good sectioning properties and improved lateral resolution, but the acquisition time is still a significant drawback.

Here, we propose a new fully optical technique, Re-scan Confocal Microscopy (RCM), that overcomes the limitations on acquisition and processing time of ISM, while maintaining the advantages in (lateral and axial) resolution improvement. RCM is based on standard confocal microscopy, extended with an optical unit (re-scanner) that projects, in a scanning way, the image directly on a camera. In the nineties, the concept of re-scanning was also implemented in microscopes with a stationary slit aperture for fast confocal imaging [9, 10]. In Re-scan Confocal Microscopy (RCM) we use a separate pair of re-scanning mirrors for a flexible optical architecture which allows de-coupling of the scanning magnification of the object and the magnification of the scanning spot. This de-coupling of magnification is the fundamental concept of RCM that gives lateral super-resolution with conservation of optical sectioning. In addition to improved resolution, RCM has superior light collection efficiency due to a relatively open pinhole and use of a sensitive EMCCD camera as detector. In contrast with Structured Illumination techniques [11], RCM is an “optics only” super resolution technique, meaning that no image reconstruction procedure is required to get sharp images. The improvement of lateral resolution in RCM was quantified by imaging of fluorescent beads of 100 nm, showing that the FWHM is reduced down to 170 nm ( ± 10 nm).

The rescan concept is very recently disclosed as well by Heintzmann and associates [12] who subsequently published a theory paper on the rescan concept during the review process of the current paper [13]. A multi-spot version of the rescan concept has been proposed by Shroff and York [14]. In contrast to ref [12] we do not use a single scanning unit three times (for scanning, de-scanning and re-scanning) but instead use a more flexible optical architecture with separate mirrors for the re-scanning, allowing for a variation in and optimization of the magnification decoupling. Furthermore, we present a theoretical investigation of the effect of pinhole size on the differences between the confocal and rescan confocal microscopes, and, finally, we demonstrate the technique on fixed and live biological samples as opposed to single bead imaging.

2. The re-scanning concept

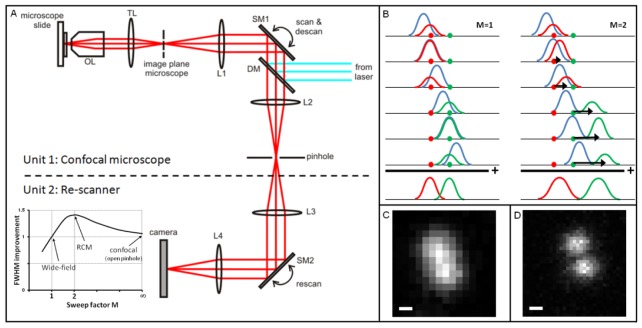
The additional scanning unit of the RCM, the “re-scanner”, re-directs the light from the pinhole to a sensitive camera for image acquisition (Fig. 1(a) ). The key to super-resolution properties of this new microscope is de-coupling of the scanning magnification of the object (M_obj) and the magnification of the scanning spot (M_spot); M_obj is determined by the angular amplitude (sweep) of the two scanners and the focal lengths of the two scan lenses, while M_spot is only determined by the focal lengths of the lenses and not by the sweep amplitude of the scanners. The re-scanning unit therefore enables adjustment of M_obj independently from M_spot by changing its sweep amplitudes, which is expressed by the sweep factor or magnification decoupling factor M (with M = M_obj / M_spot).

Fig. 1.

The Re-scan Confocal Microscope (RCM) (A) consists of two units: 1) a standard confocal microscope with a set of scanning mirrors which have double function: scanning the excitation light and de-scanning the emission light, and 2) a re-scanning unit that “writes” the light that passes the pinhole onto the CCD-camera. The ratio of angular amplitude of the two scanners, expressed by the sweep factor M, changes the properties of the re-scan microscope (see inset in A). For M = 1 the microscope has the lateral resolution of a wide-field microscope, defined by the diffraction limit. For M = 2 the RCM performs best concerning resolution. Even with a wide open pinhole the resolution is √2 times improved, which makes the system much more photo-efficient compared to conventional confocal microscopes with similar resolution (that should have pinhole < 1 Airy unit). For large values of M the system converts to a confocal microscope with open pinhole. (B) The concept of RCM is simple: For M = 1 the two scanners compensate each other and two point-objects (red and green dots) are projected on the camera without extra magnification. When the sweep-factor is set to M = 2, the extra sweep (indicated with black arrows) will smear out the spots on the camera by a factor of √2. Since the distance between the objects is 2 times larger, the relative width of the spots is reduced by a factor of √2. This resolution improvement is clearly visible by comparing C and D. Two 100 nm beads are positioned 250 nm from each other and cannot be resolved by M = 1 (C) but can easily be separated by RCM with M = 2 (D). FWHM in these two configurations was 255 nm and 185 nm, respectively. Scale bars are 100 nm.

The effect of the magnification decoupling is illustrated in the Fig. 1(b). Two nearby molecules are excited one by one by a scanning laser spot. The emitted light distributions from the two molecules are imaged in the primary image plane as two diffraction limited spots. The position of each spot in the primary image plane does not change during scanning even though the intensity of these spots changes during scanning (as the molecules will light up one by one). These static spots are subsequently imaged in the pinhole plane, via the confocal scanning unit. The re-imaged spots therefore run over the pinhole plane during a scanning sweep. The spots are subsequently re-imaged in the camera plane, via the re-scanning unit. In case the sweep factor M equals one (M = 1) the re-scanner will exactly compensate for the spot movement due to the confocal scanner and the molecules will be imaged at static positions, leading to diffraction limited resolution comparable to that of a fluorescence wide-field microscope. In case M = 2, the mirrors of the re-scanner move with double angular amplitude. This extra “sweep”, indicated by black arrows in Fig. 1(b), transfers the light to a spot that moves across the camera chip with constant velocity and therefore smears out the image of the molecules by a factor of approximately √2. However, the distance between the two molecules is doubled due to the double sweep of the re-scanner. As a result, by scanning with a sweep factor of M = 2, the width of the spot is improved by a factor of √2 relative to diffraction limited resolution (M = 1; see inset of Fig. 1(a)).

A semi-quantitative analysis of the resolution improvement as a function of sweep factor M can be made as follows. The measured spot on the camera is the sum of emission spots that have a peak height determined by the excitation spot and that are mutually displaced proportional to M-1 due to the re-scan operation. The Point Spread Function (PSF) is thus the convolution of the emission PSF with a scaled version of the excitation PSF. The separation of two points also scales with M so the effective width of the emission PSF scales as 1/M and the effective width of the excitation PSF envelope scales as (M-1)/M. A measure for the spot width W, such as the Full Width at Half Maximum (FWHM), is thus effectively given by:

$$W^2={\left(\frac{W_{em}}{M}\right)}^2+{\left(\frac{\left(M-1\right)W_{ex}}{M}\right)}^2$$ (1)

where W_em and W_ex are the widths of the emission and excitation spots. Clearly, in the limit M = 1 we find W = W_em, i.e. the resolution is determined by the emission branch only and the microscope is equivalent to a widefield fluorescence microscope (see also inset graph in Fig. 1(a)). In the opposite limit M→¥ we find W = W_ex, i.e. now the resolution is determined by the excitation branch only and the microscope’s resolution is equivalent to that of a confocal fluorescence microscope with open pinhole. The optimum (minimum) spot width is found for a magnification decoupling:

$$M=1+\frac{W_{em}{}^2}{W_{ex}{}^2}$$ (2)

For which the optimum (minimum) spot width is equal to:

$$W_{RCM}=\frac{W_{em}{W}_{ex}}{\sqrt{W_{em}{}^2+W_{ex}{}^2}}$$ (3)

In case the excitation and emission spot width are equal W_em = W_ex this boils down to M = 2 and and a √2 reduction in spot width W = W_em/√2 = W_ex/√2. A small correction can be expected for normal fluorescence microscopy due to the Stokes-shift between excitation and emission leading to an emission spot width that is a bit larger than the excitation spot width. Another small correction on the √2 reduction in spot width can be made when the here proposed Gaussian PSF approximation is replaced by a more realistic PSF (Airy-distribution).

In conventional confocal microscopy both axial and lateral resolution are determined by the diameter of the pinhole. In RCM the pinhole influences only axial resolution, not lateral resolution (apart from small deviations). In both techniques, conventional and re-scanning confocal microscopy, maximum axial resolution is obtained by setting the diameter of the pinhole at one Airy unit (AU). However, for the lateral resolution the two techniques have a quite different response to the pinhole diameter. The lateral resolution in RCM is independent of pinhole diameter, whereas in conventional confocal microscopy the lateral resolution only improves for a pinhole size smaller than one AU leading to loss of detected fluorescence signal. It turns out that for RCM, a pinhole size of 2-3 AU gives the optimum combination of high resolution, high sensitivity and good optical sectioning.

3. Theory

The image formation of the re-scan confocal microscope is governed by the following set of equations:

$$\begin{array}{c}{I}_{pin}\left(u_i,u_s\right)={\displaystyle \int d^2{u}_{o}d{v}_o{H}_{em}\left(u_i-u_o+u_s,-v_o\right)T\left(u_o,v_o\right)H_{ex}\left(u_o-u_s,v_o\right)}\\ I_{cam}\left(u_c,u_s\right)={\displaystyle \int d^2{u}_i{H}_{re}\left(u_i-M\left(u_c-u_s\right),-v_o\right)D{\left(u_i\right)}_i{I}_{pin}\left(u_i,u_s\right)}\\ I_{rec}\left(u_c\right)={\displaystyle \int d^2{u}_s{I}_{cam}\left(u_c,u_s\right)}\end{array}$$ (4)

where T( u ) is the object fluorescence, H_ex( u ) the excitation PSF, H_em( u ) is the emission PSF, H_re( u ) is the re-scan relay PSF, u _o is the object plane position, u _i the pinhole plane position, u _s the scan position, u _c the camera plane position, v₀ the axial object position, D( u _i) the pinhole transmission function, I_pin( u _i, u _s) the image intensity in the image (pinhole) plane as a function of u _i and u _s, I_cam( u _c,, u _s) the image intensity in the camera plane as a function of u _c and u _s, and I_rec( u _c) the final re-scan confocal image intensity after completion of the scanning operation. Here, the in-plane coordinates are scaled with the diffraction unit λ_ex/NA, where λ_ex is the excitation wavelength and where the NA is the numerical aperture in the object plane (for u _o), in the pinhole (image) plane (for u _i), or in the camera plane (for u _c). The axial position v₀ is the z-coordinate scaled with the axial diffraction unit nλ_ex/NA², with n the object refractive index. For the sake of simplicity we work in the scalar diffraction regime, although the NA is generally rather high.

Consider the case where the pupil stop of the re-scan relay is much higher than the re-imaged pupil stop of the objective lens. Then the re-scan relay PSF is essentially a delta-function (no additional diffraction induced blurring in that part of the imaging path), and the re-scan confocal image intensity can be written as:

$$I_{rec}\left(u_c\right)=M^2{\displaystyle \int d^2{u}_{s}D\left(M\left(u_c-u_s\right)\right)I_{pin}\left(M\left(u_c-u_s\right),u_s\right)}$$ (5)

that is, the point in the image plane at position u _i is imaged onto the point u _c = u _s + u _i /M. Now the role of M becomes clear: the magnification of the re-scan relay is different from the magnification of the re-scan operation by a factor M.

The re-scan confocal image intensity can now be rewritten as:

$$I_{rec}\left(u_c\right)={\displaystyle \int d^2{u}_{o}d{v}_o{H}_{rec}\left(u_c-u_o,v_o\right)T\left(u_o,v_o\right)}$$ (6)

with the re-scan confocal PSF:

$$H_{rec}\left(u_c-u_o,v_o\right)=M^2{\displaystyle \int d^2{u}_s}D\left(M{u}_c-M{u}_s\right)H_{em}\left(M{u}_c-u_o-\left(M-1\right)u_s,-v_o\right)H_{ex}\left(u_o-u_s,v_o\right)$$ (7)

Taking the Fourier Transform (FT) and with a little algebra it is found that:

$$H_{rec}\left(u_c-u_o,v_0\right)={\displaystyle \int d^{2}q{\widehat{H}}_{rec}\left(q,v_0\right)e^{2\pi iq\cdot \left(u_c-u_o\right)}}$$ (8)

with the re-scan confocal Optical Transfer Function (OTF):

$${\widehat{H}}_{rec}\left(q,v_o\right)={\displaystyle \int d^{2}q\text{'}\widehat{D}\left(q\text{'}\right){\widehat{H}}_{em}\left(\frac{q}{M}-q\text{'},-v_o\right){\widehat{H}}_{ex}{\left(\frac{\left(M-1\right)q}{M}+q\text{'},v_o\right)}^{*}}$$ (9)

For a magnification decoupling M = 2 we retrieve the results of Sheppard [3] and Müller and Enderlein [4], with a spatial frequency cutoff that is extended by a factor of two. The doubling of optical bandwidth is not achieved at the expense of the optical sectioning capability. The integrated intensity as a function of defocus is:

$$\begin{array}{c}{I}_{rec,tot}\left(v_o\right)={\displaystyle \int d^{2}u}{H}_{rec}\left(u,v_o\right)={\widehat{H}}_{rec}\left(0,v_o\right)\\ ={\displaystyle \int d^{2}q\widehat{D}\left(q\right){\widehat{H}}_{em}\left(q,-v_o\right){\widehat{H}}_{ex}{\left(q,v_o\right)}^{*}}\end{array}$$ (10)

For a near-zero pinhole size (FT of pinhole transmission function equal to one for all spatial frequencies) the OTF is given by the convolution of the (scaled) excitation and emission OTF so that the re-scan confocal PSF is the product of the emission and excitation PSFs:

$$H_{rec}\left(u,v_o\right)=H_{em}\left(u,-v_o\right)H_{ex}\left(u,v_o\right)$$ (11)

independent of M. For an infinite pinhole radius (FT of pinhole transmission function equal to a delta peak) the OTF is given by the product of the excitation and emission OTF:

$${\widehat{H}}_{rec}\left(q,v_o\right)={\widehat{H}}_{em}\left(\frac{q}{M},-v_o\right){\widehat{H}}_{ex}{\left(\frac{\left(M-1\right)q}{M},v_o\right)}^{*}$$ (12)

and now the integrated intensity is equal to one for all defocus values, i.e. no optical sectioning is achieved.

The performance of the re-scan confocal microscope may be compared with the standard confocal operation for which the image intensity is given by:

$$\begin{array}{c}{I}_{conf}\left(u_s\right)={\displaystyle \int d^2{u}_{i}D\left(u_i\right)I_{pin}\left(u_i,u_s\right)}\\ ={\displaystyle \int d^2{u}_{o}d{v}_o{H}_{conf}\left(u_s-u_o,v_o\right)T\left(u_o,v_o\right)}\end{array}$$ (13)

with the confocal PSF:

$$\begin{array}{c}{H}_{conf}\left(u_s-u_o,v_o\right)=\left[{\displaystyle \int d^2{u}_{i}D\left(u_i\right)H_{em}\left(u_i-u_o+u_s,-v_o\right)}\right]H_{ex}\left(u_o-u_s,v_o\right)\\ =\left[{\displaystyle \int d^{2}q\widehat{D}\left(q\right){\widehat{H}}_{em}{\left(q,-v_o\right)}^{*}{e}^{2\pi iq\cdot \left(u_s-u_o\right)}}\right]H_{ex}\left(u_o-u_s,v_o\right)\end{array}$$ (14)

which is equal to the product of the excitation PSF and the convolution of the emission PSF and the pinhole aperture function. The integrated intensity as a function of defocus is given by Eq. (10), i.e. equal to the re-scan confocal case for all defocus values.

This implies that the optical sectioning capabilities of the re-scan confocal microscope are the same as with the traditional confocal microscope. Thus, the main advantage of re-scanning is the improvement of lateral resolution, even for intermediate to large pinhole sizes, thereby maintaining a good signal to noise ratio.

Simulations have been done to investigate the effect of pinhole size on the PSF and Modulation Transfer Function (MTF, the absolute value of the OTF), of the RCM in comparison to the confocal microscope. The simulations were done with Matlab using the chirp z-transform based method for evaluating the necessary Fourier transforms [15]. The image plane was discretized with a 127 × 127 grid of size 3λ/NA, the reciprocal plane was discretized with a 256 × 256 grid of size 4NA/λ. Figure 2 shows the PSF and MTF of the confocal and re-scan confocal microscopes for different pinhole radii. The optical bandwidth for the re-scan confocal case is extended by a factor of two, but the transfer function is very low for spatial frequencies close to the cut-off, giving an effective increase with a factor of about √2. The width of the confocal spot increases with pinhole radius, whereas the width of the re-scan confocal spot remains more or less the same for different pinhole radii. This is quantified by the FWHM as a function of pinhole radius (see Fig. 3 ). Note that for pinhole radius of near to zero the FWHM of RCM equals the FWHM of the confocal microscope. For a pinhole of more than 1 AU the FWHM becomes even slightly narrower than the confocal PSF. We only measured this improvement for simulation of a realistic PSF (Airy distribution); for a Gaussian PSF approximation we did not see this improvement as expected from the theory.

Fig. 2.

PSF (A, B) and MTF (C, D) of the confocal (a, c) and re-scan confocal (b, d) microscope for different pinhole radii and defocus zero. The peak of both the MTF and PSF curves are normalized to unity. The width of the confocal microscope is only narrowed for small pinhole sizes (radius below about 1-2 AU), the same degree of narrowing is achieved in the re-scan confocal case for any pinhole size.

Fig. 3.

FWHM of the PSF as a function of pinhole radius for the confocal and re-scan confocal microscope, showing identical width for near zero pinhole size and a ratio of FWHM-values leveling off to a value a bit larger than √2 for large pinhole sizes. The data are from numerical simulations.

4. Experiments

The improvement of lateral resolution was quantified by 3D imaging of fluorescent beads of 100 nm with the pinhole set to two AU. Individual shoulder-to-shoulder beads (distance 250 nm) can clearly be distinguished with M = 2 (Fig. 1(d)) whereas they are observed as not resolved for M = 1 (Fig. 1(c)). Analysis of 25 beads shows that the FWHM is reduced from 245 nm ( ± 15 nm) for M = 1 to 170 nm ( ± 10 nm) for M = 2, which is an improvement by a factor of 1.4 ( ± 0.1), confirming the theory of RCM. Note that the FWHM in the axial direction, which is only determined by the size of the pinhole, is 500 nm ( ± 30 nm) in both cases (M = 1 and M = 2). Figure 4 shows the FWHM as well as the FWHM improvement ratio (FWHM at M = 1 divided by FWHM) as a function of sweep factor M. The data is obtained from 9 beads measured on different samples. For each value of M ≠ 1 a new data set for M = 1 is measured directly afterwards so as to mitigate effects of focus drift on the measured improvement ratio. Clearly, the model, represented by Eq. (1), fits the data well with an optimum close to M = 2, and a resolution improvement factor of 1.41 ( ± 0.13), close to the predicted factor √2. The fitted widths of the excitation and emission spots are 224 nm and 235 nm, respectively, obtained from a chi-square fits of both curves. These values are several tens of nanometers larger than the FWHM of diffraction limited spots at the excitation wavelength (488 nm) and emission wavelength (515 nm), probably due to broadening by the finite sized beads (diameter 100 nm) and small defocus errors in the light path.

Fig. 4.

Measured FWHM (A) and FWHM improvement ratio w.r.t. M = 1 (B) as a function of sweep factor M obtained from measurements on 9 beads, and the prediction of Eq. (1) with excitation and emission spot widths W_ex = 224 nm and W_em = 235 nm, showing a good agreement between the experiment and the model and a clear optimum in resolution improvement close to M = 2.

In Table 1 , we present a comparison between confocal microscopy and Re-Scan Confocal Microscopy. The theoretical data for confocal microscopy have been reported in Fig. 3 as FWHM of the PSF in λ/NA units. In Table 1 the data have been scaled for the NA (1.4) and λ (515 nm) used in the experimental setup and the obtained PSF has been convolved with a 100 nm FWHM gaussian profile in order to take into account the beads’ dimension. The theoretical data for RCM have been reported in the model plotted in Fig. 4. The experimental data for the Confocal Microscopy were obtained by using a commercial Zeiss LSM 510 Confocal Microscope with a Zeiss Plan-Apochromat, 100x /1.40 oil objective. The diameter of the pinhole has been varied from 0.2 to 2 AU, where 1 AU = 1.2λ/NA. From this comparison, it is possible to resemble the results from confocal microscopy with pinhole 0.2 AU to the results from RCM with M = 2, as predicted by the theory. In this case, it is critical to underline the importance of the improved sensitivity offered by RCM: the use of an almost closed pinhole in confocal microscopy allows a better resolution, but at the cost of a substantial reduction of photon collection. RCM with M = 1 can be compared with confocal microscopy with pinhole set at 2 AU, as predicted by the theory as well. These two comparisons show that the trade-off between sensitivity and resolution that is present in confocal microscopy is not present anymore for RCM.

Table 1. Comparison between confocal microscopy with different pinhole size and RCM. RCM allows to obtained an improvement in resolution without sacrificing sensitivity.

	Theory	Experiment
Confocal, pinhole 0.2 AU	168 nm	184 nm ( ± 17 nm)
Confocal, pinhole 1 AU	208 nm	220 nm ( ± 21 nm)
Confocal, pinhole 2 AU	212 nm	246 nm ( ± 19 nm)
RCM, pinhole 2 AU, M = 1	234 nm	245 nm ( ± 15 nm)
RCM, pinhole 2 AU, M = 2	162 nm	170 nm ( ± 10 nm)

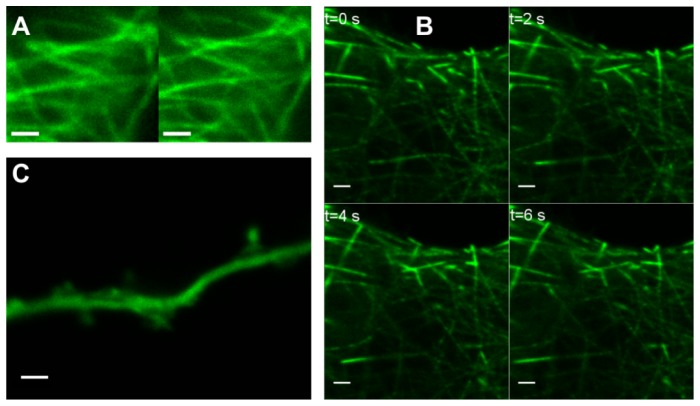
The improvement in resolution is also shown in optical sections of fluorescently labeled microtubules in HUVEC cells (Fig. 5 and Media 1 ^{(4.7MB, AVI)} ). Time lapse imaging of living HeLa cells expressing EB3-GFP, which is associated with the growing end of microtubules (Fig. 6 and Media 2 ^{(2.7MB, AVI)} and Media 3 ^{(4.4MB, AVI)} ), shows that RCM allows tracking of fast dynamic structures (0.5 μm/s) with improved resolution, high sensitivity and sufficient sample rate (2 fpm). Finally, we show that the RCM technology allows accurate observation of the mobility of dendritic spines in living primary hippocampal neurons expressing pGW1-GFP (Fig. 6 and Media 4 ^{(613.4KB, AVI)} ). Video shows mobility of spines, sub-resolution structures where communication between neurons takes place. On the right hand side two spines very close to each other appear and either fuse again move to the back-side of the dendrite. Although the distance between the spine necks is only 250 nm, they can be resolved by RCM (M = 2) and observed as individual spines, each with its specific structure. Note that the dimensions of these structures are similar to the micro beads in Fig. 1(d) which can only be resolved with RCM (M = 2), indicating that RCM will be helpful for the study of the dynamic structure of dendritic spines. With confocal microscopy, these structures can only be observed with a pinhole diameter much smaller than one AU, leading to loss of fluorescence signal and decrease of signal-to-noise ratio.

Fig. 5.

Optical sections of fluorescently labeled microtubules in HUVEC cells imaged by RCM with sweep-factor M = 1 (A), which gives an image with standard diffraction limited resolution of a wide-field fluorescence microscope. By imaging in double-sweep mode (sweep-factor M = 2) (B) gives resolution improvement by a factor of √2. Measured diameter of the microtubules is reduced from 255 nm for M = 1 to 185 nm for M = 2. The insets show junctions of microtubules (C, D) and parallel microtubules (D, F) unresolved with wide-field resolution (C, D) that can be distinguished by RCM in double sweep mode (E, F). The full 3D image stack is shown in Media 1 ^{(4.7MB, AVI)} . Scale bars are 1 μm.

Fig. 6.

(A) Screenshot from an RCM time lapse series of HeLa cells expressing EB3-GFP (Media 2 ^{(2.7MB, AVI)} ) shows that RCM allows live cell imaging with improved resolution. Left: M = 1, diffraction limited resolution, right: M = 2, improved resolution. Duration acquisition of 200 optical sections was 200 sec. (B) Screenshots from an RCM time lapse series of living HeLa cells expressing EB3-GFP (Media 3 ^{(4.4MB, AVI)} ) showing that RCM (M = 2) allows tracking of fast dynamic structures (0.5 μm/s) with sufficient sample rate (1 fps). (C) Screenshot from RCM time lapse series of a dendrite of living hippocampal neurons expressing pGW1-GFP (Media 4 ^{(613.4KB, AVI)} ). Time series is 222 sec. All scale bars (A, B, C) are 1 μm.

5. Discussion

In this study, we have proven, both theoretically and experimentally, that the lateral resolution of the Re-scan Confocal Microscope (RCM) with open pinhole equals the lateral resolution of the conventional confocal microscope with almost closed pinhole. Therefore, it has strongly improved sensitivity while the sectioning capability of conventional confocal microscopy is maintained. Moreover, post-processing of the image, which may introduce artifacts, is not required. We expect that this new technology will find its way in biological applications where superior photon economy and resolution beyond the diffraction limit is essential.

In particular, the RCM technique may be suitable for application with modern sCMOS cameras, which combine a large Field Of View (2048 × 2048 pixels) and a high frame rate (100 fps) with a reasonable Quantum Efficiency (around 70%) and low readout noise, without suffering from excess noise like EMCCD cameras [16]. This compares favorably to the photon detection efficiency of Photo-Multiplier Tubes (PMTs) generally used in confocal microscopes (up to 40%).

Appendix: Optical setup and sample preparation

Optical setup

Light from a 488 nm diode laser (Obis 488-50, Coherent Inc.) is coupled into a single mode optical fiber and collimated with a 10 mm lens (Thorlabs Inc.). The light is directed via a 488/594 nm double band dichroic mirror (ZT488/594rpc, Chroma Technology Corp.) to the first xy-scanner (VM1000, GSI Lumonics) at the telecentric point of the scan lens (Nikon Instruments Inc.). A TE2000 microscope (Nikon Instruments Inc.) stand is equipped with a 100x objective (CFI Apo TIRF 100X Oil, NA 1.49, Nikon Instruments Inc.) and Remote Focus Accessory (Nikon Inc.). Fluorescence light is, after de-scanning, focused with a 400 mm achromat (Thorlabs Inc.) on a lever-actuated iris diaphragm with an adjustable size (Thorlabs Inc.) that is used as a pinhole. Light after the pinhole is collected with a 200 mm achromat (Thorlabs Inc.) and re-scanned with a second scanner (VM500T, GSI Lumonics) and projected with a 85 mm scan lens (Thorlabs Inc.) on an EMCCD camera (iXon897, Andor Technology) with 512×512 pixels of 16×16 μm². Electronic components of the setup are interfaced by a Nidaq pci-6713 card (National Instruments Co.), LabVIEW 2012 and Micro-Manager 1.4.

The microscope magnifies both the object and the laser spot into the primary image plane with a factor M_micr. After the primary image plane the magnification of an object is determined by the angular amplitudes α_de and α_re of the de-scanner and the re-scanner, respectively and the focal distances, f₁ and f₂, of the scan lenses since the scanners are placed in the telecentric point of L1 and L4 (see Fig. 1). Resulting in the total magnification of the object:

$$M_{obj}=\frac{f_4\tan {\alpha }_{re}}{f_1\tan {\alpha }_{de}}{M}_{micr}\approx \frac{f_4}{f_1}\frac{{\alpha }_{re}}{{\alpha }_{de}}{M}_{micr}$$ (15)

The scanning spot is also magnified, first by the microscope, then by the optics of the de-scanner (f₂/f₁) and finally by the optics of the re-scanner (f₄/f₃):

$$M_{spot}=\frac{f_2}{f_4}\frac{f_4}{f_3}{M}_{micr}$$ (16)

Note that M_spot is independent of the angular amplitudes (“sweep”) of the two scanners. The sweep factor M is defined by:

$$M=\frac{M_{obj}}{M_{spot}}=\frac{f_3}{f_2}\frac{{\alpha }_{re}}{{\alpha }_{de}}$$ (17)

and can be adjusted by changing the angular amplitudes of the scanners or by replacing lenses L2 and L3.

Sample preparation

For resolution measurements on beads we used yellow-green FluoSpheres carboxylate-modified microspheres of 0.1 μm diameter (Invitrogen), mounted in VECTASHIELD (Vector Labs) on Menzel-Glaser Nr.1 coverslip. The EMCCD gain during the acquisition was set at 50, with 1 sec acquisition time and 20 μW laser intensity.

For images on microtubules, HUVEC cells (Human Umbilical Vein Endothelial cell) derived from blood vessel of human umbilical cords were grown on collagen covered coverslips in a mix of RPMI and DMEM (50-50%) with 10% fetal bovine serum (FBS) at 37°C degree at 5% CO2. The cells were fixed with 10% MeS buffer (100 mM Mes, PH6.9, 1mM EGTA and inM MgCl2) and 90% methanol for 5 minutes on ice. After Blocking with 5% BSA (Bovine Serum Albumin) for 1 hour cells were incubated in monoclonal anti Microtubules (anti-tubulin YL1/2 clone: sc-53029, Santa Cruz biotechnology, raised in Rat) for 1 hour and secondary antibody Alexa 488 donkey anti rat (Invitrogen) for 30 minutes at room temperature. 3D stack contained 41 optical sections with 100 nm interval. Acquisition time for each section was 1 s. EMCCD gain set to 150 and laser intensity to 10 μW.

For images and movies of EB3-GFP in HeLa cells, the cells (ATCC) were cultured in DMEM-Glutamax, 10% FBS, penicillin (100 U/ml) and streptomycin (100 μg/ml; Invitrogen) on 24 mm cover slips (Menzel-Gläser). Cells were transfections using Lipofectamin 2000 (Invitrogen) using 300 ng/μl EB3-GFP plasmid per sample. Cells were cultured for 24 hours before imaging in microscopy medium (20 mM HEPES (pH 7.4), 137 mM NaCl, 5.4 mM KCl, 1.8 mM CaCl₂, 0.8 mM MgCl₂, 20 mM glucose). Time series were made at sample rate of 0.5 and 1.0 fps for Media 2 ^{(2.7MB, AVI)} and Media 3 ^{(4.4MB, AVI)} , respectively. EMCCD gain was set to 200 and the laser intensity was 65 μW and 20 μW, respectively.

For images and movies of neurons, hippocampi were dissected from rat embryos (E16-19) [17]. Tissue was homogenized with trypsin (2.5% wt/vol, Gibco 15090) and cells were cultured on coverslips at 36 °C and 5% CO₂. After 3 days, half of the culture medium was replaced with culture medium containing 10 µM FUDR. 18 days later (DIV18) samples were transfected with 5 µg/ml pGW1-GFP (kindly provided by C.C. Hoogenraad, Utrecht University) using Lipofectamine (10 µl/ml; Invitrogen, cat. No.11668-027) in culture medium for 20-30 minutes. Samples were transferred to a new well with 2 ml of pre-warmed incubation medium containing 1% GlutaMax (Gibco, cat. No. 35050-038) and the transfection mix was added in a drop-wise manner. This was then left to incubate for 45 minutes at 36 °C and 5% CO₂, after which the samples were gently washed in 3 ml of culture medium and returned to their original well. One day after transfection, samples were imaged at room temperature in 2 ml of pre-warmed artificial cerebrospinal fluid. Of the brightest neurons, secondary or tertiary dendrites with dendritic spines were imaged. Time lapse imaging was performed at 0.5 fps with EMCCD gain of 200 and laser intensity set to 55 μW.