Accelerated rescaling of single Monte Carlo simulation runs with the Graphics Processing Unit (GPU)

Abstract

Abstract: To interpret fiber-based and camera-based measurements of remitted light from biological tissues, researchers typically use analytical models, such as the diffusion approximation to light transport theory, or stochastic models, such as Monte Carlo modeling. To achieve rapid (ideally real-time) measurement of tissue optical properties, especially in clinical situations, there is a critical need to accelerate Monte Carlo simulation runs. In this manuscript, we report on our approach using the Graphics Processing Unit (GPU) to accelerate rescaling of single Monte Carlo runs to calculate rapidly diffuse reflectance values for different sets of tissue optical properties. We selected MATLAB to enable non-specialists in C and CUDA-based programming to use the generated open-source code. We developed a software package with four abstraction layers. To calculate a set of diffuse reflectance values from a simulated tissue with homogeneous optical properties, our rescaling GPU-based approach achieves a reduction in computation time of several orders of magnitude as compared to other GPU-based approaches. Specifically, our GPU-based approach generated a diffuse reflectance value in 0.08ms. The transfer time from CPU to GPU memory currently is a limiting factor with GPU-based calculations. However, for calculation of multiple diffuse reflectance values, our GPU-based approach still can lead to processing that is ~3400 times faster than other GPU-based approaches.

1. Introduction

Light transport through tissue is affected by the optical properties of the underlying sample. To interpret fiber-based and camera-based measurements of remitted light from biological tissues, researchers typically use models of light transport. Applications of this approach include diffuse reflectance spectroscopy [1, 2], fluorescence spectroscopy [3, 4], Cerenkov light transport [5], Raman spectroscopy [6], and optical microscopy [7].

Researchers typically use analytical models, such as the diffusion approximation to light transport theory [8], or stochastic models, such as Monte Carlo modeling [9]. While the diffusion approximation enables fast calculation of optical fluence distributions and light reflectance and transmittance, it does not provide accurate solutions for simulated scenarios in which light absorption is appreciable, such as visible-light spectroscopy of skin cancer and port-wine stains [10, 11]. The Monte Carlo approach enables accurate, flexible modeling of light transport in biological tissues. However, it suffers from relatively long computation times required to achieve a meaningful simulation run. To solve inverse problems in which fiber- or camera-based measurements of light remittance are combined with light-propagation modeling to estimate the internal tissue optical properties, the situation is exacerbated due to the need to perform multiple Monte Carlo simulation runs [12].

To achieve rapid (ideally real-time) measurement of tissue optical properties, especially in clinical situations, there is a critical need to accelerate Monte Carlo simulation runs. We specifically are interested in integration of rapid Monte Carlo calculations with Spatial Frequency Domain Imaging (SFDI) [13, 14], which is a wide-field, camera-based method that involves analysis of multispectral reflectance images collected during structured illumination of the tissue under interest. With camera-based imaging, the computational demands are magnified due to the need for optical-property determination at each pixel.

Several peer-reviewed papers describe use of the Graphics Processing Unit (GPU) to achieve faster Monte Carlo simulation runs than those achievable on the Central Processing Unit (CPU) of the host computer. Alerstam et al. [15] published the first demonstration of GPU-based acceleration of Monte Carlo simulations. Alerstam et al. [16] then published on development of open-source GPU software designed to accelerate the popular Monte Carlo Multi-Layered (MCML) package [9]. Other groups proposed use of GPUs to perform specialized Monte Carlo simulation runs, for ionizing radiation transport [17], ultrasound-modulated light [18], fluorescence generation and detection [19], and fiber-based diffuse reflectance spectroscopy [1]. Doronin and Meglinski [20] reported on online, GPU-accelerated MC simulations.

Along with Liu et al. [21], we recently published on use of GPUs to accelerate processing of raw speckle images into maps of blood flow [22]. With complete integration of the GPU into a camera-based, laser speckle imaging system, we reported on a seven-fold reduction in the time required to convert raw speckle images to Speckle Flow Index images [22].

In this manuscript, we report on our approach using the GPU to accelerate rescaling of single Monte Carlo (sMC) runs to calculate rapidly diffuse reflectance values for different sets of tissue optical properties. The sMC method, also referred to as White Monte Carlo [15, 23, 24], involves use of a photon-pathlength rescaling approach to enable rapid calculation of diffuse reflectance, for a set of absorption (μ_a) and reduced scattering coefficients (μ_s’). With sMC, conventional Monte Carlo simulation run is performed with the medium μ_a set to zero and a specific value of μ_s ^’. For each simulation photon “i”, the exit position (r_i) and the total time of flight (t_i) are recorded. Similar to Martinelli et al. [25], we implemented a binning approach in which each remitted photon weight w_i at radial and time positions r_i and t_i was added to a reflectance matrix R(r_k,t_l), where k is the index of radial ring containing r_i and l is the index for the time interval containing t_i. To rescale the sMC simulation output for a different set of values for μ_a and μ_s ^’, we used an approach similar to that described by Alerstam et al. [15] but applied to the binned data instead of individual simulated photons. This approach enabled efficient calculation of diffuse reflectance for multiple sets of optical properties as well as multiple source-detector separations (ρ).

2. Methods

As a design goal, we wished to enable end users to perform GPU-based rescaling of sMC simulation data as easily as possible. To this end, we selected MATLAB (The Mathworks, Natick, MA) to enable non-specialists in C and CUDA-based programming to use the generated open-source code. We based this decision on our prior experience with providing open-source software for Laser Speckle Imaging calculations on the GPU [22, 26].

We developed a software package with four abstraction layers (Fig. 1 ). The first layer consisted of custom-written CUDA kernels written in C++ . The second layer consisted of CUDA host code, also written in C++ , compiled using the CUDA compiler (nvcc). The third layer consisted of C-based, MATLAB MEX code that called the CUDA binaries. The fourth layer consisted of the master MATLAB script.

Fig. 1.

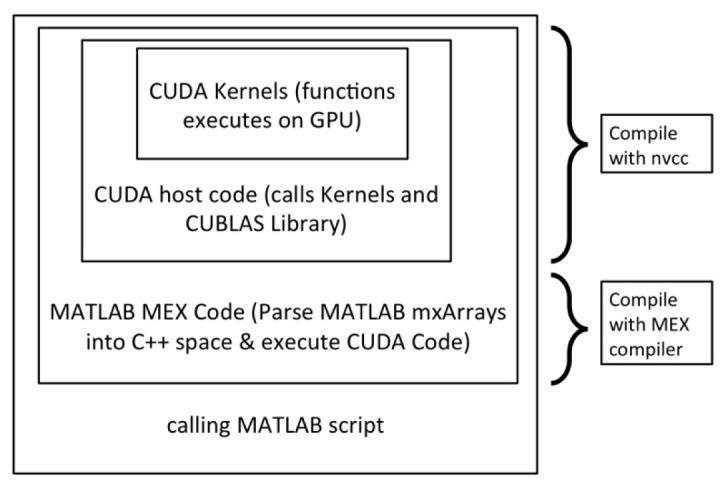
Diagram illustrating the method employed to interface MATLAB with the CUDA Monte Carlo forward model kernels. CUDA host code containing the CUDA kernels and calls to the CUBLAS library were compiled using NVIDIA CUDA Compiler (nvcc). The MATLAB MEX C/C++ code, wherein the CUDA binaries are called, were compiled subsequently with the MATLAB MEX compiler and utilized by the main MATLAB script.

In this study, we determined the time required for the CPU or the GPU to perform a single rescaling of a sMC simulation run. We performed a single sMC run consisting of 10 million simulated photons. We assumed a homogeneous medium of infinite thickness, with μ_a = 0mm⁻¹ and μ_s’ = 1mm⁻¹, and refractive index of 1.33. With conventional Monte Carlo, we calculated the binned diffuse reflectance matrix R(r_k,t_l).

We performed several applications of the rescaling approach with optical properties ranging from 0.1 to 1.0 mm⁻¹ for μ_a and 0.1 to 5.0 mm⁻¹ for μ_s’. For each set of optical properties, a total of 5000 rescaling attempts were performed on either the CPU or GPU, and the mean computation time was calculated. To simulate illumination schemes typically used with SFDI, we followed an approach described previously by Cuccia et al. [14] to calculate diffuse reflectance. The approach involves use of a zeroth-order Bessel function, to calculate the diffuse reflectance for illumination at two spatial frequencies: 0 mm⁻¹ (e.g., planar illumination) and 0.667 mm⁻¹.

We used the NVIDIA GT 650M GPU with 384 shader processing units (cores) running at 775MHz, and with 1GB of dedicated memory. The GPU ran in a MacBook Pro with an Intel Core i7 at 2.6 GHz and with 8GB of DDR3 RAM. We used MATLAB 2011b running in Windows 7, to serve as the fourth abstraction layer (Fig. 1), and the CUDA 4.1 driver and toolbox.

3. Results and discussion

To calculate the diffuse reflectance with a new set of optical properties, the GPU-enabled approach was 15 times faster. MATLAB on the CPU required 1.2 ms to rescale the sMC output to account for new optical properties. In comparison, the MATLAB/GPU approach (Fig. 1) required only 0.08 ms. The shorter computation time with the latter approach, results from the massively parallel calculations associated with rescaling the binned sMC output.

Calculation of diffuse reflectance values with our GPU-based approach is insensitive to tissue optical properties. We chose SFDI as an example for studying the effects of tissue optical properties on the time required to calculate diffuse reflectance values. We evaluated both CPU- and GPU-based rescaling approaches applied to the initial sMC output, and we used a zeroth-order Bessel function [14] to calculate the diffuse reflectance at two spatial frequencies. Over a wide range of tissue optical properties, the diffuse reflectance values associated with the GPU-based rescaling approach were similar to those of the CPU-based approach (Table 1 ). The total time required to perform GPU-based rescaling and calculate the diffuse reflectance values at the two spatial frequencies, was minimally sensitive to the tissue optical properties. In contrast, the total time associated with the CPU-based rescaling approach showed some variance with tissue optical properties. We found that the time associated with the Bessel function calculation on the CPU, showed the greatest dependence on tissue optical properties.

Table 1. Total times required to calculate diffuse reflectance values at two spatial frequencies of illumination: 0 mm⁻¹ (e.g., planar illumination) and 0.667 mm⁻¹. We performed both CPU- and GPU-based rescaling approaches of a single sMC output. Each computation time value represents the average of 5000 repetitions of the rescaling approach.

μa [mm−1]	0.1	0.1	0.1	0.5	0.5	0.5	1	1	1
μs' [mm−1]	1	2	5	1	2	5	1	2	5
Diffuse reflectance, 0 mm−1 (CPU)	0.259	0.369	0.517	0.074	0.138	0.259	0.033	0.074	0.164
Diffuse reflectance, 0 mm−1 (GPU)	0.259	0.369	0.517	0.074	0.138	0.259	0.033	0.074	0.164
Diffuse reflectance, 0.667 mm−1 (CPU)	0.208	0.332	0.500	0.069	0.134	0.256	0.032	0.073	0.163
Diffuse reflectance, 0.667 mm−1 (GPU)	0.204	0.331	0.500	0.069	0.134	0.256	0.032	0.073	0.163
Computation time (CPU) [ms]	2.62	2.65	1.94	2.62	2.62	2.54	2.63	2.61	2.23
Computation time (GPU) [ms]	0.26	0.28	0.27	0.26	0.26	0.26	0.26	0.25	0.24

To calculate a set of diffuse reflectance values from a simulated tissue with homogeneous optical properties, our rescaling GPU-based approach achieves a reduction in computation time of several orders of magnitude as compared to other GPU-based approaches. Due to 1) the advances made in GPU technology since the Alerstam et al. [15] report, and 2) the differences in complexity associated with the computational models, a direct comparison of computation times can be misleading. We propose that the work by Hennessy et al. [1], which is associated with the shortest reported run time for a Monte Carlo simulation, offers the most relevant comparison. The authors used a GPU-based approach to generate a Look-Up Table (LUT) that mapped optical properties to diffuse reflectance values. They reported a time of two min to populate a LUT with 400 values, resulting in an average of 0.3s per simulation run of one million photons per run. In comparison, our GPU-based rescaling approach generates a diffuse reflectance value in 0.00008s, or ~30,000 times faster than the Hennessy et al. approach.

For a single rescaling calculation, the transfer time from the CPU to the GPU, is the limiting factor. Our current code required the initial sMC output to be sent to the GPU device memory. The associated transfer time was 2.6ms, which is more than two times longer than the MATLAB computation time on the CPU. Hence, similar to what we observed in our previous work involving Laser Speckle Imaging calculations on the GPU (15), the transfer time is prohibitively long for a single calculation of diffuse reflectance for a new set of optical properties. However, the transfer time is a one-time penalty. Once the sMC output is transferred, the rescaling calculation can be performed on a repeated basis, with a time cost of 0.08 ms per calculation. Hence, to create a Look-Up Table similar to that created by Hennessy et al. [1], our GPU-based rescaling approach requires a total of ~35 ms to transfer the sMC output and generate diffuse reflectance values for 400 pairs of absorption and reduced scattering coefficients. Our time still is ~3400 times shorter than the GPU-based approach of Hennessy et al. [1].

We acknowledge that the computation time can change depending on CPU-related overheads, such as interrupts and cache management. Nevertheless, we propose that the GPU and CPU computational benchmarks that we report here (e.g., Table 1) provide a realistic comparison of the GPU and CPU calculation times and hence a realistic practical estimate of the potential reduction in computation time associated with GPU-based calculations.

It is important to note that our GPU-based rescaling approach provides only a rapid method to calculate diffuse reflectance at different spatial frequencies of illumination (Table 1). To date, we have not explored the use of GPU-based processing to extract other parameters of interest, such as fluence rate, energy deposition/absorption profiles, individual history of photon propagation, etc. Furthermore, for real-time, functional optical imaging, additional work is required to exploit the Look-Up Table features of the GPU, to convert maps of diffuse reflectance values efficiently to maps of tissue optical properties. This is especially important for technologies such as SFDI, which involve measurements collected at multiple spatial frequencies to hone in on estimates of both absorption and reduced scattering coefficients [27].

4. Conclusions

In conclusion, we presented a GPU-based approach that uses the rescaling approach of sMC to calculate diffuse reflectance associated with a set of optical properties. With this approach, we calculated diffuse reflectance for a given set of optical properties in ~0.08ms, which is at least ~30,000 times shorter than times reported in the literature. The transfer time from CPU to GPU memory currently is a limiting factor with GPU-based calculations. However, for calculation of multiple diffuse reflectance values, our GPU-based approach still can lead to processing that is ~3400 times faster than other GPU-based approaches. We expect that continued evolution of GPU technology will lead to shorter transfer times and lead ultimately to real-time optical-property mapping using camera-based imaging methods such as Spatial Frequency Domain Imaging (SFDI) [14]. This code and compiled binaries are freely available online for download at http://choi.bli.uci.edu/software.