Computational Simulation Strategies for Analysis of Multisubunit RNA Polymerases

1. Introduction

Multisubunit RNA polymerase (RNAP) mechanisms present challenges for current computational techniques because of their large size, complications of simulating nucleic acids and metals, and also dynamic aspects of the system. The purpose of this review is to discuss computational methods that have been applied to RNAPs and to evaluate the insight gained. Furthermore, this review seeks to anticipate some future approaches expected to give additional understanding. Because RNAPs pose challenges to available computation technology, these studies may necessitate improvements in methods and hardware applied to very large multiatom systems that include protein and nucleic acid components. Other reviews on RNAP structure/function have recently appeared but generally with a different focus.¹

This review was developed on the basis of collaborations involving the Feig, Cukier, Burton, Kashlev, and Coulombe laboratories. The attempt has been to combine sophisticated computational analyses with biochemical and genetic structure/function studies of multisubunit RNAPs. The hope was that integrating these broad approaches might enrich the science, leading to a deeper description of a complex, templated polymerization mechanism central and global in known living systems. So far, this collaborative approach has led to advances in understanding and an indication that going back and forth between simulation and experiment should prove an incisive approach to a very big problem in biology. This review can be viewed as a progress report with an eye to a bright and revealing future.

In section 13, particular emphasis is placed on quantum chemistry (QC) methods to analyze details of RNAP and DNA polymerase (DNAP) mechanisms. This section is expanded in detail relative to others because the 2-Mg mechanism is currently a subject of great general interest, but the language and methods of QC may not be easily accessible to all who may be interested. We attempt an accessible presentation of a sophisticated and developing field.

2. RNA Polymerase X-ray Crystal Structures

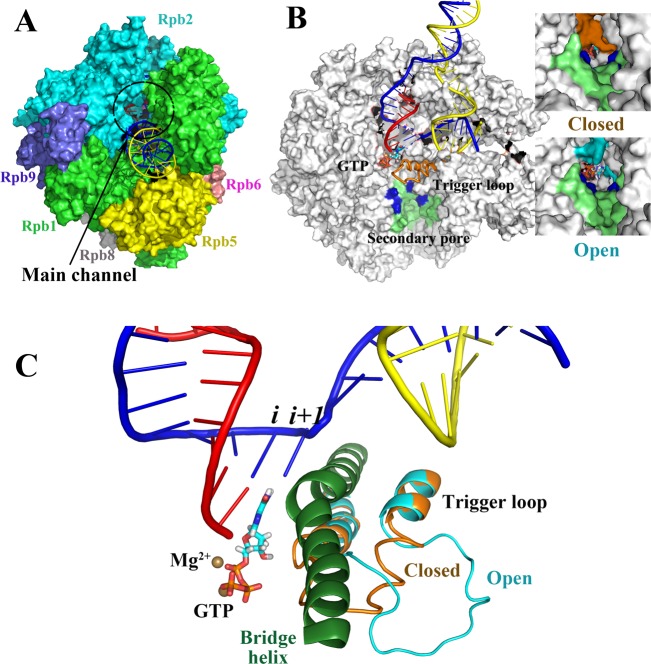
In Figure 1, images of Saccharomyces cerevisiae RNAP II are shown to illustrate features of multisubunit RNAPs. Figure 1A shows a ternary elongation complex (TEC) structure that includes 10 subunits but is missing subunits Rpb4 and Rpb7.² The active site of a RNAP is deeply buried in the structure. In Figure 1B, parts of the Rpb1 and Rpb2 subunits are cut away to reveal the transcription bubble, active site, and secondary pore. The images to the right of Figure 1B show the pore with a closed or open trigger loop conformation. It appears that closing the trigger loop closes the pore.³ Figure 1C illustrates the RNAP active site, bridge helix, and trigger loop, in closed and open conformations.²⁻⁴ Two Mg²⁺ ions are involved in the RNA polymerization mechanism. The active site includes the i and i + 1 translocation registers, which are indicated in the figure.

Figure 1.

Multisubunit RNAP (S. cerevisiae RNAP II). (A) Complex subunit structure and main enzyme channel. (B) Cutaway image (parts of Rpb1 and Rpb2 are missing) to show the transcription bubble, secondary pore (lime green; blue indicates basic residues important in PP_i release),²¹ and buried active site. RNA is red, template DNA is blue, nontemplate DNA is yellow, the closed trigger loop conformation is orange, and the open trigger loop conformation is cyan. Images to the right indicate that a TEC with a closed trigger loop (orange) mostly closes the pore, and a TEC with an open trigger loop (cyan) has a more open pore with a diameter comparable to a diffusing GTP substrate. (C) RNAP active site with closed and open trigger loop conformations overlaid. Colors are as in panel B. The bridge helix is dark green. PDB structures 2E2H and 2E2J (with the open trigger loop modeled) and a PDB file from Jens Michaelis showing the intact bubble^27b were used to make the images, by use of the program Visual Molecular Dynamics.⁹⁴.

Multisubunit RNAPs are found in eubacteria, archaea, eukarya, and also some viruses. These are large and dynamic molecules that transcribe double-stranded DNA to polymerize RNA (Figure 1). Located at a distance from the active site, RNAPs contain structural Zn²⁺. RNA is polymerized according to a 2-Mg²⁺ mechanism (Figure 2) that is closely analogous to the 2-Mg²⁺ mechanism of DNAPs, reverse transcriptases, and some simpler RNAPs (i.e., bacteriophage T7 RNAP).^1a,5 Despite similarities in RNAP and DNAP polymerization mechanisms, however, multisubunit RNAPs and DNAPs are not homologous.

Figure 2.

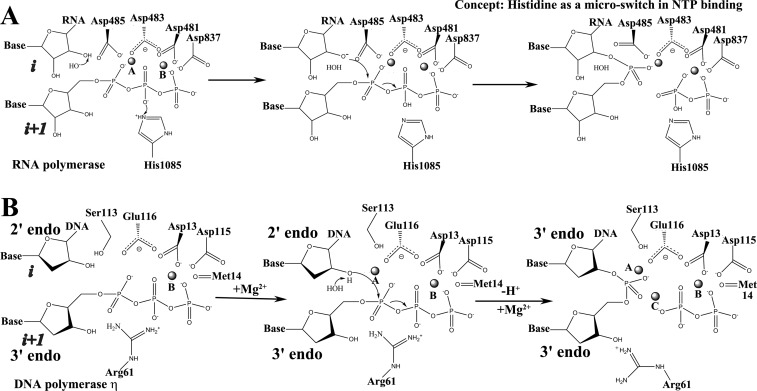
RNAPs and DNAPs have analogous 2-Mg²⁺ mechanisms. (A) Proposed mechanism for S. cerevisiae RNAP II. In the model, 3′-HO_RNA is deprotonated by OH^– proposed to be derived from solvent. Rpb1 His1085 is proposed to transfer a proton to a β-phosphate oxygen. (B) Recently proposed mechanism for human DNAP η. Water is recruited beneath the 2′-H₂ (i site sugar), interacting with the 3′-HO_DNA (i site) and the dNTP (i + 1 site) α-phosphate oxygens, which interact with Arg61. After extraction of the 3′-HO_DNA (i site) proton, the sugar pucker changes from 2′-endo to 3′-endo. Attack of 3′-O^–_DNA on the α-phosphate occurs. Arg61 shifts position and a third Mg²⁺ is recruited to PP_i.

Many RNAP structures are currently available for analysis by molecular dynamics (MD) simulation and related computational methods (Table 1). Simulation strategies extend the analysis of existing structures and allow construction of models for intermediates that may not be represented directly in crystallographic images. A particular attraction is that simulation allows many new hypotheses to be developed relating to structure, function, and dynamics based on structures. On the other hand, because multisubunit RNAPs are so large and so dynamic, they pose some challenges for all-atom computational approaches. Also, because of their large size, available RNAP X-ray crystal structures are somewhat limited in resolution, which can affect the quality of simulations. To complicate the analysis further, to be functional, RNAP structures must include DNA and RNA, Mg²⁺, and Zn²⁺. To simulate longer time scales, multiscale computational approaches can be applied, but these technologies are still in development and may not adequately substitute for all-atom methods. In some ways, RNAPs approach a worst-case scenario for computational modeling methods, making these complex enzymes a challenging subject for current technology.

Table 1. Structures of RNAPs Used in Computational Simulations.

PDB ID	resolution (Å)	organisma	protein	nucleic acid	nucleotide	state	TLb	simulationsc	refs
1I6H	3.30	Sc	10 subunits	T/R		pretranslocation	open	NMA (ENM)	(13a)
1I50	2.80	Sc	10 subunits				open	NMA (ENM)	(13a)
1HQM	3.30	Ta	α2ββ′ω				open	NMA (ENM)	(13a)
1ARO	2.80	T7		T/N				NMA (ENM)	(13)
1CEZ	2.40	T7						NMA (ENM)	(13)
1I6H	3.30	Sc	10 subunits	T/N/R		preinsertion	open	restricted MD	(19)
1IW7	2.6	Tt	α2ββ′ωσ			initiation	open	BNM	(15)
1R9T	3.5	Sc	10 subunits	T/N/R	ATP (E site)	posttranslocation	open	BD	(9)
1H38	2.9	T7		T/N/R		preinsertion		MD and umbrella sampling	(22)
1S77	2.69	T7		T/N/R	PPi	pretranslocation		MD and umbrella sampling	(22)
2E2H	3.95	Sc	10 subunits	T/N/R	GTP	posttranslocation	closed	MD, MSM,QM	(7a,16,17,21,29)
2E2J	3.5	Sc	10 subunits	T/N/R	GMPCPP	posttranslocation	open	MD, MSM,QM	(7a,16)
2O5J	3.0	Tt	α2ββ′ω	T/N/R	ATP	posttranslocation	closed	MD	(18)
2PPB	3.0	Tt	α2ββ′ω	T/N/R	AMPCPP	preinsertion	open	MD	(18a,18b)
2NVZ	4.3	Sc	10 subunits	T/N/R	UTP	posttranslocation	closed	QM	(62,73)

^aSc, Saccharomyces cerevisiae; Ta, Thermus aquaticus; T7, Enterobacteria phage T7; Tt, Thermus thermophilus.

^bTL, trigger loop configuration.

^cNMA, normal mode analysis; ENM, elastic network model; MD, molecular dynamics; BNM, block normal mode; BD, Brownian dynamics; MSM, Markov state model; QM, quantum mechanics.

X-ray crystal structures have been solved for RNAPs from eubacteria, archaea, and eukarya species. Structures are available that represent transcriptional elongation complexes and initiation complexes. Furthermore, elongation complexes with open and closed conformations of the trigger loop have been obtained.^2−4,6 The trigger loop is a mobile segment connecting two helices that is thought to enclose the RNAP active site at the time of phosphodiester bond formation (Figure 1C). The open trigger loop conformation may facilitate translocation of nucleic acids.⁷ The extent of trigger loop opening that occurs between each bond synthesis and translocation event is not yet known.

The active site of multisubunit RNAPs is buried deep within the structure (Figure 1). When the trigger loop is open, the secondary pore provides a route to solvent.^3,8 The secondary pore has been suggested to be the major or even the sole route for NTP entry, although others have proposed that NTPs may also enter through the main enzyme channel.⁸ In the ternary elongation complex (TEC), the main channel is filled with nucleic acids, limiting access to the active site via this route. Because the active site is so deeply buried and because accessibility through the pore is regulated by trigger loop opening and closing, identification of NTP loading routes, NTP rejection routes, and mechanisms of NTP exchange and pyrophosphate (PP_i) release are potentially important. For instance, if NTPs must enter and exit only through the secondary pore, this presents a potential difficulty for rapid, accurate, and efficient NTP and PP_i exchange. Potentially, loading NTPs through the main enzyme channel and releasing rejected NTPs and PP_i through the pore might be a more efficient and accurate means of exchange. The secondary pore of yeast RNAP II appears deep and narrow and negatively charged where it is most constricted,⁹ potentially making the pore a limiting channel for free NTP and PP_i exchange. As discussed below, recent studies with DNAPs provide some new ways to view this potential problem.¹⁰

3. A Brief History of Computational Studies of Multisubunit RNA Polymerases

Normal mode analysis (NMA)¹¹ is a computationally efficient and reliable method to derive protein harmonic transitions around a particular structure. An early computational approach to study RNAP, therefore, was NMA using an elastic network model (ENM),¹² which was first applied to investigate the open ↔ closed transition in all available DNAP and RNAP structures from yeast, bacterial, and phage T7 available at that time.¹³ For simpler DNAPs and RNAPs, a network of residues spanning the fingers and palm domains was detected to be involved in the open ↔ closed transition.^13b Mutation of these residues has a significant influence on polymerase activities. Block normal mode (BNM) analysis¹⁴ was then applied using an all-atom force field on bacterial RNAP¹⁵ and yeast RNAP II¹⁶ to explore intrinsic conformational flexibility.

Compared to NMA, more costly all-atom MD simulations of RNAPs can provide richer atomic details of protein conformational dynamics. All-atom MD simulations of RNAP II^7a,17 and Thermus thermophilus RNAP¹⁸ with closed and open trigger loop conformations focus on the active site and two crucial neighboring structural elements, the trigger loop and the bridge helix (Figure 1C). In agreement with crystallographic studies, the results suggest that catalysis requires a closed trigger loop and that translocation requires an open trigger loop.^7a Furthermore, the conformational changes of the bridge helix are coupled to motions of the trigger loop. Trigger loop conformations, protonation state of His1085,¹⁷ and dehydration of the active site^18c appear essential for catalysis, fidelity of NMP incorporation, and regulation of translocation. MD simulations of RNAP II with mutations on the trigger loop, such as H1085F, H1085Y, L1081G, and L1081A, influence the stability of the active site.¹⁷

Enhanced simulation techniques were used to access longer time-scale conformational movements. The diffusion of NTPs through the secondary pore⁹ and the main channel¹⁹ in RNAP II were investigated by Brownian motion simulations and restrained MD simulations respectively. The secondary pore is a narrow channel, and the estimated rate of diffusion of NTPs reaching the A site (insertion site) through the pore is very slow.⁹ So, on the basis of estimates of diffusion rates, it seems to be unfavorable for NTPs to pass through the pore to the active site, but this remains a controversial issue. On the other hand, the pore appears to be a reasonable route for pyrophosphate (PP_i) release. A Markov state model (MSM)²⁰ was established to simulate PP_i release along the secondary pore. When PP_i leaves the active site, it appears to hop between positively charged residues, such as Rpb1 Lys752 and Lys619, generating four kinetically metastable states²¹ (Figure 1B; blue residues indicate proposed PP_i hopping sites). Coupled with PP_i release, the closed trigger loop is partially opened, suggesting that PP_i release may be stimulated by opening of the trigger loop.²¹ These studies assumed a protonated trigger loop His1085, which may affect the initial movement of PP_i into the pore.

Transitions between pre-, post-, and hypertranslocation states of T7 RNAP²² and RNAP II^7a have been studied by MD simulations and umbrella sampling.²³ In multisubunit RNAPs, downstream DNA and upstream DNA/RNA hybrid translocation appear to occur separately,¹⁶ perhaps consistent with physical division of upstream RNA/DNA and downstream DNA/DNA by the bridge helix and template DNA bending (Figure 1B,C). In the presence of a cognate NTP, downstream translocation is more pronounced than upstream DNA/RNA translocation. In 10-ns simulations, observation of a partial translocation step may support a thermal ratchet mechanism, but thermal fluctuations seem to be more important in the movement of individual nucleotides, rather than in displacement of the entire hybrid. For bacteriophage T7 RNAP, based on a kinetic model with intermediates suggested by single-molecule force and various structural studies, the transition from post to pre appears to have a small energetic cost consistent with movement of Tyr639 out of the NTP binding site.^22,24

4. Transcription Cycle

The transcription cycle begins with initiation from a promoter DNA sequence. In the transition to elongation, RNAP must change from a sequence-specific DNA binding protein at the promoter to one with reduced capacity to recognize specific sequences during elongation. Initiation, therefore, is accompanied by transient association with accessory proteins that help to recognize the promoter. In bacteria, σ factors are involved in promoter recognition but are released during bulk elongation. In yeast, RNAP II utilizes a number of general transcription factors for promoter recognition. Many of these factors may dissociate during promoter escape and elongation. A crystallographic model for σ70 factor recognition of the consensus bacterial promoter −10 region (TATAATG) as single-stranded non-template-strand DNA has recently become available.²⁵

Promoter escape is the transition from initiation to productive elongation, which may involve multiple reinitiation events (abortive initiation). In eubacterial RNAP, abortive initiation implies a failure to dissociate the promoter–recognition factor σ, resulting in nascent RNA release and reinitiation. Domain 3.2 of the σ70 factor is located within the RNA exit channel, a position that must be vacated for elongation.²⁵ It is thought that as the RNA chain lengthens, domain 3.2 of the σ factor is encountered and then displaced, reducing the affinity of σ for elongating RNAP.²⁶ Sigma factor functions in promoter recognition and mechanisms to release σ factors in order to progress to elongation may vary among σ factors that recognize different promoter sequences.

During elongation, RNAP maintains a DNA template “bubble” of single-stranded DNA of 12–14 nucleotides²⁷ (Figure 1B). To date, no X-ray structure is available for the intact and native bubble. In some structures, this is due to the omission of bases during construction of nucleic acid scaffolds, and these omissions may have been necessary to construct homogeneous TECs for crystallization. In cases in which the nontemplate DNA strand is present in a crystal, this strand may be disordered. In construction of an initiating RNAP complex, the nontemplate strand appears in the structure, but it is bound to σ70, which is released during elongation.²⁵ So, in a TEC that is missing σ70, the trajectory of the nontemplate DNA strand cannot be inferred from this initiation complex. Because no X-ray structure was available for the nontemplate strand in a TEC, multiprobe single-molecule fluorescence resonance energy transfer (FRET) studies were done of S. cerevisiae RNAP II TECs to generate a structural model for the bubble.^27b From X-ray structures, RNA within the RNA/DNA hybrid is 8–9 nucleotides [8 for posttranslocated (8 + NTP in a catalytic TEC) and 9 for pretranslocated TECs] in the case of S. cerevisiae RNAP II² and 9–10 nucleotides in the case of T. thermophilus RNAP.^3,4 In the T. thermophilus RNAP TEC structure, seven unpaired RNA bases fill the RNA exit channel.

After promoter escape, the elongation phase of transcription (Figure 3) commences and, given current structures (Table 1), may be particularly amenable to simulation. Models for transcriptional elongation fall into the categories of “power stroke” and “Brownian ratchet”. In the former, the emphasis is on conformational changes, focused on helix rotations, coupled to PP_i exit to provide the driving force. In the latter, thermally driven forward and backward oscillation of the RNAP along the DNA is biased in the forward direction by nucleotide incorporation. Elucidating the balance among the energetic contributions of helix conformational changes, NTP incorporation and PP_i release that lead to RNA synthesis is an active area of investigation.²⁸

Figure 3.

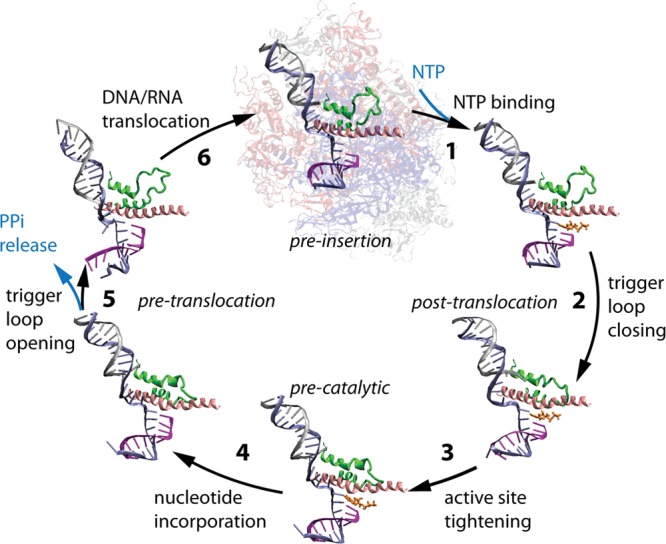
Phosphodiester bond addition cycle of S. cerevisiae RNAP II. Bridge helix is pink, trigger loop is green, NTP substrate is orange, RNA is purple, template DNA strand is blue, and nontemplate DNA strand is silver. The image is adapted from PDB files 2E2H (closed trigger loop) and 2E2J (open trigger loop). Reprinted with permission from ref (7a): Feig M.; Burton Z. F.. RNA polymerase II with open and closed trigger loops: Active site dynamics and nucleic acid translocation. Biophysical Journal 2010, 99(8), 2577.. Copyright 2010 Elsevier.

RNAPs are highly processive, tightly retaining the nascent RNA chain until a termination signal is reached. Once RNAP is dissociated, it cannot reassociate with template or RNA, because the DNA template bubble closes when the RNA is released. This is a distinction between RNAPs and DNAPs, because DNAPs can reassociate with a template-primer to continue elongation. The phosphodiester bond addition cycle is characterized by the 2-Mg²⁺ catalytic mechanism^5,29 (Figure 2), and it is thought that catalysis is supported by a closed conformation of the RNAP trigger loop³⁰ (Figures 1C and 3). Because the secondary pore appears to close when the trigger loop closes,³ it appears that a second NTP cannot load to the catalytic TEC unless it loads through the main enzyme channel rather than the secondary pore.⁸ On the other hand, if NTPs load and exchange only through the secondary pore, as some have suggested, then NTPs have no recognition of the DNA template until they are fully loaded to the active site, and significant misloading of NTPs to template must therefore occur.^8,9 Also, if the pore is the sole route for NTP loading, passive exchange of NTPs through the ∼7 Å diameter pore must occur. After bond synthesis, PP_i is initially retained in the RNAP active site. It is thought that partial or full trigger loop opening facilitates PP_i release through the pore.^21,28d Translocation is expected in a TEC with an open or partially open trigger loop.⁷ The bridge helix is thought to bend against the RNA/DNA hybrid to stimulate forward translocation, although it is not clearly known whether this motion produces a rapidly oscillating RNAP, rectifying between the pre- and post-translocation states, or whether bridge helix bending causes a more concerted push forward.^7b Some recent analyses seem to indicate that the RNAP may reside primarily in the posttranslocation register when the incoming NTP is not present, rather than oscillating rapidly pre ↔ post.^18b,28d DNAPs, by contrast, are thought to oscillate rapidly pre ↔ post.³¹

MD simulations of Thermus thermophilus RNAP TECs appear to be consistent with bridge helix bending against the RNA/DNA hybrid to stimulate the forward translocation step.^7b,18c From these simulations, bridge helix bending appears to occur mostly at a glycine hinge β′ 1076-GARKGG-1082 (T. thermophilus RNAP sequence and numbering) near the N-terminal end of the helix. Although the glycines concentrated in this region make it seem a reasonable position for bending, RNAP crystal structures tend to show bends at a more C-terminal position (see Figure 1C). The extent to which simulations and X-ray structures accurately represent bridge helix bending and generation of translocation force during elongation, therefore, is not yet known. No evidence for rapid translocation oscillation has been obtained from MD, although simulations are relatively short and may need to be extended to observe indications of reversible sliding or repeated bending and straightening of the bridge helix. Simulation of just the bridge helix of an archaeal RNAP appears to support the model for N-terminal bridge helix bending at the glycine hinge.³² In these simulations, most bending was detected at GGREG, which corresponds to GARKG in bacterial RNAPs. Bending of the archaeal RNAP bridge helix was also detected at a position further C-terminal where another glycine is present. Mutational analysis of RNAPs strongly supports the importance of bridge helix hinge glycines.^32b These Gly residues are very important for transcriptional functions because any substitutions strongly affect RNAP function.

The elongation phase of transcription involves some off-pathway states such as pausing, backtracking, and arrest. Transient pausing can occur with little or no retrograde motion of RNAP.³³ Recent work indicates that eubacterial RNAP may pause when a dGMP on the nontemplate DNA strand in the i + 1 register flips to access a groove in the β subunit. So, sequence-specific effects such as i + 1 dGMP in the nontemplate DNA strand can enhance pausing.²⁵ Backtracking involves dissociation of the 3′ end of the RNA from the DNA template and RNA extrusion into the secondary pore. With extensive backtracking, irreversible arrest may occur such that the RNA 3′ end cannot slip back into DNA contact and RNAP therefore cannot resume elongation. Protein factors that invade through the secondary pore can reactivate arrested TECs by participating in RNA endonucleolytic cleavage. For eukaryotic RNAP II, TFIIS/SII is the antiarrest and restart factor;³⁴ in eubacteria GreA and GreB, which are analogous but not homologous to TFIIS, provide this restart and editing function. Interestingly, TFIIS and Gre factors appear to recruit Mg²⁺ (Mg-B or Mg-II) to the active site to cooperate with the RNAP catalytic Mg²⁺ (Mg-A or Mg-I) in the endonuclease reaction.

In recent work on T7 RNAP elongation, an elegant combined kinetic, thermodynamic, and dynamic model was proposed.²⁴ The model was constructed to include relevant crystal structures as intermediates. Open and closed conformations of the O helix were incorporated, and flipping of Tyr639 in and out of the NTP binding site was included. On and off pathway translocation mechanisms were modeled. On pathway, translocation oscillates rapidly pre ↔ post with little energetic barrier, as observed for Phi21 DNAP.³¹ Off pathway, translocation incurs a slight thermodynamic cost because of flipping of the position of Tyr639 located at a hinge at the C-terminal end of the O helix. In T7 RNAP, it appears that NTP loading can occur only in a posttranslocated TEC, and preinsertion and postinsertion positions for a NTP substrate are considered on the basis of available structures. Potential similarities between T7 RNAP and multisubunit RNAPs were considered, although the T7 RNAP model may not precisely align with the multisubunit RNAP model for NTP loading and translocation steps, and the structures are not homologous, so details of conformational changes and development of translocation force are different. A similarly comprehensive model for multisubunit RNAPs should be developed and refined.

Termination dissociates RNA from RNAP and releases RNAP from DNA, so a terminated RNAP cannot resume transcription.³⁵ The atomic details of termination complexes have not been fully elucidated in crystal structures and are sufficiently complex that constructing a credible atomic model for a termination intermediate would present significant challenges. No crystal structure now available adequately describes a terminating TEC or termination intermediate, currently making termination a difficult subject for simulation.

5. Phosphodiester Bond Addition Cycle of DNA Polymerases

Many DNAPs have a simpler subunit composition than multisubunit RNAPs, but the details of the DNAP phosphodiester bond addition cycle remain incompletely understood. What is clear from extensive kinetic, mutational, biochemical, and structural analyses, however, is that the basic DNAP mechanism is complex, including multiple steps for substrate binding, conformational changes, catalysis, and PP_i release.^10,36 Some details of DNAP mechanisms cannot appertain precisely to RNAP mechanisms, but most features must be analogous.

A recent paper describes previously unknown details of a DNAP mechanism¹⁰ (Figure 2B), which may be general to many DNAPs and relevant to multisubunit RNAPs. Extraction of the 3′-HO_DNA/RNA proton from the i site sugar (primer strand) is expected to be a feature of both DNAP and RNAP mechanisms.²⁹ In this case, experiments were done with human DNAP η, a family Y DNAP involved in repair of ultraviolet DNA damage. Insights result from time-resolved X-ray crystallography of natural substrates and freezing crystals at different stages of a slow reaction. Notably, a detailed mechanism to extract the 3′-OH proton is described. Because 3′-O^– is a more potent nucleophile than 3′-OH, such a mechanism is expected to enhance the chemical step of phosphodiester bond synthesis, involving attack of the 3′-O^– (i site sugar) on the α-phosphate of the substrate dATP (i + 1 site). The implied mechanism for proton extraction involves recruitment of a water molecule beneath the 2′-H₂ carbon of the attacking i site sugar. Interestingly, this catalytic water recruited for 3′-OH proton extraction is also interacting with α-phosphate oxygens, indicating that the dATP substrate (i + 1 site) participates directly in the catalytic mechanism by helping to extract the 3′-OH proton, a process described as substrate self-catalysis.³⁷ This step in the mechanism cannot be identical for a RNAP, because the 2′-OH_RNA of the attacking sugar (i site) must occupy the same location as the catalytic water molecule in DNAP η; thus, RNAPs must utilize a modified water placement or an alternate mechanism for extracting a 3′-OH proton. Arg61 of human DNAP η appears to participate in 3′-OH proton extraction by contacting α- and β-phosphate oxygens and also appears to activate PP_i as a leaving group during the chemical step. Proton transfer to a β-phosphate oxygen from an Arg or Lys side chain has been proposed to be a general feature of DNAP mechanisms.³⁸ A critical histidine on the trigger loop is thought to fulfill a similar function for multisubunit RNAPs^29,38a (Figure 2A). Some multisubunit RNAPs (i.e., T. thermophilus RNAP) also have an arginine (Arg1239) positioned to participate with the histidine (His1242) in proton transfers, and this arginine appears to cooperate genetically with the neighboring histidine, such that mutation of both residues can be much more severe than mutation of one or the other.³⁹

The chemical step in the DNAP η mechanism also involves an unanticipated change in the attacking deoxyribose sugar (i site) pucker that occurs during the chemical step.¹⁰ Initially the sugar conformation is 2′-endo, but at the time of deprotonation and attack it switches to 3′-endo. The 2′-endo conformation is consistent with canonical B-form DNA, but the 3′-endo conformation is more consistent with A-form DNA.³⁷ In a previous X-ray crystal structure of a replicating, high-fidelity DNAP, a bend in the DNA primer strand was noted that seems to represent this same 2′-endo to 3′-endo conformational shift in attacking sugar pucker (i site).⁴⁰ There is reason, therefore, to consider that this dynamic change in sugar conformation may be a more general feature of DNAP mechanisms. The conformational repertoire of the polymerizing chain (i site) and the substrate (i + 1 site), therefore, are likely to be important considerations in thinking about DNAP and RNAP mechanisms. Significant discrimination between RNA and DNA bases, for instance, may be mediated by the conformational deformability of polymers and substrates.

Another unexpected insight from DNAP η is that a third Mg²⁺ appears to be recruited to interact with the PP_i leaving group after chemistry¹⁰ (Figure 2B). The third Mg²⁺ displaces Arg61 from its interactions with the α- and β-phosphate oxygens of the substrate dATP. The octahedral coordination of Mg²⁺, found at high resolution, helps to discriminate Mg²⁺ from a water molecule of similar electron density. The seemingly universal 2-Mg²⁺ DNAP and RNAP mechanism, therefore, in some cases, can involve the recruitment of an additional Mg²⁺ atom (at least three). Associating two Mg²⁺ atoms with PP_i is sufficient to neutralize the −4 charge of PP_i and to enhance nucleophilic attack on the α-phosphate.

It has also been suggested that a proton may be transferred to the β-phosphate of the substrate dNTP from a nearby Lys or Arg residue as part of the catalytic mechanism.^29,38 This conclusion is based on hydrogen–deuterium isotope effect studies of various DNAPs, but arginine has a very high pK_a and is very reluctant to give up a proton, even when buried within the hydrophobic core of a protein.⁴¹ In the DNAP η mechanism, it appears that Arg61 activates dNTP self-catalysis and then shifts position as the third Mg²⁺ is recruited to the PP_i leaving group.

6. Kinetic Studies of DNA Polymerase Mechanisms

Analysis of the kinetics of DNAP elongation points to very complex mechanisms, indicative of the DNAP η mechanism described above (Figure 2B). For instance, the pH dependence of the DNAP β (a family X DNAP) reaction is complex, implicating the transfer of multiple protons,^36a as is also suggested from the time-resolved X-ray crystallography of DNAP η.¹⁰ Observation of proton release just prior to DNAP β chemistry is also consistent with a mechanism involving deprotonation of the 3′-OH.^36a Mg²⁺ dependence is also complicated for DNAP mechanisms, consistent with recruitment of a third Mg²⁺. HIV-1 reverse transcriptase also has a complex pH dependence indicative of a reaction involving multiple proton transfers.^36b The current composite picture that arises of DNAP mechanisms, therefore, is one of multiple steps involving proton transfers, Mg²⁺ migration, 3′-OH deprotonation, substrate self-catalysis, PP_i activation, conformational changes, and specific changes of sugar pucker. Because these DNAP mechanisms are considered to be potentially simpler than multisubunit RNAP mechanisms, this elevates the degree of difficulty for computational analysis of multisubunit RNAPs.

7. Phosphodiester Bond Addition Cycle of RNA Polymerases

Many intermediate steps must be considered in the RNAP phosphodiester bond addition cycle (Figure 3), and available crystal structures do not represent all of these (Table 1). Figure 3 shows the bond addition cycle of S. cerevisiae RNAP II broken into six steps, indicating conformational changes in the NTP and trigger loop, PP_i release, and translocation associated with reaction stages. To gain insight into the mechanism, intermediates can be modeled computationally and refined by simulation. If a suitable set of snapshots could be obtained and justified, enhanced MD sampling methods such as replica exchange could be applied to obtain pathways between bond addition cycle intermediates. Currently, this job is barely begun for multisubunit RNAPs, although bacteriophage T7 RNAP, a single-subunit RNAP, has been analyzed in more detail.^22,24 A DNAP has also been analyzed for a translocation step via replica exchange.⁴² It appears that multisubunit RNAPs present a more challenging target for translocation analysis than T7 RNAP.⁷ Multisubunit RNAPs are more complex, include more atoms, appear to be in some respects more flexible and dynamic, and may have more distinct kinetic or rate-determining steps in their mechanisms. To bring computational analysis of multisubunit RNAPs into consistency with kinetic analyses may be challenging.

Kinetic studies of multisubunit RNAPs identify multiple rate-contributing steps and also rapid steps (Figure 4). At high NTP concentrations, stable NTP-Mg²⁺ loading and sequestration occurs very rapidly, as shown by millisecond chemical quench flow studies using the Mg²⁺ chelator ethylenediaminetetraacetic acid (EDTA) as a quenching agent.⁴³ After a substrate becomes committed to future incorporation, however, the timing of phosphodiester bond synthesis is delayed, as indicated by quench flow studies using HCl or other denaturing quenching agents,⁴³ which are thought to terminate the RNAP reaction mechanism immediately upon mixing. The rate-limiting step in elongation appears to be phosphodiester bond synthesis (k ∼ 30–81 s^–1),^28d which may be reversible before a bond completion conformational change. The steps in the RNAP bond addition mechanism that are quenched by EDTA and HCl are indicated in Figure 4. Comparison of EDTA and HCl quench data indicates a rate-determining step between stable NTP-Mg²⁺ loading and phosphodiester bond synthesis. Trigger loop closing is thought to occur in the interval between stable NTP-Mg²⁺ acquisition and phosphodiester bond formation. Indeed, a rapid [k ∼ 623 s^–1 (UTP), k ∼ 411 s^–1 (ATP)] intrinsic fluorescence change occurs in Escherichia coli RNAP upon NTP addition that may correspond to the trigger loop closing step.⁴⁴ Generally loop closures are rapid steps and the reaction step between stable NTP-Mg²⁺ sequestration and chemistry appears slow, so additional conformational changes may also occur in this interval. After phosphodiester bond synthesis, there is another delay before stable NTP-Mg²⁺ loading can be detected for the next bond synthesis.^43a,43b Translocation and PP_i release must occur prior to stable NTP-Mg²⁺ binding. By use of fluorescence changes to monitor RNAP translocation and also PP_i release, it was determined that a conformational change associated with PP_i release (k ∼ 82–133 s^–1) represents another rate-contributing step in the multisubunit RNAP mechanism after phosphodiester bond synthesis,^28d,44,45 but PP_i release out the pore appears to be rapid.²¹ Translocation appears to occur shortly after PP_i release, indicating that both PP_i release and translocation may depend on a conformational change that occurs after phosphodiester bond synthesis but before effective completion of product formation.^28d This step may correlate with trigger loop opening. Because multisubunit RNAPs appear reluctant to commit to completion of the phosphodiester bond, this indicates that bond formation may be reversible. Trigger loop opening and PP_i release (Figures 1C and 3) render phosphodiester bond reversal unlikely and dependent on a high concentration of PP_i to support the reverse reaction. From simulation studies, trigger loop opening is expected to enhance DNA forward sliding. TECs with open trigger loops appear to increase forward translocation, and in T. thermophilus RNAP TEC simulations, bridge helix bending appears to facilitate the forward translocation step.^7b,18c On the basis of X-ray crystal structures of TECs,⁴⁶ bridge helix bending against the RNA/DNA hybrid has been thought to be associated with forward translocation. So far, from MD, there is little indication of bridge helix bending in S. cerevisiae RNAP II simulations associated with forward translocation.^7a

Figure 4.

Simplified outline of a multisubunit RNAP elongation mechanism indicating potential rate-determining steps. Estimated or determined rate constants for elemental steps can be found in the text and references. EDTA-r/s: EDTA-resistant or -sensitive intermediates.

There remains some controversy about the order of steps between phosphodiester bond synthesis and stable NTP-Mg²⁺ binding for formation of the next bond. Using both a coupled enzyme assay and intrinsic RNAP fluorescence, the Johnson laboratory has reported that the incoming NTP-Mg²⁺ is necessary for rapid rates of PP_i release, indicating that the NTP-Mg²⁺ acts as an allosteric effector for completion of the previous bond addition step.^44,45 For instance, NTP-Mg²⁺ interaction might stimulate trigger loop opening associated with PP_i release and translocation. NTP-Mg²⁺ loading to template, therefore, would normally precede PP_i release and translocation. Because the secondary pore appears to close in a TEC with a closed trigger loop conformation (Figure 1B) and because trigger loop opening appears important for PP_i release and translocation, if NTP-Mg²⁺ loading occurs prior to PP_i release, it appears that this NTP must load through the main RNAP channel and not the secondary pore. So the timing of addition of the incoming NTP substrate and the route of NTP loading may not be fully known.

NTP-dependent PP_i release, however, was not confirmed by another group using a coupled enzyme assay.^28d Other groups have indicated that NTP-Mg²⁺ binding to the TEC may precede forward translocation.^8,43c From the point of view of simulation, however, models for NTP-Mg²⁺ binding to the pretranslocated TEC, if this occurs, will require structural models that currently are not available. These models might be constructed given current structures, but they would be speculative compared to other models of elongation intermediates for which there is more substantial support from known chemistry. Part of the challenge, therefore, in modeling intermediates for the RNAP mechanism, is judging how to construct starting structures for simulations. On the other hand, constructing accurate kinetic models requires proper ordering of steps.

8. Ionic Interactions to Support Bridge Helix Bending

In comparing T. thermophilus RNAP TECs with open and closed trigger loop conformations by all-atom MD simulations, a charge relay system was identified across the bridge helix.^7b In the closed trigger loop, catalytic structure, a chain of ionic interactions is apparent linking bridge helix residues β′ Lys1079-Asp1083-Arg1087-Asp1090. In the open trigger loop structure, which supports a different bend in the bridge α-helix, the chain of interactions involves β Asp429 (fork)-β′ Lys1079-Asp1083-Arg1087-Asp1090. It is proposed that different modes of bridge helix bending that either suppress or support forward translocation of the RNA/DNA hybrid are reinforced by these charge interactions and that Lys1079 is a key residue in mediating different bridge helix conformations. Other examples of switching contacts of ionic interactions are apparent in simulations, and these “switch” residues are likely to be important in the conformational switching of multisubunit RNAPs. Site-directed mutagenesis based on the predictions made from the simulations supports the idea that these ionic interactions are functionally important. As an example, bridge helix β′ Lys1079 is considered to be a central switch residue for eubacterial RNAPs involved in bridge helix bending and dynamics. Consistent with this idea, the substitution in E. coli RNAP corresponding to T. thermophilus K1079A (E. coli K781A) is strongly defective in transcriptional functions.⁴⁷

9. A Key Histidine on the Trigger Loop

It has been suggested that highly conserved S. cerevisiae RNAP II Rpb1 His1085, located on the trigger loop, is an important residue for RNAP function (Figure 2A). This residue appears invariant in multisubunit RNAPs and is located very close to the NTP substrate (i + 1) in the catalytic TEC. It has further been suggested that His1085 may be involved in proton transfer to the β-phosphate of the substrate NTP^29,38 (Figure 2A). There is some controversy on this point because, in some organisms, mutation of this histidine is not as deleterious to function as might be expected for such a central role in the RNAP mechanism.^30,39 Furthermore, it appears that when the trigger loop is in an open conformation, this histidine is fully exposed to solvent. In water, histidine has a pK_a of about 6.46, and a similar pK_a might be expected for His1085 on an open trigger loop. To be involved in proton transfer, His1085 would likely acquire a higher pK_a in the closed TEC configuration, at least in the presence of the NTP substrate. Modeling of the likely pK_as of His1085 in open, closed, and intermediate trigger loop conformations, therefore, might bring additional clarity to this issue.⁴⁸

Another consideration is the salt dependence of histidine pK_as. For exposed His residues, an increase from 0.01 to 1.0 M KCl often increases the pK_a of a His by ∼1 pK_a unit, making protonation of the histidine ∼10 fold more likely.⁴⁸ For buried or shielded His residues, the salt effect is less predictable. The presence of salt in the vicinity of a charged (protonated) His helps to shield the charge, explaining the strong salt dependence of the pK_a of His. Therefore, in the case in which a histidine is thought to function in the protonated state, the wild type and an uncharged mutant (i.e., H1085A) should be compared for function at different pH and at different salt concentrations. Salt can strongly stimulate elongation by RNAP II, indicating that this analysis might give insight into whether His1085 functions in a protonated state.^29,38

10. The pK_a Cooperative

Because RNAP and DNAP mechanisms are thought to be supported by specific proton and Mg²⁺ transfers within sequestered active sites and because the microenvironment of a residue may affect its pK_a, there is considerable interest in how protons can be mobilized to support chemical reactions within the enclosed active sites of these enzymes.⁴⁹ Consistent with long-standing enzymatic reaction mechanistic hypotheses, it is likely that RNAPs and high-fidelity DNAPs enclose their active site in order to orient substrates, to remove water and lower the dielectric constant of the microenvironment, and to mobilize protons of general acids and bases to accelerate the chemical step of the accurate polymerization reaction. In reactions with a noncognate substrate, it is likely that alternate pathways must develop for proton transfers, indicating that potentially multiple routes may be available within an enclosed active site to deprotonate the 3′-OH (i site) and activate the NTP substrate (i + 1 site). Also, as mentioned above, RNAPs and DNAPs may use slightly different strategies to deprotonate the 3′-OH of the attacking sugar (i site).

Because of the importance of proton transfers in catalysis, a large effort has begun in the simulation community to predict the pK_as of potentially charged amino acid residues (Asp, Glu, His, Lys, Arg) within different microenvironments in proteins.⁴⁹ These pK_as can be determined experimentally by NMR analyses combined with pH titrations. The pK_as of Asp can vary considerably.⁵⁰ In water, the pK_a of Asp is about 3.90. In one model nuclease, Asp pK_as were determined between 2.16 and 6.54, with the highest pK_a for Asp21 in a charge cluster at the active site.^50a Asp pK_as as high as 9.9 are reported.⁵¹ Glutamate has a pK_a of about 4.35 in water and may vary between a pK_a of 2.82 and 8–9 in a protein.^50a,51,52 When buried in the hydrophobic core, Glu tends to become uncharged to match its environment.^50b Aspartate tends to form stronger hydrogen bonds than Glu because of its shorter and less flexible side chain.

Anecdotally, in RNAP structures, Asp appears to form stronger ionic interactions than Glu, because Asp has a shorter side chain than Glu and is less flexible. Similarly, Arg, which is stiffer and less mobile than Lys, appears to form stronger and less plastic ion pairs than Lys. The charged Arg headgroup is larger than that of Lys, limiting Arg mobility. By contrast, Lys is very flexible and has a compact charged headgroup. Lysine, therefore, makes a more mobile switch residue than Arg, as in the case of T. thermophilus RNAP bridge helix β′ Lys1079, which can switch between β Asp429 and β′ Asp1083 contacts.^7b The Arg headgroup can also occupy a protein socket. Examples from multisubunit RNAPs include Rpb2 Arg983⁵³ and β′ Arg1078.^7b,18c

A Lys buried in a hydrophobic environment may lose its charge to match its neutral surroundings. In water, Lys has a pK_a of about 10.4. In proteins, Lys can have a pK_a that is between 5.3, buried in a protein hydrophobic core, and 10.4, exposed to solvent.^48,54 By contrast to Lys, Arg much more tenaciously maintains its positive charge within proteins.⁴¹ Via different approaches, the pK_a of Arg in water is estimated at between 11.5 and 15 and is generally considered to be >12. When buried in the core of a protein, Arg rarely if ever becomes uncharged under pH conditions tolerated by proteins.⁴¹ The larger guanidinium headgroup of Arg spreads the positive charge compared to Lys and allows access for hydrogen bonding to polar groups and water that tend to compensate for and further diffuse the charge. Therefore, Arg is often a component of active sites and sequestered positions in proteins that must retain a buried positive charge. Because of these differences comparing Lys and Arg, in DNAP mechanisms, Lys might be more likely to donate a proton directly to the dNTP β-phosphate than Arg,³⁸ which tends to maintain its charged state⁴¹ and therefore might not relinquish a proton to the PP_i leaving group. In the DNAP η mechanism (Figure 2B), Arg61 appears to switch positions as Mg²⁺ is recruited to interact with the β-phosphate of the dNTP after chemistry. So recruitment of Mg²⁺ might be another mechanism by which Arg could participate in DNAP mechanisms.

Histidine has a pK_a of about 6.46 in water. Histidine is expected to be uncharged in a hydrophobic environment, and increased salt is expected to elevate the pK_a of an exposed His. In one study, the pK_as of His vary between 4.03 and 7.16, depending on the salt concentration and the position in the protein.⁴⁸ Generally increased salt supports a higher pK_a for His because the charge on His is shielded. Clustering multiple charges around a His may help to maintain a positive charge. As an example, in human hemoglobin, β His146 is the C-terminal amino acid. In T-state hemoglobin (taut; oxygen dumping; capillaries), α Lys40−β His146(COO^–) and β His146−β Asp92 ion pairs may support the protonated state of His146 in T-state hemoglobin. In keeping with the higher pH of blood within the lungs compared to the capillaries due to dissolved carbon dioxide concentrations, β His146 is unprotonated in the R-state (relaxed; oxygen binding; lungs) hemoglobin.

Although models for specific proton transfers in RNAP and DNAP mechanisms are interesting and appealing (Figure 2), it appears that more consideration should be given to the specific properties of residues proposed to act in these schemes. Arginine may be a poor candidate for direct proton transfer to PP_i and may function more indirectly in a DNAP mechanism by facilitating proton extraction from water and by Mg²⁺ recruitment (Figure 2B). Experimental approaches and simulations may provide additional insight into the precise role of a critical trigger loop His expected to change its microenvironment in multisubunit RNAP mechanisms.

For multisubunit RNAPs, it would be of great interest to simulate the pK_a of Sc RNAP II His1085 in closed and open trigger loop conformations.²⁹ In the closed TEC, the simulations should be done with and without a NTP. A model can then be constructed and evaluated to determine the feasibility of protonation and deprotonation of His1085 in the RNAP mechanism. Because hemoglobin switches conformation between R (relaxed; oxygen binding; lungs) and T (taut; oxygen dumping; capillaries) conformational forms, and because protonation of His residues caused by changes in blood pH from the lungs to the capillaries is a key feature of the R → T switch, similar studies of hemoglobin switching, a system that may be more amenable to modeling, should be analyzed. Lowering the pH and raising the salt concentration, which are expected to favor His protonation and therefore the R → T switch, are expected to stimulate these conformational changes.

11. Model for RNA Polymerase Translocation Switches

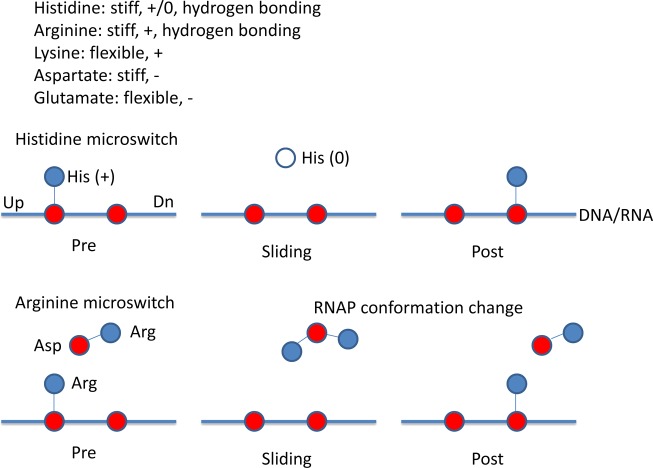
Because of the model for protonated His1085 in NTP recognition and proton transfer during chemistry (Figure 2A), we considered the idea that histidine protonation might be a more general feature of RNA and DNA interaction in RNAP mechanisms. In Figure 5, we suggest mechanisms by which His and Arg residues can act as microswitches to regulate RNAP sliding on nucleic acids. Because His can be either charged (+1) or uncharged, we consider a situation in which protonation of His depends on interaction with a DNA or RNA phosphate. In this case, His can be protonated on an upstream phosphate, deprotonated during sliding and reprotonated on the next phosphate downstream. Histidine, therefore, is a good candidate for a residue functioning as a microswitch supporting RNAP translocation. There are examples of protonated His residues functioning in specific DNA recognition. His318 of human papilloma virus type 16 E2 protein and His451 of the human glucocorticoid receptor are deprotonated when off target and protonated when binding cognate DNAs.⁵⁵ Protonation of His451 is stimulated by elevated salt. Histidine microswitches are expected to function most strongly at lower pH and at higher salt, conditions that support His protonation. Histidine microswitches that rectify DNA–protein interactions should be of practical use for maximizing the specificity of targeting, for instance, in design of genome editing nucleases.⁵⁶

Figure 5.

Model for histidine and arginine microswitches in RNAP translocation. Histidine can protonate on a DNA or RNA phosphate, deprotonate during translocation, and then reprotonate on the next phosphate downstream. Arginine remains protonated, so it requires a charge relay system and conformational effects for switching during template sliding. Red indicates negative charge; blue indicates positive charge; white indicates no charge.

Because Arg cannot easily transfer a proton, Arg is more likely to work as part of a coordinated switching mechanism involving other charged residues (Figure 5). Because Asp is less flexible than Glu, Asp is considered to be a more likely switch residue than Glu, just as Arg is generally a more likely switch residue than Lys. A phosphate-Arg-Asp-Arg microswitch, therefore, is pictured. Switching, in this case, is likely to involve movement of Arg away from the upstream phosphate and then back to the next downstream phosphate. Such a switch may require support from RNAP motions. Other details of the switch microenvironment may also contribute to switching. An Arg microswitch is expected to be resistant to pH changes and to have unpredictable salt effects.

Nucleic acids may also form microswitches for RNAP translocation because forward translocation requires opening base pairs at the i – 8 or i – 7 position of the RNA/DNA hybrid upstream and the i + 2 position of the DNA/DNA duplex downstream and closing a base pair at about i – 11 upstream (Figure 1B,C). Nucleic acid microswitches can be identified by use of mutated DNA template strands in translocation assays, that is, using exonuclease III to footprint RNAP upstream and downstream TEC boundaries on DNA.^18b Nucleic acid microswitches are expected to be stabilized at higher salt concentrations but are not expected to be highly sensitive to changes in pH.

12. Translocation

Most X-ray crystal structures of RNAP TECs indicate that the posttranslocated register is the dominant resting form.^2−4,25,57 In some TECs, the pretranslocated register can also be detected. By attaching a bromine atom to a nucleic acid strand in a crystal, the distribution of translocation states can be determined. A similar conclusion was reached on the basis of fluorescence studies of translocation.^28d Time-resolved exonuclease III mapping of TECs also supports the idea that resting TECs are primarily posttranslocated, that post → pre transitions are slow, and that pre → post transitions are rapid.^18b This may be a difference between multisubunit RNAPs and DNAPs, because, on the basis of single elongation complex studies, DNAPs appear to oscillate freely and rapidly pre ↔ post.^31a So far, single-molecule oscillation studies of multisubunit RNAPs have not been reported, although such an approach should be feasible.

13. Catalysis

13.1. Introduction

Because both RNAPs and DNAPs utilize analogous 2-Mg²⁺ mechanisms for template-dependent nucleic acid polymerization, the 2-Mg²⁺ mechanism describes a significant aspect of the core reactions in molecular biology and life. Understanding atomistic details of 2-Mg²⁺ mechanisms, therefore, is fundamental to understanding living systems and biological templated coding (replication, transcription, and translation). RNAPs and replicative and high-fidelity DNAPs have sequestered active sites with active-site opening and closing mechanisms.^2,3,30,58 A buried active site covered by a loop or protein domain might be expected to exclude and/or order water in the vicinity of substrate to change the pK_as of amino acid side chains and to mobilize proton transfers to support chemistry (Figure 2). In RNAP mechanisms, the trigger loop closes over the active site. Some DNAPs and single-subunit RNAPs close the O/O′ helices (finger domain) against the substrate to tighten the active site. Exclusion of water from a cognate base pair could be an aspect of fidelity because accurate base pairs are enhanced in stability through dehydration.^7b,18c Water competes with hydrogen bonding between purines and pyrimidines, potentially weakening or dissociating the interaction. Active-site closing mechanisms, therefore, may stabilize cognate base pairs through a dehydration mechanism. Because MD simulation in explicit solvent can model water activity in a closed TEC, potentially, insight can be obtained by simulation methods for the involvement of ordered water in RNAP catalysis and fidelity.

Although the precise mechanism is not fully elucidated, key proton transfers are thought to be important in the RNAP bond addition reaction^29,38 (Figure 2A). One model for this reaction might be the following. Deprotonation of the 3′-OH is thought to be important for attack of 3′-O^– on the α-phosphate of the NTP. Generation of OH^– in the active site, therefore, would facilitate deprotonation. Above, a DNAP η mechanism was discussed for extracting the 3′-OH proton (i site) (Figure 2B).¹⁰ This proton-transfer mechanism cannot precisely apply to RNAPs, because the placement of water acting as base in the DNAP η structure is in the position of the 2′-OH of the ribose sugar in RNAPs, but presumably in RNAPs a related mechanism might appertain. Alternatively, OH^– in the active site might be generated via trigger loop closing. An invariant His (His1085; Figure 2A) on the trigger loop might alter its pK_a through loop closure and water exclusion, so that His1085 extracts H⁺ from water to generate OH^– in proximity to the 3′-OH. The protonated histidine then is thought to transfer its proton to the β-phosphate of the NTP substrate to make PP_iH a better leaving group for attack of the 3′-O^– on the α-phosphate.^38a Protonation may also make elimination of PP_iH easier after chemistry. As described above, DNAPs are thought to support similar proton transfers in their 2- or 3-Mg²⁺ polymerization mechanisms.

13.2. Computational Approaches

A number of computational approaches to mechanisms of RNAP and DNAP catalysis have been developed. They are based on pre- and postinsertion crystal structures. Then, a combination of MD and quantum chemical (QC) methods are used to elucidate mechanism. While very instructive, there are limitations to these methods when applied to TECs, which are intrinsically complex and large, as discussed below.

The computations discussed here are focused on two metal (Mg) ion catalysis where either one proton transfers from the primer 3′-hydroxyl (3′-OH) or, additionally, another proton transfers to form a protonated pyrophosphate (PP_iH). The role of one magnesium ion, Mg-A, is to lower the pK_a of the 3′-OH group and the role of the other, Mg-B, is to provide structural support, and charge, to stabilize the phosphorane transition state and aid in PP_i release (Figure 2).

Our aim here is not an inclusive review of the chemistry but rather to concentrate on the two-metal, two-proton paradigm and consider various scenarios for the chemistry. Some issues relevant for the chemical aspects of nucleotidyl transfer include the following: (1) Which step is rate-limiting? (2) What proton acceptors of the 3′-hydroxyl group are present? (3) Is the PP_i leaving group protonated, and if so, what is its proton donor? (4) How many Mg ions are present and is their number fixed during the transfer? (5) Which residues and/or water molecules are involved in catalysis as general acids and bases, and do acidic/basic residues change their protonation states along the reaction path?

13.3. Compromises of Computation

Before we describe various mechanism-based computations that have been applied to RNAP and what may be analogous DNAP mechanisms, some cautionary statements are in order. The simulations/computations are based on X-ray crystallographic determinations that are for the most part of modest resolution, ∼4 Å. Typically, there are missing residues, often loops and other less-structured elements, that must be modeled in. Nonreactive nucleotides, used to prevent chemistry from occurring in crystallography, have to be replaced (e.g., AMPCPP replaced by ATP). At these resolutions, water identification is problematic. It should be clear that if highly charged species, such as NTP and PP_i, are entering/exiting the reaction center, then water molecules and Mg ions may also, bound to various extents to these species.

When classical MD is performed, there are always two issues: (1) accuracy of the force fields (FFs) and (2) extent of equilibration and sampling in these typically very large systems. To equilibrate a multisubunit RNAP with its protein, DNA/RNA, NTP, Mg ions, and water, starting from an (amended) X-ray structure, even when focused on the smaller rearrangements appropriate to the chemical steps discussed here, is nontrivial. When doing MD in the presence of metals such as Mg, the formal +2 charge is surely strongly modified by multiple ligands. Thus, the standard MD FF cannot be correct. Charge transfer to the metals from surrounding residues, NTP, and water molecules will change all these electrostatic charges used in the FF. Furthermore, the modifications may depend significantly on configuration. Stated otherwise, the pK_as of key residues will depend on local microenvironment. In MD, protonation states are fixed, and assigned usually on the basis of standard solution pK_as and a pH of 7, with perhaps some specific residue modifications for mainly His, based on crystal structural data, and the use of protonation state assignment programs such as PropKa (http://propka.chem.uiowa.edu/). Knowing whether a given residue is protonated or not, however, is likely to play a consequential role in the reaction mechanisms of RNAPs and DNAPs.

The focus of this section is nucleotidyl transfer chemistry that relies on bond making/breaking and proton transfer. MD force fields cannot describe such events. Thus, quantum chemistry (QC) must be introduced. Ideally, what would be used is some form of ab initio molecular dynamics (AIMD), whereby QC is used in a continually configurationally updated thermal ensemble. Then polarization and bond making/breaking would be incorporated. However, the expense of AIMD methods limits their applicability to systems on the order of 100 atoms and picosecond time scales. Thus, for the foreseeable future, reaction mechanisms are going to be studied by more conventional QC methods. These approaches center on density functional theory (DFT) -based methods that with reasonably sophisticated basis sets (including polarization) are now routinely employed to study enzyme reaction mechanisms. However, while reaction coordinates and thermodynamic and transition-state energies can be obtained, they are typically only based on otherwise fixed surrounding atoms and often are based on a crystal structure or, if MD has been done, a snapshot from the trajectory. This can produce misleading results, and use of an ensemble of structures can lead to substantially different conclusions.

Furthermore, most QC-based calculations provide energies versus free energies. Using transition-state barrier energies in an Arrhenius rate constant expression, k = A(k_BT/h) exp(−ΔF^⧧/k_BT), in which ΔF^⧧ is the activation free energy, can be misleading, and this should be kept in mind when transition-state barriers of multistep reactions are compared in order to decide on rate-limiting steps. It is also true that the pre-exponential encounter factor A can be quite variable for enzymatic reactions, and comparisons of rates based on setting A to unity may not be appropriate. Choices have to be made as to what the reaction coordinates are. That is, restraints are employed to move selected atoms along physically suggestive pathways, but these defined pathways can be outsmarted by nature and tend to produce barriers that are too large, even allowing for relaxation of the other atoms’ geometries.

Many compromises as to what to include in the QC calculation must be made. Only a small set of residues, usually represented “schematically”—for example, imidazole for histidine—can be incorporated. A method that has been applied to various enzymatic mechanistic studies is the ONIOM (our own N-layered integrated molecular orbital and molecular mechanics) method, whereby reaction center and appropriate surroundings are represented at different levels of description. Typically, an inner layer treated by DFT with a high-quality basis set and an outer layer with a lower-order quantum or molecular mechanical (MM) description is used. In this way, a compromise between the size of the system and computational practicality is found. However, these methods often freeze atoms in the outer layer and as such cannot properly describe their response to the evolving reaction chemistry in the inner layer. Immobilization of the outer layer of atoms tends to make transition-state barriers too large and, again, provides energies versus free energies. There are newer methods that avoid some of these deficiencies that will be noted below with their specific applications.

13.4. Modeling Proton Transfers

The tendency is to think of proton transfers along the lines of heavy-atom transfers. That is, a proton in a hydrogen bond between atoms A and B (A–H···B, where A–H is a covalent bond and H···B is a hydrogen bond) is thought of as forming a traditional transition state corresponding to a reaction coordinate that is the proton displacement itself. Similar considerations apply to protonated water clusters (Zundel and Eigen cations) or water chains that are hydrogen-bonded to residues and/or phosphates. This heavy-atom-transfer perspective was disputed and revised⁵⁹ to one whereby, for a AHB hydrogen bond, the proton tunnels through a barrier formed by the AB heavy atoms and its surrounding heavy atoms; here, protein, DNA, RNA, cofactors, water, and ions. The reaction coordinate then is shifted to a collective coordinate that represents the surrounding heavy atoms’ influence on the proton’s potential energy surface describing transit from reactant to product (proton covalently bonded to A and then B). This perspective relies on a Born–Oppenheimer separation of the (fast) proton coordinate from the (slow) surrounding heavy atoms. Thus, a potential surface for proton transfer from A to B can be formulated, parametric on the A, B, and all other atom coordinates. Then, the rate of proton transfer does not conform to the standard Arrhenius heavy atom transfer transition-state formulation but follows a tunneling expression similar to that used for electron transfer. One consequence is to not think of proton transition states as partially transferred protons: the proton is localized close to either atom A or atom B. An important result is that deuterium isotope effects and their magnitudes then have a very different origin. Furthermore, proton inventory expressions and their interpretations must be revised. The standard proton inventory rate expression⁶⁰ considers one transition state and formulates the rate constant k(f) dependence on deuterium atom fraction f as a ratio of products of terms from each contributing proton at the transition state to the same for the reactant state. The reactant state is assumed to not contribute to the expression. Thus, obtaining linear (quadratic) behavior of k(f) indicates that one (two) proton(s) is (are) involved in the transition state. These results are again based on a heavy atom description of the proton transfer reaction coordinate. Krishtalik⁶¹ provided another view of proton inventory rate expressions by accounting for the tunneling aspect of protons and found a formally similar expression but one that no longer invokes a classical transition state. However, there are strong assumptions involving the independence of, for example, two protons in regaining the standard form. Two points are worth stressing, therefore: (1) mechanisms that follow from this analysis need to, for quadratic dependence, rationalize a concerted (versus stepwise) transfer of the two protons, and (2) caution in reaching conclusions about proton inventory implications should be exercised.

13.5. RNA Polymerase Simulations

Carvalho et al.²⁹ performed simulations of RNAP II from S. cerevisiae based on a crystal structure (PDB ID 2E2H with 3.95 Å resolution). First, relatively long MD simulations (20 ns) were done without constraints to discover that the relative positions of the Mg²⁺ ions are maintained along with their positioning relative to NTP oxygens and with constraints that, when released, led to similar conformations. Interestingly, the 3′-OH was sometimes strongly coordinated and other times weakly coordinated to Mg²⁺. These generated configurations were then used in ONIOM calculations to investigate mechanism. In ONIOM, a division of the system into layers is made with, conventionally, the inner layer treated at a higher level of QC (here DFT-B3LYP functional) and outer layer with a lower level (here PM3MM). Energies were then calculated at DFT level for the total system, composed of GTP, 3′-OH primer, catalytic triad of Asp residues, and a number of other critical residues including the His1085 side chain (Figure 2A). A number of reactive pathways were investigated. ONIOM calculations with the strongly coordinated Mg²⁺-3′-OH led to a dead end, as the resulting stable product 3′-O^–-Mg²⁺ would not dissociate for NTP attack. Three pathways were considered:

(1) Direct proton transfer from 3′-OH to NTP Oα (NTP acts as a base). A pentavalent transition state for associative transfer was found, and the same proton then acts as an acid to form a PP_iH leaving group.

(2) A bulk hydroxide is the base for proton abstraction from the 3′-OH. That leaves a residue to protonate PP_i, here assumed to be His1085 (Figure 2A). The (free) energy of bringing in the hydroxide from bulk solvent was evaluated by a thermodynamic integration MD method.

(3) Again a hydroxyl ion is present, but now it is part of the Mg²⁺-A coordination sphere. It deprotonates the 3′-OH, and because it is closer to the NTP, it increases the pK_a of a β-phosphate oxygen that induces proton transfer from His1085. In this mechanism the pentacoordinate transition state is described by nucleophilic attack by 3′-O^– on Pα concerted with the 3′-OH protonating OH^– (Figure 2A).

Based on the various transition state energies, the most favorable mechanism is mechanism 2, with a hydroxide provided by the bulk solvent and the rate-limiting step the nucleophilic attack. However, other transition-state barriers are not much different than this one, and in view of the limitations of the QC and the mixture of barriers obtained from QC and classical MD thermodynamic integration methods, energetic barriers could potentially be reordered.

A yeast RNAP II posttranslocational active site was constructed on the basis of the crystal structure (PDB ID 2NVZ, resolution 4.3 Å) in work by Salahub and co-workers.⁶² Included were His1085, the putative base for the NTP, Arg766 that is proximate to its γ phosphate, the primer, two Mg²⁺, loop residues containing the aspartic acid triad, and water. A MD method that is capable of breaking/forming covalent bonds, ReaxFF, was used to equilibrate this system. The strength of the ReaxFF method, in contrast to conventional MD, is that covalent bonds can be formed/broken and atom charges can vary. However, methods such as ReaxFF are expensive, limiting simulation times to picoseconds, and are not yet adequately parametrized. Features of the so-generated structures do show that His1085 does hydrogen-bond with the β-phosphate and arginines hydrogen-bond to ATP either directly or through water, and water coordinates to the Mg²⁺-B ion. Methods that can both (1) simulate thermally driven atom fluctuations and (2) make/break chemical bonds are well suited to mechanistic studies. Their limitations are the parametrization of the FF and the computational cost.

Zhang and Shalahub⁷³ used the same crystal structure to first perform MD on a spherical region of 25 Å radius centered on a GTP (that replaces the original UTP) to generate starting configurations for QC DFT calculations. The DFT system consisted of two Mg²⁺ ions, three conserved aspartate residues, one ribose, a simplified RNA primer, and NTP, and, in one model, a water molecule close to the 3′-OH of the RNA primer and the α-phosphorus of the NTP, as found from the MD. In the favored reaction pathway, there is indirect proton migration from the RNA primer 3′-OH to the α-phosphate oxygen via a solvent water molecule, proton rotation to the β-phosphate oxygen, followed by primer 3′-O^– nucleophilic attack on the α-phosphate and P–O bond cleavage. In this mechanism, the initial proton transfer that deprotonates the 3′-OH proceeds through a water that protonates the α-phosphate oxygen that, when the P–O bond breaks, is transferred to a β-phosphate oxygen, providing a PP_iH leaving group, as suggested in the two-proton mechanism.³⁸ The rate-limiting step (barrier height 21.5 kcal/mol) is the RNA primer 3′-O nucleophilic attack on the α-phosphate of the NTP. The proton transfers are not found to be rate-limiting.

13.6. DNA Polymerase Simulations

Lin et al.⁶³ studied human DNAP β (Pol β) by a combination of MD to equilibrate an X-ray-based structure (PDB ID 3C2M)⁶⁴ (with two Mn) of a G·A mismatch complex followed by ONIOM QM/MM with inner layer DFT and outer Amber MM force field. dAMPCPP was replaced by dNTP and a γ-oxygen was protonated to accord with the two-proton transfer model. Attempts at a direct proton transfer from the 3′-OH to dATP failed, in agreement with the RNAP II simulation.²⁹ Thus, first a prechemistry state was formed by 3′-OH proton transfer to a residue, Asp256. Subsequently, the reaction proceeds by formation of the O3′–Pα bond, followed by breaking the Pα–O3α bond. A two-dimensional potential energy surface in these two distances provided a transition pathway that shows an associative mechanism for the nucleophilic attack and Pα–O3α bond-breaking. From the reaction barriers, the prechemistry step was rate-limiting for the misincorporated base (dG·dATP) but not for the dA·dTTP correct insertion,⁶⁵ suggesting that fidelity is enhanced by accelerating/facilitating prechemistry. As always, barriers obtained by QC-based ONIOM methods are energies, not free energies, and are not directly related to rate constants. With the assumption of γ-oxygen protonation from the outset, the sequence of reactive events that can be evaluated is limited.

In work by Cisneros et al.,⁶⁶ a human DNAP λ precatalytic X-ray structure (PDB ID 2PFO)⁶⁷ with a noncanonical dNTP was modified to create a product structure that is simulated with both Mg²⁺ and Mn²⁺ ions. First MD was carried out to provide an initial structure for subsequent QC, and a postcatalytic, product complex was also constructed from this reactant structure. With these “end-points”, a quadratic string method (QSM) was used to connect them. The virtue of the QSM is that a reaction coordinate does not have to be specified but is more objectively computed. In this way, unbiased transition states can be obtained. An inner QC layer, treated with DFT, included the active-site metals, key Asp side chains, parts of the primer dC nucleotide, and incoming dUTP nucleotide, along with two water molecules to complete the metal coordination spheres. Atoms within 20 Å of the active site were treated with an Amber MM force field. As in the work from Lin et al.,⁶³ a γ-oxygen is initially protonated in this scheme.

Three pathways for the first proton transfer, 3′-OH deprotonation, were considered: protonation of (1) Asp429, (2) Asp490, and (3) an ordered water molecule. On the basis of transition-state (TS) energies, pathway 1 is favored. Calculations were also done with a γ-oxygen that is unprotonated because PP_i pK_a values are uncertain; the scheme with the γ-oxygen protonated was favored. In the reaction path, two transition states were found, separated by a very broad plateau, with TS1 describing proton transfer to Asp490 and TS2 describing breakage of the Pα–Oβ bond. TS2 can be characterized as an associative-like, trigonal bipyrimidal phosphorane transition-state structure with the characteristic ∼1.73 Å P–O single-bond distance. The results for Mg and Mn are quite similar. From the two hypothesized TS, it appears that the initial proton transfer needs to be completed before P–O bond breakage, although the actual reaction coordinate profile, especially for the Mg case, is very flat between the two transition states. There is substantial charge transfer to the two Asp residues and the Mg²⁺-coordinated water molecule, emphasizing the importance of charge modification along the reaction pathway. An approximate energy decomposition method indicated a number of residues that participate in TS stabilization and, as noted, could be important residues to mutate.

The methods used here should be an improvement over static structure ONIOM QM/MM methods. Probing for a reaction coordinate as in the QSM, versus imposing one, is certainly a preferable strategy; however, it does require knowledge of two end-point structures, which may not be available or, if constructed, may not be accurate.

Wang and Schlick⁶⁸ simulated DNAP IV (Dpo4) from Sulfolobus solfataricus based on a crystal structure (PDB ID 2ASD) that had Ca ions. These were replaced by Mg²⁺, some missing residues were modeled in, and crystal waters were retained. The solvated structure was minimized and simulated by MD to obtain a starting structure for QM/MM as implemented in the CHARMM program coupled with GAMESS-UK (a QC method). The QM part was formed from two Asp and one Glu side chains, the two Mg ions, the dCTP nucleotide and the terminus of the DNA primer, along with four water molecules that are found to be coordinated to Mg²⁺-A and the dCTP. In this QM/MM approach, the relatively close MM atoms are allowed to fluctuate while those further away from the reaction center are constrained. Reaction coordinates probed were for transfer of the 3′-OH, and O3′–Pα and O3α–Pα distance.

The favored reaction path consisted of initial 3′-OH deprotonation via two bridging water molecules to a phosphate α-oxygen, followed by its transfer to the γ-phosphate oxygen of the nucleotide, as nucleophilic attack of the 3′-O occurs and the Pα–Oα bond breaks. Another pathway probed, whereby the 3′-OH proton directly transfers to the Oα, has a higher barrier. The rate-limiting step is found to be 3′-OH deprotonation, and as in other studies, PP_i release is through an associative transition state. Stressed in this work is that Dpo4’s active site is more open relative to other, higher-fidelity DNAPs, accounting for the presence of more water molecules in the active site that are found to be essential to the mechanism. Another insight is that active-site reorganization from the crystal to MD starting structure was important to provide a prechemistry conformation.

Wang et al.⁶⁹ simulated bacteriophage T7 DNAP from a crystal structure of 2.54 Å resolution (PDB ID 1T8E) with MD and QM/MM. The primer and incoming dCTP nucleotides were 3′-O-protonated, and then simulated by MD to provide a starting structure for the QC, with the dCTP simulated as unprotonated (−4 charge). The QM/MM was carried out with a reaction coordinate driving method⁷⁰ that, in contrast with ONIOM-based methods, does provide a reaction coordinate free-energy profile in the sense that thermal fluctuations of the MM layer are incorporated.

The QC starting structure has two water molecules, one crystallographic and another from solvent, that span the α- and γ-dNTP phosphates, and the reaction is initiated by a concerted proton transfer that protonates a γ-phosphate oxygen, leaving an OH^– coordinated to Mg²⁺-A. The 3′-OH proton neutralizes this OH^– to provide the nucleophile 3′-O^– to attack the α-phosphate and form the PP_iH leaving group. A pentavalent associative transition state is formed prior to H release. Before release, a water molecule again serves as a proton transfer bridge to reprotonate the α-phosphate by the γ-phosphate. Thus, in this “reverse” mechanism, the general base is the NTP γ-phosphate and the general acid is the 3′-OH. The net result is the same as in, for example, ref (68). Among other possibilities explored, attempts at a direct proton transfer from the 3′-OH to the α-phosphate of the NTP could not produce a stable intermediate, as found in the study of Wang and Schlick.⁶⁸ The use of a conserved Asp as the general base or a Glu as a general acid were also found to not be feasible. This result is consistent with the two-proton mechanism, but the protons come from solvent water rather than from residues. It has been found from mutational studies of a T7 RNAP that a residue is essential as a general acid.⁷¹ A possibility suggested by this reverse event mechanism would be to protonate a water molecule from an acid residue, transfer that proton to the NTP γ-phosphate oxygen through a water chain, and have that residue deprotonate 3′-OH, followed by the nucleophilic attack and PP_iH release. In this scheme, one residue acts as a general acid and base, and the acid form is automatically regenerated.

Michielssens et al.⁷² considered HIV reverse transcriptase, which also undergoes a reaction cycle of phosphodiester bond formation and PP_i release. A combined MD QM/MM simulation based on the crystal structure (PDB ID 1RTD) was carried out with a focus on the donor of the second proton, as Castro et al.^38a indicated that a Lys was the responsible acid in HIV-RT. In the 1RTD structure, the candidate Lys220 amino group is ∼15 Å from the active site. Here, explicit water MD simulations were carried out for 1 μs, a very long time for this very large system. In that time a number of different Lys conformations were found where the two hydrogens from the Lys amino group formed two hydrogen bonds to α- and γ-oxygens of the dNTP, Lys amino group hydrogens bridged an Asp carboxylate and a water that is in turn hydrogen-bonded to a γ-oxygen, and Lys is singly hydrogen-bonded to a γ-oxygen. These configurations were optimized with QM/MM and are appropriate geometrically for Lys to be the acid residue for the second proton. Of course, the pK_a of the Lys will have to be low enough to act as an acid. Active sites can and do involve Lys with reduced pK_as. The presence of an Asp could be a pK_a switch to make Lys more acidic than its nominal solvent pK_a would suggest.

13.7. RNA Polymerase/DNA Polymerase Catalysis Summary

To summarize this survey of some computational studies of two-metal two-proton mechanisms, they were strongly influenced by experiments on a diverse set of nucleic acid polymerases that indicate the involvement of two protons based on two experiments.³⁸ First, k_pol as a function of pH measurements for Mg²⁺ shows a bell shape over the accessible pH range that is indicative of two ionizable groups with, for poliovirus RNA-dependent RNAP, pK_a values of 7 and 10.5.^38a Second, proton inventory experiments, for all the studied polymerases, consistently are best fit with a two-proton form. In our view, the k_pol measurements are on firm foundation as they are based on equilibrium properties, the states of ionization of acids and bases at a given pH, based on the reasonable assumption that the actual chemical transformation (bond making/breaking) is slow compared with ionization equilibration. For reasons noted above, the proton inventory experiments are more difficult to interpret. In particular, the model that two protons participate in one transition state may not be as strongly supported by the deuterium–hydrogen exchange experiment. When properly interpreted within a tunneling framework, a scenario of a cluster of protonated water molecules, for example, H₇O₃⁺, can, by a Grotthus-like mechanism, transfer two protons (H₃O⁺H₂OH₂O ↔ H₂OH₂OH₃O⁺) in their respective covalent–hydrogen-bond configurations between their heavy atoms. However, for nucleotidyl transfer, a scenario of deprotonating the 3′-OH to some base and an acid protonating one of the NTP phosphate oxygens in a concerted process seems remote.

In all the above-discussed mechanisms of nucleotidyl transfer, a distinct separation is made between 3′-OH deprotonation and NTP protonation; reaction coordinates are proposed where the two protons follow a stepwise path separated by transition states. Among the proposed mechanisms, what does seem uniformly rejected is “direct” 3′-OH deprotonation to NTP Oα.^29,63,68,69 Thus, there is agreement that 3′-OH deprotonation occurs by a different route. In Carvalho et al.,²⁹ a bulk hydroxide is the hypothesized base. In Zhang and Salahub,⁷³ the base is a solvent water molecule that the α-phosphate oxygen activates. In Lin et al.⁶³ and Cisneros et al.,⁶⁶ transfer of the 3′-OH proton is to a residue. In Wang and Schlick,⁶⁸ the base is provided via two bridging water molecules to a phosphate α-oxygen. In Wang et al.,⁶⁹ OH^– is obtained by initial protonation of a γ-phosphate oxygen via two water molecules. Regarding the nucleotidyl transfer step by nucleophilic attack of 3′-O^–, there is general agreement that a pentacovalent associative (short ∼1.7 Å P–O bond distance) transition state is formed. That occurs under the assumption of the second proton already attached to an NTP phosphate oxygen^63,66 or being transferred from a residue²⁹ or from the initial proton binding a β-phosphate oxygen⁷³ or transfer to the γ-phosphate oxygen.⁶⁸ In another, “reverse” scenario,⁶⁹ the PP_iH leaving group’s proton is obtained from an initial step of a concerted proton transfer via two hydrogen-bonded water molecules. A number of the studies conclude that the rate-limiting step is the nucleophilic attack of the 3′-O species. Cisneros et al.,⁶⁶ however, find that their two transition states for 3′-OH deprotonation and P–O bond breaking are of almost equal energy and are separated by a broad plateau.

There are thus a variety of scenarios that have been proposed. It may well be that more tightly closed reaction complexes exclude water very effectively and rely on residues to act as proton donors and acceptors, with the pK_as of these residues structurally tuned. Other, looser reaction complexes may rely on tightly bound waters (as may be identified by crystallography of sufficient resolution) and/or more mobile waters to provide water molecules that are hydrogen-bonded to NTPs and ligands of metals. The presence of H₃O⁺ and/or OH^– as species for specific acid/base catalysis should also not be excluded. While residues in enzymes are designed to act as general acids and bases owing to their high concentration at specific locations and the low dielectric environment that tends to converge the pK_as of acid and bases toward pH 7, reaction centers in many metal-based enzymes do have water molecules present.

To conclude a long discussion, QC methods have been applied to a number of RNAP and DNAP mechanisms. There is broad agreement that, for most or all RNAPs and DNAPs, the rate-limiting step in catalysis is most likely the deprotonation of the 3′-OH of the i site sugar (Figure 2). The reaction appears to require mobilization of multiple protons, but various models have been proposed, and details of proton transfers may vary in different systems. A feature of sequestered RNAP and DNAP active sites is an environment with a reduced solvent dielectric constant and altered pK_as of amino acid side chains to promote critical proton transfers and to ensure accurate chemistry. These active sites may also be evolved to select against particularly deleterious misincorporation events. Descriptions of specific RNAP and DNAP mechanisms indicate that misincorporation events may require phosphodiester bond synthesis without active-site closing, which appears to require that alternate pathways for proton transfers be followed. The picture that emerges, therefore, is one in which sequestration within an enclosed active site enhances chemistry. Specific chemistry follows a carefully scripted and rapid mechanism. Misincorporation occurs via a slow and alternate mechanism.

14. Four-Substrate Problem

RNAPs and DNAPs also share the four-substrate problem: the utilization of four chemically distinct substrates (ATP, GTP, CTP, and UTP or dATP, dGTP, dCTP, and TTP). In these polymerization mechanisms, therefore, chemical recognition of the substrate cannot be as important as cognate base pairing and accurate base pair and triphosphate orientation. Another way of looking at this issue is that RNAPs and DNAPs must have very high selectivity for cognate versus noncognate base pairs in the active site without very strong direct chemical recognition of any particular substrate. So, RNAPs and DNAPs must maintain high polymerization fidelity with relatively low chemical recognition substrate specificity. To begin to attack this problem for RNAPs via MD, all four cognate base pairs would be simulated with a closed trigger loop in explicit water. Simulations would be analyzed for any induced-fit contacts specific to any of the four dNMP–NTP base pairs. The distribution of ordered and excluded water would be analyzed around the 3′-O^–, the cognate base pair, the ribose ring, and the triphosphate. These simulations form a frame of reference for simulations with noncognate NTPs or accurately paired 2′-dNTP or 3′-dNTP substrates.

15. A Model for Transcriptional Fidelity

A working model for transcriptional fidelity would account for dNMP–NTP alignment, hydration/dehydration, ribose/deoxyribose sugar discrimination, trigger loop opening and closing mechanisms, and clashes of the closed trigger loop with a noncognate base pair. Above, the four-substrate problem is discussed to indicate the importance of an atomistic analysis of cognate base pair alignment, at least in part, in order to begin to understand how noncognate NTPs are rejected. The issue of accurate dNMP–NTP alignment is highlighted by RNAP mutations that are expected to misalign the substrate. Because the trigger loop is expected to dehydrate the RNAP active site during closure, regulated hydration/dehydration issues are expected to be important in cognate dNMP–NTP recognition. The trigger loop is expected to be an important feature of cognate NTP recognition and noncognate NTP exclusion, so analysis of trigger loop closure in the presence of cognate and noncognate NTPs will be important. Because it appears that the trigger loop must be closed for rapid catalysis with a cognate substrate NTP, simulations should first be done with fully closed trigger loop conformations. Such a conformation of the trigger loop may induce clashes, and excessive hydration may be generated by a noncognate NTP. Because some noncognate NTPs appear to be rejected before trigger loop closing,^30,39 MD may also be done in open trigger loop conformations.

The RNAP trigger loop involvement in NTP selectivity appears to depend on the extent of difference between an inappropriate and a cognate substrate. Landick and co-workers³⁰ have argued that closing of the trigger loop and folding of the trigger helices generates a more ordered three-helix bundle that includes the bridge α-helix. In this way, trigger loop closing helps to frame and sequester the active site. They show, furthermore, that significant fidelity determination is possible with deletion of the trigger loop, indicating that trigger loop closing is not required for rejection of some inappropriate substrates. Zenkin and co-workers³⁹ demonstrate that fidelity checkpoints occur in both open and folded trigger loop conformations. Noncognate NTPs are generally rejected before the trigger loop can close. By contrast, 2′- and 3′-dNTP substrates with cognate base pairing are rejected during the late stages of active-site closure. Thermus aquaticus β′ Gln1235 on the trigger loop was shown to help select against 2′- and 3′-dNTPs, demonstrating that the trigger loop can participate directly in substrate selection.

The problems of polymerization fidelity are very similar for multisubunit RNAPs and DNAPs, particularly high-fidelity DNAPs.⁷⁴ Some DNAPs are evolved to repair damaged DNA or to incorporate noncognate dNTPs, and these DNAPs make more frequent errors in template recognition.⁷⁵ High-fidelity DNAPs (i.e., family A DNAPs) have active-site opening and closing mechanisms that are analogous to the trigger loop opening and closing mechanisms of multisubunit RNAPs.⁷⁴ More error-prone DNAPs may have more open active sites and may lack large conformational changes associated with accurate dNTP loading. DNAP fidelity has been characterized as a passive competition of cognate versus noncognate dNTPs. A simulation method termed “milestoning” has been used to characterize the energetics of accurate incorporation versus misincorporation for HIV-1 reverse transcriptase.^36b The indication is that a noncognate dNTP is rejected both during the initial encounter stage and during the chemical step. Release of the noncognate dNTP is rapid. A cognate dNTP, by contrast, is rapidly and stably bound and proceeds rapidly through chemistry, making unproductive exchange of a cognate dNTP unlikely. DNAP mechanisms are highly analogous to multisubunit RNAP mechanisms in complexity, active-site opening/closing, active-site hydration/dehydration, mechanism, fidelity and substrates, so many of the issues in DNAP and RNAP fidelity mechanisms are very similar.

16. Active versus Passive NTP Exchange

The argument against active NTP exchange by multisubunit RNAPs is that fidelity discrimination appears similar whether analyzed in the presence or absence of the cognate NTP,^7b,43b,76 indicating that the cognate NTP cannot actively displace the noncognate NTP. Passive mechanisms of NTP exchange, however, can involve NTP loading through either the secondary pore or the main channel of RNAP. However a noncognate NTP is rejected, the mechanism of release is important, as is the mechanism of PP_i release and NTP exchange. A recent study of HIV-1 reverse transcriptase indicates that noncognate dNTPs are rejected rapidly before they can undergo chemistry.^36b Cognate dNTPs, by contrast, are committed to the forward pathway much more stably and rapidly. The mechanism of exchange, therefore, appears to be passive competition in which noncognate substrates are scanned and rejected quickly and cognate substrates are rapidly sequestered and incorporated.

17. RNA Polymerase Mutant Protein Simulations

A small number of simulations of RNAP mutant proteins have been reported.^17,18c,21 In general, these approaches appear to be informative. Mutant RNAPs appear defective in simulations compared to RNAP wild type. Sometimes, defects appear to be magnified in the mutant simulation relative to observed defects in vitro and/or in vivo. One approach to such studies is to utilize MD as a controlled experiment, that is, to compare wild-type and mutant RNAPs in TECs that have open or closed trigger loop conformations. The hope, therefore, is that interpretable differences will emerge in the simulations: for instance, simulations will result in clear differences comparing open and closed trigger loop conformations and mutant and wild-type RNAPs.^7a,17,18c,21 The downside of such approaches is that all-atom simulations are computationally expensive and, so far, wild-type simulations do not appear to be perfectly done, compromising the experimental control. It does appear comforting that simulations do identify differences between mutant and wild-type RNAP, in which the wild type appears to maintain more appropriate native conformations.^18c So far, however, simulations do not provide perfect insight into mutant RNAP defects. If simulations could become much higher throughput, MD could become a more useful tool for planning and analyzing mutagenic analyses. Furthermore, detection of mutant protein defects using simulations is an important indication of the accuracy and importance of MD, so this is a verification of simulation technology.

18. Inhibitors of RNA Polymerase

There are a number of important inhibitors that might be simulated with RNAP TECs to gain insight into modes of inhibitor action. Here we discuss three examples: rifampicin, α-amanitin, and microcin J25 (Figure 6). Rifampicin is a major drug against tuberculosis (TB), and a worldwide human health challenge is to develop novel anti-TB drugs to combat multidrug-resistant TB.⁷⁷ Rifamycin and rifapentin are chemically related drugs. Many rifampicin-resistant bacterial RNAPs have been isolated. A controversy surrounding rifampicin inhibition of RNAP revolves around two models that are not mutually exclusive: (1) rifampicin affects RNAP function acting as an allosteric inhibitor, and (2) rifampicin sterically blocks early RNAP elongation at the 3–4 nucleotide RNA stage. RNAP core structures with bound rifampicin are available, so the location of rifampicin binding is known. A T. thermophilus RNAP initiation complex with σ70, a TATAATG −10 region consensus, single-stranded nontemplate strand, and a dinucleotide RNA is available, into which rifampicin could be modeled.²⁵ Therefore, it appears that appropriate structures are available to challenge these two hypotheses via MD. This project would have medical relevance.

Figure 6.

RNAP inhibitors. (A) Rifamycin, a main-line drug against TB. (B) α-Amanitin, a deadly mushroom toxin that is heavily modified through secondary enzymatic reactions. (C) Microcin J25, a naturally occurring, plasmid-encoded bacterial antibiotic. Images of α-amanitin and microcin J25 are drawn to indicate similarities in structure, including a covalently closed eight-amino-acid ring, 2-Gly residues located in analogous positions, Pro residues in analogous positions, and ring cross-bridges projecting an aromatic amino acid with a hydroxyl group.

The death cap mushroom Amanita phalloides produces the highly selective and potent RNAP II inhibitor and poison α-amanitin. There are S. cerevisiae RNAP II structures and TECs with α-amanitin bound.^57b,78 It is very likely that useful insight into α-amanitin toxicity could be gained from MD in the presence of the drug. α-Amanitin is a cyclic octapeptide with a covalent cross-bridge and other interesting covalent modifications. A related inhibitor of bacterial RNAP is microcin J25, which appears to be an α-amanitin mimic.⁷⁹ Microcin J25 is a cyclic octapeptide with an extended peptide tail that loops out, back, and then through the covalently closed eight-amino-acid ring to form a similar cross-bridge to α-amanitin (microcin J25 is described as a “lariat protoknot”)⁸⁰ (Figure 6B,C). It is very possible that microcin J25 binding to bacterial RNAP, for which there is no current RNAP–microcin J25 structure, could be modeled on the basis of RNAP II−α-amanitin structures. Understanding α-amanitin inhibition of RNAP II transcription and related microcin J25 inhibition of bacterial RNAP would contribute to understanding of mushroom toxicity and antibiotic structure and function.

19. Bacteriophage T7 RNA Polymerase

Although it is not a homologue of multisubunit RNAPs, bacteriophage T7 RNAP, a single-protein subunit of 99 kDa, provides an exceptional model system to analyze the dynamics of RNAP initiation, promoter escape, and polymerization mechanisms.⁸¹ Efforts have been made to understand T7 RNAP translocation and kinetics.^22,24 Many relevant structures are available of T7 RNAP initiation complexes⁸² and TECs^82a,83 (Table 2). T7 RNAP, which is a single subunit, solves the problem of converting from an initiating enzyme with highly specific promoter recognition capability to an elongating enzyme with reduced sequence specificity through a drastic conformational change in the N-terminal third of the protein.^82a Essentially, the domain involved in promoter recognition rotates, three separate α-helices (initiating) combine into a long single helix (elongating), and subdomain H (amino acids 170–180) remarkably translates by 70 Å and rearranges during promoter escape to become part of the RNA exit path. T7 RNAP recognizes a 17 bp promoter, and downstream DNA is bent and melted through six bases in the encounter. The RNA/DNA hybrid is 7–8 nt in length during elongation. T7 RNAP TECs are highly analogous to multisubunit RNAP TECs.

Table 2. Structures of Bacteriophage T7 RNA Polymerase.

PDB ID	resolution (Å)	nucleic acid	nucleotide	state	refs
3E2E	3.00	T/N/R		posttranslocation	(83b)
3E3J	6.70	T/N/R		pretranslocation	(83b)
2PI4	2.50	T/N	GTP	initiation	(87)
2PI5	2.90	T/N		initiation	(87)
1S76	2.88	T/N/R	ATP	posttranslocation	(71)
1S77	2.69	T/N/R	PPi	pretranslocation	(71)
1S0V	3.20	T/N/R	ATP	posttranslocation	(88)
1H38	2.9	T/N/R		preinsertion	(89)
1MSW	2.10	T/N/R		pretranslocation	(82a)
1QLN	2.40	T/N/R		preinsertion	(90)
1CEZ	2.40	T/N		initiation	(91)
1ARO	2.80			with inhibitor T7 lysozyme	(92)
4RNP	3.00				(93)

TEC structures have open and closed conformations. T7 RNAP is closely related to family A DNAPs, such as Escherichia coli DNAP I, which also have an opening and closing mechanism involving the O and O′ helices (sometimes named Y- or P-helix) of the “fingers” domain. Remarkably, there is an O helix and finger domain rotation of 22.5 Å in the pretranslocated product TEC with PP_i bound (closed conformation) and the posttranslocated TEC (open conformation). Because the absence or presence of PP_i is the only difference separating these isomorphous crystal structures, it is suggested that release of PP_i may provide the energetic driving force for T7 RNAP translocation.^81,82 Tyr639 rotates into the substrate NTP site in the open, posttranslocated TEC conformation and is displaced as the incoming NTP rotates with the O helix into a closed, catalytic conformation. Tyr639 also has a role in recruiting Mg²⁺ during the transition to the catalytically competent, closed TEC. Rotation of the O′ helix is associated with the opening of the next downstream template DNA base. T7 RNAP structures are determined at reasonably high resolution, and initiation, promoter escape, and elongation complexes are available for more extensive MD analysis (Table 2).

20. Clash of Cultures

The attempt to analyze multisubunit RNAPs by use of MD and related simulation techniques brings together computational modelers, X-ray crystallographers, single-molecule biophysicists, molecular biologists, and biochemists. Because people with different backgrounds and expertise may have different interests and goals, potentially, this could be an interesting mix of stakeholders. Without cutting corners, very long duration and elegant simulations of RNAPs may not be easily obtained, diminishing the enthusiasm of the modelers, who have the option of working on simpler systems. Additionally, multisubunit RNAPs represent an application more than an elegant model system for the development of new computational methods, although RNAPs are highly suitable subjects for developing novel multiscale methodology. X-ray crystallographers appear to gain increasing tolerance for modelers as simulation technologies advance. Increasingly, MD can be seen as a means to extract additional information and refined hypotheses from otherwise static crystal structures, making MD/QC value added to the structural data analysis.

Multisubunit RNAPs also present some issues for single-molecule biophysics approaches because of their large size and small translocation step (∼3.4 Å).^33a An outstanding issue with regard to multisubunit RNAPs is the timing for TECs to oscillate pre ↔ post. Because of the short translocation distance, a large target (RNAP) must be visualized to travel a short distance (3.4 Å), and the translocation step must be distinguished from stage drift or noise, making measurements challenging. By use of optical traps, single base-pair stepping has been recorded for RNAP elongation,^33a but this technology has not been applied to resting translocation oscillation. A DNAP has been analyzed for translocation oscillation by α-hemolysin nanopore technology.^31a DNAP oscillates pre ↔ post on a millisecond time scale, demonstrating unimpeded translocational sliding. With few modifications, the nanopore single elongation complex technology could be applied to multisubunit RNAPs. The DNA template must be customized, so that a single-stranded DNA penetrates the nanopore appropriately and the position of abasic DNA sites is optimized to detect translocation from the observed change in current flux across the membrane. Single-stranded DNA plugs the nanopore, reducing the current; exposure of abasic DNA within the pore via translocation, by contrast, opens the pore, increasing the current. This appears to be an experiment of high importance in order to understand multisubunit RNAP translocation. Multiprobe FRET could also be applied to the problem of RNAP translocation, but FRET probes are large and difficult to place on RNAP, and the translocation distance is small, making this a potentially challenging experiment.⁸⁴

Biochemists wish to believe that high-end simulation approaches will provide insight into transcriptional mechanisms that will translate into new testable models and predictions. For instance, those engaged in mutagenic studies would like to generate many useful predictions from simulations for important amino acid residues.^7b,32b Furthermore, simulations should give as much atomistic insight as possible into mutant protein defects.^7b,18c Simulations should identify flexible and dynamic hinges in functionally important parts of the protein. So far, these approaches seem to provide reasonable information, but simulations are low-throughput and expensive in computation time, limiting the number of mutant RNAPs and transcription intermediate snapshots that can be analyzed. Potentially, a single mutant could be analyzed in a closed-trigger-loop catalytic TEC and an open-trigger-loop product TEC (with PP_i bound). Advances in mutant RNAP simulation technology that allow analysis of many more mutant proteins in different contexts would be very useful for future studies.

Simulations should provide new insight into issues of RNAP and DNAP fidelity that probably cannot be obtained by any other approach. The milestoning approach applied to HIV-1 reverse transcriptase, using cognate and noncognate dNTPs, appears to provide reliable energetic information and strong correlations to experimental kinetic data,^36b indicating that this is an important approach. Many DNAPs have been analyzed for binding of cognate and noncognate dNTPs, providing some insight into DNAP fidelity.^{75b,75c,75f,85} A potential new direction for TEC studies would involve detailed analyses of each cognate base pair with more sophisticated analysis of water and counterion distributions within sequestered active sites. Improved methods to understand effective pK_a values of active-site residues and how pK_a values change upon active-site closing will be important. Because many active-site residues appear to cooperate in functional proton and Mg²⁺ transfers, understanding how these changes occur in the case of cognate substrates is necessary. Presumably, for noncognate substrates, alternate proton transfer pathways are utilized. In many cases, noncognate substrates are rejected within an open active site. Solvent distributions are, therefore, expected to be a key aspect of NTP discrimination.

Because computational models rely on empirical force fields, there is always a question about their reliability. Without enhanced modeling techniques, all-atom MD is limited to shorter time scales than a RNAP bond addition cycle. A 100 ns all-atom simulation is a very long computation for a multisubunit RNAP, and the time scale of phosphodiester bond synthesis may require milliseconds. Furthermore, typical classical MD simulations do not make or break covalent bonds without inclusion of QC calculations. Although potentially more fundamental than MD, QC treatments only apply to a small number of atoms, so these approaches are limited as well.

Explicit water models for simulating the internal hydration of proteins are considered to be well-developed, but models for divalent ions and nucleic acids may require improvement. For multisubunit RNAPs, a detailed model for hydration/dehydration functions in trigger loop opening/closing might provide insight into catalysis and fidelity. So far, it appears that water must be highly ordered and in some places specifically excluded in a closed trigger loop RNAP TEC. It should be stressed here that experimental tools to understand the specific roles of solvent in enzyme reactions are very limited and should be improved. Ordered water may be very important in deprotonating the 3′-HO_RNA/DNA. Discrimination of ribose and deoxyribose sugars in RNAPs and DNAPs may also use water.

MD simulations sample potential dynamic states of proteins. For the purposes of understanding, teaching, and experimental planning, movies of complete transcriptional processes are very helpful but, so far, these models are not fully based on MD and QC.^1b,86 In the future, complete simulations of the phosphodiester bond addition cycle based on all-atom MD and QC analyses with a cognate NTP or a noncognate NTP would be highly prized. Dynamic simulations of initiation events would also be very useful. Correlating simulations with reaction coordinate energetics and experimental kinetics should be attainable. Ultimately, of course, computational models must be challenged and/or validated by experiment to enhance their utility and reliability.

21. Looking Forward

Modeling the mechanism of elongation by multisubunit RNAPs presents many challenges, and in many respects this project appears to be a worst-case scenario for current all-atom MD approaches applied to core catalytic mechanisms. On the other hand, adequate solutions or partial solutions to problems with complex RNAPs push the limits and capabilities of dynamics studies. So far, dynamics approaches have strongly complemented biochemical and genetic studies, making simulations useful and interesting even if technical challenges and challenges of interpretation remain. Amino acid residues identified as making alternate atomic contacts or associated with dynamic hinges appear to be good candidates for mutagenesis and assays, indicating that MD can be strongly predictive for RNAP functional residues.^7b,32 Simulation of mutant RNAPs has been attempted,^17,18c,21 but simulations of wild-type RNAP remain incomplete and insufficient, indicating that many very expensive computations with RNAP mutant proteins may be premature. To gain the most information from RNAP mutant protein simulations, new approaches are likely to be necessary.

Glossary

Abbreviations

AIMD

ab initio molecular dynamics

AMBER

assisted model building with energy refinement

AMPCPP

α,β-methyleneadenosine triphosphate

BNM

block normal mode

CHARMM

chemistry at harvard molecular mechanics

DFT

density functional theory

DNAP

DNA polymerase

ENM

elastic network model

FF

force field

GAMESS-UK

a quantum chemical method

MD

molecular dynamics

MM

molecular mechanics

MSM

Markov state model

NMA

normal mode analysis

ONIOM

our own N-layered integrated molecular orbital and molecular mechanics

PP_i

pyrophosphate

PP_iH

protonated pyrophosphate

QC

quantum chemical

QM

quantum mechanics

QSM

quadradic string method

RNAP

RNA polymerase

TB

tuberculosis

TEC

ternary elongation complex: RNA, DNA, RNAP

TS

transition state

Biographies

Beibei Wang was born in Hebei, People’s Republic of China. She received her B.S. degree in applied chemistry at China University of Petroleum in 2007. She is now a Ph.D. candidate at Fudan University and a visiting scholar in Michael Feig’s lab at Michigan State University. Her research interest now mainly focuses on the molecular mechanism of RNA polymerase by computer simulations.

Michael Feig is Professor in the Departments of Biochemistry & Molecular Biology and Chemistry at Michigan State University. He also has an adjunct appointment in the Department of Computer Science & Engineering. Michael Feig began his academic training at the Technical University of Berlin, where he graduated in 1994 with a diploma in physics. He then moved to the graduate program in chemistry at the University of Houston, where he began to study computer simulations of biological macromolecules under Professor B. Montgomery Pettitt. After graduating with a Ph.D. in 1999, he moved to The Scripps Research Institute to work with Professor Charles Brooks as a postdoctoral fellow until 2003, when he started his independent career at Michigan State University. Michael Feig continues to use computational methods to study the structure and dynamics of biological systems ranging from single molecules to complex cellular environments.

Robert I. Cukier is Professor of Chemistry at Michigan State University. He received his M.S. in 1967 and Ph.D. in 1969 in chemistry from Princeton University. His scientific interests center on using statistical and quantum mechanics to create theories of and design efficient computational algorithms for the simulation and analysis of protein structure–function relations. Ongoing studies include proton-coupled electron transfer, proton translocation, large-scale protein domain movements, protein–protein interactions, and reaction mechanisms in enzymes.

Zachary Burton received his Ph.D. from UCLA in 1980, working in the laboratory of Dr. David Eisenberg. He was a postdoc in Dr. Richard Burgess’ laboratory until 1983 and a postdoc with Dr. Jack Greenblatt until 1987. Since then, he has been a professor at Michigan State University.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States