Mechanics of finger-tip electronics

Abstract

Tactile sensors and electrotactile stimulators can provide important links between humans and virtual environments, through the sensation of touch. Soft materials, such as low modulus silicones, are attractive as platforms and support matrices for arrays sensors and actuators that laminate directly onto the fingertips. Analytic models for the mechanics of three dimensional, form-fitting finger cuffs based on such designs are presented here, along with quantitative validation using the finite element method. The results indicate that the maximum strains in the silicone and the embedded devices are inversely proportional to the square root of radius of curvature of the cuff. These and other findings can be useful in formulating designs for these and related classes of body-worn, three dimensional devices.

INTRODUCTION

Tactile sensors and electrotactile stimulators mounted on the fingertips can establish natural connections between a human subject and a virtual environment. Such devices, when designed using ultrathin, skin-like properties, offer the potential to significantly improve interfaces needed in simulated surgery, therapeutic devices, and robotic manipulators.^{1, 2, 3} Tactile sensors measure the pressure created by physical contact. Together with motion detection and temperature sensing, such can serve in feedback loops with electrotactile stimulators that create artificial sensations of touch, commonly perceived as a vibration or tingling feeling.^{4, 5} Related technologies have been explored for programmable braille readers and displays for the visually impaired as well as for balance control in individuals who suffer from vestibular disorders.^{3, 6, 7, 8, 9}

The concepts of stretchable electronics have potential utility in these contexts.^{10, 11, 12, 13, 14} In particular, they create opportunities to incorporate tactile sensors and electrotactile stimulators into conformal, skin-like platforms that intimately, and non-invasively mount on the fingertips. Ying et al.¹⁵ reported materials, fabrication strategies and device designs for ultrathin, stretchable silicon-based electronics and sensors that can be mounted on the inner and outer surfaces of soft, and elastomeric closed-tube structures for integration directly on the fingertips. The active components and interconnects incorporate advanced mechanics designs, capable of accommodating large strains induced not only by natural deformations of the soft tubes during use but also during a critical step in the fabrication process in which the soft tubes, specially formed to match the shapes of fingertips, were flipped inside-out, as illustrated in Fig. 1. Figure 1a shows a finger-tube made of a very soft silicone elastomer (Ecoflex, Smooth-On, Inc.) in three dimensional forms specifically matched to those of fingers on a plastic model of the hand. The fabrication involves pouring a polymer precursor to Ecoflex onto a model finger multiple times, to create a conformal sheet with ∼500 μm thickness. As illustrated in Fig. 1b, removing the Ecoflex from the model forms a free standing finger-tube shown in Fig. 1c. Ecoflex is an attractive material for this purpose because it has a low modulus (∼60 kPa) and large fracture strain (∼900%). The former allows soft, intimate contact with the skin; the latter enables the above “flipping-over” process. Transfer printing delivers the electrotactile stimulators to the outer surface of the flipped finger-tube, while pressed into a flattened geometry (Fig. 1c). The flipped finger-tube (with the electrotactile stimulators on the outer surface) is then slipped onto the finger model (Fig. 1d), and is flipped inside-out, to move the electrotactile stimulators from the outer to the inner surface of the tube, as shown in Fig. 1e.

Figure 1.

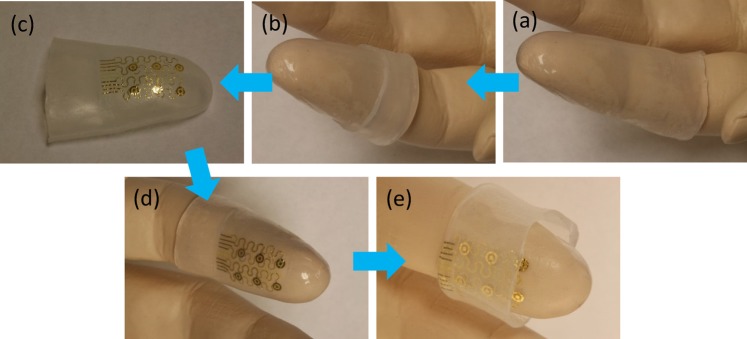
The “flipping over” process in the fabrication of finger-tip electronics: (a) a finger-tube at the natural, stress-free state on a plastic model of the hand; (b) a “flipping-over” process releases the finger-tube from the model to expose its inner surface; (c) the flipped finger-tube with the electrotactile stimulators on the outer surface; (d) the finger-tube slipped onto the finger model; (e) the “flipping-over” process for the second time moves the electrotactile stimulators from the outer to the inner surface.

This “flipping-over” process allows devices initially mounted on the outer surface of the soft tube to be reversed to the inner surface, where they can press directly against the skin when mounted on the fingers. These concepts in multifunctional fingertip devices were demonstrated with electrotactile electrode arrays multiplexed with Si nanomembrane (NM) diodes, strain sensors based on Si NM gauges, and tactile sensor arrays that use capacitors with low-modulus, elastomeric dielectrics.

This paper aims at establishing analytic mechanics models that determine the maximum strain in the “flipping-over” process. The finite element method (FEM) is used to validate the results. The predicted shape after the “flipping-over” process agrees well with experiments. A scaling law for the maximum strain in the device is established, which is useful in optimizing the design of devices to survive the “flipping-over” process used to fabricate fingertip electronics.

AN ANALYTIC MODEL FOR SOFT MATERIALS IN FINGERTIP ELECTRONICS

The schematic diagrams in Fig. 2 further illustrate the “flipping-over” process by tracking points a-h on the inner and outer surfaces of the finger-tube, where Figures 2a, 2b, 2c, 2d, 2e correspond to Figures 1a, 1b, 1c, 1d, 1e, respectively. Figure 2a shows a soft, ecoflex finger-tube at the natural, stress-free state, with points a-d on the inner and e-h on the outer surfaces, respectively, of the finger-tube. The soft finger-tube is flipped over (Fig. 2b) to expose the inner surface out and form a free standing finger-tube shown in Fig. 2c, where points a-d and e-h switch to be on the outer and inner surfaces of the flipped finger-tube, respectively. As to be shown in the following, the electrotactile stimulators transfer printed to the outer surface of the flipped finger-tube (while pressed into a flattened geometry) have very low stiffness. They have little effect on the “flipping-over” process, and are neglected in the analytic model. The flipped finger-tube (with the electrotactile stimulators on the outer surface) is then slipped onto the finger model (Fig. 2d), and points a-d and e-h remain on the outer and inner surfaces, respectively. The soft finger-tube is then flipped over again (Fig. 2e) such that the electrotactile stimulators are on the inner surface and the strain gauge arrays and tactile sensors are transfer printed on the outer surface (while pressed into a flattened geometry).

Figure 2.

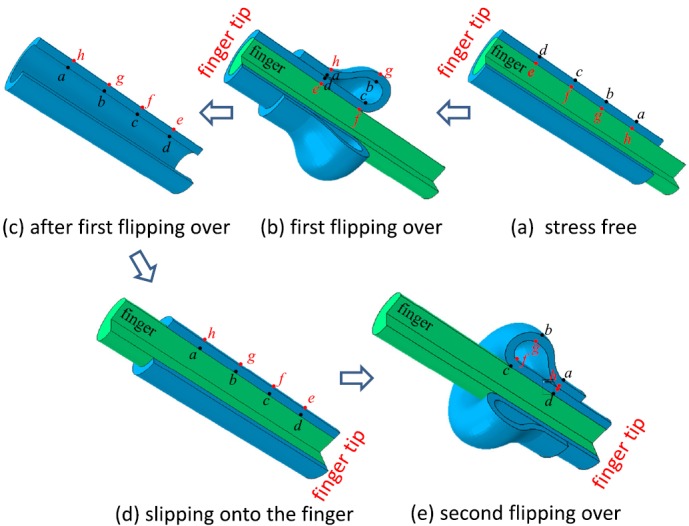
The schematic diagrams of the “flipping-over” process by tracking points a-h on the inner and outer surfaces of the finger-tube, where Figures 2a, 2b, 2c, 2d, 2e correspond to Figures 1a, 1b, 1c, 1d, 1e, respectively.

Figure 3 shows an axisymmetric model for the flipped finger-tube, where R_finger is the finger radius, t is the finger-tube thickness, a and d represent the last section of contact, and (r,z) are the axisymmetric coordinates. The contact length L with the finger, the bend radius R of the finger-tube, and contact length $L^{\prime }$ of the “flipped over” part (Fig. 3) are to be determined. The flipped figure tube consists of four parts, with the corresponding profile r = r(z) for their mid planes given in the following:

• (1)Part cd (and beyond), which is a straight line in Fig. 3 (and a cylinder wrapping around the finger in 3D), with $r=R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\left(t/2\right)$ for $0\le z\le L+L^{\prime }$.
• (2)Part bc, which is approximated by a semicircle of radius R (to be determined) in Fig. 3, with ${\left[r-R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}-R-\left(t/2\right)\right]}^2+z^2=R^2$ for $-R\le z\le 0$, or equivalently $r=R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+R+\left(t/2\right)\pm \sqrt{R^2-z^2}$, where ± are for the upper and lower halves, respectively.
• (3)Part ab, which is approximated by a sinusoidal curve with continuous slopes at its ends, $r=R_{\mathit{f}\mathit{i}\mathit{g}\mathit{u}\mathit{r}\mathit{e}}+R+t+\left(R-t/2\right)\cos \left(\pi z/L\right)$ for $0\le z\le L$ (L is to be determined).
• (4)The “straight” part beyond a, which is a straight line in Fig. 3 (and a cylinder in 3D), with $r=R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\left(3t/2\right)$ for $L\le z\le L+L^{\prime }$.

Here the axisymmetric coordinates (r,z), rather than the Gaussian coordinates in differential geometry for a curvilinear surface are used for convenience. The total length of the finger-tube is given by

$$L_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}=L+\pi R+{\displaystyle \underset{0}{\overset{L}{\int }}\sqrt{1+\frac{{\pi }^2}{L^2}{\left(R-\frac{t}{2}\right)}^2{\sin }^2\left(\frac{\pi z}{L}\right)}\hspace{0.17em}dz}+2L^{\prime },$$ (1)

where the integral represents the arc length of part ab, which can be obtained analytically as $\left(2R-t\right)E\left(\zeta \right)/\zeta$, where $E\left(\zeta \right)$ is the complete elliptic integral of second kind,¹⁶ and $\zeta ={\left\{1+\left(L^2/{\pi }^2\right){\left[R-\left(t/2\right)\right]}^{-2}\right\}}^{-1/2}$. Equation 1 gives $L^{\prime }$ in terms of L and R for a given total length L_total.

Figure 3.

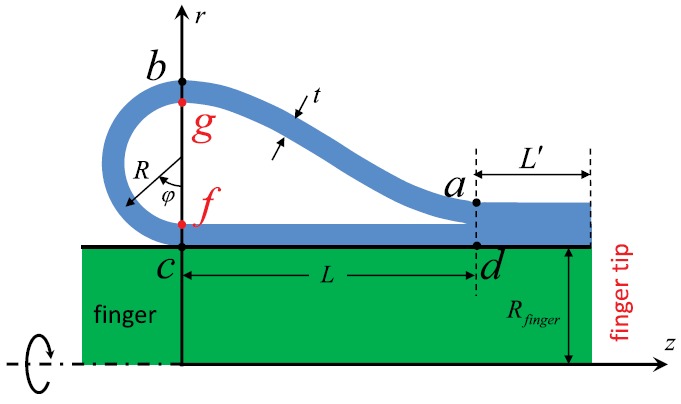
Schematic illustration of the axisymmetric model for the flipped finger-tube.

Curvatures and bending energy

The principal curvature along the meridional direction is ${\kappa }_s=\left(d^{2}r/d{z}^2\right)/{\left[1+{\left(\mathit{d}\mathit{r}/\mathit{d}\mathit{z}\right)}^2\right]}^{3/2}$ at any point [r(z),z] on the surface. The other principal curvature ${\kappa }_{\theta }$ along the circumferential direction is the negative reciprocal of the distance from the point [r(z),z] along its normal to the point of intersection with the axis of symmetry z = 0, and is given by $-{\left[r\sqrt{1+{\left(\mathit{d}\mathit{r}/\mathit{d}\mathit{z}\right)}^2}\right]}^{-1}$. The corresponding initial curvatures in Fig. 2a are ${\kappa }_{s0}=0$ and ${\kappa }_{\theta 0}=\pm {\left[R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\left(t/2\right)\right]}^{-1}$, where + is for part cd and the lower half of part bc, and − is for the upper half of part bc, and part ab and beyond. Here the opposite signs are because points a to b and c to d have the same directions (toward the finger tip) in Fig. 2a, and opposite directions in Fig. 2e (and Fig. 3) due to “flipping over” of the part ab and upper half of part bc. The above profile r = r(z) gives the principal curvatures as

• (1)Part cd (and beyond): ${\kappa }_s=0$ and ${\kappa }_{\theta }=-{\left[R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\left(t/2\right)\right]}^{-1}$.
• (2)Part bc: ${\kappa }_s=\pm R^{-1}$, where + and − are for the lower and upper halves of part bc, respectively, and ${\kappa }_{\theta }=-\sqrt{R^2-z^2}/\left(\mathit{R}\mathit{r}\right)$.
• (3)Part ab: ${\kappa }_s=-\left({\pi }^2/L^2\right)\left[R-\left(t/2\right)\right]\cos \left(\pi z/L\right)/{\left\{1+\hspace{0.17em}\left({\pi }^2/L^2\right){\left[R-\left(t/2\right)\right]}^2{\sin }^2\left(\pi z/L\right)\right\}}^{3/2}$ and ${\kappa }_{\theta }=-{\left\{R_{\mathit{f}\mathit{i}\mathit{g}\mathit{u}\mathit{r}\mathit{e}}+\hspace{0.17em}R+t+\left[R-\left(t/2\right)\right]\cos \left(\pi z/L\right)\right\}}^{-1}{\left\{1+\left({\pi }^2/L^2\right){\left[R-\left(t/2\right)\right]}^2{\sin }^2\left(\pi z/L\right)\right\}}^{-1/2}$.
• (4)The “straight” part beyond a: ${\kappa }_s=0$ and ${\kappa }_{\theta }=-{\left[R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\hspace{0.17em}\left(3t/2\right)\right]}^{-1}$.

Here the curvature in Part bc has opposite signs for the lower and the upper halves because of the use of axisymmetric coordinates (r,z). The Gaussian coordinates would give the same sign for the curvature, but they are inconvenient to describe all four parts of the flipped finger-tube.

The finger-tube is modeled as a thin shell with the Young's modulus E and thickness t. The bending energy density is¹⁷

$$u_b=\frac{D}{2}\left[{\left({\kappa }_s-{\kappa }_{s0}\right)}^2+{\left({\kappa }_{\theta }-{\kappa }_{\theta 0}\right)}^2+2\nu \left({\kappa }_s-{\kappa }_{s0}\right)\left({\kappa }_{\theta }-{\kappa }_{\theta 0}\right)\right],$$ (2)

where $D=E{t}^3/\left[12\left(1-{\nu }^2\right)\right]$ is the bending stiffness and ν is the Poisson's ratio. The bending energy in the shell is the integration of u_b over the area of finger-tube, and is given by

$$\begin{array}{c}{U}_b=2\pi \left(R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\frac{t}{2}\right)\\ *\left[{\displaystyle \underset{0}{\overset{L+L^{\prime }}{\int }}{u}_b^{\left(\mathit{c}\mathit{d}\right)}dz}+{\displaystyle \underset{-R}{\overset{0}{\int }}\left[u_b^{{\left(\mathit{b}\mathit{c}\right)}_{\mathit{l}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}}+u_b^{{\left(\mathit{b}\mathit{c}\right)}_{\mathit{u}\mathit{p}\mathit{p}\mathit{e}\mathit{r}}}\right]\sqrt{1+{\left(\frac{\mathit{d}\mathit{r}}{\mathit{d}\mathit{z}}\right)}^2}dz}+{\displaystyle \underset{0}{\overset{L}{\int }}{u}_b^{\left(\mathit{a}\mathit{b}\right)}\sqrt{1+{\left(\frac{\mathit{d}\mathit{r}}{\mathit{d}\mathit{z}}\right)}^2}dz}+{\displaystyle \underset{L}{\overset{L+L^{\prime }}{\int }}{u}_b^{\left(beyond\hspace{0.17em}a\right)}dz}\right].\end{array}$$ (3)

Membrane strains and membrane energy

The membrane strain in the circumferential direction is related to the ratio of radii by ${\epsilon }_{\theta }=r/\left[R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\left(t/2\right)\right]-1$ at any point [r(z),z] on the surface. For different parts, it is given by

• (1)Part cd (and beyond): ${\epsilon }_{\theta }=0$.
• (2)Part bc: ${\epsilon }_{\theta }=\left(R\pm \sqrt{R^2-z^2}\right)/\left[R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\left(t/2\right)\right]$, where ± are for the upper and lower halves, respectively.
• (3)Part ab: ${\epsilon }_{\theta }=\left[R+\left(t/2\right)+\left(R-t/2\right)\cos \left(\pi z/L\right)\right]/\left[R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\left(t/2\right)\right]$.
• (4)The “straight” part beyond a: ${\epsilon }_{\theta }=t/\left[R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\left(t/2\right)\right]$.

As shown in the Appendix, the membrane strain along the meridional direction is ${\epsilon }_s=-\nu {\epsilon }_{\theta }$.

The membrane energy density is¹⁷

$$u_m=\frac{\mathit{E}\mathit{t}}{2\left(1-{\nu }^2\right)}\left({\epsilon }_s^2+{\epsilon }_{\theta }^2+2\nu {\epsilon }_s{\epsilon }_{\theta }\right).$$ (4)

The membrane energy in the shell is the integration of u_m over the area of finger-tube, and is given by

$$\begin{array}{c}{U}_m=2\pi \left(R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+\frac{t}{2}\right)\\ *\left[{\displaystyle \underset{0}{\overset{L+L^{\prime }}{\int }}{u}_m^{\left(\mathit{c}\mathit{d}\right)}dz}+{\displaystyle \underset{-R}{\overset{0}{\int }}\left[u_m^{{\left(\mathit{b}\mathit{c}\right)}_{\mathit{l}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}}+u_m^{{\left(\mathit{b}\mathit{c}\right)}_{\mathit{u}\mathit{p}\mathit{p}\mathit{e}\mathit{r}}}\right]\sqrt{1+{\left(\frac{\mathit{d}\mathit{r}}{\mathit{d}\mathit{z}}\right)}^2}dz}+{\displaystyle \underset{0}{\overset{L}{\int }}{u}_m^{\left(\mathit{a}\mathit{b}\right)}\sqrt{1+{\left(\frac{\mathit{d}\mathit{r}}{\mathit{d}\mathit{z}}\right)}^2}dz}+{\displaystyle \underset{L}{\overset{L+L^{\prime }}{\int }}{u}_m^{\left(beyond\hspace{0.17em}a\right)}dz}\right].\end{array}$$ (5)

Energy minimization

The total energy U_total, which consists of bending and membrane energy, depends on L and R since $L^{\prime }$ is obtained (in terms of L and R) from Eq. 1 for a fixed total length. They are determined by minimizing the total energy, i.e.,

$$\frac{\partial U_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}}{\partial R}=\frac{\partial U_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}}{\partial L}=0,$$ (6)

which are solved numerically. For an incompressible finger-tube ($\nu =0.5$), R and L, normalized by R_finger, depend only on the normalized thickness t/R_finger, and is independent of the total length L_total for L_total ≫ L, R. They are shown in Fig. 4, and the radius R is well approximated by

$$R=\frac{1}{3}\sqrt{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}t}.$$ (7)

Figure 4.

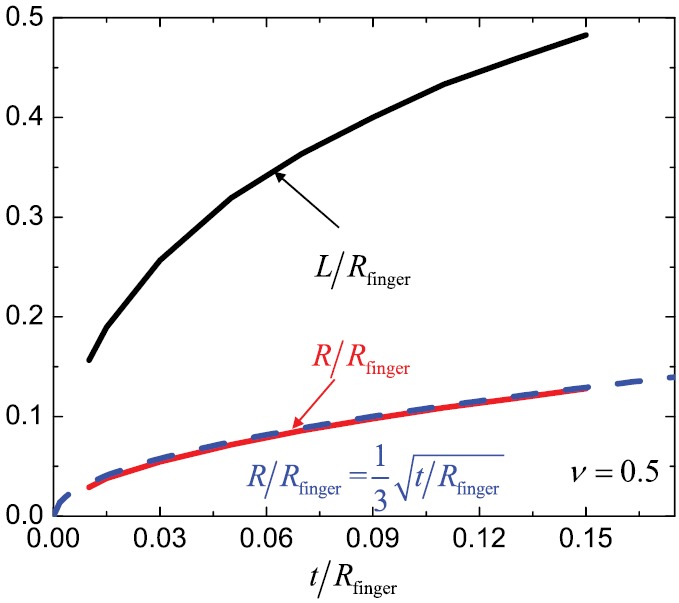
Normalized length L and radius R versus normalized ecoflex thickness.

Figure 5 compares the profile of finger-tube obtained analytically from energy minimization to that obtained by FEM (see the Appendix for details of FEM) for R_finger = 7.5 mm and t = 0.5 mm as in experiments.¹⁵ The good agreement in Fig. 5 provides validation of the analytic model.

Figure 5.

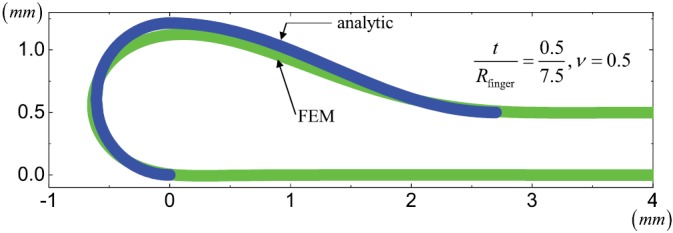
The profiles of finger-tube given by the analytic model and obtained by FEM.

Maximum strain in the finger-tube

Figure 6 gives the strain distribution in the meridional direction on the inner and outer surfaces of the flipped finger-tube obtained by FEM for R_finger = 7.5 mm and t = 0.5 mm. Its maximum tensile and compressive strains are 35.1% and −46.9%, respectively. They agree well with the maximum tensile strain ${\epsilon }_{\max }$ and compressive strain ${\epsilon }_{\min }$ obtained from the analytic model

$${\epsilon }_{\max }=\frac{3}{2}\sqrt{\frac{t}{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}}}\hspace{1em}\text{and}\hspace{1em}{\epsilon }_{\min }=-\frac{3}{2}\sqrt{\frac{t}{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}}}-\frac{2\sqrt{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}t}}{3\left(2R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}+t\right)},$$ (8)

which give the maximum tensile and compressive strains 38.7% and −47.1%, respectively.

Figure 6.

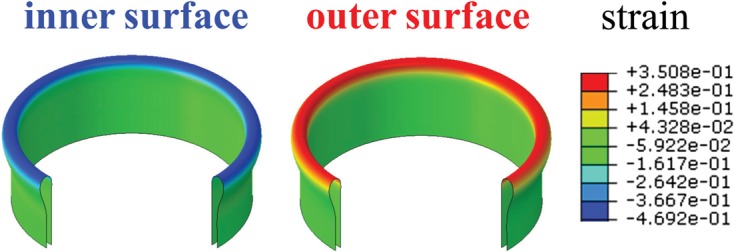
The strain distribution in the meridional direction on the inner and outer surfaces of the flipped finger-tube obtained by FEM.

MAXIMUM STRAIN IN THE ELECTROTACTILE STIMULATOR

The maximum strains in the electrotactile stimulator during the “flipping-over” process are obtained in this section. The bending moments M and membrane forces F are related to the curvatures and membrane strains given in Sec. 2 as¹⁷

$$\left\{\begin{array}{c}{M}_s\\ M_{\theta }\end{array}\right\}=\frac{E{t}^3}{18}\left\{\begin{array}{c}2\left({\kappa }_s-{\kappa }_{s0}\right)+{\kappa }_{\theta }-{\kappa }_{\theta 0}\\ {\kappa }_s-{\kappa }_{s0}+2\left({\kappa }_{\theta }-{\kappa }_{\theta 0}\right)\end{array}\right\}\hspace{0.17em}\text{and}\hspace{0.17em}\left\{\begin{array}{c}{F}_s\\ F_{\theta }\end{array}\right\}=\frac{2Et}{3}\left\{\begin{array}{c}2{\epsilon }_s+{\epsilon }_{\theta }\\ {\epsilon }_s+2{\epsilon }_{\theta }\end{array}\right\},$$ (9)

where the Poisson's ratio for the incompressible finger-tube is $\nu =0.5$. The maximum bending moment and membrane forces are reached in section bg (Fig. 3), and are given by

$$M_{s,\max }=2M_{\theta ,\max }\approx -\frac{E{t}^2}{3}\sqrt{\frac{t}{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}}},\hspace{1em}{F}_{s,\max }\approx 0 \text{and}{F}_{\theta ,\max }\approx \frac{2}{3}Et\sqrt{\frac{t}{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}}}$$ (10)

for $t\ll R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}$ as in the experiment.¹⁵

Figure 7 shows two representative cross sections of the electrotactile stimulator on the finger-tube,¹⁵ which consist of multiple layers of Au, Si, and PI. Let n denote the total number of layers, with i = 1 being the finger-tube at the bottom. The Young's modulus, Poisson's ratio and thickness of the ith layers are E_i, ${\nu }_i$, and t_i, respectively, and E₁ = E, ${\nu }_1=0.5$ and t₁ = t. The coordinate y has its origin at the bottom (Fig. 7). The strains in the electrotactile stimulator can be generally written as

$${\overline{\epsilon }}_s={\overline{\kappa }}_{s}y+{\overline{\epsilon }}_{s0}\hspace{1em}\text{and}\hspace{1em}{\overline{\epsilon }}_{\theta }={\overline{\kappa }}_{\theta }y+{\overline{\epsilon }}_{\theta 0},$$ (11)

where ${\overline{\kappa }}_s$ and ${\overline{\kappa }}_{\theta }$ are curvatures of the electrotactile stimulator, and ${\overline{\epsilon }}_{s0}$ and ${\overline{\epsilon }}_{\theta 0}$ are the strains at the bottom (y = 0). The stresses in the ith layer are given by ${\overline{\sigma }}_s=\left({\overline{\epsilon }}_s+{\nu }_i{\overline{\epsilon }}_{\theta }\right)E_i/\left(1-{\nu }_i^2\right)$ and ${\overline{\sigma }}_{\theta }=\left({\nu }_i{\overline{\epsilon }}_s+{\overline{\epsilon }}_{\theta }\right)E_i/\left(1-{\nu }_i^2\right)$, which give the membrane forces on the electrotactile stimulator as

$$\left\{\begin{array}{c}{F}_{s,\max }\\ F_{\theta ,\max }\end{array}\right\}={\displaystyle \underset{0}{\overset{\sum _{i=1}^n{t}_i}{\int }}\left\{\begin{array}{c}{\overline{\sigma }}_s\\ {\overline{\sigma }}_{\theta }\end{array}\right\}dy}\hspace{0.17em}=\left\{\begin{array}{cc}{K}_{11}& K_{12}\\ K_{12}& K_{11}\end{array}\right\}\left\{\begin{array}{c}{\overline{\epsilon }}_{s0}\\ {\overline{\epsilon }}_{\theta 0}\end{array}\right\}+\left\{\begin{array}{cc}{K}_{13}& K_{14}\\ K_{14}& K_{13}\end{array}\right\}\left\{\begin{array}{c}{\overline{\kappa }}_s\\ {\overline{\kappa }}_{\theta }\end{array}\right\},$$ (12)

where the maximum membrane forces in section bg given in Eq. 10 are used, $K_{11}={\sum }_{i=1}^n{E}_i{t}_i/\left(1-{\nu }_i^2\right)$, $K_{12}={\sum }_{i=1}^n{\nu }_i{E}_i{t}_i/\left(1-{\nu }_i^2\right)$, $K_{13}={\sum }_{i=1}^n{E}_i{t}_i\left[\left({\sum }_{j=1}^i{t}_j\right)-\left(t_i/2\right)\right]/\left(1-{\nu }_i^2\right)$ and $K_{14}={\sum }_{i=1}^n{\nu }_i{E}_i{t}_i\left[\left({\sum }_{j=1}^i{t}_j\right)-\left(t_i/2\right)\right]/\left(1-{\nu }_i^2\right)$. Similarly, the bending moments around the bottom (y = 0) in section bg can be obtained from the stresses by

$$\left\{\begin{array}{c}{M}_{s,\max }+\frac{1}{2}{F}_{s,\max }t\\ M_{\theta ,\max }+\frac{1}{2}{F}_{\theta ,\max }t\end{array}\right\}={\displaystyle \underset{0}{\overset{\sum _{i=1}^n{t}_i}{\int }}\left\{\begin{array}{c}{\overline{\sigma }}_s\\ {\overline{\sigma }}_{\theta }\end{array}\right\}ydy}=\left\{\begin{array}{cc}{K}_{13}& K_{14}\\ K_{14}& K_{13}\end{array}\right\}\left\{\begin{array}{c}{\overline{\epsilon }}_{s0}\\ {\overline{\epsilon }}_{\theta 0}\end{array}\right\}+\left\{\begin{array}{cc}{K}_{33}& K_{34}\\ K_{34}& K_{33}\end{array}\right\}\left\{\begin{array}{c}{\overline{\kappa }}_s\\ {\overline{\kappa }}_{\theta }\end{array}\right\},$$ (13)

where $K_{33}={\sum }_{i=1}^n{E}_i{t}_i\left[{\left({\sum }_{j=1}^i{t}_j\right)}^2-t_i{\sum }_{j=1}^i{t}_j+\left(t_i^2/3\right)\right]/\left(1-{\nu }_i^2\right)$ and $K_{34}={\sum }_{i=1}^n{\nu }_i{E}_i{t}_i\left[{\left({\sum }_{j=1}^i{t}_j\right)}^2-t_i{\sum }_{j=1}^i{t}_j+\left(t_i^2/3\right)\right]/\left(1-{\nu }_i^2\right)$. The solution of ${\overline{\epsilon }}_{s0}$, ${\overline{\epsilon }}_{\theta 0}$, ${\overline{\kappa }}_s$ and ${\overline{\kappa }}_{\theta }$ is obtained from Eqs. 12, 13 as

$$\left\{\begin{array}{c}{\overline{\epsilon }}_{s0}\\ {\overline{\epsilon }}_{\theta 0}\\ {\overline{\kappa }}_s\\ {\overline{\kappa }}_{\theta }\end{array}\right\}=\frac{\mathit{E}\mathit{t}}{6}\sqrt{\frac{t}{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}}}{\left\{\begin{array}{cccc}{K}_{11}& K_{12}& K_{13}& K_{14}\\ K_{12}& K_{11}& K_{14}& K_{13}\\ K_{13}& K_{14}& K_{33}& K_{34}\\ K_{14}& K_{13}& K_{34}& K_{33}\end{array}\right\}}^{-1}\left\{\begin{array}{c}0\\ 4\\ -2t\\ t\end{array}\right\}.$$ (14)

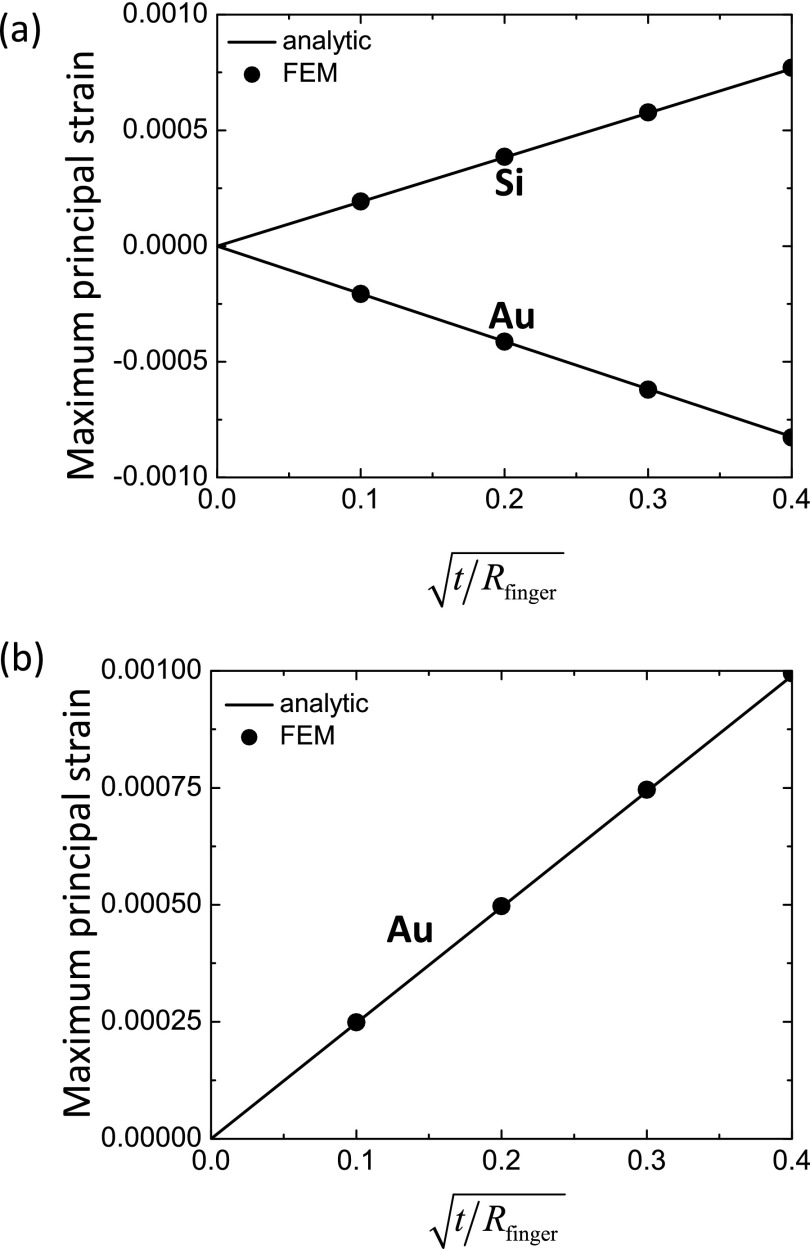
The maximum strains in the electrotactile stimulator can then be obtained from Eq. 11, and they are linearly proportional to $1/\sqrt{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}}$. Figures 8a, 8b show the maximum principal strain in Au and Si versus $\sqrt{t/R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}}$ for the two representative cross sections of the electrotactile stimulator in Fig. 7. The Young's moduli and Poisson's ratios are 78 GPa and 0.44 for Au, 168 GPa and 0.28 for Si, 2.5 GPa and 0.34 for PI, and 60 KPa and 0.5 for Ecoflex, respectively. The numerical results obtained by FEM are also shown, and they agree well with the analytic solution in Eq. 14.

Figure 7.

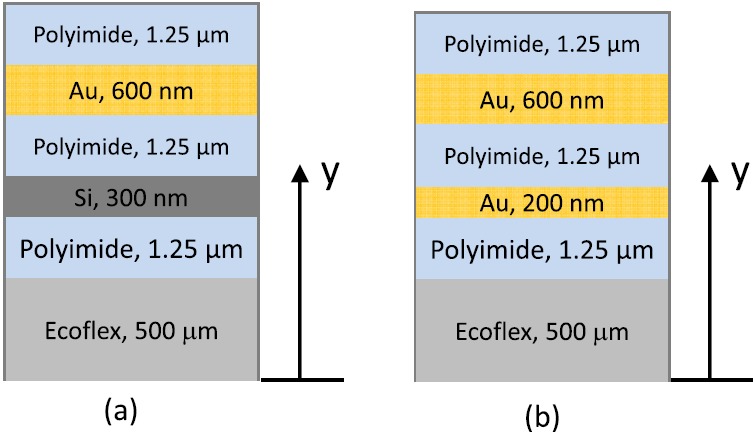
Two representative cross sections of the electrotactile stimulator on the finger-tube.

Figure 8.

The maximum principal strains in Au and Si in the electrotactile stimulator versus the normalized finger-tube radius.

CONCLUDING REMARKS

Due to their extreme deformability, soft materials, such as the classes of silicones described here, are ideal candidates for the platforms and supporting matrices of devices such as finger-tip electronics (e.g., tactile sensors and electrotactile stimulators). The process fabrication, and sometimes use, involves very large levels of mechanical deformation. The analytic models presented here give maximum strains in the finger-tube as well as in the electrotactile stimulators, as representative of wide ranging component devices that can be integrated into these systems. The maximum strains are inversely proportional to the square root of finger-tube radius, i.e., $\propto 1/\sqrt{R_{\mathit{f}\mathit{i}\mathit{n}\mathit{g}\mathit{e}\mathit{r}}}$. The analytic model, validated by FEM, can be used to guide optimal design of fingertip electronics with tactile sensors and electrotactile stimulators and other soft, three-dimensional devices.

APPENDIX: The membrane strain

The finite element method is used simulate the “flipping-over” process of the finger-tube. The finger-tube is modeled as an elastic axisymmetric shell by the element SAX1 (2-node linear axisymmetric thin or thick shell) in the finite element program ABAQUS,¹⁸ interacting with a rigid finger. The finger-tube is flipped over twice, as indicated in Figs. 1a, 1b, 1c and Figs. 1c, 1d, 1e, respectively. In each “flipping-over” process one end of the finger-tube is fixed, whereas the other end is pulled outward and toward the fixed end. The prescribed displacements at the ends are completely relaxed after the first “flipping over” process illustrated in Figs. 1a, 1b, 1c. The numerical simulations account for contact between the finger-tube and finger, and self-contact between the flipped finger-tube and that on the finger.

Numerical results show that the membrane force F_s along the meridional direction is much smaller than the membrane force $F_{\theta }$ along the circumferential direction. Therefore, the approximation $F_s\approx 0$, together with the constitutive relation $F_s=\left(2Et/3\right)\left(2{\epsilon }_s+{\epsilon }_{\theta }\right)$ in Eq. 9, give ${\epsilon }_s=-{\epsilon }_{\theta }/2$.