Artificial helical microswimmers with mastigoneme-inspired appendages

Abstract

A smooth flagellum moves in the opposite direction of the propagation of flagellar waves. Conversely, a flagellum covered with appendages perpendicular to the main flagellum, called mastigonemes, moves in the same direction as the propagation of flagellar waves. Inspired by mastigoneme structures in nature, we report the reversal of the swimming direction of magnetically actuated artificial helical microswimmers. The main flagella and mastigonemes of these microswimmers are fabricated together using three-dimensional lithography and electron beam evaporation of ferromagnetic thin films. The results show that the swimming speed and direction can be controlled by changing the length/spacing ratio of the mastigonemes.

Inertial forces become negligible at low Reynolds numbers which has required microorganisms to evolve unique swimming strategies that use viscous forces for propulsion.^{1, 2} Under this constraint, microorganisms have developed slender filaments, such as flagella and cilia, for propulsion in fluids and for the displacement of fluids around them.³ Taking inspiration from the swimming styles of natural microorganisms, magnetically actuated artificial micro- and nanoscopic swimmers have been recently proposed.^{4, 5, 6, 7, 8} These micro- and nanoscopic artificial swimmers can be wirelessly manipulated in liquid environments and have potential for biomedical applications such as targeted drug delivery and localized manipulation in microfluidic devices.^{9, 10, 11}

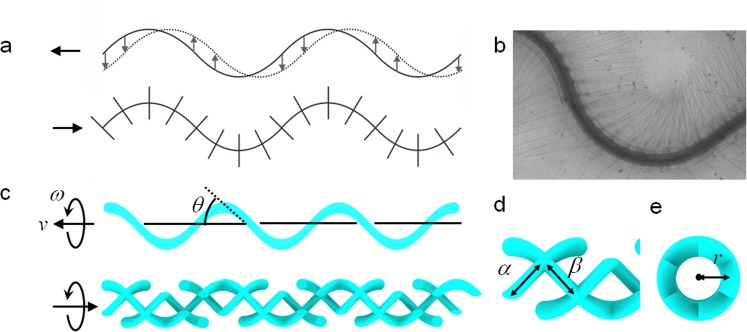
At low Reynolds numbers, anisotropic viscous drag on flagella is key to locomotion. The viscous drag coefficient parallel to the flagella ξ_∥ is smaller than the viscous drag coefficient perpendicular to the flagella ξ_⊥ (typically, ξ_⊥ ≈ 2ξ_∥).¹² Therefore, undulatory motion of a flagellum creates a thrust force in the direction of the flagellar wave. Thus, it swims in the opposite direction of the flagellar wave, as illustrated in Fig. 1a. In nature, the bacteria Ochromonas malhamensis possess flagella bearing thin rigid appendages called mastigonemes that protrude perpendicular to the main flagella (Fig. 1b).^{13, 14, 15, 16, 17} As the main flagella beat and propagate sinusoidal waves, mastigonemes follow the motion of the main flagellar filament while sustaining their orthogonal orientation to the main filament, as shown schematically in Fig. 1a. In contrast to smooth flagella, flagella with mastigonemes can locomote in the same direction as the flagellar wave when the total thrust force is dominated by the mastigonemes.

Figure 1.

(a) Schematic illustrations of a smooth flagellum and a flagellum with mastigonemes. The smooth flagellum propels in the direction opposite to the flagellar wave (left in the figure). The flagella with mastigonemes propels in the same direction as the flagellar wave (right in the figure). The dotted line on the smooth flagellum shows the movement of the wave propagation. (b) Mastigonemes of Ochromonas. (© 1971 Rockefeller University Press. Originally published in J. Cell Biology 50, 362–384 (1971).) (c) Schematic illustrations of a smooth artificial helical microswimmer and a microswimmer with mastigonemes. The smooth helical microswimmer moves in a right-handed sense (to the left in the figure). The helical microswimmer with mastigonemes moves in a left-handed sense (to the right in the figure). The helix angle is defined as θ. (d) Detailed illustration of the mastigonemes. Length and spacing of mastigonemes are denoted by α and β, respectively. (e) Frontal view of a helical microswimmer with mastigonemes. Mastigonemes have the same curvature (1/r) as the main flagellum along the helical axis.

In this study, we demonstrate tuning and direction reversal of the swimming velocity of artificial helical microswimmers with orthogonal appendages that are inspired by mastigonemes observed in nature. The fabrication process is based on two steps: printing core structures using three-dimensional lithography and subsequent ferromagnetic thin film coating using electron beam evaporation. The swimming velocity is controlled by the length/spacing ratio of the mastigonemes. Above the critical length/spacing ratio, the swimming direction is reversed. We experimentally and theoretically studied the critical length/spacing ratio where the reversal of motion occurs.

Artificial helical microswimmers with and without mastigonemes are schematically illustrated in Fig. 1c. A swimmer consists of a stem structure from negative-tone photoresists and a ferromagnetic thin film coating on the surface. All mastigoneme structures are designed to protrude perpendicularly from the main helical flagella. Rotational motion is imparted by magnetic torque induced along the helical axis by a low-strength rotating magnetic field. The rotating field is applied by an externally placed three-axis Helmholtz coil setup. Rotating helical microswimmers without mastigonemes swim forward, the same direction as a corkscrew would penetrate into a cork, as shown in Fig. 1c. However, in a rotating field of the same strength and frequency, helical microswimmers with mastigoneme structures locomote in the opposite direction to that of the smooth helical microswimmers without mastigonemes because of the thrust-reversal effect. The speed and direction of motion depend on the length and spacing of the mastigonemes. The main flagella are defined by several geometrical parameters including the radius r, helix angle θ, number of turns n, and filament thickness 2a. The mastigonemes are rigid and orthogonal to the main flagella, with a length and spacing denoted by α and β, respectively, as depicted in Fig. 1d. Figure 1e shows the frontal view of a helical microswimmer with mastigonemes. The curvature of the mastigoneme around the helical axis is the same as that of the main helical flagella (1/r).

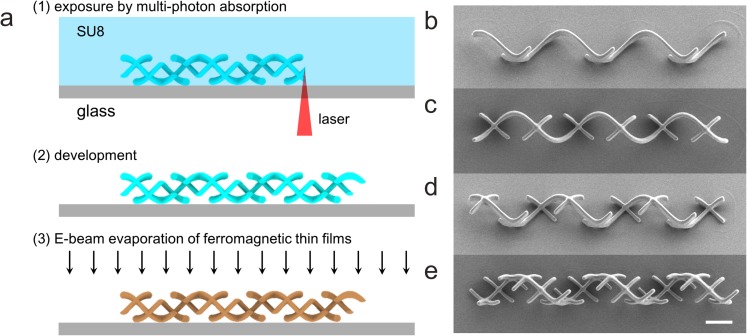
The helical microswimmers with mastigonemes are printed monolithically in a negative-tone photoresist (SU-8 50, MicroChem) using three-dimensional lithography (Photonic Professional, Nanoscribe GmbH), followed by electron beam evaporation of ferromagnetic thin films (Ni 100 nm, and Ti 5 nm), as shown in Fig. 2a.⁸ The scanning electron microscope (SEM) images of as-fabricated structures are shown in Figs. 2b, 2c, 2d, 2e. We designed the length/spacing ratios of mastigonemes of α/β = (a) 1/6, (b) 1/3, (c) 1/2, and (d) 1, at the constant α = L/6, where L is the filament length of a one-turn helix (i.e., L = 2πr/cos θ). Other design parameters are selected as r = 5 μm, θ = 45°, n = 3, and a = 0.7 μm in order to avoid connection of mastigonemes from adjacent turns and to maintain the slenderness of the mastigonemes.

Figure 2.

Fabrication of artificial helical microswimmers with mastigonemes. (a) Fabrication procedure. (b)–(e) SEM images of artificial helical microswimmers with mastigonemes. The length/spacing ratios of the mastigonemes are α/β = (b) 1/6, (c) 1/3, (d) 1/2, and (e) 1. The scale bar is 10 μm.

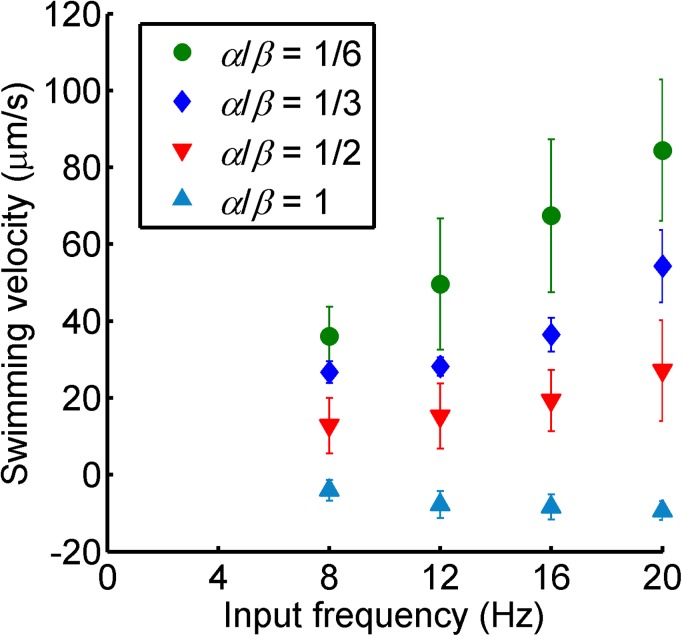
After the fabrication process, the structures are released in a tank filled with deionized water using a tungsten probe. The tank is installed at the center of the three-axis Helmholtz coil setup. The currents through the coils control the rotating fields, i.e., field strength, rotational frequency, and the two angles that define the rotational axis. The helical microswimmers subjected to the rotating field rotate synchronously with the field and produce either forward or backward translational motion. The strength of field is adjusted from 2 to 7 mT to avoid tumbling and asynchronous motions.⁸ The average translational swimming velocity is calculated by measuring the displacement of the swimmers along the rotational axis per unit time. The swimming velocity of artificial swimmers with mastigoneme structures with different length/spacing ratios as a function of input field frequency is characterized in Fig. 3. The swimming speed increases linearly with the input field frequency. The velocity decreases with the length/spacing ratio (α/β), and the velocity slope becomes negative at α/β = 1. This result shows that the mastigoneme structures generate a propulsive force opposite to the force generated by the main helical filament. Therefore, an increase in the length/spacing ratio (α/β) (in this experiment, an increase in the number of mastigoneme structures per turn) results in a decrease in the translational velocity, and eventually, in a reversal in the propulsive direction.

Figure 3.

Average translational velocity plot for different length/spacing ratios (α / β) of mastigonemes with respect to the input field frequency. The error bars show the standard deviations for three independent experiments.

The swimming velocity of the helical microswimmers with the mastigoneme structures can be estimated using the two-degree-of-freedom (2-DOF) propulsion matrix. The relation of velocity v, angular velocity ω, external force F, and external toque T, is given by the following symmetric propulsion matrix:²

$$\left[\begin{array}{c}F\\ T\end{array}\right]=\left[\begin{array}{cc}A& B\\ B& C\end{array}\right]\left[\begin{array}{c}v\\ \varpi \end{array}\right].$$ (1)

The propulsion matrix can be decomposed into two parts, the main flagella (subscript 1) and the mastigonemes (subscript 2) as follows:

$$A=A_1+A_2,\hspace{1em}B=B_1+B_2,\hspace{1em}\text{and}\hspace{1em}C=C_1+C_2.$$ (2)

The components of the propulsion matrix for the main flagella can be computed by:^{18, 19}

$$A_1=2\pi nr\left(\frac{{\xi }_{\left|\right|}{\cos }^2\hspace{0.17em}\theta +{\xi }_{\perp }{\sin }^2\hspace{0.17em}\theta }{\sin \hspace{0.17em}\theta }\right),$$ (3a)

$$B_1=2\pi n{r}^2\left({\xi }_{\left|\right|}-{\xi }_{\perp }\right)\cos \hspace{0.17em}\theta ,$$ (3b)

$$C_1=2\pi n{r}^3\left(\frac{{\xi }_{\perp }{\cos }^2\hspace{0.17em}\theta +{\xi }_{\left|\right|}{\sin }^2\hspace{0.17em}\theta }{\sin \hspace{0.17em}\theta }\right).$$ (3c)

The components for the mastigoneme structures are calculated as the main filament by reversing the handedness and replacing the helix angle θ with π/2 − θ.

$$A_2=2\pi nr\left(\frac{{\xi }_{\left|\right|}{\cos }^2\hspace{0.17em}\left(\pi /2-\theta \right)+{\xi }_{\perp }{\sin }^2\hspace{0.17em}\left(\pi /2-\theta \right)}{\sin \left(\pi /2-\theta \right)}\right)\left(\frac{2\alpha }{\beta }\right)\cot \hspace{0.17em}\theta ,$$ (4a)

$$B_2=-2\pi n{r}^2\left({\xi }_{\left|\right|}-{\xi }_{\perp }\right)\cos \left(\pi /2-\theta \right)\left(\frac{2\alpha }{\beta }\right)\cot \hspace{0.17em}\theta ,$$ (4b)

$$C_2=2\pi n{r}^3\left(\frac{{\xi }_{\perp }{\cos }^2\hspace{0.17em}\left(\pi /2-\theta \right)+{\xi }_{\left|\right|}{\sin }^2\hspace{0.17em}\left(\pi /2-\theta \right)}{\sin \left(\pi /2-\theta \right)}\right)\left(\frac{2\alpha }{\beta }\right)\cot \hspace{0.17em}\theta .$$ (4c)

The velocity of a microswimmer with mastigonemes is given by superimposing the propulsion matrices of its main flagellum and mastigonemes. From Eqs. 1, 2, the velocity is calculated without the application of any external force (F = 0) as follows:

$$v=-\frac{B_1+B_2}{A_1+A_2}\omega .$$ (5)

Thus, the velocity is computed by substituting Eqs. 3, 4 to Eq. 5. The same result can be obtained by using the apparent drag coefficients of flagella with mastigonemes: $C_{\left|\right|}={\xi }_{\left|\right|}+\left(2\alpha /\beta \right){\xi }_{\perp }$ and $C_{\perp }={\xi }_{\perp }+\left(2\alpha /\beta \right){\xi }_{\left|\right|}$.

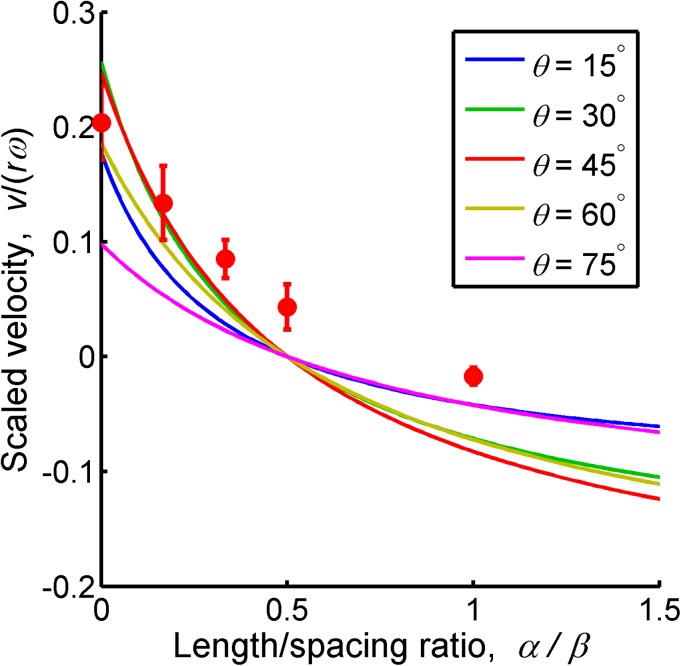
The theoretical swimming velocity in Eq. 5 is plotted with respect to the length/spacing ratio of mastigonemes (α/β) in Fig. 4. As the length/spacing ratio increases, the swimming velocity decreases and reverses, becoming negative. At all helix angles, the swimming direction is reversed at the length/spacing ratio α/β = 0.5. Figure 4 also includes experimental results for θ = 45°. The reversal effect in the experiment is smaller than the theoretical model, and, therefore, the length/spacing ratio (α/β) required for reversing the motion becomes higher. The gaps between the theoretical and experimental results increase as the length/spacing ratio α/β increases because of the unmodeled end effect and hydrodynamic interaction of the mastigonemes. As the distance between the mastigonemes decreases, the hydrodynamic interaction between each appendage becomes more significant.²⁰ In this study, we used a simple analytical model in order to capture the reversal of the swimming direction (or thrust). Detailed modeling and optimization will be required for more effective designs.²¹

Figure 4.

Scaled swimming velocity for different helix angles θ as a function of length/spacing ratio of mastigonemes (α/β). The solid lines show the theoretical simulation at θ = 15°, 30°, 45°, 60°, and 75°, and the dots show the experimental results at θ = 45°.

In conclusion, we have described thrust reversal of artificial helical microswimmers with mastigoneme-inspired appendages. The artificial helical microswimmers with mastigonemes are fabricated using three-dimensional lithography and electron beam deposition of ferromagnetic thin films. The swimming velocity is precisely tuned by changing the ratio between the length and the interval of the appendages. The design described is rigid. However, if swimmers can fold and unfold their mastigoneme structures, their swimming direction and speed can be regulated using an external stimulus or external signals. The proposed design of artificial helical nano- and microswimmers with velocity tuning will aid in the fabrication of nano- and microscopic agents that exhibit intelligent behavior in vivo and in vitro.