Abstract
Objective
A review of substance use clinical trials indicates that sub-optimal methods are the most commonly used procedures to deal with longitudinal missing information.
Methods
Listwise deletion (i.e., using complete cases only), positive urine analysis (UA) imputation, and multiple imputation (MI) were used to evaluate the effect of baseline substance use and buprenorphine/naloxone tapering schedule (7 or 28 days) on the probability of a positive UA (UA+) across the 4-week treatment period.
Results
The listwise deletion generalized estimating equations (GEE) model demonstrated that those in the 28-day taper group were less likely to submit a UA+ for opioids during the treatment period (odds ratios (OR) = 0.57, 95% confidence interval (CI): 0.39–0.83), as did the positive UA imputation model (OR = 0.43, CI: 0.34–0.55). The MI model also demonstrated a similar effect of taper group (OR = 0.57, CI: 0.42–0.77), but the effect size was more similar to that of the listwise deletion model.
Conclusions
Future researchers may find utilization of the MI procedure in conjunction with the common method of GEE analysis as a helpful analytic approach when the missing at random assumption is justifiable.
Keywords: substance use disorder treatment, psychopharmacology clinical trials, generalized estimating equations, longitudinal missing data, multiple imputation, positive urine analysis imputation
INTRODUCTION
Substance use treatment research is often characterized by having a non-trivial amount of missing data, especially in prospective randomized clinical trials (e.g., Graham et al., 1994; Wood et al., 2004; Yang and Shoptaw, 2005; Hedden et al., 2008). A review of substance use clinical trials indicates that listwise deletion and single imputation are the most commonly used procedures to deal with missing information (Wood et al., 2004; Arndt, 2009). Both listwise deletion and many imputation procedures, including “positive urine analysis (UA) imputation” (i.e., assuming that a missing value counts as evidence that the patient is using the targeted substance(s)) have been shown to produce significant bias in the estimation of predictors and their association with the primary outcomes (Nich and Carroll, 2002; Mallinckrodt et al., 2003; Cook et al., 2004; Hedeker et al., 2007). Nevertheless, these methods remain common in the analysis of substance use treatment clinical trials (Nich and Carroll, 2002; Yang and Shoptaw, 2005).
Researchers should and often do utilize multiple methods to reduce missing data in psychopharmacology substance use treatment clinical trials. However, the nature of substance use treatment research is such that a considerable amount of missing information is very common, particularly in longitudinal clinical trials. When evaluating various methods of missing data treatment, psychopharmacology clinical trial researchers should keep three primary goals in mind (Acock, 2012; Enders, 2010; McPherson et al., 2012): (i) maximize all variables used during the analysis, (ii) minimize bias during the estimation of all model parameters, and (iii) minimize bias during the estimation of standard errors to the best of the research team's ability by correctly reflecting the amount of uncertainty associated with each parameter estimate. Given that the level of missing information is typically high, and the nature of missing data in psychopharmacological substance use clinical trials is complex, optimal missing data methodologies need to be used and appropriately adapted for each unique missing data situation (McPherson et al., 2012). This is a critical step for any analysis of psychopharmacology clinical trial data in order to ensure, to the best of the research team's ability, that there is as little bias as possible contained in the reported analyses (e.g., Graham et al. 1994; Hedden et al., 2008; Arndt, 2009; Enders, 2010).
Treatment of missing data in psychopharmacology substance use disorder clinical trials
A commonly used missing data method in longitudinal clinical trials is listwise deletion (i.e., complete case analysis), which deletes patients from the analysis if they have missing data on any of the variables used in the analysis. This method assumes the data are missing completely at random (MCAR), which indicates that the data are missing because of a completely random process that cannot be explained by any variable within or outside of the data available. In the context of generalized estimating equations (GEE), patients are typically deleted using this procedure, but given that this is a longitudinal method, a patient is part of the analysis if they have two or more observations on the primary outcome. This method can cause bias and significantly reduce the level of statistical power in an analysis (Graham, 2009; Enders, 2010). This method of handling missing values is not recommended for nearly every situation (Rubin, 1987; Schafer and Graham, 2002; Molenberghs and Kenward, 2007; van Buuren, 2012) and likely all of the missing data situations faced in psychopharmacology clinical trials.
Common imputation methods, or in some instances referred to as “substitution” methods, are another very commonly used group of methods and encompass a set of different procedures (e.g., fill in the missing value with an earlier observed value; fill in the missing value UA positive score). One of these methods is known as mean imputation, wherein the mean for a given variable is used to fill in all of the missing values for a given variable. Another imputation method known as last observation carried forward (LOCF) is used commonly in longitudinal studies. This method uses the last observed data point for a patient to fill in all subsequent missing values of the outcome. A related method known as baseline observation carried forward (BOCF) uses the patient's baseline value to fill in all of the individual's missing values in a longitudinal study. Unfortunately, mean imputation, BOCF, and LOCF all suffer from producing either biased parameter estimates (e.g., odds ratios (OR) and regression weights), biased standard errors, unrealistic assumptions about the underlying mechanism of missing data (i.e., MCAR), or some combination of all three of these problems (Rubin, 1987; Schafer and Graham, 2002; Molenberghs and Kenward, 2007; van Buuren, 2012).
Regression imputation is another type of imputation methodology that fills in the missing values. This approach does so by first using the dataset (which is incomplete due to missing values) to construct a set of regression equations to predict each of the variables that contains missing values. These regression equations are then used to produce regression-generated (i.e., predicted) individual values, which are then used to fill in the missing values. Although this is an intuitive approach that has some similarities with the far superior method of multiple imputation (MI) discussed later, it suffers from an overestimation of variable correlation, inflated R2 values, and attenuated variances and covariances (Enders, 2010; van Buuren, 2012). Stochastic regression imputation is very similar to regression imputation, except that it takes the additional step of augmenting each one of the predicted values with a normally distributed error term in an effort to restore some of the lost variability (Rubin 1987; Enders, 2010; van Buuren, 2012). Indeed, this method does produce unbiased parameter estimates, but it still produces inappropriately small standard errors, which can lead to making a type I error (i.e., detection of a statistically significant treatment effect when in fact none exists; Rubin 1987; Enders, 2010; van Buuren, 2012).
There is another method that involves imputation, but this method is relatively unique for the research domain of substance use. We refer to the filling in of missing values with positive UA (UA+) values in longitudinal substance use clinical trials as positive UA imputation (McPherson et al., 2012). When using this method, the patient who fails to show up for a scheduled UA sample receives a positive UA. Thus, a missing UA value in a dataset becomes equal to a missing UA value. Although this positive UA imputation procedure and other common methods such as the LOCF procedure (i.e., another imputation procedure) have previously been considered “conservative approaches” (Hedeker et al., 2007; Enders, 2010; Smolkowski et al., 2010) to the handling of missing values in substance use disorder treatment research, these methods can produce biased treatment estimates and inappropriately small standard errors (Cook et al., 2004; Shao and Zhang, 2004; Hedden et al., 2008; Arndt, 2009). This can increase the chances of making a type I error (McPherson et al., 2012).
Multiple imputation is a potential alternative for handling missing data in longitudinal, psychopharmacology, and substance use treatment research. Although there are similarities between this methodology and the (stochastic) regression imputation methods noted earlier, these are not the same method and will likely produce markedly different results, particularly the standard errors, when applied to the same dataset. Later, we discuss the MI approach in detail, but first, we detail the different assumptions made with regard to one's missing data.
Missing data mechanisms and recommended treatment strategies
Multiple imputation is currently considered a modern approach to the handling of missing data (Enders, 2010; Graham, 2009; Schafer and Graham, 2002). This procedure assumes that the cause of missing data (i.e., the mechanism of missingness) is missing at random (MAR). If the assumption of MAR is made, this indicates that variables within the dataset can be used to account for the missing information, and when used during the analysis process, these will sufficiently account for the inherent uncertainty that comes with missing information (see Enders, 2010; McPherson et al., 2012, for a complete review of this method and mechanism), and the data are multivariate normal. The mechanism of MCAR is a special case of MAR with the primary difference being that the data are missing for a purely haphazard reason and was not the cause of any variable within or outside the dataset (Enders, 2010; Schafer and Graham, 2002). Both of these mechanisms are in contrast to when the data are assumed to be missing not at random (MNAR). This is an instance where the missing values are a function of a variable not contained in the obtained dataset, or what is more likely in clinical trials, the cause of missing data is due to the outcome itself. An example of such a situation would be individuals who choose not to report their level of depression are those who were the most depressed in a sample. Although a full explication that compares these three mechanisms is outside the scope of this paper, it is worth noting that it has been demonstrated that assumptions required for conducting MNAR analyses are just as, if not more, difficult to justify for one's analysis (see Enders, 2010, for a complete discussion of MNAR assumptions and modeling strategies).
Multiple imputation is an approach rooted in Bayesian statistics, which uses regression to predict the incomplete variables with the complete variables (see McPherson et al., 2012, for a similar explanation of the MI procedure, or Enders, 2010, for a more in-depth description). This initial phase of MI should include “auxiliary variables” as predictors in the initial regression equation (i.e., first regression equation used for imputation) in order to make the accuracy of the imputed values go up in each subsequently imputed data set (Collins et al., 2001; Graham, 2009; McPherson et al., 2012). Auxiliary variables are covariates that are potentially correlated with the missingness or are correlated with one or more of the analysis variables. Although auxiliary variables do not need to be predictors in the regression model, these variables should be correlates of the missing data mechanism (e.g., MAR) or correlates of other analysis variables responsible for the missingness. The process of including auxiliary variables will assist with refining the estimation process of missing values while also making the MAR assumption more tenable (Collins et al., 2001; Graham, 2009; Enders, 2010; McPherson et al., 2012). A strong set of auxiliary variables is usually made up of a relatively small number of variables that will ideally serve both of the following functions (Acock, 2012): (i) predict what the missing value would have been if it were observed and (ii) predict the propensity for producing a missing value. Race and gender have been demonstrated to be common correlates of missing observations (Collins et al., 2001), and their inclusion as auxiliary variables by themselves can assist greatly with justifying the MAR assumption.
These researcher-specified regression equations are carried out iteratively in order to produce multiple, newly created, complete datasets with all of the missing values filled in. The next phase of MI involves analyzing multiple, newly generated datasets, and the last phase combines the model estimates created for each dataset into one set of estimates for reporting (McPherson et al., 2012; see Enders, 2010, for a full review of the MI technical details). The MI procedure has been shown to perform exceptionally well relative to other methods of handling missing values (except for maximum likelihood (ML) estimation, e.g., see Graham, 2009, and Enders, 2010, for a detailed review of this alternative methodology) when MAR is a tenable assumption.
The only other method that is recommended by missing data experts under MAR conditions is full information ML (FIML; Schafer and Graham, 2002; Graham, 2009; Enders, 2010). Simply put, FIML is ML that uses all available information with a slight alteration to the general function wherein each individual's log likelihood contribution is based only on the information they are able to provide. This method is not a multi-step procedure like MI (e.g., no imputation of missing data), and it produces very similar results as MI assuming the models have been specified in an identical fashion (Little and Rubin, 2002; Graham, 2009; and Enders, 2010). Although FIML is available in multiple software packages (e.g., Mplus, Lisrel, Sas, and Stata) when estimating latent growth or multilevel models, it is not currently available for use with GEE procedures (Molenberghs and Kenward, 2007) in any statistical software package that the authors are aware of.
National Institute on Drug Abuse Clinical Trials Network dataset 0003
The rest of this paper is focused on demonstrating and comparing the use of multiple missing data techniques (i.e., listwise deletion, positive UA imputation, and MI procedures) for the treatment of longitudinal missing information in conjunction with GEE using the National Drug Abuse Treatment Clinical Trials Network dataset 0003 (Ling et al., 2009). This analysis served three objectives. First, the primary objective was to compare the outcomes from two common missing data handling procedures with the outcome from the MI procedure in the context of GEE. Given the prevalence of listwise deletion and positive UA imputation being used in substance use disorder psycho-pharmacology clinical trials, these are the approaches to which we compared MI later. A secondary objective was to investigate potential baseline characteristics that were predictive of longitudinal opioid use in a buprenorphine/naloxone randomized controlled trial comparing two different buprenorphine/naloxone tapering conditions. Last, Ling et al. (2009) highlighted that the method of missing data treatment in this clinical trial was a limitation of the study. Thus, another secondary objective was to build on the work of Ling et al. (2009) and that of our previous work on missing data treatment for substance use randomized clinical trials (McPherson et al., 2012) in an attempt to help address this limitation, but in a revised analysis of the primary outcome of opioid use during the entire 4-week treatment period. We have previously demonstrated that the treatment of missing information can have a meaningful impact on the interpretation of treatment (McPherson et al., 2012). However, a similar, comparative analysis has not been conducted on the primary longitudinal outcome of opioid use during the 4-week treatment period.
METHODS
Participants and procedures
A similar description of the sample, trial design, and others used for the current investigation has been reported both in the primary paper for this trial (Ling et al., 2009) and in our previous missing data work (McPherson et al., 2012).
Participants for this investigation are from National Drug Abuse Treatment Clinical Trials Network number 0003, a publicly available dataset (http://www/ctndatashare.org/). This investigation was a randomized, open-label, parallel-group study design where the procedures for the two arms of the trial being identical until the beginning of two taper periods. Eleven sites in 10 different US cities were used for the trial. Participants were a sample of opioid-dependent individuals. Nine hundred ninety individuals agreed to participate in the study with 894 being eligible and 748 eventually receiving buprenorphine/naloxone. However, 232 individuals were terminated from the trial for various reasons during the induction and stabilization phases. This resulted in a final intention-to-treat (ITT) sample of 516 participants who were potentially available for data collection at the end of the 7- or 28-day taper (Ling et al., 2009; McPherson et al., 2012).
After completing the baseline assessments, the participants were stabilized on buprenorphine/naloxone across a 4-week stabilization period. After this stabilization phase, patients were stratified across their respective maintenance dose of buprenorphine/naloxone and then randomized to the 7- or 28-day taper groups. These two groups represent 7- and 28-day stepwise decreases in the amount of administered buprenorphine/naloxone. The primary scientific question was whether it is more effective to taper opioid-dependent patients quickly (i.e., across 7 days) or more slowly (i.e., 28 days). As previously reported, we found no statistical difference between the taper groups on age, gender, ethnicity, drug use, life-time drug use, past 30 days’ drug use, withdrawal symptoms (self-reported or clinically assessed), count of concomitant medications taken during withdrawal symptoms, or opioid use during stabilization (Ling et al., 2009; McPherson et al., 2012). In addition, there were no statistically significant differences in demographics or drug use characteristics between those who dropped out and those who completed treatment (Ling et al., 2009; McPherson et al., 2012).
The primary outcome in the Ling et al. (2009) study, and in the McPherson et al. (2012) investigation, was whether there was a significant difference between the 7- and 28-day taper groups for the percentage of opioid-free urine specimens at the completion of the taper. Of the sample of 516 participants, 28% (i.e., 144 participants) were not available for urine data collection at the completion of the taper. As noted earlier, these missing values were assigned a positive UA score in the Ling et al. (2009) report. There were no missing values on any other variables, except for previous UAs collected, which were used as auxiliary variables in the MI analysis. The data used for this set of analyses included the same participants (n = 516). In our longitudinal GEE analysis, there was a total of 44.6% missing urine samples across the 4-week treatment period.
Analytic strategy
Stata 12.0 (College Station, TX) was used to conduct three separate robust logistic GEE analyses. GEE represents a somewhat similar analytic strategy as a repeated measures analysis of variance, but within the regression framework. The primary difference relevant to the current set of analyses and the reason for its use in the current investigation is that GEE can be employed for outcomes that are distributed as binary, ordinal, nominal, Poisson, and multiple other distribution types (Zeger and Liang, 1992). In addition, the model parameters are estimated using a variant of maximum likelihood (see Twisk, 2004, for a full review).
Each logistic GEE analysis regressed the binary UA score (0 = negative for opioids, 1 = positive for opioids) across the 4-week treatment period on taper condition (7 versus 28 days), sex, age, race, and multiple baseline substances (measure via UAs) including opioids, cocaine, amphetamines, and marijuana. However, amphetamines and marijuana were not significant predictors across any of the three models estimated and as a result were dropped from further consideration.
The MI estimation included several auxiliary variables (i.e., weeks 1 through 4 of opioid UAs during the stabilization period) in the initial MI phase. These covariates were not of substantive interest for our research question but were used to help demonstrate their potential use and to assist with increasing the likelihood of MAR being a tenable assumption. We included gender and race to replicate analyses conducted by McPherson et al. (2012) and Ling et al. (2009). However, these were also included to help justify the assumption of MAR given previous evidence, suggesting that their inclusion would increase the justification of making the MAR assumption. It is important to note that whereas GEE uses a variant of ML to obtain parameter estimates and standard errors when the outcome is binary (i.e., logistic GEE), our application of MI to GEE is consistent with previously described methodologies (Molenberghs and Kenward, 2007) that we have performed elsewhere (McDonell et al., 2013; Roll et al., 2013). Thus, after performing the imputation of missing data, the analysis is carried out on each newly created dataset separately using a variant of ML, but then the results are pooled using Rubin's rules (Schafer and Graham, 2002). Thus, our investigation demonstrates standard MI techniques but applied to a longitudinal analysis situation wherein the technique of choice is GEE, such as in many psychopharmacology clinical trials.
RESULTS
Listwise generalized estimation equations model
The first GEE analysis was carried out using a form of listwise deletion that is the common default for many software packages that estimate GEE models. If a participant provides at least two repeated assessments, they are included in the analysis, but otherwise, they are dropped from the analysis. The listwise GEE model included a total of n = 394 participants from the ITT sample.
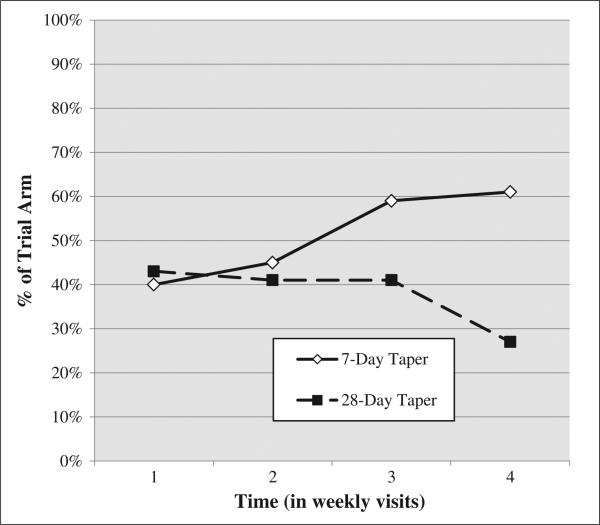
This analysis demonstrated a significant effect of trial arm such that those in the 28-day taper group showed a 45% reduction in the odds of submitting a UA+ for opioids during the 4 weeks of treatment (OR = 0.55, 95% confidence interval (CI): 0.39–0.83). Figure 1 is graphical presentation of the 4-week UA+ trajectories for both treatment arms. Those who were younger were significantly less likely (OR = 0.98, CI: 0.97–1.00) to submit a UA+ over time, and women were more likely (OR = 1.52, CI: 1.04–2.22) to submit a UA+ over time. Time was also associated with a 20% increase in the odds of submitting a UA+ (OR = 1.20, CI: 1.03–1.40), and baseline opioid UA+ was associated with an almost 900% increase in the odds of submitting a UA+ over time (OR = 8.89, CI: 5.91–13.36). No other baseline UA (i.e., cocaine, amphetamines, and marijuana) was predictive of opioid UA+ over time (Table 1, column 1).
Figure 1.
Percent of participants with a positive opioid UA using all available data across the 4-week trajectory while receiving one of two tapering schedules
Table 1.
Likelihood of a positive opioid urine analysis for 7- and 28-day buprenorphine/naloxone taper groups across the 4-week treatment period using generalized estimation equations: impact of missing data treatment choice on outcomes
| Listwise deletion (n = 394) |
Positive UA imputation (n = 516) |
Multiple imputation (n = 516) |
||||
|---|---|---|---|---|---|---|
| Covariates | Odds ratio | (95% CI) | Odds ratio | (95% CI) | Odds ratio | (95% CI) |
| Trial arm (reference = 7 days) | 0.546* | (0.371–0.802) | 0.432* | (0.341–0.549) | 0.572* | (0.424–0.775) |
| Age (per year) | 0.981* | (0.965–0.997) | 0.991 ns | (0.981–1.00) | 0.984* | (0.971–0.997) |
| Sex (reference = male) | 1.518* | (1.039–2.219) | 1.187 ns | (0.932–1.511) | 1.524* | (1.089–2.133) |
| Race (reference = Caucasian) | 0.931 ns | (0.806–1.075) | 0.920 ns | (0.841–1.005) | 0.964 ns | (0.850–1.093) |
| Time (per week) | 1.202* | (1.035–1.398) | 1.268* | (1.160–1.387) | 1.183* | (1.184–1.383) |
| Baseline opioid UA (reference = UA–) | 8.886* | (5.912–13.356) | 5.562* | (4.020–7.694) | 9.873* | (7.194–13.617) |
| Baseline cocaine UA (reference = UA–) | 1.460 ns | (0.975–2.185) | 1.358* | (1.053–1.751) | 1.191 ns | (0.867–1.639) |
The dependent measure was a negative (UA–) or positive (UA+) opioid UA at the end of the taper (0 = UA–; 1 = UA+). Trial arm represents the 7- and 28-day taper groups (0 = 7 days; 1 = 28 days).
UA, urine analysis; ns, non-significant.
p < 0.05.
Positive urine analysis imputation generalized estimation equations model
The second GEE analysis imputed a UA+ for all of the missing values across the 4-week treatment period. As a result, there were no missing values in this analysis, and the sample size used in the analysis included the entire ITT sample (n = 516).
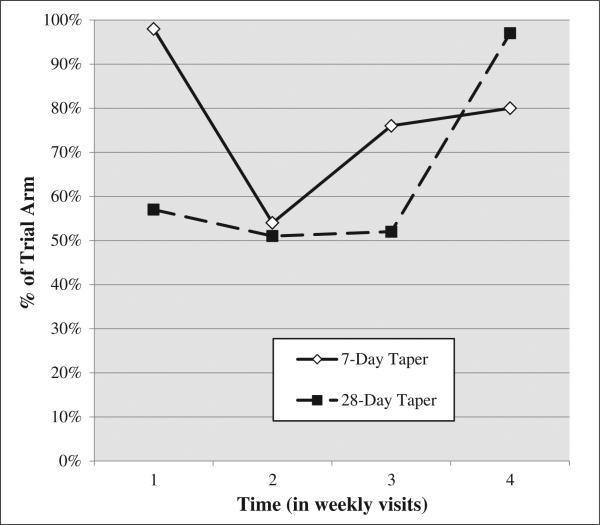
This positive UA imputation model evidenced a significant effect of trial arm. Patients in the 28-day taper group demonstrated a 57% decrease in the odds of submitting an opioid UA+ during the 4 weeks after being randomized (OR = 0.43, CI: 0.34–0.55). Figure 2 is a second depiction of the UA+ trajectories across the two treatment arms wherein all of the missing values have been filled in with UA+ values. Whereas there was no effect of age or sex, time was positively related to UA+ (OR = 1.27, CI: 1.16–1.39; Table 1, column 2). Again, baseline opioid UA+ was predictive of submitting a opioid UA+ over time (OR = 5.56, CI: 4.02–7.69), but unlike the listwise deletion model, baseline cocaine UA+ was predictive of opioid UA+ over time (OR = 1.36, CI: 1.05–1.75).
Figure 2.
Percent of participants with a positive opioid UA assuming all missing UAs were positive across the 4-week trajectory while receiving one of two tapering schedules
Importantly, the CIs are wider for the listwise deletion OR associated with trial arm (OR CI = 0.37–0.80) compared with the OR associated with trial arm in the positive UA imputation model (OR CI = 0.34–0.55). This same trend is observed when comparing the CIs of other effects (e.g., the effects of time and baseline opioid UA). This is pattern of findings is consistent with our previous discussion and with previous findings (e.g., McPherson et al., 2012), which stipulates that many types of single imputation, including positive UA imputation, produce inappropriately small standard errors. A contributing factor for this difference is the power advantage for the positive UA imputation model because this model is able to take advantage of the entire ITT sample whereas the listwise GEE model does not.
Multiple imputation generalized estimation equations model
The third and final GEE analysis used MI procedures to treat the missing observations. The first phase of MI, which involves creating several datasets with imputed values, used pre-baseline weeks 1 through 4 of opioid UAs. In addition, we used all of the other covariates shown in Table 1 (trial arm, age, sex, race, time, etc.) and the UA at baseline for other substances including amphetamine and marijuana to fill in the 50 new datasets (recommended minimum is 5; Graham et al., 2007). In this investigation, weeks 1–4 of pre-baseline opioid UAs were used as auxiliary variables. These variables were only used during the imputation phase. Thus, their only purpose was to assist with ensuring that the mechanism of missingness was more likely MAR. We imputed 50 datasets rather than five because Acock (2012) has demonstrated that relative efficiency (i.e., minimization of standard errors) increases from 90.9% with only five datasets to 97.6% with 20 datasets (assuming 50% missing data). Data presented by Acock (2012) suggest that 20 imputed datasets is a justifiable minimum number of newly created datasets in order to maximize relative efficiency. We increase the number of datasets to 50 because of the high level of missing data (46%) during the 4 weeks of treatment. A potential limitation of imputing so many datasets is the required computation time, but this is quickly becoming a non-issue with the capability of modern statistical computing evolving rapidly (Acock, 2012; Enders, 2010). Because this method uses regression-based procedures to fill in the missing values across multiple datasets before aggregating the final results, this analysis included the entire ITT sample of n = 516.
The MI model demonstrated a significant effect of trial arm. Patients in the 28-day taper group were significantly less likely to submit a UA+ during the 4 weeks after being randomized (OR = 0.57, CI: 0.42–0.78). In addition, those who were younger were significantly less likely (OR = 0.98, CI: 0.97–0.99) to submit a UA+ over time, and women demonstrated a 52% increase in the odds of submitting a UA+ over time compared with men (OR = 1.52, CI: 1.09–2.13). Again, time was positively related to UA+ (OR = 1.18, CI: 1.01–1.38), and baseline opioid UA+ was predictive of subsequent opioid UA+ submissions over time (OR = 9.87, CI: 7.19–13.62). Similar to the listwise deletion GEE model, no other baseline UA (including cocaine) was predictive of opioid UA+ over time (Table 1, column 3).
The CIs are wider for the listwise deletion OR associated with trial arm (OR CI = 0.37–0.80) compared with the OR associated with trial arm in the MI model (OR CI = 0.42–0.78). This same trend is observed when comparing the CIs of other effects (e.g., age, sex, and time). This pattern is likely the result of recovered power and precision for the MI model compared with the listwise deletion model.
DISCUSSION
Missing values are a common and pervasive problem throughout the substance use and psychopharmacology randomized clinical trial literature (Arndt, 2009; McPherson et al., 2012). Two of the most common methods of handling missing values (i.e., listwise deletion and positive UA imputation) have been shown repeatedly to be potentially problematic (Acock, 2012; Hedeker et al., 2007; Enders, 2010; Smolkowski et al., 2010). This investigation demonstrates how treatment efficacy can vary as a function of how the missing information is treated when there is a significant amount of missing information. Moreover, the variation across missing data handling strategies extends beyond the effect of Trial Arm and into other baseline predictors (e.g., demographics and baseline substance use). In fact, three of the seven predictors of longitudinal opioid use differed in statistical significance between MI and positive UA imputation, and five of the seven predictors differed by more than 10% in their OR estimation. This latter difference is particularly important given that effect size estimates are what commonly become used in quantitative reviews and meta-analyses (McPherson et al., 2012). Although this analysis demonstrated that the listwise deletion model was consistent with the MI model, the precision was lower (i.e., wider CI, as noted earlier as a common limitation of this approach), and this is not always the case as is evidenced with other missing data handling comparisons (McPherson et al., 2012). This represents evidence that missing data handling procedures can have a significant impact on the final, clinical conclusions made from substance use psycho-pharmacology clinical trials.
An important clinical finding from this analysis suggests that those in the 28-day taper group were significantly less likely to submit an opioid UA+ during active treatment. Although the effect size varied from missing data method to missing data method, a significant effect was consistent across all three approaches. This investigation presents a different picture than what has been presented previously concerning the impact of taper condition on opioid use during buprenorphine/naloxone pharmacotherapy. Indeed, this investigation presents evidence in the opposite direction (i.e., 28-day taper patients had better outcomes compared with 7-day taper patients) compared with what was found in Ling et al. (2009) and McPherson et al. (2012). However, previous investigations have only analyzed a single UA endpoint (i.e., end of tapering condition; Ling et al., 2009; McPherson, et al., 2012).
Another important clinical finding that this investigation revealed was that baseline opioid UA was the biggest predictor of opioid use during treatment, but it also varied from method to method. The effect size (OR = 9.87 in the MI model) was by far the largest compared with all other predictors in the model, including the impact of treatment. Clearly, future interventions may need to be modified in order to better engage and treat those who continue to use drugs in the days just prior to engaging in treatment. This is consistent with previous literature that has investigated the impact of baseline use on treatment outcomes (McDonell et al, 2013; McPherson et al., 2013; Roll, et al. 2013), and this adds to the call for future treatment strategies to better engage participants early in treatment. Lastly, although some of the demographic findings varied across missing data methodology, women were 52% more likely so submit a opioid UA+ during the trial (OR = 1.524 in the MI model) compared with men, and older individuals were about less 1.5% less likely (per year of age) to submit a UA+ during the trial (OR = 1.52 in the MI model).
Missing data theory and the extant literature (e.g., Rubin, 1976; Allison, 2001; Enders, 2001; Little and Rubin, 2002; Schafer and Graham, 2002; Enders, 2006; Enders, 2010) suggests that listwise deletion and positive UA imputation procedures should not be used to account for missing information. For the current study, we conclude that the MI procedure produced estimates with the greatest likelihood of reflecting reality assuming the data are MAR. By including relevant auxiliary variables (e.g., demographics, previous 4 weeks of UAs), we likely accounted for much of the reason for why missing values were present, making the MAR assumption more reasonable. This in turn makes the MI procedure more valid than procedures that assume MCAR (e.g., listwise deletion) or otherwise do not account for the inherent uncertainty of imputing missing values (e.g., positive UA imputation).
Future researchers may find utilization of the MI procedure in conjunction with the common method of GEE analysis as a helpful analytic approach compared with these commonly used procedures when the MAR assumption is justifiable. However, it should be noted that all approaches to missing values require an assumption on the part of the research team as to which missing data mechanism is the most tenable. In almost every situation, it is not possible to know for certain why missing data occurred or what the “would-be” values would have been. For example, the most likely mechanism may have been MNAR, but because of our inclusive strategy for utilizing auxiliary variables, this assisted with making the MAR assumption more justifiable (Acock, 2012; Collins et al., 2001; Enders, 2010). To the best of our knowledge, this investigation represents the first comparison of the listwise, single positive UA imputation, and MI methods with data from a psychopharmacology substance use disorder treatment trial in the context of GEE.
We do not know for certain what the missing values would have been if they were observed. Thus, it is possible that all of the missing values would have been positive had they been observed. This would indicate that the positive UA imputation model is a good approach to treating the missing values. However, we view the MI procedure as building on the positive UA imputation procedure by putting the researcher in direct control of using clinical expertise to select the best predictors of missing observations (i.e., substantively interesting covariates as well as auxiliary variables) to assist with identifying the most probable estimate using all available data (Acock, 2012; Collins et al., 2001; Enders, 2010; McPherson et al., 2012). MI gives the research team an increased level of flexibility by allowing for the selective choosing of variables that have been demonstrated to be the best predictors of missing values in each unique missing data situation.
This is important to recognize because each missing data situation is unique, and knowledge of the trial is critical in order to effectively handle the missing value. For example, a thorough exploratory analysis to identify potential correlates of missing values, and a clear understanding of the most common patterns of missing values on the outcome in question would help the research team decide how best to proceed. Future researchers should also be more explicit about not only how they handled the missing values in their analysis but also what assumptions they made about the missing data that led to such handling. Sensitivity analyses, like those presented in this investigation, will also help the clinical research team understand how the missing values impact the ultimate interpretation of the treatment effect, as well as other predictors.
We broadly define sensitivity analyses as any set of analyses wherein the research team systematically varies a singular but significant aspect of the analysis in order to determine how robust key parameters are to changes in that aspect under analysis. In this investigation, we were primarily interested in the sensitivity of Trial Arm to different methods of handling the missing data. Similar sensitivity analyses are common in order to test whether or not key clinical findings remain stable across multiple analyses (McDonell et al., 2013; Roll et al., 2013). For example, in our investigation, the effect of Trial Arm remained relatively stable across multiple methods of handling missing data (Table 1). However, baseline cocaine use was a significant predictor of opioid UAs during the treatment period when the missing values were assumed to be positive, but it was not a significant predictor when the missing data were handled in the other two ways. Thus, given the previously noted problems associated with positive UA imputation, we would conclude that baseline cocaine is likely not a meaningful predictor of opioid UAs in the current trial of buprenorphine/naloxone being used for opioid dependence. This is an example of how sensitivity analyses like those presented here have direct clinical implications, and future research teams should consider the application of sensitivity analyses to their own analysis of psychopharmacology clinical trials.
This study has notable limitations. First, this comparative study was conducted on a single psychopharmacology clinical trial, and these results may not be typical for all substance use disorder clinical trials. Yet multiple previously reported simulations would suggest that other research teams would likely find similar results when applied to other psychopharmacology clinical trials (e.g., Allison, 2001; Wood et al., 2004; Enders, 2010), but this is testable question that will hopefully be addressed by future research. Second, the validity of the MI approach relies on the MAR assumption being tenable. This assumption may be more difficult to demonstrate in other missing data situations (McPherson et al., 2012), but it is critical to understand that the alternatives (i.e., MNAR modeling strategies) require assumptions of their own that can be just as, if not more, difficult to defend (Enders, 2010; McPherson et al., 2012). Still, as alluded to earlier, MI should not be viewed as a methodology that will work in all missing data situations.
CONCLUSIONS
The missing data situation described in this investigation generalizes to many other substance use psycho-pharmacology clinical trials wherein there is missing data on the outcome of interest only. We consider these GEE analyses to be a prototype to guide future sensitivity analyses run by research teams interested in evaluating how the interpretation of treatment effectiveness and the impact of other predictors of treatment outcomes vary as a function missing data treatment. In addition to many other substance use disorder treatment researchers who have previously reported on this critical issue of missing data (Yang and Shoptaw, 2005; Hedden, et al. 2008; Arndt, 2009), we have attempted within this investigation to (i) highlight the need for researchers to understand and report the implications of missing data treatment, (ii) understand and report the assumed mechanisms at work in their own investigations, and (iii) to consider utilizing modern methods of handling missing data in their analytic approach (i.e., MI and direct maximum likelihood; McPherson et al., 2012).
ACKNOWLEDGEMENTS
This project was supported by grants from the Department of Justice, the Life Science Discovery Fund (Roll, PI), and a grant to the Clinical Trials Network Pacific Northwest Node (award number 5 U10 DA013714-10) from the National Institute on Drug Abuse (NIDA; Donovan and Roll, Co-PIs). In addition, this project was supported by funds from the Pilot Study Support Program as part of the Center for Advancing Longitudinal Drug Abuse Research (CALDAR, award number P30DA016383; McPherson, PI) from the NIDA and the Washington State University Spokane Seed Grant Program (McPherson, PI).
Footnotes
CONFLICT OF INTEREST
None of the authors have any financial, personal, or other type of relationship that would cause a conflict of interest that would inappropriately impact or influence the research and interpretation of the findings.
REFERENCES
- Acock A. What to do about missing values. In: Cooper H, editor. APA Handbook of Research Methods in Psychology. American Psychological Association; Washington, DC: 2012. [Google Scholar]
- Allison PD. Missing Data. Sage; Newbury Park, CA: 2001. [Google Scholar]
- Arndt S. Stereotyping and the treatment of missing data for drug and alcohol clinical trials. Subst Abuse Treat Prev Policy. 2009;4:2–3. doi: 10.1186/1747-597X-4-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Buuren S. Flexible Imputation of Missing Values. CRC Press; Boca Raton, FL: 2012. [Google Scholar]
- Collins LM, Schafer JL, Kam C- M. A comparison of inclusive and restrictive strategies in modern missing data procedures. Psychol Methods. 2001;6:330–351. [PubMed] [Google Scholar]
- Cook RJ, Zeng L, Yi GY. Marginal analysis of incomplete longitudinal binary data: a cautionary note on LOCF imputation. Biometrics. 2004;60:820–828. doi: 10.1111/j.0006-341X.2004.00234.x. [DOI] [PubMed] [Google Scholar]
- Enders CK. A primer on maximum likelihood algorithms available for use with missing data. Struct Equ Model. 2001;8:128–141. [Google Scholar]
- Enders CK. A primer on the use of modern missing-data methods in psychosomatic medicine research. Psychosom Med. 2006;68:427–436. doi: 10.1097/01.psy.0000221275.75056.d8. [DOI] [PubMed] [Google Scholar]
- Enders CK. Applied Missing Data Analysis. Guilford Press; New York, NY: 2010. [Google Scholar]
- Graham JW. Missing data analysis: making it work in the real world. Annu Rev Psychol. 2009;60:549–576. doi: 10.1146/annurev.psych.58.110405.085530. [DOI] [PubMed] [Google Scholar]
- Graham JW, Hofer SM, Piccinin AM. Advances in Data Analysis for Prevention Intervention Research, National Institute on Drug Abuse Research Monograph. In: Collins LM, Seitz L, editors. Analysis with missing data in drug prevention research. Natl. Inst. Drug Abuse; Washington, DC: 1994. pp. 13–63. [PubMed] [Google Scholar]
- Graham JW, Olchowski AE, Gilreath TD. How many imputations are really needed? Some practical clarifications of multiple imputation theory. Prev Sci. 2007;8:206–213. doi: 10.1007/s11121-007-0070-9. [DOI] [PubMed] [Google Scholar]
- Hedden SL, Woolson RF, Malcolm RJ. A comparison of missing data methods for hypothesis tests of the treatment effect in substance abuse clinical trials: a Monte-Carlo simulation study. Subst Abuse Treat Prev Policy. 2008;3:13–21. doi: 10.1186/1747-597X-3-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedeker D, Mermelstein RJ, Demitras H. Analysis of binary outcomes with missing data: missing = smoking, last observation carried forward, and a little multiple imputation. Addiction. 2007;102:1564–1573. doi: 10.1111/j.1360-0443.2007.01946.x. [DOI] [PubMed] [Google Scholar]
- Ling W, Hillhouse M, Domier C, et al. Buprenorphine tapering schedule and illicit opioid use. Addiction. 2009;104:256–265. doi: 10.1111/j.1360-0443.2008.02455.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. 2nd ed. Wiley; Hoboken, NJ: 2002. [Google Scholar]
- Mallinckrodt CH, Sanger TM, Dube S, et al. Assessing and interpreting treatment effects in longitudinal clinical trials with missing data. Biol Psychiatry. 2003;53:754–760. doi: 10.1016/s0006-3223(02)01867-x. [DOI] [PubMed] [Google Scholar]
- McDonell MG, Srebnik D, Angelo F, et al. Randomized controlled trial of contingency management for stimulant use in community mental health patients with serious mental illness. Am J Psychiatry. 2013;170:94–101. doi: 10.1176/appi.ajp.2012.11121831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPherson S, Barbosa-Leiker C, Burns GL, Howell D, Roll J. Missing data in substance abuse treatment research: current methods and new approaches. Exp Clin Psychopharmacol. 2012;20:243–250. doi: 10.1037/a0027146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPherson S, Packer R, Cameron J, Howell D, Roll J. Biochemical predictors are better than self-report in a smoking cessation contingency management analog study. Am J Addict. 2013 doi: 10.1111/j.1521-0391.2013.12059.x. DOI: 10.1111/j.1521-0391.2013.12059.x. [DOI] [PubMed] [Google Scholar]
- Molenberghs G, Kenward MG. Missing Data in Clinical Studies. John Wiley & Sons, Inc.; Sussex, United Kingdom: 2007. [Google Scholar]
- Nich C, Carroll KM. Intention-to-treat meets missing data: Implications of alternate strategies for analyzing clinical trials. Drug Alcohol Depend. 2002;68:121–130. doi: 10.1016/s0376-8716(02)00111-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roll JM, Chudzynski J, Cameron JM, Howell DN, McPherson S. Duration effects in contingency management treatment of methamphetamine disorders. Addict Behav. 2013;38(9):2455–2462. doi: 10.1016/j.addbeh.2013.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB. Inference and missing data. Biometrika. 1976;63:581–592. [Google Scholar]
- Rubin DB. Multiple Imputation for Nonresponse in Surveys. John Wiley & Sons, Inc.; New York: 1987. [Google Scholar]
- Schafer JL, Graham JW. Missing data: our view of the state of the art. Psychol Methods. 2002;7:147–177. [PubMed] [Google Scholar]
- Shao J, Zhang B. Last observation carry-forward and last observation analysis. Stat Med. 2004;22:2429–2441. doi: 10.1002/sim.1519. [DOI] [PubMed] [Google Scholar]
- Smolkowski K, Danaher BG, Seeley JR, Kosty DB, Severson HH. Modeling missing binary outcome data in a successful web-based smokeless tobacco cessation program. Addiction. 2010;105:1005–1015. doi: 10.1111/j.1360-0443.2009.02896.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Twisk JWR. Applied Longitudinal Data Analysis for Epidemiology. Cambridge University Press; Cambridge, UK: 2004. [Google Scholar]
- Wood AM, White IR, Thompson SG. Are missing outcome data adequately handled? A review of published randomized controlled trials in major medical journals. Clin Trials. 2004;1:368–376. doi: 10.1191/1740774504cn032oa. [DOI] [PubMed] [Google Scholar]
- Yang X, Shoptaw S. Assessing missing data assumptions in longitudinal studies: an example using a smoking cessation trial. Drug Alcohol Depend. 2005;77:213–225. doi: 10.1016/j.drugalcdep.2004.08.018. [DOI] [PubMed] [Google Scholar]
- Zeger SL, Liang K-Y. An overview of methods for the analysis of longitudinal data. Stat Med. 1992;11:1825–1839. doi: 10.1002/sim.4780111406. [DOI] [PubMed] [Google Scholar]