Modeling deterministic effects in hematopoietic system caused by chronic exposure to ionizing radiation in large human cohorts

Abstract

A new model of the hematopoietic system for humans chronically exposed to ionizing radiation allows for quantitative description of the initial hematopoiesis inhibition and subsequent increase in the risks of late stochastic effects such as leukemia. This model describes the dynamics of the hematopoietic stem cell compartment as well as the dynamics of each of the three blood cell types (leukocytes, erythrocytes, and platelets). The model parameters are estimated from the results of other experiments. They include the steady-state numbers of hematopoietic stem cells and peripheral blood cell lines for an unexposed organism, amplification parameters for each blood cell line, parameters describing the proliferation and apoptosis, parameters of feedback functions regulating the steady-state numbers, and characteristics of radiosensitivity in respect to cell death and non-lethal cell damages. The dynamic model of hematopoiesis is applied to the data on subcohort of the Techa River residents with hematological measurements (e.g., blood counts) performed in 1950–1956 (which totals to about 3,500 exposed individuals). Among well-described effects observed in these data are the slope value of the dose-effect curves describing the hematopoietic inhibition and the dose rate patterns of the fractions of cytopenic states (e.g., leukopenia, thrombocytopenia). The model has been further generalized by inclusion of the component describing the risk of late stochastic effects. The risks of the development of late effects (such as leukemia) in population groups with specific patterns of early reactions in hematopoiesis (such as leukopenia induced by ionizing radiation) are investigated using simulation studies and compared to data.

Introduction

Development of specific strategies of radiation protection is based on the detailed knowledge of population risks of adverse health effects induced by ionizing radiation (IR). The International Commission on Radiation Protection (e.g., 60th publication of ICRP) suggests distinguishing deterministic and stochastic effects of IR. For example, the deterministic effects of IR are characterized by features such as i) both the risk and severity of harm depend on dose, ii) there is a threshold in dose-effect dependence, and iii) the underlying biological process is the loss and replacement of cells. An example is the hematopoietic acute radiation syndrome. Stochastic effects of IR are characterized by the following features: i) only the risk but not the severity of harm depends on dose, ii) there is no threshold in dose-effect dependence, and iii) the underlying biological process is the accumulation of randomly occurred mutations. Leukemogenesis is an example of stochastic effects.

Effect of chronic exposure to IR on hematopoietic and other radiosensitive tissues is dual. On the one hand, IR influences kinetics of the cell populations during the early period of exposure resulting in deterministic effects. On the other hand, IR initiates and promotes stochastic late effects. Both types of effects are related, and this relationship has to be reflected in the developed models. In this paper, we develop the model for the deterministic effects in the hematopoietic system under chronic exposure to IR and demonstrate how the model can be joined to a model of the risk of development of late stochastic health effects.

Models of Deterministic Effects of Chronic Radiation Exposure in Hematopoiesis

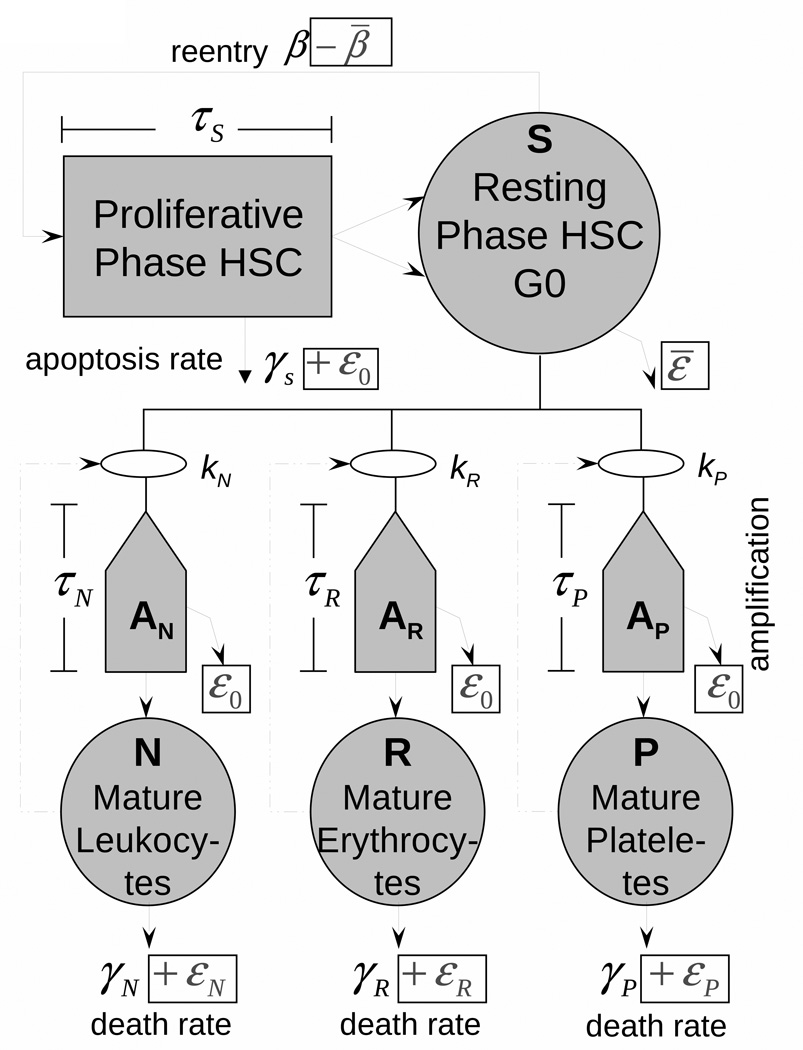
Our development is based on the models of hematopoiesis developed by Mackey and colleagues (see Colijn and Mackey (2005), Foley, Mackey (2009), and references therein). This model takes into account the dynamics of the hematopoietic stem cells (HSC) compartment as well as each of the three blood cell types (red blood cells, white cells, and platelets). The model is elaborated in detail especially with respect to i) evaluating model parameters by using available data, ii) uncovering many useful properties of the models by methods of nonlinear dynamics, and iii) explaining and quantitatively describing the cyclic phenomena in hematopoiesis, such as cyclical neutropenia and chronic myelogenous leukemia. The model compartments are those which are potentially subject to damages of exposure to IR and whose response to chronic exposure to IR is typically measured. Therefore, a model being generalized for incorporating the effects of IR is appropriate for describing the deterministic effects. The generalized model (as well as the original model) includes four compartments corresponding to HSC (S) and mature leukocytes (N), erythrocytes (R), and platelets (P) (Fig. 1). Respective system of delay differential equations is

$$\frac{dS(t)}{dt}=-(\beta (t)-\overline{\beta }(t)+k_N(t)+k_R(t)+k_P(t))S(t)+2e^{-({\gamma }_s+{\epsilon }_0){\tau }_S}(\beta (t_s)-\overline{\beta }(t_s))S(t_s)-\overline{\epsilon }S(t_d)\frac{dN(t)}{dt}=-({\gamma }_n+{\epsilon }_n)N(t)+A_N{e}^{-{\tau }_N{\epsilon }_0}{k}_N(t_n)S(t_n),\frac{dR(t)}{dt}=-({\gamma }_r+{\epsilon }_r)R(t)+A_R{e}^{-{\tau }_R{\epsilon }_0}{k}_R(t_r)S(t_r),\frac{dP(t)}{dt}=-({\gamma }_p+{\epsilon }_p)P(t)+A_P{e}^{-{\tau }_P{\epsilon }_0}{k}_P(t_p)S(t_p).$$ (1)

with initial values S_*0, N_*0, R_*0, and P_*0 corresponding to the steady-state of unexposed organism; t with subscripts define time delays: t_s = t τ_s, etc. Boxed terms at the scheme in Fig. 1 and in equations (1) show the effects of chronic exposure to IR. The Matlab solver dde23 was used for solution of the system (1) for continuous time. The properties of this solver are described and discussed by Shampine and Thompson (2001) and Bellen and Zennaro (2003).

Fig. 1.

The model of hematopoiesis under chronic exposure to IR. The circles describe four model compartments corresponding to HSC (S) and mature leukocytes (N), erythrocytes (R), and platelets (P). The pentagons denote compartments for amplification and maturation of blood cells. The square shows the compartment of HSC proliferation. Solid lines show the cell transitions between compartments, and dash-dotted lines show feedback loops regulating the blood counts.

Components of the model which are important for this study deals with mechanisms of feedback, IR induced cell effects, and time delays.

Presumptive mechanisms of negative feedback mediated by thrombopoietin, erythropoietin, and the granulocyte colony stimulating factor as well as a local regulatory loop within the pluripotent HSC population are modeled by Hill-type functions:

$$\beta (t)=\frac{{\overline{k}}_q}{1+T_{q}S{(t)}^s},k_N(t)\frac{{\overline{k}}_n}{1+T_{n}N{(t)}^n}{k}_R(t)\frac{{\overline{k}}_r}{1+T_{r}R{(t)}^m},k_P(t)\frac{{\overline{k}}_p}{1+T_{p}P{(t)}^p},$$

where s = 4, n = 1, m = 6.96, and p = 1.29 (Colijn and Mackey, 2005).

There are three types of IR induced cell effects included in the generalized model. The first is cell damages resulting in cell death (interphase (hours) or mitotic (days)) and non-lethal cell damages resulting in augmenting a compartment of injured cells. The second is the suppression of HSC proliferation (−β̄), proportional to the number of injured cells. The third is the excess cell loss resulting from increased apoptosis in HSC, peripheral blood as well as during amplification and maturation.

Five time delays are used in the model: i) stem cell proliferation time τ_s, ii–iv) maturation time of leukocytes (τ_N), erythrocytes (τ_R), and platelets (τ_P), and v) delayed cell death (τ_d) induced by IR.

Strategy of model estimation

A fine feature of the model is that almost all its parameters have clear biological sense and can be estimated using measurements. Since we intend to incorporate the measurements presented in Akleyev et al., (2009), the strategy for estimation of non-IR terms slightly differs from that used in the original paper of Colijn and Mackey (2005). First, by using measurements of the steady-state blood counts in peripheral blood (Akleyev et al., 2009) and standard values for cell flux to peripheral blood (Fliedner et al., 2002, Fliedner and Graessle, 2008), the rates of apoptosis of cells in peripheral blood are estimated. Second, parameters for hematopoietic feedback loop, amplification factors, and time delays are taken from Colijn and Mackey (2005). Third, the steady-state value S_*0 is estimated using an algebraic equation for steady-state of HSC compartment. Then estimation of parameters k̄_n, k̄_r, and k̄_p using algebraic equations for steady-states in respective blood cell lines completes the estimation of the non-IR part of the model.

Dose rate (r_d ) effects, e.g., IR induced cell death for HSC and lymphocytes, are defined by the dose rate at the moment of t and are represented as $r_d{D}_0^{-1}$, where D₀ ’s are known characteristics of radiosensitivity of HSC and peripheral lymphocytes. Effects of cumulative dose (C_d) include the rate of cell injuring resulting in increased apoptosis of peripheral blood cells and suppression of proliferation rate in HSC compartment. They are represented as αC_d, where parameters α are estimated by the data fit (manual search) or evaluated using arguments in Graessle (2000) and Fliedner and Graessle (2008). Specifically, the models for suppression of HSC proliferation, −β̄(t) = −α₁C_dβ(t), and for the excess cell loss, ${\epsilon }_0=r_d{D}_0^{-1}+{\alpha }_2{C}_d{\gamma }_s,\overline{\epsilon }=r_d{D}_0^{-1},{\epsilon }_N=r_d{D}_0^{-1}+{\alpha }_2{C}_d{\gamma }_n$, ε_R = α₂C_dγ_r, and ε_P = α₂C_dγ_p, were used in numerical analyses. Parameters were estimated as α₁ 0.1Gy⁻¹, α₂ = 0.2Gy⁻¹, and D₀ = 0.6Gy.

Properties of the model

The style of modeling is a certain trade-off between the parsimonious approach (i.e., having a tendency to keep the minimal number of parameters) and the description of three blood cell lines simultaneously. This, as well as the use of delay differential equations, are distinguishable features of our approach from the models of radiation effects in hematopoiesis by i) the group of Fliedner (see Fliedner and Graessle (2008) and references therein) and ii) Smirnova (2000, 2007).

The model permits an analytical solution of the main linear contributions (denoted as S̃, Ñ, R̃, and P̃) to the decline in blood counts in a new steady-state (denoted as S_*, N_*, etc.), i.e., the linear contributions proportional to dose rate/cumulative dose as S_* = S_*0(1 + S̃ + o(r_d, C_d)) and similar for other compartments. Declines of peripheral blood counts and HSC are:

$$\tilde{N}=\frac{\tilde{S}-{\epsilon }_0{\tau }_N-{\epsilon }_N{\gamma }_N^{-1}}{1+n},\tilde{R}=\frac{\tilde{S}-{\epsilon }_0{\tau }_R-{\epsilon }_R{\gamma }_R^{-1}}{1+m},\tilde{P}=\frac{\tilde{S}-{\epsilon }_0{\tau }_P-{\epsilon }_P{\gamma }_P^{-1}}{1+p},\tilde{S}=\frac{{\epsilon }_0{\tau }_S(f_S^{-1}+1)(k_N+k_R+k_P)+{\epsilon }_0(\overline{n}{k}_N{\tau }_N+\overline{m}{k}_R{\tau }_R+\overline{p}{k}_P{\tau }_P)+\overline{\beta }{f}_s+\overline{\epsilon }+T}{k_N(s-\overline{n})t+k_R(s-\overline{m})+k_P(s-\overline{p})}$$

where f_s 2 exp(γ_sτ_s), −1, n̄ = n/(1+n), etc., and

$$T=\overline{n}{\epsilon }_N\frac{N_{*0}}{A_N{S}_{*0}}+\overline{m}{\epsilon }_R\frac{R_{*0}}{A_R{S}_{*0}}+\overline{p}{\epsilon }_P\frac{P_{*0}}{A_P{S}_{*0}}$$

Experimental Results and Model Prediction

Experimental results which have to be described by the model can be summarized as follows (Akleyev et al. (2009), Veremeyeva et al. (2009)). First, the dose rate declines, estimated by generalized linear models, i.e., C = u + αr_d, where C and r_d are measured blood cell counts and dose rate, are: i) an absolute decline, i.e., α, in year·Gy⁻¹·10⁹·cells·L⁻¹: −5.91 for leukocytes, −1.42 for erythrocytes, and −253.8 for platelets and ii) a relative decline, i.e., α·u⁻¹, in year·Gy⁻¹: −0.77 for leukocytes, −0.33 for erythrocytes, and −1.06 for platelets. Second, the dose rate at the moment of measurement is not the best predictor of the effects of blood count decline, i.e., the effect of history of exposure is important. Third, the frequency of cytopenic states increases with the dose rate (or with another dose characteristic identified as the “best predictor”), and this increase is linear. Fourth, there are indications that the risk of late stochastic effects such as leukemia or the increase of mutations in cells is associated with an early pattern of deterministic reaction to exposure. Fifth, findings are compatible with the hypothesis that there is a subpopulation with increased radiosensitivity.

The developed model is capable of describing these findings. A relative decline in blood cell counts caused by the dose rate is found to be related as 2.3:1.0:3.2 for leukocytes, erythrocytes, and platelets, respectively. This decline can be evaluated analytically. Approximately, it is defined by the ratios of 1/(n+1):1/(m+1):1/(p+1), which is 3.9:1.0:3.2. The relation will be much better if we alternatively use n = 2. In this case 2.6:1.0:3.4

An absolute decline requires careful modeling of the pool of injured cells. We assume that the number of injured cells is proportional to the cumulative dose in Gy (C_d), such that β̄ = 0.1C_dβ (corresponds to experimental results in vitro) and excess cell losses for respective compartment (e.g., 0.2C_dγ_R).

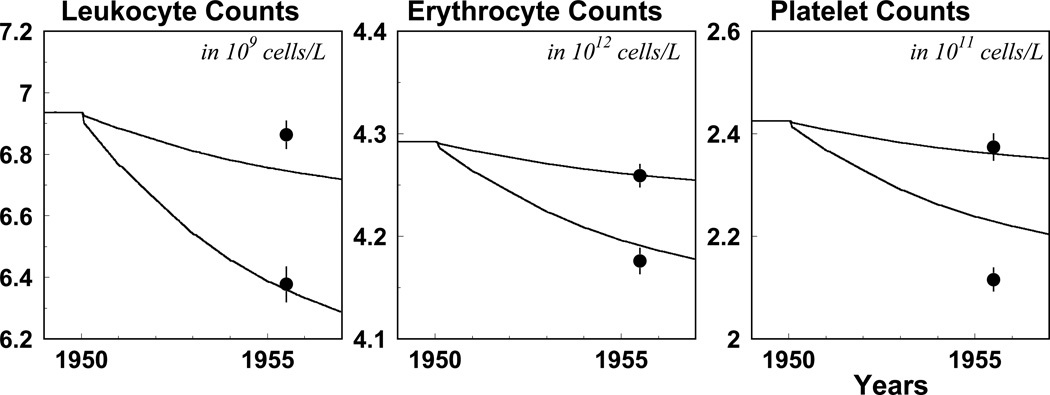
To illustrate data and model prediction compatibility, we consider data on blood counts measured in 1956 (Akleyev et al., 2009). All these measurements are separated into two dose groups (i.e., with high and low exposures), and means of exposure histories (i.e., annual trajectories of cumulative dose and dose rates) are calculated for each group. The estimated model is used for predicting blood counts in 1956 for the low and high-dose group. The results of this analysis are presented in Fig. 2. Short-term oscillations predicted by the model are not essential and, therefore, were smoothed using the Matlab function Filter. Note that the effects of dose rate and cumulative dose are compatible; therefore their joint effect can be manifested as the delay in the effect of exposure, which has also been observed byAkleyev et al. (2009).

Fig. 2.

Model prediction and blood counts measured in 1956 for two groups of dose pattern histories. The lower lines and dots correspond to the group with higher exposure histories. See the text for further details on the design of the simulation study.

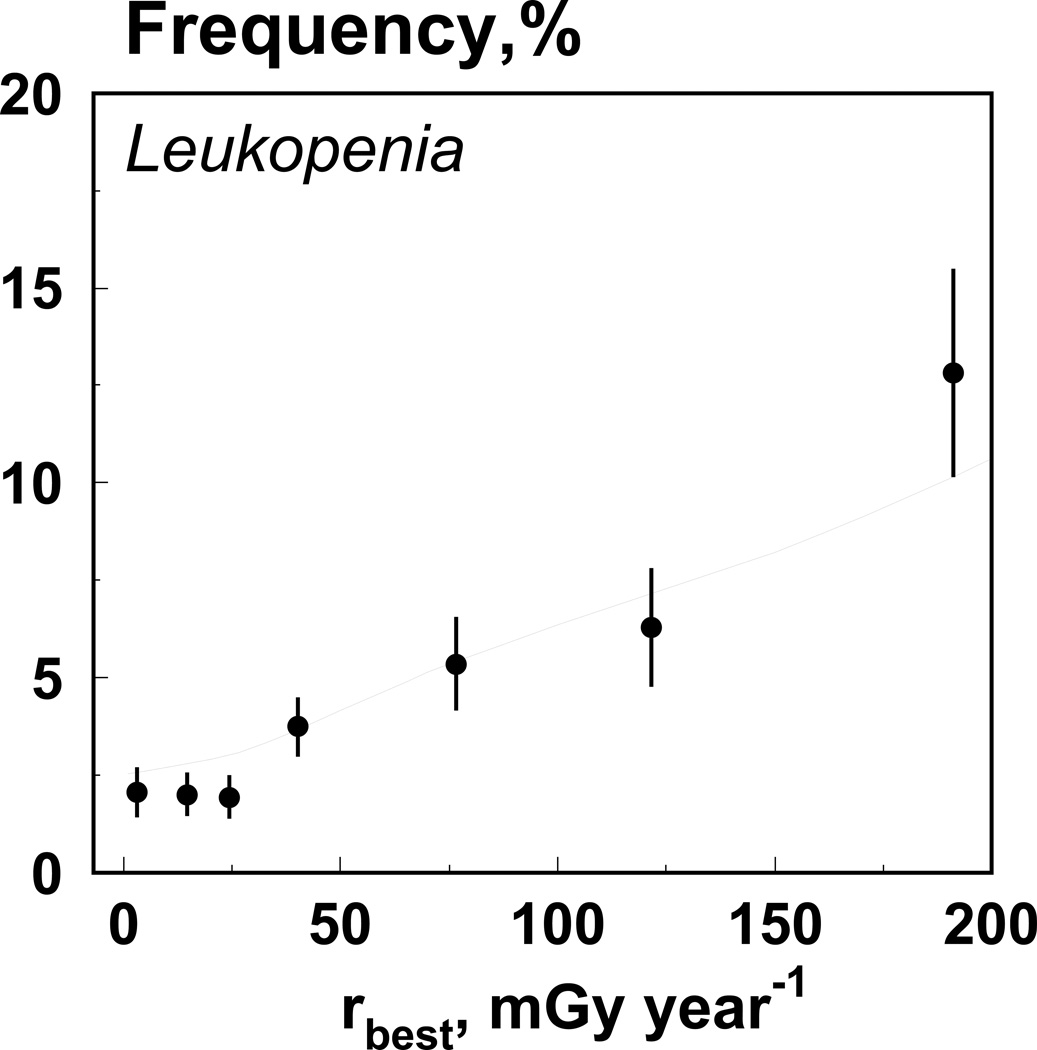
The model is capable of predicting the frequency of cytopenic states. We assume that the mean and the variance of the distribution of leukocytes in a population are known. For each dose rate, we simulate individual trajectories and estimate the frequency of leukopenia, i.e., the fraction of individuals whose new steady state of leukocytes count is below the norm. Specifically, the gamma distribution with mean=7 and standard deviation=1.75 is used for the baseline population. Fig. 3 shows data on leukopenia frequency and model prediction.

Fig. 3.

Data on leukopenia frequency (dots) and model prediction (line).

Barrier Breaking Model of Leukemogenesis

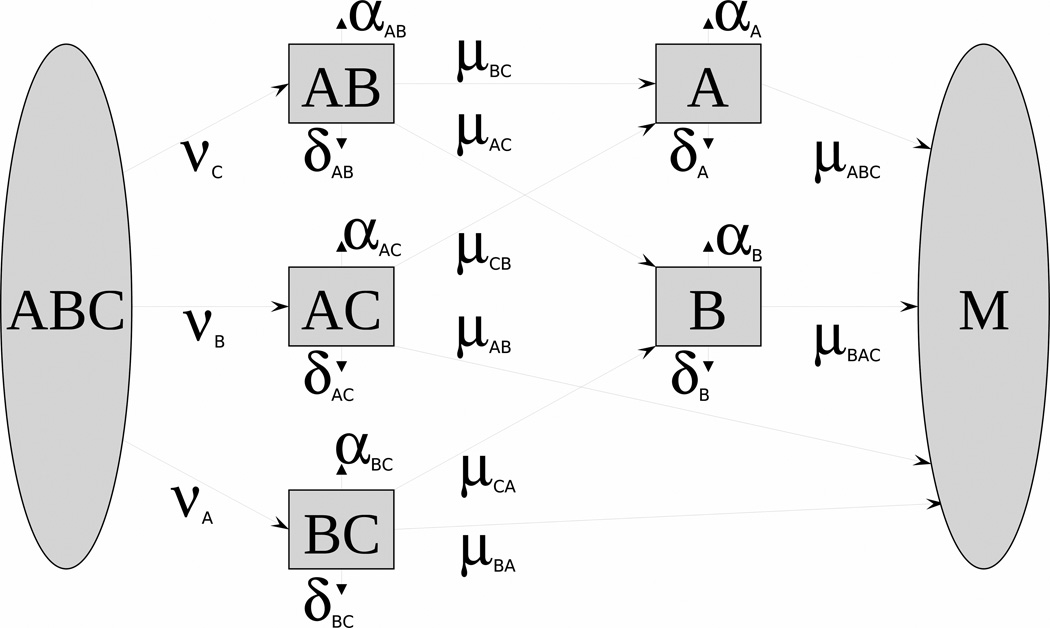
The essence of the approach to modeling stochastic effects is based on the concept of barrier mechanisms. In this approach, leukemogenesis is represented as the dynamic trade-off between two antagonistic forces or processes promoting or hindering leukemia at its different stages (initiation, promotion, conversion). The processes promoting the cell malignization are represented by mutations or adverse epigenetic events. Antagonistic processes preventing the neoplastic transformation of the cell and its forthcoming fixation in the next cell generations are represented by barrier mechanisms (e.g., apoptosis, repair, antioxidant defense). The biological concept of barrier mechanisms, details of mathematical structure, comparison to Two-Stage Clonal Expansion Model, application to SEER data, simulation studies, inclusion of IR effects, and ways to measure barrier systems are presented elsewhere (Akushevich et al, 2008a,b). For the barrier breaking model (BBM) presented in Fig. 4, the state of a healthy individual is modeled by five correlated stochastic processes X(t) = (X_BC(t), X_AC(t), X_AB(t), X_B(t), X_A(t). Observed quantities include: i) the hazard rate of cancer onset conditional to survival h̄ (t) (i.e., among surviving population), and ii) means and variances of barrier states, which are modeled by vector m(t) and matrix γ(t) as solutions of the system of ordinary differential equations:

$$\overline{h}(t)=a_0+a_{1}m(t);\frac{dm(t)}{dt}=a_0+a_{1}m(t)=\gamma (t){\mu }_1,\frac{d\gamma (t)}{dt}={\alpha }_1{\gamma }^{*}(t)+\gamma (t){\alpha }_1^{*}(t)+b{b}^{*}.$$

with initial conditions m(0) = m₀ (last measurements) and γ(0) = 0. Here a₀, μ₁, are 5-vectors, and a₁ and b are 5·5 matrices. The mathematical formalism of stochastic process modeling is described inYashin et al. (1985) and Yashin and Manton (1997).

Fig. 4.

The scheme of a compartmental model implementing the sequence of barrier breaking when a cell undergoes changes from a normal (ABC) to a malignant (M) state. Transitions correspond to the failure of a specific barrier, e.g., apoptosis (A), repair (B), antioxidant defense (C). Letters on the blocks denote which barriers are effective in a certain state.

One advantage of the modeling approach is in the application to the case of chronic low-dose irradiation, when barrier mechanisms for repair of genetic damages or elimination of cells carrying unrepaired damages play a special role. Another advantage is in the natural combining of two types of measures expressed in terms of model parameters: the age-specific hazard rate and means of barrier states. The possibility to predict measurable characteristics strongly related to leukemogenetic process (i.e., measures characterizing state of intracellular barrier mechanisms) is the distinguishing property of the model. However, since the dynamics of intracellular barriers is modeled at the level of stem cells and characteristics of barrier breaking are measured using a sample of peripheral blood, these two levels have to be linked in the correct model of the stochastic effect. Such linkage can be provided if components of the model of stochastic effects are dynamically related to the components of, and the model of, deterministic effects presented in Fig. 1. Furthermore, such a linkage allows for describing the relationship between early deterministic reaction of hematopoiesis to chronic exposure to IR and late stochastic effects such as leukemia.

Joining Models of Stochastic and Deterministic Effects

Experimental results on laboratory animals show the relations between the risk of development of late effects and individual patterns of the early effects under chronic exposure to IR (e.g., relation of the specifics of the early effects with development of hypo- and hyperplasia, and shortening longevity (Seed et al, 2002). Veremeyeva et al. (2009) revealed similar associations (e.g., between cytopenic states and an increased risk of mutations or aberrations and changes of functioning of intracellular systems) for the exposed individuals from the Techa River Cohort. These results suggest the presence of certain pathways responsible for the generation of both deterministic (or early) and stochastic (or late) effects leading to the alteration of intracellular processes responsible for genetic homeostasis (e.g., repair, apoptosis, cell cycle control) and promoting the increasing pool of cells with genetic damages.

The major hypothesis allowing for the dynamic relation of the components of IR effects (i.e., stochastic and deterministic effects) is that the rates of barrier breaking in the leukemogenesis model become dependent on certain characteristics of inhibition/recovery patterns which can be considered determinants of late stochastic effects. Specific hypothesis investigated in the simulation studies below, is: “to which extent an increased proliferation rate in hematopoietic system activated during the years of chronic exposure to IR as a response to increased cell death can lead to abnormalities of intracellular processes providing genetic homeostasis (e.g., repair, apoptosis) and promote the increase of the pool of cells with genetic damages?” We will test it by modeling the increased mutation rate and the increased risk of leukemia.

Mutation rate: linear and non-linear contributions

Two mechanisms of IR induced leukemogenesis are basically considered. IR can induce specific mutations or epigenetic events in stem cells and therefore increase the number of intermediate cells susceptible to further stages of leukemogenesis. IR can also have a promoting effect to leukemogenesis. The basic argument is that stem cells inactivated by IR may be replaced by the division of stem cells in which intermediate cells have a growth advantage (Heidenreich et.al., 2001, 2007). Increased mutation rate at acute and chronic exposure to IR is typically modeled proportionally to dose μ(dose) = μ(0) μ₁dose. In analyses of hematopoietic effects under IR there is another possible mechanism of increase of mutation rate generating non-linear dependence of mutation rate on dose. The mutation rate can be expressed as

$$\mu =\text{probability of mutation at a HSC division}\times \text{proliferation rate of HSC}$$

Since the effective number of HSC S(t) and new steady-state S_* are smaller than its initial steady state value S_*0 obtained in case of the absence of IR exposure, under chronic exposure the mutation rate can be increased even without the assumption of increase in probability of mutation at a HSC division. For the steady-state without exposure this formula is

$$\mu =\overline{\mu }·{\beta }_{*0}=\overline{\mu }\frac{{\overline{k}}_q}{1+T_q{S}_{*0}^s}$$

After the onset of IR exposure, the mutation rate becomes time dependent with non-trivial functional dependence on both dose rate and cumulative dose of chronic exposure:

$$\mu (t,\{r_d,C_d\})=\overline{\mu }(r_d)(\beta (t)-\overline{\beta }(t))=\overline{\mu }(r_d)\frac{{\overline{k}}_q(1-{\alpha }_1{C}_d)}{1+T_q{S}^s(t,\{r_d,C_d\})}$$

This dependence results from i) the number of HSCs S(t,{r_d, C_d}), which is the solution to system (1) for a specific history of exposure pattern {r_d,C_d}, ii) the correction β̄(t) to the HMC proliferation rate, which is modeled proportional to cumulative dose, and iii) possible dependence of probability of mutation at a HSC division μ̄(r_d) on current dose rate.

Dynamic relationship between mutation rate and the number of HSC allows for incorporating the dynamically changing risk of late stochastic effects (i.e., BBM model) into the hematopoiesis model. This can be performed by joining the system of DDE for hematopoiesis and the system of ODE for m(t) and γ(t). For the simplified BBM model with one barrier state representing intermediate cells, only one additional equation has to be included:

$$m\prime (t)={\overline{\mu }}_1(\beta (t)-(\overline{\beta }(t))S(t)+\mathrm{\Delta }m(t)-\overline{\mu }(\beta (t)-\overline{\beta }(t))b^2{(2\mathrm{\Delta })}^{-1}(\text{exp}(2\mathrm{\Delta }t)-1),m(0)=m_0.$$

Here μ̄₁ and μ̄ correspond to the first and second mutations, Δ describes the proliferation-apoptosis balance in the intermediate cells. The risk is calculated as h(t) = μ̄(β(t) − β̄(t))m(t).

Simulation studies: mutation rate and leukemia risk

To specify the design for a simulation study, we assume that a population is under chronic exposure with fixed dose rate r_d and adaptive effects act in such a way that the dose is accumulated for two last years of exposure. Table 1 represents the relative excess of mutation rate caused by the dynamic increase of the proliferation rate only, i.e., when μ̄(r_d) = μ̄ is assumed.

Table 1.

The excess of relative risk caused by dynamic changes in hematopoietic system due to chronic exposure to IR.

Dose rate, Gy/year	0	0.05	0.10	0.50
Relative Excess of mutation rate	1.00	1.05	1.11	1.67

Using the joined model we then simulated 9-year dynamics (1949–1957) of the four compartments and the risk of leukemogenesis for two dose rate groups (DRG) defined above (see subsection “Experimental Results and Model Prediction”). We used two modifying factors in this simulation studies: f₁ to modify the effect on the excess cell losses (i.e., 0.2C_dγ_R → f₁0.2C_dγ_R and f₂ to modify the base proliferation rate of HSC (i.e., β → f₂β, the value S_* is recalculated for each new value of f₂). In these studies we investigated the correlation between the excess relative risk f_h and the observed values of blood counts and the unobserved value of HSC counts. The results of this study are presented in Table 2.

Table 2.

Results of simulation studies for the risk of carcinogenesis caused by dynamic changes in hematopoietic system due to chronic exposure to IR for two exposure history groups (DRG) as measured in 1950–1956 in the ETRC. See the text for further details of design of the simulation study.

DRG	f1	f2	S(1957)	N(1957)	R(1957)	P(1957)	fh(1957)
Low	0.7	0.7	1.36	6.70	4.33	2.61	1.522
Low	1.0	0.7	1.36	6.66	4.32	2.60	1.526
Low	1.3	0.7	1.35	6.61	4.31	2.58	1.531
Low	0.7	1.0	1.54	6.70	4.33	2.61	1.522
Low	1.0	1.0	1.54	6.66	4.32	2.60	1.527
Low	1.3	1.0	1.53	6.60	4.31	2.58	1.531
Low	0.7	1.3	1.66	6.97	4.37	2.71	1.557
Low	1.0	1.3	1.66	6.95	4.36	2.69	1.561
Low	1.3	1.3	1.65	6.88	4.36	2.67	1.566
High	0.7	0.7	1.32	6.45	4.28	2.52	1.548
High	1.0	0.7	1.31	6.32	4.26	2.47	1.562
High	1.3	0.7	1.30	6.20	4.24	2.42	1.577
High	0.7	1.0	1.50	6.46	4.28	2.52	1.549
High	1.0	1.0	1.48	6.31	4.26	2.47	1.563
High	1.3	1.0	1.47	6.21	4.24	2.42	1.578
High	0.7	1.3	1.62	6.73	4.33	2.61	1.585
High	1.0	1.3	1.60	6.57	4.30	2.56	1.599
High	1.3	1.3	1.59	6.45	4.28	2.51	1.614

The following conclusion can be made. First, the excess of leukemia risk correlates with the decrease of blood counts in all lines of peripheral blood for the same doses. Second, this effect is held for all groups over the initial value of the number of HSC. Third, evaluated excess in mutation rate due to increased proliferation in HSC compartment can explain up to 25% of the total effect of increased cancer risk (RR=6, Krestinina et al., 2005), and the remaining increase is explained by an increase of probability of mutation at a HSC division.

Summary

An approach to comprehensive modeling of the hematopoietic system for humans exposed to IR is suggested. The approach is based on the models of hematopoiesis developed by Mackey and colleagues (Colijn and Mackey 2005) and generalizes them for inclusion of the effects of chronic exposure to IR. The crucial property and distinguished feature of our model is that it dynamically relates the HSC compartments to all lines of peripheral blood cells in conditions of chronic exposure to IR. The model is capable of describing experimental findings: i) the slope value of the dose-effect curves describing the hematopoietic inhibition due to chronic IR in the Techa River Cohort, and ii) the dose rate patterns of the fractions of cytopenic states (e.g., leukopenia,. thrombocytopenia). This model describing deterministic effects is joined with the model of late stochastic effects (such as leukemia). The risks of development of late effects were estimated using simulation studies and compared to those estimated empirically.

The developed model of hematopoiesis can be used for: i) prognoses of early effects of chronic exposure to IR such as the level of hematopoietic inhibition and dynamics of subsequent recovery after the end of exposure, and ii) estimations of the risks of late stochastic effects performed not only on the basis of the exposure characteristics (dose, dose rate) but also by taking into account the individual early reaction of an organism to the exposure during the initial exposure period. The prognoses can be used for elaborating preventive approaches in emergency situations involving exposure of large population groups.