Prior Elicitation and Bayesian Analysis of the Steroids for Corneal Ulcers Trial

Abstract

Purpose

To elicit expert opinion on the use of adjunctive corticosteroid therapy in bacterial corneal ulcers. To perform a Bayesian analysis of the Steroids for Corneal Ulcers Trial (SCUT), using expert opinion as a prior probability.

Methods

The SCUT was a placebo-controlled trial assessing visual outcomes in patients receiving topical corticosteroids or placebo as adjunctive therapy for bacterial keratitis. Questionnaires were conducted at scientific meetings in India and North America to gauge expert consensus on the perceived benefit of corticosteroids as adjunct treatment. Bayesian analysis, using the questionnaire data as a prior probability and the primary outcome of SCUT as a likelihood, was performed. For comparison, an additional Bayesian analysis was performed using the results of the SCUT pilot study as a prior distribution.

Results

Indian respondents believed there to be a 1.21 Snellen line improvement, and North American respondents believed there to be a 1.24 line improvement with corticosteroid therapy. The SCUT primary outcome found a non-significant 0.09 Snellen line benefit with corticosteroid treatment. The results of the Bayesian analysis estimated a slightly greater benefit than did the SCUT primary analysis (0.19 lines verses 0.09 lines).

Conclusion

Indian and North American experts had similar expectations on the effectiveness of corticosteroids in bacterial corneal ulcers; that corticosteroids would markedly improve visual outcomes. Bayesian analysis produced results very similar to those produced by the SCUT primary analysis. The similarity in result is likely due to the large sample size of SCUT and helps validate the results of SCUT.

INTRODUCTION

Bacterial corneal ulcers are a major cause of preventable vision loss worldwide.¹ While antibiotics are universally used, there is little evidence on the utility of adjunctive corticosteroids,^2,3 steroid use is controversial,^4,5 and the American Academy of Ophthalmology guidelines on the subject are inconclusive.⁶ In order to expand the evidence base, our group recently completed the Steroids for Corneal Ulcers Trial (SCUT, clinicaltrials.gov NCT00324168, NEI U10-EY015114).⁷ SCUT is a multicenter, international, randomized, double-masked, placebo-controlled clinical trial investigating the effect of topical corticosteroids on visual acuity in culture-positive bacterial corneal ulcers.

Before the results of this study were available, we elicited the opinions of expert clinicians via a questionnaire in order to perform a Bayesian analysis.⁸ Unlike traditional “frequentist” statistics, Bayesian methods synthesize results from observational findings and previous knowledge as a prior probability distribution. Priors can come from previous data or the opinions of experts.⁹ In this study, we used both the results from the SCUT pilot study¹⁰ and expert opinion as prior probabilities for separate Bayesian analysis, allowing comparison. We then used the objective and subjective prior distributions to perform a Bayesian analysis of the clinical trial.

METHODS

Trial Methods

Detailed methods⁷ and baseline characteristics¹¹ for SCUT have been reported. Briefly, 500 patients with culture-positive bacterial corneal ulcers were randomized to receive either topical 1% prednisolone phosphate (Bausch & Lomb Pharmaceuticals, Inc., Tampa, FL) or placebo; all patients received topical 0.5% moxifloxacin (Vigamox, Alcon, Fort Worth, TX). Patients were enrolled at the Aravind Eye Hospitals (Madurai, Coimbatore, Tirunelveli) in India, the Dartmouth-Hitchcock Medical Center in New Hampshire, and the Francis I Proctor Foundation at the University of California, San Francisco (UCSF). The trial was compliant with the Health Insurance Portability and Accountability Act, adhered to the Declaration of Helsinki, and received approval from the Institutional Review Boards at Aravind, Dartmouth, and UCSF. Informed consent was obtained from all participants.

All eligible, culture-positive patients received 48 hours of topical moxifloxacin prior to randomization. Prednisolone phosphate and placebo regimens were provided for 3 weeks, with one drop applied four times daily for the first week, twice daily the second week, and once daily for the third week. All patients received 1 drop of moxifloxacin every hour while awake for the first 48 hours, then 1 drop every 2 hours until re-epithelialization, and then 1 drop 4 times a day until 3 weeks from enrollment. Treating physicians were allowed to stop or change medications at any point during the treatment of the ulcer if they felt it was medically necessary.

The pre-specified primary outcome was logMAR 3-month best spectacle corrected visual acuity (BSCVA), controlling for acuity at presentation. A total of 1,769 patients were screened and 500 patients enrolled, 250 in each arm of the trial. Altogether, 500 patients were enrolled in SCUT in five clinical centers: the Aravind Eye Hospital at Madurai (238), Tirunelveli (156), and Coimbatore, India (91); the Dartmouth-Hitchcock Medical Center (8), and the Francis I. Proctor Foundation at UCSF (7). Complete details on baseline characteristics have been reported previously.¹¹ There was no difference between the sites in enrollment BSCVA (P = 0.98, analysis of variance, ANOVA) or 3-month BSCVA (P = 0.75, ANOVA). BSCVA was measured using an Early Treatment Diabetic Retinopathy Study “tumbling E” chart at enrollment and 3 months from enrollment by masked refractionists who were certified for the study protocol.

Prior Elicitation

The objective prior distribution comes from the results of a pilot study which included 42 patients. That study was performed at the same clinic as the largest enrolling clinic in SCUT, and used the same facilities, personnel, intervention, corticosteroid dosing, and a similar study protocol.¹⁰ The primary outcome for that trial was identical to SCUT, allowing estimation of a prior for the larger study. That study estimated a 0.09 logarithm of the minimum angle of resolution (logMAR) improvement with steroids (95% confidence interval, CI, −0.41 to 0.24). Note that in this report, ‘CI’ refers to traditional frequentist confidence intervals and is used to portray the width of probability distributions. It does not refer to Bayesian credible intervals.

A subjective prior distribution was obtained by eliciting the opinions of experts at two ophthalmologic scientific meetings prior to the results of the trial becoming publically available: The Ocular Microbiology and Immunology Group (OMIG) meeting, October 2010 in Chicago, Illinois, USA,¹² and the International Symposium on Corneal Disorders (ISCD) meeting, January 2011 in Madurai, India. Because the trial enrolled both Indian and North American patients it was important to obtain opinions from experts at scientific meetings in both India and North America. At each meeting, a speaker from our group presented the SCUT study design along with instructions to complete a paper questionnaire which was provided before the talk. The questionnaire contained two methods for obtaining a prior distribution; a multiple-choice graphical approach using normal distributions and a histogram method based on a previous questionnaire,¹³ in which participants were asked to allocate percentage points of probability to discrete intervals. Respondents were also asked for their level of training (resident, ophthalmologist, cornea specialist, etc) and their recent experience by reporting the number of corneal ulcers they had treated in the last 12 months.

Frequentist Analysis

The questionnaire responses provided data on the opinions and demographic information of experts. To that end, we performed traditional frequentist statistics to describe the responses. Note that this is presented separately from the Bayesian analysis that follows. We performed ANOVA for all response data. Differences between ISCD and OMIG responses were calculated by Welch’s t-test. Significance testing and ANOVA were computed using R 2.12 (R Foundation for Statistical Computing, www.r-project.org, Vienna, Austria).

Bayesian Analysis

Using the results of the SCUT pilot trial, we created an objective prior from a normal distribution with a mean of 0.09 and a standard deviation of 0.17. For the subjective prior, questionnaire responses were filtered to only include those that had completed a residency in ophthalmology. Individual responses from the graphical elicitation method were summed and normalized to create a prior distribution that was the arithmetic mean of many normal distributions. Responses from the histogram method were also combined by taking the arithmetic mean to produce a prior distribution composed of step functions. Posterior density for each effect size was calculated by multiplying the likelihood of having obtained the pilot study’s results by the prior distribution’s density at that effect size, and normalizing the result. We also created subsets of responses corresponding to the most enthusiastic and skeptical 10% of respondents, based on mean expectation.^14,15 This allowed us to examine the outcome from the viewpoint of the most opinionated experts.

Conversion between logMAR units and Snellen line equivalents was approximated by 10 Snellen lines = 1 logMAR. Patients with low vision were assigned the following logMAR: 1.7 for counting fingers, 1.8 for hand motion, 1.9 for light perception, and 2.0 for no light perception. All graphics, prior calculations, and posterior calculations were created in Mathematica 7 (Wolfram, Champaign, IL, USA).

RESULTS

Frequentist Analysis

At the October 2010 OMIG meeting, 46 out of approximately 80 attendees (58%) completed the questionnaire. Of the 46 respondents, 80% (37) indicated that they had completed a residency in ophthalmology and were included in the analysis. Of the 37 ophthalmologist respondents, 24% (9) completed the histogram part of the questionnaire. At the January 2011 ISCD meeting, 87 out of approximately 140 attendees (62%) completed the questionnaire. Of the 87 respondents, 86% (75) were ophthalmologists and were included in the analysis. Of the 75 ophthalmologist respondents, 19% (14) completed the histogram part of the questionnaire. Two respondents indicated in the comment section that they did not understand the questions; those responses were incomplete and were not included in the analysis.

Table 1 summarizes the questionnaire results from each meeting. Of the total 112 ophthalmologists completing the questionnaire, 53% (59) were cornea specialists, 17% (19) were cornea fellows, and 30% (34) were general ophthalmologists. OMIG respondents were more likely to self-identify as cornea specialists than ISCD respondents (73% vs 47%, P = 0.015). Among ophthalmologists, ISCD respondents treated more ulcers over the previous year than did OMIG respondents (means 177 vs 78) but the difference was not significant (P = 0.12). We examined the effect of reported level of training and ulcers treated on response to the graphical questions; the effect of these on mean expected effect was not significant for specialist (P = 0.68), fellow (P = 0.60), or number of ulcers treated (P = 0.38). The effect of these measures on the uncertainty response was similarly not significant for specialist (P = 0.61), fellow (P = 0.61), or number of ulcers treated (P = 0.57).

TABLE 1.

Summary and frequentist analysis of questionnaire responses (Note: this is distinct from the Bayesian analysis)

	OMIG (North American meeting)	ISCD (Indian meeting)
	N = 80	N = 140
Completed questionnaire, n/N (%)	46/80 (58)	87 (62)
Ophthalmologists, n/N (%)	39/46 (85)	78/87 (90)
Cornea specialists, n/N (%)	28/46 (61)*	35/87 (40)*
In fellowship, n/N (%)	4/46 (9)	16/87 (18)
Mean ulcers treated (past 1 year), n	78	177
Mean benefit estimate (of ophthalmologists), logMAR	0.124	0.121
Mean estimate of uncertainty (of ophthalmologists), logMAR	0.11	0.13

OMIG, Ocular Microbiology and Immunology Group; ISCD, International Symposium on Corneal Disorders; logMAR, logarithm of the minimum angle of resolution

^*Indicates significance at α < 0.05 by Fisher’s exact test

OMIG respondents believed there to be a mean difference of −0.124 logMAR (~1.2 Snellen lines better) with corticosteroid therapy while ISCD respondents believed there to be a mean difference of −0.121 logMAR (1.2 Snellen lines better); they did not differ significantly (P = 0.88). Note that negative numbers correspond to benefit with corticosteroid use. OMIG respondents expressed a mean uncertainty, reported as standard deviation, of 0.11 logMAR (1.1 Snellen lines) while ISCD respondents had a mean uncertainty of 0.13 logMAR (1.3 Snellen lines); they did not differ significantly (P = 0.14).

Bayesian Analysis

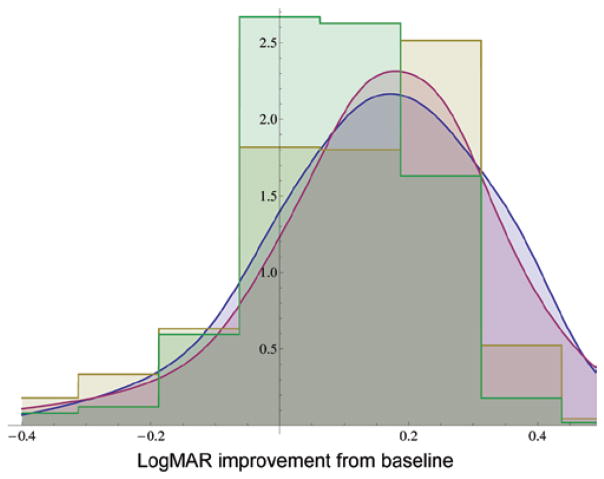
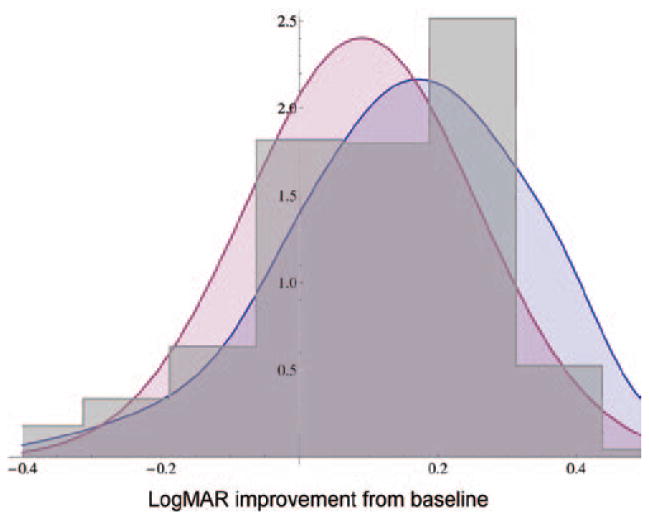
Figure 1 compares OMIG and ISCD prior distribution results for the graphical question. Because the priors elicited from these two meetings were very similar, they were pooled to create one questionnaire-based prior distribution, with equal weight given to each response. Figure 2 compares the graphical priors with the histogram priors for the two meetings. Figure 3 compares all the graphical responses with all of the histogram responses. The graphical response prior has a mean of −0.12 logMAR (1.2 Snellen lines) and a standard deviation of 0.206 logMAR (2 Snellen lines). The histogram response prior has a mean of −0.101 logMAR (1 Snellen line) and a standard deviation of 0.166 logMAR (1.6 Snellen lines). The two distributions have an overlapping area of 0.67 logMAR.

FIGURE 1.

Comparison of prior probability density functions from graphical and histogram methods from two meetings: North American graphical response (blue), North American histogram response (gold), Indian graphical response (red), and Indian histogram response (green).

FIGURE 2.

Comparison of prior probability density functions: pooled graphical response (blue), Steroids for Corneal Ulcers Trial pilot (red), and pooled histogram response (gray).

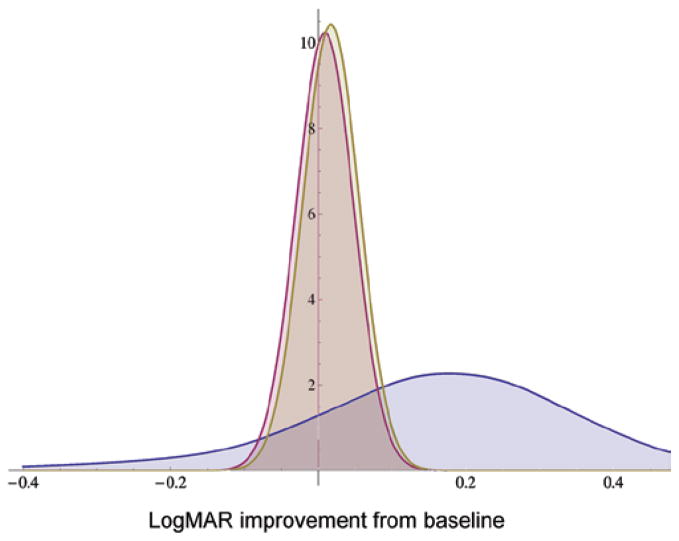
FIGURE 3.

Bayesian analysis using questionnaire graphical response as prior: pooled graphical prior (blue), likelihood of Steroids for Corneal Ulcers Trial results (red), and posterior probability distribution (gold).

The primary outcome of SCUT, 3-month BSCVA controlling for baseline BSCVA, was a benefit of 0.009 logMAR with corticosteroids (95% CI −0.085 to 0.068).¹⁶ With this result as the likelihood function, direct numerical Bayesian analysis was performed for each of the 3 priors. The graphical prior result is shown in Figure 3. Calculated areas corresponding to the probability that steroids improve outcome are 67.5% for the graphical prior, 60.6% for the histogram prior, and 63.6% for the objective prior using SCUT pilot data. The posteriors from each approach are shown on the same axis in Figure 4.

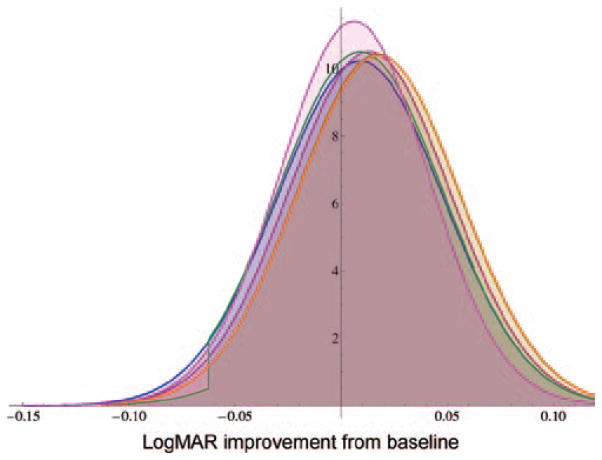
FIGURE 4.

Comparison Steroids for Corneal Ulcers Trial (SCUT) likelihood of results (blue), and posterior probabilities using SCUT pilot as prior (red), posterior using questionnaire graphical responses as prior (gold), posterior using histogram responses as prior (green), enthusiastic graphical responses as prior (orange), and skeptical graphical responses as prior (magenta).

The posterior from the enthusiastic and skeptical priors are also shown in Figure 4. The mean is −0.006 logMAR for the skeptical posterior and −0.017 logMAR for the enthusiastic posterior. Calculated areas of the posterior distribution which are below zero correspond to a 56.7% (skeptical prior) and 67.7% (enthusiastic prior) chance of steroids improving outcome.

DISCUSSION

SCUT evaluated adjunctive topical corticosteroid treatment in culture-positive bacterial corneal ulcers. Here, we gathered expert Indian and North American opinion on the effectiveness of corticosteroids in improving acuity outcomes in bacterial corneal ulcers, and used the opinions to form prior probabilities for a secondary Bayesian analysis. Indian and North American opinions on the effect of adjunctive corticosteroids in bacterial corneal ulcers were nearly identical; both expected a 1.2 Snellen line improvement with steroid treatment. Levels of reported uncertainty in this estimate were also similar. The primary analysis for SCUT found a non-significant 0.1 Snellen line benefit (0.009 logMAR); the resulting Bayesian posteriors for many different priors were not significantly different to the primary outcome.

Clinical trial results are traditionally analyzed using frequentist statistics, which were reported for the primary SCUT outcome. In a frequentist analysis, a P value represents the probability of finding an outcome as skewed as was found by the trial purely by chance, given that there is actually no difference in treatment. Alternatively, Bayesian analysis is a method which combines experimental outcome with belief before the experiment was conducted. The result of a Bayesian analysis, the posterior probability, provides a different perspective on study outcome; the probability of the underlying true effect of the treatment. A Bayesian posterior consistent with the frequentist result can serve to confirm the frequentist result, since it implies agreement between previous knowledge and outcome. Disagreement between Bayesian and frequentist results implies that previous knowledge and outcome are incompatible and both should be reexamined. Our findings confirmed the frequentist result from SCUT. As the power of a study increases, the results derived from a Bayesian posterior will asymptotically approach the results of the frequentist analysis. In our case, the posteriors approached the frequentist results regardless of our choice of the 6 informative priors we created. By calculating areas, we see that the probability that our treatment regimen improves 3-month visual outcomes in culture-positive ulcers is between 60.5% and 67.4%, using the histogram and graphical response priors, respectively. It is a different interpretation to the P value reported in the primary outcome of SCUT, and neither reaches significance.

While obtaining an objective prior distribution from pre-existing data can be straightforward, eliciting a subjective prior from experts is not a standardized procedure. It requires at least two pieces of information from each respondent, an estimate of the effect and a measure of certainty, the latter of which can be difficult to conceptualize. Many methods have been employed, such as asking respondents to assign probabilities to a histogram,¹³ estimate relative probabilities of outcomes¹⁷ or sketch a graph of the probability distribution function.¹⁸

There are a number of issues that must be considered when constructing and distributing questionnaires. For example, respondents may lack understanding of the questions asked or underlying statistical concepts, which can bias results.¹⁹ Although this effect can be mitigated by providing examples, the examples themselves may introduce bias in the form of anchoring, a phenomenon in which respondents “anchor” their response to be compatible with a suggestion. As with all surveys, there is an inherent tradeoff between thoroughness of the questionnaire and response rate; our estimated response rates were 50% for OMIG and 75% for ISCD. Our goals in designing and administering the questionnaire for SCUT were to make the responses fast, intuitive, and flexible while avoiding anchoring. A normal distribution with a checkbox for mean and a visual representation of standard deviation were chosen in order to achieve the first three goals. At each of the meetings, a discussion of the trial design, explanation of the questionnaire, and presentation of two example responses were completed in less than 5 minutes. In order to avoid anchoring, we presented two balanced examples. The histogram response, labeled optional due to time constraints, allowed greater flexibility in response.

The subjective priors were based on expert opinions. There may be more diversity of opinion than found in this group, and thus a wider prior. However, even a totally flat, non-informative (degenerate) prior would lead to a posterior which would be the likelihood itself (red distribution in Figure 3). Thus in this study, increased uncertainty in our prior would not meaningfully change the posterior. It is also important to consider the experts consulted in determining the prior in the context of the experiment being conducted. SCUT enrolled patients from North America and India, which differ in incidence of bacterial keratitis, patient characteristics, and causative organisms. To address these differences, we elicited priors from experts working in each location. In this case, we found that the two priors were remarkably similar. These results indicated that experts in India and North America, considered as two distinct groups, were approximately in agreement. The mean expectation for both groups was an approximately 1.2 Snellen line improvement at 3 months with adjunctive corticosteroid treatment. Others have reported overconfidence among inexperienced individuals which could also lead to bias.²⁰ In order to evaluate this, basic demographic information was collected for further analysis. We found no significant relationships between demographic information and expressed level of certainty. With the data from both meetings combined, the graphical and histogram responses differ but not significantly; histogram responders were more conservative about study outcomes. The histogram response was labeled optional due to time constraints, and self-selection may have led to a statistically savvy subgroup that produced a more realistically conservative estimate of study outcome.

Our method of eliciting a prior has some limitations. The survey was susceptible to acquiescence bias. To mitigate this, we made all responses anonymous.

Additionally, our respondents were a sample of experts at two conferences, and might not be a representative group of ophthalmologists. Response rates were not perfect (approximately 50% and 75%), and may have biased our prior distributions. Our sampling methods provided no information on non-respondents, so we cannot comment on how this group differed from those returning completed questionnaires.

There is also concern over respondents’ understanding of the questions and underlying concepts on the questionnaire. Two respondents commented that they did not understand. Neither had fully completed the questions, and therefore their responses were not included. It is not known how many respondents completed the questions without full understanding.

Aside from performing a secondary Bayesian analysis, there are other benefits of eliciting a prior distribution that reflects expert opinion. One can demonstrate equipoise through the use of a prior; in our case, none of the priors, including the most enthusiastic subset of the graphical responses, were significantly different from the null hypothesis. During the design phase of a study, the mean of the prior distribution is an estimate of effect size that can be used in sample size calculations; if a study is underpowered to detect the anticipated effect size, the design should be reconsidered. Elicitation, if performed early, is an opportunity to receive feedback on your research methods and outcome measures from a number of experts. Surveys can be repeated some time after the results of the study have been released to gauge their impact on expert opinion.

A criticism of subjective Bayesian methods is that since prior distributions are based on expert opinion, the outcomes are vulnerable to bias. This is a valuable consideration; the integrity of the prior distribution can be critical to the validity of the outcome. We made efforts to ensure the integrity of priors, including anonymous questionnaires, repeat elicitation, comparison with an objective prior, and analysis of optimistic and pessimistic subsets. The outcome in this case was essentially invariant in regards to the multiple priors, so it appears that prior elicitation was not critical in our case. Finally, for those who are not receptive to Bayesian methods, the prior elicitation can be interpreted as a survey, which in this case revealed a degree of community equipoise, and demonstrated that the trial was powered to detect the effect size expected by experts.

Here we presented a Bayesian analysis of a large, randomized, masked, clinical trial. We found that North American and Indian respondents were consistent in their views on the efficacy of corticosteroids; they expected a two-line improvement over placebo. In this case, the Bayesian analysis was consistent with the original, pre-specified frequentist analysis. Our survey methods allowed us to sample a large number of experts in a short period of time. Creating meaningful prior distributions is important not only for analysis but also for study design.