Quantifying Additive Interactions of the Osmolyte Proline with Individual Functional Groups of Proteins: Comparisons with Urea and Glycine Betaine, Interpretation of m-Values

Abstract

To quantify interactions of the osmolyte L-proline with protein functional groups and predict its effects on protein processes, we use vapor pressure osmometry to determine chemical potential derivatives dµ₂/dm₃ = µ₂₃ quantifying preferential interactions of proline (component 3) with 21 solutes (component 2) selected to display different combinations of aliphatic or aromatic C, amide, carboxylate, phosphate or hydroxyl O, and/or amide or cationic N surface. Solubility data yield µ₂₃ values for 4 less-soluble solutes. Values of µ₂₃ are dissected using an ASA-based analysis to test the hypothesis of additivity and obtain α-values (proline interaction potentials) for these eight surface types and three inorganic ions. Values of µ₂₃ predicted from these α-values agree with experiment, demonstrating additivity. Molecular interpretation of α-values using the solute partitioning model yields partition coefficients (K_p) quantifying the local accumulation or exclusion of proline in the hydration water of each functional group. Interactions of proline with native protein surface and effects of proline on protein unfolding are predicted from α-values and ASA information and compared with experimental data, with results for glycine betaine and urea, and with predictions from transfer free energy analysis. We conclude that proline stabilizes proteins because of its unfavorable interactions with (exclusion from) amide oxygens and aliphatic hydrocarbon surface exposed in unfolding, and that proline is an effective in vivo osmolyte because of the osmolality increase resulting from its unfavorable interactions with anionic (carboxylate and phosphate) and amide oxygens and aliphatic hydrocarbon groups on the surface of cytoplasmic proteins and nucleic acids.

Introduction

Osmotic stress is a common occurrence and an evolutionary challenge for bacteria, plants, and some types of animal cells. The α-imino acid L-proline is one of several “osmoprotectant” solutes (including the methylated α-amino acid glycine betaine [N,N,N-trimethyl glycine; GB] and the β-imino acid ectoine) that are transported from the growth medium to high concentrations in the E. coli cytoplasm in response to osmotic stress.^{1, 2} Proline is also an important plant osmolyte.^{3, 4} Increased proline synthesis makes wheat more resistant to dehydration stress⁵, and proline accumulates in drought-stressed potatoes⁶ and hot peppers⁷. Proline also increases cold tolerance of maize⁸. Proline and other osmolytes have often been called “compatible” solutes because at molar concentrations they do not greatly affect enzyme activity and do not destabilize or denature globular proteins^{9, 10}. Neverthless, these osmolytes are not inert ; proline stabilizes globular proteins and destabilizes RNA secondary and tertiary structure¹¹. Proline inhibits aggregation of the aggregation-prone P39A variant of the cellular retinoic acid-binding protein CRABP and of constructs containing a polyQ tract like that found in Huntington’s disease¹².

Previously, we quantified the preferential interactions of the solutes urea and GB with extensive sets of model compounds displaying the functional groups of biopolymers. We discovered that these interactions are quantitatively interpreted and predicted as additive contributions from interactions of urea or GB with the individual functional groups on the model compounds, using an analysis motivated by the solute partitioning model^13–15 and based on water accessible surface area^15–21. We interpreted the observed accumulation or exclusion of urea or GB in the vicinity of these groups in terms of non-covalent interactions with these groups, relative to interactions with water. Because GB lacks a hydrogen bond donor (while water has two and urea has four), we interpreted unfavorable interactions of GB with amide and anionic O as an inability to compete with water for hydrogen bonding with these groups, while favorable interactions of urea with these groups are explained by urea having more ways to form hydrogen bonds and/or stronger hydrogen bonds¹⁷. Proline provides an interesting structural comparison since, like GB, proline is zwitterionic but, unlike GB, the proline imino group can function as a hydrogen bond donor, though not as effectively as the primary ammonium group of other amino acids or the primary amine groups of urea.

In the research reported here, quantitative thermodynamic information about the preferential interactions of proline with model compounds displaying the functional groups of proteins is obtained by vapor pressure osmometry (VPO, for sufficiently soluble model compounds) and solubility assays (for sparingly soluble model compounds). Both assays determine chemical potential derivatives dµ₂/dm₃ = µ₂₃ quantifying the effect of proline on the chemical potential of the model compound; µ₂₃ also quantifies the preferential interaction of proline (component 3) with these model compounds (component 2) because the dialysis equilibrium or preferential interaction coefficient Γ₂₃ = −µ₂₃/ µ₃₃ where µ₃₃ = dµ₃/dm₃ . These µ₂₃ values are needed to interpret or predict effects of proline on biopolymer processes, for which the free energy derivative dΔG°_obs/dm₃ = m-value = Δµ₂₃. For soluble model compounds, values of µ₂₃ from VPO measurements also provide the free energy of transfer of the model compound from water to 1 molal proline solution, which cannot be accurately obtained from solubility data alone.

Values of µ₂₃ are interpreted at two levels, first using the hypothesis of additivity and a coarse-grained dissection of the model compound surface into the water-accessible area (ASA) of different functional groups. This first level of analysis yields intrinsic interaction potentials (called α-values) quantifying the interaction of proline with a unit area of each functional group. These α-values are sufficient to interpret or predict interactions of proline with protein surfaces and effects of proline on protein processes in terms of ASA information. At a second (molecular) level, these α-values are interpreted using the molecular thermodynamic analysis of the solute partitioning model (SPM) to obtain microscopic partition coefficients (K_p values) which quantify the accumulation or exclusion of proline in the water of hydration (b₁) of these groups. Comparison of K_p or α-values for interactions of proline, urea and GB with the functional groups of proteins provides significant insight into the molecular interactions that lead to accumulation or exclusion of these solutes in the vicinity of each type of functional group. These K_p or α-values not only explain why proline is an effective osmolyte in vivo and a protein stabilizer, but also allow a quantitative prediction of these effects from ASA information. We also compare α-values predictions of interactions of proline, glycine betaine and urea with the peptide backbone and amino acid side chain with those obtained from amino acid solubility data using the group transfer free energy (GTFE) analysis.²² These comparisons demonstrate the advantages of the α-value analysis to interpret or predict interactions of any solute (e.g. proline, urea, glycine betaine) with a protein, and effects of these solutes on protein processes. In particular, the α-values determined here make proline very useful in conjunction with other solutes as a probe of the amount and type of surface buried in individual steps of protein processes and mechanisms.

Materials and Methods

Details about methods and materials used (chemicals, osmometry/solubility procedures, etc.) and data analysis are provided in SI Text.

Results

Selection of Model Compounds

Preferential interactions (µ₂₃ values) of proline with thirteen soluble salts (arginine hydrochloride, potassium acetate, KCl, potassium glutamate, K₂HPO₄, potassium oxalate, lysine hydrochloride, sodium aspartate, sodium benzoate, NaCl, sodium oxamate, sodium propionate, Na₂HPO₄), eight soluble nonelectrolytes (acetyl-Ala-methylamide (aAma), glycerol, glycine, GB, glycylglycine (glygly), mannitol, urea, and zwitterionic 6-aminocaproic acid (6ACA)), and low-solubility naphthalene were determined as part of this study. Preferential interactions of proline with three low-solubility cyclic dipeptides (cycloGG, cycloAA, cycloLA) were determined from literature data. Compounds investigated here were selected to provide at least two examples of each of the seven (coarse-grained) functional groups of proteins (aliphatic and aromatic C, carboxylate, amide and hydroxyl O, and amino and cationic N), as well as two examples of anionic phosphate O, and of salts of the relevant inorganic ions, in order to vary the surface composition of these functional groups as widely as possible (e.g. urea, oxamate, aAma, and glygly to vary the ratio of amide O to amide N surface areas), and to allow interactions of proline with inorganic ions to also be determined. Preferential interactions of proline with low-solubility compounds (naphthalene, cycloGG, cycloAA, cycloLA) were determined from solubility data, and interactions with soluble compounds were determined by vapor pressure osmometry (VPO).

Determination of interactions of proline with soluble salts and polar compounds by vapor pressure osmometry (VPO)

To determine µ₂₃ for interactions of proline with soluble model compounds, osmolality differences (ΔOsm) between proline-model compound three-component solutions and the corresponding two-component solutions are determined as a function of the concentrations of model compound (m₂) and proline (m₃):

$$\mathrm{\Delta }\text{Osm}=\text{Osm}({\mathrm{m}}_2,{\mathrm{m}}_3)-\text{Osm}({\mathrm{m}}_2,0)-\text{Osm}(0,{\mathrm{m}}_3)$$ Eq. 1

At low to moderate concentrations of the two solutes, multicomponent solution thermodynamic analysis ^23–25 predicts that ΔOsm is proportional to the product of molal concentrations m₂m₃, with proportionality constant µ₂₃/RT for the proline-model compound interaction:

$$\mathrm{\Delta }\text{Osm}=({\mathrm{\mu }}_{23}/\text{RT}){\mathrm{m}}_2{\mathrm{m}}_3$$ Eq. 2

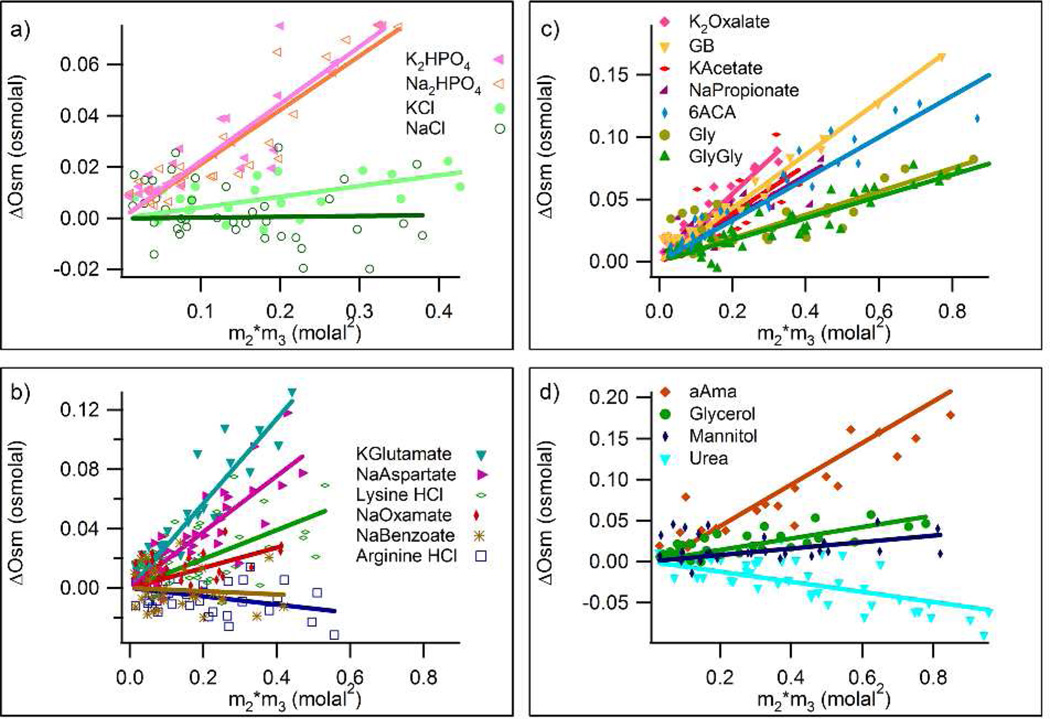
The panels of Figure 1 plot ΔOsm as a function of m₂m₃ for all twenty-one model compounds investigated by VPO. In all cases, ΔOsm is found to be proportional to m₂m₃, showing that values of µ₂₃ are independent of proline and model compound concentrations over the ranges investigated.

Figure 1.

Quantifying Interactions of Proline with Soluble Model Compounds by Osmometry. Excess osmolalities ∆Osm of three component solutions of model compound and proline, determined by VPO, are plotted as a function of m₂m₃, the product of the molal concentrations of model compound and proline. Groups of model compounds are: a) inorganic salts, b) organic salts, c) carboxylate salts and zwitterions, and d) uncharged species. Linear least-squares regression lines are shown for all compounds, with slopes equal to µ₂₃/RT (Eq.1).

Determination of preferential interactions of proline with low-solubility model compounds from solubility data

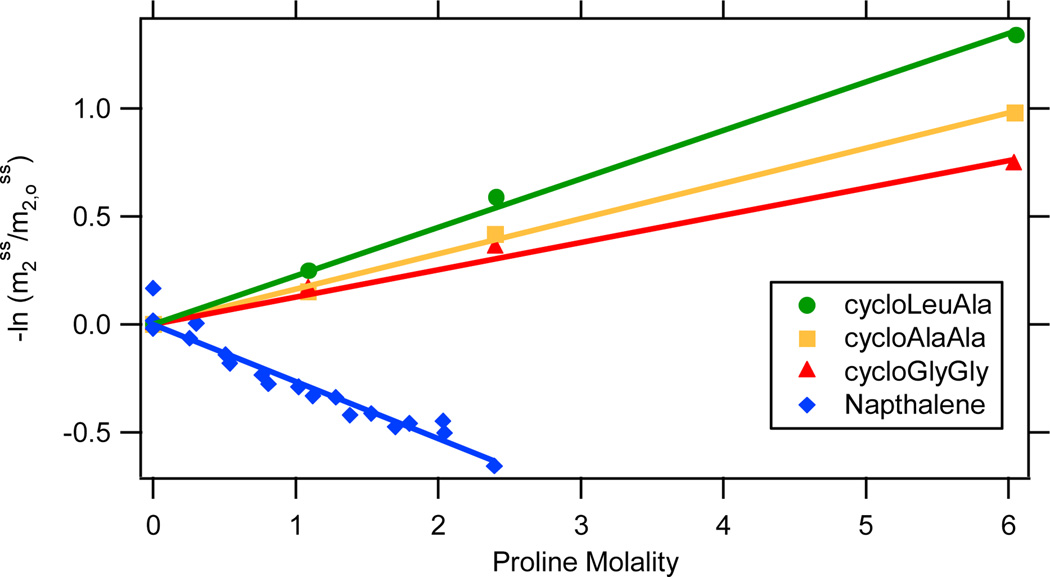
Preferential interactions of proline with four sparingly soluble model compounds (naphthalene and three cyclic dipeptides) are quantified from solubility data. An absorbance-based assay was used to determine the effect of proline on the solubility of naphthalene. Effects of proline on the solubility of three cyclic dipeptides (cycloAA, cycloGG, and cycloLA) were obtained from the literature²⁶. In Figure 2, logarithms of normalized solubilities are plotted vs. proline molality m₃. (The quantity plotted is -lnm₂^ss/m_2,0^ss , where m₂^ss is the molal concentration of the model compound in the saturated solution and m_2,0^ss is the corresponding solubility in the absence of proline.) These plots are linear for all four solutes; from the thermodynamic analysis, slopes -dlnm₂^ss/dm₃ are approximately equal to µ₂₃/RT:

$$-{{\text{dlnm}}_{\text{2}}}^{\text{ss}}/{\text{dm}}_3={\text{μ}}_{23}/[\text{RT}(1+{\text{ε}}_2)]\approx {\text{μ}}_{23}/\text{RT}$$ Eq. 3

In eq 3, the self-interaction nonideality term ε₂ = (dlnγ₂/dlnm₂)_m3 ≈ 0 provided that the saturated solution is very dilute in component 2. The linearity of the plotted data reveals that µ₂₃ is independent of proline concentration over the range examined.

Figure 2.

Quantifying Interactions of Proline with Sparingly Soluble Compounds by Solubility Assays. The negative logarithm of the molal solubility of the model compound in proline solutions (m₂^ss), normalized by its solubility in water (m_2,o^ss), is plotted vs the molality of proline (m₃). Data for cyclic dipeptides are from reference 21. Slopes of these plots are equal to µ₂₃/RT (eq. 4). In all cases, m_2,o^ss is obtained by extrapolation of the full data set to m₃ = 0.

Experimentally determined µ₂₃/RT values (slopes) for all compounds shown in Figures 1 and 2 are presented in Table S1 in the Supporting Material. In the two sections that follow, trends in these µ₂₃ values are discussed, after which they are quantitatively dissected into functional group contributions.

Qualitative deductions from µ₂₃ values about interactions of proline with functional groups of proteins

Inspection of µ₂₃/RT values (Figs. 1, 2; Table S1) that quantify the preferential interactions of proline with this range of model compounds reveals that:

1. Proline increases the chemical potential of most model compounds studied (µ₂₃>0), indicating that interactions of proline with many of the functional groups of proteins must be unfavorable relative to interactions with water.

2. Proline significantly reduces the chemical potential of naphthalene (µ₂₃<0). Therefore interactions of proline with aromatic surfaces are favorable relative to interactions with water, causing accumulation of proline (presumably a cation-π interaction).

3. 6ACA, a zwitterionic ε-amino acid analog of glycine with four additional methylene groups, interacts much less favorably with proline than glycine does, as indicated by its more positive µ₂₃ value. This indicates that the interaction of proline with aliphatic surface is unfavorable relative to water resulting in exclusion of proline from aliphatic surfaces.

4. Mannitol and glycerol have similar amounts of aliphatic surface area, but mannitol has much more hydroxyl surface area. Since the interaction of proline with mannitol is more favorable than its interaction with glycerol, the interaction of proline with hydroxyl surface must be favorable, relative to interaction with water.

5. Proline has a nearly neutral (µ₂₃∼0) interaction with NaCl and KCl so interactions with K⁺ and Na⁺ must be similar in magnitude and opposite in sign to the interaction with the Cl⁻ anion. The simplest interpretation of these results, verified by the quantitative analysis described below, is that interactions of proline with K⁺, Na⁺ and Cl⁻ are small in magnitude.

6. Preferential interactions of proline with phosphate salts (K₂HPO₄, Na₂HPO₄) and small carboxylate salts (potassium acetate, sodium propionate, potassium oxalate) are among the most unfavorable (µ₂₃>0). This indicates that proline is excluded from the vicinity of anionic carboxylate and phosphate oxygens, since its interaction with Na⁺ and K⁺ is small in magnitude.

7. Lysine hydrochloride and arginine hydrochloride both have considerable carboxylate and aliphatic surface area, yet the interaction of proline with lysine hydrochloride is only slightly unfavorable and the interaction of proline with arginine hydrochloride is slightly favorable. Therefore, the interaction of proline with ammonium and guanidinium nitrogens must be sufficiently favorable to compensate for the unfavorable carboxylate interaction deduced above, leading to accumulation. Moreover, proline interacts more favorably with 6ACA than with GB, indicating a favorable interaction of proline with the ammonium group since 6ACA and GB display similar amounts of aliphatic and carboxylate surface.

Quantifying preferential interactions of proline with functional groups of proteins and phosphate

Previous research to quantify and interpret preferential interactions of GB and urea¹⁷ with a similar model compound data set revealed that µ₂₃ values for these solutes were well-interpreted as additive contributions from interactions of these solutes with individual functional groups on the model compounds. For model compounds that are salts, additive contributions to µ₂₃ from interactions with the inorganic ions that make up the electroneutral component must be included. The contribution to µ₂₃ from the interaction of the solute (urea, GB, proline) with a particular functional group on the model compound is represented as the product of an intrinsic interaction potential per unit area (designated α_i) and the ASA of that group:

$$\frac{{\mu }_{23}}{\mathit{\text{RT}}}=\sum _i{\alpha }_i{(\mathit{\text{ASA}})}_i+\sum _{\mathit{\text{ion}}}{\nu }_{\mathit{\text{ion}}}{\beta }_{\mathit{\text{ion}}}$$ (4)

In applying Eq. 4 to salts with one or more inorganic ions, β_ion is the contribution to µ₂₃/RT from the interaction of the solute with an inorganic ion and ν_ion is the number of such ions per formula unit of the salt.

For interactions of GB¹⁶ and urea¹⁷ with model compounds displaying one or more of the functional groups of proteins, α-values obtained from Eq. 4 reproduce µ₂₃/RT values to within ±20% for most compounds in the training set. Here, values of µ₂₃/RT (Table S1) quantifying interactions of proline with 25 model compound were globally fit to Eq. 4, using ASA values in Table S2, to obtain eight interaction potentials (α-values) quantifying interactions of proline with a unit area of each of the principal functional group of proteins and anionic phosphate O, and three interaction potentials β _ion quantifying interactions of proline with each inorganic ion. Fitted values of α and β _ion are listed in Table 1, together with the corresponding α and β_ion values previously obtained for urea and GB¹⁷.

Table 1.

Solute-functional group interaction potentials (α-values) and local solute partition coefficients (K_p) by surface type or ion for proline, glycine betaine, and urea.

Surface Type (i)	104αi, (m−1·Å−2)			Partition Coefficient (Kp) a
	Proline	GB39	Urea19,17	Proline	GB	Urea
Aliphatic C	5.3±1.3	3±3	−1.1±0.5	0.85±0.04	0.92±0.08	1.03±0.02
Aromatic C	−9.2±0.9	−23±4	−8.9±0.5	1.26±0.03	1.62±0.11	1.28±0.02
Hydroxyl O	−0.7±1.3	1±2	−2.5±0.6	1.02±0.04	0.97±0.06	1.08±0.02
Amide O	14.5±4.5	28±10	−8.5±1.8	0.59±0.13	0.24±0.27	1.28±0.06
Amide N	−11.8±3.2	−20±7	−3.7±1.6	1.33±0.09	1.54±0.19	1.10±0.07
Carboxyl O	16.6±4.3	29±2	−3.7±1.6	0.53±0.12	0.22±0.06	1.13±0.05
Phosphate O	18.0±5.2	49±4	−5.8±1.2	0.49±0.15	0.00	1.18±0.04
Cationic N	−12.6±4.3	−12±4	1.6±1.7	1.36±0.12	1.32±0.11	0.94±0.05
Ionic Species (ion)	102×βion, (m−1)
Na+	−4±4	0 b	10±1
K+	−2±4	5±2	14±2
Cl	4±4	−4±4	−16±2

^aK_p calculated from the corresponding α-value using Eq. 5 and b1 =0.18 H₂O Å⁻² for the local water of hydration of these functional groups, as determined previously^28,29, except for phosphate for which a minimum b₁ =0.27 H₂O Å⁻² was determined previously ³⁹

^bβ_ion for the Na-GB interaction was set to zero.³⁹

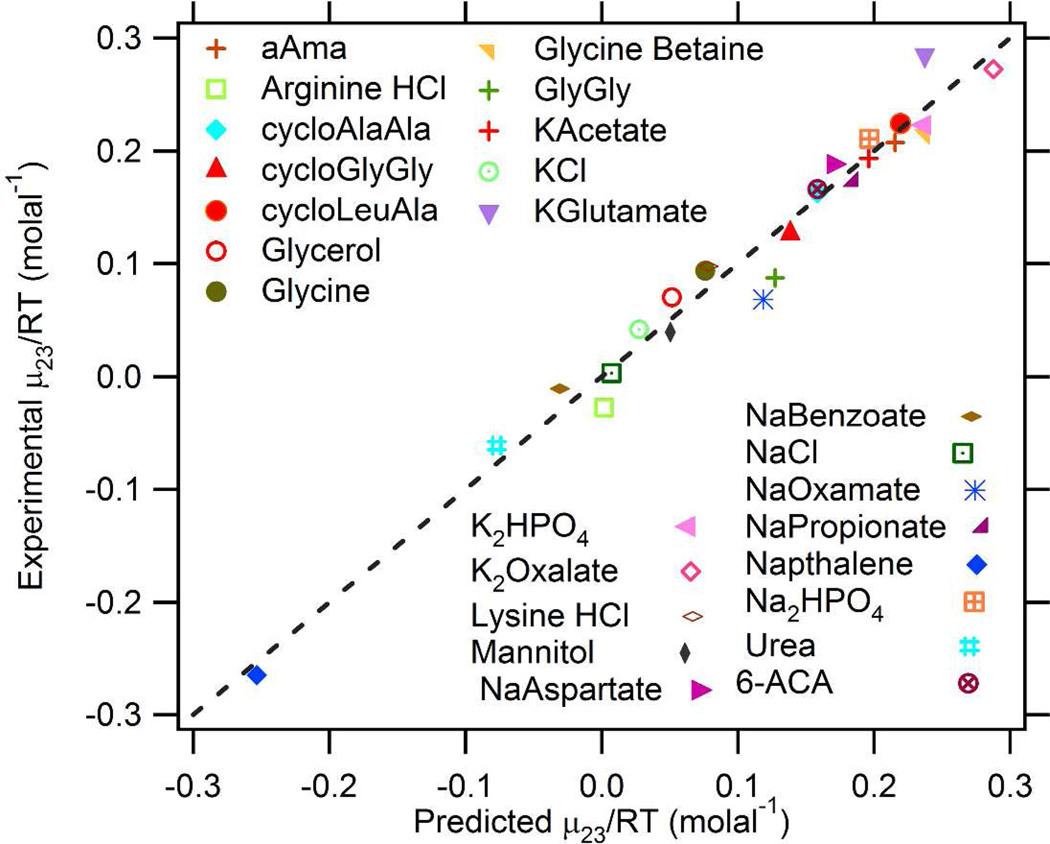
To test this additivity analysis (Eq. 4), values of µ₂₃/RT for interactions of proline with the 25 model compounds in the training set were calculated from the α_i and β_ion values given in Table 1 and ASA values given in Table S2. Figure 3 compares predicted and observed values of µ₂₃/RT, with the dashed diagonal line representing perfect correspondence. Very good agreement is obtained; the average deviation is ±17% where µ₂₃/RT is greater in magnitude than 0.03 m⁻¹, and is ± 0.03 m⁻¹ for compounds where µ₂₃/RT ≈ 0 (NaCl, arginine hydrochloride, sodium benzoate).

Figure 3.

Comparison of Observed and Predicted Proline-Model Compound Interactions. Experimentally-determined µ₂₃/RT for interactions of proline with the training set of 25 model compounds are compared with µ₂₃/RT predicted from 7 functional group α-values and 4 β_ion-values (Table 1) and ASA information (Table S2). The dashed line represents equality of predicted and experimental values.

To test the redundancy and robustness of the fit, we asked which compounds could be eliminated from the data set and be predicted from α-values obtained from analysis of the remaining twenty-four compounds. The 14 compounds cycloLA, cycloAA, cycloGG, 6-aminocaproic acid, sodium oxamate, potassium oxalate, sodium propionate, potassium glutamate, potassium acetate, lysine HCl, arginine HCl, glycine, sodium aspartate, and glycylglycine) can be removed with only small effects (±1 SE) on proline-functional group α-values, proline-ion (β_ion) interaction potentials and on predicted µ₂₃/RT values (<0.04 m⁻¹), including the prediction for the omitted compound. (Indeed at least one combination of 5 compounds (cycloAA, 6ACA, diglycine, NaOxamate, NaAspartate, 6ACA, ) is sufficiently redundant with the other 20 so that it can be eliminated without significant effect on α-values, proline-ion (β_ion) interaction potentials and on predicted µ₂₃/RT values. However, none of the 11 compounds urea, naphthalene, KCl, aAma, NaCl, NaBenzoate, mannitol, glycerol, Na₂HPO₄, K₂HPO₄, and GB can be eliminated without reducing the quality of the fit and of the prediction of their µ₂₃/RT value. NaBenzoate and naphthalene, mannitol and glycerol, and Na₂HPO₄ and K₂HPO₄ are needed to determine α-values for aromatic, hydroxyl O and phosphate O, respectively. NaCl and KCl are needed to obtain accurate β-values, and the other 3 compounds represent unique ratios of surface types needed to decouple otherwise correlated interactions.

Interpreting α-values using the SPM

According to the solute partitioning model (SPM), preferential interactions are manifested as the partitioning of the solute between the local water of hydration of a particular functional group and the bulk solution²⁷. If the preferential interaction between the solute and a functional group is favorable (α_i<0), the solute competes effectively with the water of hydration and accumulates in the vicinity of that group, resulting in a local solute concentration that exceeds its bulk concentration. If the solute-functional group preferential interaction is unfavorable (α_i>0), the solute does not compete effectively with the water of hydration and is excluded from the vicinity of that group, resulting in a local solute concentration is smaller than bulk. Accumulation has a thermodynamic effect analogous to weak binding of the solute and means that addition of solute favors the direction of a process that exposes that functional group, while exclusion favors the direction that buries that functional group.

In the context of the SPM, the accumulation or exclusion of proline in the vicinity of a functional group on a model compound (or protein) is quantified by a partition coefficient K_p,i = m_3,local/m_3,bulk where m_3,local and m_3,bulk are local and bulk concentrations of proline. Except at very high concentrations of model compound (component 2), m_3,bulk = m₃. As previously described^{16, 17,}, K_p,i is related to α_i by Eq. 5, where b_1,i is the surface density of water in the hydration layer.

$${\alpha }_i=-\frac{(K_{p,i}-1)b_{1,i}(1+\epsilon )}{55.5}$$ (5)

Analysis of µ₂₃ or α-values for highly excluded solutes and salts provide a lower bound value b₁ = 0.18 Å⁻² for both hydrocarbon and oxygen functional groups ^{16,28, 29}. Table 1 displays K_p values for proline and compares them to values obtained previously for urea and GB¹⁷ . Application of K_p values from Table 1 to predict surface maps of accumulation or exclusion of proline in the vicinity of a representative peptide (AlaPhe), comparisons of K_p values for proline with urea and GB, and chemical explanations of these K_p values are given in the Discussion.

Interaction of proline with bovine serum albumin (BSA)

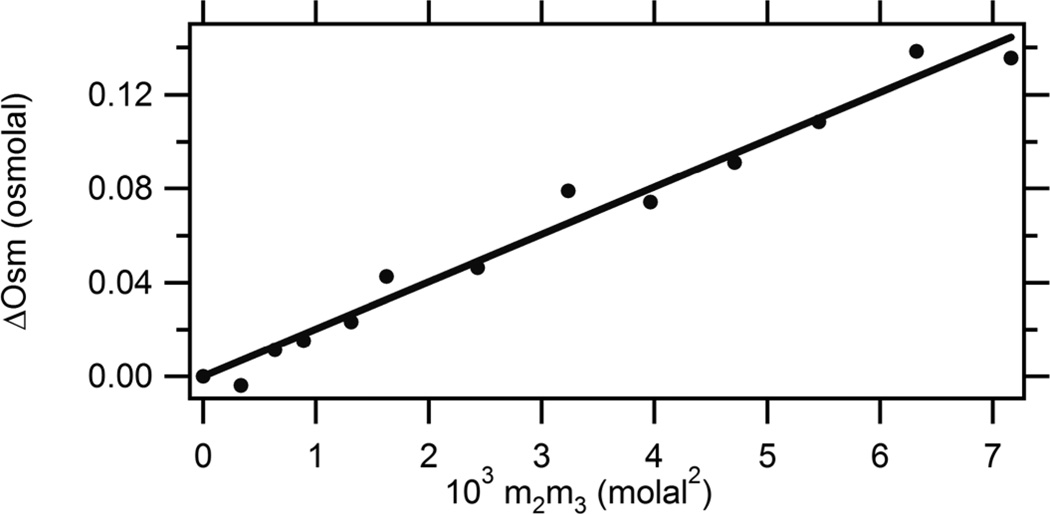
In Figure 4, excess osmolalities (ΔOsm; Eq 1) of proline-BSA solutions as a function of the concentrations of these solutes are plotted as a function of the product of proline and BSA concentrations (m₂m₃) to determine µ₂₃/RT by Eq 2. The linearity of this plot shows that µ₂₃ is independent of proline and BSA concentration; from the slope, µ₂₃/RT = 20.2 ± 0.6 m⁻¹, or µ₂₃ = 11.9 ± 0.3 kcal mol⁻¹ m⁻¹ (Table 2). When normalized by the ASA of native BSA (2.8 × 10⁴ Ų)^{20, 30}, these values are similar to those obtained for interactions of proline with GB and other small solutes from which proline is highly excluded (Table 1), indicating that the interaction of proline with the BSA component is very unfavorable. Strong exclusion of proline from the surfaces of native proteins (and presumably also nucleic acids, since the proline-phosphate interaction is highly unfavorable; Table 1) is a major reason why proline is an effective osmolyte in the concentrated intracellular biopolymer milieu.

Figure 4.

Quantifying Interactions of Proline with Bovine Serum Albumin (BSA) by Osmometry. Excess osmolalities ∆Osm of three component solutions of BSA and proline, determined by VPO, are plotted as a function of m₂m₃, the product of the molal concentrations of BSA and proline. A linear least-squares regression line is shown; from the slope µ₂₃/RT = 20.2 ± 0.6 m⁻¹ (Eq. 2).

Table 2.

Comparison of predicted and observed proline m-values for protein unfolding and µ₂₃ values for interaction of proline with native BSA surface

Protein Process	Proline			GB			Urea
	Experi- mental	α-value prediction	GTFE prediction 37	Experi- mental	α-value prediction	GTFE Predict- ion 37	Experi- mental	α-value predict- ion	GTFE Predict- ion 37
Ribonuclease T1 unfolding m-value (kcal mol−1 M−1)	0.8±0.1 22	1.1±0.5a	−0.03±0.6	0.6±0.1 22	0.7±1.1a	−0.2±0.7	−1.2±0.1 22	−2.0±0.2a	−1.2±0.6
α-chymo- trypsin unfolding m-value (kcal mol−1 M−1)	6.0±0.436	4.3±1.4a	1.8±2.2	5.6±0.336	3.9±3.1a	1.4±3.1	3.0±0.436	−4.5±0.5a	−4.4±2.0
Native BSA µ23 value (kcal mol−1 m−1)	11.9±0.3	7.7±2.0b	−6.6d	21.717	10.8±3.3b	−12.1d	−4.517	−3.6±0.8b	−2.3d

^aα-value predictions use an extended model of the unfolded state (see text)

^bα-value predictions use ASA calculated from PDB 1BM0¹⁸ and neglect interactions of the solute with the Na⁺ ions of the electroneutral BSA component.

^cCalculated as the initial slope of a quadratic fit of ∆G_obs vs urea molarity.³⁶

^dGTFE predictions use side chain and backbone values from ref 22 and ASA calculated from PDB 1BM0¹⁸; these predictions implicitly include counterions of charged amino acid side chains.³⁷

Discussion

Prediction of Interactions of Proline with Peptide and Protein Surfaces; Comparison with Urea and Glycine Betaine

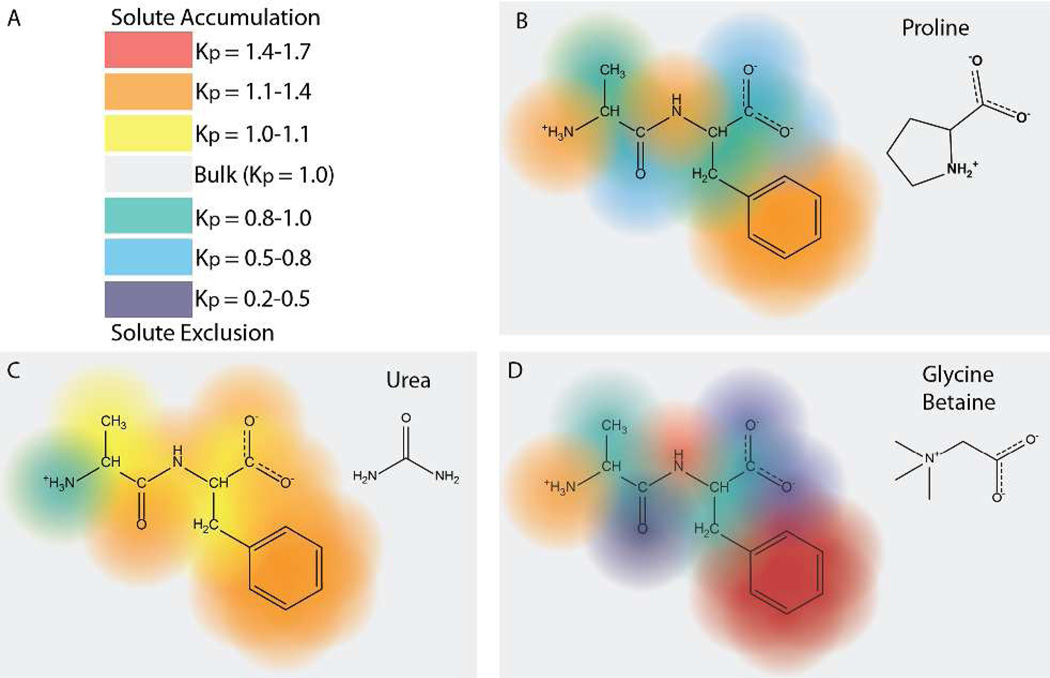
The K_p values of Table 1 allow one to predict the local accumulation or exclusion of proline in the vicinity of the functional groups of any compound displaying these groups, including any peptide or protein surface. These predictions not only provide molecular insight into the thermodynamics of these interactions but also will provide a first level of comparison with results of MD simulations or spectroscopic measurements. As one representative example, Fig. 5 shows the predicted pattern of accumulation and exclusion of proline at the surface of a model dipeptide, AlaPhe, and compares this predicted pattern with those predicted for urea and glycine betaine (GB). Red, orange and yellow indicate strong to weak accumulation; green, blue and violet indicate weak to strong exclusion. Fig. 5 shows that the pattern of accumulation and exclusion of proline in the vicinity of this peptide is more similar to that of GB than to urea. While urea is slightly-to-moderately accumulated near most of the functional groups of proteins, both proline and GB exhibit a wide range of favorable and unfavorable interactions. Both proline and GB are strongly excluded from amide and anionic oxygens and moderately (proline) or weakly (GB) excluded from aliphatic hydrocarbon. Furthermore, both are accumulated at aromatic hydrocarbon surface as strongly (proline) or more strongly (GB) than urea is. Both proline and GB are also strongly accumulated at amide and cationic nitrogens, while urea is modestly accumulated at amide N and weakly excluded from cationic N. The contrasting interactions of these three solutes with aliphatic C and amide O,N surfaces should make them collectively an excellent set of quantitative probes of the amount and composition of the surface buried in processes involving protein folding, in which ∼90% of the surface buried is hydrocarbon or amide.

Figure 5.

Predicted Accumulation or Exclusion of Proline from the Functional Groups of the AlaPhe Dipeptide; Comparison with Urea and Glycine Betaine. Panel A gives a color scale of local partition coefficients K_p (see Eq. 5) used to quantify the accumulation (K_p>1; red to yellow) or exclusion (K_p<1; green to violet) of a solute like proline in the vicinity of functional groups of a model compound or protein. Panels B – D illustrate the predictions using K_p values from Table 1 for the accumulation or exclusion of proline (B), urea (C) and GB (D) in the vicinity of individual functional groups of the AlaPhe dipeptide. Note the relatively uniform accumulation predicted for urea (except at the ammonium group), as contrasted to the large differences in accumulation and exclusion of proline and GB at the different functional groups of AlaPhe.

Molecular Interpretation of Proline Interactions; Comparison with GB and Urea

Here we propose molecular interpretations of K_p values for interactions of proline with the functional groups of proteins (cf. Table 1 and Fig 5). These molecular interpretations are supported by comparisons of K_p values for proline with those for interactions of urea and GB with these functional groups. Since these K_p values come from a “one-way” dissection of the solute-model compound µ₂₃ data, they (like the α -values they are derived from) in general are interpreted as ASA-weighted averages of interactions of all the functional groups of the solute (proline, urea or GB) with the specified model compound functional group.

The following characteristics of the molecular surfaces of proline, GB and urea appear significant for a molecular interpretation of their interactions. Zwitterionic proline, like GB, is expected to be a good hydrogen bond acceptor, with ∼80 A² of anionic carboxylate oxygen ASA (∼30% of total ASA), but the capabilities of these zwitterions as hydrogen bond donors are absent (GB) or limited (proline) as compared to urea or to amino acids with a cationic ammonium group. Cationic nitrogen ASA of proline is only 38 Ų (14% of total ASA), compared with 77 Ų for glycine and 0 Ų for GB. A majority of the ASA of both proline and GB is aliphatic carbon, which accounts for 151 Ų (56%) of total proline ASA and 197 Ų (71%) of total GB ASA, though the methyl groups bonded to the cationic N of GB may not behave like methyl groups bonded to neutral C atoms. The surface of polar urea is almost entirely amide N (129 Ų, 69%) and amide O (49 Ų , 26%) with a small exposure of the central carbon (8 Ų , 4%).

From this surface comparison, urea is expected to interact better than proline (and much better than GB) with amide or anionic oxygens that require a hydrogen bond donor (NH→O) to compete with water and form a hydrogen bond to these groups. However, urea is also expected to interact less well with amide or cationic nitrogens than proline and GB, because the larger ASA and anionic charge of the carboxylate oxygens of proline and GB should make them better hydrogen bond acceptors (O←HN-model compound) than the amide oxygen of urea. (The amide nitrogens of urea are not expected to be effective hydrogen bond acceptors, because of the delocalization of their lone pair electrons.) The contributions of the aliphatic surfaces of proline and GB (but not urea) to the interactions of these solutes with hydrocarbon (or polar) functional groups on model compounds are difficult to predict at present. “Two-way” dissections of sets of solute-model compound µ₂₃ values into additive contributions from interactions of individual functional groups on each species, in progress, are needed to elucidate these contributions and confirm the deductions reported below.

Amide, Carboxylate, and Phosphate O

Interactions of proline with amide O (K_p = 0.6 ± 0.1), carboxylate O (K_p = 0.5 ± 0.1) and phosphate O (K_p = 0.5 ± 0.2) are decidedly unfavorable and of very similar magnitude. In all three cases, the local concentration of proline in the vicinity of these oxygens is predicted to be about half (50–60%) of the bulk proline concentration. GB is much more strongly excluded from phosphate and carboxylate O than is proline. (K_p ≈ 0 for GB-phosphate O and K_p ≈ 0.2 for GB-carboxylate O; predicted local concentrations of GB near anionic O groups are therefore ≤ 20% of the bulk GB concentration). Urea, by contrast, is moderately accumulated near amide O (K_p = 1.28 ± 0.06), carboxylate O (K_p = 1.13 ± 0.05), and phosphate O (K_p = 1.18 ± 0.04).

For all three solutes, the close correspondence between K_p values for these chemically similar but coulombically different oxygens indicates that the origins of these effects are not primarily coulombic attraction or repulsion but rather are chemical (hydrogen bonding) interactions. Indeed the interactions of all three solutes with amide and anionic O are well-explained in terms of the competition between these solutes and water to interact with these oxygens by hydrogen bonding. Water is the hydrogen bond donor in its interactions with both amide and anionic oxygens, so to interact favorably with these oxygens in water the solute must be a better hydrogen bond donor (in quality or quantity of hydrogen bonds) than water.

Urea can form a NH→O hydrogen bond in four ways, as compared to the two ways to form a OH→O hydrogen bond involving water. GB lacks any hydrogen bond donor and so cannot effectively compete with water to interact with amide or anionic O. Proline falls between these extremes, having two ways (like water) to form a NH→O hydrogen bond. Water wins this competition and proline is excluded (K_p < 1) from these O groups, probably because interactions of the remainder of the proline molecule with amide or anionic O are unfavorable, and not because the NH→O hydrogen bond is less favorable than the OH→O hydrogen bond.

Amide and cationic N

Interactions of proline with amide N (K_p = 1.33±0.09) and cationic (ammonium, guanidinium) N (K_p = 1.36±0.12) are moderately and equally favorable; the local proline concentration in the vicinity of these groups is predicted to exceed its bulk concentration by about 33%. The interaction of GB with amide N is at least as favorable (K_p = 1.5 ± 0.2) as it is for proline, while the interaction of GB with cationic N (K_p = 1.32 ± 0.11) is comparably favorable to that of proline. By contrast, the interaction of urea with amide N (K_p = 1.10 ± 0.07) is only modestly favorable, while the interaction of urea with cationic N is modestly unfavorable (K_p = 0.94 ± 0.05).

Comparison of K_p values for these chemically similar but coulombically different nitrogens indicates that the origins of these effects are not primarily coulombic attraction or repulsion but rather are chemical (hydrogen bonding) interactions. Indeed the interactions of all three solutes with amide and cationic N are well-explained in terms of the competition between these solutes and water to interact with these nitrogens by hydrogen bonding. In their interactions with water, these nitrogens primarily function as hydrogen bond donors. To interact favorably with these nitrogens in water, the solute must be a better hydrogen bond acceptor (in quality or quantity of hydrogen bonds) than water.

Favorable interactions of proline and GB with amide and cationic N presumably arise from the formation of strong NH→O hydrogen bonds from these N to the carboxylates of proline and GB. Since the observed effects of all these interactions are the same within uncertainty, clearly the charge state of the N (polar or cationic) is not a major determinant of the interaction strength. Interactions of other functional groups on proline and GB with amide and cationic N, including NH→N hydrogen bonds¹⁷ involving the ammonium group of proline, are expected to be unfavorable. Interactions of urea with amide and cationic N are much less favorable than those of proline and GB with these groups, presumably because the carboxylate groups on proline and GB are better hydrogen bond acceptors than the amide oxygen on urea, and because NH→N hydrogen bonds involving the amide N of urea and cationic or amide N of the model compound are unfavorable relative to hydrogen bonds to water.

Hydroxyl O

The strength of interaction of proline and HO- groups is very similar to interactions with water (K_p = 1.02 ± 0.04), and not very different from the marginally unfavorable interaction between GB and HO- (K_p = 0.97 ± 0.06) and the favorable urea HO- interaction (K_p = 1.08 ± 0.02). These K_p values could be near unity because the interactions of the HO- functional group with all functional groups on these solutes are very similar to interactions with water, or due to compensations between stronger and weaker interactions.

Aliphatic C

Proline, like GB, is only modestly excluded from aliphatic C surface (proline K_p = 0.85 ± 0.04; GB K_p = 0.92 ± 0.08); the average local concentrations of these solutes in the vicinity of aliphatic C surface is only 8–15% smaller than their bulk concentrations. Anionic carboxylate oxygens on these amino acids, like those of sulfate and phosphate groups, are expected to be almost completely excluded from aliphatic C (i.e. K_p ≈ 0)^{17, 29}. The cationic group of proline may also be excluded from aliphatic C, based on the behavior of the ammonium ion¹⁴; interactions of alkylated ammonium cations with aliphatic C have not been quantified. Favorable aliphatic C-aliphatic C interactions must largely compensate for these unfavorable interactions.

Unlike proline and GB, urea is slightly accumulated (K_p = 1.03 ± 0.02) at aliphatic C. This favorable but small interaction is an important part of the reason that urea is a protein denaturant, since aliphatic C accounts for approximately two-thirds of the surface that gets exposed in unfolding a globular protein. It seems unlikely that the C surface of urea (4% of total) accounts for this net favorable interaction. While the interactions of amide N and O with aliphatic C are not expected to be intrinsically favorable, they must be less unfavorable than the interactions of water with aliphatic C.

Aromatic C

Proline interacts quite favorably with aromatic C (K_p =1.26 ± 0.03). By comparison, the GB-aromatic C interaction is significantly more favorable (K_p = 1.62 ± 0.11), while the urea aromatic C interaction is comparable in strength (K_p = 1.28 ± 0.02). Since the interaction of the carboxylate oxygens of proline and GB with aromatic C are expected to be highly unfavorable¹⁷, clearly the interaction of the substituted ammonium cationic groups and of aliphatic C with aromatic C must be quite favorable. For GB, this combined interaction is interpreted as a cation-π interaction¹⁶. While proline also has a formal positive charge on its ammonium group, it is expected to be a less effective cation-π donor because its ammonium hydrogens form interactions with water that must be broken to form a cation-π interaction. This conclusion is supported by enzyme inhibition studies showing that more highly substituted ammonium groups are better cation-π donors³¹ . Possible interpretations of the favorable interaction of urea with aromatic C include hydrogen bonding to and/or stacking of the urea π system on the aromatic ring.¹⁷

Prediction of Proline Interactions with Amino Acid Sidechains and Peptide Backbone of Proteins; Comparison with Urea, GB and with GTFE Approach

Interactions of proline, urea and GB with most amino acid side chains and the peptide backbone of proteins are straightforward to predict from solute-functional group α-values (Table 1) and the amount and composition of their ASA (Table S2). This allows a direct comparison between results of the α-value (µ₂₃ – based) analysis used here and the group transfer free energy (GTFE) approach to analysis of effects of urea and osmolytes on protein processes, which interprets amino acid and dipeptide solubility data to obtain free energies (∆g_tr) for transfer of amino acid side chains and the peptide backbone from water to a 1M solution of the solute in question ^{22, 32–35}. At least for sparingly soluble amino acids, values of ∆g_tr for amino acids are closely related to values of µ₂₃ for the solute-amino acid interaction on the molar scale (see Supporting Information) and are compared in Table S4.

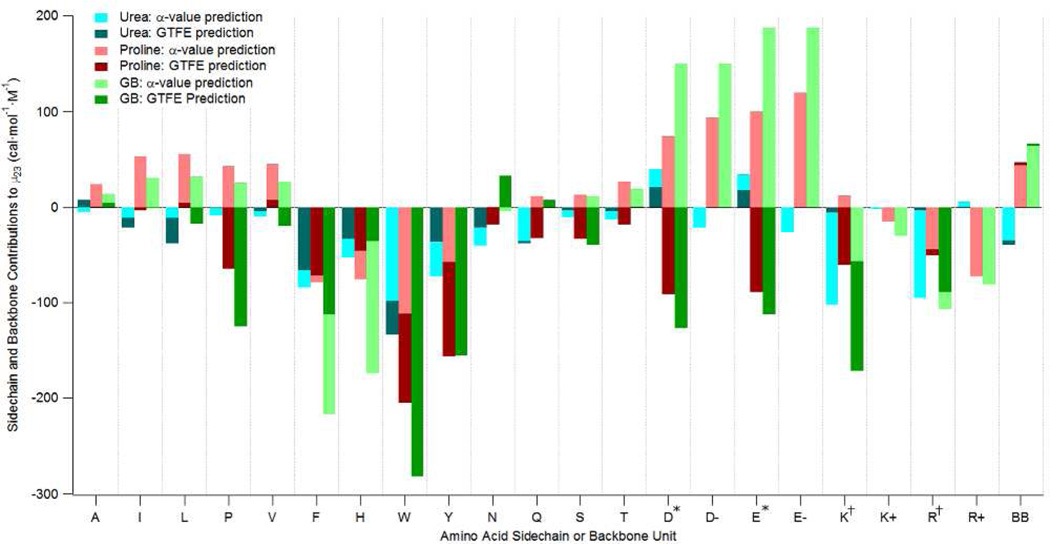
Fig 6 shows that α-value and GTFE predictions for interactions of proline, urea and GB with the peptide backbone, modeled as cGG/2, are in quantitative agreement. Interactions of proline and GB with this backbone model are moderately unfavorable, while interaction of urea is moderately favorable. Interpreted using the α-value analysis, the unfavorable interactions of proline and GB with the peptide backbone result from their unfavorable interactions with amide O and aliphatic C, which are dominant over their favorable interactions with amide N, while the favorable interaction of urea results from its favorable interactions with all backbone groups, especially amide O.

Figure 6.

Comparison of α-Value and Group Transfer Free Energy (GTFE) Predictions of Interactions of Proline, Urea and GB with Amino Acid Side Chains and the Peptide Backbone (BB). α-Value predictions use functional group α-values from Table 1 (converted from molal to molar scale at 1 M) and ASA information from Supp Table S2. GTFE predictions are from ref 29; values for W and Y side chains were not given. α-Value predictions for charged side chains are given both without counterion (specified as D−, E−, K+, R+) and with counterion (D*, E*, K^†, R^†; where * indicates Na+ and ^† indicates Cl−. For charged side chains, GTFE predictions are only available with counterion (i.e. D*, E*, K^†, R^†) Values for histidine are for the uncharged sidechain. For both α-value and GTFE predictions, the backbone is modeled as half the surface area of cyclic glycylglycine (cGG/2). Values plotted are equivalent to free energies of transfer from water to 1M solute.

Figure 6 also shows the very significant differences between α-value and GTFE predictions for interactions of proline, GB and urea with most amino acid side chains. The α-value analysis predicts that the largest unfavorable interactions of proline (and also GB) are with anionic (D⁻, E⁻) side chains; interactions of proline (also GB) with both the aliphatic C and carboxylate O of these side chains are unfavorable. α-Value predictions for the electroneutral combination of anionic side chain and Na⁺ counterion are not very different because the interactions of proline and GB with Na⁺ are small. By contrast, GTFE predictions for interactions of proline and GB with these D and E electroneutral side chains are quite favorable; these predictions are difficult to explain at the molecular level. The unfavorable interaction of proline and GB with anionic side chains predicted by α-value analysis is consistent with the function of these solutes as osmolytes in the concentrated cytoplasmic protein solution, with a high concentration of surface-exposed carboxylates.

For urea, the α-value analysis predicts favorable interactions with anionic (D⁻, E⁻) side chains because of the favorable interactions of urea with both carboxylate O and aliphatic C, but predicts that urea interacts unfavorably with the electroneutral side chain-cation combination because of the very unfavorable interaction of urea with Na⁺. GTFE analysis predicts weaker unfavorable interactions of urea with the electroneutral D and E side chains.

The α-value analysis predicts that proline (also GB) interacts moderately unfavorably with aliphatic hydrocarbon side chains (A, I, L, P, V) because the proline-aliphatic C α-value (also GB) is unfavorable. On the other hand, GTFE analysis predicts that interactions of proline and GB with these aliphatic side chains are either weakly unfavorable or favorable. The unfavorable interaction of proline (also GB) with aliphatic side chains predicted by α-value analysis is consistent with the function of these solutes as in vivo osmolytes and as protein stabilizers, since the surface of globular proteins is 50% hydrocarbon and the surface exposed in unfolding is 70% hydrocarbon. Interactions of urea with these aliphatic side chains are predicted by α-value analysis to be favorable but much smaller in magnitude than for proline and GB. On the other hand, GTFE analysis predicts a mixture of favorable and unfavorable interactions of urea with these chemically similar aliphatic side chains, mostly larger in magnitude than those predicted by α-value analysis.

Not all proline-side chain interactions are unfavorable. The α-value analysis predicts favorable interactions of proline (also GB) with aromatic (F,H,W,Y) and cationic (K+,R+) amino acid sidechains, because interactions of proline and GB with aromatic C are favorable, and interactions of these solutes with cationic N are sufficiently favorable to outweigh their unfavorable interaction with aliphatic C. Urea is also predicted to interact favorably with aromatic side chains, while its unfavorable interaction with cationic N causes it to interact unfavorably with the R+ side chain and neutrally with K+. For most of these situations, the GTFE analysis predicts the same sign but a very different magnitude than the α-value analysis, and in some cases predicts the opposite sign, as for the interaction of proline with the electroneutral K side chain.

Predictions of the alpha value analysis for the interaction of proline (also GB and urea) with the partially polar side chains of N, Q, S and T are small in magnitude. These are neutral to unfavorable for proline (also GB) because unfavorable interactions with aliphatic C and amide O outweigh the favorable interactions of these osmolytes with amide N and hydroxyl O. Urea is predicted by the α-value analysis to interact favorably, though weakly, with all functional groups of all four of these side chains. GTFE analysis also predicts modest interactions of these solutes with these four side chains, differing in some cases in sign from the α-value predictions.

Predictions of a-Value Analysis for the Contributions of the Peptide Backbone and Individual Side Chains to Proline m-Values for Protein Unfolding; Comparison with α-value Predictions for Urea and GB, with GTFE Predictions, and with Experimental Data

Proline unfolding m-values have been reported for α-chymotrypsin and RCAM (reduced, carboxymethylated) RNaseT1, and compared with urea and GB m-values ^{22, 36} Addition of proline stabilizes both proteins against unfolding, with m-values of 0.8 ± 0.1 kcal mol⁻¹ M⁻¹ for RNase T1(25 °C) and 4.3 ± 1.4 kcal mol⁻¹ M⁻¹ for α-chymotrypsin (60 °C). GB is found to be as stabilizing as proline, while urea is of course destabilizing. Urea m-values are similar in magnitude but opposite in sign to those of proline and GB. Table 2 compares these experimental m-values with those predicted from α-values for these solutes (Table 1; 25 °C) and the amount and composition of the ∆ASA, using an extended model for the unfolded state (see Methods) and the equation:

$$m-\text{value}=\mathrm{\Delta }{\mathrm{\mu }}_{23}=\text{RT}\mathrm{\Sigma }{\mathrm{\alpha }}_{\mathrm{i}}\mathrm{\Delta }{\text{ASA}}_{\mathrm{i}}$$ Eq 5

where ∆ASA_i is the change in ASA of functional group i in unfolding.

For RNase T1, the α-value analysis (Eq. 5) predicts a stabilizing proline unfolding m-value of 1.1 ± 0.5 kcal mol⁻¹ M⁻¹, in agreement with the observed proline m-value. GTFE analysis for RNase T1 predicts a small destabilizing proline m-value of −0.03±0.60 kcal mol⁻¹ M⁻¹ at 25°C ²², using an average of extended and more structured models for the unfolded state ³⁷. (The uncertainties in these RNase T1 predictions are large enough that they may not be significantly different.) Also for RNase T1, Table 2 shows that the α-value prediction for the stabilizing GB m-value agrees with the experimental value, while the α-value prediction for the destabilizing urea m-value agrees only semiquantitatively with the experimental value. The GTFE prediction for urea is in quantitative agreement with the experimental urea m-value, but GTFE predicts a small destabilizing GB m-value

For α-chymotrypsin, Table 2 shows that m-values predicted at 25°C from α-value analysis, using the structure of monomeric α-chymotrypsin (1YPH) and an extended chain model of the unfolded state, also agree reasonably well with experimental m-values, though since the temperature coefficients of the α-values are unknown this comparison cannot be made quantitatively. For proline and GB, GTFE predictions at 25°C differ from both the α-value predictions and experimental m-values; for urea, GTFE and α-value predictions agree with one another (though using different models of the unfolded state) and with the experimental m-value.

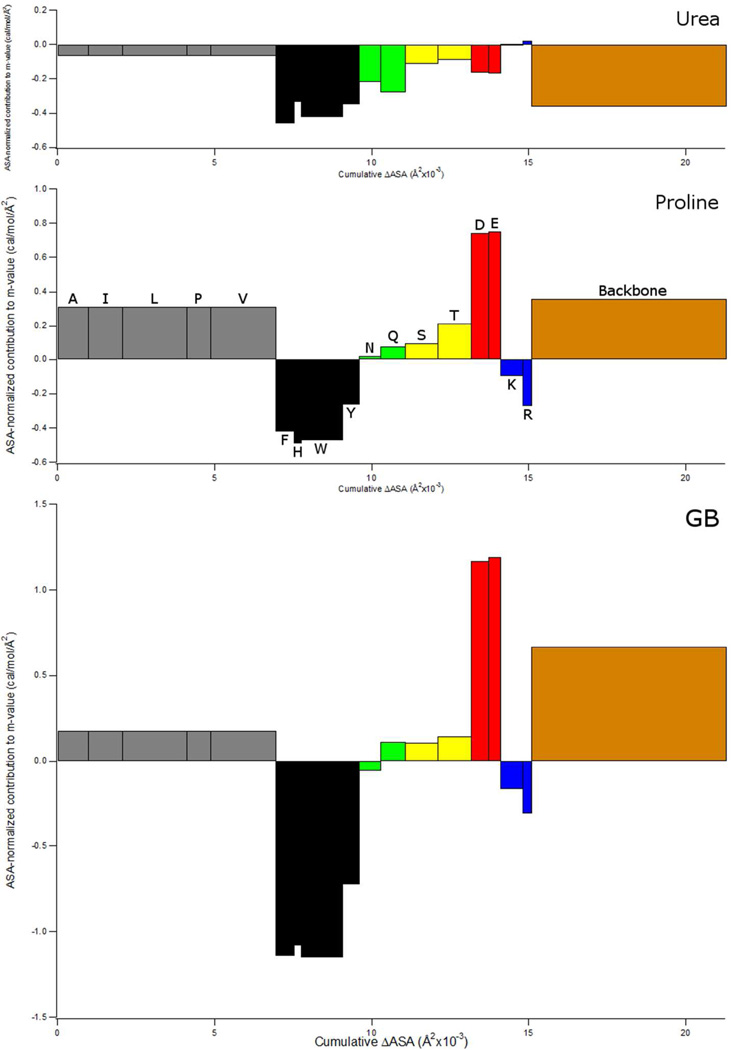
The composition of the protein surface exposed in unfolding α-chymotrypsin is quite representative of the average for globular proteins. Hence we use α-chymotrypsin unfolding and the α-values of Table 1 to predict the contributions of the peptide backbone and most of the different amino acid side chains to the proline unfolding m-value, and compare effects of proline with those of urea and GB at this level. Similar graphs for GTFE predictions for these solutes are shown in Figure 3 of reference 17. Figure 7 illustrates these results on bar graphs, using ASA-normalized contributions of each side chain and the backbone to the solute m-value as the y-axis and the ΔASA of unfolding as the x-axis. The same scale is used for the y-axis for all three solutes to allow easy visual comparison of the predicted effects. Side chains are grouped, with aliphatic and aromatic side chains on the left and polar and charged side chains as well as the polar backbone on the right. Areas of each portion of the bar graph represent the contributions of individual side chains and the peptide backbone to the predicted solute m-value for unfolding α-chymotrypsin at 25°C.

Figure 7.

Comparison of α-Value Predictions of Backbone and Side Chain Contributions to Proline (Panel B), Urea (Panel A) and GB (Panel C) m-values for unfolding chymotrypsin (PDB Code 1YPH). For each side chain or the peptide backbone, the area of the rectangle is the contribution to the m-value, and is the same as the contribution to µ₂₃ (or ∆µ₂₃) predicted from α-values and ASA information in Fig. 6. Width of rectangle is the total amount of accessible surface area of that sidechain (or backbone) exposed in unfolding chymotrypsin, and height of rectangle is the contribution per A² of that sidechain or backbone to the m-value. The same scale is used for all three solutes. Bar color denotes type of amino acid (aliphatic amino acids are grey, aromatics are black, amides are green, hydroxyls are yellow, anionic are red, cationic are blue, and the backbone is brown). Cysteine and methionine are not shown.

Figure 7 predicts that proline-backbone and net proline-sidechain contributions to the unfolding m-value are positive (unfavorable) and of similar magnitude. The group of five aliphatic (A, I, L, P, V) sidechains and the peptide backbone, whose intrinsic interactions with proline are predicted to be moderately unfavorable (∼0.3 cal/mol/A²; see Fig. 7), are predicted to make the largest positive contributions to the m-value because they make up the majority of the ΔASA (∼30% each). Intrinsic interactions of proline with anionic (D, E) sidechains are more strongly unfavorable (∼0.7 cal/mol/A²) but make a smaller contribution to the m-value because their contribution to the ΔASA is small. Intrinsic interactions of proline with aromatic (F, H, W, Y) and cationic (K, R) side chains are predicted to be favorable: these are relatively strong (∼ 0.3–0.5 cal/mol/A²) for aromatic side chains and moderately strong (∼0.1–0.3 cal/mol/A²) for cationic side chains. Intrinsic interactions of proline with polar (N, Q, S, T) side chains are predicted to be unfavorable with small to moderate magnitudes (∼0–0.2 cal/mol/A²). Of these four types of side chains (anionic, aromatic, cationic, polar) only for aromatic side chains is the product of intrinsic interaction strength and contribution to the ΔASA of unfolding (given by the area in Fig 7) sufficiently large to make a major contribution (in this case favorable) to the predicted proline m-value.

Comparison of predictions of the α-value analysis for proline with those for GB and urea in Figure 7 shows that with the exception of the asparagine sidechain, contributions to the proline and GB m-values for the different side chains and the peptide backbone exhibit the same sign but different magnitudes. Because proline interacts less favorably than GB with uncharged and cationic sidechains and more favorably than GB with anionic side chains and the backbone, the predicted m-values for these two osmolytes are very similar. For proline, contributions to the predicted m-value from unfavorable interactions with the peptide backbone and with sidechains are similarly large. For GB, on the other hand, the large favorable interaction with aromatic side chains almost completely counterbalances the smaller unfavorable interactions with aliphatic, polar, and anionic side chains, resulting in a small net contribution of side chain interactions to protein stability; the stabilizing effect of GB is largely the result of its unfavorable interactions with the backbone. The destabilizing effect of urea, as discussed previously, is distributed relatively equally between favorable interactions with the backbone and with all side chains except R, especially with aromatic side chains and the amide-containing side chains of N and Q.

Interactions of proline with native bovine serum albumin; comparison with GB and urea

In the previous section, α-value analysis was used to predict the interactions of proline, urea and GB with the functional groups exposed in unfolding a globular protein, and thereby interpret the unfolding m-value. Also important are the interactions of proline and these other solutes with the surface of native proteins and nucleic acids, which determine their ability to function efficiently as osmolytes in the concentrated biopolymer milieu of the cytoplasm. If present in the growth medium, proline and GB are imported into the E. coli cytoplasm under conditions of osmotic stress. Accumulation of proline allows the cell to maintain a larger fraction of the amount of cytoplasmic water present before the osmotic stress than the mixture of osmolytes (principally glutamate and trehalose) that is synthesized in minimal media.³⁸ GB is even more effective in this regard, is imported in preference to proline, and allows the cell to retain almost all the original amount of water (and growth rate) over a wide range of osmolality². Urea, which is membrane-permeable, is not used as an E. coli osmolyte.¹

Table 2 shows predicted contributions to µ₂₃ for the interactions of proline, GB and urea with native BSA surface. This surface (55% hydrocarbon, 20% amide, 16% carboxylate, 13% cationic) may be a useful model for the surface composition of E. coli cytoplasmic proteins. VPO measurements of the interaction of proline with BSA (Fig. S1) yield µ₂₃ = 11.9 ± 0.3 kcal mol⁻¹ m⁻¹ at 25° (Table 2). This is a significantly unfavorable preferential interaction, corresponding to modest exclusion of proline from the vicinity of BSA (average local proline concentration ∼20–25% less than bulk). From α-values (Table 1) and the surface area and composition of native BSA (Table S3) the predicted value at 25°C (neglecting the small contribution of Na⁺ counterions of the electroneutral BSA component) is µ₂₃ = 7.7 ± 2.0 kcal mol⁻¹ m⁻¹ for proline, in semiquantitative agreement with the experimental value. GB is a more effective in vivo osmolyte than proline³⁸. Consistent with this, the previously-reported preferential interaction of GB with BSA (observed µ₂₃ ≈ 21.7 kcal mol⁻¹ m⁻¹; predicted µ₂₃ = 10.8 ± 3.3 kcal mol⁻¹ m⁻¹) ³⁹ is more unfavorable than for proline, though agreement with the µ₂₃ value predicted from α-values, ASA and composition information (µ₂₃ = 10.8 ± 3.3 kcal mol⁻¹ m⁻¹) is not as good as for proline. Urea is much less effective than either proline or GB at boosting osmolality in concentrated biopolymer solutions: urea-BSA preferential interactions are favorable (observed µ₂₃ ≈ −4.5 kcal mol⁻¹ m⁻¹; predicted µ₂₃ = −3.6 ± 0.8 kcal mol⁻¹ m⁻¹). Normalized by surface area, the interactions of all three solutes with the native protein surface of BSA are more unfavorable (or, for urea, less favorable) than their interactions with the surface exposed in unfolding globular proteins (see for example Table 2). The unfavorable interactions of GB and proline with native protein surfaces and with nucleic acid phosphates² make them very good choices as osmolytes in the concentrated biopolymer environment and relatively high surface:volume ratio of the cytoplasm.²

Comparisons of α-Value and Group Transfer Free Energy (GTFE) Analyses

Figure 6 shows that the α-value and GTFE analyses yield significantly different predictions for the interactions of all three solutes with many amino acid sidechains, and thus in general give different m-value predictions (Fig 7). Table 3 presents a summary comparison of these two analyses. A first important difference is the input data for these two analyses. The GTFE analysis is based entirely on solubility data for amino acids and dipeptides; as discussed previously (^{17, 25}; also see Supporting Information), these solubility data provide a simply-interpretable transfer free energy (i.e. a direct measure of µ₂₃) only for solutes where the approximation in Eq 3 is adequate. GTFE analysis uses glycine as a reference to dissect these amino acid transfer free energies and obtain side chain contributions, which are not dissected further. (This GTFE dissection assumes that the contributions of the α-carbon, ammonium nitrogen and carboxylate oxygens of each amino acid to its transfer free energy are the same as for glycine, even though the various side chains reduce the water accessible surface area of these groups from their values for glycine (see Table S2).) By contrast, α-value analysis is based on VPO measurements for soluble model compounds displaying functional groups of proteins, and solubility data for low-solubility model compounds displaying these functional groups.

Table 3.

Comparison between α-value and GTFE-based analyses of solute effects on protein processes.

	α-value analysis	GTFE analysis 22,37
Experimental method for high- solubility model compounds	Vapor Pressure Osmometry	Solubility
Experimental method for low- solubility model compounds	Solubility or micelle formation17	Solubility
Building blocks of proteins used to quantify solute interactions	Functional groups (aliphatic and aromatic C; carboxylate, amide and hydroxyl O)	Peptide backbone, amino acid side chains
Number of model compounds	Variable (25 for proline, 27 for GB39 46 for urea17)	21 (20 amino acids+cGG)
Number of interaction values (α or GTFE/ASA) obtained from analysis	7 (7 functional groups)	20 (19 sidechains+ backbone)
Redundancy of Model Compound Set	Yes	No
Use of Hypothesis of Additivity of contributions	Yes, by unified atom or functional group(Eq. 4)	Yes, by sidechain or backbone
Test of Hypothesis of Additivity	Yes, at solute-functional group level	No
Treatment of counterions of charged amino acids	Separated from sidechain, quantified individually	Treated implicitly with sidechain; not separable
Unfolded state model	All-trans extended (but other models can be used)	Average of extended and structured (but other models can be used)
Uncertainty values	Based on error propagation from α- value uncertainty	Not reported

By comparison with the GTFE analyses, the α-value analyses of interactions of proline, GB and urea with protein functional groups are based on more extensive model compound data sets and obtain fewer parameters (α-values) quantifying interactions of the solute with the groups on the model compounds. Since the number of model compounds used in the α-value analyses greatly exceed the number of fitted α- and β-values, these analyses provide some redundancy and in each case test and validate (see for example Fig. 3) the hypothesis of additivity (Eq 4). Additivity at the level of solute-side chain and solute-backbone interactions is assumed but not tested in the GTFE analysis. Interactions of proline, GB and urea with the sets of model compounds used in the α-value analysis indeed are well-described as the sum of interactions of these solutes with the individual functional groups of the model compounds (Eq. 4). The α-values for interactions of these three solutes with the functional groups of proteins exhibit reasonable trends and make good chemical sense when interpreted in terms of noncovalent interactions (hydrogen bonding, cation-π, etc.).

At a more detailed level, α-value analysis separates interactions of the solute with charged sidechains from interactions with their counterion, not possible with the GTFE analysis. This is predicted to have only a minor effect for proline and GB, which interact only weakly with these counterions, but should have a larger effect for urea.

Finally, and most significantly, only α-value analysis can be used to obtain a quantitative interpretation of solute thermodynamic and kinetic m-values in terms of the amount and composition of the biopolymer surface buried in the steps of a protein process like folding or binding. A recent example is the use of urea and GuHCl kinetic m-values together with activation heat capacity data for folding and unfolding rate constants for 13 proteins to quantify the amounts of amide and hydrocarbon surface buried in folding to and from the high free energy transition state (TS)⁴⁰. Solute m-value data have also been obtained for protein-nucleic acid interactions, to probe for coupled folding and formation of new interfaces in the steps of transcription initiation by RNA polymerase^41–43 as well as in the binding of lac repressor to lac operator DNA⁴⁴. For a full interpretation of these data, α-values for interactions of these solutes with nucleic acid surfaces are needed; such data are now available only for urea.¹⁹

Abbreviations

GB

glycine betaine (N,N,N-trimethylglycine)

GTFE

group transfer free energy

ASA

accessible surface area

VPO

vapor pressure osmometry

SPM

solute partitioning model

TS

transition state