Extending the Peters-Belson approach for assessing disparities to right censored time-to-event outcomes

Abstract

The Peters-Belson method was developed for quantifying and testing disparities between groups in an outcome, using linear regression to compute group-specific observed and expected outcomes. It has since been extended to generalized linear models for binary and other outcomes, and to analyses with probability-based sample weighting. In this work, we extend the Peters-Belson approach to right-censored survival analysis, including stratification if needed. The extension uses the theory and methods of expected survival based on Cox regression in a reference population. Within the PB framework, among the groups to be compared, one group is chosen as the reference group, and outcomes in that group are modeled as a function of available predictors. Using this fitted model’s estimated parameters, and the predictor values for a comparator group, the comparator group’s expected outcomes are then calculated and compared, formally with testing and informally with graphics, to their observed outcomes. We derive the extension, show how we applied it in a study of incontinence in nursing home elderly, and discuss issues in implementing it. We used the “survival” package in the R system to do computations.

1. Introduction

Assessing disparities in health care is an issue of great concern to patients, families, researchers, and funding organizations. The term ‘disparity’ has had various definitions in health care research, but a commonly accepted recent definition comes from the Institute of Medicine, which defines racial/ethnic disparities as “racial or ethnic differences in the quality of healthcare that are not due to access related factors or clinical needs, preferences, and appropriateness of intervention” [1 (pp.3-4)]. Going beyond this definition, disparities may exist between groups defined by race/ethnicity, sex, age, source of payment for health care, or other characteristics. Before disparities can be addressed though policy changes or interventions, they must be defined and then measured. Statistical modeling is often employed to examine how characteristics (e.g., demographics, access to care) are associated with differences in outcome between groups, while controlling for the many aspects of health status and health care that may differ between groups but not represent a disparity [1,2].

For simplicity, in our development of this work we assume there are two groups of interest, one presumed to be preferentially treated or somehow advantaged relative to the other. Two main approaches exist for assessing disparities when other characteristics of the patients may also impact the outcome of interest. The first is a traditional regression approach, where the outcome of interest (be it binary, ordinal, count, continuous, time-to-event, or some other type) is regressed against the grouping of interest (such as race/ethnicity) along with other patient characteristics potentially relevant to the outcome; interactions of the grouping with the characteristics may or may not be included. When interactions are not present, the disparity is quantified by the group effect, which is the difference in predicted outcome between two persons with identical characteristics but from different groups. Depending on the statistical model used, “difference” may be relative or absolute. When some characteristic interacts with the group effect, the disparity between groups can be quantified at each value of the characteristic.

The second approach, the Peters-Belson (PB) method, also uses regression but in a two-stage approach. In the first stage of a PB analysis, a regression, using data for the advantaged group only, is fit including as predictors the patient characteristics (except for group membership) that are potentially relevant to the outcome. Then, for members of the presumed disadvantaged group, values of their characteristics are inserted into the advantaged group’s fitted regression model to produce predicted outcomes. Loosely speaking, these predicted outcomes represent what we would expect to see if the presumed disadvantaged group had been members of the advantaged group. In the second stage of PB analysis, the predicted outcomes for the presumed disadvantaged group are statistically compared to their own observed outcomes, and this comparison defines the unexplained disparity. The appeal of the PB approach is this explicit statistical comparison of observed to expected outcomes while allowing for typical regression adjustment for relevant characteristics. Duan et al. (2008) have proposed a different approach to defining disparities using counter-factuals that is in some aspects similar to PB, but they do not consider PB directly [2].

PB has historically been used in legal settings, but recently has been taken up by health care researchers. PB was originally developed for continuous outcome regression [3], and has since been extended to logistic regression [4] and to generalized linear models [5]. Graubard, Rao, and Gastwirth [6] introduced a weighted approach for complex survey data, appropriate for either linear or logistic regression. Recent examples of the use of PB have been in racial/ethnic disparities in cancer screening [7], racial/ethnic disparities in immunization among the elderly [8], geographic disparities in breastfeeding rates [9], equal employment opportunities [10], and geographic disparities in underinsurance among children with special health care needs [11].

The goal of the present work is to further extend PB to time-to-event outcomes in the context of Cox proportional hazards models with independent right censoring [12], with or without stratification. This was developed for use in a research project (referred to below as the REDSKIN study) on disparities among nursing home elderly in incident incontinence and in sequelae of incontinence such as pressure ulcers and dermatitis. The REDSKIN project’s purpose was to determine whether racial/ethnic groups differed in outcomes such as post-admission time to incontinence or time to pressure ulcers after adjusting for characteristics believed to be clinically associated with the outcomes. When groups appeared to differ, the PB analysis was to be followed by further analyses to determine which, if any, of the available predictors partially explained why the groups differed and if any such predictors were identified, to then propose interventions intended to remove or reduce the disparity.

To provide an intuitive analog to the current work, Section 2 gives a brief overview of PB for logistic regression. Section 3 extends PB to survival analysis based on the general theory for comparing expected and actual survival for a proportional hazards model [13]. Section 4 discusses our specific application in the REDSKIN study, some representative results, and associated complications that arose during implementation. Section 5 concludes by discussing issues in PB in general and in this extension of PB. The Supplementary Web Materials give R code [14] for computing the PB analysis using existing R packages, with output.

2. PB using logistic regression

In the United States, nursing homes certified by the Centers for Medicare/Medicaid Services must fill out a federally mandated standardized data collection form for each resident upon admission, called the Minimum Data Set (MDS) [15]; this form is also used internationally. The MDS (Version 2.0) records race/ethnicity categories as White non-Hispanic, Black non-Hispanic, Hispanic, Asian/Pacific Islander, and Native American/Native Alaskan. In our study of incontinence and related conditions, as in studies of racial/ethnic disparities generally, the supposedly advantaged group is White non-Hispanic (subsequently referred to as Whites) and the other groups are deemed potentially disadvantaged. This labeling is no more than a convention, though an understandable one, and in fact some groups we call potentially disadvantaged turn out to have better outcomes than Whites with similar characteristics. For simplicity, we will describe the PB approach for comparing binary outcomes in Whites to non-Hispanic Blacks (subsequently referred to as Blacks). The same process can be used to compare other pairs of groups defined by race/ethnicity or by any characteristic of interest.

In our nursing home context, a logistic regression approach is sensible for an uncensored outcome such as having a treatment plan in place for newly occurring dual incontinence (DI). Incident DI was captured in our data by following NH admissions without DI for up to three years, until DI was recorded on the MDS or the resident was censored. Our sample for an analysis of DI treatment is thus restricted to those Blacks and Whites with newly occurring DI, and our outcome of interest is whether they have a concurrent DI treatment plan (yes or no). The first step in the Peters-Belson method is to fit a logistic regression with this outcome using the Whites only. For the ith White resident, the logit of the probability of having DI, p_wi, is modeled as:

$$\ln (p_{\mathit{wi}}/(1-p_{\mathit{wi}}))=X_{\mathit{wi}}{\beta }_w,$$

where X_wi represents the vector of this i^th resident’s characteristics that are presumed to be related to the treatment plan outcome, and β_w represents the vector of regression coefficients for those characteristics. We use the subscript w to indicate that they are estimated using data from White residents only. (For this logistic regression overview, we ignore the fact that our sample is clustered in nursing homes.) The second step in the PB method uses this fitted logistic model to predict the treatment outcome in individual Blacks. In effect, this asks: what outcome would we expect for each Black resident if they had the same characteristics they actually do have, but they were White? (In the Discussion section, we elaborate on some hidden assumptions behind this interpretation.) For the i^th Black resident, then, we predict with:

$${\widehat{p}}_{\mathit{wi}}^b=\exp (X_{\mathit{bi}}{\widehat{\beta }}_w)/(1+\exp (X_{\mathit{bi}}{\widehat{\beta }}_w)).$$

In the simplest approach to testing whether a disparity is present, we compute this predicted probability for each Black resident in the sample, average them across the i=1,…,n_b Black residents, and use that average as our predicted outcome for the Black residents as a group:

$${\overline{p}}_w^b=\frac{1}{n_b}{\sum }_{i=1}^{n_b}{\widehat{p}}_{\mathit{wi}}^b.$$

Separately we compute the observed proportion of Black residents with this outcome, p̂^b, which has no subscript w as it depends on observed data in the Blacks only. We then carry out a one-sample test of this observed proportion p̂^b with null hypothesis $p^b={\overline{p}}_w^b$ and alternative hypothesis either one-sided (such as $p^b>{\overline{p}}_w^b$) or two-sided $(p^b\ne {\overline{p}}_w^b)$, as specified a priori. This could be done either with a normal approximation or with an exact Binomial test, depending on sample size. This simplest procedure naïvely treats ${\overline{p}}_w^b$ as a known population proportion rather than as a quantity predicted with error and correlated with the sample statistic p̂^b (because both are based on data from the Blacks), and thus will result in a test statistic that is inappropriately big, hence a p-value that is too small.

A more computationally expensive alternative is to bootstrap the calculation of expected and observed, and thus the test statistic, by re-sampling Blacks with replacement. For each re-sample, we would compute ${\widehat{p}}_{\mathit{wi}}^b$, compute ${\overline{p}}_w^b$, and test p̂^b. However, by re-sampling only the Blacks in the prediction step to get ${\widehat{p}}_{\mathit{wi}}^b$, we are still treating β̂_w as known without error, since it is estimated only once using the full sample of Whites. A more robust bootstrap approach would be to re-sample all participants (Black and White together) and repeat the entire PB process: estimate β̂_w, compute ${\widehat{p}}_{\mathit{wi}}^b$, compute ${\overline{p}}_w^b$, and test p̂^b. In our large sample of tens of thousands of Whites in the REDSKIN project, β̂_w will have very small standard errors, so the predictions ${\widehat{p}}_{\mathit{wi}}^b$ will also; hence we expect that the naïve statistical test would likely result in a significance level close to what we would get with a full bootstrapping approach. In applications with very small sample sizes, users should be cautious about applying the bootstrapping approach (as is true for use of the bootstrap in any context). We illustrate both types of tests, naïve and bootstrap, for the application of our survival analysis extension to the REDSKIN project in Section 4.

3. Extension to survival analysis

3.1 Cox proportional hazards model for an incident event

In our nursing home context, other outcomes of interest are more appropriately considered as time-to-event outcomes subject to independent right-censoring, such as time from admission to the nursing home until newly occurring dual-incontinence (DI) among residents without DI at admission. In extending the PB approach to survival analysis, by analogy with logistic regression, the first step is to fit a regression model using Whites only (hence the subscripts w in the equations that follow). We extend PB for the conventional choice of survival analysis, Cox regression, but presumably other types of analysis could be used (e.g., accelerated failure time).

A Cox proportional hazards model [12] is a semi-parametric model in which the hazard of an event for individual i at time t, h_wi(t), is associated with the adjusting characteristics through a log-linear relationship, separately from the baseline hazard of the event, h_w0(t), as follows:

$$h_{\mathit{wi}}(t)=h_{w0}(t)\exp (X_{\mathit{wi}}{\beta }_w)$$

with corresponding cumulative hazard and survivor functions

$$\begin{array}{l}{H}_{\mathit{wi}}(t)=\underset{0}{\overset{t}{\int }}{h}_{w0}(s)\exp (X_{\mathit{wi}}{\beta }_w)\mathit{ds}\\ S_{\mathit{wi}}(t)=\exp (-H_{\mathit{wi}}(t)).\end{array}$$

Estimation and properties of this model can be found elsewhere [13 (Chapter 3)]. The extension of PB that follows assumes the conventional partial-likelihood estimation of the Cox model coefficients and non-parametric estimation of the baseline cumulative hazard, as implemented in any standard statistical package. The computational details of the specific implementation of the estimation do not alter the development that follows.

3.2 Statistical test of actual versus predicted survival for Blacks

The goal in extending PB to time-to-event outcomes is to compare actual to expected survival for the group of Black residents. To test for a difference under the null hypothesis that the Black sample survivor function follows the population survivor function they would have if they were White, we used the one-sample log rank test [16]. The test statistic is a function of the observed number of events O^b and the expected number of events in the Black group. To calculate the expected number of events, we need each Black’s predicted cumulative hazard calculated from the model estimated using the White residents. At follow-up time t we thus have:

$$\begin{array}{l}{\widehat{H}}_{\mathit{wi}}^b(t)=\underset{0}{\overset{t}{\int }}{\widehat{h}}_{w0}(s)\exp (X_{\mathit{bi}}{\widehat{\beta }}_w)\mathit{ds}\\ {\widehat{S}}_{\mathit{wi}}^b(t)=\exp (-{\widehat{H}}_{\mathit{wi}}^b(t)).\end{array}$$

${\widehat{H}}_{\mathit{wi}}^b(t)$ is the predicted cumulative hazard, and ${\widehat{S}}_{\mathit{wi}}^b(t)$ is the predicted survivor function (in the REDSKIN project, time without DI), at follow-up time t for a hypothetical member of the Black population who has the same characteristics X_bi at admission to the nursing home as the i^th actual Black resident in the sample.

The test statistic is then computed as:

$${\chi }^2=\frac{{\left(O^b-{\sum }_{i=1}^{n_b}{\widehat{H}}_{\mathit{wi}}^b(T_i)\right)}^2}{\left({\sum }_{i=1}^{n_b}{\widehat{H}}_{\mathit{wi}}^b(T_i)\right)},$$

which is approximately distributed as chi-square with 1 degree of freedom under the null hypothesis. The expected number of events for the i^th Black resident at his/her end of followup T_i (either an event or censoring) is his or her predicted cumulative hazard ${\widehat{H}}_{\mathit{wi}}^b(T_i)$. The standardized mortality ratio (SMR) is equal to the ratio of observed to expected numbers of events, and as such the one-sample LRT is also a test of whether the SMR is equal to 1. An equivalent z-test statistic can be computed as the test of the intercept in a Poisson general linear model with outcome equal to the indicator of event (1) or censoring (0), the log link, offset for each individual’s predicted cumulative hazard, and no predictors; the intercept is the estimate of the log SMR.

As for the logistic regression case, this test naïvely treats the predicted hazards as known population values, rather than as quantities predicted with error and correlated with the sample statistic O^b, and thus will result in a test statistic that is inappropriately big, hence a p-value that is too small. As described in Section 2 above, a full bootstrapping approach would instead re-sample the Blacks and Whites together, estimate β̂_w from the Whites in that re-sample, calculated the predicted cumulative hazard ${\widehat{H}}_{\mathit{wi}}^b(t)$ for each Black in that re-sample, calculate χ², and calculate the SMR. A bootstrap p-value for the LRT from the original dataset, and a bootstrap confidence interval for the SMR from the original dataset, are obtained by standard methods [17].

3.3 Accounting for clustering

Explicit modeling of clusters

It is common in Cox regression to use stratification to capture clustering of the data, for example by nursing home in the REDSKIN project. A stratified analysis allows a separate baseline hazard for each cluster, here indexed by k,

$$h_{\mathit{wi}}(t)=h_{\mathit{wk}0}(t)\exp (X_{\mathit{wi}}{\beta }_w),$$

where person i is in stratum k. After partial-likelihood estimation of the stratified model for Whites, the prediction for Blacks based on that model uses the stratum-specific baseline hazard:

$$\begin{array}{l}{\widehat{H}}_{\mathit{wi}}^b(t)=\underset{0}{\overset{t}{\int }}{\widehat{h}}_{\mathit{wk}0}(s)\exp (X_{\mathit{bi}}{\widehat{\beta }}_w)\mathit{ds}\\ {\widehat{S}}_{\mathit{wi}}^b(t)=\exp (-{\widehat{H}}_{\mathit{wi}}^b(t)).\end{array}$$

A weakness of the Cox model is that having some relatively small strata (especially when the event being modeled is relatively rare) can give a partial likelihood for which the iterative estimation algorithm fails. Also, since person i is in stratum k, Black predictions from a stratified model can only be done for Black persons who happen to reside in a nursing home that also has White residents; otherwise that Black person has no estimated baseline hazard. This introduces a selection effect into the data available for analysis, which may be subtle if almost all nursing homes with Blacks also have Whites (as is true in our REDSKIN project) or substantial if many nursing homes have Blacks but no Whites.

A common alternative when stratification is infeasible is to use fixed effects for nursing home to account for the clustering. The remaining steps of the PB procedure are the same. Another alternative would be to fit a random effect for each nursing home, with a single baseline hazard, so that a nursing home’s random effect multiplies a common baseline hazard; however it is not clear how the prediction step of PB would then be carried out [13]. A further alternative would treat each nursing home’s baseline hazard as a random effect [18], and again it is not clear how the prediction step of PB would be carried out. These alternatives would be valuable research extensions of this work. The selection effect of restricting the sample to only participants in clusters having members of both groups would be present with each of these approaches, and thus these approaches are not appropriate if the subset selected for inclusion in the analyses is an unacceptably small fraction of the study population, or if this introduces a blatant selection bias. Results of the Cox model fit to the Whites should also not then be generalized to nursing homes with only Whites. Care should be taken when interpreting PB results when using only a small subset of clusters.

Cluster-based bootstrap of the test statistic

As an alternative when explicit modeling of the clusters is infeasible, a bootstrap approach that accounts for the clustering is to re-sample clusters, rather than re-sample participants as described in Section 3.2. If there are K clusters, to create each bootstrap sample we randomly re-sample K clusters, with replacement. All persons in the sampled clusters are included in that bootstrap sample; if a cluster is re-sampled more than once, those persons are included more than once in that bootstrap sample. The entire PB process is then repeated for each bootstrap sample. As described above, the bootstrap samples can be used, for example, to calculate a bootstrap p-value for the LRT and a bootstrap confidence interval for the SMR. In Section 4, we present a comparison of the naïve vs. bootstrap testing approaches for the REDSKIN project.

3.4 Graphical comparison of actual to predicted survival for Blacks

In addition to a formal statistical test, it is helpful to display actual and predicted survival graphically. For this, we must aggregate predicted survivor functions for Black individuals (which were calculated from the Cox model and used in the calculation of the LRT) into a predicted survivor function for the Black group; this is then plotted along with the observed survivor function for the Black group. This is analogous to the aggregation of the ${\widehat{p}}_{\mathit{wi}}^b$ to ${\overline{p}}_w^b$, which is then compared to the observed p̂^b, for logistic regression, as in Section 2. The actual distribution of event times for the Blacks in the sample is easily estimated and plotted as a Kaplan-Meier curve ${\widehat{S}}_{\mathit{KM}}^b(t)$ [19].

With individual predicted survival ${\widehat{S}}_{\mathit{wi}}^b(t)$ in hand (defined in Section 3.2 above) for each hypothetical Black resident, whose characteristics exactly match one of the Black residents in our sample, we considered two methods for aggregating across residents to graphically display expected survival for this hypothetical Black population [13 (Section 10.4)]: Ederer’s method [20] and Hakulinen’s method [21,22]. Both methods estimate the expected population survivor function by averaging individual expected survivor functions across the i=1,…,n_b hypothetical Black individuals at each follow-up time t, but the two methods do the averaging slightly differently. Ederer’s estimate at time t is a simple average of the survivor functions for the n_b(t) Black residents still in the risk set at time t:

$${\overline{S}}_w^b(t)=\frac{1}{n_b\left(t\right)}\sum _{i=1}^{n_b\left(t\right)}{\widehat{S}}_{\mathit{wi}}^b(t).$$

This can also be viewed as a weighted average of hazards:

$$\begin{array}{l}{\overline{H}}_w^b(t)=\underset{0}{\overset{t}{\int }}\frac{\sum _{i=1}^{n_b\left(s\right)}{\widehat{S}}_{\mathit{wi}}^b(s){\widehat{h}}_{\mathit{wi}}^b(s)}{\sum _{i=1}^{n_b\left(s\right)}{\widehat{S}}_{\mathit{wi}}^b(s)}\mathit{ds}\\ {\overline{S}}_w^b(t)=\exp (-{\overline{H}}_w^b(t)),\end{array}$$

where the weights are equal to ${\widehat{S}}_{\mathit{wi}}^b(s)$, the probability of still being in the risk set at time s. In contrast, Hakulinen’s method requires the user to specify maximum potential follow-up times for each hypothetical Black resident:

$$\begin{array}{l}{\overline{\overline{H}}}_w^b(t)=\underset{0}{\overset{t}{\int }}\frac{\sum _{i=1}^{n_b}{\widehat{S}}_{\mathit{wi}}^b(s)C_i(s){\widehat{h}}_{\mathit{wi}}^b(s)}{\sum _{i=1}^{n_b}{\widehat{S}}_{\mathit{wi}}^b(s)C_i(s)}\mathit{ds}\\ {\overline{\overline{S}}}_w^b(t)=\exp (-{\overline{\overline{H}}}_w^b(t)),\end{array}$$

where C_i(s) is 1 for times s less than the ith person’s potential censoring time and 0 afterward. If C_i(s) is set to the observed censoring history, then the Ederer and Hakulinen estimates are the same. The censoring histories C_i(s) for s in (0,t) could, for example, be set to the censoring history for the observed Blacks who were, in fact, censored, and to the maximum potential follow-up for the observed Blacks who experienced the event. In Section 4, we present some comparisons of Ederer’s method to Hakulinen’s method for our REDSKIN project.

Therneau and Grambsch [13 (Section 10.4.4)] argue that the two estimators ${\overline{S}}_w^b(t)$ and ${\overline{\overline{S}}}_w^b(t)$ will differ substantially only under certain conditions. One condition is that early entries to the study population are quite different from later entries, where ‘different’ is in terms of the covariates included in the Cox model. This is not true in the REDSKIN study, with data accrual based on a federally mandated standardized form and follow-up over a relatively narrow time frame, 2000-2002. Also, the characteristics of the nursing home population, and of care provided in a nursing home, are unlikely to have changed substantially over such a short time as there were no major regulatory changes in that period. Another condition under which the two estimates differ substantially is when a substantial fraction of the later entries to the study population are censored. While later entries are heavily censored for our DI outcome (~85% of Blacks censored among those admitted in 2002), early entries to the study population are also heavily censored (~75% of Blacks censored among those admitted in 2000 and in 2001). Many persons newly admitted to a nursing home end up being short-term residents, for example, they may be there only for rehabilitation, their condition may quickly worsen requiring hospitalization, they may transfer to a different facility, or they may die. For applications other than REDSKIN, the discussion in Therneau and Grambsch offers guidance in the selection of which estimator to use.

3.5 Calculation of ‘explained’ and ‘unexplained’ disparity

One aspect of the PB method that is commonly seen with logistic regression PB is a calculation of the percent of disparity explained by the included covariates. For a binary outcome, define the unexplained disparity as expected minus observed event rate in Blacks. Define the explained disparity as observed event rate in Whites minus the expected event rate in Blacks. The total disparity is then the sum of those two disparities, and the percent disparity explained is defined as 100*explained disparity/total disparity. Since survival curves can differ either because of number of events or timing of events or both, explained disparity has no simple analog in time-to-event models. Instead, in our REDSKIN application, we do similar computations using the proportion who are still event-free at a grid of pre-specified time points during follow-up. Disparity explained vs. unexplained is a very intuitive decomposition for clinicians, and seeing the pattern in those decompositions across the event timeline (rather than a decomposition that aggregates across the entire timeline) is informative. However, as we will see in Section 4, the calculation of disparity explained depends of course on the choice of ‘advantaged group’ and can lead to non-sensical values. This is true for either logistic or time-to-event modeling, and we are consequently unenthusiastic about its use in the PB literature.

4. REDSKIN Project

4.1 Application and interpretation

Approach

Tables 1-2 and Figures 1-3 show the results of applying the PB method as described above for the DI outcome to assess disparities between Whites and each of Hispanics, Blacks, and Asians. We accounted for clustering using the bootstrap approach, but also carried out the naïve test for comparison. For each non-White group, our sample was restricted to the non-White persons who lived in nursing homes that also had Whites. (We discuss the rationale for these modeling choices in Section 4.2.) Thus, the set of White residents included in the analysis of Blacks intersected with, but was not identical to, the set of White residents included in the analysis of Asians, since there were some homes that had Whites and Blacks but not Asians, and there were some homes that had Whites and Asians but not Blacks. Based on preliminary analyses and the input of clinical experts on the REDSKIN project, the following variables were included as predictors because they were deemed potentially important for predicting DI: resident age at admission; sex; and scales describing activities of daily living (ADL), communication ability, use of support devices and restraints, comorbidity burden (Charlson scale), medication burden (number of medications per week), and bowel function; all scales were treated as continuous. We would expect older age, greater ADL dependency on others, poorer communication ability, higher use of devices and restraints, larger comorbidity burden, higher medication burden, and poorer bowel function to be associated with increased incident DI. No NH level variables were found to be important predictors. For our graphical depiction, we present Kaplan-Meier estimates for each racial/ethnic group along with the corresponding Ederer estimates of racial/ethnic population survival.

Table 1.

Peters-Belson method applied to incident Dual Incontinence, separately for three racial/ethnic groups in elderly admissions to nursing homes: Hispanics, Blacks, and Asians.

	Hispanics	Blacks	Asians
N homes with both Whites and the racial/ethnic group	134	277	90
N residents
in the racial/ethnic group	609	2,803	560
White	16,230	30,637	12,725
N (%) events
in the racial/ethnic group	80 (13%)	569 (20%)	63 (11%)
among Whites	1,782 (11%)	3,670 (12%)	1,300 (10%)
Event rate per person-year of follow-up
in the racial/ethnic group	0.41	0.49	0.47
among Whites	0.43	0.38	0.44
Median time-to-event (days) for those with DI
in the racial/ethnic group	180.0	124.0	217.0
among Whites	148.5	150.0	141.0
Median time-to-censoring (days) for those without DI
in the racial/ethnic group	14.0	29.0	22.0
among Whites	14.0	19.0	13.0
Log rank z-test statistic	-0.71	4.04	-0.63
naïve test p-value	0.48	<0.0001	0.53
bootstrap test p-value	0.52	0.01	0.38
Standardized Mortality Ratio estimate	0.92	1.18	0.92
naïve test 95% Confidence Interval	(0.74,1.15)	(1.09,1.29)	(0.72,1.18)
bootstrap 95% Confidence Interval	(0.71,1.20)	(1.04,1.34)	(0.71,1.12)

Table 2.

Explained and unexplained disparities between Whites and each of the three racial/ethnic groups in elderly admissions to nursing homes: Hispanics, Blacks, and Asians.

	180 days	365 days	731 days
Observed proportion without DI in Whites	0.788	0.629	0.406
Observed proportion without DI in Hispanics	0.814	0.664	0.402
Expected proportion without DI in Hispanics	0.790	0.635	0.423
Total disparity (Obs. Whites – Obs. Hispanics)	-0.026	-0.035	0.004
Explained disparity (Obs. Whites – Exp. Hispanics)	-0.002	-0.006	-0.017
Unexplained disparity (Exp.– Obs. Hispanics)	-0.024	-0.029	0.021
Observed proportion without DI in Whites	0.812	0.679	0.457
Observed proportion without DI in Blacks	0.744	0.611	0.407
Expected proportion without DI in Blacks	0.806	0.672	0.459
Total disparity (Obs. Whites – Obs. Blacks)	0.068	0.068	0.050
Explained disparity (Obs. Whites – Exp. Blacks)	0.006	0.007	-0.002
Unexplained disparity (Exp.– Obs. Blacks)	0.062	0.061	0.052
Observed proportion without DI in Whites	0.777	0.625	0.402
Observed proportion without DI in Asians	0.833	0.598	0.242
Expected proportion without DI in Asians	0.755	0.596	0.380
Total disparity (Obs. Whites – Obs. Asians)	-0.056	0.027	0.160
Explained disparity (Obs. Whites – Exp. Asians)	0.022	0.029	0.022
Unexplained disparity (Exp.– Obs. Asians)	-0.078	-0.002	0.138

Disparities are calculated from the proportions of residents still without Dual Incontinence at each of 0.5, 1, and 2 years post-admission to the nursing home.

Figure 1.

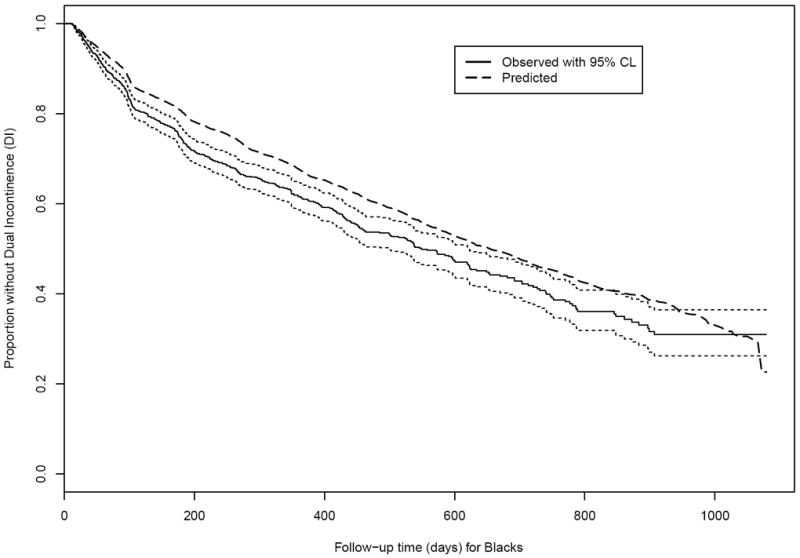
Observed and expected time without Dual Incontinence (DI) among Black non-Hispanic nursing home residents age 65+ years and free of DI at admission. (Solid black line and dotted black lines: Actual survival curve [Kaplan-Meier] for Blacks with 95% pointwise confidence limits. Dashed line: Expected survival curve for Blacks based on the Cox regression in Whites.)

Figure 3.

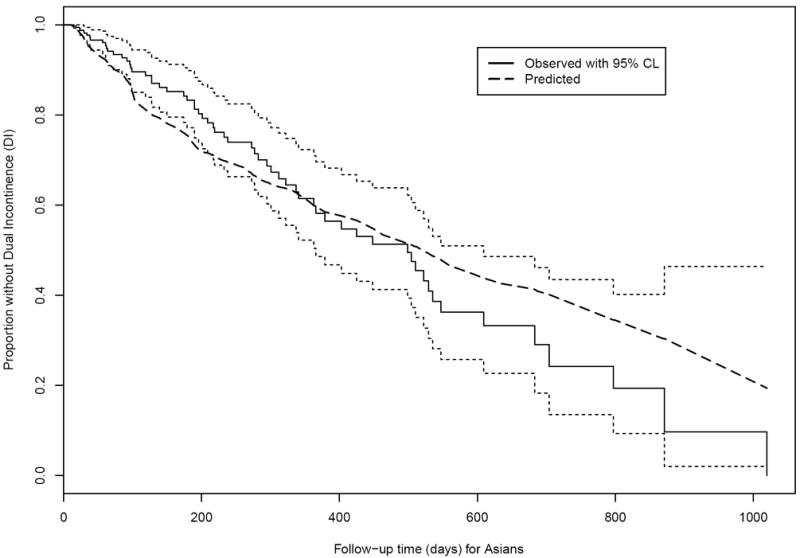
Observed and expected time without Dual Incontinence (DI) among Asian nursing home residents age 65+ years and free of DI at admission. (Solid black line and dotted black lines: Actual survival curve [Kaplan-Meier] for Asians with 95% pointwise confidence limits. Dashed line: Expected survival curve for Asians based on the Cox regression in Whites.)

Hispanic results

Among 134 nursing homes, 80 out of 609 Hispanics (13%) experienced DI, with an event rate of 0.41 events per person-year of follow-up. In those same nursing homes, 1,782 out of 16,230 Whites (11%) experienced DI, with a slightly higher event rate of 0.43 events per person-year of follow-up. Hispanics with DI experienced their event later than the Whites in their nursing homes (median 180.0 vs. 148.5 days), while median time to censoring among those censored were the same (14.0 vs. 14.0 days). The Hispanic testing results (SMR, naïve and bootstrap confidence interval, and naïve and bootstrap p-value) shown in Table 1 indicate that Hispanics did slightly better than would have been expected based on Whites in the same nursing homes. The SMR estimate of 0.92 indicates that Hispanics experienced 8% fewer DI events than would be expected based on the ‘population’ of Whites in the same nursing homes. This conclusion was robust to the choice of naïve test or bootstrap test, but note that both confidence intervals are somewhat wide, indicating a lack of precision available in estimating the SMR; an SMR greater than 1 is also plausible. A larger sample would demonstrate a more definitive result. Significant predictors of incident DI were gender, age, ADL, bowel function, communication, devices/restraints, comorbidity burden, and medication burden; these were compared between Hispanics and Whites using Mann-Whitney two-sample tests or z-tests of a difference in proportions. Hispanics were on average younger than Whites (mean 79.0 ± standard deviation 8.1 vs. 81.1 ± 7.5 years, p<0.0001), with a higher proportion male (39.9% vs. 31.7%, p<0.0001), and had slightly better bowel function (0.1 ± 0.4 vs. 0.2 ± 0.4, p=0.05), poorer communication abilities (1.0 ± 1.5 vs. 0.7 ± 1.3, p=0.0001), lower regular use of medications (1.2 ± 1.2 vs. 1.4 ± 1.2, p<0.0001), and a higher comorbidity burden (1.9 ± 1.6 vs. 1.5 ± 1.5, p<0.0001), Hispanics and Whites had similar ADL scores (10.6 ± 6.5 vs. 10.7 ± 6.1, p=0.52) and level of use of devices and restraints (0.02 ± 0.2 vs. 0.01 ± 0.2, p=0.21).

Figure 1, for Hispanics, shows that the survival curve for actual time to DI (solid line) is quite close to the survival curve for expected time to DI (dashed line, calculated via Ederer’s estimate). For a pre-specified grid of time points, the observed proportion without DI in Whites, observed proportion without DI in Hispanics, and expected proportion without DI in Hispanics are displayed in Table 2 along with the corresponding calculations of ‘explained disparity’ and ‘unexplained disparity.’ The total disparity (observed difference between Whites and Hispanics in the proportion without DI) favors Hispanics at 180 and 365 days by about 0.03, and then reverses to favor Whites at 731 days but by a very small amount (0.004). The unexplained disparity (expected minus observed difference in Hispanics) shows that expected is lower than observed at 180 and 365 days, but higher at 731 days; in Figure 1 the predicted curve for Hispanics fluctuates above and below their observed curve, so this reversal is not surprising. We can see from the breakdown of the total disparity into explained and unexplained in Table 2 that the chosen covariates do not provide much explanation of why Hispanics are experiencing DI differently than Whites. These calculations reveal an awkwardness of the PB approach: interpretation of the breakdown of total into explained and unexplained disparities if our a priori choice of the advantaged group was incorrect. This problem could be seen in a logistic regression application of PB as well, but is exacerbated in our survival setting by the calculation of disparities at each of several time points.

Black results

Among 277 nursing homes, 569 out of 2,803 Blacks (20%) experienced DI, with an event rate of 0.49 events per person-year of follow-up. In those same nursing homes, 3,670 out of 30,637 Whites (12%) experienced DI, with a lower event rate of 0.38 events per person-year of follow-up. Blacks with DI experienced their event earlier than the Whites in their nursing homes (median 124.0 vs. 150.0 days), while median time to censoring among those censored were similar (19.0 vs. 29.0 days). The SMR estimate of 1.18 indicates that Blacks experienced 18% more DI events than would be expected based on the ‘population’ of Whites in the same nursing homes. Both naïve and bootstrap tests of the SMR for Blacks showed observed incident DI significantly different from expected (Table 1), but here we have tight confidence intervals that exclude 1, indicating confidence that Blacks are at substantially higher than expected risk. Significant predictors of incident DI were cognition and ADL. Blacks had poorer cognitive scores (3.3 ± 1.3 vs. 3.0 ± 1.2, p<0.0001) and slightly better ADL scores (9.9 ± 6.6 vs. 10.1 ± 6.2, p=0.04).

Figure 2 shows that Blacks tended to have DI events earlier than would be expected based on the experience of Whites in the same nursing homes using Ederer’s estimate. The total disparity (observed difference between Whites and Blacks in the proportion without DI, Table 2) favors Whites at 180, 365, and 731 days, decreasing from 0.068 to 0.050. The unexplained disparity calculations show Blacks consistently have expected proportion without DI higher than the observed proportion without DI. The total disparity is again largely unexplained by the PB modeling; the chosen covariates do not provide much explanation of why Blacks are experiencing DI more and/or faster than Whites.

Figure 2.

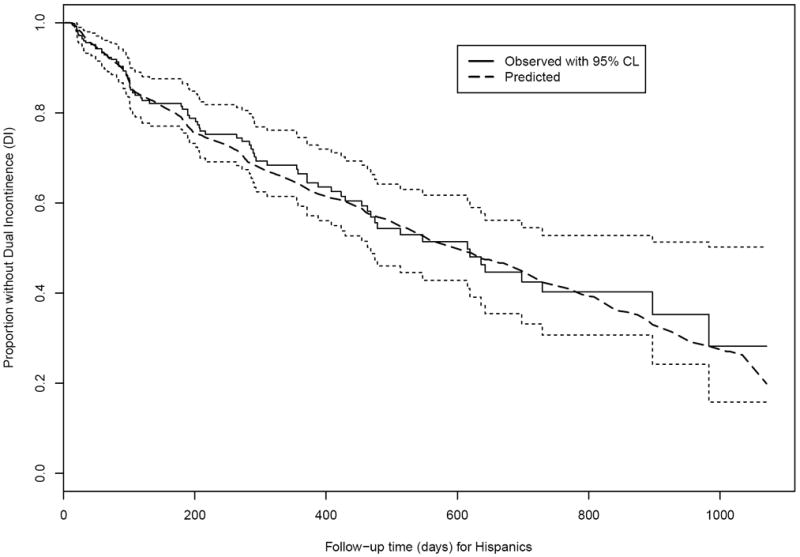
Observed and expected time without Dual Incontinence (DI) among Hispanic nursing home residents age 65+ years and free of DI at admission. (Solid black line and dotted black lines: Actual survival curve [Kaplan-Meier] for Hispanics with 95% pointwise confidence limits. Dashed line: Expected survival curve for Hispanics based on the Cox regression in Whites.)

Asian results

Among 90 nursing homes, 63 out of 560 Asians (11%) experienced DI, with an event rate of 0.47 events per person-year of follow-up. In those same nursing homes, 1,300 out of 12,725 Whites (10%) experienced DI, with a lower event rate of 0.44 events per person-year of follow-up. Asians with DI experienced their event substantially later than the Whites in their nursing homes (median 217.0 vs. 141.0 days), while median time to censoring among those censored differed by only a week between Asians and Whites (22.0 vs. 13.0 days). The SMR estimate of 0.92 indicates that Asians experienced 8% fewer DI events than would be expected based on the ‘population’ of Whites in the same nursing homes. Actual does not test different from expected for either naïve or bootstrap for Asians (Table 1) and, as for Hispanics, the confidence intervals for the SMR are relatively wide, likely reflecting the lower power due to smaller sample size. Significant predictors of incident DI were cognition and ADL. Asians had poorer cognitive scores (3.1 ± 1.2 vs. 2.9 ± 1.2, p<0.0001) and worse ADL scores (13.0 ± 5.3 vs. 11.0 ± 6.0, p<0.0001).

Figure 3 shows that for the first year after admission, Asians tended to have fewer DI events than expected (the dashed-line Ederer expected survival curve is below the solid actual survival curve), but then the actual and expected survival curves cross at about 1 year. The total disparity (observed difference between Whites and Asians in the proportion without DI, Table 2) favors Asians at 180 days, but favors Whites at 365 and 731 days. The unexplained disparities show expected lower than observed at 180 days, about the same at 365 days, and higher at 731 days. The total disparity is again largely unexplained by the PB modeling; the chosen covariates do not provide much explanation of why Blacks are experiencing DI more and/or faster than Whites.

Clinical context

For the REDSKIN project, the disparity results were as we had hypothesized before beginning the study, with Blacks showing significantly poorer outcomes, and Hispanics and Asians showing similar outcomes, compared to Whites. The log rank test is a summary across the entire event timeline, so it was also informative for our clinical collaborators to see the fluctuations in actual compared to expected event rates, for example that Asians had fewer events compared to Whites early on, but more later on, in their NH stay; this temporal pattern was evident also in the percent disparity unexplained for Asians. In addition, the project team was encouraged that many of the predictors that came up as significant predictors of incident DI (such as ADL, cognitive score, and communication ability) are potentially modifiable factors that could be intervened upon either before or after an elderly person is admitted to a NH. The magnitude of the effects were also meaningful; for example, the hazard ratio for a 2 unit higher (worse) ADL score was 1.11 for Whites in NHs with Asians, where Asians had on average a 2 unit worse score.

Ederer vs. Hakulinen for graphical display

Figure 4 presents two different Hakulinen estimates of population survival, for comparison to the Ederer estimate of population survival, for each racial/ethnic group. To use Hakulinen’s estimate, we specified the maximum potential follow-up time for censored persons as their observed censoring time and for those persons with an event we specified maximum potential follow-up time in two ways: (1) time from admission to administrative censoring, and (2) time from admission to half-way between the observed event and administrative censoring. Administrative censoring in this application corresponds to the last observed MDS record prior to database closure at the end of 31 December 2002. The first row of graphs in Figure 1 displays the entire period of follow-up, but the three curves are almost indistinguishable from each other. The second row of graphs zooms in on the second year of nursing home stay in order to see more detail. Since this study was observational and residents are censored (leave the nursing home) at various times for myriad complex reasons, e.g. related to their health status and access to nursing home alternatives, any choice of maximum follow-up is arbitrary, so our preference for the REDSKIN application is for the Ederer approach. Nonetheless, it is useful to see the impact of the censoring assumptions by comparing the Ederer and Hakulinen approaches. As we would expect, the Hakulinen and Ederer curves are very close, almost indistinguishable, for each racial/ethnic group; the first Hakulinen approach yields an aggregated survival curve that is very slightly farther from the Ederer curve than the second Hakulinen approach, because the imposed censoring dates in the first approach are later than in the second approach.

Figure 4.

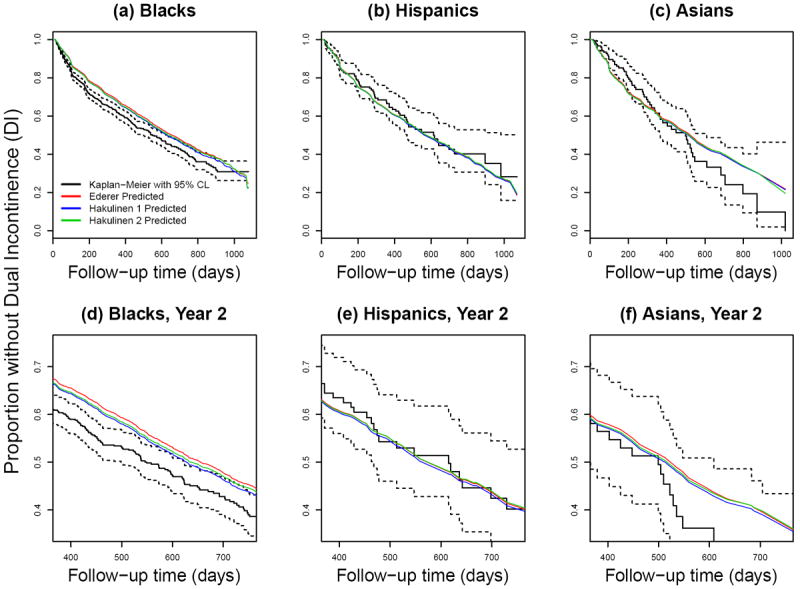
Observed and expected time without Dual Incontinence (DI) among Black non-Hispanic (a,d), Hispanic (b,e), and Asian (c,f) nursing home residents age 65+ years and free of DI at admission. (Solid black line and dotted black lines: Actual survival curve [Kaplan-Meier] with 95% pointwise confidence limits. Other lines: Expected survival curve calculated via Ederer’s estimate (red) or Hakulinen’s estimate (blue, green) based on the Cox regression in Whites; see Sections 3.4 and 4.1 for calculation details.)

4.2 Substantive complications in the REDSKIN application

Accounting for the clustering

Nursing homes can differ substantially in populations served and culture of care [23-25], so the impact of nursing home on outcomes needs to be considered. We thus restricted our sample for each race group analysis to nursing homes that had both Whites and the other race group. To account for clustering in the PB modeling, the simplest choice, conceptually and practically, was to treat nursing homes as strata in the Cox model for the Whites. In the REDSKIN project, however, nursing homes are relatively small (typically with <100 rather than several hundred residents), and the event rate was relatively low (10-20%). Thus, many nursing homes had either few White residents or few White residents with events, which resulted in very imprecise estimates of the baseline hazard for that nursing home, and hence poorly estimated expected survival for the other race groups, even the Blacks with their relatively large sample size. We also had statistical software problems with stratification, which we discuss below. In addition, one of the goals of the research project was to examine the associations of the DI outcome with nursing home characteristics (such as staffing and Census measures of the nursing home’s Census tract), so fitting fixed effects for nursing homes was not compatible with this goal. While we did consider nursing home covariates as potential predictors in the Cox model, none were significant predictors and were not discussed further.

As for any observational study, to the extent that the available nursing home covariates do not capture differences between nursing homes in the outcome being studied, using only those available could impair the validity of the naïve test of whether the SMR differs from 1. Also, simply ignoring clustering of residents into nursing homes could result in inappropriate standard errors and biased estimates of predictor effects. A bootstrap p-value and confidence interval, where bootstrap samples are drawn from the clusters and thus preserve the clustering, addresses the concern that the standard error associated with the naïve test statistic is incorrect due to the clustering. Bias can also arise if we ignore clustering and cluster size (number of DI-free admissions per NH over our 3 year follow-up) is informative about the outcome (incident DI event rate per NH) [26-28]. We checked for informative cluster size as follows: Using negative binomial regression with a log link and nursing home as the unit of analysis, we modeled incident DI event count in each NH as a function of NH (i.e., cluster) size with an offset for log total follow-up per NH (person-years). The interquartile range for NH size was approximately 50 to 125 for all racial/ethnic groups, but the largest NH size was almost 1500. The regression coefficient for NH size was very small (on the order of -0.05 per 100 higher NH size) and statistically significant, but it was determined entirely by the largest 2-4% of nursing homes. To check the effect of these largest homes, we re-ran the proportional hazards regressions without them: for each of the three racial/ethnic groups the coefficient estimates differed only negligiblyfrom when all NHs were included. Thus we judge that informative cluster size was not a problem for our project, thought it could be for others. For these reasons we opted for bootstrap adjustment to the SMR statistical test to account for clustering within nursing home.

Variable selection

As with all regression-based procedures, picking the set of covariates to include in X_w (and hence X_b) is important. We needed to employ some variable selection approach before the first step of fitting a Cox regression to the Whites, since our potential predictors numbered upwards of 60 and even with our entire sample of tens of thousands of Whites, the Cox regression would not converge. We used expert opinion in the area of wound and continence nursing care to cull potential predictors at the resident level (risk factors for the outcome, including demographics, comorbidities, clinical and functional status, etc.), and separately at the nursing home level (quality of care measures, staffing levels, neighborhood sociodemographics and socioeconomics, etc.). We also screened out predictors that were highly collinear with other predictors, and predictors that were very uncorrelated with the outcome in simple pairwise correlations. When two predictors were collinear, the predictor deemed as more clinically relevant to DI in a nursing home population by our project’s clinical team members were retained in the modeling.

Timing of censoring and events

To calculate the LRT statistic, we must compute each individual’s cumulative hazard at their end of follow-up (earlier of censoring time or event time). Censoring times that fall before the first event time have cumulative hazard of zero. To bound the smallest values away from 0, we added a small constant to all values (see Supplementary Web Materials).

4.3 Software-related complications for the REDSKIN application

We implemented this new PB procedure in the R system [13], as shown in the Supplementary Web Materials, using functions in the survival package. Our original list of potential predictors (before culling as described above) to include in the Cox model for Whites was so long that we ran up against the limit of the length of text R can parse in a model formula, so we had to shorten variable names to just a few characters each. For the problem of controlling for nursing homes, the survexp function in the most current version of the survival package does not allow Ederer predictions from a stratified model. The package author, Dr. Terry Therneau, implemented for us a version that does, but has not yet posted this version to the R project servers (personal communication).

Even after that stratification problem was solved by the modified package, stratifying on nursing home in the REDSKIN project caused the R functions to crash because many nursing homes had sample sizes or event counts (or both) that were too small. This could have been avoided by grouping nursing homes into larger clusters or by deleting small nursing homes; the former would sacrifice some of the advantage of stratifying in the first place, while the latter would sacrifice a large part of the sample and risk inducing selection bias. Instead we considered cluster level predictors and implemented the clustered bootstrap test (Section 4.1).

5. Discussion

We have extended the Peters-Belson method to right-censored time-to-event data. The proposed extension is straightforward to implement, with interpretation analogous to versions of Peters-Belson that have been developed for other types of outcomes. One advantage of our approach is a simple quantification and test of whether the observed event history in the presumed disadvantaged group is statistically different from the expected event history based on a reference, presumed advantaged, population. We used the one-sample LRT to compare observed and expected survival curves because it has some conventional status for this purpose, but other tests could be used and it is not obvious that the one-sample LRT is the best test for this purpose. The one-sample LRT is most powerful against a proportional-hazards alternative, and in some of our comparisons the actual and expected survival curves cross (e.g., Figure 3 for Asians, although far out in follow-up where there are few events).

The foregoing sections raised several issues that are relevant to PB and other statistical methods for measuring disparity based on proportional hazards models, or more generally on measuring disparity based on predictions from any model. One such issue is how to select covariates for the advantaged group model, and how sensitive the results of PB are to the variable-selection method. As far as we know, no literature exists on this specific to PB, but certainly any user of PB must be sensitive to the issue that any unexplained disparity may be due to one or more factors that were not measured or not modeled, rather than due to deliberate or inadvertent discrimination against the group shown to be disadvantaged with respect to the outcome. The risks of including too many covariates seem smaller than the risks of excluding a potentially important covariate.

A second issue is the use of the Ederer estimate, as compared to the Hakulinen estimate, of population expected survival for graphical comparison of observed to expected survival in the presumed disadvantaged group. A priori we preferred Ederer’s estimate for pragmatic reasons related to its mathematical correspondence with the LRT (although calculation of the LRT does not depend on Ederer’s estimate). The graphical displays for our REDSKIN project were almost indistinguishable between the two estimates, but this may not hold true for other datasets.

The largest hurdle we faced in REDSKIN was specific to our application of PB to a data set with clustering: how to account for nursing homes. The choices would seem to be stratification, fixed effects, random effects, and using individual- and nursing home-level predictors. We preferred stratification because it completely accounts for nursing-home effects, but this was impracticable due to small sample sizes or event counts in some homes. This failure of stratification to account for clustering was not due to PB per se; it was due to our choice to use a semi-parametric proportional hazards model, and would have occurred if we were just trying to model outcomes for these smaller groups using a stratified model. The second approach, fixed effects for homes, also led to convergence problems because of the number of homes (hundreds). We would have explored the third approach, random effects, but software for prediction in such a context does not exist and, based on conversations with Dr. Terry Therneau, it is less than obvious how to implement such an approach; this is an open topic for research. Thus, we ended up using the fourth approach, using a bootstrap-based test that adjusts for clustering. As for all observational studies, PB results are of course subject to concerns about unmeasured confounders, either individual-level characteristics or nursing-home-level characteristics.

We also quantified ‘explained’ and ‘unexplained’ disparities, as is common in the PB literature, at a grid of pre-specified time points during follow-up. However, we emphasize that the PB literature has not detailed the precise interpretation that should be given to these unexplained disparities. For example, when expected outcomes for Blacks are computed by substituting their characteristics into the outcome model fitted to the Whites, this imposes several constraints on the interpretation: (1) The choice of outcome model for the Whites is also the appropriate one for the Blacks. For example, perhaps in Blacks important predictors have a log linear relationship with the survival time (e.g., accelerated failure time model), rather than with the log hazard (as in proportional hazards model). (2) The functional forms of the predictors included in the Whites model are also appropriate for the Blacks. For example, perhaps in Blacks there is a threshold effect of a predictor on log hazard, whereas for Whites the effect is linear. (3) There are no measured predictors that were excluded from the model for Whites but which are important for predicting outcome in Blacks. (4) The associations of the predictors with outcome in the Whites (i.e., the regression coefficients) are the same for the Blacks; in other words, there are no interactions between predictors and race group. Violation of any one of these assumptions could lead to a misleading quantification of disparity. Any reporting of disparities based on a PB approach should remind the reader of these caveats.

One general argument against PB – which is more common in wage or employment contexts, and perhaps of concern in contexts where there is a history of active discrimination – is that PB quantifies what Blacks (for example) would have received under preferential treatment (i.e., Whites get better than typical care), rather than what Blacks would have received under “typical” treatment. (Of course, many would argue that the health care delivered to the preferred group should be considered typical.) Thus, under the presumption that Whites are getting superior care rather than typical care, it perhaps over-estimates how much Blacks are worse off compared to typical care. However, if the object is merely to test whether there is a difference between the actual experience of Blacks and their expected experience were they White instead, this objection seems to have no force.