Simultaneous multi-slice excitation by parallel transmission

Abstract

Purpose

A technique is described for simultaneous multi-slice (SMS) excitation using radiofrequency (RF) parallel transmission (pTX).

Methods

Spatially distinct slices are simultaneously excited by applying different RF frequencies on groups of elements of a multi-channel transmit array. The localized transmit sensitivities of the coil geometry are thereby exploited to reduce RF power. The method is capable of achieving SMS-excitation using single-slice RF pulses, or multi-band pulses. SMS-pTX is demonstrated using eight-channel parallel RF transmission on a dual-ring pTX coil at 3 T. The effect on B₁⁺ homogeneity and SAR is evaluated experimentally and by simulations. Slice-GRAPPA reconstruction was used for separation of the collapsed slice signals.

Results

Phantom and in vivo brain data acquired with FLASH and blipped-CAIPIRINHA EPI are presented at SMS excitation factors of two, four and six. We also show that with our pTX coil design, slice placement and binary division of transmitters, SMS-pTX excitations can achieve the same mean flip angles excitations at approximately 30% lower RF power than a conventional SMS approach with multi-band RF pulses.

Conclusion

The proposed SMS-pTX allows simultaneous multi-slice excitations at reduced RF power by exploiting the local B₁⁺ sensitivities of suitable multi-element pTX arrays.

INTRODUCTION

The concept of simultaneous multi-slice (SMS) acquisition in MRI was first introduced in the late 1980’s (1). SMS images can be tiled along the phase field-of-view (FOV) using Hadamard excitations and slice dependent phase modulation, provided the FOV is large enough (2). It was not until recently that developments in multi-coil receiver arrays (3) and parallel imaging reconstruction (4–6) have allowed slices to be separated using coil sensitivity rather than signal phase information (7–10). Conventional parallel imaging has been hugely successful in nearly all applications of MRI. It has, however offered very limited benefit for reducing acquisition times of single-shot 2D sequences such as echo-planar imaging (EPI) and spiral, where only the readout module of the sequence becomes shorter and the achievable TR remains largely determined by the required echo time (TE). Similar to parallel-accelerated 3D EPI acquisitions (11), SMS imaging allows entire excitation and encoding steps along the slice direction to be omitted and therefore allows TR reductions by the nominal slice acceleration factor. The speedup achieved by SMS acquisitions has therefore received particular interest in the context of BOLD fMRI (7,9,12,13) and diffusion-weighted acquisitions (7,14) based on single-shot EPI readouts and spiral imaging (15).

All previously demonstrated SMS methods have in common the need for some form of special RF pulse. Most widely used are multi-band RF (MB-RF) pulses, which can be generated by complex summation of N corresponding single-slice pulses. A limitation of this approach is that the aggregate pulse is a modulation of the original pulse shape with an N times higher peak voltage, and hence factor N² higher peak power in time. For larger N and high flip angles, this will readily exceed the capability of most clinically available RF coils and power amplifiers. The resulting higher RF power furthermore limits the in vivo use of these pulses, especially for spin-echo (T2) contrast at high field (3T and 7T). One way to manage the peak voltage of MB-RF pulses is optimal phase scheduling of the frequency bands (16); this can reduce peak voltage to scale with approximately √N instead of N (and peak power with N instead of N²), however the total pulse power remains unchanged. This has led to the proposal of the PINS (“power independent of number of slices”) RF pulse technique which has the favorable property that the required RF power does not increase with the number of slices by virtue of exciting and refocusing (13,17), or adiabatically inverting (18) magnetization along an infinite train of equidistant slices. Another way to reduce SAR in SMS applications is the use of variable rate excitations (VERSE) (10,19).

The need for B₁⁺ shimming and spatially tailored excitations has also motivated notable developments in parallel transmit (pTX) technology, especially since field strengths of 7 T and higher have become more commonplace. Multi-channel pTX systems are now commercially available and there are rapidly emerging new coil designs with even more transceiver elements arranged in multiple rings of transmitters around the head (20–22) or body (23–25), and conformal helmet shapes (26). There has also been a large body of work on the development of tailored RF pulse techniques that can utilize the spatial localization provided by pTX for improved image quality. The primary focus of most of these methods has been on improving B₁⁺ and B₀ homogeneity, primarily at high field (27–33).

The purpose of this paper is to present a novel application of pTX to achieve SMS excitation. By applying different RF frequencies on subgroups of the transmitter channels, a greater number of slices can be excited than there are frequency bands in the excitation RF pulse. It is also shown that SMS-pTX with an appropriate pTX coil design and slice placement allows SMS excitations at lower RF power by exploiting the localized sensitivity profile of the pTX array, as supported with SAR simulations and flip angle measurements. Proof of concept for the proposed SMS-pTX technique is provided using pTX with a dual-ring 8-channel coil at 3 T with FLASH and blipped-CAIPIRINHA EPI acquisitions. Images acquired at factors of two, four and six SMS-pTX are shown in phantoms and in vivo human brains. The aliased slices signals are separated using slice-GRAPPA (10).

THEORY

In conventional SMS imaging, the simultaneous excitation of N slices is usually achieved by MB-RF pulses that contain N frequency bands that match the desired slice locations for a given slice-select gradient amplitude. Under the small tip angle approximation and assuming linearity (34), adding together N single-slice pulses can generate an MB-RF pulse B(t):

$$B(t)=P(t)\sum _{n=1}^N{e}^{i{\omega }_{n}t},\text{where}{\omega }_n=\gamma G_z{z}_n.$$ [1]

Here P(t) is the RF pulse profile, G_z is the slice-select gradient, ω_n is the frequency modulation, γ is the gyromagnetic ratio, and z_n is the offset of slice n. If the pulse duration and slice-select gradient are left unaltered, a small tip angle MB-RF pulse will excite N slices with slice profiles identical to that of the single-slice pulse

$$M_{xy}(z)=i\gamma M_0\sum _{n=1}^N\underset{0}{\overset{T}{\int }}B(t)e^{i{\omega }_n(T-t)}dt=i\gamma M_0\sum _{n=1}^{N}p(z-z_n).$$ [2]

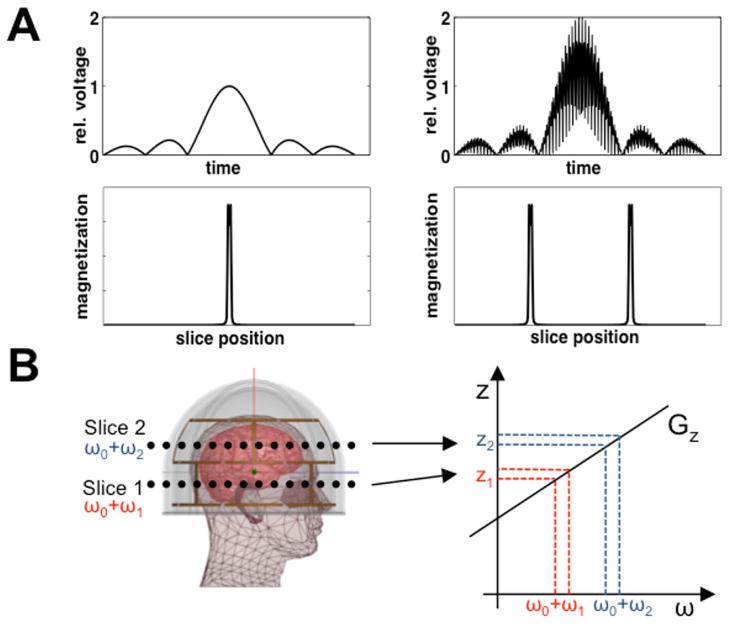
Here p(z) is the slice profile obtained and for simplicity we are assuming a uniform magnetization M₀. An example of a dual-slice MB-RF pulse is illustrated in Figure 1(A). This aggregate pulse is a modulation of the original pulse with factor N higher average pulse power and peak voltage, and factor N² higher peak power in time (2); for N >2 the peak values can be reduced by phase optimization of the frequency bands (16).

FIG. 1.

(A) Example of a conventional sinc pulse that results in excitation of a single slice (left) and MB-RF pulse to excite two slices (right). MB-RF pulses for the excitation of N slices are obtained by summation of N appropriately frequency shifted single-slice pulses. (B) SMS-pTX using multiple transmitters arranged in two rows around the head. Each row excites a different slice using a conventional single-slice pulse as shown on the left of (A). This is achieved by applying different RF frequencies to the rows in presence of a common slice select gradient G_z. In this example, frequency shifts ω₁ and ω₂ on bottom and top transmitter row simultaneously excite two slices at positions z₁ and z₂.

MB-RF designs are compatible with single-channel transmission, or in the case of a parallel transmitter the same pulse can be applied on all channels. For an acquisition of N slices excited by an MB-RF pulse applied on all L transmit elements with complex sensitivities s_l(r), the resulting aliased slice magnetization can be written as

$$M(\mathbf{r})=i\gamma M_0\sum (\mathbf{r})\sum _{n=1}^{N}p(z-z_n),\text{where}\sum (\mathbf{r})=\sum _{l=1}^L{s}_l(\mathbf{r}).$$ [3]

Eq. [3] reduces to Eq. [2] in the case of a volume transmitter because L = 1. Σ(r) is then approximately uniform, but at higher field strengths the excitation will be subject to central-brightening which increases as RF wavelength shortens.

In SMS-pTX, simultaneous excitation of multiple slices is achieved by applying the RF frequency shifts for the desired slice locations on individual, or subsets of, transmitters. This can eliminate the need for MB-RF or other multi-slice pulses if each transmitter subset excites one slice. The excited magnetization will be the sum of N overlapping slices excited by the N subsets of transmitters with composite sensitivities σ_n(r):

$$M(\mathbf{r})=i\gamma M_0\sum _{n=1}^N{\sigma }_n(\mathbf{r})p(z-z_n),$$ [4]

where ${\sigma }_n(r)={\sum }_l^L{s}_{n,l}(r)$ represents a linear combination of a subset of individual transmitters, and s_n,l(r) is the composite B₁⁺ profile of the l^th coil at the n^th slice and includes any phase and amplitude shims that might be applied to the individual transmitters within a set; the total number of transmit elements is N x L. A schematic illustration of dual-slice SMS-pTX is given in Figure 1(B). If a larger number of excited slices are needed, MB-RF pulses that excite subgroups of slices can be used. With an appropriate choice of transmitter subsets, the localization provided by pTX will demodulate the pulses and reduce RF power for a given excitation of N slices.

In Eq. [3], the B₁⁺ homogeneity and hence signal intensity and SNR with MB-RF depend on Σ(r), among other factors. However, with SMS-pTX the B₁⁺ homogeneity and SNR will depend on σ_n(r), which will typically be less uniform than Σ(r). It follows from Eq. [4], that a complex interplay of slice positioning, choice of transmitter subsets and coil geometry will determine the σ_n(r) at the excited slices. To minimize B₁⁺ inhomogeneity, a simple approach irrespective of coil geometry is to group transmitters by proximity to the slices they excite, which will also decrease the RF power required for a certain excitation flip angle to be achieved at a given slice location. In an optimal, but hypothetical situation the B₁⁺ profiles of the transmitter groups are stepwise so that the B₁⁺ profiles used for the different simultaneously excited slices have no or only minimal spatial overlap.

METHODS

HARDWARE SETUP

Experiments were performed on a clinical 3 T Siemens Magnetom TIM Trio scanner (Siemens Healthcare, Erlangen, Germany) interfaced with a custom-built 8-channel pTX system. The scanner controlled the sequence timing, gradients and acquisition, and triggered the pTX system, which was locked to the scanner’s 10 MHz clock. The pTX setup comprises a Tecmag Apollo NMR console with NTNMR software (Tecmag Inc., Houston, USA) and eight 300 W RF amplifiers (4x AMT/Herley, Lancaster, USA; 4x Tomco, Stepney, Australia). We used a custom-built 8-channel transmit-receive (TX/RX) head coil array with a snugly fitting helmet shape (Fig. 2). The coil elements are in a dual-row arrangement of four loops each around the axial plane and offset by 45 degrees; the distance between the center of the two rows is 75 mm. The three dimensional nature of this coil is well suited for SMS imaging because it provides transmit and receive sensitivity variation along both the in-plane and slice-select directions. As a proof of concept arrangement for an axial SMS-pTX excitation, two rows of the array were either driven in a birdcage (CP) mode together (“combined CP mode”) or individually (“individual CP mode”) (20). The combined CP mode was formed by using all eight elements with a 45 degree phase increment between neighboring elements, and where the two neighbors of a given element are in a different row. The individual CP mode comprised the four elements of each row driven at 90 degree increments, and 45 degree offset was applied between the two rows. The array was powered by the 8-channel pTX system or the scanner’s RF chain via power splitters and phase shifters. All eight channels were used for signal reception.

FIG. 2.

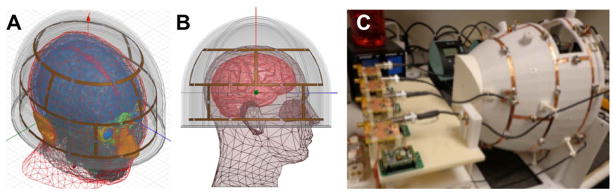
Schematics showing the geometry of the eight-channel TX/RX coil used in this study. The design comprises two rows each of four elements in a snugly fitting helmet design (A, B). The rows are offset by 45 degrees with respect to each other, allowing either the entire coil or the individual rows to be driven in a birdcage mode. Visual fMRI stimuli can be delivered through a large cutout above the eyes. A photograph of the final coil is shown in panel (C).

SIMULATION OF SPECIFIC ABSORPTION RATE

SAR simulations were performed for simultaneous dual-slice excitation with MB-RF pulses in combined CP mode, and dual-slice SMS-pTX excitation with single-slice pulses on the two rows in CP mode (each row being driven in its individual CP mode). The MB-RF generated by phase-modulating and adding two single-slice RF pulses (details under Data Acquisition below), resulting in twice the peak voltage; simulated SMS slice distance was 75 mm (frequency offset 30.5 kHz), matching our experimental scans. The same voltage was applied to each feed point, for an average target flip angle of 10 degrees over the two slices. This scenario was simulated using co-simulation strategy based on HFSS (Ansys, Canonsburg, PA) and ADS (Agilent, Santa Clara CA) (35,36). The tissue model was the realistic Ansys body model which corresponds to an average male adult and is based on a 1 mm isotropic data set. It compromises 33 tissue types including bones, eyes, white matter, grey matter and muscle compartments. The pTX coil was loaded with this model and tuned/matched/decoupled to 123.2 MHz/−30dB/−11dB. SAR matrices were computed and compressed to a smaller set of virtual observation points (37). Specifically: The B₁⁺ profiles of the combined CP modes and individual CP modes were computed from the B₁⁺ maps of the individual coil elements. These transmit profiles were used to generate the pulses to excite the two slices whereby first slice was centered in the lower coil row and the second that was centered in the upper coil row (separated by 75 mm or 30.5 kHz). For MB-RF excitation in the combined CP mode, the birdcage mode of the whole array was used to excite both slices using a single SMS pulse containing both frequency bands, i.e. the sum of the two individual pulses. This MB-RF pulse had a maximum voltage of 28 V, average power of 1.26 W and peak power of 15.68 W. For SMS-pTX using the two individual CP modes, the birdcage mode of the lower row was used to excite the first slice and the birdcage mode of the upper row was used to excite the second slice. Note that there is no cross-talk between the excitations of the two slices because of the large frequency difference between the two pulses, and that they can hence be played simultaneously on both rows without interaction. The two pulses had the same peak voltage (14 V, 0.63 W average power, 3.92 W peak power) but different frequencies in order to achieve dual-slice excitation.

To ensure adherence to the legal limits set by FDA regulations, and because our system does not support online SAR monitoring, the simulated values were used to estimate the local and global SAR for our MB-RF and SMS-pTX experiments described below, by scaling to the nominal flip angles and effective RF duty cycles.

DATA ACQUISITION

Data were acquired in phantoms and three human volunteers who provided informed consent according to the University of Hawaii/Queens Medical Center IRB protocol. At the start of each session transmitter adjustments and B₀-shims were performed using the vendor-provided routines, for which the pTX coil was driven by the scanner’s RF chain. The transmitter adjustment thus obtained was used to determine the voltages on the pTX system. Measurements with SMS-pTX excitations (in individual CP mode) and corresponding MB-RF SMS excitations (in combined CP mode) were performed using custom-written FLASH and blipped- CAIPIRINHA EPI sequences. Conventional single-slice acquisitions at the corresponding slice locations were always recorded to serve as reference for the slice-GRAPPA reconstruction (see section on Image Reconstruction below). The single-slice RF pulse shape used for excitations was a simple sinc with two side-lobes, 2.56 ms duration and a bandwidth-time product of 5.2 that yields a 5 mm slice over a gradient G_z = 9.54 mT/m; multi-band pulses were derived from this pulse as described above. The following experiments were performed:

1. FLASH SMS-pTX scans

Dual-slice FLASH images for demonstration were acquired in a structure phantom and one subject. SMS-pTX excitations of two slices in individual CP mode were done by applying single-slice RF pulses at two corresponding frequencies on the two rings. Dual-band MB-RF (N = 2) excitations were made in combined CP mode, using MB-RF pulses with a factor of two higher voltage and power than their single-slice counterparts. The slices were 75 mm apart (positioned at the center of the two rows), with slice thickness 3 mm, FOV = 192, matrix size 192×192, TE = 7 s, TR = 40 ms, nominal flip angle 37 degrees, scan time 7.7 s (15.4 seconds for the single slice scan). No CAIPIRINHA (i.e. no FOV shift between slices) by RF phase or gradient modulation was applied.

2. Flip angle mapping and calibration

Flip angle maps were acquired in a phantom covering the coil’s entire FOV of 150 mm along z. The double angle method with non-selective pre-saturation (38) was implemented into the GE-EPI sequence as described in Ref. (39). Measurements were performed in the combined CP mode and the individual CP modes of the two rows. The phantom scan was acquired on a homogenous spherical phantom filled with 4.75 mM (1.25 g/L) nickel sulfate-doped water, a diameter of 180 mm and a T1 of 750 ms. Parameters for the B₁⁺ mapping sequence were 30 slices at matrix size 64×64, 6/8 partial Fourier, TE = 13 ms, BW = 2520 Hz/px, nominal excitation flip angle 90 degrees, nominal pre-saturation flip angles α1/α2 = 22/66 degrees, and saturation TR = 5000 ms (satisfying TR ≥ 5 × T₁), scan time 5 minutes per run. Magnitude images were up-sampled to 128×128, masked and smoothed in-plane with a Gaussian kernel of four voxels FWHM. Spatial maps of the actually achieved α1 in the combined CP mode and the individual CP mode of the two rows were then calculated according to α1 = ½ * arccos((S1+S2)/2*S1), where S1 and S2 are the observed voxel intensities when pre-saturating with α1 and α2, respectively (39). To determine the effect of individual CP mode (single-row) excitation without flip angle calibration, the resulting maps were also divided to create maps of flip angle ratios. For each slice, the mean flip angle ratios of individual CP mode vs. combined CP mode excitation (prior to voltage adjustment) were incorporated into the sequence as slice-by-slice flip angle correction factors. The flip angle mapping was repeated to confirm the adjustment. This adjustment procedure did not aim to equalize the mean flip angle across all slices, but instead to achieve the same mean excitation in the individual CP modes as with the combined CP modes; this was in order to allow a direct comparison between the two. The relative increase in RF power required for the flip angle calibration directly follows from integrating over the flip angles ratios r_n of the N slices and is given by

$$P_{\mathit{rel}}=\frac{{\sum }_{n=1}^N{(\frac{1}{r_n})}^2}{N}.$$ [5]

Squaring the reciprocal of the flip angle ratios translates the necessary relative pulse voltage adjustment into the corresponding relative RF power increase. To quantify the RF power reduction that SMS-pTX can achieve while maintaining the mean flip angle per slice, we computed the RF power per imaging volume for the regular combined CP mode excitations, and the CP mode excitations that were calibrated to yield the same mean flip angles. This is achieved by replacing the denominator of Eq. 5 by 2N to reflect the doubled power of dual- vs. single band pulses.

3. EPI SMS-pTX scans

Factor two SMS-pTX with single-slice RF pulses on the two rows and corresponding MB-RF excitations in combined CP mode were obtained using an EPI sequence without and with blipped-CAIPIRINHA. Sequence parameters were 30 axial slices of 5 mm thickness, distance between simultaneous slices 75 mm, FOV 220 mm, matrix size 64 × 64, TE = 25 ms, BW = 2520 Hz/px, nominal flip angle 70 degrees, 20 volumes. No slice by slice flip angle calibration was performed. TR was 800 ms for the SMS acquisitions and 1600 ms for the single slice reference scans. The data were acquired both without FOV shift between the two slices, and with blipped-CAIPIRINHA to effect a shift of FOV/2. Two rows of receivers are sufficient to separate two axial slices, but an improved reconstruction was expected with blipped-CAIPIRINHA, which additionally draws on the in- plane receive sensitivities for the slice reconstruction.

We furthermore explored the applicability of SMS-pTX to excite a greater number of simultaneous slices than there are coil rows, which requires the use of multi-band pulses. Factor four SMS-pTX was performed by running a dual-band pulse on each coil row in individual CP mode, each exciting two slices. Similarly, factor six SMS-pTX was achieved by applying a tri-band pulse on each row. Quad- and hexa-band MB-RF excitations in combined CP mode were made for reference. For the four-slice experiment, a total of 32 slices were acquired in 8 excitations with a distance of 40 mm between simultaneous slices, TR = 450 ms, flip angle 35 degrees, and CAIPIRINHA shift was FOV/2; for the six-slice experiment, a total of 30 slices were acquired in 5 excitations with a distance of 37.5 mm between simultaneous slices, TR = 270 ms, flip angle 23 degrees, and CAIPIRINHA shift of FOV/3. Other parameters were as before.

IMAGE RECONSTRUCTION

For the flip-angle mapping, images were reconstructed online using the scanner’s standard reconstruction for EPI with sum-of-squares combination of the eight coil images. The data were exported in DICOM format and further processing as described above was performed offline in Matlab (The Mathworks Inc., Natick, MA, USA) on a dual 2.8 GHz Quad-Core Macintosh Pro (Apple, Cupertino, CA, USA) computer. The simultaneous multi-slice scans were reconstructed offline using custom Matlab routines. For the EPI data this included gridding for ramp-sampling by linear interpolation, Nyquist ghost correction (40) and frequency drift removal (41). The aliased slices were separated using slice-GRAPPA (10). FLASH data were reconstructed using 8×7 slice-GRAPPA kernels fitted to the central 64×64 k-space points of the single-slice reference scans. For the EPI data, kernels of size 4×3 were fitted once, and then applied to the entire EPI time series of aliased slice signals to reconstruct each volume. For the blipped-CAIPIRINHA EPI acquisitions, the off-resonance phase due to the blip moments was removed prior to kernel fitting and deconvolution (10).

RESULTS

Figure 3 shows simulated SAR distributions for the two cases of driving the coil in combined CP mode with a dual-band pulse on each row (left), and driving the two rows in their individual CP modes with a single-band pulse at half the voltage and power (right). The simulation confirms that the global SAR for SMS-pTX as used here is lower by about a factor of two (0.056 vs. 0.100 W/kg), which is as expected for the factor of two lower total RF power applied. Similarly the peak local SAR is predicted to be a factor of two lower (0.22 vs. 0.48 W/kg), and the SAR maps show that no unexpected hotspots arise as a consequence of the two coil rows being driven at different frequencies. The results of this simulation were used to make the local and global SAR predictions for the MB-RF and SMS-pTX scans described in the Methods section. For the in vivo FLASH scans, time-averaged global and local SAR were estimated by scaling to the flip angle of 37 degrees and the sequence’s RF duty cycle of 6.4%, yielding global/local SAR values for the MB-RF and SMS-pTX scans of 0.088/0.421 and 0.049/0.193 W/kg, respectively. For the EPI scans with the nominal flip angle of 70 degrees and the 4.83% RF duty cycle the time averaged global/local SAR for the MB-RF and SMS-pTX scans was estimated at 0.237/1.136 and 0.133/0.521 W/kg, respectively.

FIG. 3.

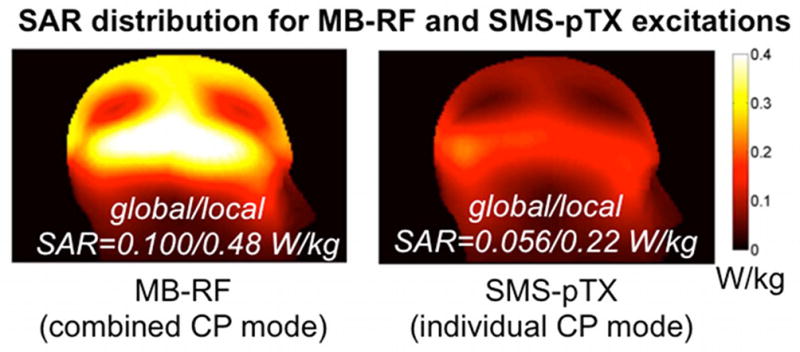
Left: SAR simulation for the pTX coil being driven in combined CP mode with a dual-band pulse on each row calibrated to achieve an average flip angle of 10 degrees over the two slices (left). Right: For the individual CP mode used for SMS-pTX excitations the two rows were independently driven with the corresponding single-band pulse at half the peak voltage hence half the total RF power, in the same manner as for the in vivo EPI experiments. Values shown represent the 10g-averaged SAR.

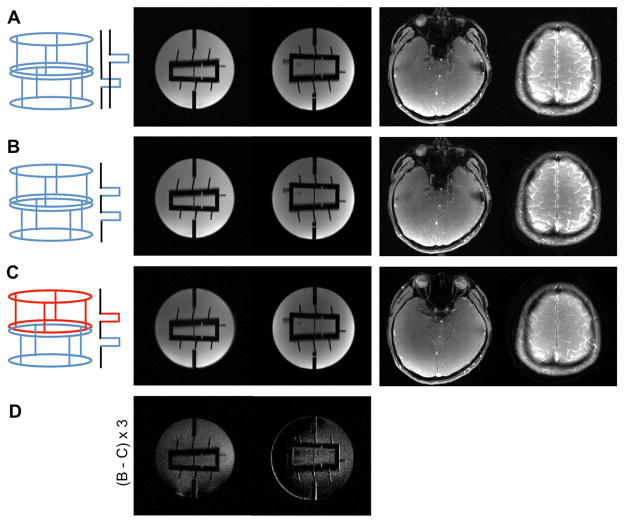
Example FLASH data of two slices at resolutions of 1×1×3mm³ (matrix 192×192) are shown in Figure 4. Panel (A) shows images obtained with conventional sequential single-slice excitation. SMS images with dual-band MB-RF excitation using both transmitter rows in combined CP mode are shown in (B), and factor two SMS-pTX images where each row excites a different slice in their individual CP modes are shown in (C). Both dual-band MB-RF and SMS-pTX excitations reduced scan time by a factor of two as compared to a single-slice scan. The SMS-pTX was set to transmit at the same RF power per excitation as a conventional single-slice scan, whilst it was factor of two higher for the MB-RF excitations. For the total RF power during the measurement, this translates to the same total power being applied in the MB-RF and single-slice scans, and a 50% lower power was applied in the SMS-pTX scans, without flip angle calibration. In particular for the region of the coil where the B₁⁺ sensitivities of the two rows overlap, a reduction in excitation flip angle would be expected. For the phantom image, this can qualitatively be seen from the scaled-up difference image in panel (D), which shows the difference between the MB-RF (B) and SSMS-pTX image (C). The in vivo SMS-pTX example to the right of panel (C) shows some degree of alteration in the intensity and tissue contrast, which is indicative of a change in excitation flip angle and/or flip angle distribution. A less than 50% RF power reduction would therefore result when making sure that the mean flip angle remains constant throughout the coil volume. The exact amount of power reduction is subject to the amount of overlap between the B₁⁺ sensitivity profiles at the slice locations of interest.

FIG. 4.

This figure shows example FLASH images of two slices (matrix size 192×192) obtained with conventional sequential single-slice excitation (A), dual-band MB-RF excitation using both transmitter rows in combined CP mode (B), and factor two SMS-pTX where each row excites a different slice in their individual CP modes (C). The in vivo SMS-pTX images to the right of panel (C) show a slight alteration in intensity and tissue contrast that is indicative of a reduced excitation flip angle and/or flip angle distribution. This is also indicated by the difference image in panel (D), which shows the difference between the MB-RF (B) and SMS-pTX image (C) for the phantom and is scaled up by a factor of three for better visibility.

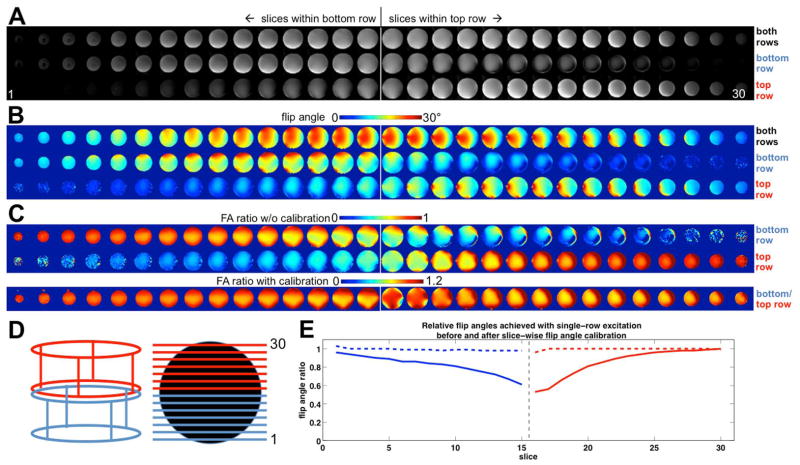
To investigate this further, the flip angle maps acquired for the combined CP mode and individual CP mode excitations are shown in Figure 5. The top panel (A) shows axial EPI images spanning across the coil volume along the z-axis. Images in the top row of (A) were excited with both transmitter rows in combined CP mode, whereas only one transmitter row at a time was used to excite the slices shown in the middle and bottom row of panel (A). The locations where the two transmitter rows join are indicated in the figure by the white vertical lines, and panel (D) provides a schematic of coil row selection, slice location and numbering; red and blue colors indicate excitation with the top and bottom row. The flip angle maps corresponding to the EPI images in panel (A) are shown in panel (B). The decreasing flip angle observed in slices that lie outside the active transmitter row indicate that the extent in the B₁⁺ sensitivity profile beyond the transmitter row, and hence the overlap of the two rows’ sensitivity profile, is not as pronounced as the intensity of the EPI images in (A) may imply. The relative flip angles achieved when transmitting only on one row at a time vs. the combined CP mode are shown in the top and middle row of panel (C). From these ratio maps we calculated the average flip angle ratio for each slice, which are plotted as solid lines in panel (E). The reciprocal of the ratios was then applied as a correction factor to adjust the flip angle (RF voltage) for each slice, to ensure the same mean flip angles are being achieved with transmission on a single transmitter row and in the coil’s combined CP mode. The aim was thus not to equalize the mean angle across all slices. The flip-angle mapping was repeated after calibrating the voltages, and resulting ratio maps are shown at the bottom of panel (C). Plotting the slice mean values (broken lines in panel (E)) demonstrates the efficacy of the calibration, accurate to within 2%. It is however evident from the maps with and without calibration (C) that this procedure does not homogenize the flip angle distributions within each slice.

FIG. 5.

Flip angle maps and calibration. Panel (A) shows 30 EPI slices spanning the entire coil volume (150 mm). The top row shows the images obtained when using the coil in its combined CP mode (both rings excite each slice); the middle and bottom row show the corresponding slices when exciting with only the bottom or top row in their individual CP modes, respectively, with no flip angle adjustment. The divide between the slices that fall within bottom and top rows is indicated by the vertical line. (B) shows the corresponding flip angle maps obtained with the dual-angle method. The nominal target flip angle is 22 degrees. Ratios of the flip angle achieved with single-row excitation vs. combined mode excitation without transmitter adjustments are shown in the top two rows of (C). As expected, a reduced B1+ is observed especially in the region where both rows contribute significantly to the excitation, but not in the lower and upper slices. The bottom row of (C) shows the ratio maps after adjustment of the RF pulse voltage for each slice to give the same mean flip angle as the combined-mode excitation. A plot of the flip angle ratios for each slice before (solid lines) and after (broken lines) flip angle adjustment is shown in (E), demonstrating successful restoration of mean flip angle. Throughout, red and blue colors indicate excitation with top and bottom row, respectively. (D) shows a schematic of the coil row selection, and slice positioning and numbering.

Calculation of the relative power increase required for this calibration yields P_rel = 1.408, thus a 41% higher RF power (on average per measurement) is required when using the calibrated flip angles for exciting the bottom half of slices with the bottom row, and exciting the top half of the slices with the top row. Comparing the calibrated voltages to standard MB-RF excitations yields P_rel = 0.703 which shows that SMS-pTX achieves the same mean flip angles at a 30% lower RF power per measurement than the MB-RF excitations. The same therefore holds true for the time averaged SAR. For SMS-pTX excitations, the RF power needed to excite the different slice pairs is the sum of the power needed for the individual slices are being excited together, and SAR of the different excitations scales accordingly. The plot of relative flip angles in Figure 5(E) clearly illustrates that effectively no power savings or SAR reductions can be gained near the interface of the coil rows (where their sensitivities strongly overlap), whereas the gains for slices near the distant ends of the rows (where their sensitivities do not overlap) is significant and approaches 50%.

Figure 6 shows EPI SMS-pTX images acquired in three subjects, at a slice acceleration factor of two. Images acquired with MB-RF excitations are also shown for comparison. Regular planar EPI without CAIPIRINHA blips was used in panel (A), while a FOV/2 shift between slices was imposed for the data shown in (B). Image quality of the SMS-pTX scans compares well to that of the MB-RF scans throughout. Careful inspection reveals a reduced signal and a discontinuity in signal intensity in the transition area between the two slice stacks. This is better illustrated in panel (C), which depicts the relative signal reduction of the SMS-pTX as compared to the MB-RF images. The effect on excitation flip angle in the transition region is not unexpected, and can be attributed to the corresponding B₁⁺ discontinuity near the interface of the two coil rows. Performing the MB-RF and SMS-pTX same experiments with blipped-CAIPIRINHA did not visibly impact the separation for aliased slices and image quality (panel (B) vs. (A)). This demonstrates that the receive sensitivities provided by the dual-row geometry along the z-axis alone are well capable of separating two axial slices without gradient spatial encoding. The image quality observed without blipped-CAIPIRINHA is in agreement with the reconstruction quality obtained for the FLASH scans in Figure 4, and also motivated the subsequent SMS-pTX experiments with blipped-CAIPIRINHA to excite and separate four and six simultaneous slices.

FIG. 6.

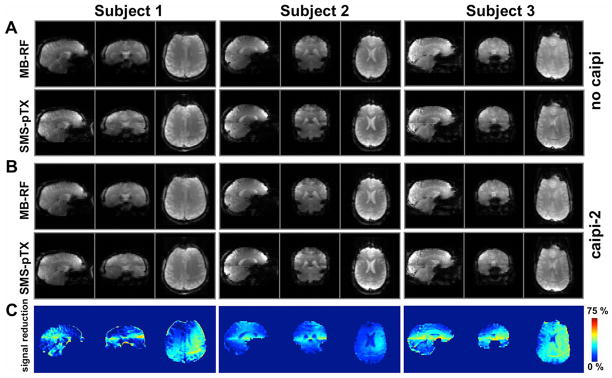
Three-plane view of the whole-brain EPI acquisitions with axial slices in three subjects, acquired at factor-2 slice acceleration with MB-RF and SMS-pTX excitations. Data acquired without FOV-shift between simultaneous slices are shown in panel (A); repeating the same experiment with blipped-CAIPIRINHA (FOV/2-shift between slices; panel (B)) did not visibly affect image quality, which demonstrates the suitability of the dual-row geometry to separate two axial slices. Overall apparent image quality between the MB-RF and SMS-pTX methods is comparable, but signal reductions and discontinuities in image intensity can be observed in the transition areas between the two slice groups. This is attributable to the reduced B₁⁺ especially near interface of the two coil rows and also the step function in B₁⁺ profile, as is evident from the maps in panel (C), which show the relative signal reduction of SMS-pTX vs. MB-RF (for the case without CAIPI).

Example SMS-pTX EPI images at slice acceleration factors of four and six are shown in Figure 7(A) and (B), and conventional MB-RF acquisitions are again provided for comparison. At both slice acceleration factors the image quality compares very well between SMS-pTX and MB-RF excitations. Slice separation with blipped-CAIPIRINHA EPI and slice-GRAPPA worked robustly at slice factor four, and even the six simultaneous slices could be reconstructed reliably despite there being a total of only eight receiver channels. The lower image intensity of the factor six SMS data is caused by a lower flip angle of 23 degrees, which was used due to peak voltage limitations with the hex-band MB-RF pulse.

FIG. 7.

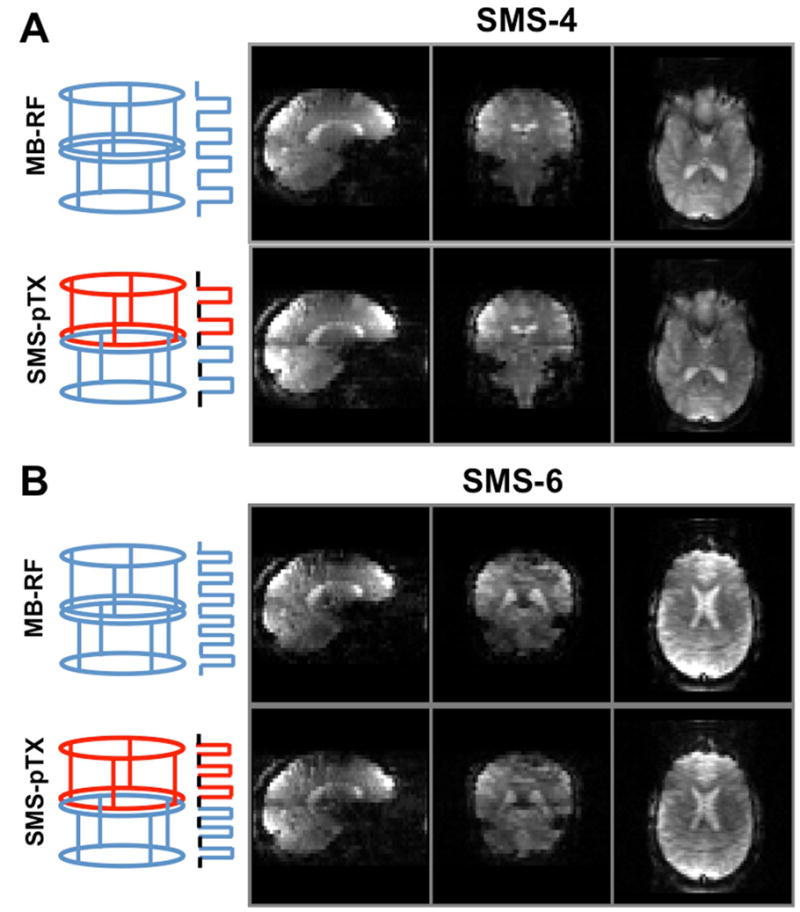
This figure shows three-plane views of the axially acquired blipped-CAIPIRINHA EPI acquisitions at slice acceleration factors of (A) four and (B) six. Four-slice MB-RF (A, top) was achieved by using regular quad-band pulses in combined CP mode, while SMS-pTX (A, bottom) was achieved by simultaneously applying dual-band pulses at different frequencies on the two coil rows. Analogously, hexa-band pulses were used for six-slice MB-RF, and two tri-band pulses for SMS-pTX. The receive sensitivities of the dual rows along z allow only for the separation of two axial slices, therefore CAIPIRINHA shifts of FoV/2 and FoV/3 were needed to reconstruct four and six simultaneous slices by drawing on the in-plane coil sensitivities.

DISCUSSION AND CONCLUSIONS

We have introduced the concept for SMS-pTX and demonstrated its use on an 8-channel pTX system at 3 T. Using a dual-row pTX/RX coil, SMS-pTX excitations were applied to multi-slice FLASH and EPI sequences. It was shown that SMS-pTX allows for a reduction in RF power deposition and SAR as compared to MB-RF excitations, by taking advantage of the local B₁⁺ sensitivities inherent the pTX coil geometry. We observed a 30% reduction in RF power after flip angle calibration, but at a tradeoff in B₁⁺ homogeneity. The dual-row coil naturally lends itself to the simultaneous excitation and acquisition of two-slices, and a larger number of slices can be separated using the CAIPIRINHA technique. Phantom and in vivo FLASH images were shown at slice acceleration factors of two, four and six.

We found that RF power can be reduced by exploiting the localized transmit sensitivities of the pTX array. SMS-pTX does this by exciting slices using only the transmitters that are nearby, and not the transmitters that are further away and contribute fully to SAR while contributing little to nothing to exciting the target slice. Those transmitters are instead used to excite another slice closer to them, at the same time. The choice of pTX coil geometry and transmitter grouping as well as slice orientation are clearly important considerations that will affect the ability to reduce transmit power and achieve acceptable B₁⁺ homogeneity as well as the number of slices that can reliably be separated during the reconstruction. We employed a coil with the arrangement of transmitters in two axial rows stacked along the z-axis (20,21). This is a design that naturally lends itself to the excitation of two axial slices or two slice groups since the B₁⁺ sensitivities are relatively smooth within the axial plane (the prerequisite for retaining B₁⁺ homogeneity with SMS-pTX) but do not overlap so strongly between the rows (the prerequisite for realizing RF power reductions). An axial slice orientation is also common for many SMS applications such as fMRI. For the case of two rows and two slices with non-overlapping transmit sensitivities, RF power is reduced by 50%. However, since there is typically overlap in the sensitivities of the transmitter groups, the binary channel selection will have consequences on the flip angle that is achieved with SMS-pTX. Slice location specific flip angle adjustment is hence desirable, which on our dual-row setup still resulted in an RF power per volume that was about 30% lower than for corresponding excitations on both rings.

Non-axial slice orientations still need to be explored with the dual-row coil used here, and it is conceivable that more flexibility regarding transmitter grouping and slice orientation would be provided by other 3D pTX coil geometries including the head conformal helmet design by Gilbert et al. (26). If axial slices are to be excited and more pTX elements are available, the addition of more transmitter rows to increase the 3D transceiver sensitivities might be preferable. A practical advantage of a multi-row geometry is that each row can be driven in a CP mode (20), which in principle reduces the number of required RF transmit channels to the number of rows, with the elements of each row simply being driven via power splitters. In contrast to two- or more row design, the more common pTX coil arrangement in a single axial row lacks sensitivity variation along the z-axis, and has therefore no or limited capability of providing appreciable power reductions or coil spatial encoding for any type of SMS excitations of axial slices. There will however be some benefit with sagittal and coronal slices.

Many other approaches to reducing SAR with various pTX strategies are also actively being researched. This includes the reduction of total SAR by using different RF pulses for different k-space regions (46) or reducing local time-averaged SAR by toggling between different RF pulses for different lines and/or slices such that the E field distribution of subsequently applied pulses does not strongly overlap (36,47). Neither approach has yet been explored in the context of SMS acquisitions. The advantages of reduced SAR should especially pertain to high field or T2 weighted imaging.

How SMS-pTX impacts B₁⁺ homogeneity depends on how the transmitter subgroups are selected and the locations of the slices excited by them. In general, a greater overlap of the B₁⁺ profiles of the subgroups will result in a stronger effect on B₁⁺ homogeneity when dedicating only a subset of transmitters to exciting a given slice. Also in our setup with two coil rows in their CP mode there naturally is some discontinuity in B₁⁺ at the transition between the SMS-pTX slice stacks. This is reduced, but not removed by flip angle adjustment, as was seen from the bottom row of Figure 5(C) and also explains the intensity variation around the midline of the sagittal views of the SMS-pTX EPI data (Figure 6). For typical EPI applications with gradient echo contrast, such as BOLD fMRI this may not be a practical concern as they rely on signal stability over time, rather than absolute image intensity. For example, the much stronger dark bands in a fast multi-slab fMRI sequence (43) was found to be unproblematic in practice. For applications that require a higher degree of B₁⁺ homogeneity such as spin-echo based diffusion acquisitions, one will have to consider more complex excitation schemes that go beyond the “binary” selection of transmitters that was used here. This is the main limitation of the present approach that future work needs to address.

B₁⁺ shimming or the application of a more general pTX framework may help remove the limitations brought by forming rigid transmitter groups. While this is necessary if single-band RF pulses are to be used for SMS excitation as we did here for the dual-slice SMS-pTX, other strategies are conceivable. Slice specific B₁⁺ shims have been shown to yield superior homogeneity for 2D acquisitions (44,45) and are particularly necessary at high field or for quantitative applications based on spin-echo contrast. To realize fully B1+ shimmed SMS-pTX, one could first determine the optimal amplitude and phase modulations for each transmitter and slice as for a slice-by-slice B₁⁺ shim with single-slice excitations. Subsequently, multi-band RF pulses would be formed by complex addition of the individual pulse shapes of the slices that are to be excited simultaneously, to obtain different multi-band pulse shapes (with different amplitude and phases on the different frequency bands) for each transmitter and SMS slice group. The additional degrees of freedom should allow the best possible B₁⁺ calibration at the minimum required power per excitation, or the two can be traded off against each other at will.

This study is intended as a proof of concept, and we have hence not investigated exhaustively how SMS-pTX can best be utilized to reduce SAR, maximize number of simultaneous slices, or incorporate full B₁⁺ shims. These are open questions for future work and there may also be coil designs with 3D pTX sensitivities that are better suited to this purpose. Especially in conjunction with slice specific B₁⁺ shims on more complex coil geometries, and at high field, full simulation of local SAR should be performed to ensure that legal power limits are not exceeded. For our gradient-echo EPI scans, the simulated peak local SAR of 1.14 W/kg for the conventional MB-RF pulses was well within the FDA regulations (factor of >7 lower), but limits will quickly be reached in experiments with spin-echo contrast, a large number of simultaneously excited slices or when B₁⁺ homogenization is desired. In these cases the proposed SMS-pTX or improvements thereon will be very valuable.

Single-shot acquisitions benefit the most from acceleration along the slice direction, which is why SMS has primarily been used in EPI sequences. This motivated the choice of EPI for this study, and fMRI and diffusion imaging are good candidate applications of SMS-pTX. We chose to reconstruct the SMS EPI acquisitions with a blipped-CAIPIRINHA EPI sequence as recently described by Setsompop et al. (10). Primarily aimed at managing the g-factor penalty in SMS acquisitions by reducing the spatial overlap between the aliased slices as described in the original CAIPIRINHA work (48), the method facilitates undersampling factors that are greater than the receiver coils dimensionality along the same imaging direction. Here, slice factors of four and six were achieved with only two axial coil rows, by using controlled aliasing to redistribute part of the undersampling into the slice plane. It may be regarded remarkable that six simultaneous slices could be disentangled at such high fidelity using only eight receive channels; clearly this prohibits the use of phase-encode acceleration in addition to the slice acceleration. A setup with separate transmit- and receive coil arrays may allow a larger number of receive channels and facilitate even larger acceleration factors. We chose slice-GRAPPA for slice unfolding due to its ability to reconstruct FOV-shifted slices, but alternatives include SENSE reconstruction as used in the original SMS work by Larkman et al. (8), a hybrid SENSE/GRAPPA approach (49), GRAPPA (9) and a generalized iterative SENSE framework that recognizes the 3D-encoding nature of CAIPI acquisitions. Analogous to the B₁⁺ sensitivities, the B₁⁻ receive profiles along z allow for separation of two simultaneous slices without the need for gradient encoding, as evident from our dual slice acquisitions without CAIPIRINHA.

To summarize, this paper has introduced the concept of SMS-pTX. This new method allows RF power reductions in SMS excitations by taking advantage of the B₁⁺ variations the pTX coil geometry. We applied the technique to SMS FLASH and EPI sequences at 3 T using an eight-channel dual-row pTX coil. RF power reductions of 30% were achieved compared to regular multi-band RF excitations while maintaining the mean flip angle. The tradeoff is a reduced B1+ homogeneity especially between the stacks of simultaneous slices, which also constitutes the main limitation of the current approach. Future work needs to address this with a full pTX multi-slice B1+ shim which will allow a flexible tradeoff of B1+ homogeneity and RF power reductions.