Abstract
It seems unlikely that the immune system can actively avoid the generation of self-reactive cells in the primary, pre-selected repertoire. On the contrary, by generating a very high proportion of self-reactive B cells in its primary repertoire, the immune system may be pursuing the most efficient strategy for building a repertoire capable of optimally recognizing nonself, as discussed here by David Nemazee.
The fact that autoreactive B cells are efficiently eliminated by tolerance mechanisms1 has far-reaching implications for the formation of the lymphocyte repertoire. However, these mechanisms introduce waste. The waste in B-cell development is massive, both at early stages of development in the bone marrow2 and later, after potentially responsive B cells have been generated and exported to the periphery3. To what extent is this waste due to tolerance? Or, to put it another way, what proportion of generated B cells is Likely to be autoreactive and suppressed by deletion? This article suggests that it is reasonable to expect that most generated B-cell receptors are self-reactive and are eliminated by tolerance.
The B-cell repertoire is highly diverse; thus, the concept that there is extensive self-reactivity, which is subject to strong negative selection, might imply that B-cell tolerance is extraordinarily sensitive, perhaps having a low affinity/avidity threshold. This possibility has been explored experimentally using mice transgenic for anti-major histocompatibility complex (MHO class I-specific immunoglobulin (Ig) genes4, in which self-tolerance of B cells bearing a defined receptor can be followed. The Ig genes used to generate these transgenic mice are derived from a B-cell hybridoma (3–83), which itself was derived from a fusion of spleen cells from an H-2d mouse strain immunized with H-2k spleen cells5. The 3–83 Ig binds with moderate affinity to H-2Kk and only very weakly to several other MHC class I molecules. The 3–83 crossreactive interaction with Kbm3 and Dk molecules is particularly weak and, even at the highest concentrations of Ig, it is difficult to demonstrate any binding to these antigens. The avidity of the bivalent form of 3–83 for these antigens is much less than 10−6 M, and the single-site affinity is below the detection limits of our assays (>10−5 M). This allowed a comparison of the tolerance-inducing ability of antigens of similar structure, valency and tissue distribution that varied only in their relative affinities for the B-cell's receptor. The results of these experiments were clear: when 3–83-transgenic mice were bred onto the low-avidity ligand backgrounds bearing Kb, Dk or Kbm3, autoreactive B cells were deleted from the peripheral lymphoid organs (Refs 4, 6; J. Lang and D. Nemazee, unpublished). These results are rather surprising given the reported ubiquity and prevalence of low-affinity autoreactive B cells (reviewed in Refs 7, 8), and may suggest a countervailing antigen-driven positive selection for certain specificities.
The capacity model
A deeper significance of self-tolerance in repertoire development emerges from a consideration of the well-known concepts of degeneracy and crossreactivity9. An individual antibody or B cell must bind to many different antigens, which can be related or unrelated to one another. This property is probably a function of both the size and the flexibility of the antigen-combining site10. Clearly, many of the generated antigen-combining sites must cross-react with self. Is it possible to devise a model that describes the amount of self-reactivity in the pre-selected repertoire, and provides the most efficient use of the cells that are not deleted? With this aim, the following discussion analyses the relationship between two key numbers: (1) the fraction of B cells that must be inactivated; and (2) the degeneracy of the antigen-combining site.
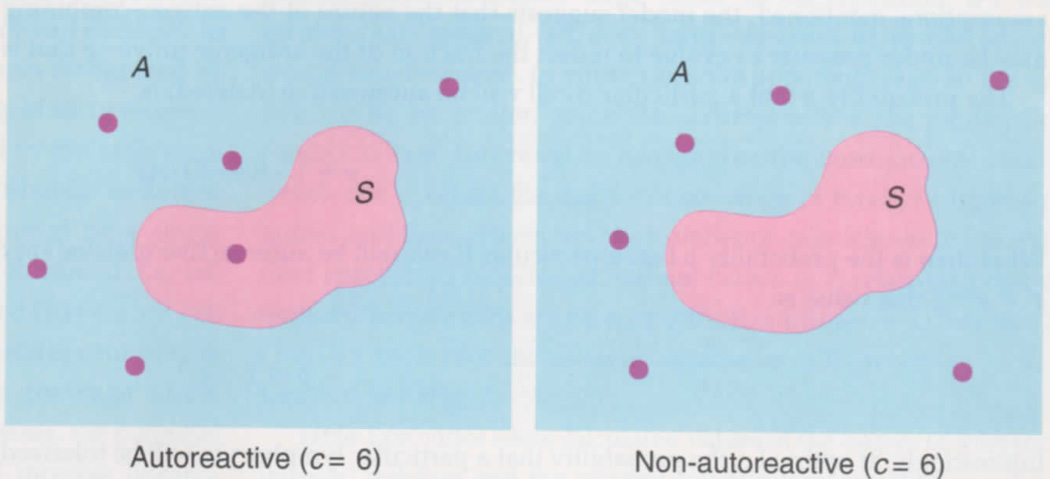
In Fig. 1, the rectangle A represents the total number of potential antigen epitopes, and S represents the subset of self-epitopes to which tolerance is induced. The number of epitopes recognized by an individual receptor is defined as c, the capacity of an Ig receptor. According to this model, the epitopes recognized by the individual B cells in Fig. 1 are represented as a random distribution of dots of number c, and a fraction of the epitopes recognized by a single B cell may or may not bind self at a 'deletable' threshold, i.e. fall within S. Assuming that A is large, but finite, and that each B cell has the same value for c, what would be the best strategy for the immune system to adopt in order to maximize the 'coverage' of the foreign universe of antigens? As the size of c increases, the potential coverage that each permitted B cell affords will increase linearly, but the probability that it will be eliminated by tolerance, and that its potential coverage of the foreign antigens will be lost, will ultimately increase more rapidly. This means that there should be an optimal value of c.
Fig. 1.
Scheme illustrating the capacity model for describing selection of the B-cell repertoire. Rectangles (termed A) represent the totality of antigenic epitopes, of which subsets (termed S) represent self-antigens. The lymphocyte represented by the left-hand panel has a capacity (c) of six (shown as dots), reacting with six different epitopes, one of which is included among the self-antigens. This cell will be subjected to self-tolerance and eliminated, preventing its potential reactivity to the remaining five, foreign epitopes. The lymphocyte represented by the right-hand panel has a similar c value, but fails to see self and is tolerated. As c increases, the likelihood that a cell will be autoreactive tends to rise more rapidly than does the coverage of foreign epitopes that the increased value of c imparts.
Optimal degeneracy leads to massive deletion
A simple mathematical formula can be used to determine optimal c (see Box 1). Remarkably, at the optimal value of c, the majority of B cells (~63.2%) are eliminated by tolerance. Thus, the system should provide the most complete coverage or protection from foreign antigens when most (1 — e−1= ~63.27%) of the B cells are forbidden! If c were suboptimal, the immune response would be more specific and delete a smaller percentage of cells, but would require far more cells to avoid intolerably large 'holes' in the repertoire. If c were greater than optimal, an even larger fraction of produced cells would be eliminated. In either case, the apparent waste in the system would be greater, given the assumptions of the model. This concept is best illustrated by considering the most general case, in which one specifies the degree of coverage of foreign antigens required and then determines the number of cells (clones of independent specificity) required at various values of c, relative to that required when the cells are monospecific (i.e. where c = 1) (see Box 2). One can then plot the relative number of cells required, n, as a function of c (Fig. 2).
Box I. Is there an optimal level of antigen receptor degeneracy?
Assumptions:
self-epitopes are a subset of the finite set of all epitopes;
self-epitopes induce tolerance;
antigen receptors recognize a random collection of epitopes of number c;
the signaling threshold for tolerance and activation is identical;
the generation of the B-cell repertoire is selected by evolution to provide the maximum 'coverage' of the foreign antigenic set by potentially reactive B cells.
On the basis of these assumptions, it follows that the fraction, F, of the foreign antigenic universe recognized by some functional B cell in the system is:
| (1) |
Equation 1 expresses the value of one minus the probability that a portion of the foreign epitopes will fail to be seen by the produced lymphocytes, either because of chance or because the cells are disallowed due to self-tolerance. This second term of Eqn 1 is the first term of the Poisson series (representing the class with zero events) and the exponent m represents the mean number of 'events' per foreign epitope (i.e. the number of cells recognizing a particular foreign epitope). This value is seen to be nc/(A–S) (where A is the totality of antigenic epitopes and S represents the subset of self-antigens) multiplied by a correction factor to include only the fraction of clones that are non-self-reactive, which is [(A–S)/A]c. Thus:
| (2) |
where n is the total number of clones of independent specificities in the system before selection (in practice, n is equivalent to the number of B cells generated prior to selection). By differentiating F with respect to c and setting to zero, one can determine the value of c that maximizes the coverage of the foreign epitopic universe. We find an optimal c:
| (3) |
which is a function of the ratio of self to nonself. (This value is well approximated by A/S for values of S<A/4.) Thus, based on the few assumptions mentioned, the model suggests that the nature of the antigen-combining site, which is the biochemical expression of c, may be under pressure to evolve to reflect the fraction of the antigenic universe that is self.
The probability p that a particular B cell will be autoreactive (deleted) is:
| (4) |
What then is the probability p that a particular B cell will be autoreactive (deleted) at optimal c? Substituting for c (and recalling that ax = exlna, this value is:
| (4a) |
Interestingly, at optimal c, the probability that a particular lymphocyte will be tolerized is a dimensionless number (~63.2%), the value of which is independent of n, A and S.
De Boer and Perelson27 and Whitaker and Renton28 have arrived at similar conclusions based on somewhat different assumptions and parameters. Unlike the theories of these authors, the present model does not impose the assumption that S is small relative to A, and it takes into account the likely possibility that much more than minimal 'coverage' may be required for immunological protection (see text and Box 2 for details.)
Box 2. Assessing the costs and benefits of degeneracya.
In a more general model, one can specify a particular level of 'coverage' of the foreign antigens and determine the effect of c on the relative number of lymphocyte clones required to achieve this level. This can be done by rearranging Eqn 1 thus:
| (5) |
and solving for the ratio: n (at an arbitrary value of c): n (when c = 1), which yields:
| (6) |
This relation is graphically demonstrated in Fig. 2 for several ratios of self to nonself. It is easy to show that the optimal value of c for the minimization of n required in Eqn 5 is the same as that found in Eqn 3. In addition, similar high rates of deletion are obtained if one assumes either a normal distribution of values of c or a highly skewed bimodal distribution of c, suggesting again that the generation of massive autoreactivity in the pre-selected repertoire is the most cost-effective strategy to maximize coverage of nonself.
a For definition of variables c, n, F, A and S, see Box 1.
Fig. 2.
The effect of the capacity (c) of the antigen-combining site on the relative number of lymphocytes required to obtain comparable coverage of foreign antigens. Optimal c provides comparable coverage at lower cost (relative number of independent clones, n) and is sensitive to the proportion of epitopes that are self. At 1% self, higher values of c than those plotted here will lead to an eventual rise in relative n. This graphic was generated using the JMP statistical analysis program (SAS Institute Inc., Cary, NC).
Table 1 provides some calculated values of the degree of tolerance-induced deletion and the relative cell numbers required as a function of the proportion of antigens that are self and the values of c. For example, if self constitutes 1% of all epitopes, optimal c leads to 63-fold more cell deletion relative to a c value of 1 (monospecificity), but requires only 2.7% as many cells in the pre-selection repertoire to yield comparable coverage of foreign antigens compared with that required by a monospecific repertoire.
Table 1.
The relationship between antigen receptor capacity (c), the pre-selection cell numbers required to achieve comparable 'coverage' of foreign antigens (n) and the probability of deletion
| 1% self-antigensa | 5% self-antigens | 10% self-antigens | ||||
|---|---|---|---|---|---|---|
| c | n requiredb | % B cells deletedc | n required | % B cells deleted | n required | % B cells deleted |
| 1 | 100.0 | 1.0 | 100.0 | 5.0 | 100.0 | 10.0 |
| 2 | 50.5 | 2.0 | 52.6 | 9.8 | 55.5 | 19.0 |
| 5 | 20.8 | 4.9 | 24.6 | 22.6 | 30.5 | 40.9 |
| 10 | 10.9 | 9.6 | 15.9 | 40.1 | 25.8 | 65.1 |
| 20 | 6.1 | 18.2 | 13.3 | 64.2 | 37.0 | 87.8 |
| 50 | 3.3 | 39.4 | 24.7 | 92.3 | 349.3 | 99.5 |
| 100 | 2.7 | 63.4 | 160.5 | 99.4 | 33883.7 | 99.99 |
As assumed by the model, tolerance plays a central role in establishing the form of the optimal repertoire. It is interesting to note that, in the absence of self-tolerance, the best strategy for the immune system would be to generate a single clone bearing a receptor with infinite c, providing a universal 'glue' capable of binding to all antigens.
Implications of the model
Several additional points can be made regarding the implications of the model (see Eqns 1 and 2 in Box 1). First, maximizing F (the fraction of the foreign antigenic universe recognized by a functional cell) is achieved by maximizing m (the average number of B cells recognizing any given epitope); in other words, maximizing the breadth of coverage is achieved concomitantly with maximizing, on average, the depth of coverage. Augmenting depth through clonal proliferation may be less desirable initially because it limits breadth and is lacking in heterogeneity of functional affinity, potentially limiting the pre-mutational pool available for the affinity maturation of late primary responses.
Second, the value m increases linearly with increasing n. This satisfies conditions that solve what Langman and Cohn call 'the elephant:tadpole paradox', namely that B-cell function is concentration dependent11. Thus, a single rare B cell reactive to a pathogen is useless to combat primary infection in a large animal, and the responding cells must represent a reasonable proportion of cells, and be present at a minimal copy number per unit volume, in order to generate a sufficent primary response11. Assuming that optimal c is selected by economy, the values of S are similar for all vertebrates, and n increases with organism size, then m should be proportional to the volume of the animal. [The latter assumption is probably correct because: (1) the concentration of lymphocytes in blood is similar in birds, reptiles and mammals of different sizes12; and (2) in the cases where information is available, the B-cell number never approaches the size of the potential repertoire13–15.] If an organism increases in size over its lifetime, or through evolutionary time, m would increase proportionately, and this increase would be sufficient to achieve a comparable unit concentration of reactive B cells to any particular antigen.
Third, since optimal c is the same for different organisms, once a workable antigen-combining site with sufficent size/flexibility to yield optimal c has been selected over evolutionary time, further changes in c would not be heavily selected. What should be selected in evolution is a potential receptor diversity that exceeds a minimum threshold, i.e. diversity itself should be selected. In practice, this means that the potential receptor diversity must never drop below the total number of cells present, but need not be vastly greater than the total cell number. This might explain why 'N' nucleotide additions in variable (V)-gene assembly are not found in early development16,17 because the B-cell number is not sufficient to require the additional diversity generated. Thus, diversity that is adequate for the cell numbers required, coupled with an appropriate c value, would provide broad and deep coverage of the antigenic universe.
The problem posed by the antigenicity of V-regions themselves18 predicts that, during the development of the immune system, the effective S set should change, and perhaps grow, through the loss of maternal Ig and the accumulation of self V-region proteins. Should self-idiotypes generate an increase in the effective self-determinants with age, c should decrease accordingly. In any case, B cells with receptor epitopes mimicking self should be favored.
One difficulty that might be imposed by a high level of receptor crossreactivity (c value) is that B cells undergoing antigen-driven V-region hypermutation may frequently acquire reactivity to self. The potential importance of tolerance induction in B cells that have undergone V-gene mutation has long been recognized19 and tolerance may be induced in such B cells20–22.
Massive cellular negative selection induced by self-antigens may manifest a pattern of antigen receptor V-gene usage in the surviving cells that is difficult to distinguish from that which may arise as a result of self-antigen-induced 'positive selection'. Thus, the plausibility of massive, tolerance-induced deletion provides an alternative hypothesis that may explain some published results (e.g. Ref. 23).
Concluding remarks
Is tolerance-related cell loss unavoidable? The B-lymphoid system could partly compensate for the potential waste caused by self-tolerance by using receptor editing to screen out useless receptors, without cell loss, at an early developmental stage6,24–26. This would partially overcome the theoretical difficulty proposed above: namely, that even an efficient immune system should generate huge numbers of autoreactive receptors destined for deletion.
Acknowledgments
This work was supported by grants from the Arthritis Foundation and the National Institutes of Health (RO1GM44809, KO4AI01161, AI33608-02). The author thanks P. Archer of the University of Colorado Health Sciences Center for checking the mathematical model; and P. Lane, M. Weigert, S. Litwin, A. Perelson, K. Karjaleinen, D. Gray, V. Kouskoff and L. Wysocki for encouraging the publication of this work and for commenting on the mathematical model.
References
- 1.Nossal GVJ. Adv. Immunol. 1992;52:283–331. doi: 10.1016/s0065-2776(08)60878-0. [DOI] [PubMed] [Google Scholar]
- 2.Osmond DG. Semin. Immunol. 1990;2:173–180. [PubMed] [Google Scholar]
- 3.Förster I, Rajewsky K. Proc. Natl Acad. Sci. USA. 1990;87:4781–4784. doi: 10.1073/pnas.87.12.4781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Russell DM, Dembic Z, Morahan G, Miller JFAP, Bürki K, Nemazee D. Nature. 1991;354:308–311. doi: 10.1038/354308a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ozato K, Mayer N, Sachs DH. J. Immunol. 1980;124:533–540. [PubMed] [Google Scholar]
- 6.Tiegs SL, Russell DM, Nemazee D. J. Exp. Med. 1993;177:1009–1020. doi: 10.1084/jem.177.4.1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Avrameas S. Immunol. Today. 1991;12:154–159. doi: 10.1016/S0167-5699(05)80045-3. [DOI] [PubMed] [Google Scholar]
- 8.Schwartz RS, Stollar BD. Immunol. Today. 1994;15:27–32. doi: 10.1016/0167-5699(94)90022-1. [DOI] [PubMed] [Google Scholar]
- 9.Yoshioka M, Lifter J, Hew CL, et al. Biochemistry. 1973;12:4679–4685. doi: 10.1021/bi00747a021. [DOI] [PubMed] [Google Scholar]
- 10.Foote J, Milstein C. Proc. Natl Acad. Sci. USA. 1994;91:10370–10374. doi: 10.1073/pnas.91.22.10370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Langman RE, Cohn M. Mol. Immunol. 1987;24:675–697. doi: 10.1016/0161-5890(87)90050-2. [DOI] [PubMed] [Google Scholar]
- 12.Altman PL, Dittmer DS, editors. Biology Data Book. 1964:272–274. , FASEB. [PubMed] [Google Scholar]
- 13.Du Pasquier L. Curr. Opin. Immunol. 1993;5:185–193. doi: 10.1016/0952-7915(93)90003-b. [DOI] [PubMed] [Google Scholar]
- 14.Reynaud CA, Bertocci B, Dahan A, Weill JC. Adv. Immunol. 1994;57:353–378. doi: 10.1016/s0065-2776(08)60676-8. [DOI] [PubMed] [Google Scholar]
- 15.Reynaud CA, Garcia C, Hein WR, Weill JC. Cell. 1995;80:115–125. doi: 10.1016/0092-8674(95)90456-5. [DOI] [PubMed] [Google Scholar]
- 16.Komori T, Okada A, Stewart V, Alt FW. Science. 1993;261:1171–1175. doi: 10.1126/science.8356451. [DOI] [PubMed] [Google Scholar]
- 17.Gilfillan S, Dierrich A, Lemeur M, Benoist C, Mathis D. Science. 1993;261:1175–1178. doi: 10.1126/science.8356452. [DOI] [PubMed] [Google Scholar]
- 18.Jerne NK. Ann. Immunol. Inst. Pasteur. 1974;125C:373–389. [PubMed] [Google Scholar]
- 19.Diamond B, Scharff MD. Proc. Natl Acad. Sci. USA. 1984;81:5841–5844. doi: 10.1073/pnas.81.18.5841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Walker SM, Weigle WO. Cell. Immunol. 1985;90:331–338. doi: 10.1016/0008-8749(85)90198-4. [DOI] [PubMed] [Google Scholar]
- 21.Linton P-J, Rudie A, Klinman NR. J. Immunol. 1991;146:4099–4104. [PubMed] [Google Scholar]
- 22.Pulendran B, Karvelas M, Nossal GJV. Proc. Natl Acad. Sci. USA. 1994;91:2639–2643. doi: 10.1073/pnas.91.7.2639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gu H, Tarlinton D, Müller W, Rajewsky K, Förster I. J. Exp. Med. 1991;173:1357–1371. doi: 10.1084/jem.173.6.1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gay D, Saunders T, Camper S, Weigert M. J. Exp. Med. 1993;177:999–1008. doi: 10.1084/jem.177.4.999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Radic MZ, Erikson J, Litwin S, Weigert M. J. Exp. Med. 1993;177:1165–1173. doi: 10.1084/jem.177.4.1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chen C, Radic MZ, Erikson J, et al. J. Immunol. 1994;152:1970–1982. [PubMed] [Google Scholar]
- 27.De Boer RJ, Perelson AS. Proc. R. Soc. London Ser. B. 1993;252:171–175. doi: 10.1098/rspb.1993.0062. [DOI] [PubMed] [Google Scholar]
- 28.Whitaker L, Renton AM. J. Theor. Biol. 1993;164:531–536. doi: 10.1006/jtbi.1993.1171. [DOI] [PubMed] [Google Scholar]