Joint detection of association, imprinting and maternal effects using all children and their parents

Abstract

Genomic imprinting and maternal effects have been increasingly explored for their contributions to complex diseases. Statistical methods have been proposed to detect both imprinting and maternal effects simultaneously based on nuclear families. However, these methods only make use of case-parents triads and possibly control-parents triads, thus wasting valuable information contained in the siblings. More seriously, most existing methods are full-likelihood based and have to make strong assumptions concerning mating-type probabilities (nuisance parameters) to avoid over-parametrization. In this paper, we develop a partial Likelihood approach for detecting Imprinting and Maternal Effects (LIME), using nuclear families with an arbitrary number of affected and unaffected children. By matching affected children with unaffected ones (within or across families) having the same triad/pair familial genotype combination, we derive a partial likelihood that is free of nuisance parameters. This alleviates the need to make strong, yet unrealistic assumptions about the population, leading to a procedure that is robust to departure from Hardy–Weinberg equilibrium. Power gain by including siblings and robustness of LIME under a variety of settings are demonstrated. Our simulation study also indicates that it is more profitable to recruit additional siblings than additional families when the total number of individuals is kept the same. We applied LIME to the Framingham Heart Study data to demonstrate its utility in analyzing real data. Many of our findings are consistent with results in the literature; potentially novel genes for hypertension have also emerged.

Introduction

Genomic imprinting and maternal effects are two important epigenetic factors in the etiology of complex diseases, which may hold some promise in research for finding missing heritability.¹ Genomic imprinting is the effect of an epigenetic process leading to imprinted genes that express in a parental-origin-specific manner. That is, for an imprinted gene, a particular genetic variant may have different effects on disease susceptibility depending on which parent transmits it to the offspring.² The first imprinted gene in humans was found 20 years ago.³ After that, more and more imprinted genes have been identified, and a number of genetic diseases have been confirmed to be associated with these imprinted genes. Classic examples include Beckwith–Wiedemann syndrome, and Prader–Willi and Angelman syndromes.⁴ In fact, it has been estimated that about 1% of all mammalian genes are imprinted,⁵ but only a limited number have been identified thus far.

Maternal effect refers to the phenotype of an individual being influenced by the genotype of the mother. It has been well established that in the etiology of some complex diseases, such as childhood cancers, certain psychiatric illness, congenital malformations, and pregnancy complications, both the maternal genome and the fetal genome have important roles, and thus both need to be considered in the analysis.^{6, 7, 8} On the other hand, genomic imprinting has emerged as one of the most informative paradigms in understanding the interplay between the genome and the epigenome.² However, in analyzing genomic imprinting of complex diseases, maternal effects may be confounded with genomic imprinting because both can produce the same parent-of-origin patterns of phenotypic variation.⁹ Therefore, genomic imprinting and maternal effects, the consequences of two different underlying epigenetic mechanisms, should be distinguished and studied jointly to avoid false positives and false negatives.¹⁰

To study genomic imprinting and/or maternal effects, there are different designs, including the designs that recruit extended families,^{11, 12} as well as designs that consider case-parents/control-parents triads, case-mother/control-mother pairs and a mixture of them.^{10, 13, 14, 15} In analyzing triads and/or pairs data, both nonparametric and parametric statistical methods have been proposed. Nonparametric methods are mainly proposed to detect imprinting effects under the assumption of no maternal effects,^{13, 16} but type I error may be inflated and power may also be affected when the assumption is violated.¹² On the other hand, although parametric method can detect imprinting and maternal effects jointly, they usually need to make some stringent and unrealistic assumptions about mating-type probabilities. A log-linear likelihood ratio test was the first method proposed to detect imprinting and maternal effects simultaneously by using only case-parents triad data.¹³ However, it is necessary to assume mating symmetry (MS) when using this method to avoid estimating many parameters. For case-mother and control-mother pairs data, a log-linear relative risk model has also been proposed; it also needs to assume MS and parental allelic exchangeability (AE).¹⁴

The above-mentioned methods are all full-likelihood based, and thus they have to make many stringent assumptions to avoid over-parametrization. To overcome the limitation, Yang and Lin¹⁰ proposed a partial likelihood approach. They used a design containing a mixture of case-parents/control-parents triads and case-mother/control-mother pairs to derive a robust and powerful partial likelihood without any unrealistic assumption about mating-type probabilities. Their method uses information on one child, affected or not, together with both parents, or only mother if the father is missing. However, it is not uncommon that there may be other siblings in each family. Therefore, it would be desirable to incorporate the additional information from siblings into the analysis to boost statistical power. To this end, we have extended the partial Likelihood approach for detecting Imprinting and Maternal Effects (LIME) to accommodate additional sibling data to jointly test for association, imprinting and maternal effects. The proposed test makes no assumption concerning mating-type probabilities and can use all children's (affected or unaffected) information. We carried out an extensive simulation study to validate the test empirically and to study the power under a variety of settings. While keeping the total number of individuals to be the same, we compare power with respect to two sampling schemes, one recruiting additional children and the other recruiting additional families, and the former is shown to be more powerful.

We applied LIME to the Framingham Heart Study (FHS) data and several interesting findings emerged in testing for association/imprinting/maternal effects. Some of them are consistent with results in the literature, whereas some are novel that merit further investigation.

Materials and methods

Consider a candidate diallelic marker. Denote the two alleles by M₁ and M₂, where M₁ is taken to be the variant allele. There are three genotypes M₁M₁, M₁M₂ and M₂M₂ at this marker. For convenience, we call each of these three genotypes by the number of M₁ allele, that is, 0=M₂M₂, 1=M₁M₂ and 2=M₁M₁. Let F, M and C denote the genotypes of the father, mother and a child of a nuclear family, respectively. Let D=1(0) be the disease status of an affected (unaffected) child. Note that if there are multiple children in a family, C and D have subscripts to distinguish the children. When discussing a child-parents triad in general, however, the subscript is dropped for simplicity where ambiguity does not occur. We use the following multiplicative relative risk model of disease penetrance:¹⁰

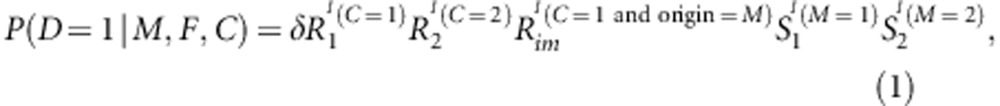where δ is the phenocopy rate of the disease; I (.) is an indicator function, taking value of 1 or 0, depending on whether the condition within the parentheses is met or not; R₁ and R₂ are the variant allele effects of 1 and 2 copies carried by the child, respectively; R_im is the effect when the single copy of the variant allele carried by the child is inherited from the mother; S₁ and S₂ are the maternal effect when the mother carries 1 and 2 copies of the variant allele, respectively.

Consider a sample with N₁ case families (ie, nuclear families that are recruited through an affected child, the case proband) and N₀ control families (ie, nuclear families recruited through an unaffected child, the control proband.) We then collect the affection status of their siblings and also the familial genotypes, if available. For convenience, a family with both parents is termed as a complete family. In contrast, a family with only mother is termed as an incomplete family. More specifically, we collect 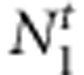case-sibling-parents families, 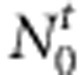control-sibling-parents families, 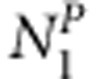case-sibling-mother families and 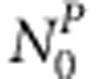control-sibling-mother families. Two special cases of this general sampling procedure are: all families are complete or all families only have mother's genotype available.

Conditional probability for complete family

For simplicity of exposure of the likelihood function, we fix the number of children per families at two (proband and one sibling). We consider complete families in this subsection, whereas the incomplete setting is given in the following subsection. Let us calculate the probability for proband-sibling-parents family conditional on the affection status of the proband using the following factorization:

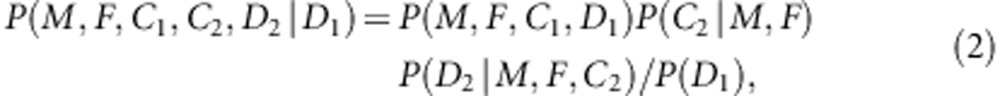where C₁(C₂) and D₁(D₂) are the genotype and affection status of the proband (sibling). The notations of D₁ and D₂ are completely general. The values they take (0 or 1) depend on the specific affection status of the children in a family. The transmission probability P(C₂|M,F) follows the Mendelian law of segregation, and the penetrance probability P(D₂|M, F, C₂) is calculated using the multiplicative relative risk model as defined in equation (1). For the calculation of P(M, F, C, D), there are 15 possible combinations of (M, F, C) triad; their enumeration and label (type) are listed in the top segment of Table 1. For all 15 types, the specific joint probabilities of triad genotypes and child's affection status for the case-parents families and control-parents families are listed in the last two columns of the top segment of Table 1. From the top panel of Table 1, it is obvious that the parameters concerning the mating-type probabilities are factored out nicely from the parameters of the disease model, both for case-parents and control-parents triads. We assume here that the disease prevalence, P(D=1), in the source population is known. Therefore, in the expression of the conditional probability P(M,F,C₁,C₂,D₂|D₁), the nuisance parameters and the risk parameters can be perfectly separated.

Table 1. Joint probability of triad genotypes and disease status of the childa.

Type	M	F	C	P(M, F, C, D=1)	P(M, F, C, D=0)
1	0	0	0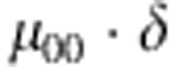
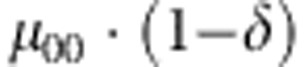2	0	1	0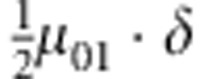
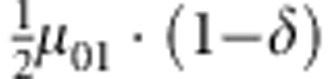3	0	1	1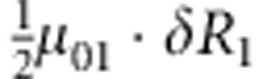
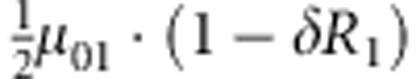4	0	2	1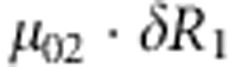
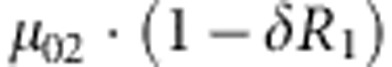5	1	0	0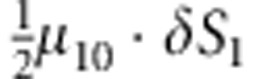
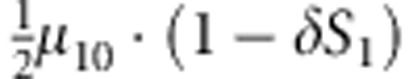6	1	0	1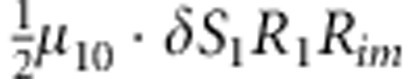
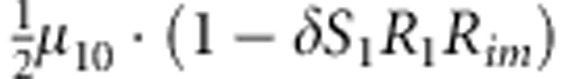7	1	1	0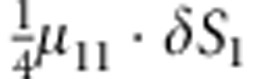
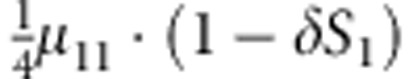8	1	1	1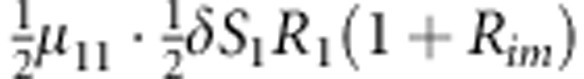
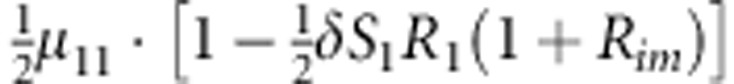9	1	1	2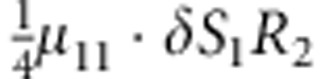
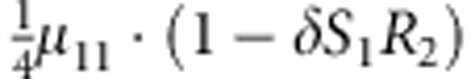10	1	2	1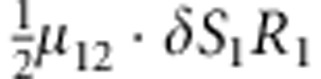
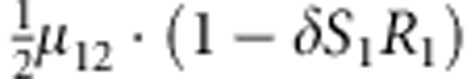11	1	2	2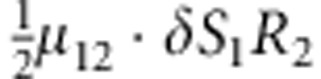
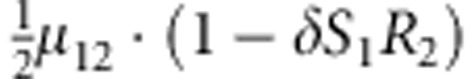12	2	0	1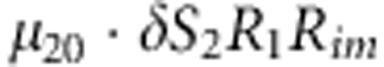
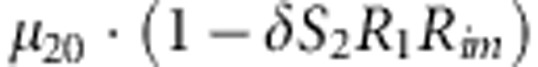13	2	1	1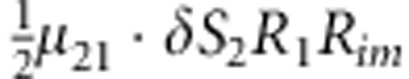
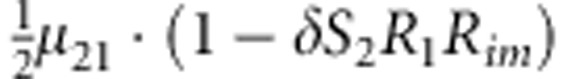14	2	1	2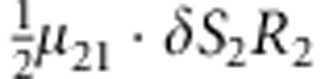
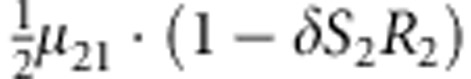15	2	2	2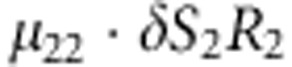

				P(M, C, D=1)	P(M, C, D=0)
1,2	0	—	0
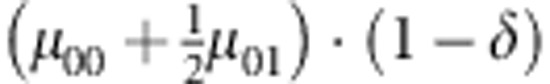3,4	0	—	1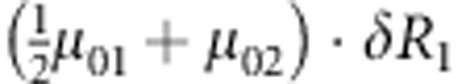
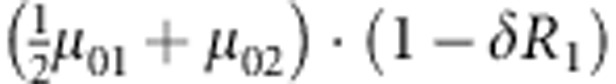5,7	1	—	0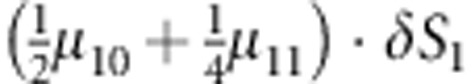
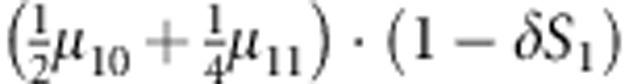9,11	1	—	2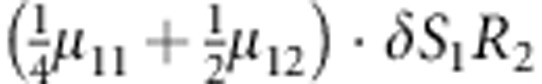
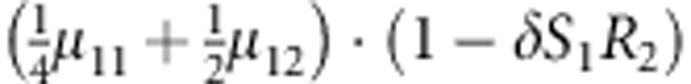12,13	2	—	1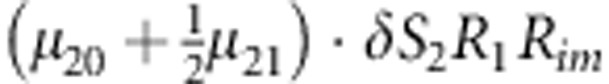
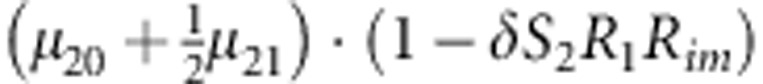14,15	2	—	2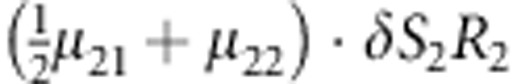

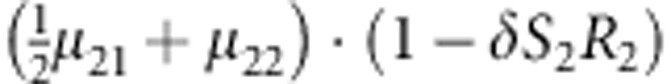^aM, F and C are the number of variant allele(s) carried, respectively, by the mother, father and the child in a triad, which take values of 0, 1 or 2. Mating-type probability of (M, F )=(m, f ) is denoted by μ_mf. For the disease model, δ is the phenocopy rate; R₁ and R₂ are relative risks of having 1 and 2 two copies of the variant allele, respectively; R_im is the relative risk of having a single copy of the variant allele inherited from the mother; S₁ and S₂ are the maternal effect of 1 and 2 copy of the variant allele carried by the mother, respectively. In the bottom segment of the table, F=− indicates paternal genotype being missing. Moreover, note that type (M, C )=(1, 1) (combination of 6, 8, 10 from top segment) is not given, as this type cannot be used in the partial likelihood formulation.

Now consider all triads composed of the proband (affected or unaffected) and their parents. Denote the counts of triads with M=m, F=f, C₁=c₁ and D₁=1 (or 0) by 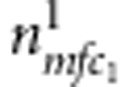(or 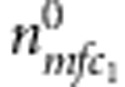). Similarly, for all triads composed of the sibling and their parents, denote the counts of triads with M=m, F=f, C₂=c₂ and D₂=1 (or 0) by (or 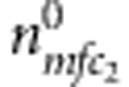). The full likelihood for 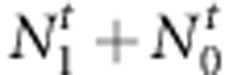complete families is

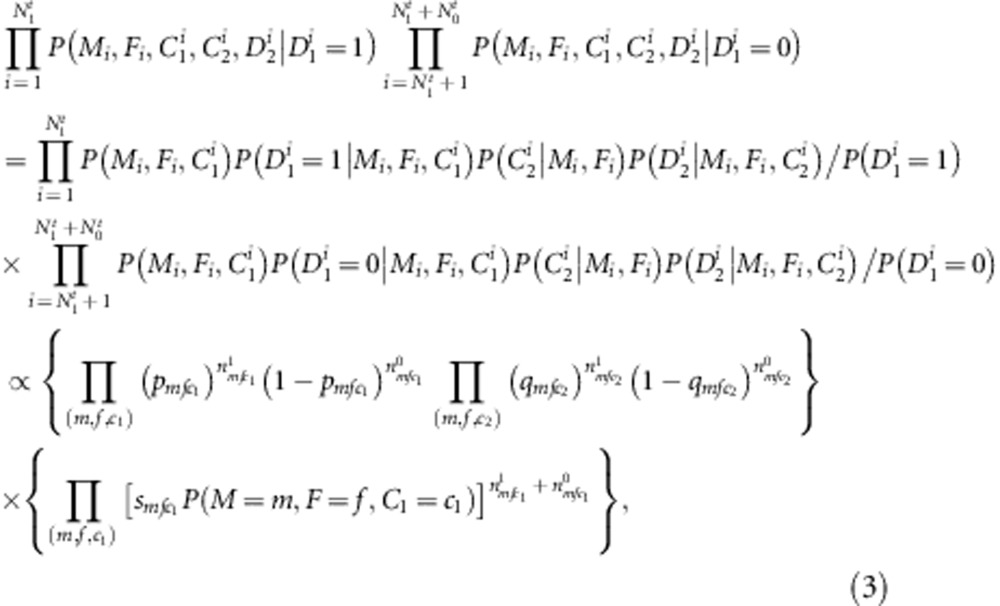where

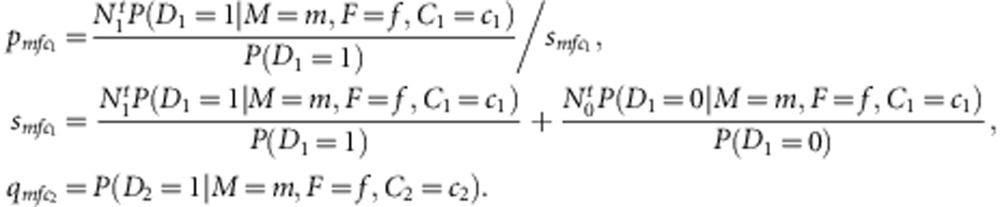It can be seen that the nuisance parameters are only present in the second component of the likelihood (factors within the second set of curly brackets in the last formula (equation (3)). Thus, the first component (factors in the first set of curly brackets in equation (3)) is our partial likelihood for complete families, each with two children. This formulation can be generalized to accommodate more than two children. For each additional child i, the contribution is 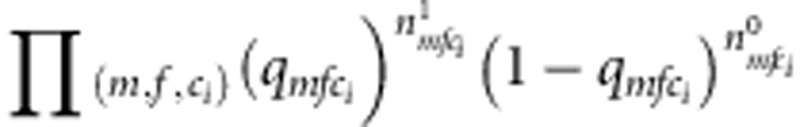, where 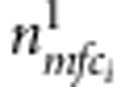, 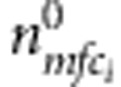and 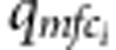are as defined above.

Conditional probability for incomplete family

To calculate P(M, C₁, C₂, D₂|D₁) for a case-sibling-mother family or a control-sibling-mother family, let us first express it as the summation of P(M, F, C₁, C₂, D₁, D₂)/P(D₁) over all possible F, or more explicitly as

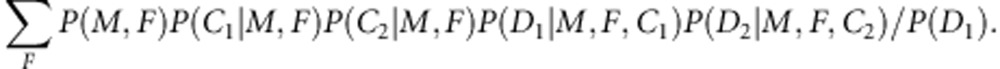Based on the results observed in Table 1, we find that the conditional probability P(D|M, F, C ) is the same for any F value as long as (M, C )≠(1, 1). Thus, we defined P(D|M, C )≡P (D|M, F, C ). Then for (M, C₁)≠(1, 1) and (M, C₂)≠(1, 1), we have

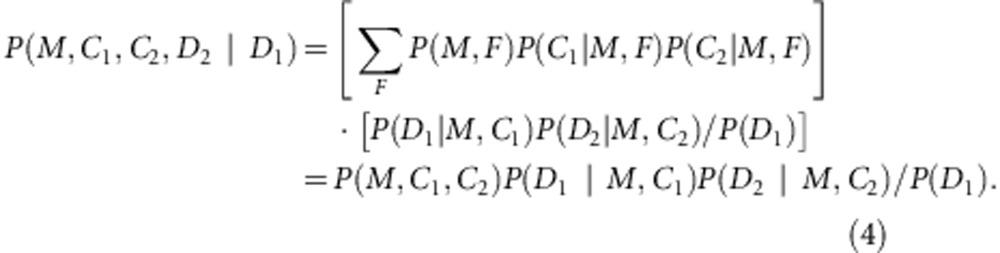From the bottom panel of Table 1 (which is obtained by collapsing of the top panel, but excluding the (M, C)=(1,1) combination), it can be seen that P(D|M, C) involves no nuisance parameters. All the 17 genetically possible combinations of (M, C₁, C₂) are listed in the first four columns of Table 2. The joint probabilities are shown in the last column of Table 2, when D₁=1 and D₂=0. The corresponding joint probabilities for the situations in which D₁=1 and D₂=1, D₁=0 and D₂=1, D₁=0 and D₂=0 can be obtained similarly (see Supplementary Tables S1–S3).

Table 2. Joint probability of mother-children genotypes, and affection status of a case proband and a control sibling in an incomplete familya.

Type	M	C1	C2	P(M, C1, C2, D1=1, D2=0)
1	0	0	0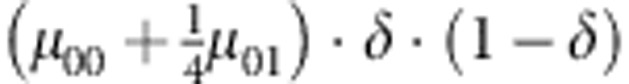
2	0	1	0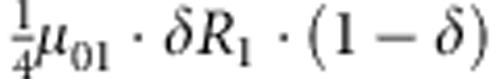
3	0	0	1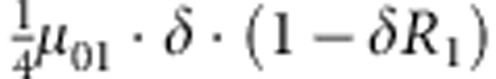
4	0	1	1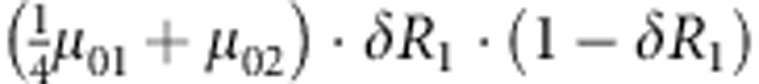
5	1	0	0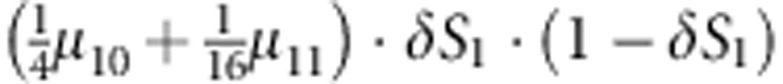
6	1	0	1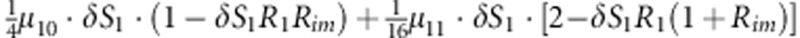
7	1	0	2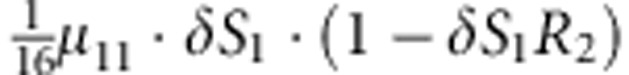
8	1	1	0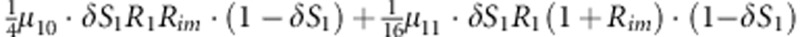
9	1	1	1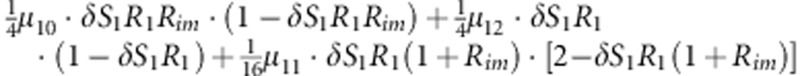
10	1	1	2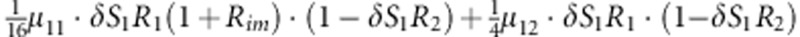
11	1	2	0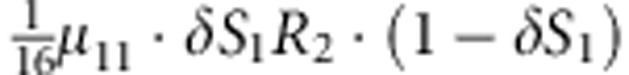
12	1	2	1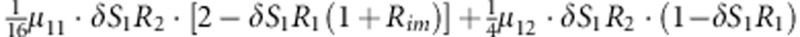
13	1	2	2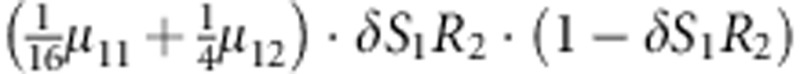
14	2	1	1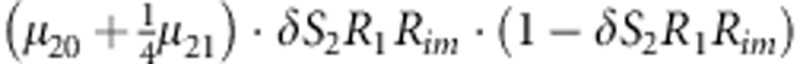
15	2	1	2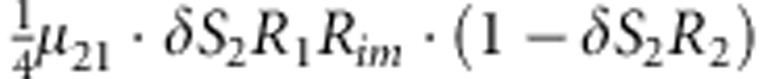
16	2	2	1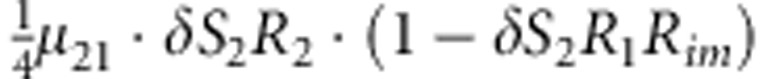
17	2	2	2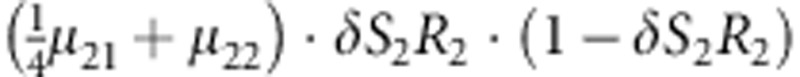

^aParameters μ_mf, δ, R₁, R₂, R_im, S₁ and S₂ are as given in the footnote of Table 1.

Denoting the counts of mother-proband pairs with M=m, C₁=c₁ and D₁=1 or 0 by 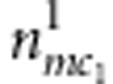or 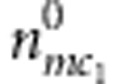for the affected and unaffected child, respectively. For the mother-sibling pairs with M=m, C₂=c₂ and D₂=1 or 0, the counts are 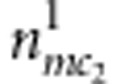or 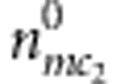, respectively, for the affected and unaffected child. Similarly, as for complete families, we can extract out a partial likelihood component free of nuisance parameters:

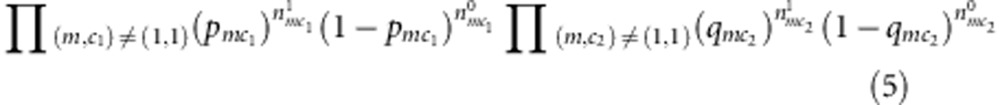Where

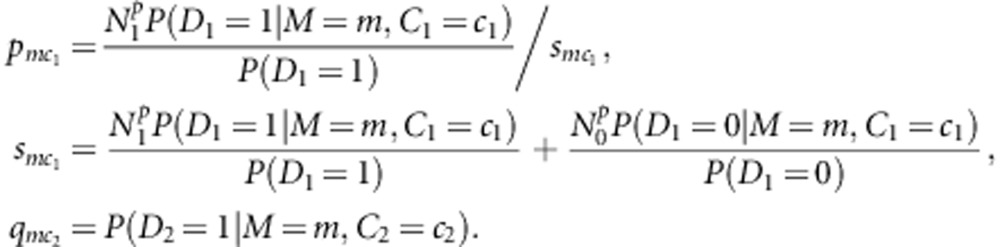This partial likelihood can easily accommodate contributions from additional children, as in the case of complete families.

Finally, if we collect both complete and incomplete families, the overall partial likelihood is the product of the partial likelihood for complete families and that for incomplete families. Based on this overall partial likelihood, the likelihood ratio test is employed to test for association, imprinting and maternal effects by setting up appropriate null and alternative hypotheses.¹⁰ Note that when there is only one child per family, the partial likelihood function reduces to that in Yang and Lin.¹⁰ LIME has been implemented as an R package, which is freely available at http://www.stat.osu.edu/∼statgen/SOFTWARE/LIME.

Results

Simulation study

Simulation settings and data generation

To evaluate the performance of LIME and to compare it with existing methods, we create eight simulation settings of relative risks due to variant allele, imprinting and maternal effects (Table 3). The first three settings neither have imprinting nor maternal effects. Setting 4 has maternal effect, but no imprinting effect. Settings 5 and 6 have paternal and maternal imprinting effects, respectively, but no maternal effect. Settings 7 and 8 have paternal and maternal imprinting effects, respectively, and also maternal effect.

Table 3. Eight simulation settings of relative risksa.

	Settings
Parameter	1	2	3	4	5	6	7	8
R1	1	1.5	1	1	1	1	1	1
R2	1	2	2	2	2	2	2	2
Rim	1	1	1	1	2	0.5	2	0.5
S1	1	1	1	2	1	1	1.5	2
S2	1	1	1	2	1	1	2	2

^aParameters R₁, R₂, R_im, S₁ and S₂ are as described in the footnote of Table 1. Settings 1–3 do not have imprinting nor maternal effects; setting 4 has maternal effect, but no imprinting effect; settings 5 and 6 have paternal and maternal imprinting effects, respectively, but no maternal effect; settings 7 and 8 have paternal and maternal imprinting effects, respectively, and also maternal effect.

Firstly, we generate the parental genotypes M and F under the following two scenarios. Under the first scenario, the population is in Hardy–Weinberg equilibrium (HWE) and the probabilities of a paternal or maternal genotype score being 0, 1 and 2 are (1−p)², 2(1−p)p and p², respectively, where p is the variant allele frequency and is taken to be 0.3 in this study. As the population is in Hardy–Weinberg equilibrium, (AE) and (MS) are implied. Under the second scenario, the probabilities of a genotype score being 0, 1 and 2 are (1−p)²(1−ζ)+(1−p)ζ, 2p(1−p)(1−ζ) and p²(1−ζ)+pζ, respectively, where ζ is the inbreeding parameter, which is set to be 0.1 and 0.3 for male and female subjects, respectively. Thus, neither AE nor MS holds in the population under this scenario. In other words, the parents are sampled from an inbred population under the latter scenario. This setting may better reflect the true state of nature in some situations, such as in the FHS data as we discussed in the Application Section. Based on the generated parental genotypes M and F, the genotypes of their children, C₁, C₂, ... are created according to the transmission probability. Affection status D₁, D₂, … are determined by a Bernoulli trial, with the success probability being equal to the phenocopy rate multiplied by the relevant relative risks. Here, we do not specify the number of children in each family and this number could be different in different samples, as described below. Note that the phenocopy rate can be solved by expressing the prevalence in terms of the relevant relative risks. The disease prevalence is fixed at 0.15 in the simulation. Consistent with the terminology used in describing the method, a family with D₁=1 (case) is termed a case family, whereas a family with D₁=0 (control) is termed a control family. The process of generating M, F, C₁, C₂, …, D₁, D₂, … is repeated until we collect sufficient case families and control families to meet the preset sample size.

Eight different types of family samples are considered to study type I error and to compare power. FS1 consists of 150 case-sibling-parents families and 150 control-parents families (no sibling), where the father's genotype may be missing, with probabilities 0.5 and 0.7 in the case and control families, respectively. The setting of allowing for missing paternal genotype is more realistic in genetic epidemiology studies. The subset of complete families from FS1 makes up FS2, whereas the collection of incomplete ones leads to FS3. These three family samples are mainly for the purpose of checking the validity of the procedure. The nominal significant level is set at 5%, and 1000 replicated samples are created in each simulation setting to estimate empirically the type I error rates or powers.

For extensive investigation of the power of LIME, we also generate the following five family samples based on the aforementioned data generation procedure. FS4: 150 case-2 siblings-parents families and 150 control-parents families; FS5: FS4 with the removal of the last sibling in each case family (same as FS2, but with a different sample size); FS6: FS4 with the removal of both siblings in each case family (same as in Yang and Lin¹⁰ for complete families); FS7: 200 case-parents families and 150 control-parents families; FS8: 175 case-parents families and 175 control-parents families. Family samples FS4–FS6 are used to investigate the effect of including one or two siblings of cases in the analysis on the size/power of LIME. On the other hand, FS7, FS8 and FS5 are used to make size/power comparison when the total numbers of individuals in all three samples are equal to 1050.

Simulation results

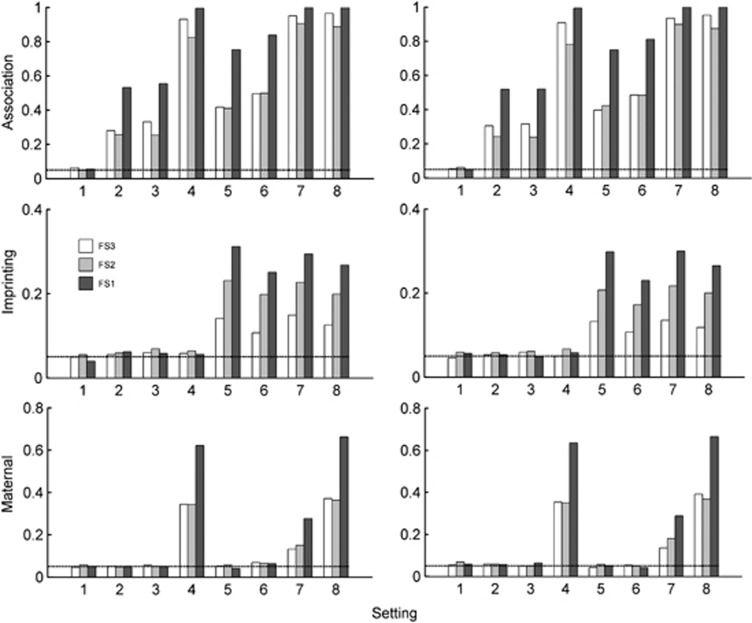
Figure 1 plots the size/power of LIME based on family samples FS1–FS3. Among the 8 settings considered, setting 1 corresponds to no association; settings 1–4 correspond to no paternal/maternal imprinting effect, and settings 1–3 and 5–6 correspond to no maternal effect. They are, therefore, used to gauge type I error rates for the corresponding effects. Figure 1 shows that regardless of the family sampling scheme (all fathers missing, all fathers present or a mixture of the two), the type I error rates are around the nominal value set at 5%, regardless of whether AE and MS hold or not. It is not surprising to observe from Figure 1 that the power of testing for association/imprinting/maternal effects based on sample FS1 are always higher than those based on FS2 or FS3, because FS1 is the combined samples of FS2 and FS3.

Figure 1.

Type I error rate and power of LIME having family samples FS1–FS3. FS1 comprises of 150 case-sibling-parents families and 150 control-parents families, with the probabilities of father missing being 0.5 and 0.7 in the case and control families, respectively. FS2 is the subsample composed of complete families, whereas FS3 is the one with incomplete families. In the left panel, neither AE nor MS holds, and in the right panel, both AE and MS hold. The prevalence is 0.15. The X-axis represents the eight simulation settings of relative risks given in Table 3. The horizontal line marks the nominal α level of 0.05.

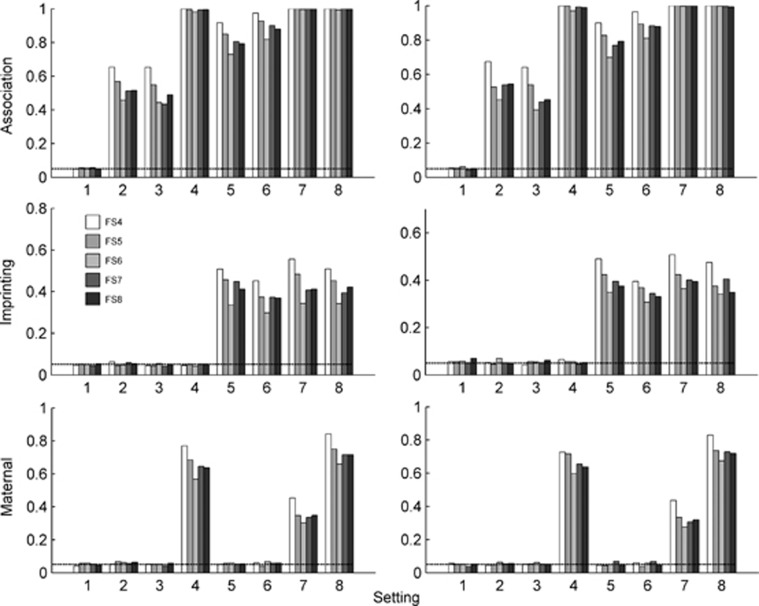
The size/power of the proposed method based on family samples FS4–FS8 are presented in Figure 2. It is found that the type I error rates are reasonable, based on the family sample FS4 in which the number of children in each case family is 3. In fact, we conducted a series of simulation studies for a variable number of children in the case families to further investigate the performance of LIME, and we found that all type I errors are well-controlled (results not shown). The power gain for testing for imprinting and maternal effects is clearly exhibited in Figure 2, when one sibling of the cases are included in the analysis (FS5 vs FS6), and when two siblings of cases are included in the analysis (FS4 vs FS5). Taking setting 8 as an example for family sample FS4/FS5/FS6, the power is 0.509/0.453/0.342 for imprinting and 0.842/0.750/0.659 for maternal effect, when neither AE nor MS holds.

Figure 2.

Type I error rate and power of LIME having family samples FS4–FS8. FS4: 150 case-2 siblings-parents and 150 control-parents families. FS5: 150 case-sibling-parents and 150 control-parents families. FS6: 150 case-parents and 150 control-parents families. FS7: 200 case-parents and 150 control-parents families. FS8: 175 case-parents and 175 control-parents families. In the left panel, neither AE nor MS holds, and in the right panel, both AE and MS hold. The prevalence is 0.15. The X-axis represents the eight simulation settings of relative risks given in Table 3. The horizontal line marks the nominal α level of 0.05.

Now, suppose we have extra resources to genotype more individuals in order to improve the power of a statistical test. We evaluate the performance of the test based on FS5, FS7 and FS8, in which the numbers of individual are all the same (4 × 150+3 × 150=1050, 3 × 200+150 × 3=1050, 3 × 175+3 × 175=1050). It can be seen from Figure 2 that the power based on family sample FS5 is almost always higher than that based on FS7 or FS8. It may suggest that collecting more siblings rather than more families is a more effective way to increase statistical power. The statistical power based on FS7 and FS8 are similar, although FS8 is slightly better in most cases, suggesting that equal sizes of case families and control families might be a better choice.

Application to FHS data

To demonstrate the utility of LIME, we apply it to the FHS data. These data were made available through the database of Genotypes and Phenotypes (dbGap) supplied by the Genetic Analysis Workshop 16 (http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?studyid=phs000128.v3.p3). Some studies have indicated that there is ancestrally related positive assortative mating in the FHS.¹⁷ Fortunately, our method is neither influenced by assortative mating nor by non-random mating, a major advantage clearly demonstrated in our simulation. There are three groups of the FHS participants, the original cohort, the offspring cohort and the third generation cohort, which consist of 5209, 5124 and 4095 participants, respectively. In other words, the FHS is a prospective, community-based, multigeneration family study. There are 1538 pedigrees in the data set; the mean pedigree size is 10. Note that although there are 14 428 participants, some of them were not available to participate in the genetic studies, and therefore, only 6849 of them have genotype data at 48 060 single nucleotide polymorphism (SNP) markers over the 22 autosomes.

The objective of the FHS is to identify common risk factors of cardiovascular disease. Here, we focus on hypertension, a multifactorial complex disease influenced by the interaction between genetic and environmental factors. Hypertension is usually defined as systolic blood pressure ≥140 mm Hg or diastolic blood pressure ≥90 mm Hg. In the FHS, as a prospective cohort study, the systolic blood pressure and diastolic blood pressure of the original cohort and the offspring cohort were measured in four examinations, wereas the third generation only once. Therefore, the definition of one's phenotype, either affected or not, is based on the highest measurement among all available ones for each individual in our analysis to minimize medication effect. Prior to using LIME, we need to obtain the disease prevalence based on an external data. The disease prevalence used here is 23.9%, based on the result of a population study.¹⁸

As LIME can only use two-generation nuclear families, we first split every multigenerational pedigree into two-generation nuclear families and include only one nuclear family from each pedigree to guarantee that all the nuclear families in our analysis sample are independent. For each nuclear family and each specific SNP, we discard members with missing genotypes and siblings with missing phenotypes. Further, all nuclear families with missing mothers are excluded in the analysis. For each nuclear family contained in our sample, we randomly select a child and label the family as a case family or a control family based on the affection status of the child. The effect of the uncertainty of this ascertainment procedure on the analysis will be elaborated in the Discussion section.

Table 4 provides a summary of the top-10 significant findings, each in testing for association, imprinting and maternal effects, using LIME. We discuss the results for association first. Several of the SNPs have been previously implicated in hypertension or other cardiovascular-related diseases. For example, SNP rs11149562 (P=2.24 × 10⁻⁵), residing in the intron region of gene CDH13 on chromosome 16, has been reported to be a candidate hypertensive susceptibility gene in two European populations, and is associated with both long-term systolic blood pressure and diastolic blood pressure.^{19, 20} In fact, CDH13 encodes for an adhesion glycoprotein T-cadherin, which is a regulator of vascular wall remodeling and angiogenesis, and is compatible with the blood pressure biology. Another SNP, rs7559838 (P=1.32 × 10⁻⁵), located in the intron region of gene HPCAL1 on chromosome 2, has also been linked to hypertensive phenotype in the Japanese population.²¹ HPCAL1 encodes for the hippocalcin-like 1 protein. It is well known that hippocalcin protein, along with neuronal apoptosis-inhibitory protein, protects neurons against calcium-induced death stimuli.²²

Table 4. Top-10 significant results each for testing for association (top panel), imprinting (middle panel) and maternal effect (bottom panel) with hypertension using LIME.

Effect	Rank	SNP a	Chr	Position (BP)	Gene symbol b	−log10(P-value)
Association	1	rs684596	12	108070244	TCTN1	5.19
	2	rs2229188	7	86371063	CYP51A1	5.18
	3	rs1112438	3	39194263	TTC21A	4.93
	4	rs7559838	2	10367571	HPCAL1	4.88
	5	rs2736483	4	66100289		4.82
	6	rs16881524	5	49858593	NDUFS4	4.70
	7	rs7657817	4	89668859	FAM13A	4.67
	8	rs11149562	16	69190863	CDH13	4.65
	9	rs1112438	3	39194263	TTC21A	4.63
	10	rs17717907	7	89739016	ASB4	4.51
Imprinting	1	rs684596	12	108070244	TCTN1	6.64
	2	rs1040461	6	56889411	RAB23	5.50
	3	rs12932514	16	985885		5.26
	4	rs3024391	6	6124947	F13A1	5.18
	5	rs11774465	8	1277951	DLGAP2	4.66
	6	rs2266131	11	86157811		4.58
	7	rs6706091	2	38861436		4.58
	8	rs2103731	21	14912824		4.50
	9	rs12204317	6	134621215		4.33
	10	rs380417	21	12675653	APP	4.31
Maternal	1	rs7559838	2	10367571	HPCAL1	6.26
	2	rs2736483	4	66100289		5.47
	3	rs4559524	1	132402540	PVRL4	5.30
	4	rs6706091	2	388614361		5.23
	5	rs11767450	7	90043270	DYNC1I1	5.00
	6	rs470306	18	21139588		4.72
	7	rs9511484	13	6255208	RNF17	4.72
	8	rs1112438	3	39194263	TTC21A	4.49
	9	rs9406074	6	7882930		4.47
	10	rs12414948	10	84312391	STAMBPL1	4.29

^aSNPs that are in at least two of the top-10 lists are in bold type.

^bGene symbol gives the name of the gene in which the SNP resides.

The second segment of Table 4 shows the top-10 genes with the most significant imprinting effect. One of them is SNP rs3024391 (P=1.26 × 10⁻⁵), which lies in the intron region of a housekeeping gene called F13A1 on chromosome 6. Although no direct evidence about hypertension has been discussed before, the gene has been studied intensively for its association with cardiovascular disease, such as myocardial infarction, ischemic stroke and atrial fibrillation.^{23, 24, 25} Interestingly, this SNP has a rather small P-value (8.75 × 10⁻⁵) for association (even though it did not make the top-10), suggesting that F13A1 is perhaps an associated imprinted gene, whose significant effect might have been masked without properly accounting for the imprinting effect. Therefore, further study about the association and imprinting effect of F13A1 on hypertension etiology is warranted. On the other hand, SNP rs380417 (P=4.90 × 10⁻⁵) is located in the intron region of a known imprinted gene APP on chromosome 21.⁵ Hereditary cerebral haemorrhage with amyloidosis-Dutch type (HCHWA-D), an autosomal dominant disorder caused by a single base change in APP, has a higher mortality rate when paternally transmitted.²⁶ Another study found that there is a stronger relative risk (1.48) of African–American with hypertension at rs380417.²⁷

The top-10 most significant findings for maternal effects are given in the bottom segment of Table 4. In particular, gene HPCAL1 is the most significant one, suggesting that HPCAL1 bears maternal effect (P=4.22 × 10⁻⁷). This gene has also been implicated for association with hypertension,²¹ and is among the top-10 most-significant findings in our association testing. As we have pointed out earlier, maternal effect and genomic imprinting, though both can lead to apparent parent-of-origin effect, arise from two very different underlying genetic mechanisms. Therefore, it is not surprising to see that there is only one common SNP (rs6706091) between their top-10 lists. Further, although it has been widely recognized that imprinting and maternal effects are two essential epigenetic factors in the etiology of many complex diseases, only a limited number of imprinted genes or genes bearing maternal effects have been reported in the literature. In fact, for the hypertensive trait, little research has looked into parent-of-origin effect to date.¹¹ Therefore, further studies are warranted to investigate the most outstanding genes found in this study to be potentially imprinted and/or bearing maternal effects. It is well known that association studies are not consistently reproducible due to false positives, false negatives or heterogeneity among different populations, and thus validation studies are crucial.

Discussion

Complex diseases with a genetic predisposition are known to exhibit familial aggregation, which frequently manifests itself as having affected sibling(s) of a case. Therefore, it is valuable to develop methods that can accommodate information from the siblings, regardless of their affection status. It is anticipated that the inclusion of siblings will improve the power of a statistical test. To profit from such potential gain, we develop a partial likelihood-based approach that can utilize all children, affected and unaffected, and their parents to jointly test for association, imprinting and maternal effect. LIME possesses a number of desirable properties, and is indeed more powerful by utilizing additional data from siblings if such information is available. In particular, LIME circumvents certain unrealistic assumptions about the population, such as AE and MS, as the parameters of interest and the nuisance parameters can be completely separated. The dimension of the parameter space is thus reduced greatly.

Extensive simulation studies were conducted to check the validity and to evaluate the performance of the proposed test based on various family samples. The simulation results illustrate that the test is applicable to a sample including multiple affected/unaffected children along with their parents, or just their mothers, or a mixture of the two. The power gain is clearly shown when more and more siblings are included in the analysis. We also compared the performance of the statistical test based on two different sampling schemes, one recruiting extra siblings and the other recruiting extra families, while keeping the total number of subjects involved the same. Based on the results, we may draw the conclusion that collecting more siblings is more efficient compared with collecting more families, if siblings are available.

The proposed LIME was applied to the FHS data and some interesting findings have emerged. Among the genes identified, some have been documented in the literature for the hypertensive phenotype, whereas some have been discussed in the literature but for a different trait, and yet there are others that are identified for the first time. The latter two categories are novel findings for the hypertensive trait, which merit further investigations to substantiate the findings.

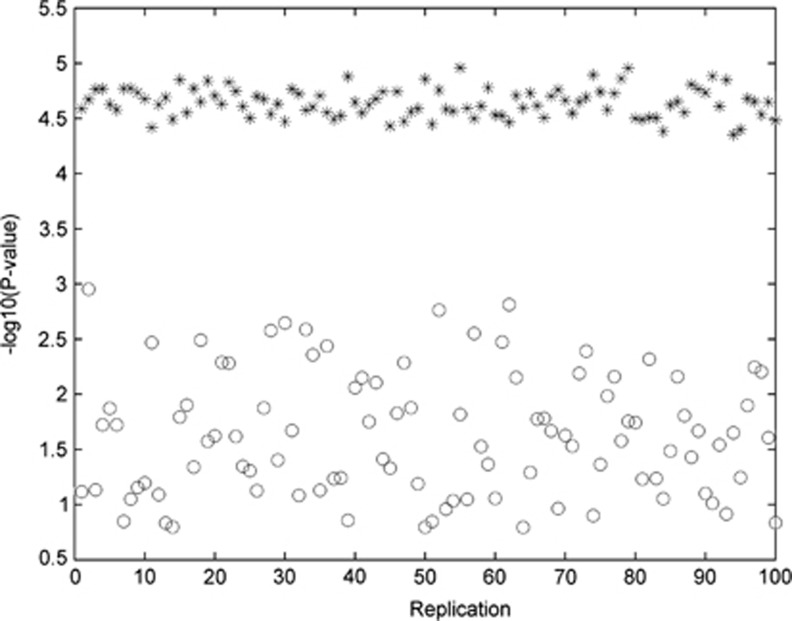
As the formulation of the partial likelihood depends on the ascertainment event (ie, who is the proband in each family), and as this designation is somewhat contrive and arbitrary in our analysis of the FHS data, we investigated the sensitivity of LIME by studying the variability of the outcomes of LIME with multiple sets of random proband labeling. Taking SNP rs11149562 as an example, we conducted 100 replications of testing for association. In each replication, a child is randomly chosen from every nuclear family and designated as the proband. We calculated the P-values of the proposed statistical test when the probands and their siblings were all included in the analysis, and as a comparison, we also performed a test when only the probands were analyzed. Figure 3 plots the replication index against the −log₁₀ (P-value), where the *'s denote the results including the siblings, whereas the o's represent those with the probands only. Two observations are apparent from the figure. First, the variation across the 100 replications is much smaller for the analysis with more data (ie, including sibling information). Second, the power for detecting association is smaller when only probands were used. These results provide confidence, to a certain degree, that although the formulation is conditional on the probands, the outcome does not depend heavily on the conditioning event, given there are additional siblings. Further, the results re-enforce the central theme of this work, that is, including sibling information can lead to substantial power gain.

Figure 3.

Variation of the P-values from 100 replications when all children are included in the analysis (represented by *), compared with variation of P-values, also from 100 replicates, when only probands are included in the analysis (represented by o).

Given the successful extension of LIME to including data from siblings, and the encouraging results from both simulation and real data analysis, it is warranted to investigate whether the capability of LIME can be further extended to other data types. Of immediate interest is whether we can do away with independent control families, as they are more difficult to collect than case families. However, ‘control families' are indispensable for LIME as it relies on them to create ‘internal matches' stratified by familial genotypes.¹⁰ To balance the two competing elements, one may consider families in which both affected and unaffected children are present to explore whether ‘internal matches' can be created in such a setting for LIME to be applicable. Ascertainment criterion and corresponding ascertainment correction have important roles in such an investigation. Further, although LIME can utilize data from multiplex families, each family unit is assumed to be ascertained through a single proband. Thus, further study is needed to study LIME's applicability to multiplex families and its relative performance with various ascertainment criteria.

The authors declare no conflict of interest.