Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2013 May 8;21(12):1396–1402. doi: 10.1038/ejhg.2013.84

Human X-chromosome inactivation pattern distributions fit a model of genetically influenced choice better than models of completely random choice

Nisa K E Renault 1,*, Sonja M Pritchett 2, Robin E Howell 3, Wenda L Greer 4, Carmen Sapienza 5, Karen Helene Ørstavik 6,7, David C Hamilton 2
PMCID: PMC3831084  PMID: 23652377

Abstract

In eutherian mammals, one X-chromosome in every XX somatic cell is transcriptionally silenced through the process of X-chromosome inactivation (XCI). Females are thus functional mosaics, where some cells express genes from the paternal X, and the others from the maternal X. The relative abundance of the two cell populations (X-inactivation pattern, XIP) can have significant medical implications for some females. In mice, the ‘choice' of which X to inactivate, maternal or paternal, in each cell of the early embryo is genetically influenced. In humans, the timing of XCI choice and whether choice occurs completely randomly or under a genetic influence is debated. Here, we explore these questions by analysing the distribution of XIPs in large populations of normal females. Models were generated to predict XIP distributions resulting from completely random or genetically influenced choice. Each model describes the discrete primary distribution at the onset of XCI, and the continuous secondary distribution accounting for changes to the XIP as a result of development and ageing. Statistical methods are used to compare models with empirical data from Danish and Utah populations. A rigorous data treatment strategy maximises information content and allows for unbiased use of unphased XIP data. The Anderson–Darling goodness-of-fit statistics and likelihood ratio tests indicate that a model of genetically influenced XCI choice better fits the empirical data than models of completely random choice.

Keywords: X chromosome inactivation, genetic models, population genetics, statistical genetics

Introduction

Eutherian females have two X-chromosomes, while males have only one. To compensate for the gene dosage inequality between the sexes, one X in every XX somatic cell in females is transcriptionally silenced early in embryologic development.1 An early step in this process, X-chromosome inactivation (XCI), is the choice of which X, maternal (Xm) or paternal (Xp), to inactivate (reviewed in Morey and Avner2). An X-linked, cis-acting, non-coding RNA, XIST (or Xist in mouse), located within the X-inactivation centre (XIC),3 is thought to respond to this choice. It directs the epigenetic reprogramming of the future inactive X, silencing nearly all X-linked genes, in cis.4 The choice of which X to inactivate is faithfully maintained during mitosis (reviewed in Heard et al5). Females are thus functional mosaics of cells expressing paternal X genes and cells expressing maternal X genes. This can affect disease expression in females,6, 7, 8 sparking interest in the mechanism of XCI choice and the factors that influence X-inactivation patterns (XIP). The XIP is defined as the relative abundance of cells with the Xp active phase. When the parental origin of each X-chromosome (the phase) is unknown, this is arbitrarily assigned.

When first described, the XCI hypothesis supposed that XCI choice is completely random, based on the observation that most females appear to have XIPs near 0.5 (ie, 50% of cells have the Xp active).1 However, further analysis indicated that XIPs in mice are influenced by genetic background.9, 10, 11, 12 Cattanach and Isaacson9, 10 proposed that a cis-acting X-controlling element (Xce) biases XCI choice by influencing the propensity for each X-chromosome to be inactivated. They determined that there are at least three co-dominant Xce alleles, Xcea, Xceb, and Xcec, where the Xcea allele has the weakest association with the active X and the Xcec allele the strongest. Xce-homozygous mice have XIPs close to 0.5 (balanced XIP), whereas heterozygous mice have XIPs differing significantly from 0.5 (skewed XIP), where the X with the strongest Xce is active in a greater number of cells.

It is not clear whether human XCI choice is genetically influenced or the mouse Xce paradigm is applicable. If it is genetically influenced, this would have important implications for the risk of disease expression in some females. Experimental data do support a human XCE hypothesis,13, 14, 15, 16, 17 though definitively answering the question has been difficult due to the challenges in defining and assigning XIP phenotypes. Defining XIP phenotypes is challenging because of its continuous nature. Often, an arbitrary threshold is defined, typically 0.7518 or 0.80,14 above which XIPs are considered to be skewed and below which XIPs are considered to be random. However, these thresholds have no theoretical basis, and the terminology is confusing in that it implies that randomness results exclusively in XIPs near 0.50, and that skewedness arises purely from aberrant XCI. Further, the threshold method defines only two XIP phenotypes, which may not be sufficient to study the XCI process. An approach examining XIP distributions may be more appropriate.

Defining XIP phenotypes may be facilitated by elucidating the precise number of cells (c) undergoing XCI choice. For technical and ethical reasons, it has not been possible to observe the onset of human XCI to precisely determine the timing of XCI choice. Several groups have attempted to calculate c based on the standard deviation (SD) of XIPs sampled from large populations of females, with estimates ranging from 7 to 16 cells.19, 20, 21, 22 One study also estimated c to be between 10 and 12 cells by graphically comparing the distribution of XIPs in a population of newborns, represented by a histogram, with various normal distributions defined by discrete values of c.21 However, the generation of the histogram required sorting XIPs into phenotype bins of arbitrary, and in that case inconsistent, size. This reduces the information content of the distribution and may inappropriately group some XIPs together. Further, both of these approaches rely on a simple normal model of XCI choice in which a discrete binomial distribution is approximated by a normal distribution.19 This is only appropriate if XCI choice is independent in each cell and if Xm and Xp have an equal probability of being chosen for inactivation, assumptions that do not explain all of the available data. Also, for both the calculated and graphical approaches, the directionality of the ratio of cell populations is arbitrarily assigned in cases where phase is unknown. This is not the most rigorous approach, and could artificially skew XIP distributions.

Assigning individuals to XIP phenotypes is challenging as the XIP at the time of measurement (typically adulthood) can differ from the primary XIP established at the onset of XCI. Proliferation or survival differences between the maternal- and paternal-X-active populations can result in changes to the XIP during development (secondary skewing). This is particularly striking in carriers of X-linked diseases such as Wiskott-Aldrich Syndrome, who have completely skewed XIPs in peripheral blood.23 Also, XIPs become more skewed with age (age-associated skewing, AAS24), particularly in individuals over 55 years of age and in hematopoietic cell lineages.13

To address these technical issues and explore the nature of human XCI choice, we (1) describe a new XIP data treatment strategy that does not require binning XIP phenotypes or arbitrarily assigning phase when this is unknown, (2) propose modifications and extensions of the model of completely random XCI choice that accommodates secondary skewing, (3) compare these models with XIP distributions in populations of phenotypically normal females using an Anderson–Darling (AD) goodness-of-fit test, and (4) develop models of genetically influenced XCI choice based on the principles of the mouse Xce paradigm and use statistical methods to test whether these models fit the empirical data and or they offer significant improvements over the models of completely random choice.

Materials and Methods

For detailed Materials and methods, see the Supplementary material.

Permissions

This project was approved by the research ethics boards concerned.

Data

Two data sets of individual age and peripheral blood XIP data were generated from previously published data: Utah (n=183),25 and Denmark (n=258).13 XIP data are folded about 0.5 to allow for correct use of unphased cases and represented as cumulative distribution functions (Supplementary Figure 1).

Statistical models

Two classes of statistical models are generated: models of completely random XCI choice, and models of genetically influenced XCI choice. Briefly, each model describes (1) a discrete primary XIP distribution, and (2) a continuous secondary XIP distribution that allows for changes to the XIP arising during development and aging (Supplementary Figure 2). (1) For models of completely random choice, the possible primary XIPs are dependent on the number of progenitor cells c, where their probabilities are given by the binomial theorem. For models of genetically influenced choice, the primary XIPs are determined by genotype, where homozygotes have balanced XIPs, and heterozygotes with alleles i and j have primary XIPs shifted away from 0.5 by δij>0 toward the dominating allele. The probabilities of each phenotype are given by the allele frequencies, pi, assuming HWE. (2) For simple normal and simple beta models, a continuous secondary distribution is generated by approximating the discrete model with a normal or beta curve, respectively. A mixed beta model is also generated where each peak in the discrete distribution defines the mode of an individual beta curve, and the overall distribution is a probability-weighted mean of the individual component densities. The variance of each individual component is assumed to decrease with increasing primary skewing in relation to a multiplicative factor, τ2. Similarly, secondary skewing is accommodated in models of genetically influenced choice using beta distributions centred at the primary skewing values. Again, the variances are related to τ2. Parameters c, δij, pi and τ2 are estimated from the data.

Statistical tests

The models above are symmetric around XIP=0.5. The probability above 0.5 is folded onto the [0, 0.5] interval to be compared with the folded XIP data. A two-sample t test is used to compare the mean age for Utah and Denmark samples. Lowess curves and linear regression are used to determine whether there is a significant correlation between age and XIP. The AD statistic26 is used to test for goodness-of-fit of the models (one sample), and to compare the distributions of folded XIPs for the Utah and Denmark samples (two samples). Comparisons between models are based on likelihood ratio statistics. A likelihood ratio test is used to determine whether the primary XIP shifts δij are the same for the Utah and Denmark data sets by comparing the fit of a model that assumes these shifts are the same in both data sets with a model using two sets of shifts.

Results

Analysis of XIPs

XIP data from two large populations of normal adult females were available for analysis: the Utah data set25 and the Denmark data set.13 Using the thresholds defined elsewhere, both data sets have similar proportions of ‘skewed' and ‘extremely skewed' XIPs as other adult populations with comparable age ranges (see Supplementary Table 1 and references therein). Consistent with the hypothesis of AAS in peripheral blood,27, 28 these proportions are larger in the Utah and Denmark data sets than in populations of neonates and young children, and less than that in populations of exclusively elderly females.

Analysis of folded XIPs

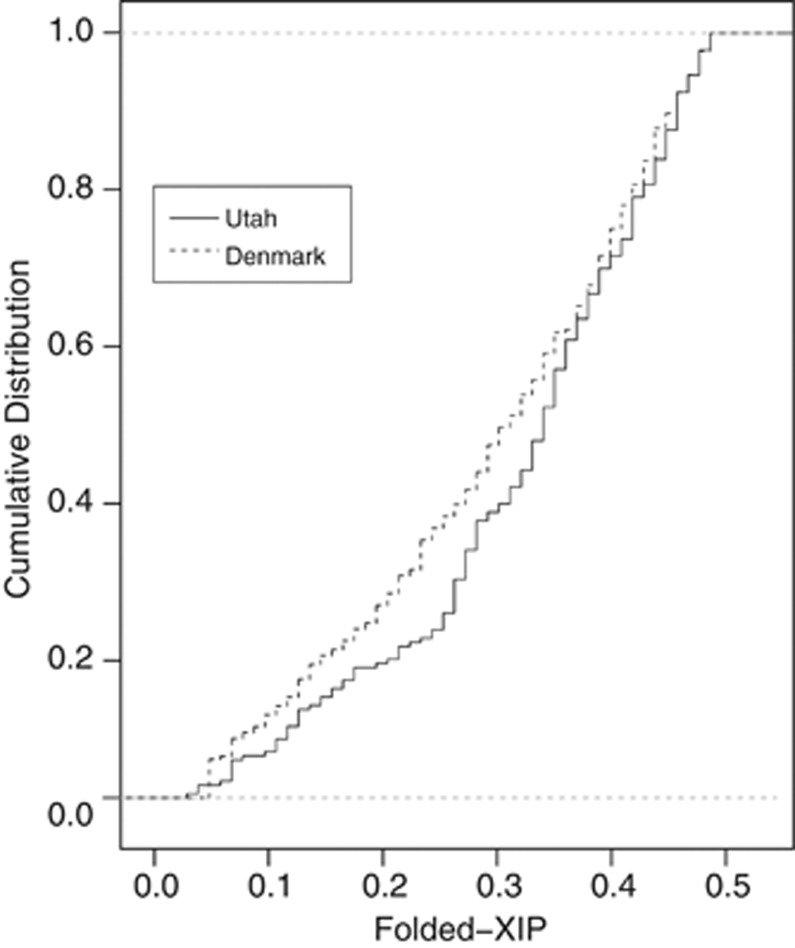
Folded XIPs for the Utah and Denmark data sets range from 0.03 to 0.50 (mean=0.33, SD=0.12) and from 0.05 to 0.50 (mean=0.30, SD=0.13), respectively (Figure 1). A two-sample AD goodness-of-fit statistic shows that there is some evidence that the Utah and Denmark data sets were not drawn from the same distribution (P=0.086). This difference suggests that elements other than randomness are affecting XIP distributions and that simple random models of human XCI choice inadequately describe empirical adult XIP distributions. This putative departure from the simple model could be due to a primary non-random mechanism, or due to secondary effects. Differences between these distributions could also be due to inter-laboratory experimental differences; however, should such differences exist, they are expected to be small, as both laboratories utilise equivalent positive and negative controls, methods and reagents.13, 25

Figure 1.

Figure 1

Open in a new tab

Empirical cumulative distribution functions for the Utah and Denmark folded-XIP data. A two-sample Anderson-Darling (AD) goodness-of-fit statistic shows some evidence that the two samples are not drawn from the same distribution (P=0.086).

Fits of completely random models of XCI

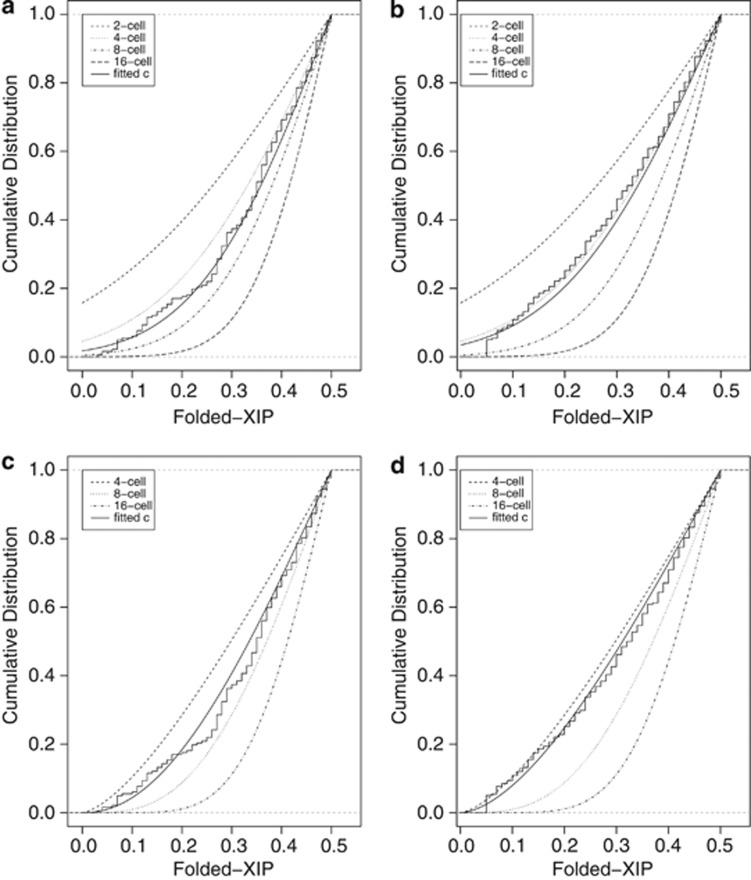
In order to directly test whether empirical data are consistent with completely random XCI choice, we compare the Utah and Denmark data sets with models of completely random XCI choice. We first consider the simple normal model using various integer values for c (Supplementary Figure 2a and b). While the Denmark data set is consistent with c=4 cells (P=0.132), the Utah data set is not (P=0.021) (Table 1, Figures 2a and b). Further, the AD goodness-of-fit test indicates that the Utah data set does not fit any simple random model using c values of 2, 4, 8 or 16, and increasing cell numbers does not improve the fit to either data set (data not shown). To assess whether a modified model of completely random XCI can be found that fits both data sets, we investigate various extensions and modification of the simple random models. First, we extend the simple random model to allow c to be any real number and estimate its value from the empirical data. From both the Utah and Denmark data sets, the most likely progenitor pool size is estimated to be a non-integer between 4 and 6 cells (Table 2). The fitted c values are not significantly different from one another (z test, P=0.06) and cannot be rejected by the AD test (Utah: P=0.373, Denmark: P=0.063). An unsatisfactory aspect of any normal model, however, is that a small amount of probability is assigned to XIP values outside the permissible [0, 1] interval. A remedy for this is to use the beta distribution, which assigns probability only to values between 0 and 1, and looks much like the normal distribution when its two parameters α and β are equal and sufficiently greater than 1 (Supplementary Figure 2b). To test this alternative model of completely random XCI choice, simple beta models, with c=2, 4, 8 and 16, are compared with the Utah and Denmark data sets (Table 1, Figures 2b and c), and the likelihood function is maximized to estimate c, allowing for non-integer values. There is some indication that the beta model with c=8 could fit the Denmark data (P=0.0525). However, the Utah data set fails to fit any simple beta model using the discrete values for c tested, and increasing c does not improve the fit (data not shown). Again, non-integer progenitor pool sizes between 4 and 6 cells best fit both data sets (Table 2). The fitted values for the simple beta model are not significantly different from one another (P=0.072) and cannot be rejected by the AD test (Utah: P=0.139, Denmark: P=0.179). A non-integer value for c could be consistent with models where XCI choice is asynchronous within the embryo or between embryos. Alternatively, cell loss or developmental bottlenecks could create the appearance of a non-integer c at the time of choice. However, such low c values are inconsistent with recent biological data that indicate that XCI has not occurred even in very late human blastocyst embryos.29 A small c could be consistent with this latest finding if the progenitor pool in question is not the total number of cells in the embryo at the time of choice, but the number of cells in a subpopulation giving rise to the blood cells from which the XIP is determined. However, several studies show a good correlation between XCI ratios in tissues derived from each of the three germ layers,17, 30 suggesting that if choice occurs completely randomly, it must occur in a progenitor pool giving rise to all three germ layers. Therefore, c would have to represent at least the number of cells giving rise to the embryo proper. Taken together, these data suggest that there is no biologically relevant c for which a simple normal or simple beta model of completely random XCI will fit the data examined here, supporting the hypothesis that simple random models inadequately describe XIPs in adult populations.

Table 1. Goodness-of-fit tests for simple models of completely random XCI choice applied to the Utah and Denmark data sets.

  Simple normal Simple beta
  Utah Denmark Utah Denmark
c AD P-value AD P-value AD P-value AD P-value
2 28.26 0 81.29 0 79.52 0 152.51 0
4 3.2672 0.021 1.7434 0.132 9.4774 0 3.0051 0.017
8 6.9225 0 28.9596 0 6.3747 0.0004 30.2274 0.0525
16 51.97 0 128.92 0 58.15 0 152.51 0
Open in a new tab

P-values for models with no significant lack of fit are set in bold.

Figure 2.

Figure 2

Open in a new tab

Fits of the simple models of completely random choice. Simple normal models: (a) For the Utah data set, only the fitted c shows no significant lack of fit to the data (ĉ=5.656, P=0.373). (b) For the Denmark data set, both the 4-cell and fitted-c models show no significant lack of fit (4-cell: P=0.132; fitted-c: ĉ=4.4685, P=0.063). Simple beta models: (c) For the Utah data set, only the fitted-c model shows no significant lack of fit to the data (ĉ=5.4064, P=0.139). (d) For the Denmark data set, both the 8-cell and fitted-c models show no significant lack of fit (8-cell: P=0.0525; fitted c: ĉ=4.4325, P=0.179).

Table 2. Estimated progenitor pool size obtained from simple models of completely random XCI choice for Utah and Denmark data sets.

  Simple normal Simple beta
  Utah Denmark Utah Denmark
ĉ 5.6560 4.4658 5.4064 4.4325
se(ĉ) 0.54458 0.3247 0.4713 0.2678
AD 0.9466 2.3550 1.6737 1.4828
P 0.373 0.063 0.1390 0.1790
Open in a new tab

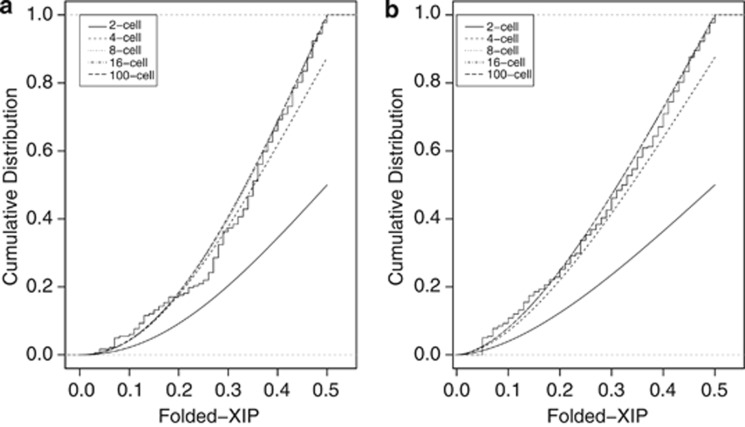
It is possible that the lack of fit of the simple normal and beta continuous models is due to a poor representation of the process of secondary skewing. A potentially more realistic mixture model was therefore developed. In the mixed beta model, the primary XIP distribution is again defined by a binomial distribution and is dependent on the number of progenitor cells (Supplementary Figure 2a). Throughout development and aging, individual XIP values shift away from their primary value to some secondary value with a probability defined by a beta distribution (Supplementary Figure 2a, dashed line). The overall distribution of XIPs in a population then becomes a probability-weighted sum of the component distributions (Supplementary Figure 2c, solid line). Parameter estimates, AD goodness-of-fit statistics, and associated P values are shown for mixed beta models for various values of c (Table 3). An interesting feature of the mixture model is that increasing the cell numbers beyond a certain threshold, in this case around 8 or 16 cells, does not significantly alter the fit (Table 3, data not shown). This mixture model could therefore accommodate very high cell numbers.29 Visually, the mixed beta model fits the Utah and Denmark data better than the simple models for integer values of c (Figure 3). Non-integer c values cannot be accommodated by this statistical model. There is some indication that c values >12 could fit the Denmark data. However, all mixture models of the Utah data set with integer values of c can be rejected by the AD test, even for large c (c=100).

Table 3. Goodness-of-fit tests for mixed beta models applied to the Utah and Denmark data sets for c=4–100.

  Utah Denmark
Model AD P-value AD P-value
4 13.366 0 13.421 0
6 2.742 0.003 2.600 0.012
7 1.766 0.028 1.828 0.021
8 1.542 0.033 1.606 0.035
9 1.520 0.034 1.540 0.034
10 1.540 0.036 1.516 0.044
12 1.584 0.039 1.496 0.053
16 1.619 0.038 1.478 0.050
24 1.629 0.044 1.467 0.045
50 1.641 0.036 1.471 0.048
100 1.654 0.024 1.476 0.059
Open in a new tab

P-values for models with no significant lack of fit are set in bold.

Figure 3.

Figure 3

Open in a new tab

Fits of the mixed beta models of completely random XCI choice. (a) The mixed beta models approach, but never reach, a significant fit to the Utah data, even for large c. (b) Mixed beta models with c≥12 may fit the Denmark data (c=12, P=0.053).

Overall, none of the models of completely random XCI choice is wholly satisfactory, as the only model fitting both data sets, the simple beta model, estimates a c between 4 and 6 cells, and this low value is inconsistent with the biological data.

Fits of genetically influenced models

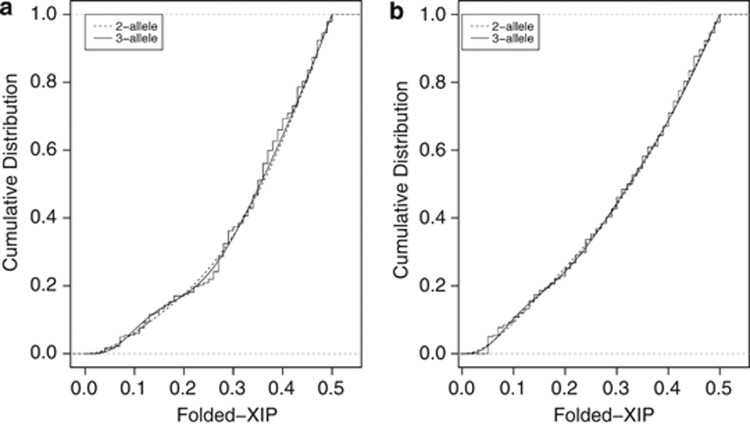
Various studies suggest that XCI choice is genetically influenced in humans, possibly through a co-dominant mechanism similar to the mouse Xce.13, 14, 15, 16, 17 In order to test whether distributions of XIPs in large populations of unrelated females would also be consistent with the human XCE hypothesis, models of genetically influenced XCI choice were generated. That is, models representing a single, co-dominant locus with large effect. Two- and three-allele models were generated (Supplementary Figure 2 d–g) and fitted to the Utah and Denmark data sets (Table 4). From the Utah data set, the two-allele genetic model estimates a dominant allele frequency of 0.89 and a primary folded-XIP of 0.10 in heterozygotes (this is equivalent to a ratio of 10:90 or 90:10). From the Denmark data set, the dominant allele frequency is 0.79 with a primary shift of 0.39, giving a primary folded XIP of 0.11 in heterozygotes (ratio of 11:89). The visual fits of the models to the data are good (Figure 4, dotted lines), and the model cannot be rejected by the AD test for the Utah data (P=0.066). However, the Denmark data show significant lack of fit (P=0.039). For the three-allele models, primary shifts and allele frequency estimates for the Utah and Denmark data sets are shown (Table 4). It is estimated that 35% of the Utah population are homozygous (1|1, 2|2, and 3|3) with balanced primary XIPs (folded XIP=0.5, ie, a ratio of 50:50). An estimated 50% have genotypes 1|2 or 1|3, with a primary folded XIP of 0.32 (ratio of 32:68). The 2|3 genotype has the largest shift, giving a primary folded XIP of 0.095 (ratio of 9.5:91.5), present in 17% of the population. The visual fit of the three-allele model is excellent and there is no lack of fit (P=0.174) (Figure 4a, solid line). Similarly, for the Denmark data set, it is estimated that 34% of the population are homozygous with balanced primary XIPs, and that genotypes 1|2, 1|3, and 2|3 are present in 25, 23, and 19% of the population, with primary folded XIPs of 0.32, 0.24, and 0.08, respectively. Again, the visual fit of the 3-allele model is excellent (Figure 4b, solid line) and there is no lack of fit (P=0.656).

Table 4. Parameter estimates for the two- and three-allele models of genetically influenced XCI choice for the Utah and Denmark data sets.

Model Parameters τ P1 P2 P3 δ12 δ13 δ23 P-value (AD)
Two-allele Utah 0.31 0.11 0.89   0.398     0.066
Two-allele Denmark 0.31 0.21 0.79   0.388     0.039
Three-allele Utah 0.17 0.43 0.29 0.286 0.179 0.000 0.405 0.174
Three-allele Denmark 0.18 0.39 0.32 0.29 0.176 0.257 0.420 0.656
Open in a new tab

P-values for models with no significant lack of fit are set in bold.

Figure 4.

Figure 4

Open in a new tab

Fits of the two- and three-allele models of genetically influenced XCI choice. (a) Both the two- and three-allele models show no significant lack of fit to the Utah data set (2-allele: P=0.066; 3-allele: P=0.174). (b) The three-allele model also shows no significant lack of fit to the Denmark data set (3-allele: P=0.6564).

If the 3-allele genetic model is valid, the same allelic variants and primary shifts δij are expected in the Utah and Danish populations. The allele frequencies pi, i=1, 2, 3, and variance scaling factor τ2 could differ. A model with these features was fitted to the combined data sets from Utah and Denmark. The likelihood ratio test, which compares this fit with the more complicated model that allows different shifts in the two populations, is not significant (P=0.57). This suggests that the genotype–phenotype relationships estimated from the data are the same in both populations, supporting the validity of the 3-allele genetic model.

Three-allele model of genetically influenced choice provides the best overall fit

To determine which of the models tested provides the best overall fit to both data sets, we compare the best fits of the models of completely random choice and genetically influenced choice with each other. Among the simple random models tested, the beta models are the most reasonable as the predicted XIP values are restricted to the permissible [0, 1] interval. The only simple beta models not rejected by the AD test for both data sets are for non-integer fitted values for c; thus, the fitted c simple beta models are selected to represent the best simple random models. Among the mixed beta models tested, all values of c are rejected by the Utah data set. For completeness sake, however, we wanted to include at least one mixture model in our comparative analysis. As there was some indication that some c ≥12 could not be rejected by the Denmark data set (Table 3), we selected c=16 to represent the best-fitting mixture models. This value was selected because it represents a true stage of development, and as the analysis suggests that no other value of c would provide a significantly better fit. Among the genetic models tested, the 3-allele genetic model is preferred, as the 2-allele genetic model is rejected for the Denmark data set (P=0.039). The likelihood ratio test was used to determine whether the 3-allele genetic model (alternative hypothesis) is a significant improvement over the best models of completely random choice (null hypotheses). This test takes into consideration the number of parameters estimated by each model to account for the fact that a model with more parameters will typically fit better. The genetic model was found to be superior to each of the models of completely random choice tested for both data sets (P values: simple beta (fitted ĉ), Utah=0.020, Denmark=0.01; Mixed beta (c=16), Utah=0.010, Denmark=0.014), suggesting that, among the models tested, the 3-allele co-dominant model of genetically influenced XCI choice provides the best overall fit to the empirical data examined, further supporting the hypothesis that human XCI choice is genetically influenced.

Discussion

The present study explores the nature of secondary XIP distributions in large populations of females in order to illuminate the nature of XCI choice. Using a statistical modelling approach, we have explored secondary folded-XIP distributions in populations from Utah and Denmark and compared these with models of completely random and genetically influenced XCI choice. By folding XIP data and utilizing continuous, cumulative distribution functions, we avoid some of the pitfalls of previous studies, and our statistical analyses, which utilize entire distributions, are preferred over threshold-based approaches.

We test various models of completely random XCI choice and find none to be satisfactory. We therefore do not favour the hypothesis that XCI choice is completely random. Consequently, we conclude that the number of cells undergoing choice, c, cannot be calculated based on XIP distributions alone. We do find a model of genetically influenced XCI choice that fits all of the available data. A three-allele model of genetically influenced XCI choice, based on the mouse Xce paradigm, fits both data sets, provides the best overall fit of all the models tested, estimates similar genotype–phenotype relationships from two independent populations, allows for secondary skewing, and can accommodate a large c. We therefore favour the hypothesis that human XCI choice is genetically influenced, possibly through an XCE-like mechanism. Whether this represents a true human ortholog of the mouse Xce or a phenocopy remains to be seen.

While we have used the term ‘allele', other variants, such as epi-alleles or environmental exposures, could potentially fit the model as well. Other genetic models would be interesting to explore in future work, as would a four-allele model.

In the mixture models studied here, it is assumed that the variance of the individual component densities decreases as the primary XIP becomes more extreme. A longitudinal study examining the change in XIPs over time as a function of the initial XIP could be used to determine whether this assumption is accurate.

One potential confounder of XIP studies in humans is age. AAS may be due to a true shift in XIP due to changes in the survival or proliferation of the maternal and paternal X populations25 or could be due to a progressive demethylation of the human androgen receptor locus in peripheral blood.28 Using continuous functions, our models do allow for shifts away from the primary XIP due to any number of phenomena, including age. However, we did not specifically include an age-dependent parameter in our models. To determine whether the addition of such a parameter could significantly affect our general conclusions, we examined the impact of AAS on XIP distributions. We find that there is a significant correlation between age and folded XIP among individuals in the Utah and Denmark data sets for whom age is known (Utah: r=−0.204, P=0.009; Denmark: r=−0.269, P=0.00002). However, a Lowess curve illustrates that the change in folded XIP is ∼0.1 over 70 years, or 0.0014 per year. Therefore, while there is a definite effect, it is small. AAS is not likely to have a serious impact on our models where, for example, the primary shifts estimated by the 3-allele genetic model for the Utah data are ≥ 0.18, and deviations away from the primary shifts due to secondary skewing are already taken into consideration in the continuous models. It would, however, be interesting to analyse neonatal populations in future work as these individuals would be the least affected by AAS.

Our conclusion that XIPs could be genetically influenced is consistent with several other studies. Kristiansen et al13 compare XIPs in monozygotic and dizygotic twins. They find a heritability of 0.63 and evidence for a dominant genetic effect. These findings are consistent with our genetically influenced models in which genotype determines the XIP at the time of choice (primary XIP), and other factors (environment, stochastic events, AAS etc) shift the pattern away from its primary value to the observable secondary XIP. Further studies14, 15, 16, 17 find that the inheritance pattern of XIPs in families can be explained by a co-dominant model following the rules of the mouse Xce model. Our findings contrast with a recent report by Bolduc et al,31 however, which stated that XIPs result from completely random XCI and selective pressures, and are not heritable through a single cis-acting locus such as the XCE. However, their analysis appears to consider only purely dominant and recessive modes of inheritance and includes only mother–daughter pairs, rather than whole families. Our three-allele model shows that empirical data can be consistent with a genetic model with a co-dominant mode of inheritance in which a difference in allele strength defines the phenotype. As such, the phenotype of the daughter cannot be predicted without knowledge of the paternal contribution. The findings of Bolduc et al31 could be consistent with our co-dominant model if three allelic variants are present in the examined population at approximately equal allele frequency, and they define primary skewing shifts similar to those found in our study.

How genetics could influence XCI choice remains a fascinating question. Several molecular models of XCI choice are discussed in the literature (for a review, see Starmer and Magnuson32). It may be that a single autosomal ‘blocking factor' or a single complex of blocking factors33 binds the future active X, inhibiting XCI in cis. Alternatively, an X-linked competence factor, such as Rnf12,34 may be required at some threshold concentration to trigger inactivation on a single X in trans. Cohesin may also have a role in the molecular mechanism of human XCI choice.17 One model suggests that cohesin could bind together the two X-inactivation centres (XIC) during their obligatory co-localisation35 prior to XCI initiation, and, given the asymmetrical structure of the cohesion complex, could potentially affect transcriptional activity within a single XIC.17 Genetics could influence choice by altering the expression, stability, localisation, orientation, or binding of any of these elements. Additional biological data and mathematical modelling will be required to determine if any of these possibilities is accurate.

Our study illustrates potential improvements to the data treatment strategies employed in human XCI research, and describes new models of XCI choice and a novel statistical modelling approach for XCI model testing. We find that models of completely random XCI choice inadequately describe folded-XIP distributions in large populations of adult human females and that a 3-allele co-dominant model of genetically influenced XCI choice based on the mouse Xce paradigm can be consistent with these distributions. Our results support the concept that XCI choice is genetically influenced.

Acknowledgments

Manuscript preparation: Marc Renault. Funding: Canadian Institutes of Health Research (CIHR), the Killam Foundation, the Natural Sciences and Engineering Council (NSERC) of Canada.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

Supplementary Material

Supplementary Figure 1
Click here for additional data file. (45.9KB, pdf)
Supplementary Figure 2
Click here for additional data file. (106.2KB, pdf)
Supplementary Table 1
Click here for additional data file. (21.8KB, pdf)
Supplementary Information
Click here for additional data file. (434.4KB, pdf)

References

  1. Lyon MF. Gene action in the X-chromosome of the mouse (Mus musculus L.) Nature. 1961;190:372–373. doi: 10.1038/190372a0. [DOI] [PubMed] [Google Scholar]
  2. Morey C, Avner P. The demoiselle of X-inactivation: 50 years old and as trendy and mesmerising as ever. PLoS Genet. 2011;7:e1002212. doi: 10.1371/journal.pgen.1002212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Brown CJ, Lafreniere RG, Powers VE, et al. Localization of the X inactivation centre on the human X chromosome in Xq13. Nature. 1991;349:82–84. doi: 10.1038/349082a0. [DOI] [PubMed] [Google Scholar]
  4. Carrel L, Willard HF. X-inactivation profile reveals extensive variability in X-linked gene expression in females. Nature. 2005;434:400–404. doi: 10.1038/nature03479. [DOI] [PubMed] [Google Scholar]
  5. Heard E, Clerc P, Avner P. X-chromosome inactivation in mammals. Annu Rev Genet. 1997;31:571–610. doi: 10.1146/annurev.genet.31.1.571. [DOI] [PubMed] [Google Scholar]
  6. Morleo M, Franco B. Dosage compensation of the mammalian X chromosome influences the phenotypic variability of X-linked dominant male-lethal disorders. J Med Genet. 2008;45:401–408. doi: 10.1136/jmg.2008.058305. [DOI] [PubMed] [Google Scholar]
  7. Migeon BR. The role of X inactivation and cellular mosaicism in women's health and sex-specific diseases. JAMA. 2006;295:1428–1433. doi: 10.1001/jama.295.12.1428. [DOI] [PubMed] [Google Scholar]
  8. Orstavik KH. X chromosome inactivation in clinical practice. Hum Genet. 2009;126:363–373. doi: 10.1007/s00439-009-0670-5. [DOI] [PubMed] [Google Scholar]
  9. Cattanach BM, Perez JN, Pollard CE. Controlling elements in the mouse X-chromosome. II.Location in the linkage map. Genet Res. 1970;15:183–195. doi: 10.1017/s0016672300001518. [DOI] [PubMed] [Google Scholar]
  10. Cattanach BM, Isaacson JH. Controlling elements in the mouse X chromosome. Genetics. 1967;57:331–346. doi: 10.1093/genetics/57.2.331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cattanach B, Rasberry C. Identification of the mus castaneus Xce allele. Mouse Genome. 1994;92:114. [Google Scholar]
  12. Cattanach BM, Williams CE. Evidence of non-random X chromosome activity in the mouse. Genet Res. 1972;19:229–240. doi: 10.1017/s001667230001449x. [DOI] [PubMed] [Google Scholar]
  13. Kristiansen M, Knudsen GP, Bathum L, et al. Twin study of genetic and aging effects on X chromosome inactivation. Eur J Hum Genet. 2005;13:599–606. doi: 10.1038/sj.ejhg.5201398. [DOI] [PubMed] [Google Scholar]
  14. Naumova AK, Olien L, Bird LM, et al. Genetic mapping of X-linked loci involved in skewing of X chromosome inactivation in the human. Eur J Hum Genet. 1998;6:552–562. doi: 10.1038/sj.ejhg.5200255. [DOI] [PubMed] [Google Scholar]
  15. Cau M, Addis M, Congiu R, et al. A locus for familial skewed X chromosome inactivation maps to chromosome Xq25 in a family with a female manifesting LOWE syndrome. J Hum Genet. 2006;51:1030–1036. doi: 10.1007/s10038-006-0049-6. [DOI] [PubMed] [Google Scholar]
  16. Renault NK, Dyack S, Dobson MJ, Costa T, Lam WL, Greer WL. Heritable skewed X-chromosome inactivation leads to haemophilia A expression in heterozygous females. Eur J Hum Genet. 2007;15:628–637. doi: 10.1038/sj.ejhg.5201799. [DOI] [PubMed] [Google Scholar]
  17. Renault NK, Renault MP, Copeland E, Howell RE, Greer WL. Familial skewed X-chromosome inactivation linked to a component of the cohesin complex, SA2. J Hum Genet. 2011;56:390–397. doi: 10.1038/jhg.2011.25. [DOI] [PubMed] [Google Scholar]
  18. Abkowitz JL, Taboada M, Shelton GH, Catlin SN, Guttorp P, Kiklevich JV. An X chromosome gene regulates hematopoietic stem cell kinetics. Proc Natl Acad Sci USA. 1998;95:3862–3866. doi: 10.1073/pnas.95.7.3862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Fialkow PJ. Primordial cell pool size and lineage relationships of five human cell types. Ann Hum Genet. 1973;37:39–48. doi: 10.1111/j.1469-1809.1973.tb01813.x. [DOI] [PubMed] [Google Scholar]
  20. Tonon L, Bergamaschi G, Dellavecchia C, et al. Unbalanced X-chromosome inactivation in haemopoietic cells from normal women. Br J Haematol. 1998;102:996–1003. doi: 10.1046/j.1365-2141.1998.00867.x. [DOI] [PubMed] [Google Scholar]
  21. Amos-Landgraf JM, Cottle A, Plenge RM, et al. X chromosome-inactivation patterns of 1,005 phenotypically unaffected females. Am J Hum Genet. 2006;79:493–499. doi: 10.1086/507565. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Prchal JT, Prchal JF, Belickova M, et al. Clonal stability of blood cell lineages indicated by X-chromosomal transcriptional polymorphism. J Exp Med. 1996;183:561–567. doi: 10.1084/jem.183.2.561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Wengler G, Gorlin JB, Williamson JM, et al. Nonrandom inactivation of the X chromosome in early lineage hematopoietic cells in carriers of Wiskott-Aldrich syndrome. Blood. 1995;85:2471–2477. [PubMed] [Google Scholar]
  24. Busque L, Mio R, Mattioli J, et al. Nonrandom X-inactivation patterns in normal females: lyonization ratios vary with age. Blood. 1996;88:59–65. [PubMed] [Google Scholar]
  25. Sandovici I, Naumova AK, Leppert M, et al. A longitudinal study of X-inactivation ratio in human females. Hum Genet. 2004;115:387–392. doi: 10.1007/s00439-004-1177-8. [DOI] [PubMed] [Google Scholar]
  26. D'Agostino R, Stephens M. Goodness-of-fit Techniques. Marcel Dekker, Inc.; 1986. [Google Scholar]
  27. Fey MF, Peter HJ, Hinds HL, et al. Clonal analysis of human tumors with M27 beta, a highly informative polymorphic X chromosomal probe. J Clin Invest. 1992;89:1438–1444. doi: 10.1172/JCI115733. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Swierczek SI, Agarwal N, Nussenzveig RH, et al. Hematopoiesis is not clonal in healthy elderly women. Blood. 2008;112:3186–3193. doi: 10.1182/blood-2008-03-143925. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Okamoto I, Patrat C, Thepot D, et al. Eutherian mammals use diverse strategies to initiate X-chromosome inactivation during development. Nature. 2011;472:370–374. doi: 10.1038/nature09872. [DOI] [PubMed] [Google Scholar]
  30. Bittel D, Theodoro M, Kibiryeva N, Fischer W, Talebizadeh Z, Butler M. Comparison of X-chromosome inactivation patterns in multiple tissues from human females. J Med Genet. 2008;5:309–313. doi: 10.1136/jmg.2007.055244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Bolduc V, Chagnon P, Provost S, et al. No evidence that skewing of X chromosome inactivation patterns is transmitted to offspring in humans. J Clin Invest. 2008;118:333–341. doi: 10.1172/JCI33166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Starmer J, Magnuson T. A new model of random X chromosome inactivation. Development. 2009;1:1–10. doi: 10.1242/dev.025908. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nicodemi M, Prisco A, Self-assembly DNA. binding of the blocking factor in X chromosome inactivation. PLoS Comput Biol. 2007;11:e210. doi: 10.1371/journal.pcbi.0030210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Jonkers I, Barakat T, Achame E, et al. RNF12 is an X-encoded dose-dependent activator of X chromosome inactivation. Cell. 2009;5:999–1011. doi: 10.1016/j.cell.2009.10.034. [DOI] [PubMed] [Google Scholar]
  35. Bacher CP, Guggiari M, Brors B, et al. Transient colocalization of X-inactivation centres accompanies the initiation of X-inactivation. Nat Cell Biol. 2006;8:293–299. doi: 10.1038/ncb1365. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure 1
Click here for additional data file. (45.9KB, pdf)
Supplementary Figure 2
Click here for additional data file. (106.2KB, pdf)
Supplementary Table 1
Click here for additional data file. (21.8KB, pdf)
Supplementary Information
Click here for additional data file. (434.4KB, pdf)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES