Nonequilibrium landscape theory of neural networks

Significance

The brain map project aims at mapping out human brain neuron connections. Even with given wirings, the global and physical understandings of the function and behavior of the brain are still challenging. Learning and memory processes were previously globally quantified for symmetrically connected neural networks. However, realistic neural networks of cognitive processes and physiological rhythm regulations are asymmetrically connected. We developed a nonequilibrium landscape–flux theory for asymmetrically connected neural networks. We found the landscape topography is critical in determining the global stability and function of the neural networks. The cognitive dynamics is determined by both landscape gradient and flux. For rapid-eye movement sleep cycles, we predicted the key network wirings based on landscape topography, in agreement with experiments.

Abstract

The brain map project aims to map out the neuron connections of the human brain. Even with all of the wirings mapped out, the global and physical understandings of the function and behavior are still challenging. Hopfield quantified the learning and memory process of symmetrically connected neural networks globally through equilibrium energy. The energy basins of attractions represent memories, and the memory retrieval dynamics is determined by the energy gradient. However, the realistic neural networks are asymmetrically connected, and oscillations cannot emerge from symmetric neural networks. Here, we developed a nonequilibrium landscape–flux theory for realistic asymmetrically connected neural networks. We uncovered the underlying potential landscape and the associated Lyapunov function for quantifying the global stability and function. We found the dynamics and oscillations in human brains responsible for cognitive processes and physiological rhythm regulations are determined not only by the landscape gradient but also by the flux. We found that the flux is closely related to the degrees of the asymmetric connections in neural networks and is the origin of the neural oscillations. The neural oscillation landscape shows a closed-ring attractor topology. The landscape gradient attracts the network down to the ring. The flux is responsible for coherent oscillations on the ring. We suggest the flux may provide the driving force for associations among memories. We applied our theory to rapid-eye movement sleep cycle. We identified the key regulation factors for function through global sensitivity analysis of landscape topography against wirings, which are in good agreements with experiments.

A grand goal of biology is to understand the function of the human brain. The brain is a complex dynamical system (1–6). The individual neurons can develop action potentials and connect with each other through synapses to form the neural circuits. The neural circuits of the brain perpetually generate complex patterns of activity that have been shown to be related with special biological functions, such as learning, long-term associative memory, working memory, olfaction, decision making and thinking (7–9), etc. Many models have been proposed for understanding how neural circuits generate different patterns of activity. Hodgkin–Huxley model gives a quantitative description of a single neuronal behavior based on the voltage-clamp measurements of the voltage (4). However, various vital functions are carried out by the circuit rather than individual neurons. It is at present still challenging to explore the underlying global natures of the large neural networks built from individual neurons.

Hopfield developed a model (5, 6) that makes it possible to explore the global natures of the large neural networks without losing the information of essential biological functions. For symmetric neural circuits, an energy landscape can be constructed that decreases with time. As shown in Fig. 1, started in any initial state, the system will follow a gradient path downhill to the nearest basin of attractor of the underlying energy landscape (local minimum of energy E) that contains the storage of the complete information formed from learning with specific enhanced wiring patterns. This can be the memory retrieval process from a cue (incomplete initial information) to the corresponding memory (complete information). The Hopfield model shows us a clear dynamical picture of how neural circuits implement their memory storage and retrieval functions. This theory also helps in designing associate memory Hamiltonians for protein folding and structure predictions (10, 11). However, in real neural networks, the connections among neurons are mostly asymmetric rather than symmetric. Under this more realistic biological situation, the original Hopfield model fails to apply. This is because there is no easy way of finding out the underlying energy function. Therefore, the global stability and function of the neural networks are hard to explore. In this work, we will study the global behavior of neural circuits with synaptic connections from symmetric to general asymmetric ones.

Fig. 1.

The schematic diagram of the original computational energy function landscape of Hopfield neural network.

Here, we will first develop a potential and flux landscape theory for neural networks. We illustrate that the driving force of the neural network dynamics can be decomposed into two contributions: the gradient of the potential and a curl probability flux. The curl probability flux is associated to the degree of nonequilibriumness characterized by detailed balance breaking. This implies the general neural network dynamics is analogous to an electron moving in an electric field (potential gradient) and magnetic field (curl flux). The curl flux can lead to spiral motion, the underlying network dynamics deviating from the gradient path, and even generate coherent oscillations, which are not possible under pure gradient force. We show a potential landscape as Lyapunov function of monotonically decreasing along the dynamics in time still exists even with asymmetric connections (12–14) for the neural networks. Our approach is based on the statistical probabilistic description of nonequilibrium dynamical systems. The global natures are hard to explore by just following the individual trajectories. Due to the presence of intrinsic and extrinsic fluctuations, exploring probability and its evolution is more appropriate rather than the trajectory evolution.

The probabilistic landscape description can provide an answer to the global stability and function because the importance of each state can be discriminated by its associated weight. In the state space, the states with locally highest probability (lowest potential) represent the basins of attraction of the dynamical system. Each point attractor state surrounded by its basin represents a particular memory. The stability of the attractor states is crucial for memory storage and retrieval under perturbations and fluctuations. The escape time from the basin quantifies the capability of communications between the basins. The barrier heights are shown to be associated with the escape time from one state to another. Therefore, the topography of the landscape through barrier height can provide a good measurement of global stability and function (12, 14–17).

Such probability landscape can be constructed through solving the corresponding probabilistic equation. However, it is difficult to solve the probabilistic equation directly due to the exponentially large number of dimensions. Here, we applied a self-consistent mean field approximation to study the large neural networks (13, 18, 19). This method can effectively reduce the dimensionality from exponential to polynomial by approximating the whole probability as the product of the individual probability for each variable and be carried out in a self-consistent way (treating the effect of other variables as a mean field). Lyapunov function can characterize the global stability and function of the system. Here, we construct a Lyapunov function from the probabilistic potential landscape.

We constructed nonequilibrium thermodynamics for the neural networks. Quantifying the main thermodynamical functions such as energy, entropy, and free energy is helpful for addressing global properties and functions of neural networks. As an open system that constantly exchanges energy and materials with the environment, entropy of the network system does not necessarily increase all of the time. We found the free energy of the network system is monotonically decreasing. Therefore, rather than entropy maximization, we propose that the free-energy minimization may serve as the global principle and optimal design criterion for neural networks.

The original Hopfield model shows a good associative memory property that the system always goes down to certain fixed point attractors of the dynamical storing memories. However, more and more studies show that oscillations with different rhythms in various nervous systems also play important roles in cognitive processes (8, 20). For example, theta rhythm was found to be enhanced in various neocortical sites of human brains during working memory (21), and enhanced gamma rhythm is closely related to attention (22, 23). Studying the oscillations may give rise to new insights toward how the various neural networks in the nervous system work. Our studies will provide a way to explore the global properties of various dynamical systems, in particular the oscillations (12, 13). We will apply our method to study asymmetric Hopfield circuits and their oscillatory behaviors, and tie them with the biological functions.

After the theoretical potential and flux landscape framework established, we will next study a Hopfield associative memory network consisting of 20 model neurons. The neurons communicate with each other through synapses, and the synaptic strengths are quantitatively represented by the connection parameters T_ij (5, 6). In this paper, we will focus more on how the circuits work rather than how they are built. So we used constant synaptic strengths here. We constructed the probabilistic potential landscape and the corresponding Lyapunov function for this neural circuit. We found that the potential landscape and associated Lyapunov function exists not only for symmetric connection case of the original Hopfield model where the dynamics is dictated by the gradient of the potential, but also for asymmetric case where the original Hopfield model failed to explore. We discussed the effects of connections with different degrees of asymmetry on the behaviors of the circuits and study the robustness of the system in terms of landscape topography through barrier heights.

One distinct feature that has often been observed in neural networks is the oscillation. We found oscillations cannot occur for the symmetric connections due to the gradient natures of the dynamics. The neural circuit with strong asymmetric connections can generate the limit cycle oscillations. The corresponding potential landscape shows a Mexican hat closed-ring shape topology, which characterizes the global stability through the barrier height of the center hat. We found the dynamics of the neural networks is controlled by both the gradient of the potential landscape and the probability flux. Although the gradient force attracts the system down to the ring, the flux is responsible for the coherent oscillations on the ring (12, 13). The probability flux is closely related to the asymmetric part of the driving force or the connections.

We also discussed the period and coherence of the oscillations for asymmetric neural circuits and its relationship with landscape topography to associate with the biological function. Both flux and potential landscape are crucial for the process of continuous memory retrievals with certain directions stored in the oscillation attractors. We point out that flux may provide driving force for the associations among different memory basins of attractions. Furthermore, we discuss how the connections with different degree of asymmetry influence the capacity of memory for general neural circuits.

Finally, we applied our potential and flux theory to a rapid-eye movement (REM) sleep cycle model (24, 25). We did a global sensitivity analysis based on the landscape topography to explore the influences of the key factors such as release of acetylcholine (Ach) and norepinephrine on the stability and function of the system. Our results are consistent with the experimental observations, and we found the flux is crucial for both the stability and the period of REM sleep rhythms.

Potential Landscape and Flux Theory, Lyapunov Function, and Nonequilibrium Thermodynamics for Neural Networks

In general, when exploring the global dynamics of a neural network, there are several approaches: one is to follow individual deterministic or stochastic trajectories, and the other one is to describe the system from thermodynamics perspectives with energy, entropy, and free energy for global characterization of the system. Hodgkin and Huxley proposed a model that quantifies how individual neurons evolve with time based on their biological features, and the theoretical predictions are in good agreement with experimental results. Many simplified models have been proposed to explore complex neural networks. The neural networks are often under fluctuations from intrinsic source and external environments. Rather than individual trajectory evolution, the probabilistic evolution can characterize the dynamics globally and therefore often more appropriate. We can start with a set of Langevin equations considering the stochastic dynamics of neural networks under fluctuations: 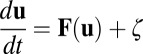. Here, 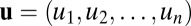is a vector variable representing each individual neuron activity u_i, for example each individual neuron’s action potential. The 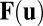represents the driving force for the dynamics of the underlying neural network. ζ represents here the stochastic fluctuation force with an assumed Gaussian distribution. The autocorrelations of the fluctuation are assumed to b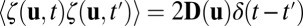e . The 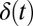is the δ function. The diffusion matrix 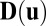is defined as 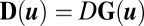, where D is a scale constant giving the magnitude of the fluctuations and 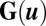represents the scaled diffusion matrix. Trajectories of individual neuron activities can be studied under fluctuations and quantified.

As we know, it is the circuits in the brain instead of individual neurons carrying out different cognitive functions. Therefore, we should focus on the global properties of the whole neural circuits. For a general equilibrium system, we can always get the energy function and the driving force is a gradient of an energy function. Once the energy is known, the equilibrium partition function and the associated free-energy function to study the global stability of the system can be quantified. In fact, the Hopfield associative memory model provides such an example (5, 6). By assuming the symmetric connections between neurons, Hopfield is able to find such an underlying energy function and use it to study the global stability and function for learning and memory through equilibrium statistical mechanics. However, in reality, the connections of the neurons in the neural networks are often asymmetric. Hopfield model with symmetric connections does not apply in this regime. There is no easy way of finding out the energy function determining the global nature of the neural networks in such general case.

Realistic neural networks are open systems. There are constant exchanges of the energy and information with the environment, for example, the oxygen intake of the brains for the energy supply. So the neural network is not a conserved system. The driving force therefore cannot often be written as a gradient of an energy function in such nonequilibrium conditions. However, finding an energy-like function such as a Lyapunov function (monotonically going down as the dynamics) is essential for quantifying the global stability of the system. Therefore, the challenge is whether such a potential function exists and can be quantified to study the global function for the general neural networks.

We will meet the challenge by developing a nonequilibrium potential landscape and flux theory for neural networks. Rather than following a single deterministic trajectory, which only gives local information, we will focus on the evolution of the probability distribution, which reflects the global nature of the system. Then we can establish the corresponding Fokker–Planck diffusion equation for probability evolution of state variable u_i:

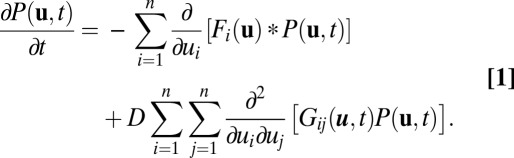With appropriate boundary condition of sufficient decay near the outer regime, we can explore the long-time behavior of Fokker–Planck equation and obtain steady-state probability distribution P_ss. The Fokker–Planck equation can be written in the form of the probability conservation: 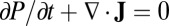, where J is the probability flux: . From the expression of the flux J, the driving force of the neural network systems can be decomposed as follows: 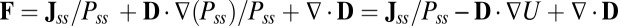. Here, divergent condition of the flux is satisfied for steady state. We see the dynamical driving force F of neural networks can be decomposed into a gradient of a nonequilibrium potential [the nonequilibrium potential U here is naturally defined as related to the steady-state probability distribution, analogous to equilibrium systems where the energy is related to the equilibrium distribution through the Boltzman law] and a divergent free flux, modulo to the inhomogeneity of the diffusion, which can be absorbed and redefined in the total driving force (12–15). The divergent free force J_ss has no source or sink to go to or come out. Therefore, it has to rotate around and become curl.

When the flux is divergent free 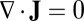in steady state, it does not necessarily mean the 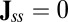. There are two possibilities, one is 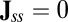and one is 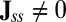. When 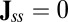, the detailed balance is satisfied and the system is in equilibrium. Furthermore, the dynamics is determined by purely the gradient of the potential. This is exactly the equilibrium case for Hopfield model for neural networks of learning and memory assuming underlying symmetric connections between neurons. However, when 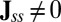, the detailed balance is broken. The nonzero flux is the signature of the neural network being in nonequilibrium state. The steady-state probability distribution can quantify the global natures of the neural networks, whereas the local dynamics is determined by both the gradient of the nonequilibrium potential landscape and the nonzero curl flux.

To quantitatively study the global stability and functions of neural networks, we need to find out whether a Lyapunov function of monotonically going down in time exists (12, 13, 18, 19, 26–34) and how it is related to our potential landscape. We expand the with respect to the parameter for the case of weak fluctuations 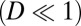in realistic neural networks and substitute it to the steady-state Fokker–Planck diffusion equation; then we obtain the D⁻¹ order part and this leads to Hamilton–Jacobi equation for (28, 29, 34–36):

We can then explore the time evolution dynamics of . Notice that this derivation is based on weak fluctuation assumptions 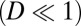. The temporal evolution 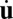can be written as 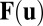here and therefore is deterministic without the noise term ζ. We see that decreases monotonously with time due to the positive defined diffusion matrix G. The dynamical process will not stop until the system reaches a minimum that satisfies 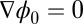. In general, one has to solve the above Hamilton–Jacobi equation for 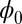to obtain the Lyapunov function. Finding the Lyapunov function is crucial for studying the global stability of the neural networks. For point attractors, 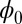will settle down at the minimum value. For limit cycles, the values of 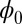on the attractors must be at constant (34). Therefore, the limit cycle cannot emerge from Hopfield model for neural networks with a pure gradient dynamics because there is no driving force for the coherent oscillation. However, the nonzero flux can provide the driving force for the oscillations on the cycle. 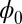being a Lyapunov function is closely associated with the population nonequilibrium potential landscape U under the small fluctuation limit. Therefore, the function 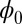reflects the intrinsic properties of the steady state without the influences from the magnitude of the fluctuations. Because 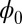is a Lyapunov function that decreases monotonically with time, the 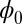has the physical meaning of the intrinsic nonequilibrium potential that quantifies the global stability for neural networks. When the underlying fluctuations are not weak, we can no longer expand the nonequilibrium potential U with respect to the fluctuation amplitude parameter D as shown above and the noise term ζ cannot be neglected in the derivation. Therefore, there is no guarantee that is a Lyapunov function for finite fluctuations. We will see next that the nonequilibrium free energy always decreases with time without the restriction of weak fluctuation assumption.

In a manner analogous to equilibrium thermodynamics, we can construct nonequilibrium thermodynamics (27, 30, 32–35, 37, 38) and apply to neural networks. We can define the potential function 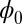and connect to the steady-state probability P_ss as 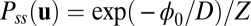, where Z can be defined as the time-independent (steady-state) nonequilibrium partition function for the neural network quantified as 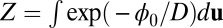. The diffusion scale D measures the strength of the fluctuations and here plays the role of k_BT in the Boltzmann formula. We can define the entropy of the nonequilibrium neural networks as follows: . We can also naturally define the energy 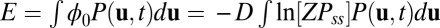and the free energy 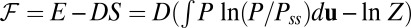for the nonequilibrium neural networks.

We can explore the time evolution of the entropy and the free energy for either equilibrium or nonequilibrium neural networks. We see the free energy of the nonequilibrium neural networks ℱ always decreases in time 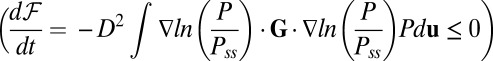until reaching the minimum value 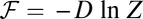(34). Therefore, the free-energy function ℱ is a Lyapunov function for stochastic neural network dynamics at finite fluctuations. The minimization of the free energy can be used to quantify the second law of thermodynamics for nonequilibrium neural networks. Therefore, the free energy is suitable to explore the global stability of the nonequilibrium neural networks.

The system entropy of the neural networks, however, is not necessarily maximized. This is because the time derivative of the system entropy dS/dt is not necessarily larger than zero all of the times. We can see that the system entropy evolution in time is contributed by two terms: 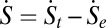. Here, the entropy production rate is defined as 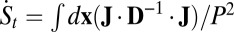, which is either positive or zero. The heat dissipation rate or entropy flow rate to the nonequilibrium neural networks from the environment defined as 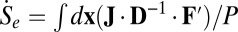can either be positive or negative, where the effective force is defined as 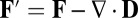. Although the total entropy change rate of the neural network (system plus environment) 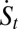is always nonnegative, consistent with the second law of thermodynamics, the system entropy change rate 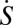, however, is not necessarily positive, implying the system entropy is not always maximized for the neural networks. Although the system entropy is not necessarily positive, the system free energy does minimize itself for neural networks. This may provide an optimal design principle of the neural networks for the underlying topology of wirings or connections.

The Dynamics of General Neural Networks

The Dynamics of Networks at Fixed Synaptic Connections.

The methods to construct global probability potential function and the corresponding Lyapunov function discussed above can be applied to general dynamical systems. Now we will explore the potential landscape and Lyapunov function for general neural networks. We start with the dynamical equations of Hopfield neural network of N neurons (6) as follows: 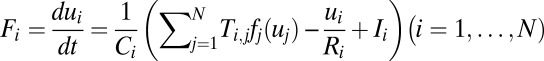. The variable u_i represents the effective input action potential of the neuron i. The action potential u changes with time in the process of charging and discharging of the individual neuron, and it can represent the state of the neuron. C_i is the capacitance and R_i is the resistance of the neuron i. T_i,j is the strength of the connection from neuron j to neuron i. The function 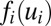represents the firing rate of neuron i. It has a sigmoid and monotonic form. The strength of the synaptic current into a postsynaptic neuron i due to a presynaptic neuron j is proportional to the product of 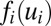and the strength of the synapse T_i,j from j to i. So the synaptic current can be represented by 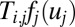. The input of each neuron comes from three sources: postsynaptic currents from other neurons, leakage current due to the finite input resistance, and input currents I_i from other neurons outside the circuit (6).

Notice that there is a very strong restriction in the Hopfield model, which is the strength of synapse T_i,j must be equal to T_j,i. In other words, the connection strengths between neurons are symmetric. In this paper, we will discuss more general neural networks without this restriction and include the asymmetric connections between neurons as well.

By considering fluctuations, we will explore the underlying stochastic dynamics by writing down the corresponding Fokker–Planck equation for the probability evolution; then we can obtain the Lyapunov function for a general neural network by solving the same equation shown as Eq. 2.

For a symmetric neural network 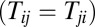, we can see there is a Lyapunov function, which is the energy E of the system as follows (5, 6): 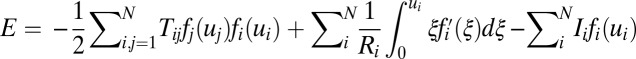. For a symmetric situation, it is easy to get the following: 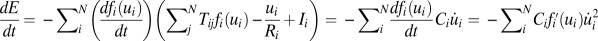. C_i is always positive and the function f_i increases with variable u_i monotonously, so the function E always decreases with time. The Hopfield model, although successful, assumes symmetric connections between neurons. This is not true for realistic neural circuits. As we see, unlike the energy defined by Hopfield, is a Lyapunov function no matter whether the circuit is symmetric or not. In fact, 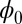as the general Lyapunov function is reduced to the energy function only when the connections of neural network are symmetric such as Hopfield model. In general, one has to solve the Hamilton–Jacobi equation to get the information on 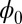because there is no general analytical solution for the Lyapunov function one can write down explicitly as in the symmetric connection case as Hopfield model.

For a symmetric circuit, the driving force can be written as a gradient, 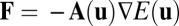, where 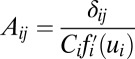. For a more general asymmetric circuit, the driving force cannot be written as the form of pure gradient of the potential. We have mentioned before that the driving force can be decomposed into a gradient of a potential related to steady-state probability distribution and a curl divergent free flux. As we will discuss in Results and Discussion, complex neural behaviors such as oscillations emerge in an asymmetric neural circuit, although this is impossible for the Hopfield model with symmetric neural connections. The nonzero flux J plays an important role in this situation.

The Dynamics of Neural Networks with Adaptive Synaptic Connections.

In real brains, genes program synaptic connectivity, whereas neural activity programs synaptic weights. We used constant synaptic connections before. We should notice that the synaptic connections actually vary all of the time. In addition, learning is exactly implemented by changes in the strengths of feedforward connections between different layers in feedforward networks or recurrent connections within a layer in feedback networks (39). Therefore, it is crucial to construct frameworks for networks with adaptive connections, which also helps people understand the mechanisms of prediction and reward (40). Actually, how the connections vary with time depends on the learning rules we choose. If we take the adaptive synaptic connections into consideration, based on Hebbian rules for example, we can write the dynamical equations as follows: .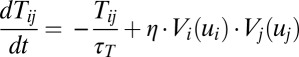

V_i here is the output potential of neuron i, and η is the learning rate. If the connection T_ij varies much more slowly than the state variable u, we can approximate the connections as constants. However, when the connection T_ij varies as fast as or even faster than the state variable u, the synaptic connections become dynamical and their evolution should not be ignored. Fortunately, our method provides a way to explore a general neural network no matter whether the synaptic connections are adaptive or not. This can be simply realized by including the above dynamical equation for the neuron connections T_ij and couple together with the dynamical equation for u_i. Then we write down the corresponding stochastic dynamics and the Fokker–Planck probability evolution diffusion equation and the corresponding Hamilton–Jacobi equation for the nonequilibrium intrinsic potential 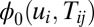. We can obtain the potential landscape 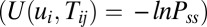and curl flux for the enlarged state space of 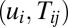beyond neural activity (potential) variable u_i along with the connections T_ij. The advantage of this is that we can quantitatively uncover the dynamical interplay between the individual neural activity and the connections in between in the general neural networks in shaping their global function.

Results and Discussion

Potential and Flux Landscape of Neural Network.

From the dynamics of the general neural networks described above, we established the corresponding probabilistic diffusion equation and solved steady-state probability distributions with a self-consistent mean field method. Then we can quantitatively map out the potential landscape [the population potential landscape U here is defined as 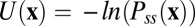] (12–15). It is difficult to visualize the result directly because of the multidimensionality of the state variable space of neural activity u. We selected 2 state variables from 20 in our neural network model to map out the landscape by integrating out the other 18 variables. We used more than 6,000 initial conditions in this study to collect statistics and avoid local trapping in the solution.

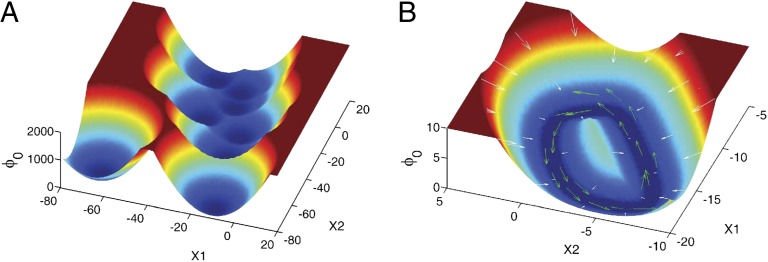
We first explored a symmetric circuit as what Hopfield did (6). Fig. 2A shows the potential landscape of the circuit and we can see that this symmetric circuit has eight basins of attractors. Each attractor represents a memory state that stores a complete information. When the circuit is cued to start with an incomplete information (initial condition), it will go “downhill” to the nearest basin of attractor with a complete information. This dynamical system guarantees the memory retrieval from a cue to the corresponding memory.

Fig. 2.

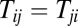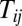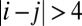The 3D potential landscape figures from restricted symmetric circuit to totally unrestricted circuit. (A) The potential landscape of symmetric neural circuit. (B and C) The potential landscapes of asymmetric circuits that for negative when and 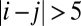, respectively. (D) The potential landscape of the asymmetric circuit without the restrictions on the connections. 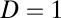for multistable case and 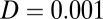for oscillation.

As we discussed in the above section, we constructed a Lyapunov function 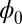from the expansion of the potential 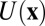on the diffusion coefficient D. It is difficult to solve the equation of 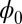directly due to its huge dimensions. We applied the linear fit method for the diffusion coefficient D versus the DU to solve the approximately. Fig. 3A shows the intrinsic potential landscape 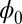of the symmetric neural circuit. In Fig. 3A, we can see there are also eight basins of attractor. Because 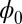is a Lyapunov function, the potential 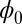of the system will decrease with time and settle down at a minimum at last. This landscape looks similar to the Hopfield energy landscape shown in Fig. 1. However, asymmetric circuits are more general and realistic. Unlike the computational energy defined by Hopfield, which only works for the neural networks with symmetric connections, 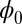is a Lyapunov function irrespective to whether the circuit has symmetric or asymmetric connections. Our landscape provides a way to capture the global characteristics of asymmetric neural circuits with Lyapunov function .

Fig. 3.

(A) The potential landscape of the symmetric circuit. (B) The potential landscape 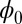as well as corresponding force: the green arrows represent the flux, and the white arrows represent the force from negative gradient of the potential landscape.

The pattern of synaptic connectivity in the circuit is a major factor determining the dynamics of the system. Hopfield defined an energy that is always decreasing with time during the neural state changes in a symmetric circuit. However, we know that having the sign and strength of the synaptic connection from neuron i to j the same as from j to i is not reasonable in a realistic neural system. So we focus here on the neural circuits without the restriction of symmetric connections. We chose a set of T_ij randomly. First, we set the symmetric connections, 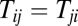when . Here, T_ii is set to zero, representing that the neuron does not connect with itself. Fig. 2A shows the potential landscapes of this symmetric circuit, and we can see eight basins of attractor. The number of memories stored in this symmetric neural circuit is eight. Next, we relaxed the restrictions on T_ij. We set 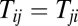for negative T_ij when 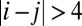and 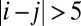, and we mapped out the landscapes in Fig. 2 B and C, respectively. The landscapes show that the number of stored memories decreases gradually. When we explored the original circuit without any restrictions on T_ij, there is a possibility in which all of the stable fixed points disappear and a limit cycle emerges in Fig. 2D. We can see the potential landscape has a Mexican-hat shape. These figures show that, as the circuit becomes less symmetric, the number of point attractors decreases. Because there are many ways of changing the degree of asymmetry, this result does not mean the memory capacity of an asymmetric neural network must be smaller than a symmetric one. We will discuss the memory capacity of general neural networks later in this paper.

As shown in Fig. 2D, oscillation can occur for unrestricted T_ij. Obviously, the system cannot oscillate if it is just driven by the gradient force of the potential landscape resulting from the symmetric connections. The driving force F in the general neural networks cannot usually be written as a gradient of a potential. As we have mentioned earlier in this paper, the dynamical driving force F can be decomposed into a gradient of a potential related to steady-state probability distribution and a divergent free flux (12–15).

We obtained the Lyapunov function 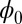of this asymmetric neural network. The landscape 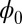of the limit cycle oscillations from an unrestricted asymmetric circuit is shown in Fig. 3B. We can see again the Mexican-hat shape of the intrinsic landscape 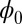. The potential along the deterministic oscillation trajectories are lower, and the potentials inside and outside of the ring are higher. Therefore, this Mexican-hat topography of the landscape attracts the system down to the oscillation ring. The values of 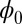are almost constant along the ring. This result is consistent with the property of 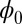being Lyapunov function. In Fig. 3B, the green arrows represent the flux, and the white arrows represent the force from negative gradient of the potential landscape. We can see the direction of the flux near the ring is parallel to the oscillation path. The direction of the negative gradient of the potential is almost perpendicular to the ring. Therefore, the landscape attracts the system toward the oscillation ring, and the flux is the driving force and responsible for coherent oscillation motion on the ring valley.

Generally, a neural network dynamics will stop at a point attractor where the Lyapunov function reaches a local minimum. We have shown that the neural network can also oscillate for some cases in which the values of Lyapunov function 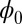on the oscillation ring are homogeneous constant. Our Lyapunov function 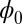provides a good description of the global intrinsic characteristics. Although the population potential U is not a Lyapunov function, the population landscape potential U captures more details of the system because it is directly linked to the steady-state probability distribution. For example, U reflects the inhomogeneous probability distribution on the oscillation ring, and this implies the inhomogeneous speed on the limit cycle oscillation path. 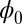being global Lyapunov function does not capture this information.

For a symmetric circuit, the system cannot oscillate, because the gradient force cannot provide the vorticity needed for oscillations (6). However, from our nonequilibrium probabilistic potential landscape, we can clearly see that the flux plays an important role as the connections between neurons become less symmetric. The flux becomes the key driving force when the neural network is attracted onto the limit cycle oscillation ring.

Quantifying Global Stability of Neural Network.

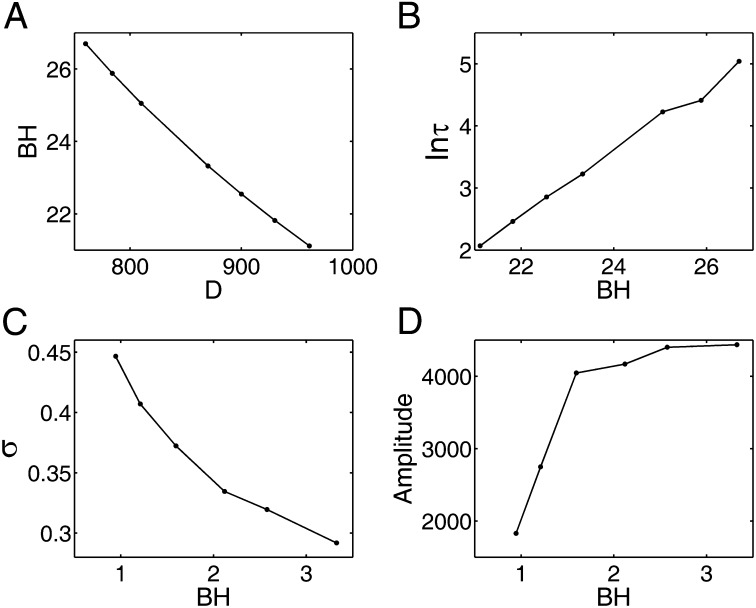
Consistent with the symmetric Hopfield model, the memories in neural networks are stored in attractors. Having quantified the potential landscape, we can further study the robustness of the neural network by exploring the landscape topography. We found that barrier height correlated with the escape time is a good measure of stability. In Fig. 4A, we can see that, when the fluctuation strength characterized by the diffusion coefficient D increases, the population barrier height decreases. Barrier height here is defined as . U_max is the maximum potential between the basins of attractions, and U_min is the potential at one chosen basin of attractor. We also followed the trajectories of this dynamical neural network starting with one selected basin of attractor, and obtained the average escape time from this basin to another with many escape events. Fig. 4B shows the relationship between barrier height of one selected basin and the escape time under certain fluctuations. We can see that, as the barrier height in potential landscape increases, the escape time becomes longer. Therefore, larger barrier height means it is harder to escape from this basin, and the memory stored in this basin is more robust against the fluctuations.

Fig. 4.

(A) The potential barrier height in U versus the diffusion coefficient D. (B) The logarithm of the average escape time versus the barrier height in potential barrier height U for symmetric circuits. (C) The barrier height versus the SD σ of period for asymmetric circuits. (D) The barrier height versus the amplitude of the power spectrum.

For the oscillation case, we discuss the barrier height with respect to the period distribution. Barrier height here is also defined as 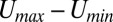. U_max is the maximum potential inside the closed ring (the height of the Mexican hat), and U_min is the minimum potential along the ring. When the fluctuations increase, the period distribution of the oscillations becomes more dispersed and the SD increases. Fig. 4C shows higher barrier height leads to less dispersed period distribution. We can use the Fourier transforms to find the frequency components of a variable that changes periodically. For the oscillation case, there should be one distinct peak in the frequency domain after Fourier transforms. If the oscillation is coherent, the corresponding magnitude of the peak is large. We discuss the relationship between the barrier height and the amplitude of the peak in the frequency domain. Fig. 4D shows that the amplitude of the peak increases as the barrier height increases. Larger barrier height makes it more difficult to go outside the ring, and this ensures the coherence and robustness of the oscillations. The barrier height provides a quantitative measurement for the global stability and robustness of the memory patterns.

Flux and Asymmetric Synaptic Connections in General Neural Networks.

Because we have shown that the flux is a major driving force and crucial for the stability of oscillations, we will explore the origin of the flux in general asymmetric circuits. What we know is there is only gradient force but no flux in Hopfield’s symmetric neural network. So, naturally, the flux suggests to us the asymmetric part of the network. We also explain this in mathematics. As we discussed before, we can decompose the driving force as 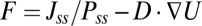(assuming constant diffusion without the loss of generality). Furthermore, for a symmetric neural circuit, the driving force can be written as 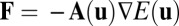, where 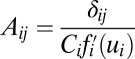. Comparing the above two equations, it is not difficult to find that the term 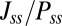may be generated by the asymmetric part of the driving force. So we decomposed the driving force into the symmetric part and the asymmetric part: 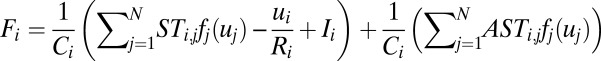, where .

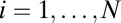Here, we constructed a connection matrix ST (symmetric matrix) as the form of 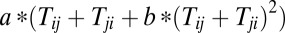(a, b are constants). Clearly, the matrix ST satisfies 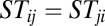and 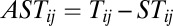. Notice that the resulting symmetric part of the driving force 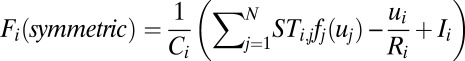has the general form of Hopfield model for a symmetric neural circuit. 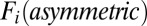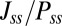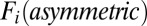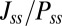To explore the relationship between the asymmetric part of driving force and the flux term , we calculated the average magnitude of and along the limit cycle for different asymmetric circuits. 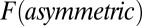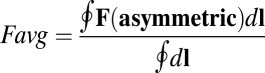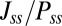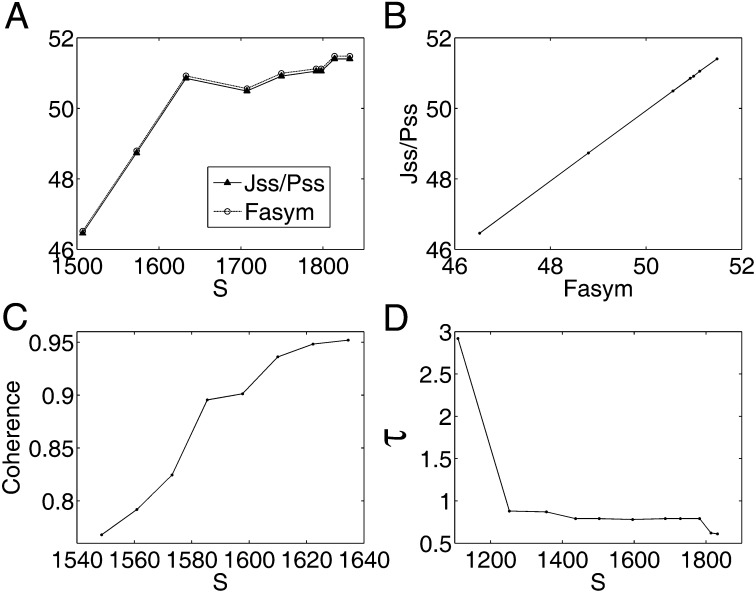Here, the average magnitude of is defined as , and the definition of average is similar (details are in SI Text). We also use S, which is defined as 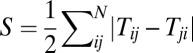, to describe the degree of asymmetry of a neural circuit. In Fig. 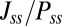5A, we can see when S increases (the network becomes less symmetric), the average and along the limit cycle increases. It is not difficult to understand that the asymmetric part of driving force becomes stronger when the circuit is more asymmetric. The similar trend of average 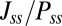versus S in Fig. 5B shows that the asymmetric part of driving force and the flux are closely related. The result is consistent with our view that the nonzero probability flux 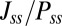are generated by the asymmetric part of the driving force.

Fig. 5.

(A) Average 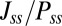(asymmetric part of driving force F) along the limit cycle with solid line (dotted line) versus the degree of asymmetry S. (B) Average 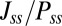versus asymmetric part of driving force F along the limit cycle. (C) The phase coherence versus the degree of asymmetry S. (D) The period τ of the oscillations versus the degree of asymmetry S.

Next, we explored how the system is affected when the degree of asymmetry of the circuit changes. The coherence is a good measure of the degree of periodicity of the time evolution (the definition of coherence is shown in SI Text). The larger value of coherence means it is more difficult to go in a wrong direction for oscillations. Fig. 5C shows the coherence increases when the degree of asymmetry S increases. Asymmetric connections ensure the coherence is good, which is crucial for the stability of the continuous memories with certain direction. For example, it is more likely to go in the wrong direction along the cycle for a less coherent oscillation, and this may cause fatal effects on the control of physiological activities or memory retrieval.

We also explored the period of the oscillation. Fig. 5D shows the period τ of oscillation decreases as the degree of asymmetry S increases. As we have discussed before, the system is mainly driven by the flux after attracted to the oscillation ring by the gradient force. Larger force 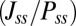leads to shorter period of a cycle. Besides, larger force means the system cannot be easily influenced by the fluctuations around. The oscillation becomes more stable as the circuit is more asymmetric. It is natural to expect that shorter period of the oscillation means higher frequency of some repetitive actions. If so, the flux is also the key of controlling factor for the frequency of some crucial physiological activities such as breath and heartbeat. However, uncovering the relation between neuronal oscillators and the much slower biochemical–molecular oscillators, such as circadian rhythms, is still a challenge.

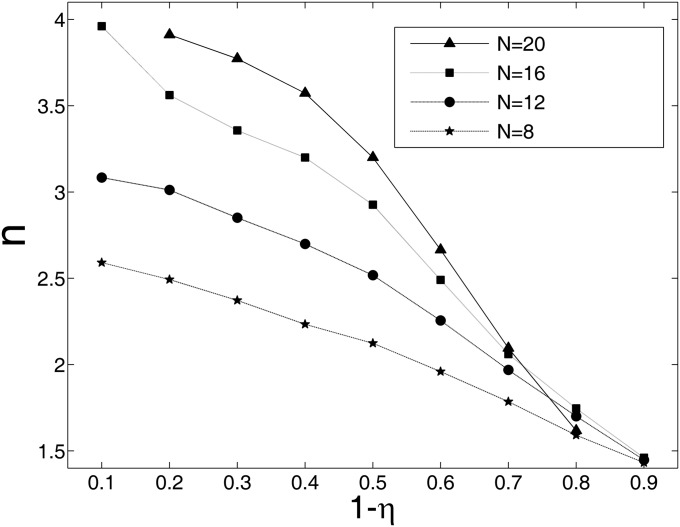
Furthermore, we explored whether the degree of asymmetry affects the capacity of memories. Here, we use a statistical method to show the memory capacity in general asymmetric neural circuits. For any special set of connections T_ij that are given randomly, we follow the trajectory of evolution with time to find its steady state and we do the calculation with more than 6,000 different initial conditions. For the generality of our results, we explored four networks with different sizes, whose number of neurons are N = 8, 12, 16, and 20, respectively. Here, we provide the results from 10,000 different random sets of connections for each network. Here, we introduce a measure of the degree of symmetry 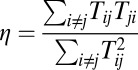to be consistent with the previous studies (41, 42). In Fig. 6, we use 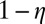to describe the degree of asymmetry. We can see that, for a certain network size, the capacity (average number of point attractors) decreases as the network connections become more asymmetric. For certain degree of asymmetry, the capacity increases as the network size increases. Our results are consistent with the previous studies (41–43). Some details of the dynamical behavior of a system with weak asymmetric are studied in ref. 44.

Fig. 6.

The memory capacity versus the degree of asymmetry for networks with different sizes. The y axis indicates the average number of point attractors.

We point out here that the flux that correlates with the asymmetric parts of the driving force for neural networks is a measure of how far away the system is from equilibrium state from our study. The presence of the flux that breaks the detailed balance of the system reduces the number of point attractors available and therefore the memory capacity of the neural networks. Larger fluxes, although not favoring the point attractors, do lead to continuous attractors such as limit cycle oscillations for storing memory in a sequential form, which means better associativity between different memories. Furthermore, previous studies have hinted that the relationship between storage capacity and associativity is determined by the neural threshold in spin system (45). Our results suggest that the flux provides a quantitative measure of the competition between storage capacity and memory associativity. We will explore more details on this in future work.

Concluding the results, we found that asymmetric synapse connections break the detailed balance and the asymmetric part of driving force becomes larger as the circuit is less symmetric. Larger asymmetric part of driving force leads to larger flux, which can generate the limit cycle. Here, we need both the potential landscape and flux to guarantee a stable and robust oscillation.

The oscillatory pattern of neural activities widely exists in our brains (8, 46–48). Previous studies have shown much evidence that oscillations play a mechanistic role in various aspects of memory including the spatial representation and memory maintenance (21, 49). The continuous attractor models have been developed to uncover the mechanism of the memory of eye position (50–52). However, understanding how sequential orders are recalled is still challenging (53, 54), because the basins of the attractions storing the memory patterns are often isolated without connections in the original symmetric Hopfield networks. Some studies indicated that certain asymmetric neural networks are capable of recalling sequences and determining the direction of the flows in the configuration space (55, 56). We believe that the flux provides the driving force for the associations among different memories. In addition, our cyclic attractors and flux may also help to understand phenomena like “earworm” that a piece of music sticks in one’s mind and plays over and over. Synchronization has been important in neuroscience (57). Recently, phase-locking among oscillations in different neuronal groups provides a new way to study the cognitive functions involving communications among neuronal groups such as attention (58). We notice that the synchronization can only happen among different groups with coherent oscillations. As shown in our study, the flux is closely related to the frequency of oscillations. We plan to apply our potential and flux landscape theory to explore the role of the flux in modulation of rhythm synchrony in the near future.

Potential and Flux Landscape for REM/Non-REM Cycle.

After exploring a general but somewhat abstract neural network model, we also apply our potential and flux landscape theory to a more realistic model describing the REM/non-REM cycle with the human sleep data (24, 25, 59). The REM sleep oscillations are controlled by the interactions of two neural populations: “REM-on” neurons [medial pontine reticular formation (mPRF), laterodorsal and pedunculopontine tegmental (LDT/PPT)] and “REM-off” neurons [locus coeruleus (LC)/dorsal raphe (DR)]. A limit cycle model of the REM sleep oscillator system is similar to the Lotka–Volterra model used to describe the interaction between prey and predator populations in isolated ecosystems (60, 61). The mPRF neurons (“prey”) are self-excited through Ach. When the activities of REM-on neurons reach a certain threshold, REM sleep occurs. Being excited by Ach from the REM-on neurons, the LC/DR neurons (“predator”) in turn inhibit REM-on neurons through serotonin and norepinephrine, and then the REM episode is terminated. With less excitation from REM-on neurons, the activities of LC/DR neurons decrease due to self-inhibition (norepinephrine and serotonin). This leads to the REM-on neurons to release from inhibition. Thereafter, another REM cycle starts.

This circuit can be described by the following equations: 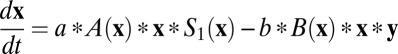and 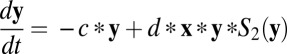. Here x and y represent the activities of REM-on and REM-off neural population, respectively. The detailed form of the interactions such as 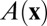and 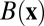is shown in SI Text.

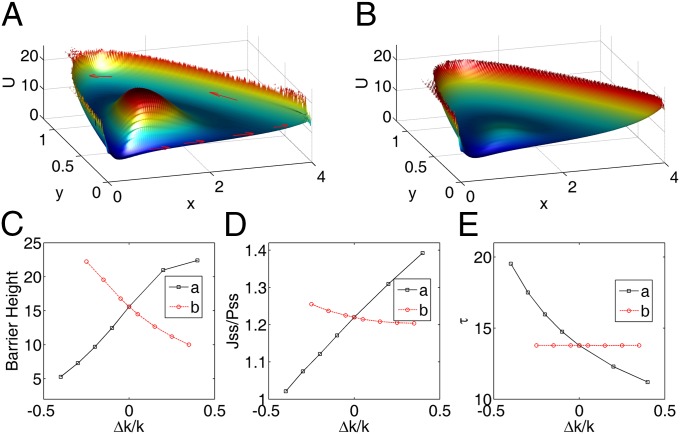
Based on the above dynamics of REM sleep system, the potential landscape and the flux of the REM/non-REM cycles are quantified. As shown in Fig. 7A, the potential landscape U has a Mexican-hat shape, and the oscillations are mainly driven by the flux indicated by the red arrows along the cycle. Because how initial conditions (circadian phase) influence the duration and intensity between the first and other REM periods, as well as how the changes of the parameters representing specific physiological situations influence the dynamics of REM oscillations have been discussed by the previous studies (24), here we mostly focused on the global stability and sensitivity of the REM oscillations using our potential and flux theory. We did a global sensitivity analysis to explore the influences of parameter changes on the stability of the system through changing the interaction strength a and b. The global stability is quantified by the landscape topography represented by the barrier height of the center island of the Mexican-hat landscape. When the center island is high, the chance of escaping from the oscillation ring valley to outside is low and the system is globally stable. We can see in Fig. 7 A and B, the potential inside the ring (the height of the center island of the Mexican hat) becomes lower when the parameter a decreases from 1 to 0.6. This means oscillations are less stable and less coherent. As we have discussed above, barrier height is a good measurement of the robustness. The effects of a and b on the barrier height are shown in Fig. 7C. We can see the increase of a makes the system more stable, and the system becomes less stable for larger b. In our model, raising the level of a means increasing the Ach release within mPRF, and the connection b is associated with the norepinephrine release (24). Much evidence has shown that Ach plays an important role in maintaining the REM sleep, and the REM sleep is inhibited when Ach decreases (62). Previous studies have also shown increased norepinephrine is ultimately responsible for REM sleep deprivation (63). Our theoretical results are consistent with these experimental data. We have also shown that the flux plays a key role for the robustness of oscillations, and Fig. 7D shows this explicitly: the barrier and the average flux along the ring is larger as a increases [the system is more stable and oscillations are more coherent (Fig. 5C)]. Both the potential landscape and the flux are crucial for the robustness of this oscillatory system. Furthermore, we investigated the effects of the parameters on the period of REM sleep cycles. We can see in Fig. 7E, the larger a leads to shorter period due to the increase of the flux as the main driving force of the oscillation on the ring valley. Previous investigators have shown the REM sleep rhythm can be shortened by repeated infusions of Ach agonist such as arecholine (64). The period almost remains unchanged as b changes because the strength of flux is affected less by the parameter b. These results showed again the flux is not only crucial for the stability of oscillations but can also provide a way to explore the period of biological rhythms. Exploring such a system may also give new insights to the understanding of the mechanism of gamma oscillations in the hippocampus where the theory and experiment have converged on how a network can store memories, because the interactions between REM-on and -off neurons share some similarities with the interactions between excitatory pyramidal cells and inhibitory interneurons in hippocampal region CA3 (65).

Fig. 7.

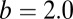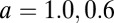(A and B) The potential landscape for and , respectively. The red arrows represent the flux. (C) The effects of parameters a and b on the barrier height. (D) The effects of parameters a and b on flux. (E) The effects of parameters a and b on period.

The application of our landscape and flux framework to the specific REM sleep cycle system provides us more information on what we can do with our general theory. By quantifying the potential landscape topology, we can measure the global stability in terms of barrier height. For oscillatory systems, both potential landscape topology and the flux are crucial for maintaining the robustness and coherence of the oscillations. From the global sensitivity analysis of the landscape topography, we are able to uncover the underlying mechanisms of neural networks and find out the key nodes or wirings of such networks for function. Our theory can be used to explain experimental observations and provide testable predictions. Furthermore, quantifying the flux can provide a new way to study the coherence and period of biological rhythms such as the REM sleep cycles and many others. This quantitative information cannot be easily obtained by previous studies. Our theory can be applied to other neural networks. For example, the flux may also provide new insights to the mechanism of the retrieval of sequential memories processes. We will return to this in future studies.

Models and Methods

To explore the nature of probabilistic potential landscape, we will study a Hopfield neural network composed of 20 model neurons (5, 6). Each neuron is dynamic, which can be described by a resistance–capacitance equation. In the circuit, the neurons connect with each other by synapses. The following set of nonlinear differential equations describes how the state variables of the neurons change with time in the circuit:

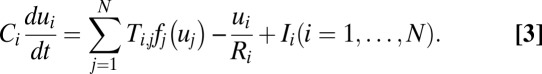This model ignores the time course of the action potential propagation and synapses’ change for simplicity; these simplifications make it possible to compute a complicated circuit with more neurons. Besides, this model reflects some important properties of biological neurons and circuits. In this paper, we use the Hill function as the form of the sigmoid and monotonic function 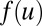. All C_i and R_i are equal to 1. For simplicity and stressing the effects of connections here, we also neglect the external current I. The strengths of connections here are all chosen randomly from 0 to 30 for general circuits. Details are given in SI Text.

To obtain the underlying potential landscape that is defined as 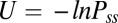, we first calculated the probability distribution of steady state. The corresponding diffusion equation describes the evolution of the system that can give the exact solution of steady-state probability. However, it is hard to solve this equation directly due to the huge dimensions. We therefore used the self-consistent mean field approximation to reduce the dimensionality (13, 14).

Generally, for a system with N variables, we have to solve a N-dimensional partial differential equation to obtain the probability 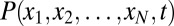. This is impossible for numerical calculation. If every variable has M values, then the dimensionality of the system becomes M^N, which is exponential in size of the system. Following a mean field approach (14, 18, 19), we divide the probability into the products of individual ones: 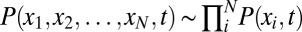and solve the probability self-consistently. Each neuron feels the interactions from other neurons as an average field. Now the degrees of freedom are reduced to 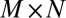. Therefore, the problem is computationally feasible due to the dimensional reduction from exponential to polynomials.

The self-consistent mean field approximation can reduce the dimensionality of the neural network for computational purposes. However, it is still often difficult solve the coupled diffusion equation self-consistently. The moment equations are usually relatively easy to get. If we have the information of all of the moments, then in principle we can uncover the whole probability distribution. In many cases, we cannot get the information of all of the moments. We then start from moment equations and make simple ansatz by assuming specific relation between moments (14, 19) or giving specific form of the probability distribution function. Here, we use Gaussian distribution as an approximation. We need two moments to specify Gaussian distribution, mean and variance.

Let us consider the situation where the diffusion coefficient D is small; the moment equations for neural networks can then be approximated as follows:

Here u, 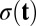, and 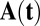are vectors and tensors representing the mean, variance, and transformation matrix, respectively, and 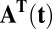is the transpose of 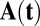. The matrix elements of A are 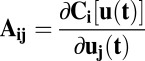. According to this equation, we can solve 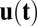and 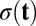for the neural networks. We consider here only the diagonal element of 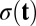from the mean field approximation. Therefore, we can obtain the evolution of distribution for one variable using the mean and variance by Gaussian approximation:

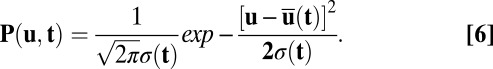The total probability is equal to the product of probability for each individual variable from the self-consistent mean field approximation. Furthermore, the weight of each point stable state is not equal for a multistable system. This indicates that the probability of some stable states are higher than others. We need to find the weight of these attractors relative to the others. We do so by calculating the percentage of each final attractor state starting from many different initial conditions. We check how many different initial states eventually go to specific basins. These quantify the weight coefficient of each stable state. Finally, once we have the steady-state probability distribution, we construct the potential landscape by adding those individual Gaussian distributions around each attractors with the relative weights collected from the multiple initial conditions.

Once we obtain the probability distribution, we solve the Lyapunov function approximatively based on linear fitting. As discussed before, the potential can be expanded on small D as 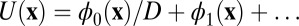. We use the data of 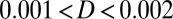to fit a line (the diffusion coefficient D versus the ). In addition, the slope of this line is the value of .

Conclusion

We have established a potential and flux landscape theory for general neural network dynamics. We quantify the probabilistic potential landscape and the corresponding Lyapunov potential landscape for a general asymmetric Hopfield neural network consisting of 20 model neurons (5, 6). We applied a self-consistent mean field approximation method to reduce the degrees of freedom of the system for solving the steady-state probability distribution that determines the probabilistic potential landscape. Based on the probabilistic potential landscape, we constructed a Lyapunov function characterizing the global stability and function of the neural circuit. The point attractor states with the highest probability represent memories stored in the circuit. We quantified the landscape topography with the barrier heights that are correlated with the escape time and used that to study the robustness of the stored memories against the fluctuations.

We quantified the potential landscape of the neural circuits without the restriction of symmetric connections. The oscillations can emerge for a neural network circuit with asymmetric synaptic connections. Being different from Hopfield’s associate memory energy function, the Lyapunov function we constructed is not restricted to the symmetric connections, and therefore the circuits can be either symmetric or asymmetric. In other words, the Lyapunov function characterizes the global behavior of not only symmetric but also the asymmetric neural networks. The values of Lyapunov function along the oscillation ring are constant.

We found that the driving force for local dynamics of neural networks can be decomposed into the gradient of the potential and the curl flux. For oscillations, the landscape attracts the neural network toward the closed ring and the probability flux drives the neural network for coherent oscillation along the closed-ring valley. We found the flux is closely associated with the asymmetric part of the driving force. The flux is crucial for the coherent oscillatory pattern of neural activities associated with repetitive continuous memories. The flux is the key to understand the synchronization among neurons and brain rhythms. Our result indicates asymmetric neural networks may store less distinct memories than a symmetric one for point attractors. However, continuous attractors that store continuous memories with certain directions can appear in general asymmetric neural circuits, but not in symmetric neural circuits. Furthermore, the flux may provide the origin and driving force for the associations among different memories.

We have applied our potential and flux landscape theory to an REM sleep cycle model (24, 25). We did a global sensitivity analysis based on the global topography of the landscape to explore the influences of key factors such as the release of Ach and norepinephrine on the stability and function of the system. Our theoretical predictions are consistent with the experimental observations. Quantifying the flux is not only crucial for exploring the robustness of neural systems but also provide a tool to study the period of biological rhythms such as the REM sleep cycles.

In the future, we hope to apply our general potential and flux landscape theory in this study to other complex neural networks.