Making sense of big data

As scientists, each of us faces the question of how best to summarize and display data. This question has become increasingly vexatious, because we now find ourselves in an age of “big data,” where technology has enabled us to measure an ever-increasing volume and variety of variables. Even so, modern attempts to answer this question began as early as the turn of the last century, with the introduction of mathematical methods designed to reduce data dimensionality. In 1901, Pearson (1) introduced principal components, which would become a mainstay of 20th century data analysis. Motivated by Gauss’s method of least squares a century earlier, Pearson showed how to solve the equations of a plane that best describes a cloud of points—a low-dimensional summary of a high-dimensional dataset. Fifty years later, Torgerson (2) proposed multidimensional scaling, which uses pairwise comparisons of similar measured variables to create a low-dimensional visualization of their overall relationship. In PNAS, Aflalo and Kimmel (3) present another advance in our understanding of how to reduce the computational costs of big data analysis methods like these in a principled manner.

Such advances open the door to crucial unanswered questions about the algebraic, geometric, and topological structures underpinning the mathematics of big data. On the practical side, we must of course acknowledge that our notion of “big” is relative as well as absolute. Pearson, with typically British understatement, touted of his approach that “the labor is not largely increased if we have a considerable number of points.” In at least one sense he remains correct: the cost of determining the principal components of a cloud of points grows like the cube of the dimension of the point cloud. There is only a weaker dependence on the actual number of points forming the cloud. By the standards of our contemporary theory of computation, this result could hardly be better.

What, then, has changed since the time of Pearson? Why are contributions such as those in the present study (3) important? First, the sheer size of modern datasets means that even this cubic cost can be prohibitive, particularly in nascent fields ranging from high-throughput biology to neuroimaging to computational social science. By comparison, the fast Fourier transform—one of the most ubiquitous mathematical methods of the last 50 y—costs only slightly (logarithmically) more than the dimension of its input data. Second, advances in mathematics have generated new answers to the question of how best to summarize and display data.

In particular, dimension reduction methods based on multidimensional scaling—because they depend on pairwise similarities between measured variables—have a computational cost that is dominated by the number of data points, rather than their dimensionality (4). Not all pairwise similarities turn out to be equally important, however. Small distances among near neighbors matter more than long-distance relationships! For this reason, we may reduce computation by strategically choosing a small subset of representative data points or landmarks and then basing our analysis solely on this sample.

Partly as a result of this insight, and following the advent of modern computing, the early 2000s witnessed a resurgence of interest in dimension reduction methods (5–9). Although their details differ, all are driven by a single essential mathematical idea: aggregating purely local relationships in a large dataset, to build a simplified picture of its global structure. This same idea underlies the present study (3). To see it, consider how we might discover that the Earth is round by measuring only short point-to-point distances along our various modern transport networks. The local structure of the Earth is flat and appears so when we travel point to point. However, by aggregating many straight-line distances from one city, airport, or seaport to the next, we would eventually uncover the Earth’s spherical structure.

The beauty of this approach is that it turns the enormity of a dataset—in this case, the points on our global transport networks—from a liability into an asset. Clearly if we sample only a few points on the Earth’s surface, the method will not work; we would have trouble determining that the Earth is indeed a sphere. However, nor do we require a measurement of every point on the Earth’s surface; as long as our transport network points are sufficiently dense and relatively uniformly spaced, so that they do not leave too many holes (Antarctica, for example!), we will be able not only to recover this global structure, but also to unfold it into a lower dimension, such as a plane.

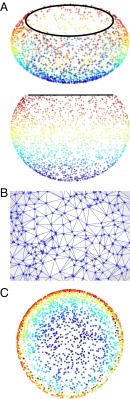
Thus we arrive at the mapmaker’s problem discussed by Aflalo and Kimmel: how best to represent a curved surface by a flat one. Mathematically, this means embedding one space into another of lower dimension while preserving important aspects of its structure. Fig. 1 illustrates the main idea by unfolding a 3D set of points that describe a “fishbowl”—a sphere with its top cap removed (Fig. 1A)—into two dimensions. Because these data exhibit nonlinear rather than linear structure, Pearson’s method of principal components—unlike its modern competitors—will fail to correctly summarize them (10).

Fig. 1.

Global structure from local information (after ref. 10). (A) Two views of a prototypical point cloud taking the shape of a 3D fishbowl. (B) A close-up of the graph that is induced by connecting neighboring points on the bottom of the fishbowl via a Delaunay triangulation. (C) A successful unfolding of the fishbowl structure into two dimensions, based on using this graph structure to approximate geodesic paths. Note how the unfolding respects the original orientation of the data points relative to one another, as denoted by their coloring.

In the context of big data analysis, we must discover the underlying structure in our data to successfully unfold it. This makes the problem addressed by Aflalo and Kimmel particularly challenging and exciting. At the same time, promising advances in pure mathematics are beginning to help us understand and categorize precisely what types of global structure can be determined from point clouds and pairwise similarities (11).

To understand how such similarities give insight into global structure, some definitions are required. Typically we model our point cloud in terms of a manifold: a structure that may curve smoothly but, like the Earth, appears from any point on its surface to be locally flat. We then infer the global geometric and topological structure of our “unknown data manifold” from local distances between points that are near to one another or otherwise similar according to an appropriate mathematical generalization of nearness.

This generality is part of the power of the approach: classical theorems by the likes of Bochner, Hilbert, Mercer, and Schmidt combine to give us very flexible recipes for constructing pairwise similarities or distances (12) beyond the purely straight-line Euclidean ones originally proposed by Torgerson. A picture of global structure then emerges by aggregating these pairwise distances or path lengths to obtain what we call a geodesic—a shortest path between two points on a curved surface. To bring this discussion back down to Earth(!), geodesics are precisely the great circle routes flown by transcontinental aircraft.

How do the authors and their predecessors obtain a picture of global structure from a great many purely local similarities? The key lies in the construction of a sparse graph to connect neighboring data points (Fig. 1B). Graphs approximate geodesics, as we have reasoned in our earlier example using the Earth’s transport networks. In fact, viewing the World Wide Web itself as a form of big data, this same principle originally inspired Internet search—in particular PageRank (13) and its now-famous notion of an “idealized Web surfer,” which led to Google’s first search engine algorithm to rank Web pages.

In the approach of Aflalo and Kimmel (3) and those that it builds on (5–9), we imagine this idealized surfer randomly visiting data points (Web pages) in proportion to the number and length of graph edges (Web links) that connect them to their neighbors. Under appropriate technical conditions, this procedure defines what is known as a Markov chain, and the Perron and Frobenius theorem, known for over 100 years, asserts that after sufficiently many random surfings, our surfer will have spent a proportion of time at each point roughly equal to the corresponding coefficient of the principal eigenvector of the underlying graph.

This eigenvector (and others like it) thus yields information on the global structure of our data. Limiting the graph to local similarities ensures that it is sparse and reduces computation while at the same time effectively linearizing the problem. We then obtain from the principal eigenvectors a low-dimensional embedding of our data (Fig. 1C); by analogy, in a Web search, they provide the global structure that allows each Web page to be ranked in importance relative to all others.

What makes the contribution of the present report (3) unique is the way in which the authors couple the idea of manifold embedding with a strategy alluded to earlier: operating only on a selected subset of data points. Aflalo and Kimmel do so by parameterizing the pairwise distance function representing geodesics on the assumed manifold in terms of the manifold’s eigenfunctions—or rather, those of its Laplace–Beltrami operator, which can be approximated by the eigenvectors of a data-derived graph in various ways, one of which we have just described.

In this way, the authors’ contribution allows us to reduce computation while respecting the global structure underlying our data. Along with the illustrative examples the authors provide from computer vision and pattern recognition, the present study (3) provides increasing evidence that it is in fact possible to reduce the computational costs of big data analysis in a principled manner. An important next step will be to make these results fully rigorous, thereby adding to our understanding of the fundamental limits of manifold embedding methods for dimensionality reduction and enabling us to quantify their accuracy–complexity tradeoffs (14). Equally important is the need to transfer this broad class of methods from conceptual to practical settings. We currently have little sense of how such techniques behave when their underlying mathematical assumptions are violated, as is inevitably the case in many practical settings of interest. To make sense of big data, we will need to determine the intellectual underpinnings of a common analysis framework and then show that this framework can achieve genuine, significant impact across a range of scientific problems.

In summary, the present study (3) exemplifies both the challenges and the opportunities inherent in 21st century data analysis. Complementary recent work in PNAS focuses on extending many of its central concepts, from the application of pairwise distances to phylogenetic inference (15) to techniques for further reducing the computational costs associated with constructing nearest-neighbor graphs (16). Recent research in PNAS also shows how families of manifold embedding techniques such as those described here can be generalized to datasets with time-dependent structure (17, 18). Together, these varied contributions serve to reinforce the timeliness and importance of the advances reported by Aflalo and Kimmel in PNAS (3), giving us a tantalizing hint as to what we may expect from the scientific future of big data.