Mechanistic analysis of the function of agonists and allosteric modulators: reconciling two-state and operational models

Abstract

Two-state and operational models of both agonism and allosterism are compared to identify and characterize common pharmacological parameters. To account for the receptor-dependent basal response, constitutive receptor activity is considered in the operational models. By arranging two-state models as the fraction of active receptors and operational models as the fractional response relative to the maximum effect of the system, a one-by-one correspondence between parameters is found. The comparative analysis allows a better understanding of complex allosteric interactions. In particular, the inclusion of constitutive receptor activity in the operational model of allosterism allows the characterization of modulators able to lower the basal response of the system; that is, allosteric modulators with negative intrinsic efficacy. Theoretical simulations and overall goodness of fit of the models to simulated data suggest that it is feasible to apply the models to experimental data and constitute one step forward in receptor theory formalism.

Linked Articles

Another recent review on allosteric modulation can be found at:

Kenakin, T (2013). New concepts in pharmacological efficacy at 7TM receptors: IUPHAR Review 2. British Journal of Pharmacology 168: 554–575. doi: 10.1111/j.1476-5381.2012.02223.x

And in this issue of BJP there is an article on a new allosteric modulator:

Newman AS, Batis N, Grafton G, Caputo F, Brady CA, Lambert J, Peters JA, Gordon J, Brain KL, Powell AD and Barnes NM (2013). 5-Chloroindole: a potent allosteric modulator of the 5-HT3 receptor. British Journal of Pharmacology 169: 1228–1238. doi: 10.1111/bph.12213

Introduction

Agonists, neutral antagonists and inverse agonists are compounds that bind the receptor at the orthosteric site, that is, the site where the endogenous hormone or neurotransmitter binds. The affinity for a common site leads to competition between orthosteric ligands if we accept that, in principle, two of these molecules cannot occupy the receptor site simultaneously. Allosteric modulators (AMs) are compounds that bind the receptors at sites other than the orthosteric site. Because of this, AMs do not compete directly with the endogenous ligand for the receptor but rather modulate its activity indirectly across a subsidiary receptor region. AMs can be classified as either positive (PAMs) or negative (NAMs) depending on whether they increase or decrease the activity of the endogenous ligand respectively. AMs can also have intrinsic efficacy by themselves, which can be either positive or negative. AMs are at the centre of present pharmaceutical research in the GPCR field because they are not so affected by the selectivity limitations between receptor subtypes for drugs acting on the orthosteric site. Moreover, the functional dependence of AMs lacking intrinsic efficacy on the presence of the endogenous ligand may present temporal and spatial activity advantages over orthosteric ligands (Christopoulos and Kenakin, 2002; Melancon et al., 2012).

Mathematical models are instrumental for the characterization of drug action. To briefly summarize, we can cite among other topics, the analysis of curve shape and its effect on the determination of agonist parameters (Black et al., 1985; Giraldo et al., 2002); the characterization of inverse agonism/neutral antagonism and the estimation of agonist affinity constants (Leff, 1995; Kenakin, 2004; Giraldo, 2010; Ehlert et al., 2011); the description of functional selectivity either by operational models (Rajagopal et al., 2011; Kenakin et al., 2012) or by mechanistic analyses involving the asymmetric/symmetric activation of receptor dimers (Rovira et al., 2010); and, particularly and directly relevant to the present study, the quantification of co-operativity effects of AMs on agonist function (Keov et al., 2011; Kenakin, 2012).

Currently, there are two main approaches for modelling the effect of allosteric modulation: a two-state-based model (Hall, 2000) and an operational-based model (Leach et al., 2007). It has been argued that most mass-action-based molecular models of allosteric modulation contain too many parameters to be fitted to real experimental data and, therefore, it is more practical to use an operational model of allosterism, which contains a minimum number of experimentally accessible parameters (Melancon et al., 2012). The pharmacological property responsible for the difference in the number of parameters is constitutive receptor activity, which is present in the two-state (Hall, 2000) but not in the operational model of allosterism developed by Leach et al. (2007). Importantly, constitutive receptor activity has recently been incorporated into the operational model of agonism and proved to be useful for the analysis of agonist effects at chemokine receptor CCR4 (Slack and Hall, 2012). Of note, an operational model of allosteric interactions including constitutive receptor activity was derived earlier (Hall, 2006) from limiting cases of the ternary complex model (De Lean et al., 1980), paving the way for subsequent simulations and analysis.

Constitutive receptor activity has increasingly become a key issue in modern GPCR pharmacology and efforts have been made to incorporate this property into mathematical analyses. However, the different approaches and modelling techniques used by authors active in the field may pose some difficulties in the understanding and application of a variety of equations. Accordingly, with the aim of clarifying mathematical aspects and singular pharmacological concepts of agonism and allosterism, a comparative analysis with a common rationale is made between two-state and operational models. To this end, an alternative derivation of the (Hall, 2006) operational model of allosterism, including constitutive receptor activity, is provided with the aim of reducing the complexity of mathematics as much as possible and facilitating a comparison between models. It is shown that two-state- and operational-based models are describing essentially the same pharmacological features, with the former providing a more microscopic focus and the latter a more macroscopic approach. Moreover, the comparative analysis reveals that there is a correspondence between the two models in each of their parameters if constitutive receptor activity is present in both. Detailed examination of the pharmacological parameters of efficacy and co-operativity in each of the models can help to better understand the complex mechanism of allosteric action and clarify concepts that are currently under debate (Canals et al., 2012).

Although we are mainly interested in the analysis of allosteric action, it may be useful to start the comparison between the two approaches from the very beginning, that is, from the analysis of agonism. For a proper comparison between the models, we tried to unify the common notation, thus, we used dissociation equilibrium constants in all cases, and the same symbols, K for agonists and M for AMs. In addition, a value of n equal to 1 was used for the operational function translating receptor occupation/stimulus into response. Fractional responses were expressed as hyperbolic rectangular (linear rational) (a + b[A])/(c + d[A]) functions, with [A] being agonist concentration, in which the coefficients may depend on the concentration of the modulator in the case of allosteric modulation.

Finally, it should be noted that all the work presented herein refers to equilibrium situations. Thus, the model equations developed are not valid for non-equilibrium situations such as, for instance, those involving measurements of calcium transients or slow dissociating prebound insurmountable antagonists.

Modelling the function of agonists

The two-state model of agonism

The two-state model was originally developed for ion channels (del Castillo and Katz, 1957; Monod et al., 1965) and later applied to receptors (Karlin, 1967; Colquhoun, 1973; Thron, 1973) (see Leff, 1995 for a detailed review). The model is based on the assumption that the receptor can reversibly interconvert between two states, one inactive, R, and the other active, R* (Figure 1A). This simple proposal has proved extremely useful for the analysis of agonist action, allowing a functional distinction between agonists, neutral antagonists and inverse agonists. It is worth mentioning that inclusion of constitutive receptor activity essentially leads to a revision of many of the classical equations in pharmacology that were based on the absence of a basal response. In this regard, the Schild and Cheng-Prusoff methods for binding affinity estimation, which were originally developed for (neutral) antagonists, have been updated for inverse agonists in the context of the two-state model (Giraldo et al., 2007). Moreover, and of especial relevance, we can cite Ehlert et al. (2011), in which an extension of receptor theory from a two-state model enabled the authors to estimate observed affinities and relative efficacies of orthosteric ligands, including agonists, neutral antagonists and inverse agonists, in receptor systems exhibiting constitutive activity.

Figure 1.

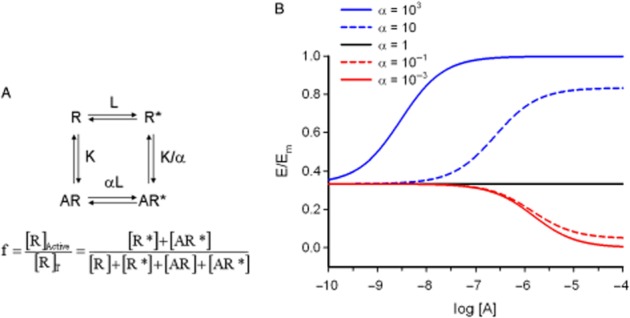
(A) The two-state model of agonism: four receptor species, two free (R, inactive and R*, active) and two ligand-bound (AR, inactive and AR*, active). Because of the thermodynamic cycle, there are four equilibrium constants but only three independent parameters, L, K and α. L measures the propensity of the free receptor to form active states; K, the affinity of the ligand A for the inactive receptor state; and α, the intrinsic efficacy of the ligand viewed either as the capacity to alter L in the complexed relative to the free receptors (horizontal equilibria) or the differential affinity for binding to inactive and active receptors (vertical equilibria). The functional response, f, is defined as the fraction of active receptors, [R]_Active/[R]_T (Appendix 1). (B) Simulation with the two-state model of agonism (Equation 1). A basal response, which depends on the L-value, is inherent to the model and ligands are agonists, neutral antagonists or inverse agonists if they increase, not change or decrease the basal response (α greater, equal or lower than 1, respectively). Concentration-effect curves for full agonist (α = 10³), partial agonist (α = 10), neutral antagonist (α = 1), partial inverse agonist (α = 10⁻¹) and full inverse agonist (α = 10⁻³). Fixed parameters: K = 10⁻⁶ and L = 0.5.

In the two-state model, the system is comprised of four receptor species, two free and two ligand-bound, whose concentrations are determined by four chemical equilibria governed by three independent constants L, K and α (Appendix 1.1). L measures the propensity of the free receptor to form active states; K, the affinity of the ligand A for the inactive receptor state; and α, the intrinsic efficacy of the ligand. As can be seen in Figure 1A, the latter property can be interpreted in one of two equivalent mechanistic hypotheses, either the induction approach (horizontal chemical equilibria: the propensity of the complexed receptors to become active relative to the free ones) or the selection approach (vertical chemical equilibria: the differential affinity of the ligand for active and inactive receptors) (Giraldo, 2004). Values of α greater, equal or lower than one, lead to an increase, no change or decrease in the proportion of active receptors respectively.

It is common to analyse the receptor function in terms of the fraction of active receptors, f, which ranges between 0 and 1 (Equation and Appendix 1.2).

(1)

Equation contains the L, K and α parameters defined above. Values of α greater, equal and lower than one, lead to asymptotic top f-values greater, equal and lower than basal reference, which are the effects defining the behaviour of agonists, neutral antagonists and inverse agonists respectively (Appendix 1.3). In addition, it can be seen that [A₅₀], the value for half-maximum f, is lower, equal and greater than K (the dissociation constant for the inactive state of the receptor) for agonists, neutral antagonists and inverse agonists respectively. It can be proved (see Appendix 1.3) that the apparent dissociation constant of the ligand matches [A₅₀].

To illustrate the model, Figure 1B displays the response profiles of five ligands, a full agonist, a partial agonist, a neutral antagonist, a partial inverse agonist and a full inverse agonist, which differ only in the value of the α parameter. Variations in α determine both the maximum or minimum responses (agonists or inverse agonists) and the potency of the ligands (location of the curves along the X-axis through the [A₅₀] quantity).

The operational model of agonism

The operational model of agonism (Black and Leff, 1983) contains two steps: the binding of an agonist to the receptor and a transducer function for the conversion of receptor occupation into response (Figure 2A and Appendix 2a). Equation 2 embodies the concentration-fractional effect relationship for the operational model of agonism, with E_m being the maximum effect of the system.

Figure 2.

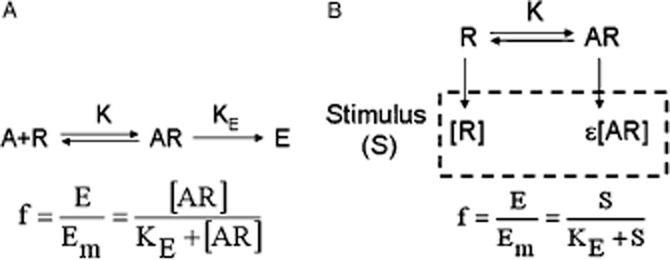
(A) The operational model of agonism. The ligand A binds the receptor R with a dissociation equilibrium constant K. A rectangular hyperbolic function f = E/E_m = [AR]/(K_E + [AR]) transduces receptor occupation into response, where K_E is the value of [AR] for half the maximum possible effect, Em. K_E is then a measure of the efficiency of transduction of receptor occupation into response (Appendix 2a). (B) The operational model of agonism including constitutive receptor activity. Constitutive receptor activity is incorporated in the model by including the concentration of free receptors within the definition of stimulus (S = [R] + ε[AR]). A rectangular hyperbolic function f = E/E_m = S/(K_E + S) transduces stimulus into response, where K_E is the value of S for half the maximum possible effect, Em, then is a measure of the efficiency of transduction of stimulus into response (Appendix 2b).

(2)

Equation 2 contains two parameters, K (the equilibrium dissociation constant of the ligand for the receptor) and τ (the operational efficacy of the system determining the asymptotic top f-value). τ is the quotient between two quantities, [R]_T (the total concentration of receptors) and K_E (an index of the intrinsic efficacy of the agonist for a given receptor). Thus, τ contains a tissue-dependent term and a molecular-dependent term. It is worth considering why a rectangular hyperbolic (E/E_m = [AR]/(K_R + [AR])) rather than a linear (E/E_m = K_R[AR]/[R]_T) relationship for the transduction of receptor occupancy into response was proposed in this model. It can be shown that if a linear relationship for the transducer function were used then the concentration for half maximum effect [A₅₀] would be equal to K, which is not consistent with agonist behaviour.

The operational model of agonism contains one parameter less than the two-state model of agonism but with a functional cost, constitutive receptor activity, and, consequently, the behaviour of an inverse agonist cannot be derived from this model. It is worth mentioning that although basal response has been included in the operational model as an ad hoc parameter in some studies (Eq. 3) (Gregory et al., 2012), this does not allow the characterization of inverse agonism because the equation cannot produce effects lower than basal.

(3)

The operational model of agonism including constitutive receptor activity

To allow the operational model of agonism to account for constitutive receptor activity, an extension of the model has recently been proposed (Slack and Hall, 2012). Constitutive receptor activity was included in the model by defining a stimulus, S, as S = [R] + ε[AR], which is related to the observed effect by the rectangular hyperbolic function E/E_m = S/(K_E + S) (Figure 2B and Appendix 2b). Equation 4 embodies the concentration-fractional effect relationship for the operational model of agonism including constitutive receptor activity.

(4)

Equation contains three parameters, χ = R_T/K_E (a parameter determining the capacity of the free receptors of generating the (basal) response), K (the equilibrium dissociation constant of the ligand for the receptor) and ε (a parameter measuring the different capacity of the ligand-bound receptor of generating a stimulus relative to the free receptor). Values of ε greater, equal or lower than one, lead to asymptotic top values greater, equal or lower than basal response, which are the effects found for agonists, neutral antagonists and inverse agonists respectively (Appendix 2b.3).

Because of the mathematical equivalence between Equations 1 and 4, identical curve profiles are obtained for the two-state and the operational model of agonism including constitutive receptor activity if the same values are used for K, χ and ε (operational) and K, L and α (two-state) respectively. Thus, Figure 1B can be described in terms of the operational model in a fashion similar to the two-state model: the variation of the ε parameter (α in the two-state model) determines the asymptotic top values of the curves.

Modelling the function of allosteric modulators

The allosteric two-state model of receptor activation

The allosteric-two state model of receptor activation (Hall, 2000) was constructed as an extension of the two-state model of agonism by including a second binding site, that for the allosteric modulator (Figure 3A). By denoting the orthosteric ligand as A and the allosteric ligand as B, the model basically consists of the following parameters: the receptor isomerization constant, responsible for constitutive receptor activity (L); the equilibrium dissociation constants of A and B for the free receptor (K and M, respectively); the binding cooperativity between A and B (γ); the intrinsic efficacies of A and B (α and β respectively); and the activation co-operativity between A and B (δ). Solving the model leads to the fraction of activated receptors (Equation ), which will eventually determine the observed pharmacological effect (Appendix 3). Consistently, the expression for f condenses to that for the two-state model of agonism if [B] = 0.

Figure 3.

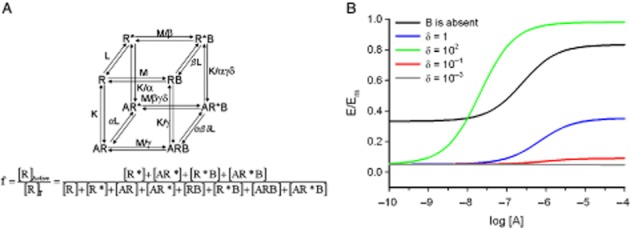
(A) The allosteric two-state model of receptor activation (adapted from Hall, 2000). Eight receptor species, two free (R, inactive and R*, active), four singly ligand-bound (AR and BR, inactive and AR* and BR*, active) and two doubly bound (ARB, inactive and AR*B, active), with A and B being the agonist and the modulator, respectively. Because of the thermodynamic cycles, there are 12 equilibrium constants but only seven independent parameters, L, K, M, γ, α, β and δ. L measures the propensity of the free receptor to form active states; K and M the affinities of A and B for the inactive free receptor, respectively; α and β, the intrinsic efficacies of A and B, respectively; γ, the binding co-operativity between A and B; and δ, the activation co-operativity between A and B. The functional response, f, is defined as the fraction of active receptors, [R]_Active/[R]_T. (B) Simulation with the allosteric two-state model of receptor activation (Equation 5). A basal response, which depends on L-value, is inherent to the model and ligands A and B are agonists, neutral antagonists or inverse agonists if they increase, not change or decrease the basal response (α or β greater, equal or lower than 1, respectively). Agonist concentration-effect curves in the absence and presence of an AM, B, with intrinsic negative efficacy. All the parameters are fixed except the activation co-operativity parameter δ, which varies among the curves. Fixed parameters: [B] = 10⁻⁴ except for the black curve for which [B] = 0, K = 10⁻⁶, M = 10⁻⁶, L = 0.5, α = 10, β = 10⁻¹, γ = 1. Variable parameter: δ = 1, δ = 10², δ = 10⁻¹, δ = 10⁻³.

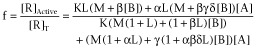(5)

Three asymptotes can be considered for f curves: basal, if [A] and [B] are 0; bottom, if [A] but not [B] is 0; and top, the limit of f as [A] increases for fixed [B]. We see (Appendix 3.3) that (i) the basal response is determined by L; (ii) the bottom depends on L (the reference value), [B] and the affinity and intrinsic efficacy of B (M and β, respectively); obviously, no parameter for [A] is present either for the binding or for activation co-operativities between B and A (γ and δ, respectively); (iii) the top contains all the parameters of the system with the exception of K because as [A]→∞ all the receptor is A-bound and the value of the agonist-receptor dissociation constant is irrelevant.

The agonistic properties of the allosteric modulator B are determined by β. If B is a pure modulator lacking intrinsic efficacy then β = 1 (bottom = basal), whereas if B is an agonist β > 1 (bottom > basal) and if it is an inverse agonist β < 1 (bottom < basal). The δ values relative to 1 will influence the effect of the modulator on the top relative to the curve with [B] = 0. In the particular case that both β and δ are equal to 1, then top = Lα/(1 + Lα) and no effect of B on the top is produced. However, if the β and δ B-dependent efficacy parameters are different from one then the top of the curve will depend on [B] and on the M and γ B-dependent affinity parameters.

To illustrate the behaviour of the model, we have performed some simulations for a particularly interesting group of ligands, that in which B bears intrinsic negative efficacy but the activation co-operativities between A and B are either neutral (δ = 1), positive (δ > 1) or negative (δ < 1) (Figure 3B). For simplicity, there is neutral binding co-operativity between A and B (γ = 1). In comparison to the reference ([B] = 0) curve, the curves including B show (i) the bottoms (left asymptote) are below the basal response because β < 1; (ii) if δ = 1, a down-shift displacement of the whole curve is obtained; (iii) if δ = 10², both a left and upward shift (A becomes more potent and efficacious to the right of a particular [A] value, that for which the curves for B either absent or present cross); it is worth noting that, in general, the maximal response will increase relative to the control when the product βδ > 1; (iv) if δ = 10⁻¹, a nearly complete blocking of receptor effect. Interestingly, for sufficiently low δ values (for instance, δ = 10⁻³) the ‘top’ of the curve (right asymptote) drops below its ‘bottom’ (left asymptote): the effect when both A and B are present is lower than when only B is present.

There are a large number of examples in the literature showing the effects of PAMs and NAMs in different receptor systems. We can cite two examples taken from class C GPCRs, MPEP acting as a NAM of the agonist quisqualate on mGlu5 receptors (Bradley et al., 2011) and CDPPB analogues acting as PAMs of glutamate on the same receptor (Chen et al., 2007). Recent reviews of allosteric modulation in A, B and C GPCR classes are presented in the following publications (Kenakin and Miller, 2010; Keov et al., 2011; Melancon et al., 2012). Typically, NAMs are found to cause rightward shifts and/or decreases in the asymptotic maximum values of agonist concentration-response curves and PAMs to do the opposite. However, and as has been shown in Figure 3B, complex behaviours resulting from intrinsic efficacies and co-operativities of a different character are obtained.

The operational model of allosterism

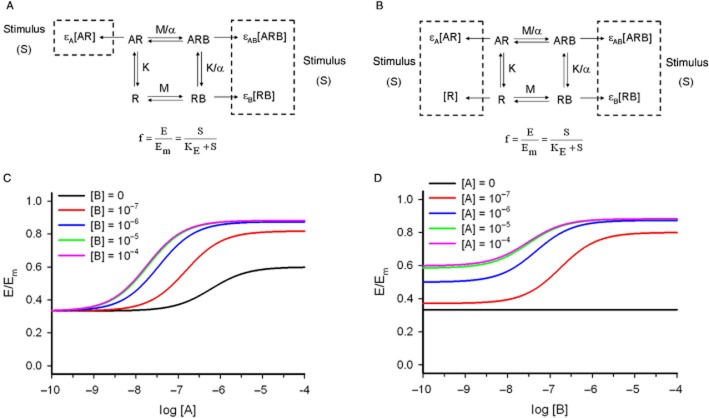
The operational model of allosterism (Ehlert, 2005; Kenakin, 2005; 2007; Price et al., 2005; Leach et al., 2007) was constructed as an extension of the operational model of agonism (Black and Leff, 1983) by including a second binding site, that for the allosteric modulator (Figure 4A and Appendix 4a). This leads to three independent dissociation constants, two for the binding of the agonist A and the allosteric modulator B to the free receptor (K and M, respectively) and a third one involving the doubly occupied receptor. The dissociation constant regulating the latter equilibrium can be expressed in terms of K or M, depending on which is the complex receptor to which the second ligand binds and a co-operativity binding factor (α). Following the rationale in Leach et al. (2007), a total stimulus S is defined as the sum of the stimulus of all the ligand-bound receptor species, S = ε_A[AR] + ε_B[RB] + ε_AB[ARB] (Appendix 4a.2). The connection between stimulus and fractional effect is made by the rectangular hyperbolic function E/E_m = S/(K_E + S).

Figure 4.

(A) The operational model of allosterism. Four receptor species, one free (R), two singly bound (AR and RB) and one doubly bound (ARB). Because of the thermodynamic cycle, there are four equilibrium constants but only three independent parameters, K, M and α. K and M measure the affinities of the agonist and the modulator for the free receptor, respectively, and α, the binding co-operativity between A and B. Stimulus is defined including only the occupied receptors (S = ε_A[AR] + ε_B[RB] + ε_AB[ARB]). A rectangular hyperbolic function f = E/E_m transduces stimulus into response, with K_E defined as in Figure 2B. (B) The operational model of allosterism including constitutive receptor activity. Constitutive receptor activity is incorporated in the model by including the concentration of free receptors within the definition of stimulus (S = [R] + ε_A[AR] + ε_B[RB] + ε_AB[ARB]). A rectangular hyperbolic function f = E/E_m transduces stimulus into response, with K_E defined as in Figure 2B. (C,D) Simulation with the operational model of allosterism, including constitutive receptor activity (Equation 8). Fixed parameters: receptor system, χ = 0.5; partial agonist A, K = 10⁻⁶, ε_A = 5; AM B, M = 10⁻⁶, ε_B = 1; agonist-modulator co-operativity parameters, α = 10, δ = 5. (C) Agonist concentration-effect curves in the absence and presence of increasing concentrations of AM B. (D) Modulator concentration-effect curves in the absence and presence of increasing concentrations of the agonist A, with the same pharmacological parameters for the system and the ligands as in Figure 4C.

Equation 6 embodies the concentration-fractional effect relationship for the operational model of allosterism. Apart from the K and M dissociation constants and α binding co-operativity, the equation includes the operational efficacies τ_A = ε_A[R]_T/K_E, τ_B = ε_B[R]_T/K_E and τ_AB = ε_AB[R]_T/K_E = βε_A[R]_T/K_E = βτ_A. As in the operational model of agonism, τ includes both molecular and tissue components. It is worth noting that ε_AB was defined as ε_AB = ε_Aβ, another possibility being ε_AB = ε_Aε_Bδ. The chosen parameters have a different meaning, β describes the ability of B to alter the signalling capacity of A (asymmetric interaction: its value would be different if it had been defined as ‘the ability of A to alter the signalling capacity of B’, that is ε_AB = ε_Bβ) whereas δ describes the activation co-operativity between A and B in the ARB complex (symmetric interaction: it does not measure the influence of one compound on the other but their mutual effects on each other). However, only the former (ε_AB = ε_Aβ) definition is satisfactory in this modelling approach in terms of curve fitting as the latter (ε_AB = ε_Aε_Bδ) leads to an additional parameter in the final equation, after intrinsic efficacies are combined with system parameters into operational (τ) efficacies.

(6)

As constitutive receptor activity is not included in the model, the effect for [A] and [B] equal to 0 (basal response) is 0 (Appendix 4a.3). To account for this issue without changing the mechanistic nature of the model, basal response has been included as an ad hoc parameter, as was also done in the operational model of agonism (Equation 7) (Bradley et al., 2011). However, as also occurred with the operational model of agonism, effects lower than the basal response are outside the scope of the model.

(7)

It is worth noting that constitutive receptor activity was not incorporated into the model because as the authors stated (Leach et al., 2007), the resultant number of parameters makes the model impractical for fitting to experimental data. Interestingly, the operational model of agonism including constitutive receptor activity (vide supra) has been applied to describe experimental data, the effects of agonists at CC-chemokine receptor 4, with overall satisfactory fitting parameters (Slack and Hall, 2012). These positive results encouraged us to incorporate constitutive receptor activity into the operational model of allosterism. This would allow us to model the behaviour of allosteric modulators with intrinsic negative agonist efficacy (inverse agonists).

The operational model of allosterism including constitutive receptor activity

To incorporate constitutive receptor activity in the operational model of allosterism, we followed a rationale similar to that adopted by Slack and Hall in the operational model of agonism (Slack and Hall, 2012): the concentration of free receptors was included in the definition of the total stimulus S, S = [R] + ε_A[AR] + ε_B[RB] + ε_AB[ARB], which, in turn, was related to the observed effect by the rectangular hyperbolic function E/E_m = S/(K_E + S) (Figure 4B and Appendix 4b.2). Equation 8 embodies the concentration-fractional effect relationship for the operational model of allosterism including constitutive receptor activity. It is worth mentioning that the equation is an alternative derivation of one previously obtained in Hall (2006). By comparing Equations 6 and 8, we see that including constitutive receptor activity leads to a model in which intrinsic efficacies (εs) are included instead of operational efficacies (τs) and a parameter (χ = [R]_T/K_E) to account for basal response appears. Ligands A and B are agonists, neutral antagonists or inverse agonists if they increase, not change or decrease the basal response (ε_A or ε_B greater, equal or lower than 1 respectively). Finally, for proper comparison with the allosteric two-state model, the intrinsic efficacy of ARB is defined as ε_AB = ε_Aε_Bδ, with δ measuring the activation co-operativity between A and B in the ARB complex.

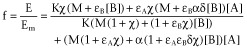(8)

Because of the mathematical equivalence between Equations 5 and 8, identical curve profiles are obtained both for the allosteric two-state model of receptor activation and the operational model of allosterism including constitutive receptor activity if the same values are used for χ, K, M, ε_A, ε_B, α and δ (operational) and L, K, M, α, β, γ and δ (two-state) respectively (see Table 1 for parameter terminology). Thus, Figure 3B can be described in terms of the operational model in a manner similar to the two-state model by the same variations of the δ parameter.

Table 1.

Parameter correspondence between the allosteric two-state model (Equation 5) and the operational model of allosterism including constitutive receptor activity (Equation 8)

Pharmacological property	Allosteric two-state model	Operational model of allosterism
Constitutive receptor activity (basal response)	L	χ
Agonist concentration	[A]	[A]
Allosteric modulator concentration	[B]	[B]
Agonist dissociation constant	K	K
Allosteric modulator dissociation constant	M	M
Intrinsic efficacy of A	α	εA
Intrinsic efficacy of B	β	εB
Binding cooperativity between A and B	γ	α
Activation cooperativity between A and B	δ	δ

Note the α used has two different meanings: intrinsic efficacy of A in the allosteric two-state model and binding co-operativity between A and B in the operational model of allosterism. This was done as a compromise to preserve consistency with conventional model parameters used in reference publications (Hall, 2000; Leach et al., 2007).

We would like you to note that, during the revision of this paper, an article was published which includes the derivation of the generalization of Equation 8 to transducer functions with arbitrary Hill coefficient (Hall, 2013). Inclusion of an exponential parameter will provide additional flexibility for fitting purposes. However, in the present study this was not considered because its use would preclude the isomorphism between two-state and operational models. This correspondence, which is the key message of this article, holds only for the important, but still specific, case of a rectangular hyperbolic (linear rational) transducer function [E/E_m = S/(K_E + S)].

To further examine the models under particular conditions, the pharmacological interactions between a partial agonist and a PAM were considered. Figure 4C shows the concentration-effect curves for a titrated partial agonist A in the absence and presence of a PAM B and Figure 4D shows the curves for a titrated PAM B in the absence and presence of the partial agonist A. In the simulations, it is supposed that B has no intrinsic efficacy (ε_B = 1). The latter property is reflected in Figure 4C in that the left asymptote does not change as [B] increases. The parameter δ > 1 means that the right asymptote increases in the presence of B making the agonist more efficacious. In addition, a leftward shift of the curves is observed resulting from both α > 1 and δ > 1.

The absence of intrinsic efficacy of B is reflected in Figure 4D in that the response for [A] = 0 is a horizontal line equal to basal response. Increasing [A] leads to sigmoid curves with left asymptotes greater than basal response.

Two-state and operational models: two sides of the same coin

Two-states and operational models including constitutive receptor activity describe the same pharmacological phenomena in a parallel manner. Two-state models circumvent the biochemical complexity to the formation of active receptor states whereas operational models include explicit functions for the transduction of stimulus into response. Thus, two-state models consider only chemical equilibria between receptor and ligand species (a molecular approach) whereas operational models take into account the transduction capabilities of the whole pharmacological system (a pharmacological tissue approach).

An examination of the equations provided by both models of agonism shows a correspondence between their parameters. In this way, we note that Equation 1 and 4 are mathematically identical. There is a correspondence between L and χ and between α and ε parameters. The ability of the free receptor to produce the pharmacological effect (basal response) is determined by L in the two-state model and by χ in the extended operational model. In the former case, L is the equilibrium constant for the interconversion between inactive and active free receptor states whereas, in the latter case, χ contains the total receptor concentration and the capability of the system of transforming stimulus into response. Furthermore, the intrinsic efficacy of the ligand (the ability of the ligand to increase or decrease the basal response) is determined by α (an index measuring the capability of the ligand-bound receptor to induce the active state relative to the free one) in the two-state model and by ε (an index measuring the capability of the ligand-bound receptor to induce a stimulus relative to the free one) in the extended operational model.

In an analogous fashion to the phenomenon of agonism, the analysis of allosterism by the two-state and operational models displays similar features. By comparing Equations 5 and 8, we see the correspondence between L and χ (basal response), α and ε_A (intrinsic efficacy of the agonist A), β and ε_B (intrinsic efficacy of the allosteric modulator B), γ and α (the binding co-operativity between A and B) and δ (the activation co-operativity between A and B). In order to make the correspondence between the two models more evident, we have used the expression ε_AB = ε_Aε_Bδ for the definition of the intrinsic efficacy of ARB instead of ε_AB = ε_Aβ, which was used in the operational model of allosterism (Leach et al., 2007). It is not merely a matter of notation because the parameters have a different meaning; β describes the ability of B to alter the signalling capacity of A whereas δ describes the activation co-operativity between A and B in the ARB complex. It is worth noting that the definition ε_AB = ε_Aε_Bδ in the operational model of allosterism including constitutive receptor activity does not increase the number of parameters. However, the same definition in the operational model of allosterism without including constitutive receptor activity (Leach et al., 2007) leads to an increase in the number of parameters when intrinsic efficacies are combined with system parameters into operational efficacies (τs), thus, making curve fitting unproductive.

As the inclusion of constitutive receptor activity in both the operational and two-state models (and the use of a symmetric activation co-operativity parameter in the former) results in mathematically comparable models, then the question arises as to whether one should be considering one model above the other. To address this issue there are two points that should be taken into consideration: (i) the left members of Equations 5 and 8 (fractional active receptor concentration and fractional functional response respectively) correspond to different properties; however, if the linear relationship [R*]/[R]_T = E/E_m is proposed then the models would become identical and (ii) operational models allow the inclusion of an exponential parameter in the transducer function, which can improve curve fitting.

Data fitting with overparameterized models

Overparameterization is a characteristic of operational models. It has been shown that neither Equation 2 nor Equation 4 can be used to directly fit a single experimental E/[A] curve if E_m, the maximum effect of the system, is unknown (Leff, 1987; Slack and Hall, 2012; Roche et al., 2013). Because of the correlation between parameters, to obtain reliable parameter estimates at least two E/[A] curves with differentiable asymptotic maximum responses are needed and this can be done by using the receptor inactivation method (Furchgott, 1966). Decreasing the number of available receptors has the effect of lowering both the τ parameter in the operational model of agonism and the χ parameter in the operational model of agonism including constitutive receptor activity. In both cases this leads to concentration-effect curves with asymptotic maximum values lower than that of the control curve.

Fitting E/[A] curve data under the operational model of agonism with constitutive receptor activity

To examine the fitting capability of Equation 4, two steps were followed: (i) data generation and (ii) curve fitting.

1. For data generation the Monte Carlo method was used; it was assumed the experimental situation we are simulating involves an agonist and a constitutively active receptor (Equation 4). A rationale similar to that employed in Slack and Hall (2012) was used and five χ parameter values were included (one for the control curve and the remaining four for those curves after receptor inactivation). The input or true theoretical values were E_m = 10, K = 10⁻⁹, ε = 10², χ₁ = 0.5, χ₂ = 0.1, χ₃ = 0.05, χ₄ = 0.01 and χ₅ = 0.005. Fifty E/[A] data sets, each composed of five χ-varied curves and log[A] ranging between −15 and −4 with an increment of 0.5, were generated by Monte Carlo method; it was assumed the pharmacological effects follow normal distributions with the proposed input value and standard deviations equal to 3% of the mean.

2. For curve fitting, a hybrid approach composed of two (global and local) optimization methods was used. Global methods are especially indicated for exploring the parameter space whereas local methods are suitable for finding a local minimum close to an initial seed point (Ashyraliyev et al., 2009). Differential Evolution (DE), an algorithm belonging to Evolutionary Computation methods and with proven efficiency over continuous spaces (Storn and Price, 1997), and gradient-based non-linear regression (NLR) were used for global and local optimizations respectively. DE and NLR were used sequentially with the aim of the former providing the latter with good quality seed points.

Table 2 includes the theoretical parameter values and the mean and standard deviations of the parameter estimates. Results show an excellent agreement between estimated and input parameters. Figure 5A shows the Monte Carlo simulated data points (mean and standard deviations for each agonist concentration) and the curves obtained from Equation 4 using the mean values of the parameter estimates. Because the ligand is a full agonist (εχ > >1 or, equivalently, εχ/(1 + εχ) ≍ 1) the asymptotic maximum response for the control curve is close to E_m. We see that the effect of receptor inactivation on the χ parameter translates into both left (free receptor) and right (saturating agonist concentration) asymptotes.

Table 2.

Theoretical values and parameter estimates for a pharmacological system described by the operational model of agonism including constitutive receptor activity (Equation 4)

Parameter	Theoretical (population mean) values	Parameter estimates Mean ± SD
Em	10	10.01 ± 0.10
log(K)	−9	−9.00 ± 0.03
log(ε)	2	2.00 ± 0.04
log(χ1)	−0.30	−0.30 ± 0.01
log(χ2)	−1	−1.00 ± 0.01
log(χ3)	−1.30	−1.30 ± 0.02
log(χ4)	−2	−2.00 ± 0.03
log(χ5)	−2.30	−2.30 ± 0.03

Fifty E/[A] data sets, each composed of five χ-varied curves and log[A] ranging between −15 and −4 with an increment of 0.5, were generated by Monte Carlo method from theoretical (population mean) values assuming normal distributions with SDs 3% of the mean. A hybrid global/local method Differential Evolution (DE)/gradient-based non-linear regression (NLR) was used for curve fitting. All parameters except E_m were assumed to be log-normally distributed. The parameter space for exploration with DE was defined as: E_m, (5,100); log(K), (−15,−3); log(ε), (0,4); log(χ₁) to log(χ₅), (−5,5). In addition, the 3-parameter DE/rand/1/bin scheme reported in (Storn and Price, 1997) was used. For a real search space of dimension D (being D the number of parameters; eight in our simulation), the population is randomly initialized with NxD vectors. In our simulations, we used the common n = 40 value. Each vector in the population is allowed to evolve by mutation and recombination operators. The mutation rate is given by a parameter F ∈ [0; 2] and the combination rate by CR ∈ [0; 1]. Following (Das and Konar, 2005), F = 0.9 and CR=0.5 parameter values were chosen for DE algorithm. All programmes were conducted under the R software environment (R Development Core Team, 2012).

Figure 5.

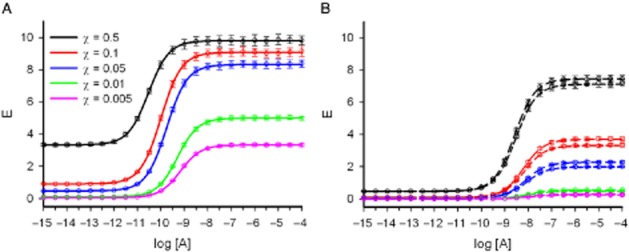
This figure illustrates a simulated experiment in which curves in Figure 5A (the allosteric modulator B is absent) are the control curves for Figure 5B (the allosteric modulator B is present). The whole set of curves of the experiment is separated into two (Figure 5A and Figure 5B) for clarity. (A) Monte Carlo data (mean ± SD) and curve fitting (solid lines) under the operational model of agonism with constitutive receptor activity. Fifty sets each composed of five χ-varied (χ = 0.5, 0.1, 0.05, 0.01 and 0.005) curves were generated for an agonist-receptor system, in which E_m = 10, K = 10⁻⁹ and ε = 10², by assuming that responses follow Equation 4 under a normal distribution with mean equal to the former theoretical values and SD equal to 3% of the mean for log[A] ranging between −15 and −4. For curve fitting a hybrid approach between a global Evolutionary Computation method and a local gradient-based non-linear approach was used (see Table 2). (B) Monte Carlo data generation and curve fitting under the operational model of allosterism with constitutive receptor activity. As in Figure 5A, 50 sets each composed of five χ-varied (χ = 0.5, 0.1, 0.05, 0.01 and 0.005) curves were generated for an agonist-receptor system with parameters equal to those in Figure 5A (E_m = 10, K = 10⁻⁹ and ε = 10²) in the presence of an allosteric modulator with M = 10⁻⁹ and ε_B = 10⁻¹ that interacts with the agonist as determined by α = 10⁻¹ and δ = 0.5, at two fixed concentrations, [B] = 10⁻⁶ and [B] = 10⁻⁴. Monte Carlo response data were generated as in Figure 5A using Equation 8 and the defined system, agonist and modulator parameters. Curve fitting was performed as in Figure 5A, keeping the parameter estimates obtained for the agonist when acting alone fixed (see Table 3): long-dashed lines [B] = 10⁻⁶ and short-dashed lines [B] = 10⁻⁴, colour code as in Figure 5A.

Fitting E/[A] curve data under the operational model of allosterism with constitutive receptor activity

To exemplify this case, we will assume that we are working with the same input data as in the previous case (the same tissue, the same receptor and the same agonist) but in the presence of an AM at a defined (10⁻⁴) concentration (Equation 8). Thus, curves in Figure 5A are the control curves for Figure 5B. The theoretical parameters of the modulator are M = 10⁻⁹, and ε_B = 10⁻¹ and those for the agonist-AM interaction α = 10⁻¹ and δ = 0.5. Monte Carlo simulated data were generated as in the previous case (distributions for pharmacological effects were assumed to be normal with standard deviations equal to 3% of the mean) and the same hybrid fitting procedure was used. On the fitting procedure, the parameter values estimated in the previous case (E_m, χ, ε_A, K) were assumed to be known and kept fixed. Of note, the NLR part of the algorithm performed badly and convergences were not achieved. Accordingly, we decided to test whether using two concentrations (10⁻⁶ and 10⁻⁴) of the AM rather than a single one could circumvent the problem. As it can be seen in Table 3, the hybrid DE-NLR approach produced excellent results. Comparison between Figures 5A and 5B shows the effect of compound B as a NAM with negative intrinsic efficacy and negative co-operativities both for binding and activation: left and right asymptotes are lowered and a right-shift displacement of the curves is observed.

Table 3.

Theoretical values and parameter estimates for a pharmacological system described by the operational model of allosterism including constitutive receptor activity (Equation 8)

Parameter	Theoretical (population mean) values	Parameter estimates Mean ± SD
Log(M)	−9	−9.01 ± 0.05
log(εB)	−1	−1.00 ± 0.01
log(α)	−1	−1.00 ± 0.02
log(δ)	−0.30	−0.30 ± 0.01

System- (E_m and χ) and agonist-dependent (K, ε_A) parameters were taken from parameter estimates in Table 2 and kept fixed [Curves from Table 2 (Figure 5A) represent the control curves from those from Table 3 (Figure 5B)]. Two concentrations (10 and 10⁻⁴) were used for the allosteric modulator. Details for Monte Carlo simulated data generation and curve fitting as described at the bottom of Table 2. All parameters were assumed log-normally distributed. The parameter space for exploration with DE was defined as: log(M), (−15,−3); log(ε_B), (−4,0); log(α), (−4,4) and log(δ), (−4,4).

Concluding remarks

A comparison between concentration-effect equations for two-state and operational models have revealed their equivalence when constitutive receptor activity is included in the operational model; and, in addition, the conceptual link present between pure molecular- and pharmacological tissue-dependent models. Importantly, the extension of the operational model of allosterism by including constitutive receptor activity allows the characterization of response curves with bottom values lower than the basal response arising from allosteric modulators with negative intrinsic efficacy.

The overparameterized nature of operational models together with the increase in the number of parameters after including constitutive receptor activity inevitably results in difficulties for the fitting to experimental curves. To solve this problem, the combination of experimental conditions (such as receptor inactivation method and examination of the system in the absence and presence of multiple concentrations of AMs) and computational strategies (such as the use of hybrids of global and local optimization methods) can be useful. To this end and because of the increasing complexity of modern pharmacology, it would be useful if experimental and theoretically-orientated pharmacologists work together in close collaboration with computer scientists in order to develop pharmacological models that are both robust and reliable.

Glossary

AM

allosteric modulator

DE

differential evolution;

NAM

negative allosteric modulator

NLR

non-linear regression

PAM

positive allosteric modulator

Appendix

1. The two-state model of agonism

The two-state model is shown in Figure 1.

1.1. The equilibrium constants of the model

Note that the quotient K/α is the equilibrium dissociation constant of the ligand to the active receptor.

1.2. The fraction of active receptors

where [R]_Active = [R*] + [AR*]

and [R]_T = [R] + [AR] + [R*] + [AR*]

1.3. Geometric descriptors of the curves

• Left asymptote (Basal response: f for [A] = 0)

• Right asymptote, the asymptotic f-value as [A] increases (Top: )

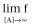• The midpoint, the [A] value for half maximum f-value

[A₅₀] is lower, equal and greater than K for agonists (α > 1), neutral antagonists (α = 1) and inverse agonists (α < 1) respectively.

• The apparent dissociation constant, a conditional constant considering all the free and ligand-bound receptor species

It can be seen that K_app and [A₅₀] are coincident.

2a. The operational model of agonism

The operational model of agonism contains a single chemical equilibrium, the binding of the ligand to the receptor.

2a.1. The equilibrium constant of the model

Note that the constant K in the operational model and in the two-state model of agonism does not define the same parameter. In the two state-model, active (R*) and inactive (R) receptor states are considered and, in this model, K defines the affinity of the agonist for the inactive receptor state. In this regard, the presence of active receptor states induced by agonist binding has been considered in a recent article and the apparent affinity constants obtained analysed (Roche et al., 2013).

2a.2. The fractional observed effect

A rectangular hyperbolic equation is proposed for the relationship between the concentration of complex receptors and the observed effect.

With 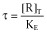and [R]_T = [R] + [AR]

2a.3. Geometric descriptors of the curves

• Left asymptote (Basal response: f for [A] = 0)

The receptor does not have constitutive activity. The model cannot describe the function of inverse agonists.

• Right asymptote, the asymptotic value as [A] increases (Top: )

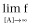τ defines the operational efficacy of the ligand, as greater is τ greater is the asymptotic top values of the agonists. Full agonists yield top values close to 1 whereas partial agonists produce top values significantly lower than 1.

• The midpoint, the [A] value for half maximum effect

[A₅₀] is lower than K and as more efficacious the agonist is greater is the difference between K and [A₅₀].

2.b. The operational model of agonism including constitutive receptor activity

The model contains a single chemical equilibrium, the binding of the ligand to the receptor.

2b.1. The equilibrium constant of the model

2b.2. The fractional observed effect

A receptor stimulus is defined which includes the concentration of both the free and the ligand-bound receptors.

A rectangular hyperbolic equation is proposed for the relationship between the receptor stimulus and the observed effect.

With 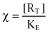and [R]_T = [R] + [AR]

2b.3. Geometric descriptors of the curves

• Left asymptote (Basal response: f for [A] = 0)

• Right asymptote, the asymptotic f-value as [A] increases (Top: )

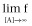• The midpoint, the [A] value for half maximum effect

[A₅₀] is lower, equal and greater than K for agonists (ε > 1), neutral antagonists (ε = 1) and inverse agonists (ε < 1) respectively.

3. The allosteric two-state model of receptor activation

The allosteric two-state model of receptor activation is shown in Figure 2.

3.1. The equilibrium constants of the model

3.2. The fraction of active receptors

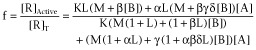where [R]_Active = [R*] + [AR*] + [R*B] + [AR*B]

and [R]_T =[R] + [AR] + [RB] + [ARB] + [R*] + [AR*] + [R*B] + [AR*B]

3.3. Geometric descriptors of the curves

• Left asymptote in the absence of A and B (Basal response: f for [A] = 0 and [B] = 0)

• Left asymptote in the absence of A (Bottom: f for [A] = 0)

• Right asymptote, the asymptotic f-value as [A] increases (Top: )

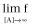It is worth noting that if γ = 0, that is, [ARB] = [AR*B] = 0, then 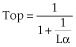. Note that this is an extreme negative co-operativity situation resulting in mutually exclusive binding of the ligands.

• The midpoint, the [A] value for half maximum effect

4.a. The operational model of allosterism

The operational model of allosterism (Leach et al., 2007) contains four chemical equilibria, corresponding to the binding of the agonist or the allosteric modulator to the free receptor or to a receptor occupied by the other compound. However, because of thermodynamic closure, there are only three independent equilibrium constants.

4a.1. The equilibrium constants of the model

4a.2. The fractional observed effect

The individual stimuli are given by

S_AR = ε_A[AR]. S_RB = ε_B[RB] and S_ARB = ε_AB[ARB]

And the total stimulus by

A rectangular hyperbolic equation is proposed for the relationship between the total stimulus and the observed effect.

With

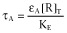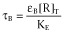, and 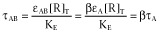and [R]_T = [R] + [AR] + [RB] + [ARB]

4a.3. Geometric descriptors of the curves

• Left asymptote in the absence of A and B (Basal response: f for [A] = 0 and [B] = 0)

• Left asymptote in the absence of A (Bottom: f for [A] = 0)

• Right asymptote, the asymptotic f-value as [A] increases (Top: )

• The midpoint, the [A] value for half maximum effect

4.b. The operational model of allosterism including constitutive receptor activity

As in the operational model of allosterism (Leach et al., 2007) included in Appendix 4a, the operational model of allosterism including constitutive receptor activity contains four chemical equilibria, corresponding to the binding of the agonist or the allosteric modulator to the free receptor or to a receptor occupied by the other compound.

4b.1. The equilibrium constant of the model

The same equations as in Appendix 4a.1.

4b.2. The fractional observed effect

The individual stimuli are given by

S_R = [R], S_AR = ε_A[AR], S_RB = ε_B[RB] and S_ARB = ε_AB[ARB]

In comparison with Appendix 4a.2, the free receptor produces a stimulus with an intrinsic efficacy of 1.

And the total stimulus by

A rectangular hyperbolic equation is proposed for the relationship between the total stimulus and the observed effect.

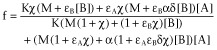With 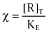, ε_AB = ε_Aε_Bδ and [R]_T = [R] + [AR] + [RB] + [ARB]

4b.3. Geometric descriptors of the curves

• Left asymptote in the absence of A and B (Basal response: f for [A] = 0 and [B] = 0)

  

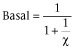
• Left asymptote in the absence of A (Bottom: f for [A] = 0)

  

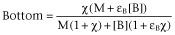
• Right asymptote, the asymptotic f-value as [A] increases (Top: )

  

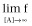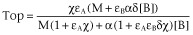
• The mid-point, the [A] value for half maximum effect

Conflict of interest

None.