Calculated treatment

Abstract

Mathematical modelling linked with patient data suggests that combination therapy is more effective than sequential treatment at preventing drug resistance in cancer. This predictive approach may pave the way for personalized therapies.

In a study published in eLIFE, Bozic et al.¹ use a mathematical approach to examine tumour evolution and response to chemotherapy. In one example, they describe a patient who had the skin cancer melanoma characterized by an estimated tumour burden of 9.8 × 10¹⁰ cells and 8 metastatic lesions. Their modelling predicts a 0% chance of disease control using a single drug, but that the likelihood of successful treatment could rise to 88% during combined therapy with two drugs. The approach offers a brave, quantitative look at designing targeted therapy for cancer.

The search for cancer treatments has traversed a long and thorny path, with more failures and disappointments than glimpses of success. A major breakthrough was achieved with the development of a drug called imatinib in the 1990s. This inhibitor of tyrosine kinase enzymes showed breathtaking success for treating chronic myelogenous leukaemia (CML). Imatinib and other small-molecule inhibitors ‘recognize’ and attack cancer cells, but spare normal cells, thereby reducing side effects compared with traditional chemotherapy. Since the discovery of imatinib, dozens of other such inhibitors have been developed for treating different cancers. However, the initial excitement surrounding these drugs was tempered by the appearance of drug resistance — the phenomenon in which disease returns a few months after initial treatment success².

Cancer is a process of Darwinian evolution played out in a particular organ. Normal cells divide and die, and each division brings a small chance of genetic change. Most such mutations are deleterious, and the cells die without leaving offspring, but some confer new properties that promote growth or survival and can lead to cancer. The greatest challenge for drugs targeted at such cells is the further evolution of mutations that confer drug resistance. Combining multiple drugs that have distinct mechanisms of action might provide a solution to this problem. The concept of a ‘drug cocktail’ was introduced in 1996 in the context of treating AIDS. There, the emergence of viral strains resistant to single drug treatments rendered all previous attempts to control the disease unsuccessful. Viral evolution in a patient is conceptually similar to the evolution of cancer cells, so similar treatment strategies might work well for both diseases.

Current common practice for treating cancers with small-molecule inhibitors is to administer the agents sequentially, starting with a ‘first-line’ drug and switching to ‘second-line’ therapies if the tumour relapses. Bozic et al. assessed the effectiveness of this approach using sophisticated mathematical techniques and data from patients with melanoma or with pancreatic or colorectal cancers. They convincingly demonstrate that a sequential strategy “precludes any chance for cure”, even in the best-case scenario in which no single mutants confer resistance to both drugs. However, they show that simultaneously combining two or more drugs can provide much-needed hope for patients.

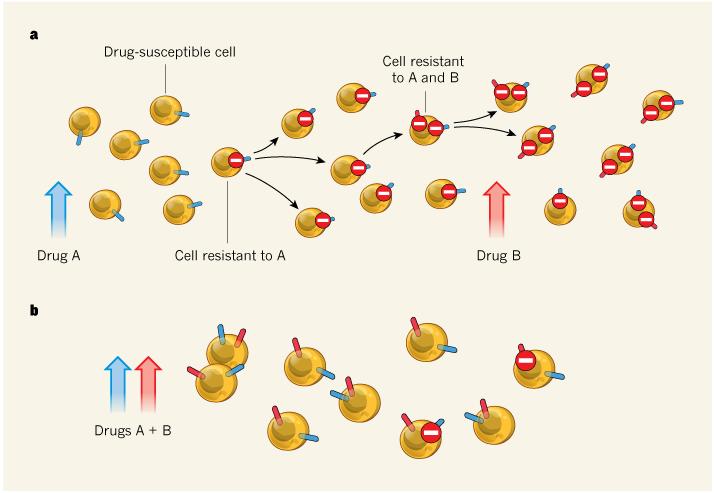
As demonstrated last year³, drug-resistant mutants typically exist at low levels in tumours before the beginning of treatment. Treatment with a single drug gives a competitive advantage to mutants resistant to that drug, such that by the time of the switch to a second-line therapy, there is a high chance that a mutant that is also resistant to the second drug (a doubly resistant mutant) has already emerged (Fig. 1). But combination therapy eliminates cells that are singly resistant to either drug and therefore — because the likelihood of a doubly mutated cell emerging in such a population is low — greatly increases the chance of success.

Figure 1. Single-drug versus combination therapy.

a, During therapy with one drug alone, a cell that acquires a mutation that confers resistance to that drug will be at a proliferative advantage. By the time this is recognized and treatment with a second drug is started, it is likely that a cell resistant to both drugs will already have emerged. b, Starting therapy with both drugs simultaneously means that cells acquiring single resistance will be immediately eliminated by the other drug. Bozic et al.¹ use mathematical modelling to show that this approach increases the chance of effective treatment.

The greatest obstacle for combination treatments is the phenomenon of cross-resistance, in which a single mutation confers resistance to more than one drug. But even if such mutants are generated, the authors estimate that combination treatment can be beneficial in some cases, whereas single-drug and sequential strategies offer no hope.

Previous mathematical analyses have also shown⁴ that cyclic treatments are ineffective compared with combination treatments, and have led to the proposal⁵ that a combination of three anticancer drugs would be needed to treat CML. It has also already been argued⁶ that, even in the presence of cross-resistant mutations in CML, combination treatments give patients a better chance of cure than do single-drug treatments. And in-vitro studies⁷ that compared CML cells treated with one small-molecule inhibitor with those treated with a combination of two or three demonstrated that the combined therapy suppressed cell proliferation more effectively. But with Bozic and colleagues’ success in synthesizing theoretical and experimental methods and applying the analysis to solid tumours, these modelling studies have taken a leap forward.

Even more significantly, the authors’ paper outlines a roadmap for future personalized therapies, by showing that specific parameters for a patient can be measured and used in a mathematical model to calculate the probability of treatment success and to design the best possible treatment strategy. The authors extracted tumour parameters — including its size at presentation, cellular division and death rates, and changes in the associated kinetic parameters following treatment — from 20 patients with melanoma who were treated with the small-molecule inhibitor vemurafenib. With this information, they were able to predict the most likely outcome of single, dual and triple therapies for each patient.

There is a bright future for this approach. As new drugs and more information on the exact mechanisms of drug action become available, the model can be iteratively improved. For example, there is currently a strong research focus on cellular plasticity, the heterogeneity of cells within a tumour and the role of cancer stem cells. But it is not known how the presence of cancer cells with differing properties affects a tumour’s susceptibility to targeted treatments. Moreover, the evolutionary costs of resistance for a cell have not been quantified in most cases, nor have mutation rates for molecular changes of various kinds, although estimates have been made for the number of mutations conferring resistance to certain drugs in CML^7,8. The potential complications of drug cocktails — including toxicity and undesirable drug interactions — must also be taken into account. But the overall message is loud and clear: mathematics can help to calculate treatment strategies, and the best hope so far lies in combination therapies.