Significance
Intuition suggests that many interesting phenomena in physics, chemistry, and materials science are “short-sighted”—that is, perturbation in a small spatial region only affects its immediate surroundings. In mathematical terms, near-sightedness is described by functions of finite range. As an example, the so-called Wannier functions in quantum mechanics are localized functions, which contain all the information about the properties of the system, including its spectral properties. This work’s main research objective is to develop theory and numerical methods that can systematically derive functions that span the energy spectrum of a given quantum-mechanical system and are nonzero only in a finite spatial region. These ideas hold the key for developing efficient methods for solving partial differential equations of mathematical physics.
Abstract
This article describes a general formalism for obtaining spatially localized (“sparse”) solutions to a class of problems in mathematical physics, which can be recast as variational optimization problems, such as the important case of Schrödinger’s equation in quantum mechanics. Sparsity is achieved by adding an 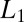 regularization term to the variational principle, which is shown to yield solutions with compact support (“compressed modes”). Linear combinations of these modes approximate the eigenvalue spectrum and eigenfunctions in a systematically improvable manner, and the localization properties of compressed modes make them an attractive choice for use with efficient numerical algorithms that scale linearly with the problem size.
regularization term to the variational principle, which is shown to yield solutions with compact support (“compressed modes”). Linear combinations of these modes approximate the eigenvalue spectrum and eigenfunctions in a systematically improvable manner, and the localization properties of compressed modes make them an attractive choice for use with efficient numerical algorithms that scale linearly with the problem size.
Significant progress has been recently achieved in a variety of fields of information science using ideas centered around sparsity. Examples include compressed sensing (1, 2), matrix rank minimization (3), phase retrieval (4), and robust principal component analysis (5), as well as many others. A key step in these examples is use of a variational formulation with a constraint or penalty term that is an 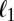 or related norm. A limited set of extensions of sparsity techniques to physical sciences and partial differential equations (PDEs) have also appeared recently, including numerical solution of PDEs with multiscale oscillatory solutions (6) and efficient materials models derived from quantum mechanics calculations (7). In all of these examples, sparsity is for the coefficients (i.e., only a small set of coefficients are nonzero) in a well-chosen set of modes (e.g., a basis or dictionary) for representation of the corresponding vectors or functions. In this article, we propose a use of sparsity-promoting techniques to produce “compressed modes” (CMs)—modes that are sparse and localized in space—for efficient solution of constrained variational problems in mathematics and physics.
or related norm. A limited set of extensions of sparsity techniques to physical sciences and partial differential equations (PDEs) have also appeared recently, including numerical solution of PDEs with multiscale oscillatory solutions (6) and efficient materials models derived from quantum mechanics calculations (7). In all of these examples, sparsity is for the coefficients (i.e., only a small set of coefficients are nonzero) in a well-chosen set of modes (e.g., a basis or dictionary) for representation of the corresponding vectors or functions. In this article, we propose a use of sparsity-promoting techniques to produce “compressed modes” (CMs)—modes that are sparse and localized in space—for efficient solution of constrained variational problems in mathematics and physics.
Our idea is motivated by the localized Wannier functions developed in solid state physics and quantum chemistry. We begin by reviewing the basic ideas for obtaining spatially localized solutions of the independent-particle Schrödinger’s equation. For simplicity, we consider a finite system with N electrons and neglect the electron spin. The ground state energy is given by 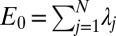 , where
, where 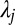 are the eigenvalues of the Hamiltonian,
are the eigenvalues of the Hamiltonian, 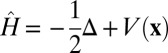 , arranged in increasing order and satisfying
, arranged in increasing order and satisfying 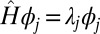 , with
, with 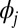 being the corresponding eigenfunctions. This can be recast as a variational problem requiring the minimization of the total energy subject to orthonormality conditions for wave functions:
being the corresponding eigenfunctions. This can be recast as a variational problem requiring the minimization of the total energy subject to orthonormality conditions for wave functions:
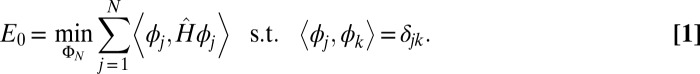 |
Here, 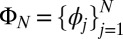 and
and 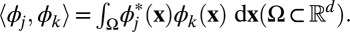
In most cases, the eigenfunctions 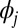 are spatially extended and have infinite support—that is, they are “dense.” This presents challenges for computational efficiency [as the wave function orthogonalization requires
are spatially extended and have infinite support—that is, they are “dense.” This presents challenges for computational efficiency [as the wave function orthogonalization requires 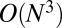 operations, dominating the computational effort for
operations, dominating the computational effort for 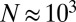 electrons and above] and is contrary to physical intuition, which suggests that the screened correlations in condensed matter are usually short-ranged (8). It is well understood that the freedom to choose a particular unitary transformation (“subspace rotation”) of the wave functions
electrons and above] and is contrary to physical intuition, which suggests that the screened correlations in condensed matter are usually short-ranged (8). It is well understood that the freedom to choose a particular unitary transformation (“subspace rotation”) of the wave functions 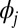 can be used to define a set of functions that span the eigenspace of
can be used to define a set of functions that span the eigenspace of 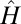 , but are spatially localized or sparse. Methods for obtaining such functions have been developed in solid state physics and quantum chemistry, where they are known as Wannier functions (9).
, but are spatially localized or sparse. Methods for obtaining such functions have been developed in solid state physics and quantum chemistry, where they are known as Wannier functions (9).
Mathematically, the Wannier functions are obtained as a linear combination of the eigenfunctions:
 |
where the subspace rotation matrix U is unitary, 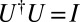 . Currently, the most widely used approach to finding
. Currently, the most widely used approach to finding 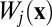 is the one proposed in ref. 10 for calculating maximally localized Wannier functions (MLWFs). This approach starts with the precalculated eigenfunctions
is the one proposed in ref. 10 for calculating maximally localized Wannier functions (MLWFs). This approach starts with the precalculated eigenfunctions 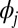 and determines
and determines 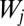 by minimizing the second moment:
by minimizing the second moment:
where 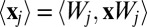 . More recently, a method weighted by higher degree polynomials has been discussed in ref. 11. Although this approach works reasonably well for simple systems, constructing optimally localized real-valued Wannier functions is often difficult because the minimization problem (Eq. 3) is nonconvex and requires a good starting point to converge to the global minimum. Another difficulty is that when the resulting MLWFs are used to construct efficient numerical algorithms, they need to be cut off “by hand,” which can result in significant numerical errors when the MLWFs are calculated “on the fly” and their range is not known in advance. It would be highly desirable to devise an approach that does not require the calculation of the eigenfunctions and would converge to localized functions, while simultaneously providing a variational approximation to the total energy
. More recently, a method weighted by higher degree polynomials has been discussed in ref. 11. Although this approach works reasonably well for simple systems, constructing optimally localized real-valued Wannier functions is often difficult because the minimization problem (Eq. 3) is nonconvex and requires a good starting point to converge to the global minimum. Another difficulty is that when the resulting MLWFs are used to construct efficient numerical algorithms, they need to be cut off “by hand,” which can result in significant numerical errors when the MLWFs are calculated “on the fly” and their range is not known in advance. It would be highly desirable to devise an approach that does not require the calculation of the eigenfunctions and would converge to localized functions, while simultaneously providing a variational approximation to the total energy 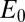 .
.
In this article, we propose a method to create a set of localized functions 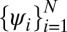 , which we call CMs, such that
, which we call CMs, such that 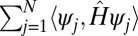 approximates
approximates 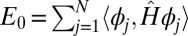 . Our idea is inspired by the
. Our idea is inspired by the 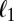 regularization used in compressive sensing. As a convex relaxation of
regularization used in compressive sensing. As a convex relaxation of 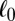 regularization,
regularization, 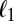 regularization is commonly used for seeking sparse solutions for the underdetermined problem
regularization is commonly used for seeking sparse solutions for the underdetermined problem 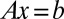 (2, 12). Motivated by advantages of the
(2, 12). Motivated by advantages of the 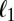 regularization for the sparsity in the discrete case, we propose a modification of the objective functional given by Eq. 1, which can immediately obtain functions with compact support and calculate approximate total energy “in one shot,” without the need to calculate eigenfunctions. This is accomplished by introducing an
regularization for the sparsity in the discrete case, we propose a modification of the objective functional given by Eq. 1, which can immediately obtain functions with compact support and calculate approximate total energy “in one shot,” without the need to calculate eigenfunctions. This is accomplished by introducing an 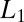 regularization of the wave functions:
regularization of the wave functions:
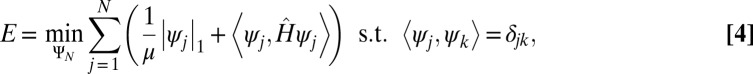 |
where 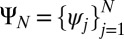 and the
and the 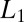 norm is defined as
norm is defined as 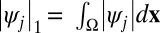 . For simplicity, we are requiring that the wave functions
. For simplicity, we are requiring that the wave functions 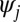 are real; generalization to complex-valued wave functions, required to handle relativistic effects, is straightforward. The parameter μ controls the tradeoff between sparsity and accuracy: larger values of μ will give solutions that better minimize the total energy at the expense of more extended wave functions, whereas a smaller μ will give highly localized wave functions at the expense of larger errors in the calculated ground state energy. Due to the properties of the
are real; generalization to complex-valued wave functions, required to handle relativistic effects, is straightforward. The parameter μ controls the tradeoff between sparsity and accuracy: larger values of μ will give solutions that better minimize the total energy at the expense of more extended wave functions, whereas a smaller μ will give highly localized wave functions at the expense of larger errors in the calculated ground state energy. Due to the properties of the 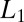 term, the functions that minimize Eq. 4 will have compact support. In contrast to other approaches that use manually imposed cutoff distances, the main advantage of our scheme is that one parameter μ controls both the physical accuracy and the spatial extent, while not requiring any physical intuition about the properties of the solution. In other words, the wave functions
term, the functions that minimize Eq. 4 will have compact support. In contrast to other approaches that use manually imposed cutoff distances, the main advantage of our scheme is that one parameter μ controls both the physical accuracy and the spatial extent, while not requiring any physical intuition about the properties of the solution. In other words, the wave functions 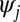 are nonzero only in those regions that are required to achieve a given accuracy for the total energy and are zero everywhere else. Furthermore, due to the fact that exponentially localized Wannier functions are known to exist, the solution to Eq. 4 will provide a good approximation to the true total energy of the system (in fact, it converges to
are nonzero only in those regions that are required to achieve a given accuracy for the total energy and are zero everywhere else. Furthermore, due to the fact that exponentially localized Wannier functions are known to exist, the solution to Eq. 4 will provide a good approximation to the true total energy of the system (in fact, it converges to 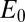 as
as 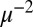 ).
).
As a major contribution in this article, we propose localized CMs using an 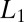 regularized variational formula. In addition, we propose a numerical algorithm to solve the proposed nonconvex problem.
regularized variational formula. In addition, we propose a numerical algorithm to solve the proposed nonconvex problem.
Variational Model for Compressed Modes
Free-Electron Case.
Consider a 1D free-electron case defined on 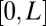 with periodic boundary conditions. Namely, the Schrödinger operator is
with periodic boundary conditions. Namely, the Schrödinger operator is 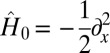 . It is clear that
. It is clear that 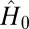 has eigenfunctions
has eigenfunctions  with the corresponding eigenvalues
with the corresponding eigenvalues 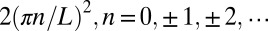 . With a unitary transformation
. With a unitary transformation 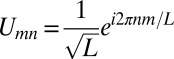 , one can construct quasi-localized orthonormal functions as
, one can construct quasi-localized orthonormal functions as
 |
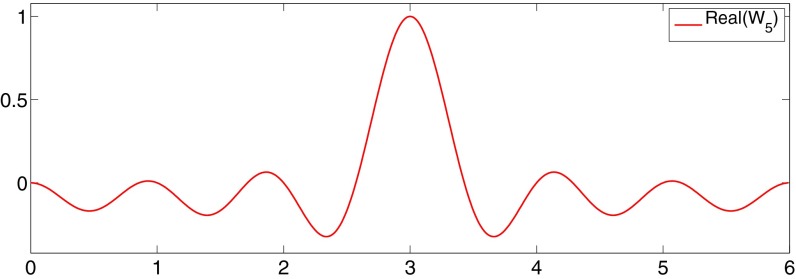
Fig. 1 illustrates the real part of one of the resulting quasi-localized functions obtained from the above unitary transformation. It is evident that the resulting 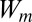 are not even exponentially localized, as expected for metallic systems with continuous energy spectrum at zero temperature (8).
are not even exponentially localized, as expected for metallic systems with continuous energy spectrum at zero temperature (8).
Fig. 1.
A quasi-localized Wannier function for 1D Laplace operator.
As an example, we can analytically check that the 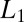 regularization introduced in Eq. 4 can localize the resulting functions. Let’s again consider the 1D free-electron model defined on
regularization introduced in Eq. 4 can localize the resulting functions. Let’s again consider the 1D free-electron model defined on 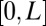 with the Schrödinger operator
with the Schrödinger operator 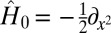 . Then the lowest mode satisfies:
. Then the lowest mode satisfies:
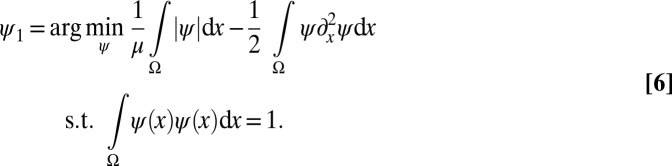 |
The solution of the above minimization problem will be a sparse solution—that is, the Dirac delta function when 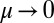 —and will approach the first eigenfunction of
—and will approach the first eigenfunction of 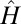 when
when 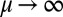 . Intuitively, we expect to be able to express the solution of Eq. 6 as an approximation to a truncated diffusion of Dirac delta function via the Schrödinger operator
. Intuitively, we expect to be able to express the solution of Eq. 6 as an approximation to a truncated diffusion of Dirac delta function via the Schrödinger operator 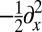 , which is a compactly supported function. Indeed, the Euler–Lagrange equation corresponding to Eq. 6 is:
, which is a compactly supported function. Indeed, the Euler–Lagrange equation corresponding to Eq. 6 is:
 |
If we further assume that 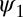 is symmetric around
is symmetric around 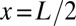 , the solution of Eq. 6 is:
, the solution of Eq. 6 is:
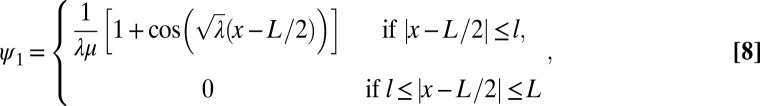 |
where 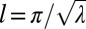 and
and 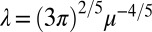 . Here
. Here 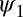 has compact support
has compact support 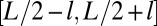 if μ is small enough satisfying
if μ is small enough satisfying 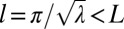 . Note that
. Note that 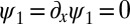 and
and 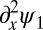 has a jump of
has a jump of 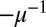 at the boundary
at the boundary 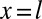 of the support of
of the support of 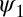 , which are all consistent with Eq. 7. From this simple 1D example, it is clear that
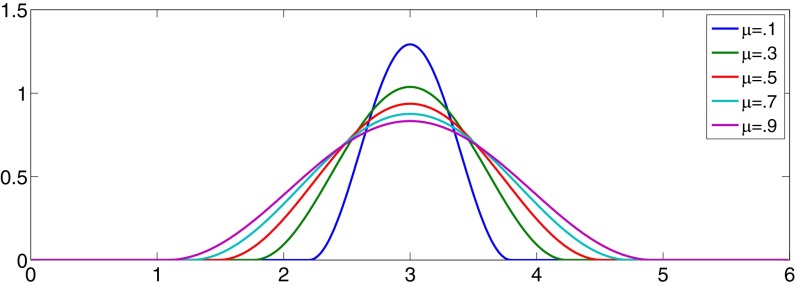
, which are all consistent with Eq. 7. From this simple 1D example, it is clear that 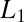 regularization can naturally truncate solutions to the variational problem given by Eq. 6. Moreover, we also observe that the smaller μ will provide a smaller region of compact support. Fig. 2 shows
regularization can naturally truncate solutions to the variational problem given by Eq. 6. Moreover, we also observe that the smaller μ will provide a smaller region of compact support. Fig. 2 shows 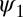 for different values of μ.
for different values of μ.
Fig. 2.
Theoretical 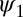 in the 1D free-electron model (Eq. 6) for different values of μ.
in the 1D free-electron model (Eq. 6) for different values of μ.
The 1D solution Eq. 8 can be generalized to dimension 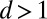 , as:
, as:
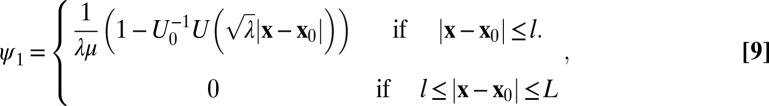 |
in which 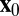 is the center of the cube
is the center of the cube 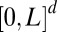 and
and 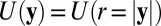 (for
(for 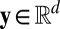 ) is the solution of
) is the solution of  —that is:
—that is:
and 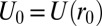 ,
, 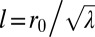 ,
,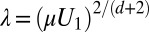 . Here
. Here 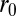 is the smallest (nonegative) solution of
is the smallest (nonegative) solution of 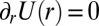 and
and 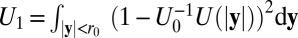 in which
in which 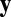 is in
is in 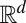 . For
. For 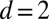 ,
, 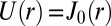 is the 0-th Bessel function of the first kind, and for
is the 0-th Bessel function of the first kind, and for 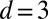 ,
, 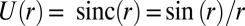 .
.
Generalization to Nonzero Potential.
The simple free-electron example inspires us to consider 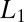 regularization of the wave functions proposed in Eq. 4 for a general Schrödinger operator
regularization of the wave functions proposed in Eq. 4 for a general Schrödinger operator 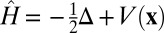 defined on
defined on 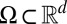 .
.
For definition 1, we call 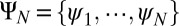 , defined in the variational model Eq. 4, the first N CMs of the Schrödinger operator
, defined in the variational model Eq. 4, the first N CMs of the Schrödinger operator 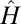 .
.
By analogy with the localized Wannier functions described in the opening paragraphs, we expect that the CMs have compact support and can be expressed as orthonormal combinations of the eigenmodes of the original Schrödinger operator. In other words, let 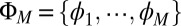 be the first M eigenfunctions of
be the first M eigenfunctions of 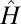 satisfying:
satisfying:
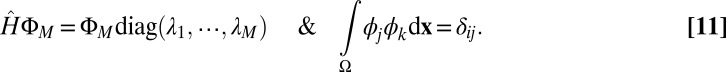 |
We formulate the following conjecture to describe the completeness of the CMs. Given 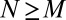 , consider the
, consider the 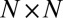 matrix
matrix 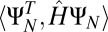 with the
with the 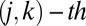 entry defined by
entry defined by 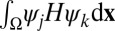 and let
and let 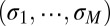 be its first M eigenvalues; then:
be its first M eigenvalues; then:
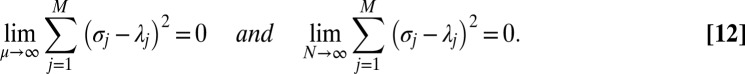 |
Numerical Algorithms
To numerically compute the proposed CMs, we consider the system on a domain 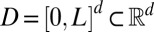 with periodic boundary conditions and discretize the domain D with n equally spaced nodes in each direction. Then, the variational formula (Eq. 4) for the first N CMs can be reformulated and discretized as follows:
with periodic boundary conditions and discretize the domain D with n equally spaced nodes in each direction. Then, the variational formula (Eq. 4) for the first N CMs can be reformulated and discretized as follows:
 |
in which 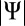 is the
is the 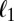 norm of the matrix
norm of the matrix 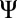 .
.
We solve this optimization problem by splitting orthogonality constraint (SOC) using the algorithm proposed in ref. 13. By introducing auxiliary variables 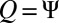 and
and 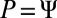 , the above problem Eq. 6 is equivalent to the following constrained problem:
, the above problem Eq. 6 is equivalent to the following constrained problem:
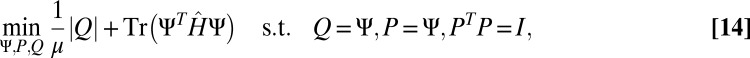 |
which can be solved by the SOC algorithm based on split Bregman iteration (14–16).
For algorithm 1, initialize 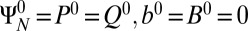 ; while “not converged” do:
; while “not converged” do:
1)
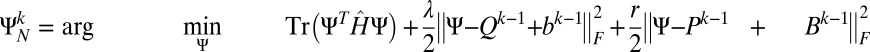
2)
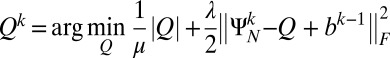
3)
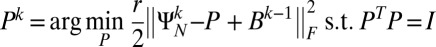
4)
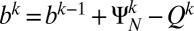
5)
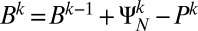 .
.
Solutions to the minimization subproblems 1–3 can be expressed as follows:
and
where 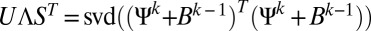 and the “Shrink” (or soft-threshholding) operator is defined as
and the “Shrink” (or soft-threshholding) operator is defined as 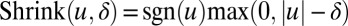 . Because the matrix
. Because the matrix 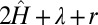 in Eq. 15 is sparse and positive definite, in practice a few iterations of either Gauss–Seidel or conjugate gradient are sufficient to achieve good convergence. Thus, Eqs. 15 and 16 can be solved very efficiently with long operation counts linearly dependent on N. The only time-consuming part in our algorithm is Eq. 17, which involves a singular value decomposition (SVD) factorization and can be straightforwardly solved with an
in Eq. 15 is sparse and positive definite, in practice a few iterations of either Gauss–Seidel or conjugate gradient are sufficient to achieve good convergence. Thus, Eqs. 15 and 16 can be solved very efficiently with long operation counts linearly dependent on N. The only time-consuming part in our algorithm is Eq. 17, which involves a singular value decomposition (SVD) factorization and can be straightforwardly solved with an 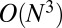 algorithm. For a moderate size of N, the proposed algorithm can solve the problem efficiently.
algorithm. For a moderate size of N, the proposed algorithm can solve the problem efficiently.
For a large number of modes N, a possible approach to accelerating the computation is to use graphs processing unit (GPU)-based parallel processing to perform the SVD factorization in Eq. 17. Here, we propose another method to speed up the third step of the proposed algorithm, which takes advantage of the special structure of the solution. We find that each of the resulting functions  has compact support, so that the support of each
has compact support, so that the support of each 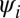 overlaps with only a finite number of its neighbors. This allows us to replace to the full orthogonality constraint
overlaps with only a finite number of its neighbors. This allows us to replace to the full orthogonality constraint 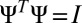 by a system of banded orthogonality constraints.
by a system of banded orthogonality constraints.
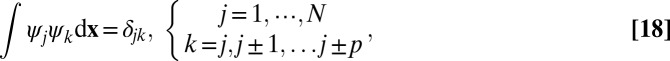 |
where p is the bandwidth. Thus, the 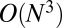 algorithm for SVD factorization in Eq. 17 can be replaced by N factorizations of
algorithm for SVD factorization in Eq. 17 can be replaced by N factorizations of 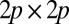 matrices, which is an algorithm with
matrices, which is an algorithm with 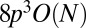 long operations.
long operations.
Numerical Results
We illustrate our scheme for two representative cases. The first is the free-electron model, which approximates the behavior of valence electrons in a metallic solid with weak atomic pseudopotentials; the potential function in the Schrödinger operator is simply set to zero. Because the allowed energy spectrum of free electrons is continuous in the limit of infinite system size, the conventional Wannier functions decay as an inverse power law. The second case is that of a periodic one-dimensional crystal, of which the famous Kronig–Penney (KP) model (17) is the most widely used example. The KP model describes the states of independent electrons in a one-dimensional crystal, where the potential function 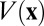 consists of a periodic array of rectangular potential wells. For simplicity, in our experiments we replace the rectangular wells with inverted Gaussians so that the potential is given by
consists of a periodic array of rectangular potential wells. For simplicity, in our experiments we replace the rectangular wells with inverted Gaussians so that the potential is given by 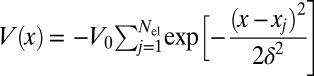 . We choose
. We choose 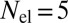 ,
, 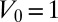 ,
, 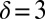 , and
, and 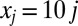 in our discussion below and, despite the different potential, continue to refer to this case as the 1D KP model. This model exhibits two low-energy bands separated by finite gaps from the rest of the (continuous) eigenvalue spectrum, and the Wannier functions corresponding to these bands are exponentially localized.
in our discussion below and, despite the different potential, continue to refer to this case as the 1D KP model. This model exhibits two low-energy bands separated by finite gaps from the rest of the (continuous) eigenvalue spectrum, and the Wannier functions corresponding to these bands are exponentially localized.
In our experiments, we choose 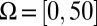 and discretize
and discretize  with 128 equally spaced nodes. The proposed variational model Eq. 4 is solved using algorithm 1, where parameters are chosen as
with 128 equally spaced nodes. The proposed variational model Eq. 4 is solved using algorithm 1, where parameters are chosen as 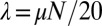 and
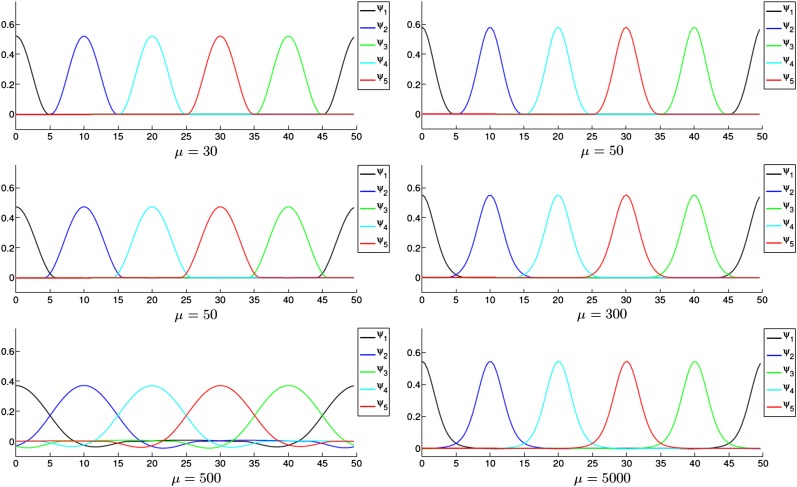
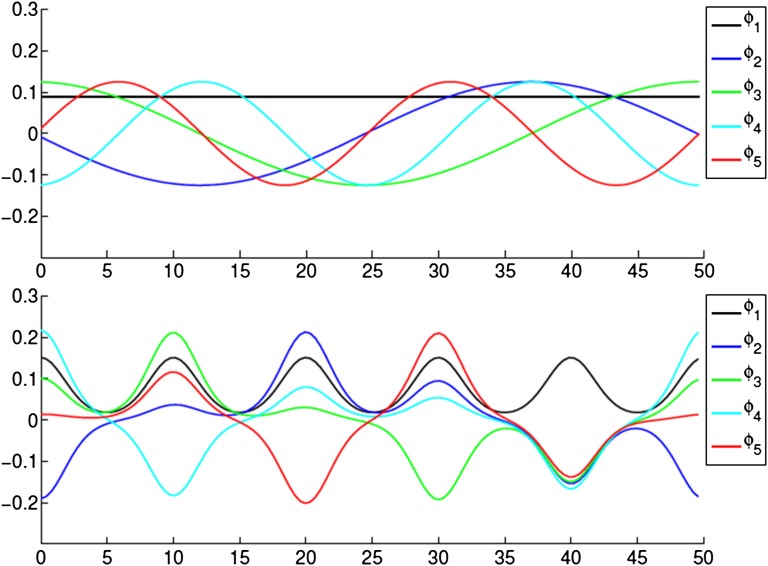
and 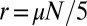 . We report the computational results of the first five CMs of the 1D free-electron model (the first column) and the 1D KP model (the second column) in Fig. 3, where we use five different colors to differentiate these CMs. To compare all results more clearly, we use the same initial input for different values of μ in the free-electron model and the 1D KP model. We flip the CMs if necessary such that most values of CMs on their support are positive, as sign ambiguities do not affect minimal values of the objective function in Eq. 4. For comparison, Fig. 4 plots the first five eigenfunctions of the Schrödinger operator used in the free-electron model and KP model. It is clear that all these eigenfunctions are spatially extended without any compact support. However, as we can observe from Fig. 3, the proposed variational model does provide a series of compactly supported functions. Furthermore, all numerical results in Fig. 3 clearly show the dependence of the size of compact support on μ, as suggested by general considerations based on the variational formula Eq. 4. In other words, the model with smaller μ will create CMs with smaller compact support, and the model with larger μ will create CMs with larger compact support. In addition, we find that the resulting CMs are not interacting for small μ (the first row of Fig. 3). By increasing μ to a moderate value, the modes start to interact with each other via a small amount of overlap (the second row of Fig. 3). Significant overlap can be observed using a big value of μ (the third row of Fig. 3).
. We report the computational results of the first five CMs of the 1D free-electron model (the first column) and the 1D KP model (the second column) in Fig. 3, where we use five different colors to differentiate these CMs. To compare all results more clearly, we use the same initial input for different values of μ in the free-electron model and the 1D KP model. We flip the CMs if necessary such that most values of CMs on their support are positive, as sign ambiguities do not affect minimal values of the objective function in Eq. 4. For comparison, Fig. 4 plots the first five eigenfunctions of the Schrödinger operator used in the free-electron model and KP model. It is clear that all these eigenfunctions are spatially extended without any compact support. However, as we can observe from Fig. 3, the proposed variational model does provide a series of compactly supported functions. Furthermore, all numerical results in Fig. 3 clearly show the dependence of the size of compact support on μ, as suggested by general considerations based on the variational formula Eq. 4. In other words, the model with smaller μ will create CMs with smaller compact support, and the model with larger μ will create CMs with larger compact support. In addition, we find that the resulting CMs are not interacting for small μ (the first row of Fig. 3). By increasing μ to a moderate value, the modes start to interact with each other via a small amount of overlap (the second row of Fig. 3). Significant overlap can be observed using a big value of μ (the third row of Fig. 3).
Fig. 3.
Computation results of CMs with different values of μ. The first column, the first five CMs of the 1D free-electron model; the second column, the first five CMs of the 1D KP model.
Fig. 4.
The first five egienfunctions of the Schrödinger operator 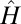 in the free-electron model (Upper) and the KP model (Lower).
in the free-electron model (Upper) and the KP model (Lower).
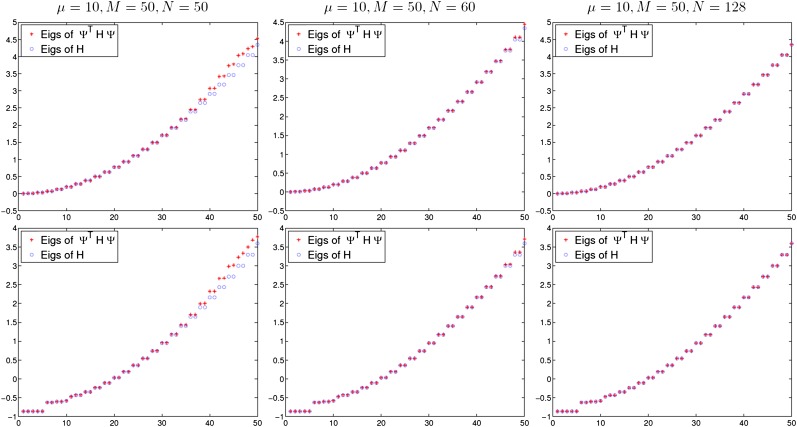
We further test conjecture 1 (Eq. 12) numerically—that is, unitary transformation of the derived compactly supported CMs can represented the eigenmodes of the Schrödinger operator. We compare the first M eigenvalues 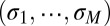 of the matrix
of the matrix 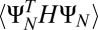 obtained by the 1D KP model and 1D free-electron model with the first M eigenvalues
obtained by the 1D KP model and 1D free-electron model with the first M eigenvalues 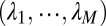 of the corresponding Schrödinger operators. Fig. 5 illustrates the comparisons with a relative small value
of the corresponding Schrödinger operators. Fig. 5 illustrates the comparisons with a relative small value 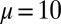 , when the CMs are highly localized. We can clearly see that
, when the CMs are highly localized. We can clearly see that 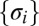 gradually converges to
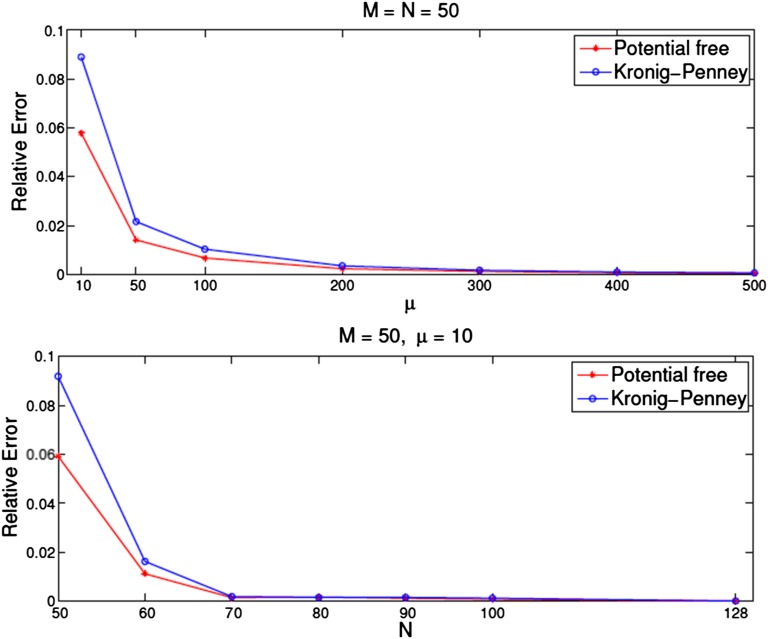
gradually converges to 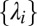 with increasing number N of CMs. In addition, we also plot the relative error
with increasing number N of CMs. In addition, we also plot the relative error 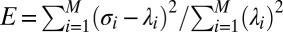 in Fig. 6. As we speculated in conjecture 1, the relative error will converge to zero as
in Fig. 6. As we speculated in conjecture 1, the relative error will converge to zero as 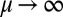 for fixed
for fixed 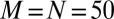 , which is illustrated in the upper panel of Fig. 6. The relative error will also converge to zero as
, which is illustrated in the upper panel of Fig. 6. The relative error will also converge to zero as 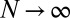 for fixed
for fixed 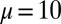 and
and 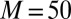 , which is illustrated in the lower panel of Fig. 6.
, which is illustrated in the lower panel of Fig. 6.
Fig. 5.
Comparisons of the first 50 eigenvalues of the 1D free electron model (the first row) and the 1D KP model (the second row).
Fig. 6.
Relative eigenvalue error of the 1D free-electron model (red dots) and 1D KP model (blue circles). (Upper) Relation of the relative error via different values of μ for fixed 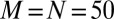 . (Lower) Relation of the relative error via different values of N for fixed
. (Lower) Relation of the relative error via different values of N for fixed 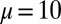 and
and 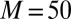 .
.
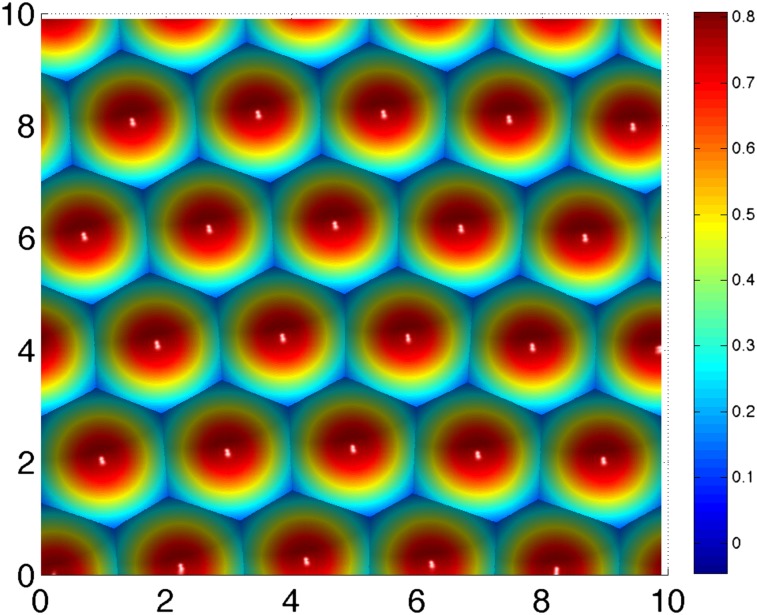
Moreover, the proposed model and numerical algorithm also work on domains in high dimensional space. As an example, Fig. 7 shows computational results of the first 25 CMs of the free-electron case on a 2D domain 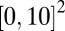 with
with 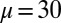 . All of the above discussions of 1D model are also true for 2D cases. In addition, our approach can also be naturally extended to irregular domains, manifolds, as well as graphs, which will be investigated in our future work.
. All of the above discussions of 1D model are also true for 2D cases. In addition, our approach can also be naturally extended to irregular domains, manifolds, as well as graphs, which will be investigated in our future work.
Fig. 7.
The first 25 CMs of free-electron case on a 2D domain 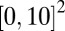 with
with 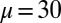 . Each CM is color-coded by its height function.
. Each CM is color-coded by its height function.
In conclusion, the above numerical experiments validate the conjecture that the proposed CMs provide a series of compactly supported orthonormal functions, which approximately span the low-energy eigenspace of the Schrödinger operator (i.e., the space of linear combinations of its first few lowest eigenmodes).
Discussions and Conclusions
In conclusion, we have presented a method for producing CMs (i.e., modes that are sparse and spatially localized with a compact support) for the Laplace operator plus a potential V, using a variational principle with an 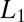 penalization term that promotes sparsity. The tradeoff between the degree of localization and the accuracy of the variational energy is controlled by one numerical parameter, μ, without the need for physical intuition-informed spatial cutoffs. The SOC algorithm of ref. 13 has been used to numerically construct these modes. Our tests indicate that the CMs can be used as an efficient, systematically improvable orthonormal basis to represent the low-energy eigenfunctions and energy spectrum of the Schrödinger operator. Due to the fact that the CMs are compactly supported, the computational effort of total energy calculations increases linearly with the number of modes N, overcoming the
penalization term that promotes sparsity. The tradeoff between the degree of localization and the accuracy of the variational energy is controlled by one numerical parameter, μ, without the need for physical intuition-informed spatial cutoffs. The SOC algorithm of ref. 13 has been used to numerically construct these modes. Our tests indicate that the CMs can be used as an efficient, systematically improvable orthonormal basis to represent the low-energy eigenfunctions and energy spectrum of the Schrödinger operator. Due to the fact that the CMs are compactly supported, the computational effort of total energy calculations increases linearly with the number of modes N, overcoming the 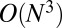 orthogonalization bottleneck limiting the performance of methods that work by finding the eigenfunctions of the Schrdinger operator.
orthogonalization bottleneck limiting the performance of methods that work by finding the eigenfunctions of the Schrdinger operator.
In addition, note that the discretized variational principle in Eq. 13 is related to sparse principal component analysis (SPCA) (18, 19). SPCA, however, does not involve an underlying continuum variational principle, and the sparse principal components are not localized, as the component number does not correspond to a continuum variable.
These results are only the beginning. We expect that CM-related techniques will be useful in a variety of applications in solid state physics, chemistry, materials science, and other fields. Future studies could explore the following directions:
i) Use CMs to develop spatially localized basis sets that span the eigenspace of a differential operator, for instance, the Laplace operator, generalizing the concept of plane waves to an orthogonal real-space basis with multiresolution capabilities. More details will be discussed in ref. 20.
ii) Use the CMs to construct an accelerated [i.e.,
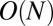 ] simulation method for density-functional theory electronic structure calculations.
] simulation method for density-functional theory electronic structure calculations.iii) Construct CMs for a variety of potentials and develop CMs as the modes for a Galerkin method for PDEs, such as Maxwell’s equations.
iv) Generalize CMs for use in PDEs (such as heat type equations) that come from the gradient descent of a variational principle.
v) Extend CMs to higher dimensions and different geometries, including the Laplace–Beltrami equation on a manifold and a discrete Laplacian on a network.
Finally, we plan to perform an investigation of the formal properties of CMs to rigorously analyze their existence and completeness, including the conjecture 1 (Eq. 12) that was hypothesized and numerically tested here.
Acknowledgments
V.O. gratefully acknowledges financial support from the National Science Foundation under Award DMR-1106024 and use of computing resources at the National Energy Research Scientific Computing Center, which is supported by the US Department of Energy (DOE) under Contract DE-AC02-05CH11231. The research of R.C. is partially supported by the US DOE under Contract DE-FG02-05ER25710. The research of S.O. was supported by the Office of Naval Research Grant N00014-11-1-719.
Footnotes
The authors declare no conflict of interest.
References
- 1.Donoho DL. Compressed sensing. IEEE Transactions on Information Theory. 2006;52(4):1289–1306. [Google Scholar]
- 2.Candès EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory. 2006;52(2):489–509. [Google Scholar]
- 3.Recht B, Fazel M, Parrilo P. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010;52(3):471–501. [Google Scholar]
- 4.Candès EJ, Eldar YC, Strohmer T, Voroninski V. Phase retrieval via matrix completion. SIAM Journal on Imaging Sciences. 2013;6(1):199–225. [Google Scholar]
- 5.Candès EJ, Li X, Ma Y, Wright J. Robust principal component analysis? J ACM. 2011;58(3):1–37. arXiv:0912.3599v1. [Google Scholar]
- 6.Schaeffer H, Caflisch R, Hauck CD, Osher S. Sparse dynamics for partial differential equations. Proc Natl Acad Sci USA. 2013;110(17):6634–6639. doi: 10.1073/pnas.1302752110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nelson LJ, Hart G, Zhou F, Ozoliņš V. Compressive sensing as a paradigm for building physics models. Phys Rev B. 2013;87(3):035125. [Google Scholar]
- 8.Prodan E, Kohn W. Nearsightedness of electronic matter. Proc Natl Acad Sci USA. 2005;102(33):11635–11638. doi: 10.1073/pnas.0505436102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wannier GH. The structure of electronic excitation levels in insulating crystals. Phys Rev. 1937;52(3):191–197. [Google Scholar]
- 10.Marzari N, Vanderbilt D. Maximally localized generalized Wannier functions for composite energy bands. Phys Rev B. 1997;56(20):12847–12865. [Google Scholar]
- 11.Weinan E, Li T, Lu J. Localized bases of eigensubspaces and operator compression. Proc Natl Acad Sci USA. 2010;107(4):1273–1278. doi: 10.1073/pnas.0913345107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Donoho DL, Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via l minimization. Proc Natl Acad Sci USA. 2003;100(5):2197–2202. doi: 10.1073/pnas.0437847100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lai R, Osher S. A splitting method for orthogonality constrained problems. J Sci Comput. 2013 in press. [Google Scholar]
- 14.Osher S, Burger M, Goldfarb D, Xu J, Yin W. An iterative regularizatoin method for total variation-based image restoration. Multiscale Model Simul. 2005;4(2):460–489. [Google Scholar]
- 15.Yin W, Osher S, Goldfarb D, Darbon J. Bregman iterative algorithms for l1-minimization with applications to compressed sensing. SIAM Journal on Imaging Sciences. 2008;1(1):143–168. [Google Scholar]
-
16.Goldstein T, Osher S. The split bregman method for
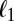 -regularized problems. SIAM Journal on Imaging Sciences. 2009;2(2):323–343. [Google Scholar]
-regularized problems. SIAM Journal on Imaging Sciences. 2009;2(2):323–343. [Google Scholar] - 17.Kronig RdeL, Penney WG. Quantum mechanics of electrons in crystal lattices. Proc R Soc Lond, A Contain Pap Math Phys Character. 1931;130(814):499–513. [Google Scholar]
- 18.d’Aspremont A, El Ghaoui L, Jordan MI, Lanckriet G. A direct formulation for sparse PCA using semidefinite programmingpca using semidefinite programming. SIAM Rev. 2007;49(3):434–448. [Google Scholar]
- 19.Qi X, Luo R, Zhao H. Sparse principal component analysis by choice of norm. J Multivariate Anal. 2013;114:127–160. doi: 10.1016/j.jmva.2012.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ozoliņš V, Lai R, Caflisch R, Osher S. Compressed Plane Waves—Compactly Supported Multiresolution Basis for the Laplace Operator. 2013. preprint. [DOI] [PMC free article] [PubMed] [Google Scholar]