High-performance, low-voltage electroosmotic pumps with molecularly thin silicon nanomembranes

Significance

Electroosmotic pumps (EOPs) are a class of pumps in which fluid is driven through a capillary or porous media within an electric field. Current research on EOPs concerns the development of new materials in which high electroosmotic flow rates can be achieved for low voltages. Such pumps could be used for portable microfluidic devices. Porous nanocrystalline silicon (pnc-Si) is a material that is formed into a 15-nm-thick nanomembrane. pnc-Si membranes are shown here to have high electroosmotic flow rates at low applied voltages due to the high electric fields achieved over the ultrathin membrane. A prototype EOP was designed using pnc-Si membranes and shown to pressurize fluid through capillary tubing at voltages as low as 250 mV.

Abstract

We have developed electroosmotic pumps (EOPs) fabricated from 15-nm-thick porous nanocrystalline silicon (pnc-Si) membranes. Ultrathin pnc-Si membranes enable high electroosmotic flow per unit voltage. We demonstrate that electroosmosis theory compares well with the observed pnc-Si flow rates. We attribute the high flow rates to high electrical fields present across the 15-nm span of the membrane. Surface modifications, such as plasma oxidation or silanization, can influence the electroosmotic flow rates through pnc-Si membranes by alteration of the zeta potential of the material. A prototype EOP that uses pnc-Si membranes and Ag/AgCl electrodes was shown to pump microliter per minute-range flow through a 0.5-mm-diameter capillary tubing with as low as 250 mV of applied voltage. This silicon-based platform enables straightforward integration of low-voltage, on-chip EOPs into portable microfluidic devices with low back pressures.

Electroosmotic flow results from the interaction between an electric field and the diffuse layer of ions at a charged surface. In capillaries or pores, the migration of the diffuse layer toward the oppositely charged electrode causes the bulk fluid within the channel to flow through viscous drag. Electroosmotic pumps (EOPs) are designed to generate high flow rates in microchannels using these principles (1, 2). EOPs present a number of advantages over mechanical pumps, including the lack of mechanical parts, pulse-free flows, and ease of control through electrode actuation. EOPs have been suggested as pumps for cooling circuits (3) and microfluidic devices that aid in drug delivery (4, 5) or diagnostics (2, 6). Microfluidic devices enable the miniaturization of multistep laboratory processes into small, low-cost, disposable units (6, 7). The inclusion of multiple steps into a single device increases the need for the precision pumping of fluids on-chip.

High voltages (>1 kV) are often required for direct current (dc) EOPs to achieve sufficient flow rates in microchannels (8, 9). However, devices with high-voltage EOPs require bulky external power supplies and a skilled technician to operate, which defeats the ease of use and portability aims of a microfluidic diagnostic tool. For these reasons, the development of a low-voltage EOP is a current focus in the literature. Several recent low-voltage EOPs have been fabricated from porous silicon (10), alumina (11–13), track-etched polymer (14), and carbon nanotube membranes (15). These low-voltage EOPs are much thinner than their high-voltage predecessors (60–350 μm compared with >10 mm). Yao et al. suggest that further thinning of EOPs will enable better voltage-specific characteristics (16). Here, we examine the electroosmotic pumping by nanoporous membranes that are more than two orders of magnitude thinner than any membrane material previously used in an EOP.

We have recently developed an ultrathin (15–30 nm), nanoporous membrane material called porous nanocrystalline silicon (pnc-Si) (17). pnc-Si membranes are fabricated on silicon wafers using techniques standard to the microelectronics industry. The silicon platform enables control of freestanding membrane area (Fig. 1A) and industrial-scale manufacturing (18). Pore distributions are controlled by fabrication temperatures and ramp rates during a rapid thermal crystallization step (19). Pores can be directly viewed in the ultrathin membrane and characterized with transmission electron microscopy (TEM). The silicon platform also enables the integration into a number of devices and fluidics systems. Previously, pnc-Si membranes have been shown to present little resistance to the diffusion of small molecules (17, 20–22) and have high permeability to water (18) and air (23).

Fig. 1.

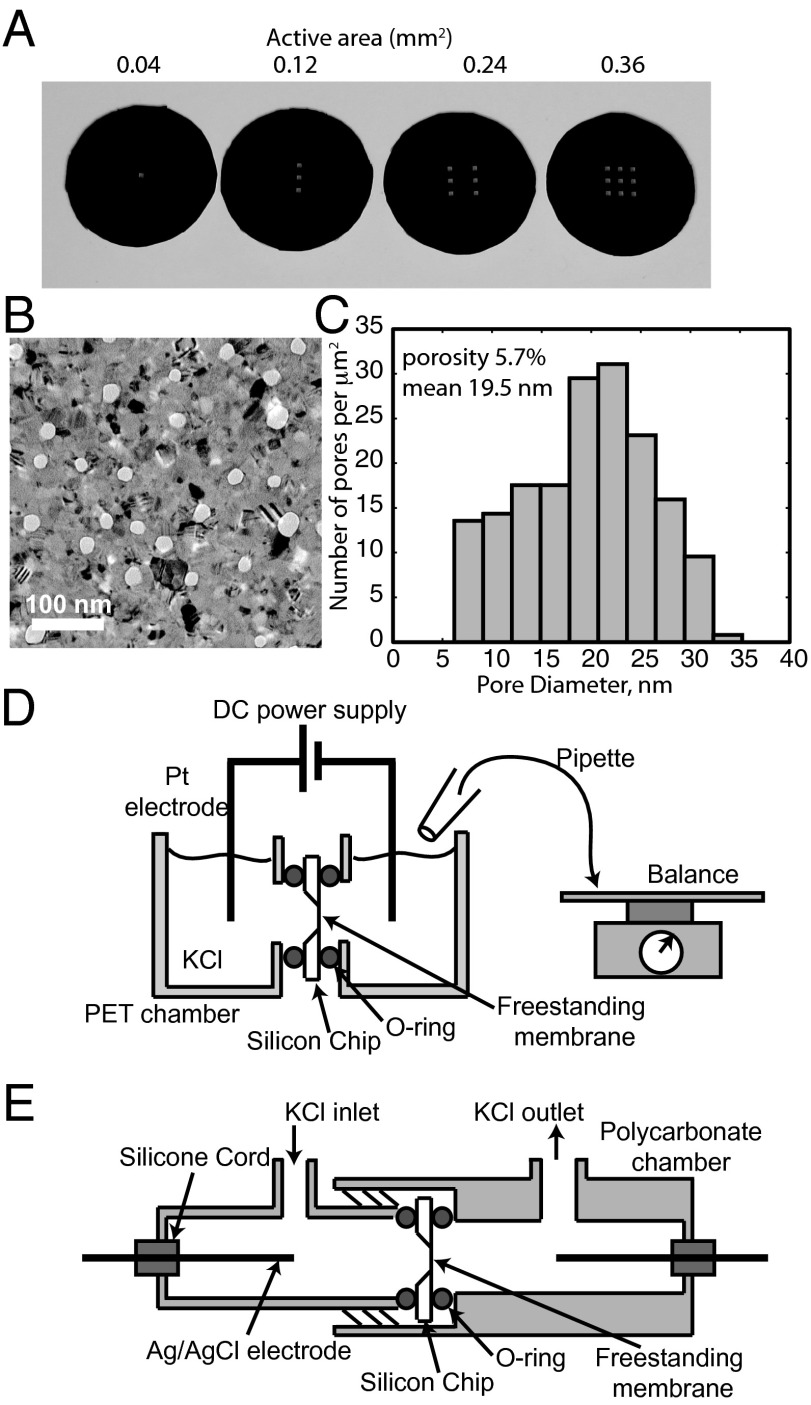
pnc-Si membranes and testing devices. (A) pnc-Si chips with one, three, six, or nine 200 × 200-μm windows of freestanding membrane. A 15-nm-thick pnc-Si membrane extends over each window on the silicon chips. (B) Transmission electron micrograph of pnc-Si membrane. White spots are pores and black regions are diffracting nanocrystals. (C) Pore diameters as determined by MATLAB image processing of a 1.7 × 1.1-μm TEM image of the membrane depicted in B. (D) Electroosmosis testing device. pnc-Si chips are sealed between two PET chambers, and a dc power supply maintains a constant voltage across two Pt electrodes. KCl solution that flows into the receiving chamber was continuously removed and weighed at intervals to determine electroosmosis rate. (E) Streaming potential testing device. pnc-Si chips are sealed between two threaded polycarbonate chambers. Ag/AgCl electrodes measure voltage difference between cells as KCl is pressurized through chamber.

In this work, we show that pnc-Si membranes with low active areas (0.36 mm²) generate electroosmotic flow rates of 10 μL/min at voltages of 20 V or lower. These flow rates are compared with electroosmotic theory by calculating electroosmotic flow using pore distributions from TEM micrographs. Surface modifications are shown to change the zeta potential of the material and influence the electroosmotic flow rates. EOPs developed using pnc-Si membranes and Ag/AgCl electrodes were shown to pump fluids through capillary tubing at applied voltages as low as 250 mV. The thermodynamic efficiency of pnc-Si EOPs was shown to be less than 0.01% due to low stalling pressures. Theoretically, the thermodynamic efficiency could be improved orders of magnitude by bringing the electrodes closer to the membrane and reducing the applied voltage. Our work suggests pnc-Si EOPs can provide ultralow voltage and on-chip pumping in microfluidic systems with low back pressures.

Results and Discussion

Electroosmosis Flow Rates.

pnc-Si membrane chips with different amounts of freestanding membrane (one, three, six, or nine 200 × 200-μm windows) were fabricated as described in Methods (Fig. 1A). Characterization by electron microscopy determined that membranes had an average pore size of 19.5 nm and a porosity of 5.7% (Fig. 1 B and C).

The electroosmosis testing device was built by milling vertical wells into two pieces of polyethylene terephthalate (PET) (Fig. 1D). Access points were drilled into the side of the two PET blocks, each with a recessed ledge to hold an O-ring. pnc-Si membranes were placed between viton O-rings at the two access points and the devices were sealed using screws with wing nuts. Experiments were performed with 100 mM KCl, as this system is envisioned as a pump for microfluidic chips and molecules that require physiological salt concentrations. A Hewlett Packard E3612A dc power supply was used to apply a constant voltage of 20 V, and the volume of aqueous KCl passed into the receiving chamber was measured on a balance at specific time intervals. The supply chamber was continuously replenished so that pressure gradients between the two chambers were negligible. The chamber was open to atmosphere to prevent trapping of bubbles at the membrane caused by electrolysis at the platinum electrodes. Control experiments with solid silicon chips confirmed that the chambers were well sealed with no leakage current. Control experiments using chips with freestanding membranes removed did not exhibit any flow (Fig. 2A), indicating that the pores in the material are necessary for electroosmosis.

Fig. 2.

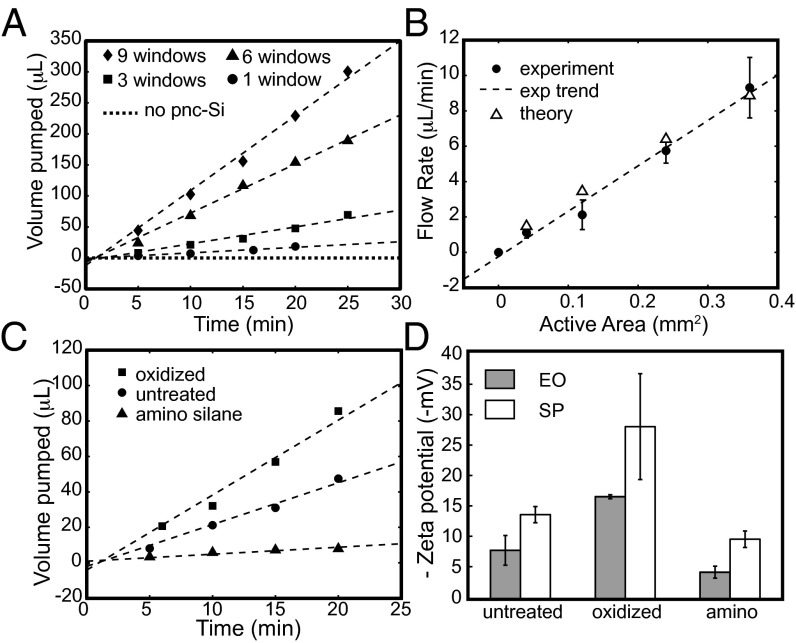
(A) Electroosmotic transport of KCl measured over time for untreated pnc-Si chips with active areas shown in Fig. 1A. All measurements were performed at an applied voltage of 20 V. Dotted line indicates a nine-window chip without pnc-Si material. (B) Electroosmotic flow rates of untreated pnc-Si membranes as a function of active area at an applied voltage of 20 V. Theoretical points are calculated using the pore characteristics, current, and zeta potential of the particular experimental point. (C) Electroosmotic transport of modified pnc-Si membranes. Higher flow rates are observed for oxidized membrane. Amino silanization reduces the flow rate, but does not change the direction of the flow. (D) Zeta potential measured through electroosmotic (EO) and streaming potential (SP) experiments. As expected, oxidation increases the zeta potential whereas amino silanization reduces the zeta potential.

Representative volume vs. time curves are plotted in Fig. 2A for the four chips with different active membrane areas. Volumetric electroosmotic flow rates were determined from the slope of these curves. We observe in Fig. 2B that the relationship between volumetric flow rate and active area is linear. Because an increase in active area results in a proportional increase in the number of pores, maximizing the active membrane area occupying a channel cross-section will maximize flow rates. Although the active areas are small compared with other EOPs, this active area is scalable using photolithography techniques and can be fabricated to match channel dimensions in future applications. Even in this small size format, pnc-Si membranes achieved flow rates up to 10 μL/min with an active area of 0.36 mm².

Theoretical Comparison.

We compare our experimental results to Rice–Whitehead theory for electroosmosis in narrow pores (24). Volumetric electroosmotic flow, V, through a narrow capillary in the absence of an external pressure gradient can be described by the following:

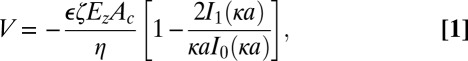where ϵ is the product of the dielectric constant of the solution and the permittivity of free space, ζ the zeta potential of the capillary walls, E_z the electric field through the capillary, A_c the cross-sectional area of the capillary, η the viscosity, a the capillary radius, and I₀ and I₁ modified Bessel functions of the zeroth- and first order, respectively. κ is the reciprocal of the Debye length and is found using

where k is the Boltzmann constant, T the temperature, q the charge of an ion in a symmetrical salt, N_A Avogadro’s number, and c the concentration of the counterion (in mol/m³). The multiplier on the right-hand side of Eq. 1 takes into account the reduction in electroosmotic velocity of the region within the diffuse layer at the edge of the pore wall, although if κ⁻¹ << a, this term vanishes and the equation reduces to the classical Helmholtz–Smoluchowski description of electroosmosis (25). In our case, the nanopores within the membrane are similar in dimension to the Debye length and we must consider this scaling factor. As this theory is developed using the Debye–Hückel approximation, it is applicable for zeta potentials of up to 50 mV (8, 24), and EOPs with higher zeta potentials require alternate solutions (2). As shown below, the magnitude of zeta potential for pnc-Si is less than 30 mV and so the Debye–Hückel approximation is valid.

Volumetric electroosmotic flow through a porous medium can be determined by expanding Eq. 1 to describe a bundle of capillaries in a manner similar to the use of Darcy’s law for pressurized flow (25). Because we can obtain pore distributions from TEM images that are representative of the entire membrane area, we can sum Eq. 1 over all of the pores in the image and scale by the ratio of membrane area to image area, A_tot/A_im, to obtain a total volumetric flow,

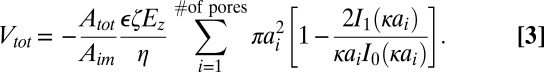Rice–Whitehead theory gives the following expression for current I in a system with electroosmotic flow but lacking pressurized flow:

where β is 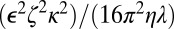. At the physiological salt concentrations used in the experiments, β is very small and the electric field for the porous membrane is

where χ is the membrane porosity and λ is the conductivity of the solution. Experimental currents were found using a TEK DMM252 multimeter (Tektronix). Conductivity was measured with a CON6 conductivity meter (Oakton Instruments) in bulk solution. We note that this measurement for the conductivity is an approximation, as the conductivity inside the nanopores could potentially deviate from the bulk solution. The results indicate electric fields of 8 × 10⁵ V/m across the membranes. These high electric fields are likely obtained for relatively low applied voltages because pnc-Si is only 15 nm thick. Because electroosmotic flow rates increase in proportion to the electric field strength (Eq. 1), high electric fields across the membrane enhance pump performance. The benefit of using thin materials for electroosmosis is further examined in our following comparison with other EOPs.

The zeta potential of the pore walls was determined from streaming potential measurements. In these experiments, pnc-Si chips were inserted into the polycarbonate streaming potential device in Fig. 1E and were sealed by threading the two chambers together and compressing two O-rings. Ag/AgCl electrodes were prepared using the method of Burns and Zydney (26) and sealed into the device with silicon cord compressed with a polycarbonate screw. The chamber was filled with 100 mM KCl and pressurized with N₂ through an entry port fitted with Tygon tubing. For each measurement the pressure was allowed to stabilize for 30 s, as displayed by a VWR digital manometer, and the potential difference across the membrane was measured with a multimeter.

Streaming potential can be described using Rice–Whitehead theory, and if β once again is very small, we can use the expression

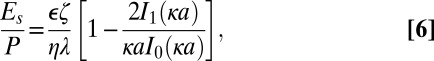where E_s is the streaming potential measured at zero current and P is the applied pressure through the membrane (24, 27). In Eq. 6 the pore size a is taken to be the average pore size. The slope of a streaming potential versus pressure plot can be substituted for the left-hand side of Eq. 6, allowing for the determination of the zeta potential (Fig. S1). By this method we find that the zeta potential of untreated pnc-Si membranes is −13.9 mV, consistent with a native oxide surface.

Theoretical flow rates for each experiment were calculated using the electric field (Eq. 5), average zeta potential (Eq. 6), and pore characteristics as obtained from image processing of TEM micrographs. The theoretical flow rates are very similar to the experimental flow rates, indicating that theory developed for infinitely long pores (24, 25) also holds for pore radii that are on the same order as their length. If entrance and exit effects exist for electroosmosis in short nanopores, they were not observable by our methods.

Surface Modifications.

Modifying the surface of a material can change the zeta potential and alter the rate of electroosmotic flow. To investigate the ability to change the rate of electroosmosis through surface modifications, we treated pnc-Si membranes with both plasma oxidation and aminosilanization (Fig. 2C). Oxidation increased flow rates by about two times over the untreated samples, whereas aminosilanization reduced the flow rates almost to zero.

The effects of plasma oxidation can be understood as an enhancement of the intrinsic negative charge of pnc-Si. pnc-Si is expected to grow a negatively charged native oxide as silicon surfaces typically do in the presence of oxygen (28). This expectation is consistent with the negative zeta potential of untreated pnc-Si and the fact that electroosmostic flow is directed toward the negative electrode. Plasma oxidation, a treatment that is commonly used to remove carbonaceous substances from inorganic surfaces (29), has been previously shown to slow the diffusion of negatively charged molecules (17), indicating a stronger negative charge than untreated membranes. Treatment in oxygen plasma has been shown to create negatively charged silanol groups on the surface of poly(dimethyl siloxane) microfluidic channels, thereby allowing them to generate electroosmotic flow (30). In the pnc-Si membranes used in this study, plasma oxidation resulted in a larger measured zeta potential compared with untreated membranes (Fig. 2D), suggesting that the oxide layer formed during this process is denser than the native oxide layer.

Aminosilanization treatment causes a reduction of electroosmotic flow by reducing the native negative surface charges on pnc-Si. Silanization, a chemical reaction that enables a silicon-containing organic compound (or silane) to be covalently bonded to a silica surface, allows for a myriad of functionalization possibilities due to the abundance of silanes. Previous work with capillary electrophoresis and microfluidic chips has shown that surface modification with various silanes reduces the electroosmotic flow rates and the zeta potential of silica (31, 32). In this study, we have grafted aminopropyltriethoxysilane (APTES) to the surface of the plasma-oxidized pnc-Si membranes. This modification results in a terminal amino group on the surface that carries a positive charge at neutral pH. The aminosilanization treatment greatly reduced the rate of electroosmosis, but did not change the direction of fluid flow or reverse the sign of the zeta potential (Fig. 2 C and D). This suggests that the positive amino groups reduced the net surface charge within the pores, but that the modification was not complete enough to invert the native negative charge.

Note that in this study we calculated zeta potential from streaming potential (Eq. 6) and electroosmosis measurements (Eq. 3). Streaming potential measurements are the most common form of zeta potential calculation, although we include electroosmotic calculations for comparison. pH changes induced by electrolysis at the electrodes and the effects of ion migration through the device can influence the zeta potential as calculated from electroosmosis (33). We do see an agreement in the trend of the zeta potentials as calculated by the different methods for the treated membranes, although electroosmosis calculations lead to lower zeta potentials for all membrane types.

Intrinsic Electroosmotic Flow Rate.

pnc-Si is more than 100 times thinner than other membrane materials used for dc electroosmotic pumping, and it is expected that thinner materials would result in higher electroosmotic flow rates. However, the test devices used in this work were not optimized and thus do not take advantage of the intrinsic rate of electroosmosis for this material. Here, we calculate this potential rate by normalizing the flow rate by active area and transmembrane voltage. Note that only a small portion of the applied voltage V_app falls across the membrane. One method to determine the transmembrane voltage V_TM is through the electrical resistance in the system (11, 16),

The resistance R_b occurs within the bulk fluid in the chambers, R_c is the resistance of the orifice within the silicon chip, and R_m is the resistance of the membrane. V_dec is the decomposition potential, or the voltage required to initiate electrolysis at the Pt electrodes. The transmembrane voltage is the product of the membrane resistance and current: 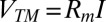. Current-voltage (I-V) curves (Fig. 3, Inset) can be used to determine the parameters in Eq. 7; the slope of an I–V curve of a system with an intact membrane gives 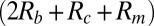and the slope of an I–V curve using an equivalent geometry chip in which the membrane was removed gives 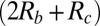. Thus, the difference in resistances calculated in these two cases is attributed to the membrane itself (R_m).

Fig. 3.

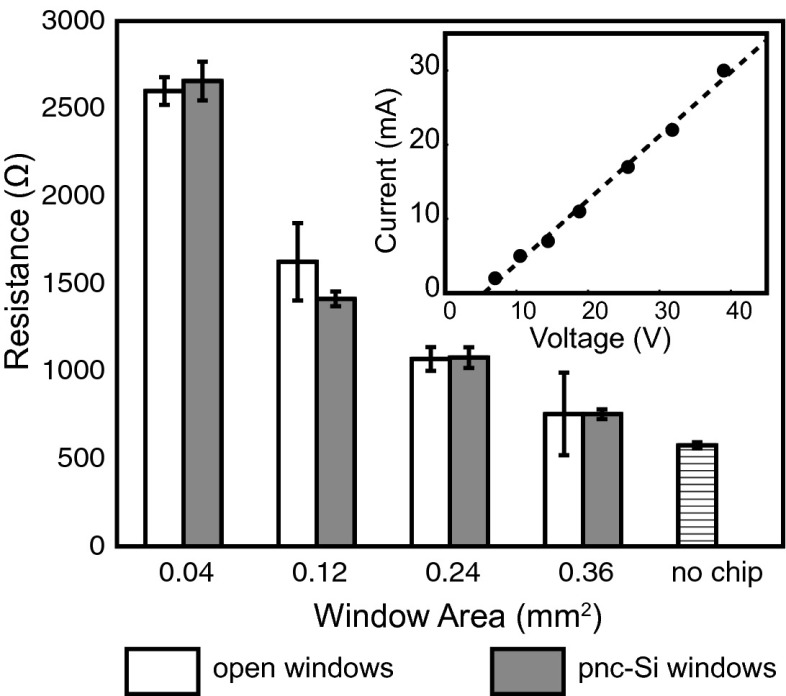
pnc-Si electrical resistance. Resistance of pnc-Si membranes is compared with identical form factor chips with windows lacking freestanding pnc-Si material. pnc-Si membranes impart negligible resistance to the system. The “no chip” bar indicates the resistance of the system lacking a silicon chip. (Inset) Typical I–V curve from a six-window (0.24-mm² active area) pnc-Si chip. Error bars are SDs.

In Fig. 3 we report the resistances as calculated from I–V curves for different active area chips both with and without membranes. In each case the difference is within the SE of the measurements (∼60 Ω), indicating that the transmembrane voltage is no greater than 600 mV given experimental currents of 10 mA. However, the actual transmembrane voltage appears to be much smaller than this estimate. The electric field strength (8 × 10⁵ V/m) and a 15-nm-thick membrane require a transmembrane voltage of only 12 mV. Low membrane resistance compared with all other resistances in the system has been observed for diffusive transport through pnc-Si (17, 18, 20, 22). In these studies, the ultrathin dimension of the membrane results in a transmembrane resistance to diffusion that can be neglected compared with bulk resistances. Analogously, the low electrical resistance of pnc-Si in electroosmosis experiments follows from the ultrathin quality of the membrane, as other resistances in the system are much higher by comparison. It is striking that the insertion of a vanishingly thin membrane is necessary to generate microscale flow, yet does not significantly alter the current or power consumed by the system.

We normalize the electroosmosis flow rate by the calculated transmembrane voltage and the active area of the chip to obtain a figure of merit of 260 mL⋅min⁻¹⋅cm⁻²⋅V⁻¹. In Table 1 we show that this figure of merit exceeds low-voltage EOPs fabricated from porous silicon (10), alumina (11), and track-etched polymer (14) by three orders of magnitude. Normalized flow rates for ultrathin pnc-Si EOPs are also 20 times higher than carbon nanotube (CNT) EOPs, which are considered to have unique properties due to a slippery surface (15). Recent advances in alternating current (ac) electrode arrays have enabled the development of ac EOPs. Whereas the flow rates of ac EOPs increase nonlinearly compared with dc EOPs, at the low voltages used in this paper the figure of merit for pnc-Si EOPs exceeds that of an ac EOP by 70 times. (34). In addition, electroosmotic flow through ac EOPs is hampered by high salt (>10 mM) (35), which reduces their utility in solutions with physiological ionic concentrations. pnc-Si EOPs are also inexpensive to fabricate (∼$1 per chip), as hundreds of functioning membrane chips can be produced per 6-inch wafer.

Table 1.

Normalized electroosmotic flow rates for low-voltage EOPs

EOP	Normalized flow rate, mL⋅min−1⋅cm−2 V−1
pnc-Si	260
Porous Si (10)	0.13
Alumina (11)	0.125
TE polymer (14)	0.12
CNT (15)	9.6
ac EOP (34)	3.6

The low electrical resistances and high electrical fields achieved across the ultrathin pnc-Si membranes enable the high normalized flow rate. To realize the full potential of pnc-Si-based EOPs, fluidic channel cross-sections and active membrane areas must be of similar dimensions. Electrodes also could be brought closer to or sputtered directly on the membrane surface to further minimize the applied voltage. Unlike ac EOPs, Faradaic reactions in dc EOPs can cause sample or fluid contamination, and this drawback could be a greater problem for smaller scale EOPs with electrodes closer to the membrane surface. By keeping the applied voltages low and using Ag/AgCl electrodes, we can minimize electrolysis and bubble formation within the pores of smaller scale EOPs.

Development of pnc-Si EOP Prototype.

To demonstrate the applicability of pnc-Si membranes as pumps in microfluidic systems, we designed and tested a low-voltage EOP (Fig. 4 A and B). Ag/AgCl electrodes were prepared by coating 200-μm-diameter silver wire with Ag/AgCl ink (Conductive Compounds), which were allowed to dry before insertion into the device. The electrodes were sealed in the polycarbonate enclosure with silicone gaskets, and 500-μm-diameter tubing was connected to the inlet and outlet ports. The device was filled with 100 mM NaCl under vacuum. A double-slit pnc-Si membrane was inserted into the device between two viton O-rings in solution at atmospheric pressure. Once assembled, the device was left submerged in solution for at least 12 h before testing.

Fig. 4.

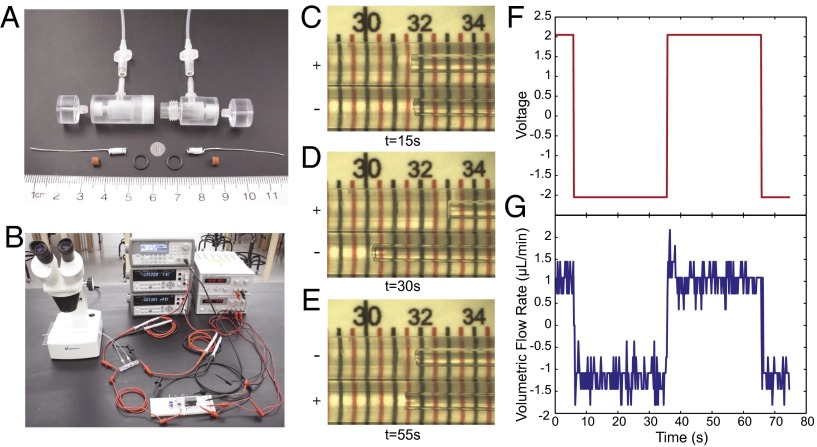
Micro-EOP prototype. (A) A prototype pump was developed using a polycarbonate housing that seals a circular pnc-Si membrane chip between two viton O-rings. Silver wire electrodes were wound to produce more surface area and painted with AgCl. Tubing with a 1-μm diameter was attached to the inlet and outlet ports of the device. (B) The pump was driven with a constant-current circuit that switched polarity using a relay (on breadboard). The flow rate was visualized by filming the movement of the solution front in the tubing under a dissection microscope. (C) Screen capture from Movie S1 of the prototype pumping fluid. The inlet and outlet tubes are shown side by side, and the fluid is moving left toward the negative electrode in the bottom tube (current 0.6 mA, voltage 2.05 V changing polarity every 30 s; scale, mm). (D) Screen capture at 30 s. The fluid has moved 1.5 mm in the 15 s between images C and D. (E) An image at 55 s. The polarity has changed at this point and the fluid is flowing left toward the negative electrode in the top tube. (F) Voltage during the time span of Movie S1. (G) Volumetric flow rate as calculated from individual screen captures from Movie S1.

Both Ag/AgCl electrodes of the EOP were connected to an Agilent 33220A arbitrary waveform generator, which was used as a controllable voltage source. The current measurement was performed by using an Agilent 34410A digital multimeter. Both waveform generator and digital multimeter were connected to a personal computer and controlled remotely. This software, written in C/C++, was developed specifically to provide a constant dc voltage ranging from −5 V to +5 V and simultaneously record the current readouts from the multimeter.

Electroosmosis was visualized by tracking the movement of the menisci in inlet and outlet capillary tubes under a microscope equipped with a CCD camera. In Fig. 4 C–E, we show images of the menisci at three different time points during an experiment in which the voltage polarity was switched every 40 s (Movie S1). The fluid flowed toward the negatively charged electrode at a rate of 1 μL/min at an applied voltage of 2 V (Fig. 4 F and G). With the Ag/AgCl electrodes, fluid flow through the capillary tubes was achieved at voltages lower than the hydrolysis of water, and no gases were generated in the chamber during the experiments.

Thermodynamic Efficiency.

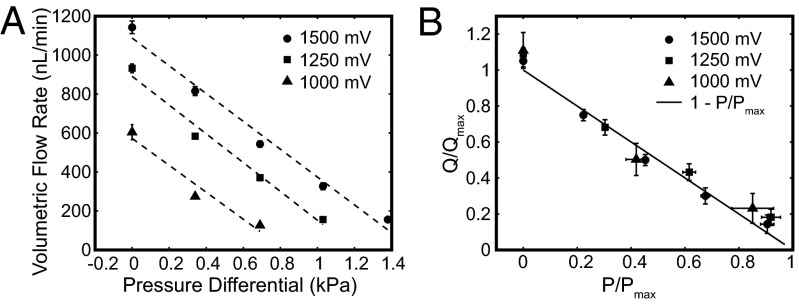
We tested the capability of the EOP to pump against back pressures supplied by a precision air pressure regulator type 70 (Marsh Bellofram). Electroosmosis flow rates in the presence of back pressure were measured from the meniscus movement in the inlet tube (Fig. 5A). Application of pressure linearly reduced the electroosmotic flow rate for applied voltages of 1,000–1,500 mV (Fig. 5A). In Table S1 we show the maximum flow rate at zero pressure Q_max, the maximum pressure at zero flow P_max, and the power consumption. We use Q_max and P_max to normalize the flow rate and pressure, respectively, and plot this relationship in Fig. 5B. Our data compare well with the accepted relationship (12) between flow rate and pressure,

which is plotted as a solid line in Fig. 5B.

Fig. 5.

Comparison of flow rate under applied pressure. (A) Electroosmotic volumetric flow rate was measured under regulated air pressure in the micro-EOP prototype for three applied voltages and a single direction through the EOP. The applied pressure reduces the flow rate and stalls electroosmotic flow in the range of 0.5–1.5 kPa for voltages 1,000–1,500 mV. (B) Normalized volumetric flow rate (Q/Q_max) is plotted against normalized pressure (P/P_max). The plotted solid line represents Eq. 8.

The thermodynamic efficiency is the ratio of hydraulic to electrical power for an EOP, or

Using the data from the back pressure analysis and the applied voltages, we calculated the thermodynamic efficiencies to be on the order of 0.00075%. Thermodynamic efficiency has been shown to range from 0.005% to 2% experimentally in aqueous buffers (10, 14, 36, 37). In our case, the thermodynamic efficiency could be improved by orders of magnitude by moving the electrodes to either side of the membrane. The efficiency may also be improved by increasing the amount of membrane occupying the channel cross-section (currently 5% or less). Increasing the active area will raise both the flow rate and the current, but the current increase is expected to plateau as the resistance does (Fig. 3).

To address whether the low back pressures supported by pnc-Si EOPs were related to membrane thickness, we conducted experiments with both 15- and 30-nm membranes. Surprisingly, we discovered that the 30-nm membranes exhibited lower stall pressures than the 15-nm membranes (Table S1), indicating that thickness was not the only variable that determined stall pressures. By characterizing the pore distributions of the two membranes, we were able to calculate a significantly higher hydraulic permeability for the 30-nm membrane (Table S2) (18). Whereas the porosities of the 15- and 30-nm membranes were similar, it has been shown that larger pores naturally form in thicker membranes due to looser geometric constraints (19). Thus, the low stall pressure seen with pnc-Si is directly related to the permeability. Low porosity, rather than greater thickness, may be the most effective way to improve this aspect of pnc-Si performance. Despite a low thermodynamic efficiency and low stall pressures in the current version, pnc-Si EOPs were used to produce flow rates of 1 μL/min through 10 cm of microcapillary tubing in voltages lower than 2 V. Thus, by installing pnc-Si EOPs in microfluidic chips with low back pressures, high microfluid flow rates can be achieved under low applied voltages. pnc-Si could therefore find uses as in-line pumps to move reagents and samples between locations within microfluidic chips.

Conclusions

Ultrathin pnc-Si membranes operate as high-flow-rate EOPs with low applied voltages. This is due to the small electrical resistance presented by the membrane and high electric fields across the molecularly thin membrane. The normalized flow rates were shown to be 20 times to several orders of magnitude higher than recent low-voltage EOPs. Pore distributions of pnc-Si membranes can be imaged via TEM, and we show using Rice–Whitehead theory that flow rates can be predicted for a given membrane. Surface modification through oxidation and silanization techniques was used to change the zeta potential of the material and the electroosmotic flow rates. A prototype pnc-Si EOP was shown to produce flow through capillary tubing with applied voltages as low as 0.25 V, although stalling pressures were in the range of 1 kPa. This EOP can be optimized by bringing the electrodes closer to the surface and maximizing active membrane area to channel dimensions. Due to scalable silicon fabrication methods, pnc-Si EOPs can be fabricated cheaply and can be easily integrated on silicon- or silica-based microfluid chips. pnc-Si EOPs will potentially enable low-voltage, on-chip electroosmotic pumping in microfluidic devices.

Methods

pnc-Si Fabrication.

The pnc-Si membranes in this study were made on 200-μm-<100> silicon-thick wafers using the methods developed in Striemer et al. (17). The photoresist was spin-coated on the surface of the wafers, and chrome masks were used to define the geometry of the 6.5-mm-diameter experimental chips and 3-mm-diameter imaging chips. The masks also defined the intended internal windows of freestanding pnc-Si membranes (one, three, six, or nine windows of 200 × 200 μm or two slits of 2 mm × 100 μm for experimental chips and four windows of 100 × 100 μm for imaging chips). A three-layer 20-nm SiO₂/15- or 30-nm amorphous Si/20-nm SiO₂ stack was sputtered onto patterned wafers via rf magnetron sputtering. The wafers were annealed at 1000 °C at a rate of 100 °C/s to induce crystallization and form nanopores in the reorganized silicon film. The bulk patterned silicon was anisotropically etched with ethylene diamine pyrocatechol, and protective oxide layers were removed with buffered oxide etchant. Pore distributions were obtained from TEM micrographs using an open-source MATLAB (The MathWorks) image processing program (http://nanomembranes.org/resources/software/) (Fig. 1 B and C).

Plasma Oxidation and Aminosilanization.

pnc-Si chips were oxidized using a 1224-P Yield Engineering Systems chemical vapor deposition (CVD) system with plasma capabilities. pnc-Si chips were placed in the 150 °C chamber and a vacuum of 0.3 Torr was drawn. A plasma of 0.198 kV was struck in the chamber with a 20 standard cubic centimeters per min flow of oxygen for 5 min.

Aminosilanization was performed in the CVD system with a process temperature of 150 °C. The chips were first dehydrated with two pump/purge cycles of the chamber with high-purity nitrogen. An oxygen plasma cleaning was then performed using the procedure described above. The surface was then rehydrated by injection of water vapor at a pressure of 0.5 Torr and soaked for 5 min. Then, 1 mL of APTES was vaporized and injected into the chamber at a pressure of 1.4 Torr and allowed to soak for 5 min. Spectroscopic ellipsometry measurements on SiO₂-coated reference chips indicate that a highly reproducible 0.5-nm-thick silane layer is deposited with this process.