Plasmonic antennas as design elements for coherent ultrafast nanophotonics

Significance

The focus of ultrafast science is rapidly moving toward increasingly complex systems, both on a fundamental level (such as quantum networks in diamond or excitonic coherence in photosynthesis) and in applied physics (such as multiphoton microscopy in membranes and cells). However, to disentangle the heterogeneous contributions to dynamics in such complex structures, femtosecond time resolution needs to be accompanied by nanometric spatial excitation volumes. Here we present preengineered plasmonic structures to amplitude-phase shape excitation pulses in a designed way, and thus deliver simultaneous deterministic spatial and temporal control. We expect these results to establish the reproducibility that ultrafast plasmonics needs to serve as a reliable and accurate tool for the investigation of femtosecond nanoscopic dynamics in complex systems.

Abstract

Broadband excitation of plasmons allows control of light-matter interaction with nanometric precision at femtosecond timescales. Research in the field has spiked in the past decade in an effort to turn ultrafast plasmonics into a diagnostic, microscopy, computational, and engineering tool for this novel nanometric–femtosecond regime. Despite great developments, this goal has yet to materialize. Previous work failed to provide the ability to engineer and control the ultrafast response of a plasmonic system at will, needed to fully realize the potential of ultrafast nanophotonics in physical, biological, and chemical applications. Here, we perform systematic measurements of the coherent response of plasmonic nanoantennas at femtosecond timescales and use them as building blocks in ultrafast plasmonic structures. We determine the coherent response of individual nanoantennas to femtosecond excitation. By mixing localized resonances of characterized antennas, we design coupled plasmonic structures to achieve well-defined ultrafast and phase-stable field dynamics in a predetermined nanoscale hotspot. We present two examples of the application of such structures: control of the spectral amplitude and phase of a pulse in the near field, and ultrafast switching of mutually coherent hotspots. This simple, reproducible and scalable approach transforms ultrafast plasmonics into a straightforward tool for use in fields as diverse as room temperature quantum optics, nanoscale solid-state physics, and quantum biology.

The intriguing prospect of resolving and using nanoscale and quantum-mechanical processes in large, complex, and disordered systems pushes physics, biology, chemistry, and engineering to ever smaller length scales and ever shorter time scales (1–3). A promising route to unlocking this regime is the marriage of ultrafast spectroscopy with nanoplasmonics (4–6), as evidenced by various experiments aimed at controlling localization or measuring ultrafast dynamics of hotspots, such as polarization control of localization (7, 8), measurements of plasmon dephasing (9–11), and adiabatic compression of pulses at plasmonic tips (12). However, for ultrafast nanoplasmonics to find widespread application in physics, biology, and material sciences, the ability to engineer a plasmonic system at will to provide a desired ultrafast response in a predetermined nanoscale hotspot is crucial: only then will the technique reach the necessary reproducibility, flexibility, and simplicity to be broadly usable. The achievement of this goal requires three conditions be met: localization of a broadband pulse in a nanoscale volume, deterministic near-field dynamics for a given plasmonic structure, and the ability to tune the near-field dynamics by plasmonic design. To prove the achievement of these first three goals, a fourth ability, measuring the ultrafast field dynamics in a given hotspot, is also required.

Large inroads have been made toward achieving those goals individually. Nanoscale field dynamics have been measured using photoelectron emission microscopy (PEEM), two-photon photoemission, or second harmonic spectroscopy (12–14); closed-loop coherent control has had large successes in creating (time-dependent) localization on nanostructures (7); nanofocusing of shaped ultrafast pulses has been achieved using near-field tips (12); and plasmonic structures have been used to, for example, design vortex beams or create controllable nonlinear emission (15, 16). However, the achievement of all goals simultaneously, let alone in a simple, flexible, and reproducible manner, has proved elusive. This has caused ultrafast plasmonics to remain a challenging topic of research, rather than fulfilling its potential as a tool that can unlock the fascinating regime of nano and quantum phenomena in complex physical, chemical, and biological systems.

We endeavor to experimentally reach this desired regime by coupling calibrated nanoantennas into plasmonic structures that deterministically shape the spectral amplitude and phase, and therefore the ultrafast dynamics, of the near field in a predetermined hotspot.

Plasmonic antennas are widely explored for applications in sensing and imaging owing to their ability to confine far-field illumination to near-field hotspots, with properties determined by antenna geometry (17–20), material (21, 22), and the excitation scheme (23–25). Furthermore, plasmonic antennas sustain coherent excitation (4, 8) and the antenna resonances exhibit broad bandwidths. Based on Fourier’s principle, this renders plasmonic antennas inherently suited for the investigation of ultrafast processes and coherent control (16, 26): A wide bandwidth in the frequency domain offers the potential for an ultrashort pulse in the time domain.

With a nonlinear measurement, we determine the amplitude and phase response of single nanoantennas to ultrafast excitation, and we use calibrated antennas as building blocks to engineer two examples of deterministic ultrafast nanoscale pulse shaping by a plasmonic system: a subwavelength resolution phase modulator and an ultrafast hotspot switch. With this, we show that it is possible to create tunable, deterministic, ultrafast hotspot dynamics based on plasmonic design and an a priori defined, simple pulse.

Experimental Procedures

The key to using nanoantennas in ultrafast plasmonic designs is a systematic measurement of the complex spectral modulations that antennas of increasing lengths add to the hotspot field. To measure this, we create a two-photon excitation in gold using a customized 4f-shaper and detect the two-photon photoluminescence (TPPL) in a confocal microscope setup (27). We detect the full spectral modulation as follows.

For a femtosecond pulse with spectral amplitude and phase 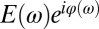, the probability of a two-photon absorption at a particular two-photon frequency ω_TP = 2ω is determined by the second derivative of the spectral phase at frequency ω: the signal at a particular ω_TP will be maximum if 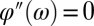. To measure the spectral phase in a hotspot, we expand 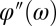into a known phase added in a femtosecond pulse shaper and an unknown antenna dispersion 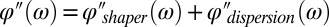, and we thus need to solve

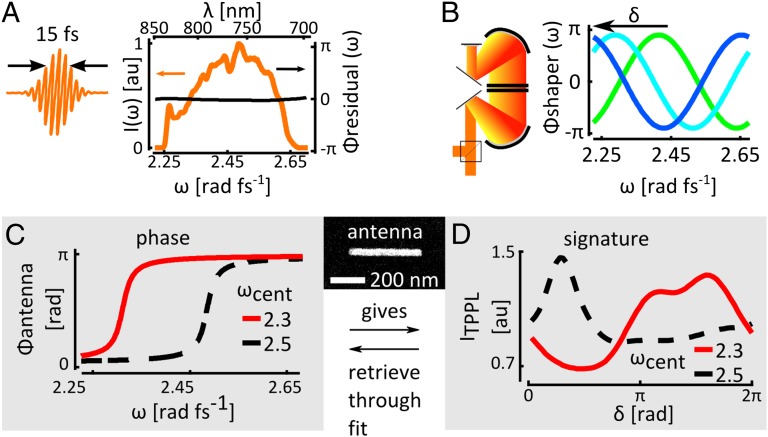
Analogous to the multiphoton intrapulse interference phase scan (MIIPS) method (28, 29), we add a series of cosinusoidal phase functions to a pulse (Fig. 1A) in a 4f-pulse shaper: 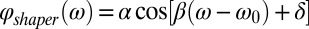(Fig. 1B). α is the amplitude of the phase function and determines the resolution with which the phase can be retrieved; ω₀ is the central frequency of the pulse; 2π/β is the periodicity of the phase function in frequency space, determining the bandwidth over which the phase can be measured; δ is a phase offset.

Fig. 1.

Characterization of spectral amplitude and phase in nano-antenna hotspots. (A) A gold nanoantenna (Inset) is excited with a Fourier limited 15-fs pulse with depicted spectrum and residual phase Φ_residual that is flat within 0.05π rad. (B) A series of cosinusoidal phases with shifting offset δ is added to the pulse in double-pass 4f-pulse shaper. (C) The antenna resonance adds a particular phase to the field in a hotspot. (D) The shifting cosinusoidal phase samples the antenna phase, which gives an antenna signature that can be fitted to retrieve the phase profile (see also Fig. S1).

Scanning the phase offset δ from 0 to 2π (Fig. 1B) samples the frequencies ω for which 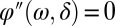(Eq. 1 and Fig. 1C), because those frequencies will dominate the TPPL signal (Materials and Methods). This allows us to record an antenna “signature” (Fig. 1D): a TPPL signal as a function of δ that traces the spectral probability of two-photon absorption. Because 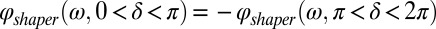, two measurements are performed: one with a “positive” phase and one with a “negative” phase. This means we are obtaining a quasi-2D solution to the 2D problem of measuring an unknown amplitude and phase; in other words, provided we know the spectral amplitude and phase of the pulse before interaction with the antenna, comparing the two halves of the measurement allows disentangling the amplitude and phase modulation of the hotspot field by the antenna (see Materials and Methods for elaboration and the procedure of pulse calibration before interaction with the antenna). There are similarities between our frequency domain measurement and interferometric time-resolved PEEM (ITR-PEEM) (14), although ITR-PEEM would be analogous to a time domain autocorrelation measurement using TPPL as a readout. Our double measurement in the spectral domain contains as much information as a cross-correlation in time domain, measured twice with different color probe pulses.

Results and Discussion

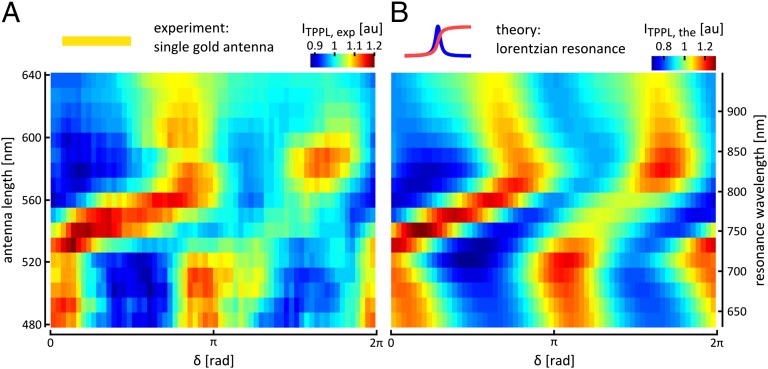
A fundamental antenna geometry that has been tested and analyzed particularly rigorously is that of single- and coupled-bar antennas (15, 21, 30–34) (Fig. 1, Inset). Thus, in a first experiment, we focus on the bar antenna as building block and determine the complex spectrum in the near-field hotspots on bars of varying lengths. Fig. 2A presents the antenna signatures of single-bar antennas with increasing lengths from 480 to 640 nm, recorded with Fourier limited laser pulses of 15 fs width (corresponding to a spectral bandwidth of 120 nm at 776 nm; Fig. 1A and Materials and Methods). The parameters for the cosinusoidal phase are 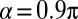and 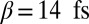. An intuitive understanding of these data can be gained by considering that the highest TPPL signal occurs when the shifting cosinusoidal phase 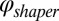compensates for the spectral phase of the antenna resonance best. The particular shape of the band of maximum intensity that starts at 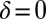rad for 480-nm rods and curves toward 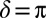for longer rods (Fig. 2A) can thus be interpreted as the phase jump that the excitation light at carrier wavelength 776 nm experiences when it drives the antenna above or below the resonance frequency.

Fig. 2.

Coherent ultrafast dynamics of single nanoantenna hotspots. (A) Antenna signatures of gold nano-antennas of increasing lengths. The signatures measure the spectral phase and, therefore, through the Fourier transform, the ultrafast dynamics of the hotspot. Recording the signature between 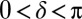and 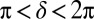allows differentiating between the effect the antenna has on the spectral amplitude and on the spectral phase of the field; this can clearly be seen in, for instance, the case of a 560-nm antenna: When δ is ∼π/2 the cosine function compensates best for the dispersion of the antenna, and the combination with a good overlap of the excitation spectrum with the resonance of the antenna provides for a high two-photon signal. In contrast, when δ is ∼3π/2, the overlap between the excitation spectrum and the antenna resonance is equally good but the cosine function adds to the antenna dispersion, and the two-photon signal is very low. (B) Corresponding signatures calculated for Lorentzian resonances at different wavelengths with a width of 0.13 ± 0.02 rad⋅fs⁻¹ (41 ± 6 nm at 776 nm).

To retrieve the spectral resonance profiles of the antennas, the measured signatures are compared with fits based on Lorentzian resonances that are given by 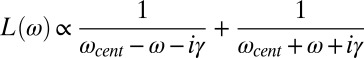. Here, ω_cent is the central frequency of the resonance, 2γ is the FWHM of the imaginary (i.e., absorptive) part of the resonance, and the antenna phase is defined as 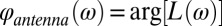. The best fits (Fig. 2B) are obtained if the width of the Lorentzian is kept at 2γ = 0.13 ± 0.02 rad⋅fs⁻¹ (corresponding to Δλ= 41 ± 6 nm at 776 nm central wavelength) while the resonance wavelength is varied from 640 nm for antennas of 480-nm length to 940 nm for antennas of 640-nm length (corresponding, respectively, to ω_cent = 2.95 rad⋅fs⁻¹ and 2 rad⋅fs⁻¹).

The measurement depicted in Fig. 2 is a systematic exploration of the complex spectral modulation that calibrated nano-antennas impose on an impinging ultrafast pulse. This realization now allows us to create plasmonic structures with tailored and predetermined ultrafast responses by coupling antennas. The field in each hotspot in such a system is influenced by the resonances of the building blocks, modified by the dispersion and absorption of the coupled system. One feasible application is a subwavelength resolution phase modulator: a plasmonic structure that imparts a predefined spectral phase on the field in a hotspot for use in high-resolution, small-volume nonlinear experiments.

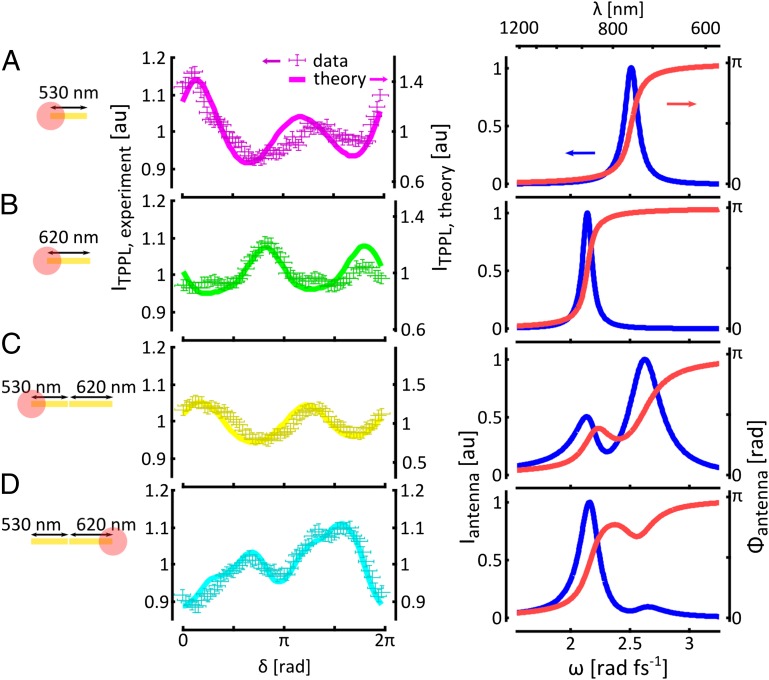
This concept of engineering ultrafast nanophotonic systems is demonstrated in Fig. 3, in which we present the measured and fitted TPPL signature and the retrieved amplitude-phase modulation added to a hotspot by a single-bar antenna of 530-nm (Fig. 3A) and 620-nm length (Fig. 3B), as well as to the hotspot on the 530-nm (Fig. 3C) and 620-nm side (Fig. 3D) respectively, by a coupled antenna with a gap of ∼30 nm. The best fits for the signatures were obtained by significantly broadening the single-antenna resonances from 0.13 ± 0.02 rad⋅fs⁻¹ to 0.26 ± 0.06 rad⋅fs⁻¹ for coupled antennas, indicating that the total dispersion of the combined antenna determines the width of the resonances in each profile. The losses in the metal, giving rise to the broadening, are a vital property of the design, because they in part determine the range of the spatial mode associated with the resonance and therefore its strength in a particular hotspot. The spectral phase modulation the antenna imprints on the hotspot-sized field can directly be controlled by adapting the strength and separability of the resonances of the constituent antennas in the hotspot of interest through a wide range of readily accessible parameters (i.e., antenna dimensions, material, geometry, and gap widths).

Fig. 3.

Shaping the phase in hotspot on a plasmonic structure using the resonances of the constituent antennas. (A) Antenna signature measured in a hotpot on a 530-nm single antenna (Left) and the resonance profile retrieved from the fit (Right). (B–D) Corresponding signatures (Left) and resonance profiles (Right) for a 620-nm single antenna and different positions on a coupled 530- to 620-nm asymmetric antenna, demonstrating the engineering of spectral phase in antenna hotspots by mixing resonances with different strengths.

Coupled plasmonic nanoantennas can be used in this way as a subwavelength resolution phase modulator, as shown in Fig. 3 C and D, Right); the reconstructed modulation functions in the hotspots give insight into the role of the spatial range of resonant antenna modes. This allows controlled realization of another anticipated application of ultrafast plasmonics: hotspot switching. This can be achieved by addressing localized resonances at different times in an excitation pulse through application of a spectral chirp (e.g., by adding dielectric material in the beam path). To demonstrate this concept, we engineer an asymmetric coupled antenna to function as a sub-100-fs spatial hotspot switch.

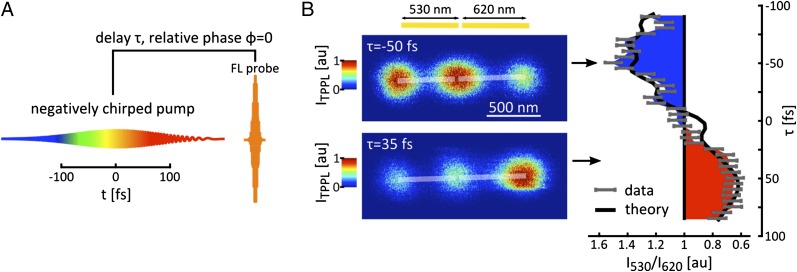
Antennas with 530-nm and 620-nm lengths are chosen as suitable building blocks owing to their resonances at the high- and low-frequency ends, respectively, of the excitation spectrum. The coupled antenna is excited with a −500-fs² chirped pulse. The dynamics of the field is resolved in a pump-probe experiment (Fig. 4A and Materials and Methods). The ratio between the TPPL intensity from the outermost hotspots on the constituent bar antennas is depicted in Fig. 4B (Right, gray points) as a function of pump-probe delay. The spatial asymmetry in the resonances (Fig. 3 C and D, Right) makes the hotspot intensity switch from the short antenna bar to the long antenna bar between τ = −50 fs and τ = +35 fs with contrast ∼2.8. Comparison between experiment and theory based on the resonance structure of the hotspots and the chirp in the excitation pulse (Fig. 4B, Right, solid black line) shows a good agreement between the actual hotspot switching of the antenna and the theoretical behavior for which the antenna was designed. The ultrafast switching can directly be visualized by imaging the antennas with fixed pump-probe delay at −50 fs (Fig. 4B, Upper Left) and 35 fs, respectively (Fig. 4B, Lower Left). This demonstrates the utility of a coupled plasmonic antenna as an ultrafast hotspot switch.

Fig. 4.

A sub-100-fs plasmonic switch. (A) The dynamics of the hotspots are resolved in a pump-probe experiment. (B) Between a pump-probe delay of −50 fs and 35 fs the luminescence intensity switches from the 530-nm antenna bar to the 620-nm antenna bar with a contrast ratio ∼2.8 (Right). Imaging the antenna with these delays fixed demonstrates the sub-100-fs plasmonic switching (Left).

In an intricate plasmonic structure, the local field potential is determined by the eigenmodes of the structure and the dielectric constants of the materials involved (4). In other words, the local spectral amplitude and phase in a hotspot on a plasmonic system are determined by the amplitude and phase profiles of the resonant modes contributing to the hotspot. These modes and the timing with which they are addressed then control the dynamics of the field in the hotspot. Hence, local complex spectra can be readily interpreted by decomposition of the structure into constituent antenna building blocks with specific resonances and coupling constants; consequently, local spectra can be designed in a bottom-up approach by coupling antennas with well-defined resonances. This also implies that, although the control of the dynamics of the near-field ultrafast pulse is based on resonances, an arbitrary shape can be imposed upon the field in a particular hotspot by picking the right combination of structure shapes and material for the constituent antennas.

There are several limitations to this approach. A plasmonic structure does not allow transformation of one arbitrary pulse shape into another arbitrary pulse shape. This means we are designing a particular structure to imprint one particular pulse shape on an impinging, Fourier limited pulse in a particular hotspot (i.e., currently this would be a static “pulse shaper”). The occurrence of absorption in plasmonic structures means that there is a limit on the applicability of time reversal, meaning that there are in fact limitations on the pulse shapes that can be created in a predefined hotspot, starting from, for instance, a Fourier limited pulse.

However, here we have concerned ourselves with the simplest possible incarnations of coupled plasmonic structures and show that the simplest possible designs (single- and double-bar antennas) already lead to a wide variety of possible phase shapes and high-fidelity control over nanoscale field dynamics, using Fourier limited or linearly chirped pulses. With this, we aim to simplify ultrafast plasmonics enough for it to make the transition to a useful research tool for nanometric and femtosecond physics. Investigations at these ultrafast timescales and ultrasmall length scales are rapidly being embraced in fields as diverse as material science, cell biology, and quantum optics. What unites these areas is the transition from research on phenomena in isolated or uniform systems (molecular jets, ultracold atoms, and bulk materials) to nanoscale components interconnected in larger systems (nanostructured surfaces, supramolecular complexes, cells, and nitrogen-vacancy center networks). The concept of plasmonic antennas as elements in near-field femtosecond pulse shapers feeds this paradigm shift with its potential for, for example, nanoscopic coherent control, spatially selective ultrafast spectroscopy, quantum information in complex systems, pulse-shaped scanning probe microscopy, and the possibility of integration in chip-based constructs. For successful transition into these regimes, femtosecond time resolution needs to be combined with high spatial selectivity and complete control of the time evolution of fields with nanometer precision, as we have demonstrated here.

Materials and Methods

Gold nanoantennas, created via e-beam lithography, evaporation, and liftoff, were excited with a 85-MHz pulse train of 120-nm bandwidth, Fourier limited 15-fs pulses on an inverted confocal microscope. Pulse amplitude and phase were measured in the plane of the experiment using a micrometric beta barium borate (BBO) slice and using the MIIPS method. Two-photon photoluminescence (TPPL) of the hotspot of interest was collected in epiconfocal configuration, separated from the excitation light with suitable dichroic mirrors and filters, and focused on a pair of polarization-split avalanche photodiodes (APDs). Excitation power was limited to stay in the quadratic regime. Pulse compensation, creation of the sinusoidal measurement shapes, and delay-line implementation were all done in an adapted, double-pass 4f-pulse shaper. At the start of each experiment the sample was scanned through the focus of the microscope objective with a piezo scanner, yielding TPPL images of the matrices of antennas with each hotspot lighting up. The experiments described in the paper were then performed by positioning one of the hotspots in the focus with the piezo scanner. Subsequently, the phase shape of the pulse was changed, and the corresponding TPPL response of the antenna was recorded. More details are given in SI Materials and Methods.