Cell responses only partially shape cell-to-cell variations in protein abundances in Escherichia coli chemotaxis

Significance

The relationship between form and function is ubiquitous in biology. Using a method (maximum entropy) from statistical physics, we investigated how function regulates form in the context of Escherichia coli chemotaxis. We found that the nearly perfect and robust chemotaxis behavior (function) does not fully determine the cell-to-cell variations of chemotaxis protein abundances (form) in E. coli. We show that additional constraints imposed by the protein synthesis machinery and nonchemotactic cell functions in conjunction with the constraints imposed by the chemotaxis program are required to determine the observed variations of protein abundances. This demonstrates that properties of a modular component (e.g., the chemotaxis signaling module) in a biological network also depend on the system of which the module is a part.

Abstract

Cell-to-cell variations in protein abundance in clonal cell populations are ubiquitous in living systems. Because protein composition determines responses in individual cells, it stands to reason that the variations themselves are subject to selective pressures. However, the functional role of these cell-to-cell differences is not well understood. One way to tackle questions regarding relationships between form and function is to perturb the form (e.g., change the protein abundances) and observe the resulting changes in some function. Here, we take on the form–function relationship from the inverse perspective, asking instead what specific constraints on cell-to-cell variations in protein abundance are imposed by a given functional phenotype. We develop a maximum entropy-based approach to posing questions of this type and illustrate the method by application to the well-characterized chemotactic response in Escherichia coli. We find that full determination of observed cell-to-cell variations in protein abundances is not inherent in chemotaxis itself but, in fact, appears to be jointly imposed by the chemotaxis program in conjunction with other factors (e.g., the protein synthesis machinery and/or additional nonchemotactic cell functions, such as cell metabolism). These results illustrate the power of maximum entropy as a tool for the investigation of relationships between biological form and function.

Cell-to-cell variations in protein abundances or copy numbers are commonly found in genetically identical cells (1, 2). Because protein abundances directly regulate cell responses through signaling networks, a logical form–function relationship would imply that in the context of an adaptive behavior of a cell population (function), these variations among individual cells (form) should themselves be under selection pressures. However, functional implications of cell-to-cell variations of protein abundances are generally not understood well (3).

The relationship between form and function is an abiding theme of biological research (4, 5). The most common way to probe this relationship is through manipulation of form [e.g., perturbing parameters of the system and observing the effects on function (this can be done in vivo, in vitro, or in silico)]. Experiments of this type in recent years have indeed demonstrated functional consequences of cell-to-cell variation in protein abundances; that is, differences in protein abundances can produce distinct lineage commitments in hematopoietic stem cells (6), and covariation in protein abundances has been shown to increase the efficiency of chemotactic responses in Escherichia coli (E. coli) (7, 8). This type of experiment can be illuminating, but it can also be incomplete because the range of perturbations considered is subject to practical limitations as well as the limits of our imaginations regarding what other possibilities exist.

Here, we turn this procedure around and instead ask the question: If we start from an evolutionarily favored function, what general features of form must then exist? In other words, rather than asking what is the impact on function of some selected features of form, we ask what constraints are imposed on form by selective factors operating at the level of function. In the context of cell-to-cell variations of protein abundances, this question becomes the following: How does the ability of individual cells to respond to changes in the local environment shape the nature of variations of protein abundances in a cell population? Addressing this question is important to acquire a better understanding regarding the functional role of the cellular heterogeneity.

We develop a general methodology for asking such questions, based on maximum entropy (MaxEnt) (9, 10). To illustrate, we apply the method to one particular feature of form, cell-to-cell variation in protein abundances or copy numbers in genetically identical cells, in the context of a very well-characterized and highly robust system: chemotaxis in E. coli (11, 12). Using experimental data from cell population-based assays as well as single cell experiments available in the published literature (7, 8, 13–16), we use MaxEnt to ask two distinct but related questions. First, we investigate whether the observed chemotactic responses are sufficient to explain the variations in protein abundances. We find that the answer to this question is “no,” and we hypothesize that additional constraints on the relationships among protein abundances are required, above and beyond the constraints inherent in the chemotactic response itself. The second question we ask relates to the nature of these additional constraints. We show that when constraints jointly imposed by the chemotaxis program itself and by cell functions and processes not directly related to chemotaxis (e.g., processes involved in protein synthesis) determine mean values and pair correlations of the chemotaxis protein abundances in individual cells, the cell population remarkably reproduces the measured chemotactic responses. These results demonstrate the role of nonchemotactic functions in shaping the form of the chemotaxis signaling network module in E. coli, which is widely believed to be relatively isolated (17). This adds another important example of an emerging theme in biology, namely, that properties of a modular component in a biological network depend on the system of which the module is a part (18). In addition to shedding additional light on E. coli chemotaxis, these results illustrate the power of the MaxEnt methodology as a general tool for the investigation of relationships between biological form and function.

Results

E. coli Chemotaxis and the MaxEnt Method.

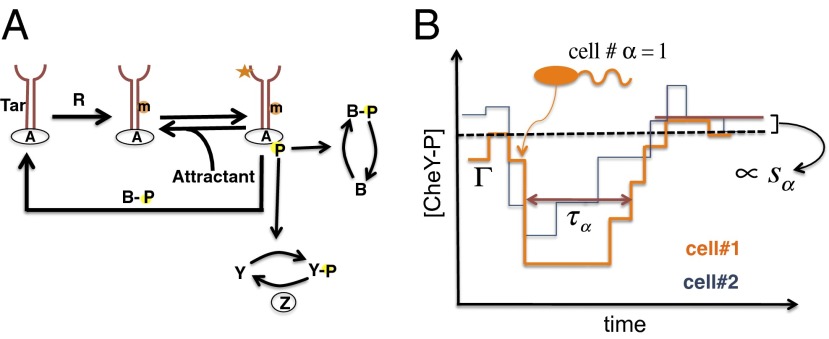
Single E. coli cells sense the presence of attractants such as amino acids in the medium and swim toward the nutrient source. Upon reaching the region of higher nutrient concentrations, the cells return to their prestimulus state of random movements, displaying a nearly perfect adaptive behavior. In individual E. coli cells, membrane-bound chemoreceptor Tar binds to attractant molecules and initiates a series of biochemical signaling reactions (Fig. 1A) leading to a transient dephosphorylation of the phosphorylated form of a key cytosolic protein CheY or CheY-P. CheY-P controls the direction of rotation (clockwise or anti-clockwise); a decrease in CheY-P abundance favors anti-clockwise rotations and propels the single cell toward the attractants (Fig. 1B). The CheY-P abundance slowly increases back to its prestimulus level as the copy number of methylated Tar receptors, which lead to phosphorylation of CheY at an increased rate, is gradually elevated due to a decrease in the demethylation rate in the presence of attractants (Fig. 1A). Throughout the signaling, the methylation/demethylation processes are executed by the enzymes CheR/CheB and the phosphorylation/dephosphorylation processes are carried out by the enzymes CheA-P/CheZ. Because CheY-P abundances in single cells regulate flagellar rotations, the chemotactic response in single E. coli cells can be characterized by variables describing the time scale and the adaptive behavior of the CheY-P kinetics (Fig. 1B); specifically, (i) adaptation time, τ_α, defined as the time the CheY-P abundance (denoted by [CheY-P]) in an E. coli cell (indexed by α) takes to rise up to half of its prestimulus value from the time when attractants were added; (ii) precision of adaptation, s_α, calculated as the absolute value of the relative difference in the steady-state abundance of CheY-P in a single E. coli cell at the prestimulation ([CheY-P]_prestim) and poststimulation ([CheY-P]_poststim) conditions (i.e., s_α = |([CheY-P]_poststim − [CheY-P]_prestim)|/[CheY-P]_prestim); and (iii) the variation of the prestimulus steady-state abundance of CheY-P (or p_α) in an E. coli cell relative to its value at the optimal condition as a relevant variable for characterizing chemotactic responses for the reasons below. Previous experiments and mathematical models pioneered by Barkai and Leibler (19) (henceforth referred to as the BL model) (SI Appendix, Fig. S1 and Tables S1 and S2) demonstrated the robustness of the perfect adaptive nature of the chemotactic response to variations of protein abundances and kinetic rates. However, single cell experiments of the E. coli flagellar motor response showed that the motor can work properly within a 30% variation from the optimal steady-state concentration of CheY-P at about 3 μM (13). The BL model produces substantial changes to steady-state CheY-P abundances against large variations of protein abundances, and thus is unable to explain the robustness of the motor function for such large perturbations. Sourjik and colleagues (7) modified the BL model (the modified BL model; henceforth referred to as the MBL model) to account for the proper functioning of the flagellar motor. A key extension of the MBL model over the BL model was the inclusion of a CheZ-dependent deactivation of CheY-P dephosphorylation (Fig. 1A).

Fig. 1.

Chemotactic response in E. coli. (A) Chemotaxis signaling network for the MBL model. CheA, CheB, CheR, CheY, and CheZ are abbreviated as A, B, R, Y, and Z, respectively. (B) Adaptive kinetics of copy number of CheY-P vary from cell to cell due to variations of protein abundances in individual cells as well as intrinsic noise fluctuations in the signaling reactions. The signaling proteins follow a unique stochastic trajectory, 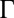, describing the kinetics of chemotaxis signaling in an individual E. coli cell indexed by α. The dashed line shows the cell population-averaged value of steady-state CheY-P abundance. For each stochastic trajectory, we calculate the adaptation time, τ_α (or τ_Γ); the precision of adaptation, τ_α (or s_Γ); and the percentage variation of steady-state abundance of CheY-P, p_α (or p_Γ) (not shown in the figure).

We develop a MaxEnt-based method to quantify the minimally structured cell-to-cell variations in total protein abundances required to reproduce the observed chemotactic responses in single cell- and cell population-based experiments. We considered cell-to-cell variations of total abundances of chemotaxis proteins (20, 21), as well as intrinsic fluctuations in copy numbers of signaling proteins within individual E. coli cells that arise due to the stochastic nature of biochemical chemotaxis signaling reactions (20–22). Upon addition of attractants in the medium at time t = t₀ in an individual cell containing total protein abundances, given by 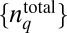(q = 1… N_T, representing the chemotaxis proteins Tar, CheA, CheB, CheR, CheZ, and CheY), the copy numbers of signaling molecules change with time due to the signaling reactions. We define a stochastic trajectory, Γ, representing changes in the abundances of signaling proteins with time in an individual cell by a set ({n_j}, t_n ;{n_j}, t_n−1 ; {n_j}, t_n−2 ; ….; {n_j}, t₁ ; {n_j}, t₀ ; 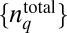) where copy numbers of different proteins, {n_j} [j = 1…N_P; N_P = total number (#) of distinct signaling proteins] change at the times {t₀, t₀ + Δ, t₀ + 2Δ, \x{2026}, t₀ + nΔ}. Δ is taken to be smaller than or of the same order of the smallest reaction time scale (Fig. 2). N_P ≥ N_T, because a protein species can be modified during signaling (e.g., CheY-P is generated from the protein CheY during signaling). We use the MaxEnt technique to estimate the probability distribution of these trajectories (P_Γ), specifically by maximizing Shannon’s entropy (S):

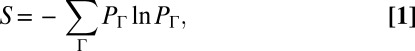in the presence of constraints imposed by experimental measurements pertaining to chemotactic responses or chemotaxis protein abundances. Eq. 1 is also known as the path entropy, and the constrained maximum is also referred to as the maximum caliber (10). We carried out maximization of S in the presence of two types of constraints that capture relevant information (23) regarding E. coli chemotactic responses and the nature of the cell-to-cell variations of total protein abundances:

• i) Constraints characterizing chemotactic responses. Because the essential features of chemotactic responses in a single cell (indexed by α) are described by the variables τ_α, s_α, and p_α, we used average values and variances of these variables over a cell population as constraints.

• ii) Constraints describing the shape of cell-to-cell variations of total protein abundances. We used the average values, as well as the variances and covariances of the protein abundances, as constraints.

Because P_Γ represents the joint distribution P({n_j}, t_n ;{n_j}, t_n−1 ; {n_j}, t_n−2 ; ….; {n_j}, t₁ ; {n_j}, t₀ ; 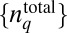), any change in the shape of cell-to-cell variations of total protein abundances or 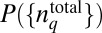will produce changes in P_Γ. We sought to estimate the maximally varying, or the least structured, distribution 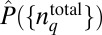consistent with constraints imposed by the available experimental data as described in i or ii (an explicit derivation of the underlying equations is provided in Materials and Methods). Therefore, 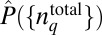represents a probability distribution that is sufficient to characterize what is known about the underlying system (the constraints), without the imposition of any additional assumptions not directly justified by the available empirical data (9, 10). The constraints in i estimate the minimal structure imposed by the chemotactic responses themselves on the distribution of total protein abundances in E. coli cells, whereas the constraints in ii probe the minimal structure in cell-to-cell variations of total protein abundances that is able to reproduce the measured chemotactic responses while remaining consistent with the observed protein abundances. If the distribution of the protein abundances is entirely shaped by the chemotactic responses, the estimated 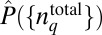will be the same using the constraints in i and the constraints in ii. Our results show, however, that this is not the case. We describe our results in the next sections.

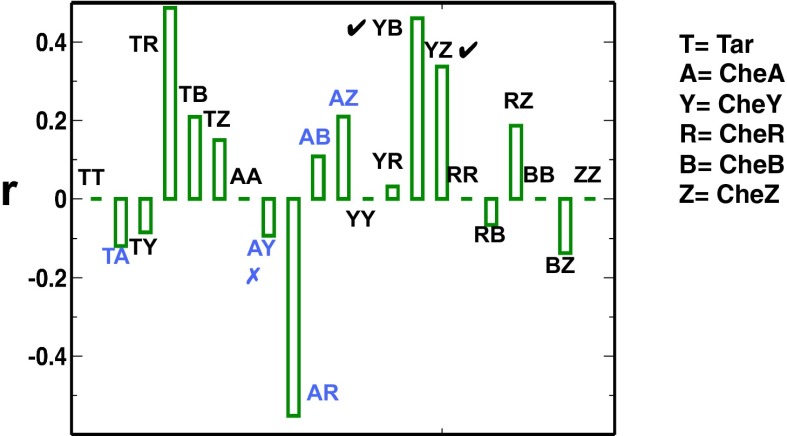
Fig. 2.

Observed chemotactic response imposes pairwise correlations between proteins. We constrained mean values of τ, τ², s, p, and p² to the respective values measured in experiments, that is, 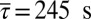, , 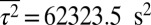, , 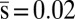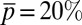and 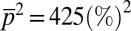, for estimating distributions of protein abundances using our MaxEnt approach. The pairwise Pearson correlation coefficients are calculated for six chemotactic proteins using the MaxEnt distributions (r_MaxEnt) for the MBL model and the a priori uniform distribution (r_uni). We show the difference, 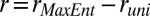for different protein pairs. When cross-correlations between protein pairs are considered, r_uni ≈ 0. Because, by definition, r_MaxEnt = r_uni =1, r = 0 when correlations between the same protein pairs (or variances) are considered. The protein pairs encoded by genes in the same and different operons are shown in black and blue, respectively. The agreement and disagreement with experiments assaying protein expression in single cells and in in vitro cloned gene pairs are shown with a tick and a cross symbol, respectively.

Chemotaxis Itself Is Not Sufficient to Explain Observed Protein Abundance Distributions.

We maximized the entropy (Eq. 1) to evaluate (details are provided in Materials and Methods) the least structured cell-to-cell variations in protein abundances required to produce experimentally observed chemotactic responses and then compared the inferred distribution with the available data pertaining to cell-to-cell variations of E. coli proteins from experimental observations. Specifically, we compared the mean values, variances, and covariances of the least structured distribution with the available measurements. Because all six chemotactic proteins (Tar, CheA, CheR, CheB, CheZ, and CheY) regulate the variables τ_α, s_α, and p_α in single cells, constraining averages and variances of these variables, in principle, could constrain variations of total protein abundances of the chemotactic proteins. When average values of {τ_α} (or 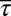), {s_α} (or 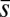), and {p_α} (or 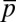) were constrained individually, the corresponding least structured distribution of protein abundances produced small correlations, both positive and negative, between the protein abundances (SI Appendix, Fig. S2). This was in stark contrast to the experimental observation that shows strong positive correlations (≈1) between the proteins CheY and CheZ or CheA and CheY (7, 8) or between CheY and CheB as observed in in vitro experiments using cloned gene pairs (8). The average values of the protein abundances in the inferred distribution showed much larger values compared with their experimental counterparts (SI Appendix, Table S3). 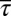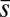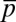When , , and were constrained at the same time, the qualitative features of the least structured distribution of protein abundances did not change (SI Appendix, Fig. S2). Including the variances of the variables, 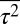, , 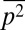and 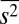in the set of constraints in different combinations increased the magnitude of the correlations between the protein abundances; however, the correlations contained both positive and negative values, and the average values of the protein abundances were still larger compared with their experimental counterparts (SI Appendix, Figs. S2 and S3 and Table S3).

We describe results from a particular case in which the variables 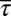, , 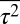, , 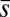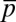and 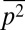were constrained as detailed below to discuss specific agreements and disagreements of the variations of protein abundances with experimental observations and their biological implications. The above constraints produced correlated variations in the protein abundances (Fig. 2 and SI Appendix, Fig. S4); however, the magnitude of the correlations was smaller compared with that observed in experiments. Positive correlations were obtained between abundances of multiple protein pairs (Fig. 2 and SI Appendix, Table S4), including the protein pairs (e.g., CheY-CheZ, CheY-CheB, CheY-CheR, CheR-CheZ, Tar-CheR, Tar-CheB, Tar-CheZ) that are encoded by genes (cheY, cheZ, cheB, mcp, and cheR) residing in the meche operon (7, 8) and the protein pairs (e.g., CheA-CheB, CheA-CheZ) that are encoded by genes residing in two different operons, meche and mocha (contains cheA) (7, 8). When E. coli chemotaxis proteins are encoded by genes in the same operon, they are translated by the same polycistronic mRNA (24); thus, abundances of those proteins are likely to be positively correlated. Therefore, the observed positive correlations for the MBL model between the protein abundances encoded by the meche operon are qualitatively consistent with the notion of coregulated gene expressions for the genes in the same operon. The positive correlation between CheY and CheZ is in direct qualitative agreement with single cell experiments measuring CheY and CheZ simultaneously (7, 8). Positive MaxEnt correlations between other pairs of protein abundances have not been directly measured in single cell experiments. However, the predicted positive correlations between the abundances of CheY-CheB and CheY-CheZ are consistent with in vitro experiments assaying correlations in protein expression using cloned gene pairs (8) (Fig. 2 and SI Appendix, Table S4). Most of the protein pairs producing positive correlations (SI Appendix, Table S4) in the inferred distribution also showed strong pairwise co-occurrence of the encoding genes in 527 bacterial genomes containing at least one chemotaxis gene (8), supporting the concept that the chemotactic functions partially produce the observed correlated variations between these protein pairs qualitatively.

However, the MaxEnt model also produced negative correlations between protein abundances (Fig. 2) for protein pairs (CheB-CheZ, CheR-CheB, and Tar-CheY) encoded by the meche operon and protein pairs (Tar-CheA, CheA-CheY, and CheA-CheR) encoded by the mocha and meche operons. This disagrees with experiments (7), which have demonstrated a positive correlation between abundances of CheA and CheY, and between CheR and CheB, and it also disagrees with in vitro protein expression measurements for cloned gene pairs (8). In addition, the negative correlations between CheB-CheZ, CheR-CheB, and Tar-CheY would seem to contradict the idea that genes in the same operon are likely to produce positive correlations between corresponding protein expressions.

Furthermore, by comparison with data from single cell experiments, the univariate MaxEnt distributions of protein abundances showed larger means and variances and higher order moments for the abundances of CheY, CheZ, and CheA (Fig. 3 A and B and SI Appendix, Figs. S5 and S6). Similarly, the second and higher order moments calculated from the predicted joint distributions of CheY and CheZ (Fig. 3C) or CheA and CheZ abundances showed a similar increased spread of protein abundances in single cells compared with the experiments. In addition, the mean abundances for the other proteins in the inferred distribution were consistently larger than for their measured counterparts. Constraining all six variables, 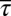, , 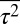, , 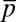, 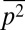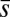and 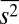, did not produce any qualitative change in the results (SI Appendix, Fig. S2 and Table S3). This shows that regardless of the combination of the constraints, involving the variables describing the chemotactic responses consistently produces a broader distribution with larger mean values and positive and negative covariances and including additional constraints does not lead to a qualitatively better agreement between the inferred distribution and the experiments. This tells us that the distribution of protein abundances in E. coli is subject to additional constraints not yet incorporated into the MaxEnt calculation.

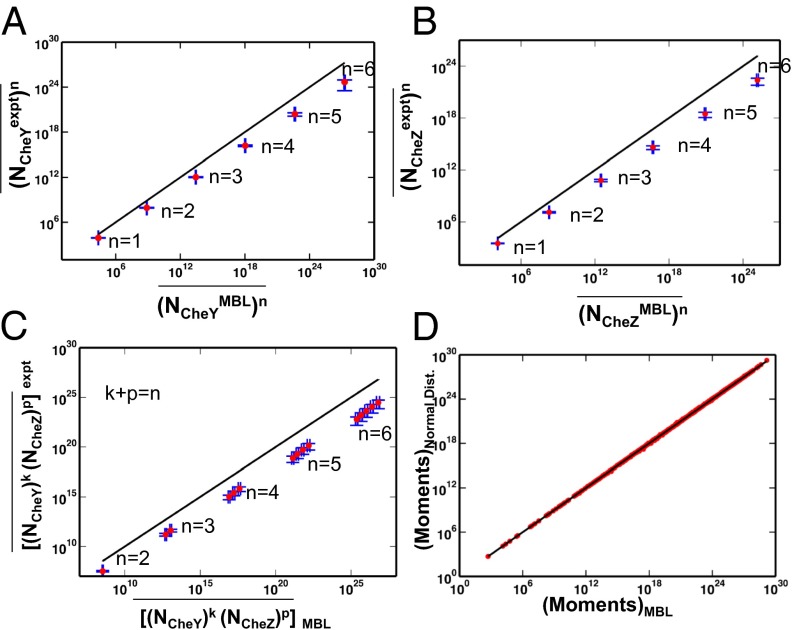
Fig. 3.

Minimally structured distribution of protein abundances enforced by E. coli chemotaxis is broader compared with the observed cell-to-cell variations. (A) Comparison of the moments of CheY abundances calculated from the MaxEnt distribution with the data from single cell experiments by Kollman et al. (7). The y = x line (solid black) is shown for comparison. (B) Similar comparison as in A for CheZ abundances. (C) Similar comparison as in A for the joint distribution of CheZ and CheY abundances. We further quantify the differences between inferred distribution and the experimental observations using χ² (SI Appendix, Table S6) (D) Comparison of the MaxEnt distribution with a multivariate normal distribution. The multivariate distribution is constructed with the mean values and pair correlations equal to those of the MaxEnt distribution. We calculate all the moments up to the sixth order for all six proteins for the MaxEnt and the constructed multivariate normal distribution. The y = x line (solid black) is shown for comparison.

Because the chemotactic program itself does not sufficiently constrain the protein abundance distribution, we hypothesize the importance of additional constraints arising from physical and biochemical processes that control synthesis and other nonchemotactic functions of these different proteins in a cell. Taking a clue from the result that a multivariate normal distribution can be used to approximate to a reasonable extent the inferred distribution 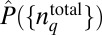in protein abundances (Fig. 3D), we hypothesized that the efficient chemotactic program in individual E. coli cells, along with processes not directly related to the chemotaxis, regulates the mean values and the pair correlations in the chemotaxis protein abundances. We turn to these in the next section.

Mean Values and Pairwise Correlations in Protein Abundances Regulate Chemotactic Responses in E. coli.

Here, we again use the MBL model, but we do not impose constraints on the chemotactic parameters. Instead, we introduce constraints directly on the protein abundances and compare the resulting MaxEnt model with the observed chemotactic response.

We first considered the MaxEnt distribution subject only to constraints on the means of the protein abundances taken from cell population measurements. The model showed exponentially distributed protein abundances with vanishing covariations (details are provided in SI Appendix). This distribution generated chemotactic responses with values for s, p, and τ (in individual cells) that were substantially different from those observed in experiments for WT E. coli (SI Appendix, Fig. S7 and Table S5). We then further constrained the variances and covariances between different protein abundances. Magnitudes of variances and covariances for most of the chemotaxis protein pairs, except CheY-CheA and CheY-CheZ (7), were not directly available from the published experiments. However, as suggested by Kollman et al. (7), a log-normal distribution for all proteins similar to that of CheY and CheZ reproduced the observed average values of s, p, and τ, as well as their distribution, reasonably well (SI Appendix, Fig. S7). Thus, we used covariances calculated from the log-normal distribution for those protein abundances that have not been directly measured in single cell experiments.

With these additional constraints in place, the MaxEnt distribution was a multivariate normal for the protein abundances, and the resulting chemotactic response produced distributions of s, p, and τ that showed excellent agreement with experiments (Fig. 4 A–C and SI Appendix, Fig. S8). We tested this conclusion further by leaving covariances between different pairs of protein unconstrained. Our results show that as long as covariances that minimally connect all the protein abundances are constrained, the generated chemotactic response is in reasonable agreement with the experiments (SI Appendix, Figs. S7, S9, and S10). This represents the minimal set of constraints in protein abundances required to produce the observed chemotactic response (details are provided in SI Appendix). This supports the hypothesis that a combination of constraints imposed by an efficient chemotactic response and other factors (e.g., the protein synthesis machinery and/or the nonchemotactic functions of the chemotaxis proteins) determines the mean values, variances, and covariances that minimally connect all the chemotaxis protein abundances in the WT E. coli.

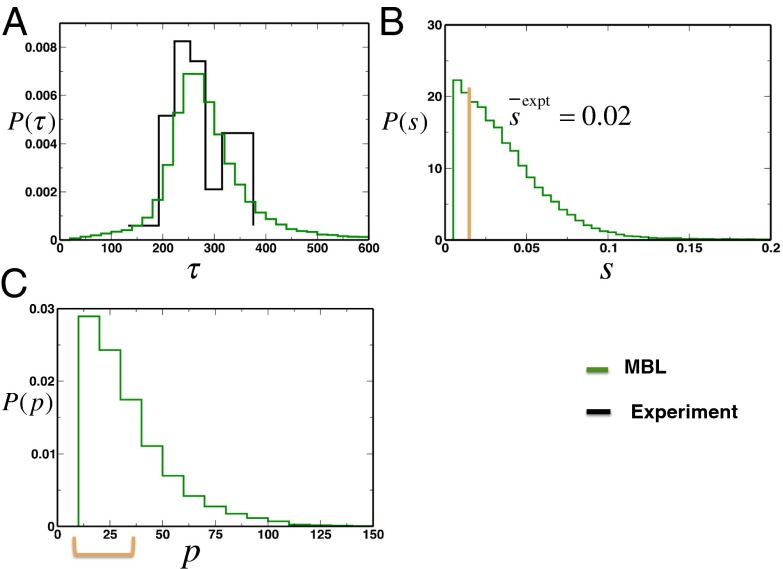
Fig. 4.

Pairwise correlations between protein abundances produce remarkable agreement between the predictions for chemotactic response and experiments in single cells. (A) Distribution of the adaptation time, τ, for the MBL model is shown, along with the experimental data (average value = 245 s; black stairs). (B) Distribution of the precision of adaptation, s, for the MBL model (15). The orange bar indicates the average precision of adaptation observed in WT RP437 (16). (C) Distribution of the percentage variation p in the prestimulus steady state of CheY-P abundance measured from an optimal value (details are provided in Materials and Methods and SI Appendix). The distribution shows that 70% of the cells are within the working range (p = 30%) of the flagellar motor. The allowed range of percentage variation is shown with an orange bar.

Discussion

Examples of form constraining function are ubiquitous in living systems (5). Here, we addressed the inverse question of “how function constrains form” in the context of E. coli chemotaxis. Specifically, using a MaxEnt-based approach, we studied the minimal restriction imposed on cell-to-cell variations of protein abundances by the measured chemotactic response in individual E. coli cells. We found that the observed chemotactic response imposed both positive and negative correlations between protein abundances (Fig. 2 and SI Appendix, Table S4). The positive correlations suggest that the requirement to execute an efficient chemotaxis program, crucial for increased growth or fitness of an E. coli population, leads to selection of processes that can coregulate protein expressions in E. coli. Formation of operons could provide a potential mechanism to generate positively correlated protein expressions (24) because genes in an operon transcribed by the same mRNA are likely to produce coregulated gene expressions. E. coli chemotaxis proteins are encoded by genes residing in two operons, meche and mocha (7, 8). Therefore, the positive correlations of protein abundances in the MBL model in the pairs CheY-CheZ, CheY-CheB, CheY-CheR, CheR-CheZ, Tar-CheR, Tar-CheB, and Tar-CheZ indicate that the requirement of efficient chemotaxis helped in formation of the mocha operon. Also, proteins encoded by genes in different operons can become correlated during translation (8, 25, 26). Therefore, the positive correlations between CheA-CheB or CheA-CheZ could assist in evolutionary selection of such processes.

An intriguing aspect of our results is the imposition of negative correlations in protein abundances by the observed chemotactic behavior. Functional implications of the negative correlations in the chemotaxis signaling kinetics are evident in most of the cases (SI Appendix, Table S4) (e.g., the negative correlation between CheA and CheY abundances; because CheA activates CheY, an increase in the abundance of CheA accompanied by a decrease in the abundance of CheY keeps the abundance of CheY-P unchanged, and thus increases robustness). Surprisingly, this result contradicted the results of single cell experiments, which showed a positive correlation between the protein abundances (7). Furthermore, the same minimally structured distribution produced much larger mean values and higher order moments compared with the experiments (Fig. 3). This led us to hypothesize that mean values and the pair correlations in protein abundances whose primary function is to execute chemotactic signaling in E. coli are largely determined by constraints imposed by both an efficient chemotaxis program and functions directly unrelated to chemotaxis (Fig. 5). Limitations such as a finite pool of RNA polymerases and ribosomes in individual cells (27, 28) or energetic costs for protein synthesis (29) imposed by the protein synthesis machinery could restrict protein expression. These restrictions are manifested in a reduction in cell growth rate when abundances of nonfunctional proteins are increased in bacterial cells (27, 30). A tight regulation of protein abundances is also demonstrated in the results showing that the steady-state protein abundances are remarkably conserved across species (31). Moreover, a chemotaxis protein could be involved in nonchemotactic function as well as cell metabolism [e.g., CheY is linked with the metabolic state of the cell (32)].

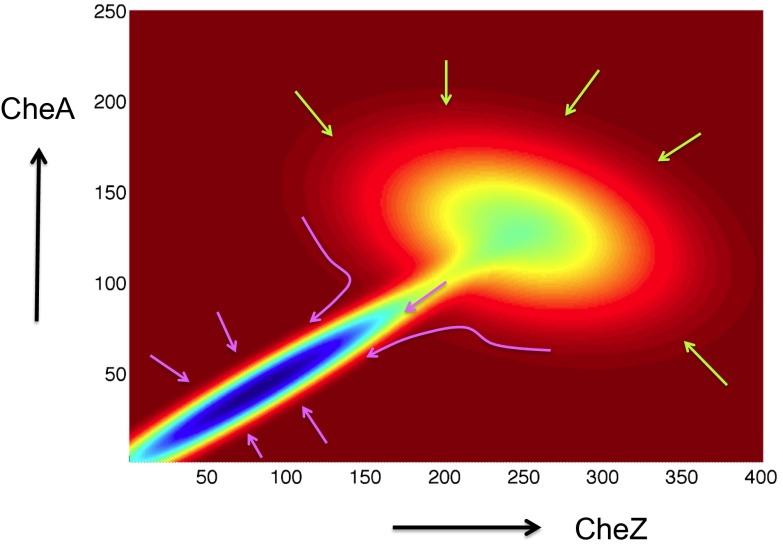
Fig. 5.

Chemotaxis program in combination with nonchemotactic phenotypes shapes the cell-to-cell differences in chemotaxis protein abundances. A schematic diagram shows the dependence of the E. coli fitness (z axis, cooler colors indicate higher values) landscape on variations of CheY and CheA abundances in individual cells. The observed chemotactic response leads (indicated by the green arrows) to the selection of processes that impose correlations between the abundances. However, biochemical and biophysical processes regulating synthesis of chemotactic proteins and additional nonchemotactic cell functions in which chemotaxis proteins also participate drive (indicated by the pink arrows) the E. coli cells to a higher fitness value at lower and more restricted values of protein abundances.

We found that the mean values and the pair correlation functions between protein abundances that minimally connect all the protein abundances are required to be constrained to be able to produce the measured chemotactic responses in individual E. coli cells (SI Appendix, Figs. S7, S9, and S10). In this case, all the pair correlations needed to be constrained to large positive values. Therefore, these nonchemotactic functions lead to selection of a distribution of protein abundances that links all the chemotactic proteins simultaneously with strong positive correlations. This is chosen over the distribution containing weaker pair correlations with positive and negative values as preferred by the chemotactic responses alone. This result, in addition to emphasizing the role of nonchemotactic functions in shaping protein abundances involved in a relatively insulated chemotaxis signaling module, lends support to an emerging theme in biology that properties of a biological module can be influenced by the system in which the module is embedded (14).

Recent work by Salman et al. (33) showed that protein abundances in E. coli and yeast that are involved in metabolism can be scaled to a “universal” non-Gaussian scaling function when protein abundances are scaled with the mean values and the variances. This result urges us to speculate if the scaling of distributions of protein concentrations to a universal scaling function reflects the adequacy of the mean values and the pairwise correlations to produce the essential variations in the phenotype primarily regulated by those proteins in individual cells. It will be worthwhile to investigate the generality of these results for other phenotypes in other cell types. The proposed MaxEnt method is general and can be used to probe such function–form relationships in other living systems.

Materials and Methods

Calculation of MaxEnt (Maximum Caliber) Solutions.

We seek to determine the least structured distribution of total protein abundances, or 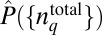, that maximizes S in Eq. 1 in the presence of constraints imposed by the chemotactic response in E. coli. P_Γ is related to 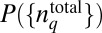by the relation

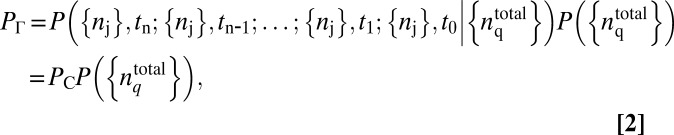where, 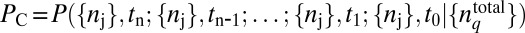is the conditional probability of occurrence of the trajectory, Γ_C, represented by the set, ({n_j}, t_n ; {n_j}, t_n−1 ; …. ; {n_j}, t₁; {n_j}, t₀) for a specific choice of total protein abundances, 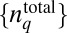. When a variable, f_Γ, describes a chemotactic response (e.g., τ) that depends on the stochastic trajectory Γ produced in a single E. coli cell indexed by α, the cell population-averaged value of f_Γ is given by:

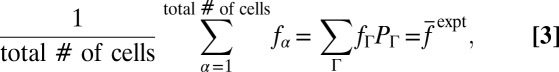where 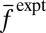denotes the average value of f measured in experiments. We show the result that 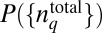maximizes S in Eq. 1 for the constraint in Eq. 3 for simplicity. The result, including additional constraints, is shown in SI Appendix.

Because P_Γ depends on 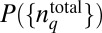via Eq. 2, it is possible to choose different shapes of 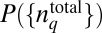that will satisfy the constraint imposed by Eq. 3. We seek to estimate the maximally varying or the least structured distribution 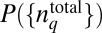, where the minimal structure in the distribution arises solely due to the constraints imposed. For the constraint in Eq. 3, the 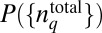that maximizes S (Eq. 1) is given by (a detailed derivation and discussion are provided in SI Appendix):

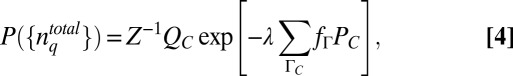where 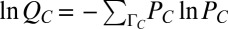. The sum over Γ_C essentially denotes averages over variations of stochastic trajectories due to intrinsic noise fluctuations. The conditional probability P_C can be calculated by solving the master equation (22) describing the biochemical reactions in the signaling model. Q_C is then calculated from P_C. The Lagrange multiplier λ is calculated by substituting the estimated 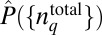in the constraint equation (Eq. 3) and then solving the resulting nonlinear equation. We could also extend this method to a more general scenario, where the underlying intrinsic fluctuations are not quantifiable due to uncharacterized interactions in the signaling network. In such cases, P_C can be inferred by imposing further constraints on lnQ_C, provided data from repeated experiments on the same sample (or individual cell) (34) are available. Additional details are provided in SI Appendix (section IIIA) and refs. 35–37.

When the mean values and the higher order moments of the total protein abundances are constrained instead of the chemotactic responses, the minimally structured distribution 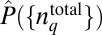is calculated by maximizing the entropy:

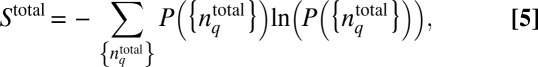instead of Eq. 1 because the structure of 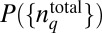is independent of the chemotactic response in this case. The estimation of 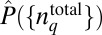for this case is detailed in SI Appendix.

In our simulations, we evaluate the distribution 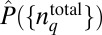in Eq. 4 in the following way. First, we generate a priori distribution 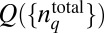by drawing total protein abundances from a uniform distribution U(0, U_H), where U_H is chosen to be roughly 10-fold larger than the experimentally measured mean abundance of the corresponding chemotactic protein (14). Then, the signaling kinetics in each individual cell are simulated by solving the deterministic biochemical reactions for the MBL model in the prestimulus condition (zero attractant concentration) using the rule-based software package BIONETGEN (www.bionetgen.org) (38). Once the kinetics reach the steady state, attractants are added in the medium and the stochastic kinetics of the signaling reactions are simulated using BIONETGEN for a long time when the kinetics reach a steady state. In the sample size (∼70,000 single cells) we considered, each E. coli cell produces a unique chemotactic response composed of a stochastic trajectory Γ describing the time evolution of abundances of signaling proteins; therefore, we identified each trajectory by the single cell that generated it (Fig. 1). The summation over Γ_C in Eq. 4 is performed using this unique association of any trajectory with a single cell. Further details regarding the numerical scheme for constructing 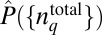in Eq. 4 are provided in SI Appendix (section III and Figs. S11–S13). We carry out simulations for the BL and fine-tuned (39) models following the same scheme.

Data from E. coli Experiments.

The distribution of τ was obtained from Min et al. (15) by digitizing Fig. 3C in that paper using an online Web plot digitizer (http://arohatgi.info/WebPlotDigitizer/). The values of 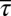and 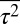are calculated from the distribution thus obtained. The value of 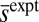for WT RP437 strain was obtained from the work of Alon et al. (16). The average values of the chemotactic protein abundances were taken from Li and Hazelbauer (14). The single cell distributions of CheY, CheZ, CheY-CheZ, and CheA-CheY for the WT RP437 strain were extracted from the work of Kollman et al. (7) using the same graph digitizer.