Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2004 Apr;14(4):507–516. doi: 10.1101/gr.1975204

Reconstructing the Genomic Architecture of Ancestral Mammals: Lessons From Human, Mouse, and Rat Genomes

Guillaume Bourque 1, Pavel A Pevzner 2, Glenn Tesler 3,4
PMCID: PMC383294  PMID: 15059991

Abstract

Recent analysis of genome rearrangements in human and mouse genomes revealed evidence for more rearrangements than thought previously and shed light on previously unknown features of mammalian evolution, like breakpoint reuse and numerous microrearrangements. However, two-way analysis cannot reveal the genomic architecture of ancestral mammals or assign rearrangement events to different lineages. Thus, the “original synteny” problem introduced by Nadeau and Sankoff previously, remains unsolved, as at least three mammalian genomes are required to derive the ancestral mammalian karyotype. We show that availability of the rat genome allows one to reconstruct a putative genomic architecture of the ancestral murid rodent genome. This reconstruction suggests that this ancestral genome retained many previously postulated chromosome associations in the placental ancestor and reveals others that were beyond the resolution of cytogenetic, radiation hybrid mapping, and chromosome painting techniques. Three-way analysis of rearrangements leads to a reliable reconstruction of the genomic architecture of specific regions in the murid ancestor, including the X chromosome, and for the first time allows one to assign major rearrangement events to one of human, mouse, and rat lineages. Our analysis implies that the rate of rearrangements is much higher in murid rodents than in the human lineage and confirms the existence of rearrangement hot-spots in all three lineages.

Molecular evolution studies are usually based on the analysis of individual genes rather than entire genomes. An alternative approach is to infer the evolutionary history of entire genomes, rather than individual genes, on the basis of the analysis of gene orders. Human, mouse, and rat genomic sequences, for the first time, provide the opportunity to accurately estimate the extent of rearrangement events and to derive the putative genomic architecture of ancestral mammalian genomes.

Every genome rearrangement study involves solving a combinatorial puzzle to find a series of genome rearrangements to transform one genome into another. For multichromosomal genomes, the most common rearrangements are reversals (also known as inversions), translocations, fusions, and fissions, and the number of such rearrangements in a most parsimonious scenario is known as the genomic distance between multichromosomal genomes. Finding the genomic distance is a difficult combinatorial problem. The shortcoming of early genome rearrangement studies is that they considered breakpoints independently without revealing combinatorial dependencies between related breakpoints. Kececioglu and Sankoff (1995) were the first to recognize the importance of dependencies between breakpoints and to come up with an approximation algorithm for the genomic distance problem in the case of unichromosomal genomes (reversals only). Hannenhalli and Pevzner (1995a), Tesler (2002a), and Ozery-Flato and Shamir (2003) further developed a polynomial-time algorithm for the genomic distance problem, that is, for computing a most parsimonious scenario to transform one genome into another by reversals, translocations, fusions, and fissions of chromosomes. These results, although useful, do not yet yield a meaningful estimate of the number of the rearrangement events. The problem is that the genomic sequences provide evidence for both microrearrangements (e.g., intrachromosomal rearrangements with a relatively small span) and macrorearrangements (e.g., intrachromosomal rearrangements of larger span, as well as interchromosomal rearrangements). The existing rearrangement algorithms do not distinguish between these two types of rearrangements. Because some microrearrangements may be caused by fragment assembly errors, mixing micro- and macrorearrangements within one rearrangement scenario may produce a distorted picture greatly influenced by errors in assembly of draft genomic sequences. It is widely acknowledged that the existing draft genomic sequences are not free from assembly errors. Because the human assembly was subject to finishing and the mouse assembly was verified (to some extent) by existing physical maps, we believe that these errors do not affect the order of synteny blocks, but rather, rearrange regions within synteny blocks. Such local assembly errors are manifested as fictitious microrearrangements.

Multiple microrearrangements within synteny blocks call for development of new synteny block generation algorithms that adequately address the complex rearrangement history of mammalian genomes. Recently, Waterston et al. (2002) and Pevzner and Tesler (2003a) described two different approaches to synteny block generation that produced remarkably similar results. Kent et al. (2003) described another approach to analyze similar data, but produces something different than synteny blocks. The GRIMM-Synteny algorithm described in Pevzner and Tesler (2003a) has two important features; (1) it preserves information about microrearrangements within synteny blocks and allows one to analyze microrearrangement history of every synteny block; (2) it can be extended easily from analysis of synteny blocks in two genomes to analysis of three or more genomes. As a result, GRIMM-Synteny allows one to study micro- and macrorearrangements separately and to estimate the number of both macrorearrangements and microrearrangements between human, mouse, and rat. This separation into macro- and microrearrangements is an artificial one depending on the choice of parameters, and we hope that in the future, more natural criteria will be found to separate them.

METHODS AND RESULTS

Synteny Blocks

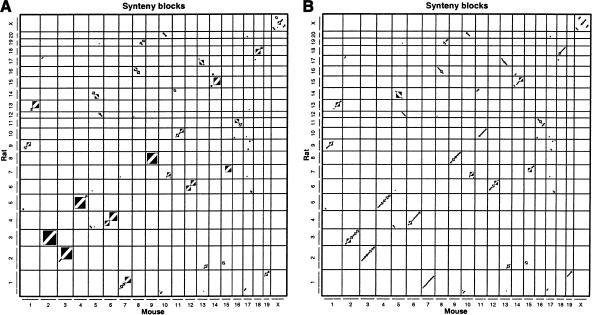
We demonstrate that human and rat share 417 synteny blocks of size at least 300 kb, on the basis of the current assemblies. (Human and mouse share 394, whereas mouse and rat share 162.) Rearrangements in the mouse lineage further break some of the human–rat synteny blocks into smaller blocks, thus creating an even more granular representation of comparative genomic architecture of three species (Fig. 1). However, many of these newly formed synteny blocks are too short to pass the 300-kb block-length threshold, so the number of three-way human–mouse–rat synteny blocks of length 300 kb or longer is reduced to 391 (see Tables 1 and 2 for details).5

Figure 1.

Figure 1

Open in a new tab

(A) The 162 two-way synteny blocks between mouse and rat, of size at least 300 kb, computed by direct two-way comparison of mouse and rat. Synteny blocks are shown as rectangles with a diagonal stripe to indicate direction. (B) The 391 three-way human–mouse–rat syntenic blocks of size at least 300 kb, shown in their mouse–rat coordinates. Introducing human splits of many of the synteny blocks in A into smaller ones in B, and also removes regions that do not have a human homolog. Higher quality versions of these plots are available in the Supplemental materials.

Table 1.

From Alignments to Two-Way Synteny Blocks

Human—mouse Human—rat Mouse—rat
# PatternHunter alignments 2,155,195 2,202,096 14,612,360
# Two-way anchors 642,542 598,632 1,379,600
300 kb two-way synteny blocks:
   # Blocks 394 417 162
   # Macro-rearrangements 340 344 123
   # Micro-rearrangements 3,744 4,116 7,421
   # Breakpoint region re-uses 265 254 77
   # Breakpoints per breakpoint region H: 1.64—1.83 H: 1.59—1.75 M: 1.46—1.73
      (with chromosome ends-w/o chromosome ends) M: 1.64—1.81 R: 1.59—1.74 R: 1.46—1.74
   Mean synteny block length (kb) H: 6,851 H: 6,400 M: 15,288
M: 6,133 R: 6,108 R: 16,348
   Maximum synteny block length (kb) H: 79,289 H: 55,358 M: 157,726
M: 64,401 R: 49,813 R: 169,760
   Total synteny block length (kb) H: 2,699,430 H: 2,668,876 M: 2,476,643
M: 2,416,552 R: 2,546,960 R: 2,648,380
   Total synteny block length (% of genome) H: 89.40% H: 88.39% M: 96.10%
M: 93.76% R: 93.64% R: 97.37%
   Mean breakpoint region length (kb) H: 569 H: 610 M: 254
M: 253 R: 393 R: 406
   Maximum breakpoint region length (kb) H: 26,092 H: 26,110 M: 3,549
M: 6,469 R: 7,555 R: 4,057
   Total breakpoint region length (kb) H: 211,214 H: 240,150 M: 36,103
M: 94,731 R: 155,580 R: 57,251
   Total breakpoint region length (% of genome) H: 6.99% H: 7.95% M: 1.40%
M: 3.68% R: 5.72% R: 2.10%
1 Mb two-way synteny blocks:
   # Blocks 280 278 105
   # Macro-rearrangements 246 243 84
   # Micro-rearrangements 4,270 4,796 8,216
   # Breakpoint region re-uses 193 190 56
   # Breakpoints per breakpoint region H: 1.65—1.91 H: 1.64—1.91 M: 1.50—1.98
      (with chromosome ends-w/o chromosome ends) M: 1.65—1.89 R: 1.64—1.89 R: 1.50—2.00
   Mean synteny block length (kb) H: 9,821 H: 9,820 M: 23,876
M: 8,682 R: 9,265 R: 25,457
   Maximum synteny block length (kb) H: 79,917 H: 88,198 M: 157,726
M: 64,954 R: 84,258 R: 169,760
   Total synteny block length (kb) H: 2,749,840 H: 2,729,972 M: 2,507,026
M: 2,430,879 R: 2,575,550 R: 2,672,970
   Total synteny block length (% of genome) H: 91.07% H: 90.41% M: 97.27%
M: 94.32% R: 94.69% R: 98.27%
   Mean breakpoint region length (kb) H: 605 H: 680 M: 58
M: 315 R: 488 R: 393
   Maximum breakpoint region length (kb) H: 25,096 H: 25,821 M: 3,340
M: 6,073 R: 43,357 R: 10,614
   Total breakpoint region length (kb) H: 155,553 H: 172,629 M: 4,905
M: 81,913 R: 125,515 R: 32,994
   Total breakpoint region length (% of genome) H: 5.15% H: 5.72% M: 0.19%
M: 3.18% R: 4.61% R: 1.21%
Open in a new tab

The information in this table only considers two species at a time; alignments with the third species are not considered. Quantities that differ between the two species are marked with H, R, or M, to denote the separate measurements. The lengths of breakpoint regions include those between synteny blocks, and exclude those at chromosome ends.

Table 2.

Three-Way Human–Mouse–Rat Synteny Blocks of Size of Least 300 kb or 1 Mb in Human

Human Mouse Rat
Chromosomes included 1—22, X 1—19, X 1—20, X
Total length (Mb) 3020 2577 2720
300 kb three-way synteny blocks
   # Blocks 391 391 391
   Mean synteny block length (kb) 6,702 5,994 6,358
   Maximum synteny block length (kb) 79,235 64,310 71,003
   Total synteny block length (kb) 2,620,531 2,343,664 2,486,156
   Total synteny block length (% of genome) 86.79% 90.94% 91.41%
   Mean breakpoint region length (kb) 763 446 548
   Maximum breakpoint region length (kb) 26,140 6,489 11,270
   Total breakpoint region length (kb) 280,751 165,616 202,601
   Total breakpoint region length (% of genome) 9.30% 6.43% 7.45%
1 Mb three-way synteny blocks
   # Blocks 289 289 289
   Mean synteny block length (kb) 9,225 8,156 8,643
   Maximum synteny block length (kb) 79,879 64,895 71,394
   Total synteny block length (kb) 2,666,132 2,357,154 2,497,941
   Total synteny block length (% of genome) 88.30% 91.46% 91.84%
   Mean breakpoint region length (kb) 883 560 716
   Maximum breakpoint region length (kb) 26,140 6,897 11,383
   Total breakpoint region length (kb) 235,003 150,575 191,757
   Total breakpoint region length (% of genome) 7.78% 5.84% 7.05%
Open in a new tab

The lengths of breakpoint regions include those between synteny blocks, and exclude those at chromosome ends.

Although the Hannenhalli-Pevzner theory provided efficient tools to study rearrangements between two genomes, integration of data from multiple genomes (genome phylogeny) represent a more difficult task. Initial work on this topic was based on breakpoint distances between pairs of genomes (Blanchette et al. 1997; Sankoff and Blanchette 1997; Moret et al. 2001). Recently, Bourque and Pevzner (2002) proposed a new approach, the Multiple Genome Rearrangement Algorithm (MGR), and demonstrated important advantages of the genomic distance over the previously used breakpoint distance. Alternative methods have also been developed for the study of rearrangement scenarios in multiple genomes (Siepel et al. 2001; Moret et al. 2002; Caprara 2003), but so far, these methods have only been applied to unichromosomal genomes.

Using the 391 three-way blocks, MGR reveals evidence of at least 293 pairwise macrorearrangements between human and mouse, 299 between human and rat, and 100 between mouse and rat (these are different from the figures for macrorearrangements in Table 1, which were based on GRIMM-Synteny's two-way synteny blocks that were constructed without regard to the third genome), and constructs a three-way rearrangement scenario between human, mouse, and rat. The constraints of fitting all three genomes into the same scenario increase the pairwise distances slightly to 298, 303, and 107, respectively, within the three-way scenario. Within the 391 three-way blocks, there is evidence of at least 1070 microrearrangements between human and mouse, 1533 between human and rat, and 1260 between mouse and rat (although many of them may be artifacts of incorrect assemblies).

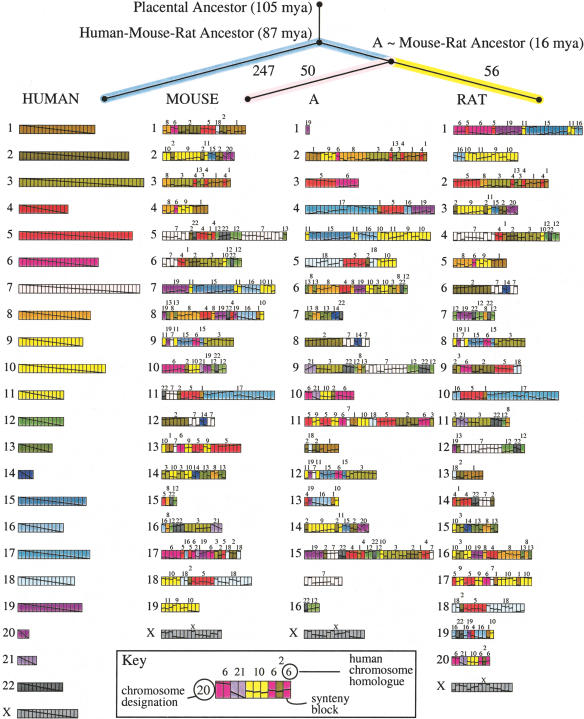
MGR further identifies the putative murid rodent ancestor (more precisely, it computes a possible median ancestor of human, mouse, and rat; this median is a close approximation to the last common ancestor of mouse and rat; see the tree in Fig. 3, below) and estimates the number of rearrangement events on the evolutionary path from the ancestor to human, mouse, and rat. This reconstruction suggests that the ancestral murid rodent genome retained many previously postulated chromosome associations of the placental ancestor. This analysis gives an estimated rate of 3.2 chromosomal rearrangements per million years on the mouse branch from the murid rodent ancestor; 3.5 chromosomal rearrangements per million years on the rat branch; and 1.6 chromosomal rearrangements per million years on the human branch (these rates are estimated by taking the ratio between the number of rearrangements in the putative scenario recovered and the estimated time of divergence). Our results imply that rodents may have unusually rapid chromosome alterations. The sequencing data for chimpanzee and dog may soon shed further light on the comparative rates of rearrangements in different branches of the mammalian evolutionary tree. Our three-way analysis of rearrangements within particular regions, such as the X chromosome or a large preserved region of human chromosome 17, mouse chromosome 11, and rat chromosome 10 (h17/m11/r10) leads to a reliable reconstruction of the genomic architecture of the murid ancestor of these regions, and for the first time, allows one to assign the major rearrangement events to one of human, mouse, and rat lineages.

Figure 3.

Figure 3

Open in a new tab

Ancestral murid rodent genome (A) and evolutionary tree computed by MGR, using mouse and rat with human as an outgroup. Each genome is represented as an arrangement of 391 synteny blocks (longer than 300 kb) as computed by GRIMM-Synteny. The synteny blocks are each represented as one unit, regardless of their length in nucleotides. Chromosomes with too many blocks are split into two lines. Each human chromosome is assigned a unique color, and a diagonal line is drawn through the whole chromosome. In other genomes, this diagonal line indicates the relative order and orientation of the rearranged blocks. The phylogram at the top of the figure indicates the number of rearrangements required to convert each genome (human, mouse, rat) into A, as computed by MGR. The estimated dates of divergence are from Springer et al. (2003).

Summary of Methods

We compared the following assemblies: Human (April 2003, NCBI build 33); Mouse (Feb. 2003, NCBI build 30); and Rat (June 2003, Baylor HGSC v. 3.1). They were first repeat masked by the UCSC Genome Bioinformatics group (Kent et al. 2002) using RepeatMasker (A.F.A. Smit and P. Green, unpubl.) and TandemRepeatFinder (Benson 1999). A number of software tools have become available recently to generate all interesting local alignments for entire mammalian genomes (Schwartz et al. 2000; Kent 2002; Ma et al. 2002; Couronne et al. 2003). Local alignments used in this study were produced by Bin Ma using PatternHunter (Ma et al. 2002).

PatternHunter generated ∼2.1 million human–mouse alignments, 2.2 million human–rat alignments, and 14.6 million mouse–rat alignments, with sizes ranging from 30 to ∼24,000 bp. We discriminate between alignments of segments that are present in a single copy in each of the genomes (such alignments are called anchors in Waterston et al. 2002) and alignments of segments that are repeated in at least one of the genomes. For the goals of rearrangement analysis, the latter alignments have to be removed from further consideration.

Because the existing repeatmasking tools are far from perfect, PatternHunter's output, similar to other genome-scale alignment tools, is contaminated by repeats. We remove this contamination and combine the remaining similarities into two- and three-way anchors by the algorithm described below. We ran these anchors through GRIMM-Synteny (Pevzner and Tesler 2003a) to produce two- and three-way synteny blocks at various resolutions. We further analyzed rearrangements of these blocks, estimated the number of macrorearrangements and microrearrangements in human, mouse, and rat lineages, and reconstructed a putative genomic architecture of the murid rodent ancestor. The three-way blocks were used to create a putative rearrangement scenario for three species using MGR (Bourque and Pevzner 2002). The three sets of two-way blocks were analyzed for breakpoint reuse.

Some of these steps are illustrated for h17/m11/r10 in Figure 2. A related illustration for X chromosome evolution will appear in the Rat Genome Sequencing Project Consortium 2004.

Figure 2.

Figure 2

Open in a new tab

Region on human chromosome 17, mouse chromosome 11, rat chromosome 10. (A) Local two-way similarities produced by PatternHunter (darker ones are longer; some short mouse–rat ones were removed for legibility). Synteny blocks appear as ±45° diagonals. Repeats tend to appear as discrete grids with irregular spacing. (B) After removing repeated regions and combining close alignments, GRIMM-Synteny computes 19 large-scale synteny blocks (at least 300 kb). The same synteny blocks are shown in each pair of species, using consistent colors. (C) The arrangement (order and orientation) of the 19 synteny blocks in this region is shown for each genome. MGR determined that there is a unique median ancestor associated with the most parsimonious evolutionary scenarios of the three genomes in this region; note that it coincides with mouse. The arrangement of blocks in this region implies there were at least 12 inversions between human and the median, and at least two inversions between rat and the median. The chronological order of the inversions cannot be inferred from this method. Note also that the minimum number of inversions required to convert the human block order in this region into the rat order is 14, so the solution shown is optimal, and all optimal solutions have equal block arrangements on median and mouse.

From Local Alignments to Anchors

Constructing Two-Way Anchors

The assemblies were repeat masked and PatternHunter produced local alignments between two repeat-masked sequences. However, as repeat masking is not perfect, many repeats still survived masking, resulting in multiple hits on the same genomic coordinates. The genome rearrangement algorithms are not designed to work with repeated regions, and all repeats have to be discarded before the rearrangement analysis starts. We separated the unique hits from the repeats by the following algorithm, which we explain using human and mouse.

The PatternHunter alignments are base-by-base alignments between an interval of a human chromosome and an interval of a mouse chromosome. Each alignment is between an interval chromosome; start...end for human and chromosome, start...end for mouse, and has a sign σ = 1 if these are aligned in the forward direction or σ = -1 if one of these is aligned to the reverse complement of the other. Dot plots of their locations in h17/m11/r10 are shown in Figure 2A. Some of the local similarities produced by PatternHunter correspond to similarities between nonrepetitive regions, whereas others consist of repeated regions. There are also local similarities that are combinations of repeated and unique regions.

The unique hits and repeats are separated as follows.6

GRIMM-Anchors-2d

  1. Form the union of all human intervals. Two positions in this union are contiguous if they are one nucleotide apart on the same chromosome and some alignment contains them both. Decompose this union into maximally contiguous regions. Call each region a superinterval.

  2. Form mouse superintervals in the same fashion.

  3. Form a bipartite graph whose vertices are the human and mouse superintervals. Connect a human superinterval to a mouse superinterval by an edge if PatternHunter reported any alignments between portions of these superintervals. Such alignments are called supporting alignments.

  4. Graph components consisting of a single edge correspond to alignments of unique regions. (They also may correspond to tandem repeats only found in one region of each genome, which is acceptable for our purposes.) If all of its supporting alignments have the same sign σ, we output a two-way anchor whose coordinates are the coordinates of the superintervals and whose sign is σ. If they do not all have the same sign (due to near-palindromatic sequences or other causes), we discard it.

  5. Graph components consisting of more than one edge are considered to be repeat families and are discarded. Ideally, a repeat family should give a component that is a complete bipartite graph between its human and mouse superintervals.

We formed 642,542 human–mouse anchors, 598,632 human–rat anchors, and 1,279,600 mouse–rat anchors by this procedure, ranging in size from 30 bp up to about 14,000 bp. (Although PatternHunter reported some larger alignments, they were classified as repeat families by this procedure and discarded.) Next, these were input to GRIMM-Synteny to construct two-way synteny blocks for breakpoint reuse analysis (see below), and separately, they were combined into 291,000 three-way human–mouse–rat anchors, as described below.

We emphasize that the produced anchors do not necessarily represent similarities within human and mouse genes, but may also represent similarities between noncoding regions. This is a departure from the previous gene order comparison approach of genome rearrangement studies. It allows us to bypass the difficult issues of gene annotation and ortholog identification, which are not necessary for genome rearrangement studies.

The processing of PatternHunter local alignments described above may remove some unique regions if such regions are combined with repeats in the PatternHunter output. However, the number of such discarded unique regions is typically small compared with all unique regions, and removing such regions does not have a serious effect on the constructed synteny blocks. This shortcoming of available repeat-masking tools can be addressed by a more involved analysis of the graph components with multiple edges, and we will consider them in future research, unless the accuracy of repeat masking improves.

From Two-Way Anchors to Three-Way Anchors

Constructing Three-Way Anchors

The GRIMM-Anchors-2d algorithm identifies three sets of two-way anchors—human–mouse, human–rat, and mouse–rat. For example, there is a human–mouse anchor (H,M,σ) with H representing the interval on human chromosome 1, positions 1009893 through 1010038; M representing the interval on mouse chromosome 4, positions 152700531 through 152700679; and σ = -1 to indicate that either of these intervals is aligned to the reverse complement of the other.

The three sets of two-way anchors were combined into 291,000 three-way anchors as follows.

We first identify certain triples of two-way anchors between human–mouse, human–rat, and mouse–rat as follows: (H1,M1,σ1), (H2,R2,σ2), (M3,R3,σ3), in which Hi, Mi, Ri represent coordinate intervals and σi = ± 1. Specifically, we identify anchors such that the intervals H1, H2 overlap, M1, M3 overlap, and R2, R3 overlap. If the signs are consistent (σ1σ2σ3 = + 1), then we output a three-way anchor whose coordinates are (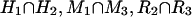Inline graphic). The signs are 1 for human, σ1 for mouse, σ2 for rat.

This procedure generalizes to producing k-way anchors from two-way anchors in a straightforward way, but the details are tedious and will not be stated here.

From Anchors to Synteny Blocks

Current genomic sequences provide evidence that the human, mouse, and rat genomes are significantly more rearranged (as compared with each other) than previous studies (on the basis of lower-resolution gene order data) revealed. Moreover, they indicate that a large proportion of previously identified conserved segments (i.e., segments with identical order of orthologous genes and other genomic regions whose counterparts in each genome can be unambiguously defined) are not really conserved, as there is evidence of multiple microrearrangements in many of them. We study synteny blocks instead of conserved segments. Intuitively, the synteny blocks are segments that can be converted into conserved segments by microrearrangements. The synteny blocks do not necessarily represent areas of continuous similarity between all of the genomes. Instead, they usually consist of short regions of similarity that may be interrupted by non-similar regions and gaps. Most synteny blocks are subject to microrearrangements within these blocks.

Synteny blocks do not cover the entire genome, as typically, there is a gap (called a breakpoint region) between every two consecutive synteny blocks. Although in some cases, there is either no gap or a very small one, they can also be quite large; our 300-kb human–mouse–rat blocks have 112 human breakpoint regions <100 kb and 256 >100 kb (not counting chromosome ends). The largest breakpoint region is 26 Mb long. The exact positions of breakpoints within these regions are unknown.

In this section, we assume that a set of nonoverlapping three-way anchors is given, and the goal is to construct the synteny blocks on the basis of these anchors. False ortholog assignments, missing orthologs in one of the species, and microrearrangements make it nontrivial to find synteny blocks conserved across all three species. In Pevzner and Tesler (2003a), we described the GRIMM-Synteny algorithm for determining large-scale synteny blocks from two-way anchors. It combines anchors that are close, even if their ordering in the two genomes is not consistent due to microrearrangements. In the present study, we applied the exact same procedure to three-way anchors. GRIMM-Synteny combines collections of close anchors together, and those whose span is at least the minimum block size C (another user-specified parameter) are output as synteny blocks, whereas the smaller ones are discarded. However, it is necessary to define when three-way anchors are close.

The distance between two points (h1,m1,r1) and (h2,m2,r2) in the same chromosome triple is defined as the Manhattan distance |h2-h1|+|m2-m1|+|r2-r1|. The distance between two points in different chromosome triples is defined as infinity. The distance between two anchors on the same chromosome triple is the distance between their nearest endpoints. Two anchors are regarded as close when their distance is less than the gap threshold G, which is a user-specified parameter.

The number of synteny blocks found by GRIMM-Synteny depends on parameters, G and C. For example, with the 291,000 three-way anchors, at C = 300 kb and G = 450 kb, we found 391 synteny blocks, whereas at C = 100 kb and G = 150 kb, we found 662 synteny blocks. However, smaller syntenic blocks assignments are less reliable, as they may be caused by false orthologs and sequencing errors. We emphasize that the shorter the synteny block, the larger the chance that it reflects spurious similarities (as produced by genomic-scale similarity search tools as PatternHunter) or duplications/gene loss events that remain beyond our genome rearrangement analysis. As a result, short synteny blocks have to be discarded. Three-way blocks are verified by similarities in all three genomes, and are therefore more reliable than two-way blocks.

The chosen values of G and C result in a classification of the anchor arrangements. We define microrearrangements as rearrangements of anchors within a synteny block, and macrorearrangements as rearrangements of the order and orientations of the synteny blocks.

DISCUSSION

From Synteny Blocks to Rearrangement Analysis

In the context of an analysis of rearrangements, genomes are viewed as signed permutations, in which each integer corresponds to a unique gene/marker or, as in the current study, a unique synteny block and the sign corresponding to its orientation. The goal is to recover a most parsimonious scenario that can explain the observed data. The MGR (Multiple Genome Rearrangements) algorithm (Bourque and Pevzner 2002) constructs an evolutionary tree, whereas seeking to minimize the number of reversals, translocations, fissions, and fusions. It is based on the Hannenhalli-Pevzner theory of rearrangements (Hannenhalli and Pevzner 1995a,b) and uses a fast modification of their algorithm (Tesler 2002a,b; Ozery-Flato and Shamir 2003) available via the GRIMM Web server at http://www-cse.ucsd.edu/groups/bioinformatics/GRIMM/index.html.7

In the current application, with only three genomes, the problem is to find the ancestral synteny block order that minimizes the total number of rearrangements required to convert each of the three genomes into the median ancestor. The algorithm finds this ancestor by iteratively performing rearrangements in one of the three genomes in a manner such that they are slowly merged together. The choice of the rearrangements to be carried out and their order is of utmost importance. See Bourque and Pevzner (2002) for a full description of the procedure.

MGR identifies the putative murid rodent ancestor and estimates the number of rearrangement events on the evolutionary path from this ancestor to human, mouse, and rat (Fig. 3). A step-by-step breakdown of the rearrangement events along the edges of this tree for h17/m11/r10 is shown in Figure 2C.

Running MGR on the 391 three-way synteny blocks of at least 300 kb common to human, mouse, and rat produced the median ancestor (A, shown in Fig. 3).8 At this level of granularity, A is the mouse–rat ancestor and is close to the last common murid ancestor. The recovered scenario requires a total of 353 rearrangements (247 from A to human, 50 from A to mouse, and 56 from A to rat). The path from human to the mouse–rat ancestor consists of two subpaths (one from human to human–mouse–rat ancestor and another from the human–mouse–rat ancestor to the mouse–rat ancestor). A recent study (Stanyon et al. 2003) implies that most of the 247 rearrangements from A to human may have occurred on the latter path, most likely on the subpath of this path leading from the squirrel–mouse–rat ancestor to the mouse–rat ancestor. Human acts as an outgroup and we can consider the mouse–rat ancestor recovered as an approximate murid rodent ancestor.

We define a chromosome association as synteny blocks from two different human chromosomes that are adjacent on a single chromosome in another genome [i.e., fragments of human chromosomes 3 and 21 fused together (denoted 3/21) on mouse chromosome 16] or in an ancestor. The reconstruction suggests that the ancestral murid rodent genome retained many previously postulated chromosome associations of the placental ancestor like 3/21, 4/8, 12/22, 16/19 (Murphy et al. 2003; Stanyon et al. 2003). Because human is so distant from the putative murid rodent ancestor, features of this ancestor can also be studied by looking at how mouse chromosomes are conserved or perturbed in the rat genome and in the ancestor recovered. Some mouse chromosomes are associated both in rat and in A (synteny blocks from different mouse chromosomes adjacent in another genome), such as mouse chromosomes 1/4, 1/17, 5/6, 7/19, 8/14, and 10/17. These associations are probably older than the murid rodent ancestral genome. Mouse chromosome syntenies that are well preserved in both rat and A are also of interest. They consist of mouse chromosomes 3, 4, 6, 9, 12, 19, X. A different version of Figure 3, color-coded based on mouse chromosomes (instead of human chromosomes), can be found in the Supplemental materials available online at www.genome.org.

The Mouse–Rat ancestor is located ∼16 million years ago (Mya) and the Human–Mouse–Rat ancestor ∼87 Mya (Springer et al. 2003), giving an estimated rate of 3.2 chromosomal rearrangements per million years on the mouse branch from A; 3.5 chromosomal rearrangements per million years on the rat branch from A; and 1.6 chromosomal rearrangements per million years on the human branch from A.9 Our results imply that rodents may have unusually rapid chromosome alterations. The sequencing data for chimpanzee and dog may soon shed further light on the comparative rates of rearrangements in different branches of the mammalian evolutionary tree.

Our previous analysis (Pevzner and Tesler 2003a) of human and mouse X chromosomes revealed 11 synteny blocks of 1 Mb and longer and provided evidence for at least seven inversions on the evolutionary path from human to mouse. Our current analysis of the human, mouse, and rat genomes reveals 16 three-way blocks of length 300 kb and longer; we decided to use the 300-kb threshold for synteny block length in this three-way comparison, as three-way alignments are less likely to be caused by spurious similarities. A possible step-by-step breakdown of the rearrangement events with these markers along the edges of this tree for the X chromosome is shown in the Rat Genome Sequencing Project Consortium 2004. There are five events on the branch from A to mouse and five events on the branch from A to rat. There are five events on the path from A up to the human–mouse–rat ancestor (HMR) and then back down to human; low-resolution outgroup data from the dog genome (Kirkness et al. 2003) and the cat and cow genomes (Murphy et al. 2003) suggests that either all five of these events occurred on the HMR to A edge, or that four of them did, and just one was on the HMR to human edge. The former possibility would be consistent with Lahn and Page (1999).

Our analysis of h17/m11/r10 reveals 19 three-way blocks of length 300 kb and longer. A possible step-by-step breakdown of these rearrangement events are shown in this work (Fig. 2C). The scenario recovered is guaranteed to be optimal, as the pairwise distances in the tree equal the pairwise distances disregarding the constraints of the tree. Moreover, in all most parsimonious scenarios, the median ancestral chromosome fragment containing this region coincides with this region in present-day mouse.10 This three-way analysis of rearrangements within h17/m11/r10 leads to a reliable reconstruction of the genomic architecture of the murid ancestor of this region and, for the first time, allows one to assign rearrangement events to particular lineages (see Fig. 2C). Determining how the events on the A to human branch were split between human and rodent lineages requires use of additional outgroups (relative to the HMR node). Low-resolution data from the dog genome (Kirkness et al. 2003) suggests that the reversal of block 13 was on the HMR to MR edge, and all other events on the A to human path (except possibly those involving blocks 4–8, for which sufficient data was not present) occurred on the HMR to human edge.

Microrearrangement analysis can indirectly reveal the problematic regions in assembly. For example, a perfectly conserved synteny block in human and mouse that is disrupted by many microrearrangements in rat may be an indication of an assembly error in rat. The analysis of human–mouse–rat microrearrangements implies that the rate of microrearrangements in the rat lineage is significantly higher than in mouse lineage (in our three-way blocks, 8.8 microrearrangements per million years between human and rat vs. 6.1 microrearrangements per million years between human and mouse), thus pointing either to (1) problematic assembly of some synteny blocks in rat, or (2) a very high microrearrangement rate in rat.

Breakpoint Reuse in Human, Mouse, and Rat Evolution

In a landmark paper, Nadeau and Taylor (1984) estimated that there are roughly 180 synteny blocks in human and mouse and provided convincing arguments in favor of the random breakage model of genomic evolution postulated by Ohno (1973). The model assumes a random (i.e, uniform and independent) distribution of chromosome rearrangement breakpoints, and is supported by the observation that the lengths of synteny blocks shared by human and mouse are well fitted by the predicted distribution imposed by the random breakage model. This fit between predicted and observed human–mouse data (with progressively increasing levels of resolution) made the random breakage model the de facto theory of chromosome evolution.

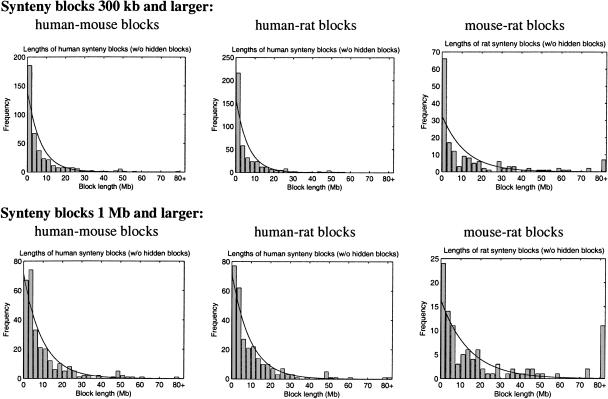
Of course, histograms of synteny block lengths in our pairwise comparisons (Fig. 4) deviate from the exponential distribution, but in the human–mouse and human–rat comparisons, these deviations are small enough to accept the random breakage model as the first approximation of the evolutionary process. However, even a visual inspection of the histogram of the mouse–rat synteny lengths reveals significant deviations from the exponential distributions and raises a question about applicability of the random breakage model. In all cases (human–mouse, human–rat, and mouse–rat), the histograms significantly deviate from exponential distributions if the number of inferred hidden synteny blocks (arising from breakpoint region reuse) is added to the analysis (Pevzner and Tesler 2003b).

Figure 4.

Figure 4

Open in a new tab

Histograms of lengths of two-way synteny blocks for each pair of species, fitted by the exponential distribution predicted by the statistical model in Nadeau and Taylor (1984). The mouse–rat block lengths appear to deviate from this model.

Because every rearrangement creates at most two new breakpoints, the genomic distance is at most half the number of the breakpoints in the genome. However, the estimate of genomic distance in terms of breakpoints is inaccurate, as it assumes that the breakpoints are not reused in evolution.11 The previous studies of human and mouse genomic sequences revealed extensive reuse of breakpoints from the same short regions. The human–mouse–rat rearrangement analysis confirms this conclusion and reveals extensive breakpoint reuse in evolution of each of the three lineages, summarized in Table 1.12

Acknowledgments

We thank Bin Ma for providing us with the PatternHunter runs and Bill Murphy for many helpful suggestions. We also thank the referees for many additional suggestions.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1975204.

Footnotes

[Supplemental material is available online at www.genome.org.]

5

Table 1 illustrates some potential pitfalls of the artificial separation of large-scale and small-scale rearrangements. Increasing the minimum synteny block length filters out smaller blocks and reduces the number of large-scale rearrangements of those that remain. We concurrently increased the gap threshold (described later) by a proportionate amount to the minimum synteny block length, which allowed more anchors into these larger synteny blocks and resulted in more microrearrangements. Apart from these issues, there is ambiguity in how to treat the chromosome ends; because the teleomeres have not been sequenced (too many repeats), we do not know whether rearrangements involving them are bounded at the exact end of the chromosome, or somewhere within the end regions. The lack of sequence data precludes us from computing the blocks (if any) at the ends and the rearrangements involving them. Some chromosome ends do not participate in rearrangements, so there is ambiguity in whether to call them breakpoint regions.

6

In Pevzner and Tesler (2003a), we used anchors produced by Michael Kamal (Waterston et al. 2002) for using another procedure, which did not output the signs of the anchors nor information on the repeat familes. We used heuristics to guess the signs of those anchors when possible, and discarded the 2% of the anchors for which this determination was not possible. Some of the guessed anchor signs may have been incorrect, leading to an undercount of microrearrangements.

7

Although the Hannenhalli-Pevzner algorithm finds a most parsimonious rearrangement scenario for two genomes, the real scenario is not necessarily a most parsimonious one, and the order of rearrangement events within a most parsimonious scenario usually remains uncertain. Availability of more than two genomes remedies some of these limitations and provides a means to infer the gene order in the mammalian ancestor (Bourque and Pevzner 2002).

8

In many cases, MGR does not provide an exact solution. It attempts to determine a most parsimonious tree based on macrorearrangements of the synteny block orders in the genomes. The synteny block order of the computed ancestral nodes is only approximate, because there are other possible orders that give identical tree scores, although exploration of neighboring alternative solutions suggests that most of the adjacencies (including all of the chromosome associations) are valid. Localizing the analysis to particular regions of the genome, or including data from appropriate additional species acting as outgroups, can help resolve these issues.

9

The rate of rearrangements on the path from the placental ancestor to human may be significantly smaller than 1.6, as most of the rearrangements on the human branch in Figure 3 may have been acquired on the path from the placental to the murid rodent ancestor.

10

The scenario being optimal, and the ancestor being unique are not typical. With arbitrary data, MGR approximates an optimal scenario, but does not guarantee it will achieve it. In general, distances between two genomes in the computed tree equal or exceed their pairwise distance if the tree constraints are ignored; in this case they are equal, proving the scenario is optimal. Also in general, the recovered ancestor may not be unique.

11

We emphasize that by reusing breakpoints, we do not mean multiple use of exactly the same genomic position as an endpoint of rearrangements, but rather the fact that the breakpoint regions host endpoints for multiple rearrangement events.

12

The breakpoint reuse analysis depends crucially on the accurate generation of synteny blocks and separation between macro- and microrearrangements (Sankoff and Nadeau 2003). Our breakpoint reuse estimates assume this separation is accurate and is not blurred by microrearrangements on the border between breakpoint regions and synteny blocks.

References

  1. Benson, G. 1999. Tandem repeats finder: A program to analyze DNA sequences. Nucleic Acids Res. 27: 573-580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Blanchette, M., Bourque, G., and Sankoff, D. 1997. Breakpoint phylogenies. In Genome informatics workshop (eds. S. Miyano and T. Takagi), pp. 25-34. University Academy Press, Tokyo, Japan. [PubMed]
  3. Bourque, G. and Pevzner, P.A. 2002. Genome-scale evolution: Reconstructing gene orders in the ancestral species. Genome Res. 12: 9748-9753. [PMC free article] [PubMed] [Google Scholar]
  4. Caprara, A. 2003. The reversal median problem. INFORMS J. Comput. 15: 93-113. [Google Scholar]
  5. Couronne, O., Poliakov, A., Bray, N., Ishkhanov, T., Ryaboy, D., Rubin, E., Pachter, L., and Dubchak, I. 2003. Strategies and tools for whole-genome alignments. Genome Res. 13: 73-80. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hannenhalli, S. and Pevzner, P.A. 1995a. Transforming men into mice (polynomial algorithm for genomic distance problem). In Proceedings of the 36th Annual IEEE Symposium on Foundations of Computer Science, pp. 581-592. Milwaukee, WI.
  7. ———. 1995b. Transforming cabbage into turnip (polynomial algorithm for sorting signed permutations by reversals). In Proceedings of the 27th Annual ACM Symposium on the Theory of Computing, pp. 178-189. (full version appeared in J. of ACM 46: 1-27, 1999).
  8. Kececioglu, J. and Sankoff, D. 1995. Exact and approximation algorithms for the inversion distance between two permutations. Algorithmica 13: 180-210. [Google Scholar]
  9. Kent, W.J. 2002. BLAT—the BLAST-like alignment tool. Genome Res. 12: 656-664. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Kent, W.J., Sugnet, C.W., Furey, T.S., Roskin, K.M., Pringle, T.H., Zahler, A.M., and Haussler, D. 2002. The Human Genome Browser at UCSC. Genome Res. 12: 996-1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Kent, W.J., Baertsch, R., Hinrichs, A., Miller, W., and Haussler, D. 2003. Evolution's cauldron: Duplication, deletion, and rearrangement in the mouse and human genomes. Proc. Natl. Acad. Sci. 100: 11484-11489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kirkness, E.F., Bafna, V., Halpern, A.L., Levy, S., Remington, K., Rusch, D.B., Delcher, A.L., Pop, M., Wang, W., Fraser, C.M., et al. 2003. The dog genome: Survey sequencing and comparative analysis. Science 301: 1898-1903. [DOI] [PubMed] [Google Scholar]
  13. Lahn, B.T. and Page, D.C. 1999. Four evolutionary strata on the human X chromosome. Science 286: 964-967. [DOI] [PubMed] [Google Scholar]
  14. Ma, B., Tromp, J., and Li, M. 2002. PatternHunter: Faster and more sensitive homology search. Bioinformatics 18: 440-445. [DOI] [PubMed] [Google Scholar]
  15. Moret, B.M.E., Wyman, S., Bader, D.A., Warnow, T., and Yan, M. 2001. A new implementation and detailed study of breakpoint analysis. In 6th Pacific Symposium on Biocomputing (PSB 2001), Hawaii, pp. 583-594. [DOI] [PubMed]
  16. Moret, B.M.E., Siepel, A.C., Tang, J., and Liu, T. 2002. Inversion medians outperform breakpoint medians in phylogeny reconstruction from gene-order data. In Proceedings of the 2nd International Workshop on Algorithms in Bioinformatics (WABI'02). (Lecture Notes in Computer Science 2452), pp. 521-563, Rome, Italy.
  17. Murphy, W.J., Bourque, G., Tesler, G., Pevzner, P.A., and O'Brien, S.J. 2003. Reconstructing the genomic architecture of mammalian ancestors using multispecies comparative maps. Human Genomics 1: 30-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Nadeau, J.H. and Taylor, B.A. 1984. Lengths of chromosomal segments conserved since divergence of man and mouse. Proc. Natl. Acad. Sci. 81: 814-818. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ohno, S. 1973. Ancient linkage groups and frozen accidents. Nature 244: 259-262. [DOI] [PubMed] [Google Scholar]
  20. Ozery-Flato, M. and Shamir, R. 2003. Two notes on genome rearrangement. J. Bioinform. Computat. Biol. 1: 71-94. [DOI] [PubMed] [Google Scholar]
  21. Pevzner, P.A. and Tesler, G. 2003a. Genome rearrangements in mammalian evolution: Lessons from human and mouse genomic sequences. Genome Res. 13: 13-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. ———. 2003b. Human and mouse genomic sequences reveal extensive breakpoint reuse in mammalian evolution. Proc. Natl. Acad. Sci. 100: 7672-7677. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Rat Genome Sequencing Project Consortium. 2004. Genome sequence of the Brown Norway Rat yields insights into mammalian evolution. Nature (in press). [DOI] [PubMed]
  24. Sankoff, D. and Blanchette, M. 1997. The median problem for breakpoints in comparative genomics. In Computing and combinatorics. Proc. of COCOON '97, Lecture Notes in Computer Science, pp. 251-263. Springer Verlag, New York.
  25. Sankoff, D. and Nadeau, J.H. 2003. Chromosome rearrangements in evolution: From gene order to genome sequence and back. Proc. Natl. Acad. Sci. 100: 11188-11189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Schwartz, S., Zhang, Z., Frazer, K.A., Smit, A., Riemer, C., Bouck, J., Gibbs, R., Hardison, R., and Miller, W. 2000. PipMaker—A web server for aligning two genomic DNA sequences. Genome Res. 10: 577-586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Siepel, A.C. and Moret, B.M.E. 2001. Finding an optimal inversion median: Experimental results. In Proceedings of the First International Workshop on Algorithms in Bioinformatics (WABI'01), Vol. 2149 of Lecture Notes in Computer Science, pp. 189-203. Springer Verlag, New York. [Google Scholar]
  28. Springer, M.S., Murphy, W.J., Eizirik, E., andO'Brien, S.J. 2003. Placental mammal diversification and the Cretaceous-Tertiary boundary. Proc. Natl. Acad. Sci. 100: 1056-1061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Stanyon, R., Stone, G., Garcia, M., and Froenicke, L. 2003. Reciprocal chromosome painting shows that squirrels, unlike murid rodents, have a highly conserved genome organization. Genomics 82: 245-249. [DOI] [PubMed] [Google Scholar]
  30. Tesler, G. 2002a. Efficient algorithms for multichromosomal genome rearrangements. J. Comp. Sys. Sci. 65: 587-609. [Google Scholar]
  31. ———. 2002b. GRIMM: Genome rearrangements web server. Bioinformatics 18: 492-493. [DOI] [PubMed] [Google Scholar]
  32. Waterston, R.H., Lindblad-Toh, K., Birney, E., Rogers, J., Abril, J.F., Agarwal, P., Agarwala, R., Ainscough, R., Alexandersson, M., An, P., et al. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420: 520-562. [DOI] [PubMed] [Google Scholar]

WEB SITE REFERENCES

  1. http://www-cse.ucsd.edu/groups/bioinformatics/GRIMM/index.html; genome rearrangements Web server. [DOI] [PubMed]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES