Patterns of Insertions and Their Covariation With Substitutions in the Rat, Mouse, and Human Genomes

Abstract

The rates at which human genomic DNA changes by neutral substitution and insertion of certain families of transposable elements covary in large, megabase-sized segments. We used the rat, mouse, and human genomic DNA sequences to examine these processes in more detail in comparisons over both shorter (rat–mouse) and longer (rodent–primate) times, and demonstrated the generality of the covariation. Different families of transposable elements show distinctive insertion preferences and patterns of variation with substitution rates. SINEs are more abundant in GC-rich DNA, but the regional GC preference for insertion (monitored in young SINEs) differs between rodents and humans. In contrast, insertions in the rodent genomes are predominantly LINEs, which prefer to insert into AT-rich DNA in all three mammals. The insertion frequency of repeats other than SINEs correlates strongly positively with the frequency of substitutions in all species. However, correlations with SINEs show the opposite effects. The correlations are explained only in part by the GC content, indicating that other factors also contribute to the inherent tendency of DNA segments to change over evolutionary time.

Many functional DNA sequences are very similar between related species because of purifying selection that removes sequence changes that are detrimental to organisms (Jukes and Kimura 1984). Thus, reliable indicators that sequences are under selection can be used as predictors of functional genomic sequences (Pennacchio and Rubin 2001). A major complication in developing such reliable measures is that the rate of neutral evolution varies within genomes (Wolfe et al. 1989; Ellegren et al. 2003), and thus, the probability that a particular level of similarity reflects the effects of purifying selection varies with amount of background sequence similarity (Li and Miller 2002). Better understanding of this regional variation in evolutionary rates should improve the ability to find functional genomic sequences (Mouse Genome Sequencing Consortium 2002; Kolbe et al. 2004).

The whole-genome alignments of rat (Rat Genome Sequencing Project Consortium 2004), human (International Human Genome Sequencing Consortium 2001), and mouse (Mouse Genome Sequencing Consortium 2002) provide an opportunity to better understand rates and mechanisms of eutherian evolution. Previous analysis of whole-genome alignments between human and mouse showed that the rates of several processes by which DNA diverges, including neutral nucleotide substitution, insertions of transposable elements, and recombination, vary significantly in large (megabase-sized) segments of the human genome (Mouse Genome Sequencing Consortium 2002; Hardison et al. 2003). Moreover, most of these rates covary, showing that large regions that are more susceptible to change by one process also tend to change more by other processes. Because substitutions were measured at sites likely to be neutral, and protein-coding regions comprise a small minority (on average 1.5%) of each megabase-sized region, differences in selective pressure do not easily account for the relative tendency for change. Rather, the tendency to change at a given rate appears to be a local property of DNA, such that some segments are relatively “rigid” and others are relatively “flexible” in evolutionary terms (Chiaromonte et al. 2001). Smith et al. (2002) showed that variation in substitution rates correlated down the human and chimpanzee lineages, indicating that the rate variation is deterministic. Recently, Hellman et al. (2003) demonstrated that substitutions between human and chimp correlate positively with recombination rates, which also argues for a neutral explanation for the covariation in different processes that change DNA.

Most measures of divergence showed strong covariation in the genome-wide analyses of human and mouse DNA, but the density of repetitive elements showed more complex relationships. For example, whereas the density of lineage-specific LTR repeats has a strong positive correlation with the deduced rates of other divergence processes (Mouse Genome Sequencing Consortium 2002; Hardison et al. 2003), the density of all lineage-specific repeats has a negative correlation with the rates of neutral substitutions and recombination (Hardison et al. 2003). To better resolve this apparent contradiction, we explored the covariation of divergence measures in more closely related species, rat and mouse. Rodents should be particularly informative for this analysis because of their intense retrotranspositional activity recently in evolution, which exceeds that seen in the human genome (Mouse Genome Sequencing Consortium 2002; Rat Genome Sequencing Project Consortium 2004).

RESULTS

Alignments Among Rat, Mouse, and Human Genomes

The rat, mouse, and human genomes were aligned in all pairwise combinations using BLASTZ (Schwartz et al. 2003). These alignments were constructed using information about the ages of interspersed repeats, which allows their origin to be assigned to individual branches of the phylogenetic tree (Fig. 1). Methods for assigning the repeats to recent and ancestral branches are described in the next section. Nucleotide substitution rates were deduced from the alignments and used to study their covariation with insertions of repeats.

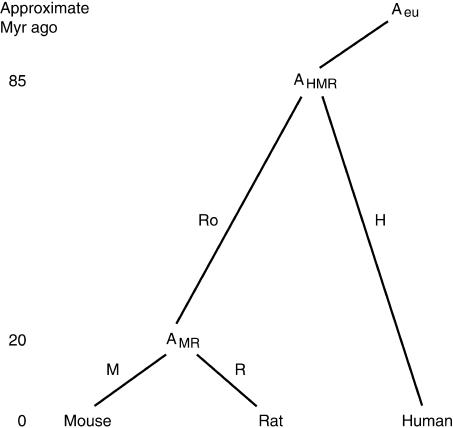
Figure 1.

Phylogenetic tree for rat, mouse, and human and their last common ancestors. The last common ancestor for human, mouse, and rat is A_HMR, and the last common ancestor for mouse and rat is A_MR; A_HMR and the ancestors to other eutherian mammalian orders diverged earlier from the last common eutherian ancestor A_eu. The branch from A_HMR to human is defined as “human” and is referred to by the suffix “H”, the branch from A_HMR to A_MR is defined as “rodent” and is referred to by the suffix “Ro”, the branch from A_MR to rat is defined as “rat” and is referred to by the suffix “R”, and the branch from A_MR to mouse is defined as “mouse” and is referred to by the suffix “M”. Average approximate times for the divergence from A_HMR and A_MR (Adkins et al. 2001; Mouse Genome Sequencing Consortium 2002; Springer et al. 2003) are given in millions of years.

Lineage-Specific and Ancestral Repeats in Rat, Mouse, and Human Genomes

About half of each of the human, mouse, and rat genome sequences is comprised of interspersed repeats, which primarily are the remnants of transposable elements. Copies of those elements active before a speciation event can be found at orthologous sites in both species (unless a later deletion has removed the element), whereas copies that arrived later are lineage specific. No evidence for selective deletion of individual repetitive elements has been reported in mammals; thus, such deletion events are larger than an individual element. Only one example of a specific deletion of a mammalian repeat has been reported, deleting part of an Alu repeat in the human CD4 gene (Edwards and Gibbs 1992). Even in this case, the signature of the Alu element was left behind in the genome. Alignments between mammalian genomes are dramatically improved by the removal of lineage-specific repeats (Schwartz et al. 2003). Oftentimes, such a deletion reconstructs the ancestral situation, thereby reducing the number of gaps in an alignment and increasing sensitivity. Furthermore, many lineage-specific repeats in rodents and primates (specifically copies of the abundant Alu/B1 SINEs and the LINE1s) match each other closely and can create confounding, ectopic alignments.

For analyzing the mouse and rat genomes, we considerably expanded the rodent repeat libraries, from 136 rodent-specific repeats (175 kb of consensus sequence) in Jan 2002 to 391 (579 kb) in August 2003.

Each interspersed repeat family in the three genomes was labeled as either ancestral or lineage specific, on the basis of the observed presence or absence, respectively, of copies at orthologous sites in both species. For alignments between a rodent and human sequence, ancestral repeats are those present in the last common ancestor to rodents and primates (A_HMR in Fig. 1). The high substitution level in the rodent lineages limits the sensitivity of finding repeat elements ancestral to the rodent–primate divergence from these genomes; therefore, all A_HMR-ancestral repeats have been established from copies in the human genome. Human repeat families with copies that are 12%–18% diverged from their consensus were transpositionally active around the time of the rodent–primate divergence (Mouse Genome Sequencing Consortium 2002). All such human repeat families were examined for copies present at orthologous sites in mouse or rat. Those families with orthologous rodent copies were assigned as ancestral, those without orthologs were assigned as lineage specific. Less-diverged families of repeats were automatically assumed to be lineage specific, and more-diverged families were assumed to be ancestral. For alignments between rat and mouse, ancestral repeats are those present in the last common ancestor to mouse and rat (A_MR in Fig. 1). In this case, repeat families with copies that are 7%–12% diverged from their consensus in mouse or rat (hence, were active around the time of the rat–mouse divergence) were examined for copies present at orthologous sites in the other rodent species. Assignments of A_MR-ancestral, mouse-specific and rat-specific repeats were made using the same logic as for those at the rodent–primate divergence. The establishment of age is greatly helped by the fact that evolutionary trees can be built for retroposon families in mammalian genomes (Smit 1993; Smit et al. 1995); families that are ancestral to those for which copies can be found at orthologous sites are necessarily ancestral to the speciation as well, whereas families derived from elements that are lineage specific must be lineage specific as well.

The net result of this analysis is that repeats can be assigned as appearing on the human, rodent, mouse, and rat branches of the phylogenetic tree (Fig. 1). The August 2003 release of RepeatMasker (Smit and Green 1999) has initial phylogenetic tags with each mammalian repeat consensus to designate the assigned branch. The composition of the primate and rodent repeat databases is listed in Table 1.

Table 1.

Composition of the August 2003 RepeatMasker Database by Lineage-Specific and Ancestral Repeats

Repeat class	Mammalian-wide	Primate-specific	Rodent-wide	Rat-specific	Mouse-specific
SINE	3 (1)	26 (7)	20 (3)	8 (1)	7 (1)
LINE	64 (102)	36 (55)	25 (52)	12 (23)	18 (28)
LTR	156 (241)	221 (475)	110 (140)	84 (182)	94 (154)
DNA	100 (105)	26 (25)	8 (4)	-	-

Note: The number of repeat families in each class is given for each category of repeats (lineage-specific or ancestral), and the number of kilobase of family consensus sequence is given in parentheses. A few unclassified elements are left out.

Normal RepeatMasker output can be modified with the RepeatDater script (distributed with RepeatMasker) to indicate whether an annotated repeat is likely to be shared or lineage specific. This information was used before each BLASTZ alignment.

Differences in the Patterns of Lineage-Specific Interspersed Repeats Among Rat, Mouse, and Human

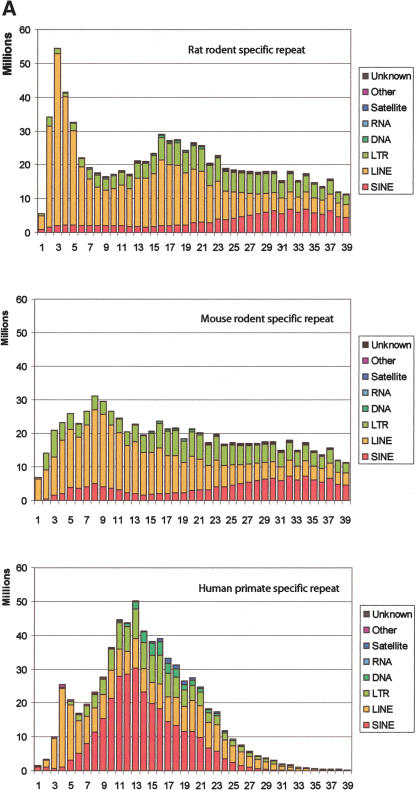
The predominant class of interspersed repeats in rodents consists of LINEs, whereas SINEs (Alu repeats) predominate in humans (Fig. 2A). LINE1 activity surged in the rat lineage between 5 and 15 million years ago, as indicated by a peak of LINE1 copies that are 2%–5% diverged from the six reconstructed rat-specific source genes. LINE1 activity remained relatively stable in mouse. In contrast, LTR repeats have been more transpositionally active in mouse than in rat. The rodent repeats whose divergence from the consensus exceeds 12% were largely in the A_MR ancestor. Thus, the classes of repeats in the 13%–39% divergence range are those that accumulated along the rodent branch (Fig. 1), and their distributions are similar for both rat and mouse, as expected.

Figure 2.

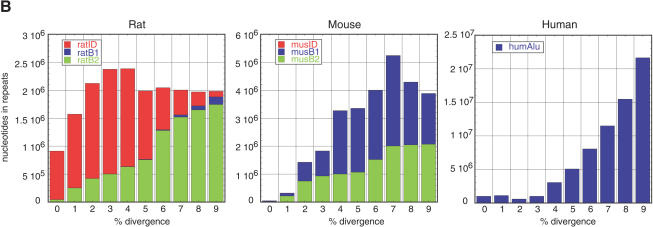
Age distribution of repeats in rat, mouse, and human that have inserted since their divergence from A_HMR. The x-axis represents divergence from consensus sequences, corrected for multiple hits at a single site using the Jukes-Cantor model (Jukes and Cantor 1969). This model was chosen for this analysis to be consistent with previous publications (International Human Genome Sequencing Consortium 2001; Mouse Genome Sequencing Consortium 2002). The y-axis is the number of nucleotides occupied by each repeat family at each divergence level. (A) Distribution for all repeat families that have accumulated since the divergence from A_HMR. For rat, the repeats are those that accumulated along both the rodent and the rat branches (Fig. 1); for mouse, the repeats are those that accumulated along both the rodent and the mouse branches (Fig. 1); for human, the repeats are those that accumulated along the human branch (Fig. 1). (B) Distribution of recent mammalian SINEs by age and family. The number of nucleotides in each family is plotted by percent divergence from the consensus sequence for each family. Only recent SINEs (0%–9% divergence) are examined in rat (left), mouse (middle), and human (right). The rat recent SINEs consist of IDs (red), B1s (blue), and B2s (green). The recent SINEs in mouse consist of B1s (blue) and B2s (green); the mouse IDs are not visible on the plot. Recent SINEs in humans are exclusively Alu repeats (blue).

The transpositional activity of all repeats has decreased gradually in the recent human lineage (repeats with less than 11% divergence from the consensus in Fig. 2A, human), although a small spike of activity is seen at 3%–4% divergence. In contrast, the rate of transposition in rodents has remained high during recent evolution. The decline in the amount of repetitive DNA in the 1%–3% divergence categories is expected, given that the small number of source genes for each family differs by 2%–3% among each other (Matera et al. 1990; Arcot et al. 1995). Thus, at its birth, each new repeating element generated from one source gene differs from new elements derived from other source genes for that same family. The different source genes are not defined sufficiently well for RepeatMasker to distinguish among their progeny.

Whereas LINEs account for much of the recent transpositional activity in both rodents, different SINEs have remained active. In fact, a new family of SINEs, the ID repeats, has arisen in the rat lineage (Kim and Deininger 1996; Fig. 2B). Like the B2 repeats, this family is derived from a tRNA-like gene, in contrast to the rodent B1 and human Alu families, which are derived from a 7SL RNA gene. Concomitantly with the advent of ID repeats in rats, the B1 family declined in activity, whereas in mice, the B1 repeats remained moderately active. In both rodents, the B2 repeats show a similar gradual decline in activity, although the lower number of less-diverged copies may again (partially) reflect an incomplete definition of recent source genes.

Difference Between Rodents and Humans in Local GC-Content Preference for Insertion of SINEs

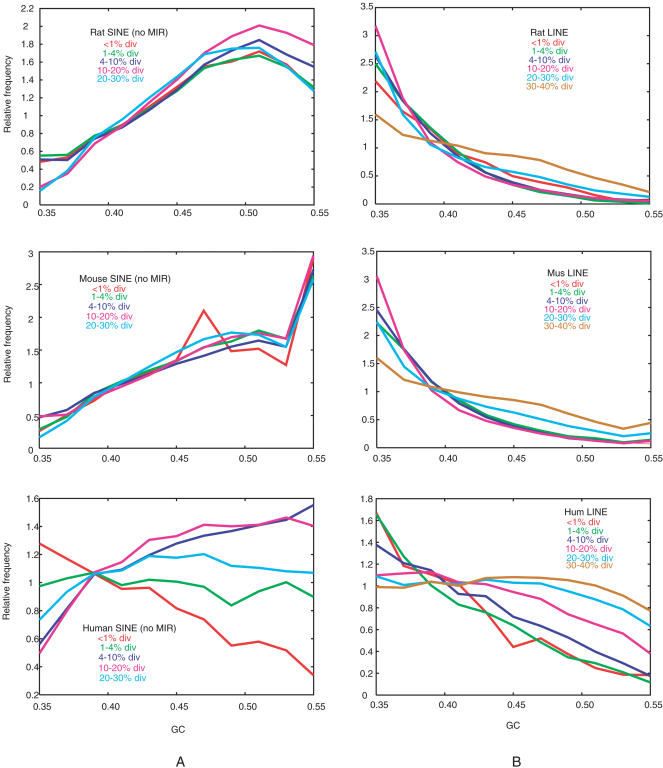
The continued activity of SINEs in rats provides enough repeats to expand the analysis of the genomic context preferred for insertion of repeats. Previous studies (International Human Genome Sequencing Consortium 2001) showed that very young human SINEs (Alu repeats) are more prevalent in DNA of low GC content, but the older SINEs are markedly enriched in DNA of high GC content. This result is recapitulated with a more recent and more complete human assembly (Fig. 3A). In contrast, the very young SINEs in rats (ID repeats) are much more frequent in high GC DNA, indicating that they prefer to insert into GC-rich DNA. The distribution of repeats does not change for older rodent SINEs (Fig. 3A), indicating that they also are retained in GC-rich DNA. A similar pattern is seen for the mouse SINEs (Fig. 3A). Examination of the distribution of each rodent SINE family (ID, B1 and B2 repeats) by age and GC content of the surrounding DNA shows that all three families are inserted and retained preferentially in high GC DNA (data not shown). LINEs show a different pattern, preferring to insert into low GC DNA in all three genomes (shown by the distribution of low divergence repeats, Fig. 3B) and to be retained there (shown by the distribution of higher divergence repeats, Fig. 3B). Thus, the preference for rodent SINEs inserting in high GC DNA is the opposite of that shown by LINEs.

Figure 3.

Frequency of occurrence of different ages and families of interspersed repeats in regions of different GC-content. The local GC-content (measured as the fraction of G or C in the surrounding 50 kb) was determined for each member of a repeat family, the number of repeats in intervals of GC-content was counted and then divided by the abundance of all genomic DNA in that interval to obtain the relative frequency of repeats. Repeats of different ages (measured by their divergence from the consensus) were examined for SINEs (A) and LINEs (B) for the rat (top), mouse (middle), and human (bottom) genomes.

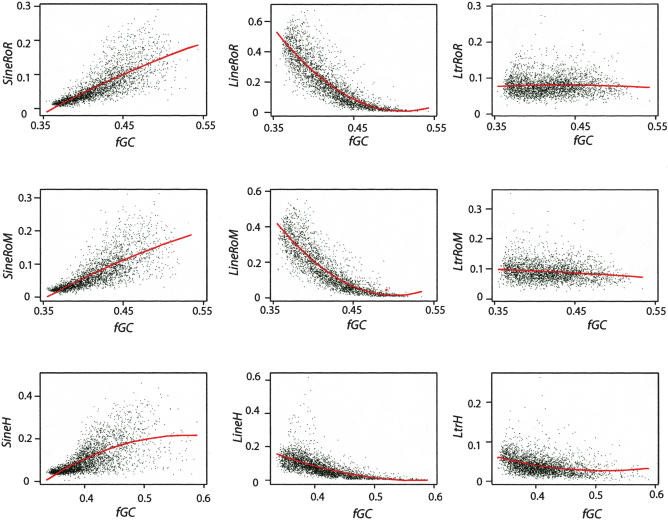
The insertion and retention preference of SINEs and LINEs is reflected in their current distribution by GC content in rat, mouse, and human, whereas density of LTR repeats shows little dependence on GC content (Fig. 4). Each genome was divided into large (1 Mb) nonoverlapping windows, and the local densities of each class of repeats were determined as the fraction of nucleotides in the window occupied by the lineage-specific members of that class of repeats. The repeat densities were further separated by the branch of the phylogenetic tree on which they arose. For example, the local density of SINE elements that arose along the rodent plus rat branches is referred to as SineRoR, that for SINES that arose along the rodent plus mouse branch is SineRoM, and that for SINEs that arose along the human branch is SineH. Similar calculations were done for LINEs and LTR repeats. When plotted against fGC, the fraction of nucleotides in the 1-Mb window that are G or C, the strong enrichment of lineage-specific SINEs in GC-rich DNA and LINEs in AT-rich DNA is clear (Fig. 4). The enrichment of LINEs in AT-rich DNA is more dramatic in rat and mouse than in human, with a particularly steep negative slope below an fGC of 0.45. This reflects the greater abundance of LINEs in the rodent genomes, which are largely concentrated in the AT-rich DNA. In contrast to the striking enrichment of SINEs and LINEs in high and low fGC, respectively, the plots of density of lineage-specific LTR density are essentially flat versus fGC.

Figure 4.

Scatter plots of lineage-specific repeat densities in 1-Mb nonoverlapping windows by family (SINEs, LINEs, and LTRs) against GC content of the window in rat, mouse, and human. The fraction of nucleotides in the 1-Mb window occupied by each family of lineage-specific repeat is the density plotted on the y-axis; the fraction of nucleotides in the window that are G or C is the fraction GC (fGC) plotted on the x-axis. For mouse and rat, the lineage-specific repeats are those that accumulated on both the rodent and mouse (suffix RoM) or rodent and rat (suffix RoR) branches. A quadratic fit (red curve) is superimposed on each plot.

Local Variation in Rates of Substitution and Insertions

The rate of likely neutral substitutions between rodents and between human and rodent genomes was computed using previously described methods (Mouse Genome Sequencing Consortium 2002; Hardison et al. 2003). In brief, the whole-genome pairwise alignments and RepeatMasker output was used to compute all mismatches in the relevant ancestral repeats, that is, those in A_HMR for human–rodent comparisons and those in A_MR for comparisons between rodents (Fig. 1). The fraction of mismatches in aligned regions was converted to substitutions per site using the REV model to correct for multiple hits at a single site (Tavare 1986; Yang 1997). The local measure of substitutions per site in aligned ancestral repeats (in this case, nonoverlapping 1-Mb windows) is called t_AR (Mouse Genome Sequencing Consortium 2002; Hardison et al. 2003). The ancestral repeats are a good, but not perfect, model for neutral DNA (for review, see Ellegren et al. 2003). One advantage is their abundance. Our analysis examines 180–189 million, 53–58 million, and 285–287 million aligned sites in ancestral repeats, respectively, for the human–rodent, rodent–human, and between rodent comparisons. The densities of lineage-specific repeats (RepH, RepRoR, RepRoM, and analogous densities of the different classes) also were computed in 1-Mb nonoverlapping windows as described above and in the Methods section.

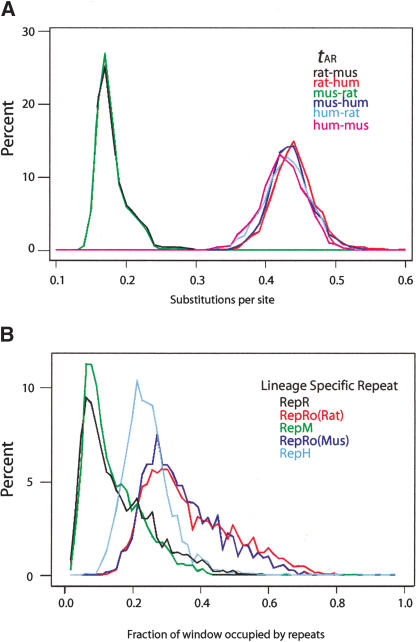
The amounts of change by substitution and insertions of lineage-specific transposable elements vary substantially across 1-Mb nonoverlapping windows both over short (rat–mouse) and longer (rodent–primate) comparisons. All of these parameters present a wide variation range; histograms for t_AR and lineage-specific repeat densities are shown in Figure 5. Because of the shorter phylogenetic distance, the histograms for the substitution rate t_AR derived from alignments within rodents are shifted to the left (lower values, Fig. 5A). The distribution of t_AR from the rat–human alignments is shifted slightly to the right of that from mouse–human alignments, consistent with the ∼6% faster rate in the rat branch compared with the mouse branch (Rat Genome Sequencing Project Consortium 2004).

Figure 5.

Distributions of divergence rates for pairwise comparisons among rat, mouse, and human. (A) Histograms of t_AR, the local nucleotide substitution rate in aligned ancestral repeats, for alignments between rat and mouse (black line), mouse and rat (green line), rat and human (red line), mouse and human alignments (dark blue line), human and rat (light blue line), and human and mouse (violet line). (B) Histograms of the density of lineage-specific interspersed repeats on the rat branch (RepR, black line), the mouse branch (RepM, green line), the human branch (RepH, light blue line), and the rodent branch (RepRo). The latter was computed in the rat genome to determine RepRo(Rat), the red line, and in the mouse genome to determine RepRo(Mus), the dark blue line. All measures were computed in 1-Mb nonoverlapping windows.

The distributions for densities of lineage-specific repetitive DNA are wide for all branches (Fig. 5B), and they show striking differences. The densities of rat- and mouse-specific interspersed repeats (RepR and RepM) generally are lower than older repeats (RepRo) because they have been active for shorter times. These distributions reflect the intense activity of rodent retrotransposons before (RepRo) and after (RepR and RepM) the mouse–rat divergence (Fig. 2; Mouse Genome Sequencing Consortium 2002). The distribution for human-specific repeats (RepH) is shifted to the left of the distributions for the older rodent-interspersed repeats (Fig. 5B), consistent with lower transpositional activity of the long transposable elements such as LINEs along the human branch (Fig. 2A).

Covariation in Rates of Substitution and Insertions Except SINEs

Given the wide local variation presented by likely neutral substitutions (t_AR) and lineage-specific transpositional insertion rates in all three genomes, we measured the extent to which these rates vary together. We calculated the correlations between pairs of these measurements for all pairwise alignments.

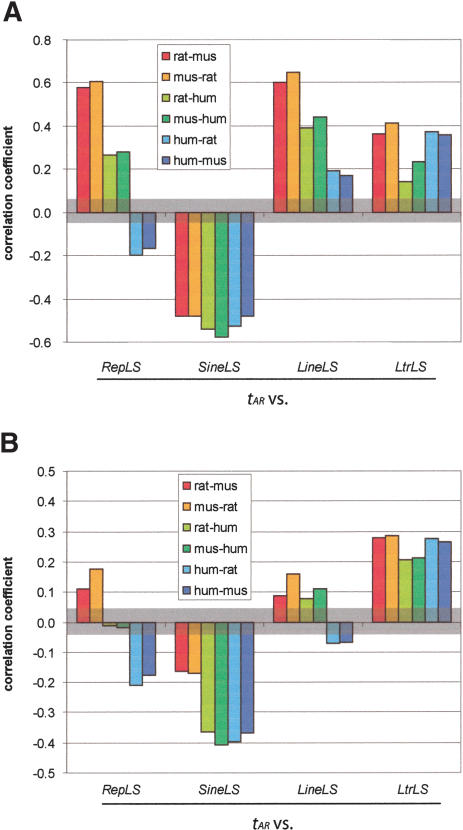
The substitutions per site (t_AR) and repeat densities (RepLS, where LS refers to the relevant lineage-specific repeats in the first species in an alignment) show strong positive, highly significant pairwise correlations for alignments between rodents (Fig. 6A). These comparisons involve the two genomes that are phylogenetically closest (Fig. 1) and have the most similar patterns of transpositional activity (Figs. 2, 3, 4). The correlations are less strong, but they are still positive and significant when rodent genomes are compared with human (rat–human and mouse–human alignments). These comparisons cover a larger phylogenetic distance, and transposition in the reference (rodent) genome is still active and dominated by LINE insertions.

Figure 6.

Pairwise correlations among measures of sequence divergence in comparisons among mammals. (A) Analysis of the original data. The amount of change by three processes was quantified in about 2500 1-Mb nonoverlapping windows genome-wide in two-way alignments among rat, mouse, and human. The function t_AR is the substitutions per site in aligning ancestral repeats within each window, and RepLS is the portion of each window of the first (reference) species occupied by lineage-specific repeats. The portions occupied by lineage-specific LINEs, SINEs, and LTRs are given by LineLS, SineLS, and LtrLS, respectively. Correlation coefficients for each comparison are plotted. The brackets between roughly -0.05 and +0.05 denote the region in which the correlations lose statistical significance (P value more than 0.05) (B) Pairwise correlations among measures of sequence divergence in comparisons among mammals, after removing the effects of (1) G+C content in the first species, and (2) change in G+C content between the two species, using quadratic regressions.

Consistent with our previous report (Hardison et al. 2003), the correlations between t_AR and RepLS are negative for human–mouse and human–rat alignments (Fig. 6A). Because the human–mouse comparison covers an identical phylogenetic distance as the mouse–human comparison, the distance is not the determinant of the negative correlations seen between t_AR and RepLS for human–rodent alignments. RepLS measures the combined densities of all lineage-specific repetitive elements, but the regional insertion preferences differ between classes of repeats and between species in some cases. In particular, SINEs dominate the pattern of transpositional insertion in humans, whereas LINEs dominate that for rodents (Fig. 2), and the SINEs show a different GC-related regional insertional preference between humans and rodents (Fig. 3).

Thus, we focused on deconvoluting RepLS as a potential confounding factor by examining the densities of the three major classes of repeats (SINEs, LINEs, and LTRs) separately in these comparisons. The correlations between SINE density (SineLS) and substitutions per site are negative for all pairwise alignments (Fig. 6A). In contrast, all correlations of LINE density (LineLS) and LTR density (LtrLS) with t_AR are positive, regardless of the alignment examined. These results explain the negative correlation between substitution rate and density of all interspersed repeats previously observed in human–mouse comparisons (Hardison et al. 2003). SINEs, which are the dominant repeat in the human (reference) genome, are most abundant in GC-rich DNA (the opposite of the pattern seen for LINEs and LTRs), and they also are more abundant in more slowly changing DNA (small values for t_AR). Thus, the major classes of repeats differ in their regional preference for GC content (high GC for SINEs, but low GC for LINEs) and the inherent tendency to change (low t_AR for SINEs, but high t_AR for LINEs).

Additional studies (data not shown) examined the covariation after separating different classes of repeats by age (measured as divergence from the consensus). The effects were substantially less than those observed when separating repeats into different classes.

Relationships Between Divergence Measures and GC Content

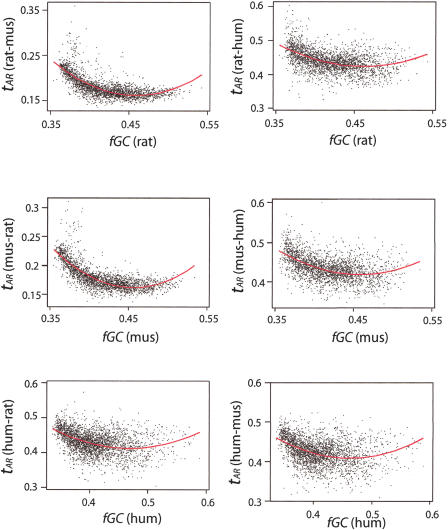
Given the striking differences in the relationships between the major classes of repeats and GC content (Fig. 4), it was important to examine the behavior of substitutions with GC content for each species, again measured in 1-Mb nonoverlapping windows. The substitutions per site (t_AR) decrease over the fGC interval of 0.35 to ∼0.40 for all of the alignments (Fig. 7); note that fGC refers to the fraction of G or C nucleotides in the reference (first) sequence. For alignments with rat as the reference sequence, the plots are flat above an fGC of 0.40, but for mouse–human and human–mouse alignments, the trend is slightly increasing in this interval. A fit to a quadratic is appropriate for all the comparisons, even when the increase at higher fGC is modest, and is used in the following section.

Figure 7.

Scatter plots of t_AR against GC content of the window (fGC) in alignments among rat, mouse, and human for 1-Mb nonoverlapping windows. A quadratic fit (red curve) is superimposed on each plot.

Amount of Covariation Among Divergence Measures Explained by GC Content

Previous studies showed that human GC content and related variables can only partially account for the covariation of divergence measures observed in human–mouse alignments (Mouse Genome Sequencing Consortium 2002; Hardison et al. 2003). It was important to re-examine this issue for the comparisons with additional genomes and, in particular, with respect to the major classes of repeats, which have pronounced and distinctive dependence on GC content (Fig. 4). Considering the various pairwise alignments, we found that the GC content of surrounding DNA accounts for some but not all of the covariation.

For each collection of pairwise alignments and each divergence measure (t_AR, RepLS, SineLS, LineLS, and LtrLS), we fitted a quadratic regression with two predictors as follows: (1) fGC, the GC fraction in the first species (scatter plots shown in Figs. 4 and 7), and (2) change in GC content (dGC) between the two species (Mouse Genome Sequencing Consortium 2002). Correlations were then calculated on residuals from these regressions, instead of the original divergence measures (Fig. 6B). In most of the cases, after removing the GC-related effects in this way, correlation coefficients decreased compared with those for the original divergence measures, but retained the same sign. The decrease in correlation coefficients reflects the extent to which GC content can explain the covariation. In alignments between rodents, GC-related parameters account for over half of the covariation between t_AR and RepLS, SineLS, and LineLS. This fits with the substantial dependence of each of these measures on fGC (Figs. 4 and 7). In contrast, the correlations on residuals are modestly reduced compared with the original data for t_AR and LtrLS, in keeping with the lack of dependence of LtrLS on fGC (Fig. 4).

At the larger phylogenetic distance between rodents (reference sequences) and human, the GC-related parameters explain all of the covariation between t_AR and RepLS, so that the correlation on the residuals is no longer significant. However, the effects differ depending on the class of repeats. The GC-related parameters explain much of the covariation of t_AR with LineLS (and hence, RepLS, of which LineLS is the dominant component for rodents), but they explain none of the correlation between t_AR and LtrLS (Fig. 6B). Again, this fits with the GC-dependence of LineLS, but GC-independence of LtrLS.

When the correlations are examined using alignments with human as the reference sequence, the distinctive negative correlation between t_AR and human RepLS, which is dominated by human SineLS (Alu) repeats, is still strong even after removing GC-related effects (Fig. 6B). Thus, for most of the comparisons, GC content explains some of the inherent tendency for DNA segments to change, but properties other than GC content also contribute. These relationships are clearer at the shorter phylogenetic distance covered by rat–mouse alignments.

DISCUSSION

Adding the rat genome (Rat Genome Sequencing Project Consortium 2004) to the mouse and human genomes opens many opportunities for new insights into mammalian evolution. The generality of observations about genome structure and function can be tested. For example, we show that the substantial variation in nucleotide substitution rates and repeat density observed for human–mouse comparisons is also seen for comparisons over a smaller evolutionary distance (within rodents) and when using rodent sequences as the references. Given the differences in patterns of repetitive elements between rodents and humans, it was important to show the local variation in these rates for rodents on the basis of genome-wide alignments. The current study also clarifies some issues that were confounding previous analyses of the covariation between substitution rates and repeat densities. We find that the densities of various classes of repeats show different correlations with nucleotide substitutions. The density of LINEs correlates positively with substitutions, whereas the density of SINEs shows the opposite relationship. Thus, for comparisons with a rodent genome as the reference sequence, for which the density of interspersed repeats is dominated by LINEs, a positive correlation is observed. In contrast, for comparisons with the human genome as the reference sequence, for which the density of interspersed repeats is dominated by SINEs, a negative correlation is obtained. This explains the failure to see a positive correlation between the density of all repetitive elements and nucleotide substitutions in human–mouse alignments in previous studies (Hardison et al. 2003).

We have measured nucleotide substitutions in one model for neutral DNA, aligned repeats that predate the divergence of the species being examined (Mouse Genome Sequencing Consortium 2002; Hardison et al. 2003). Thus, it is unlikely that different selective pressures over large regions cause the differences in evolutionary rate. Instead, one can interpret the covariation as reflecting an inherent tendency for change in some regions of the DNA. These regions are very large, megabase-sized segments. The inherent tendency to change can be termed the evolutionary flexibility of genomic segments (Chiaromonte et al. 2001), with more flexible regions changing fast and evolutionarily more rigid regions changing slowly by almost all processes that change DNA. Smith et al. (2002) showed that the substitution rate in likely neutral sites also varies at smaller scales in comparisons among human, chimpanzee, and baboon sequences. Importantly, the rate variation correlated along both the human and chimpanzee lineages, indicating that some property of the sequences, not selection on individual sites, determines the rate variation. The authors call this deterministic rate variation, which is equivalent to our conclusion that regions show an inherent tendency to change. Covariation of substitution rates and recombination rates was also observed between human and chimpanzee genome sequences (Hellmann et al. 2003), consistent with variation in the rate of neutral evolution (Lercher and Hurst 2002). The search for an explanatory mechanism is the subject of other studies; one interesting possibility is that double-strand breaks on chromosomes such as those that form during recombination are also mutagenic (Nachman 2001; Lercher and Hurst 2002). Ellegren et al. (2003) point out that these regions of different neutral rates may be subject to regional selection, such that some classes of genes tend to accumulate over evolutionary time in, say, more slowly changing regions. This is consistent with the clustering of housekeeping genes in the human genome (Lercher et al. 2002; Pal and Hurst 2003).

Each model for neutral DNA has distinctive advantages and disadvantages (Ellegren et al. 2003). Aligned ancestral repeats are abundant and fairly evenly distributed across the genome, and the vast majority of them are unlikely to have a biological function, thus, we currently prefer to use them as a model for neutral DNA. Nevertheless, it is important to realize some of the real and potential shortcomings of this model. Some repeats do play a role in gene regulation (Jordan et al. 2003), and HS4 of the HBB locus control region (Li et al. 1999) is largely comprised of an ancestral repeat (data not shown). Given the very large number of sites in aligned ancestral repeats, it is likely (but unproven) that such functional sites are a considerable minority. Another limitation comes from the alignment technologies. The alignments between human and rodent are sensitive, but one cannot determine that all orthologous sequences have been aligned (Schwartz et al. 2003). Thus, the ancestral repeats that align between human and rodent may be enriched for those in more slowly changing regions. Finally, the estimates of substitutions in repeats could be affected by gene conversions, but it is not possible at this time to measure the magnitude of this effect. Gene conversion has been clearly documented in young Alu repeat families (Deininger and Batzer 2002). Instances of a young Alu repeat in humans having an orthologous copy in a primate species whose time of divergence predates the expansion of that young Alu subfamily result from a member of an older Alu subfamily undergoing a gene conversion with a member of the young Alu subfamily member in humans (Roy-Engel et al. 2002). Some members of the young Alu subfamilies have a mosaic structure that can be explained by gene conversion with members of other Alu subfamilies (Roy et al. 2000; Carroll et al. 2001). However, these examples of gene conversion are rare relative to the total number of Alu repeats, and they tend to be seen in younger Alu subfamilies whose estimated time of origin is ∼5.3 million years ago (Carroll et al. 2001). The rate of gene conversion between repeats as old as ancestral repeats and young repeats should be much lower than conversions among young repeats because of the greater sequence divergence. At the present time, one should consider the assignments of repeats as lineage specific or ancestral as the best one can do in a high-throughput manner. We cannot rule out the possibility that some of the assignments of individual repeats are incorrect. Repeats that are actually young, but which undergo gene conversion with an ancestral repeat, will lead to an overestimate of substitutions. However, it seems unlikely that this is a frequent occurrence.

SINEs accumulate in the opposite part of the genome as most other repeats, that is, in the GC-rich regions containing highly expressed genes (Smit 1996). Consistent with that, our current results show that, unlike other repeats, they tend to be in regions that accumulate fewer nucleotide substitutions. Although the cause of this distribution pattern is unknown, it must be a conserved feature, given that the locations of independently inserted, lineage-specific SINEs in rodents and primates (Mouse Genome Sequencing Consortium 2002) and in rat and mouse (Rat Genome Sequencing Project Consortium 2004) are strongly correlated, far stronger than the correlation with GC level.

The fact that all rodent SINEs, including very young (<1% diverged) copies show this distribution pattern suggests that it is caused by a regional insertion bias, rather than by post-integration selection or mutation patterns. This contrasts sharply with observations in the human genome, where the youngest Alus show a bias toward AT-rich DNA similar to that of LINE1 copies, whereas older copies are enriched properly in GC-rich DNA. The current observations in rodents could indicate that the preference for insertion into GC-rich, slow-changing DNA may be ancestral, and that the insertion pattern of Alus in our genome has recently changed. Study of SINE distribution in other mammalian genomes should confirm or reject this hypothesis.

Several interesting hypotheses have been offered for the enrichment of SINEs in GC-rich DNA of rodents and humans. To explain the shifting patterns in human DNA, it was suggested that Alus, although lost through genetic drift from AT-rich DNA, may be retained in GC-rich DNA, because SINEs landing in open chromatin or highly expressed regions of the genome have a beneficial effect on the genome (International Human Genome Sequencing Consortium 2001). This benefit could be rapid expression under stress conditions. For instance, the RNA products of Alu repeats have been implicated in stress-induced control of translation (Chu et al. 1998; Rubin et al. 2002). The selective enrichment in GC-rich regions could be explained if only SINEs in the right place were expressed under stress. The organism would benefit from having a large number of SINEs that can be readily expressed, so that the selection is on the whole (individuals with many Alu copies are healthier) and not on each element, which would constitute a grave genetic load.

A second explanation is that Alu repeats tend to be lost from AT-rich DNA, perhaps because it is advantageous to maintain large AT-rich isochores, but the GC-rich Alu repeats disrupt them. However, other GC-rich repetitive elements do not accumulate in GC-rich DNA, whereas rodent SINEs, which are not particularly GC-rich, are dramatically underrepresented in AT-rich DNA.

Alternatively, the prevalence of SINEs in GC-rich DNA may reflect their historical (human and rodent) and current (rodent) regional preference for insertion. However, this leaves several questions to be answered as well. Both SINEs and LINEs tend to insert at staggered breaks that are AT-rich (Jurka 1997), and this and other evidence has led to the model that SINE retrotransposition depends on the reverse transcriptase and integrase encoded by LINE1. The fact that young Alu repeat elements in humans have a similar regional GC insertion preference to that seen for LINE repeats is consistent with the Alu repeats piggy-backing on the enzymatic machinery of the LINEs. Recent results show that Alu elements can be transposed in human cells using the LINE enzymatic machinery (Dewannieux et al. 2003).

The apparent change in regional GC insertion preference in human Alus, and the contrast with that of rodent SINEs, raises the question of what enzymatic machinery is being used by rodent repeats. The target-site duplications for all rodent SINEs are identical to those of human Alus and human and rodent LINE1s (data not shown). It is highly likely that the rodent SINEs are using the retrotransposition machinery encoded by LINE1 repeats, thereby explaining the similarity of target sites. Perhaps differences in abundance of the classes of repeats could play a role in explaining the shift in insertion preference. The large number of Alu repeats in human GC-rich DNA may have reached a critical limit, such that additional Alu repeats are detrimental (Batzer and Deininger 2002). Thus, newer copies tend to go to other regions, such as the more AT-rich DNA.

Other explanations for the shift in regional GC preference for SINE insertion may lie in the different demographic histories between rodents and humans. Analysis of the pattern of GC preference for Alu insertion in another primate, such as the chimpanzee, could test this possibility, as chimpanzees have had a less-constricted demographic history than humans.

Further studies are needed to find explanations for the insertion preferences of different classes of retrotransposons and to understand the mechanistic bases for the inherent tendency for genomic regions to change. Even without understanding the molecular bases for these effects, the available quantitative descriptions of these variables, in particular the neutral substitution rate inferred from aligned ancestral repeats, can be used to improve prediction of functional DNA sequences. For example, the local neutral rate is included in calculations that refine estimates of probabilities that a given sequence alignment reflects purifying selection (Mouse Genome Sequencing Consortium 2002). Inclusion of a local neutral rate correction also improves the ability to discriminate alignments in regulatory regions from those in non-functional DNA (Kolbe et al. 2004).

METHODS

Generating Whole-Genome Two-Way Alignments

The whole-genome alignments were computed on the February 2003 assembly of the mouse (Mouse Genome Sequencing Consortium 2002), the April 2003 assembly of human NCBI Build 34 (produced by the International Human Genome Sequencing Consortium 2001), and the June 2003 assembly (version 3.1) of the rat genome (produced by the Atlas group at Baylor Human Genome Sequencing Center, Rat Genome Sequencing Project Consortium 2004).

Our whole-genome alignment protocol (Schwartz et al. 2003) uses the program BLASTZ in an all-versus-all alignment procedure, allowing any segment of the first sequence (e.g., rat) to align with any segment of the second sequence (e.g., human). Lineage-specific repetitive elements are excluded from the alignment procedure. Because of duplications, more than one segment in the second sequence may align with the same segment in the first sequence, so the program axtBest is used to filter out all but the best alignment within a sliding window of 10 kb. The resulting alignments are not symmetric; hence, divergence measurements must be computed on both sets of alignments (e.g., rat–human and human–rat). For the three mammalian genomes available, six different pairwise alignments were performed.

Calculation of Regional GC Preference for Repeats

The regional GC preference for repeats was calculated as the relative frequency of repeats distributed by local GC content. This was computed in four steps. First, the local GC content of a 50-kb window surrounding each repeat, fGCrep, was calculated. This is the count of G or C in the 25-kb upstream of a repeat plus the count of G or C in the 25-kb downstream of the repeat, divided by 50 kb. The local GC content for all 50-kb windows, fGCall, was also computed. Then, the number of repeats falling in ranges of fGCrep was counted, in intervals of 1% fGCrep (e.g., from 50% to 51% GC content), and the number of all windows falling in the corresponding ranges of fGCall were counted. The relative frequency for the repeats in each GC range is the frequency of repeats in that range of fGCrep (count of repeats in a range of fGCrep divided by the count of all repeats) divided by frequency of all windows in that GC range (count of windows in a range of fGCall divided by the count of all windows). These were computed for each class of repeat, subdivided by the amount of divergence from the consensus sequence.

Calculation of Substitution and Lineage-Specific Repeat Insertion

The sets of alignments were analyzed to compute the number of mismatches within aligning regions in 1 Mb nonoverlapping windows throughout each genome. From the pairwise alignments, nucleotide substitutions are assigned to the sum of the branches connecting the two species, for example, for rat–human alignments, the substitutions could have occurred on the human, rodent, or rat branch (Fig. 1). Only mismatches (transitions and transversions) were counted; gaps in the alignment were excluded. For mismatches in likely neutral sites, the counts were limited to intervals assigned by RepeatMasker as being repetitive elements present in the A_HMR ancestor for human–rodent comparisons, or present in the A_MR ancestor for comparisons between mouse and rat. Windows that contain less than 300,000 sequenced nucleotides or fewer than 400 sites in aligned ancestral repeats were removed from the analysis. The fraction of aligning nucleotides that are in mismatches was corrected for multiple hits at a single site to generate a measure of the nucleotide substitutions per site, using the REV model (Tavare 1986; Yang 1994; Whelan et al. 2001). The average substitution per site in ancestral repeats in a 1-Mb window was computed as the function t_AR. Applying the Jukes-Cantor correction (Jukes and Cantor 1969) gave very similar results.

Individual repetitive elements and their class were determined by RepeatMasker (Smit and Green 1999), and they were assigned to the human, rodent, mouse, or rat branches by RepeatDater. The fraction of each 1-Mb window in a genome occupied by lineage-specific repeats was computed as the function RepLS. The fractions of each window occupied by the lineage-specific members of each major family of repeats were also computed (SineLS, LineLS, and LtrLS).

Analysis of Covariation

Correlation computations, tests, and regressions were performed using the programs packaged in Minitab (Ryan and Joiner 2000).