Characterization of Evolutionary Rates and Constraints in Three Mammalian Genomes

Abstract

We present an analysis of rates and patterns of microevolutionary phenomena that have shaped the human, mouse, and rat genomes since their last common ancestor. We find evidence for a shift in the mutational spectrum between the mouse and rat lineages, with the net effect being a relative increase in GC content in the rat genome. Our estimate for the neutral point substitution rate separating the two rodents is 0.196 substitutions per site, and 0.65 substitutions per site for the tree relating all three mammals. Small insertions and deletions of 1–10 bp in length (“microindels”) occur at ∼5% of the point substitution rate. Inferred regional correlations in evolutionary rates between lineages and between types of sites support the idea that rates of evolution are influenced by local genomic or cell biological context. No substantial correlations between rates of point substitutions and rates of microindels are found, however, implying that the influences that affect these processes are distinct. Finally, we have identified those regions in the human genome that are evolving slowly, which are likely to include functional elements important to human biology. At least 5% of the human genome is under substantial constraint, most of which is noncoding.

The availability of a third complete mammalian genome sequence (Rat Genome Sequencing Project Consortium 2004) presents a wealth of opportunities for understanding mechanisms of mammalian molecular evolution, and for extending methodologies for comparative sequence analysis. Fundamental phenomena such as rates of nucleotide substitution, sizes and frequencies of small insertions and deletions, and lineage-specific shifts in evolutionary patterns can be uncovered, in some cases definitively, by such comparisons. Whereas this was previously accomplished with direct comparison of the human and mouse genomes (Waterston et al. 2002), the rat genome provides a chance to refine and extend these analyses.

In addition to facilitating insights into basic mechanisms of nucleotide evolution, such comparisons have the capacity to improve the annotation of the human genome. Comparative sequence analyses leverage the fact that functional DNA is constrained because of purifying selection. They have facilitated, and will continue to do so, the discovery of elements in the genome that play a functional role in human biology (Gottgens et al. 2002; Sidow 2002; Boffelli et al. 2003; Cooper and Sidow 2003; Thomas et al. 2003).

It is with these goals in mind that we present a comparative analysis of the rat genome. It was accomplished on the basis of global multiple sequence alignments that cover the bulk of the human, mouse, and rat genomes. These alignments are described in detail elsewhere (Brudno et al. 2004) and will be available electronically (http://pipeline.lbl.gov/).

The first step in quantifying rates and dissecting patterns of nucleotide evolution is selection of aligned sites for analysis. To estimate the neutral rate of point substitution, for example, criteria must be established to exclude positions that are likely to be under constraint. Exons, for example, cannot be used because protein-coding regions are generally subject to strong purifying selection. Thus, previous studies (Waterston et al. 2002; Hardison et al. 2003) have used synonymous sites within exons, or sites within remnants of ancient mammalian repeats (ARs). Synonymous sites may be under very weak selection because of codon bias (Li 1997), and their relative scarcity in the genome precludes high resolution estimates of the neutral rate in local genomic regions. Remnants of ARs, on the other hand, are generally free of constraint and occur at a higher density in the genome than synonymous positions. However, their discovery may introduce biases because they must be confidently identified by similarity to a previously built consensus sequence.

As an alternative to ARs and synonymous sites, we leveraged a combination of two nonoverlapping data sets that does not require annotation of any sort (Fig. 1). The first data set includes all sites that are confidently aligned among all three sequences. It was generated from our global alignments (Brudno et al. 2004) by eliminating regions that contain long gaps (>19 bp) in either the human or the rodent sequences (Fig. 1). These regions will include a mixture of constrained and unconstrained positions, most of which originated prior to the last common ancestor of human, mouse, and rat. The second data set contains only sites present in the rodents, and none that are also present in human (Fig. 1). This data set is heavily enriched for neutrally evolving sites because the vast majority of functional regions, including coding exons, noncoding RNAs, and regulatory elements, is aligned with the human genome and therefore eliminated from this set. To minimize potential alignment artifacts, we also eliminate regions that are heavily gapped in either rodent. (An analysis that goes beyond the scope of this study showed that evolutionary estimates derived from these sites are robust to alignment parameters used.) In addition, we require the length of each region to be at least 20 bp to eliminate most sites that correspond to microdeletions in the human lineage. Dataset 2, therefore, predominantly consists of rodent insertions that originated after the last common ancestor of human and the rodents, but before the divergence of the mouse and rat lineages. Although some rodent-specific constrained elements may remain, we expect these positions to constitute a trivial fraction. We therefore refer to Dataset 2 as “rodent-specific neutral sites,” a designation that is supported by their comparatively high rates of evolution (see Results).

Figure 1.

Description of data sets used in this study, which represent specific subsets of sites of the MLAGAN whole-genome alignments (Brudno et al. 2004). One hypothetical alignment is shown; (H) human; (M) mouse; (R) rat. Excluded sites are shaded gray. The remainder is kept, with the final number of sites in each set shown. Dotted lines represent gaps, which are not drawn to scale. Dataset 1 consists of all those regions that are shared among all three species. Excluded are regions that are gapped in human, or in one or both rodents, for at least 20 consecutive bases. The number of positions shown refers to those scored in the microindel analysis; for analyses of rates of substitution, gapped sites were eliminated, leaving 1,071,376,029 sites. Dataset 2 consists of “rodent-specific” sites, explicitly defined as those regions in our global alignments across from a human gap of at least 20 bases in length, and in which the rodent sequences contain less than 10% gap characters. Note that these two data sets are mutually exclusive, and therefore constitute independent sites.

Using these data sets, we describe the patterns and rates of various microevolutionary features, such as point substitutions, insertions, and deletions, along all three branches of the unrooted tree that relates human, mouse, and rat. We furthermore estimate rates of evolution in 25-bp windows across our alignments, and use these windows to comprehensively annotate slowly evolving regions of the human genome. These regions include many protein-coding exons, but also capture many noncoding elements, with a vast majority awaiting even basic functional characterization. Finally, we analyze the variability of these evolutionary features across a portion of the rat genome, and highlight the importance of the interaction between local genomic context and rates of evolution.

RESULTS

Global Patterns of Nucleotide Substitution

The GC content of the nonrepetitive fraction of the rat genome differs subtly from that of the mouse genome, with rat having 0.35% more GC than mouse (41.26% vs. 41.61%). This difference is perhaps surprising, given their close evolutionary relationship, and is statistically highly significant given the large number of sites in the nonrepetitive genome (>1.4 Gb). It indicates a slightly skewed mutation bias either toward AT in the mouse lineage, or toward GC in the rat lineage, since their last common ancestor. There is also a shift in the CpG dinucleotide content of the nonrepetitive fraction of these two genomes, with CpGs constituting 0.92% of all dinucleotides in the mouse, but 1.06% in the rat. Compared with all other dinucleotides, CpGs exhibit the largest such difference (data not shown).

To determine whether these shifts are due to specific or general biases in the mutation spectrum, we performed a quantitative analysis of substitution patterns in the two genomes. We considered all those positions within Dataset 1 (Fig. 1) in which human and one of the rodents share a common base that is different from that of the second rodent. The vast majority of these sites represents single events in which one of the rodents experienced a point substitution, while human and the other rodent share the ancestral base. We classified these sites according to which lineage exhibits the difference, and what type of difference is represented (see Methods).

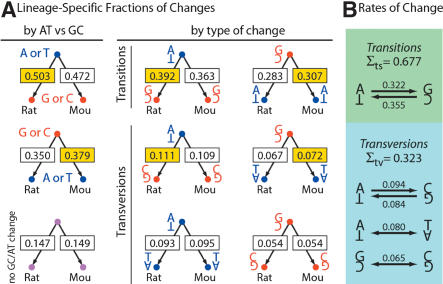
More than 117 million positions across Dataset 1 exhibited such single differences in either rodent, with ∼60 million representing a change in the rat lineage compared with 57 million representing a change in the mouse lineage. (The difference in point substitution rates between the rodents is discussed below.) The inferred substitutions exhibit a consistent bias toward elevated GC content in the rat genome compared with the mouse genome. Cumulatively, 50.3% of the changes inferred to have occurred in the rat lineage produced a G/C base pair from an A/T, compared with 47.2% of the changes in the mouse lineage (Fig. 2A, left side, top tree). For changes from G/C to A/T, the mouse lineage exhibits the relative excess (Fig. 2A, left side, middle tree). No substantial difference between the mouse and rat lineage is seen for those changes that do not alter GC content (Fig. 2A, left side, bottom tree). This consistent bias does not appear to be confined to particular types of transitions or transversions, as each type of change exhibits the same trend (Fig. 2A, right side).

Figure 2.

Fractions and rates of nucleotide substitution events observed within the mouse and rat lineages. (A) Fractions of various nucleotide changes within each lineage. Larger fractions are colored yellow if the change alters base composition. (Left panel) Sums of changes that result in the same change in base composition (A or T to G or C, e.g., which includes both transitions and transversion events). (Right panel) A more detailed classification of these data by the exact type of change (two transitions, four transversions), with base pairs shown to unambiguously describe the type of change. (B) Relative rates of each transition and transversion, corrected for base composition and averaged between the two rodents (see Methods). Counts of the given substitution events were divided by the frequency of the departing nucleotide, and subsequently normalized such that the values for all changes from the two lineages sum to 1. Note that either transition is approximately fourfold more likely than any given transversion.

Given the difference in CpG content between the genomes, we then asked whether this bias could be primarily caused by differential behavior of CpG dinucleotides between the two lineages, as these are sites that are known to mutate much faster than others (Sved and Bird 1990). It is possible, for example, that much of the observed discrepancy could be a result of an accelerated rate of CpG deamination in the mouse lineage (giving TpG) or, alternatively, more efficient protection or mutation repair for CpG sites in the rat. To address this, we analyzed the distributions of aligned dinucleotides between the rodents (Supplemental Table 1 available online at www.genome.org), considering only dinucleotides aligned between the rodents that show a single change (the human sequence was not used). Of all 24 possible dinucleotide alignment patterns, 16 result in a change of GC content between the two species. Of these 16, 15 favor creating a higher GC in the rat genome than in the mouse (Supplemental Table 1). The lone dinucleotide pattern that opposes this trend (GC/GC vs. GA/TC) has one of the smallest mouse–rat differentials. Although CpGs clearly play a major role in this phenomenon (Supplemental Table 1, top row), as would be expected because of their substantially accelerated rate of evolution, the trend is more general with respect to the affected type of dinucleotide.

Thus, we find evidence for a global shift in the mutation spectra between mouse and rat that is consistent with the difference in their GC and CpG content. Furthermore, we find that this shift is not confined to specific transitions or transversions or to CpGs. We conclude that it is a general shift differentiating the lineages of mouse and rat whose causative factors, selective or otherwise, remain to be elucidated.

Rates of Transitions and Transversions in the Rodents

Our counts of single nucleotide changes also afford the possibility to estimate average rates of transitions and transversions between the two rodents. Notwithstanding the lineage-specific differences discussed above (which clearly illustrate that substitution processes exhibit shifts during evolution even between closely related species), we sought such estimates because they are useful for molecular evolutionary studies. This is because most methods of phylogenetic inference model point substitutions on the basis of stationary Markov processes, and many require user-specified substitution parameters such as the ratio of transitions to transversions.

Therefore, we calculated the average relative rates of all types of transition and transversion between the two rodents (Fig. 2B; see Methods). As expected, transitions are more likely than transversions, with either transition being approximately fourfold more likely than any transversion. The magnitude of the transition bias appears stronger than in old estimates (Li et al. 1984) but is consistent with more recent analyses using likelihood modeling and multiple sequence alignments of mammalian DNA (Siepel and Haussler 2003). To our knowledge, this represents the first genome-wide estimate of these rate parameters for mammalian DNA.

Rates of Neutral Point Substitution

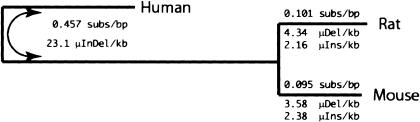
We then sought to determine the amount of neutral divergence, in terms of nucleotide substitution events per site, that occurred in the lineages of mouse and rat since their last common ancestor. For this purpose, we quantified point substitution events in rodent-specific neutral sites (Dataset 2) under a Jukes-Cantor model (Jukes and Cantor 1969; more sophisticated models have a negligible effect on our estimates; data not shown). The average rate of nucleotide substitution between mouse and rat is 0.196 substitutions per site (Table 1; Fig. 3), based on the 407,005,868 positions of Dataset 2.

Table 1.

Rates of Small Insertions and Deletions and Neutral Point Substitutions

	Human + ancestral rodent branch	Mouse branch	Rat branch	Total	Mouse/rat
Nucleotide subs per site	0.457	0.095	0.101	0.653	0.941
Microdeletions per site	n/a	0.00277	0.00336	n/a	0.824
Microinsertions per site	n/a	0.00184	0.00167	n/a	1.102
Ins/Del	n/a	0.664	0.497	n/a	1.336
Ins + Del	0.023	0.00461	0.00503	0.033	0.963
(Ins + Del)/Subs	0.051	0.049	0.050	0.050	0.974

Figure 3.

Tree of human, mouse, and rat, drawn to the scale of point substitutions estimated from Dataset 1 (Fig. 1). Tree is rooted for display purposes, but analyses were performed assuming an unrooted tree (note the arrow connecting the ancestral rodent and human branches). Each branch is annotated with the neutral substitution rate, as estimated using rodent-specific sites. For the mouse and rat branches, rates of small insertion and deletion are also shown, whereas for the human/ancestral rodent branch, the sum of small insertions and deletions is shown.

In addition to estimating the neutral rate between the rodents, we also determined the neutral rate for the evolutionary tree relating human, mouse, and rat. Instead of using ARs, we chose to use a previously used two-step approach (Cooper et al. 2003) because we felt that the introduction of biases, possibly owing to the annotation or alignment process during the identification of ARs, has not been adequately studied to date. The first step is to estimate the distance between mouse and rat using rodent-specific neutral sites (Dataset 2). The second step is to extrapolate this rate over a tree of human, mouse, and rat using relative branch lengths estimated from Dataset 1. This tree is unrooted, and we therefore refer to the branches by the species names. Note that the “human” branch is the sum of the two branches representing the human lineage and the ancestral (shared) lineage of the two rodents.

To estimate the relative branch lengths of this tree, we obtain all positions from Dataset 1 that do not have a gap in any of the three sequences (N = 1,071,376,029). We then obtain the maximum likelihood estimate of the unrooted tree (see Methods). The total tree length is 0.504 substitutions per site, with the human, mouse, and rat branches contributing 0.353, 0.073, and 0.078 substitutions per site, respectively. Note that Dataset 1 includes a mixture of constrained and neutral DNA, implying that the tree length estimated from it is an estimate for the lower bound of the neutral rate between human, mouse, and rat. Normalized such that the rat branch is 1 unit in length, the relative lengths of the human and mouse branches are 4.52 and 0.94, respectively, consistent with branch length estimates using different alignments (Rat Genome Sequencing Project Consortium 2004). Under the assumption, then, that this ratio remains constant across different classes of DNA (Cooper et al. 2003), we estimate the total neutral rate for the tree of human, mouse, and rat as 0.65 substitutions per site (Table 1; Fig. 3).

Rates of Microinsertion and Microdeletion

Microdeletions and microinsertions, here defined as lesions no larger than 10 bp, are the other types of small-scale evolutionary change. We sought to estimate the rates at which they occur and compare them with rates of point substitutions. This goal, too, is facilitated by the availability of the two closely related rodent genomes in conjunction with that of human.

We first determined the number and size of all gaps of <11 bp present in the aligned sequences of Dataset 1. Then, from an analysis of the lengths and relative positions of the gaps, the rates of microinsertion and microdeletion (“microindels”) were inferred under a parsimony assumption. For example, a gap in the rat not shared by mouse or human was scored as a rat deletion, whereas a gap shared by rat and human is classified as a mouse insertion. More complicated scenarios are classified such that the size and number of implied indel events are minimized (see Methods).

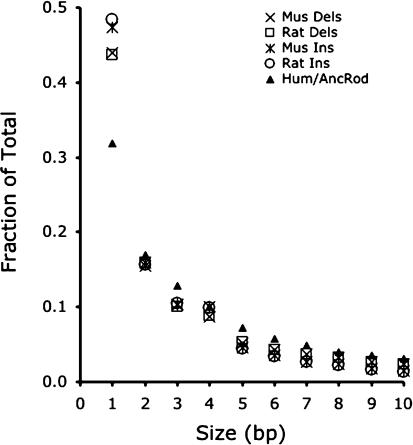
The frequency of small insertions and deletions drops dramatically as a function of the size of the event, for all classes of gap analyzed (Fig. 4); this pattern is consistent with other studies (Rat Genome Sequencing Project Consortium 2004), including those using nonmammalian sequences (Petrov et al. 2000). Consider that nearly half of all indels of <11 bp are single base events in both the mouse and rat lineages, whereas only a few percent are 10 bp in size. Furthermore, there is nearly perfect concordance in the shapes of the frequency plots between insertions and deletions, and between the two rodent lineages. This reflects fundamental similarities in the processes that generate these types of mutations. Note that the relatively large decrease in the frequency of single base events along the human branch is unlikely to be a meaningful biological difference, but rather an artifact of multiple hits, which will systematically obscure our ability to detect single base events.

Figure 4.

Number of gaps as a function of size in the mouse, rat, and human/ancestral rodent lineages. The frequencies of insertions and deletions <11 bp in length are plotted for the mouse and rat lineages, whereas the frequencies of insertions + deletions are plotted for the human/ancestral rodent branch. Note the rapid decline in the relative numbers of indel events as size increases, with events of size 1 occurring at a rate of >40% along both the mouse and rat lineages. Also note that the size distribution of small insertions and deletions behave very similarly to each other within each rodent lineage, as well as between lineages.

We also determined the rates of indels that have occurred along the three branches of the unrooted tree. To this end, we counted the number of events within each of our alignments, and normalized by the length of alignment. Although the length of the alignment is clearly not the length of the ancestral genome sequence in that region, it is a reasonable approximation, especially given the fact that we exclude those regions that have experienced large insertion and deletion events. Furthermore, because all rates are calculated relative to the same alignment, they are directly comparable between lineages. The rat lineage has experienced an increase in the rate at which small deletions occur when compared with the mouse, whereas the opposite is true for small insertions (Table 1), although at lesser magnitude. Microdeletions occur more frequently than microinsertions, on average by a factor of 2, in each of the lineages.

Finally, it is interesting to note that the summed rate of microindels relative to the rate of neutral point substitution is remarkably consistent for each branch at 5% (Table 1). Given that the average size of these small events is ∼3.3 bases, the per-base level of genomic change due to insertions and deletions (<11 bp) is on the order of 17% that of point substitutions. Including all insertions and deletions up to 20 bp in length, which are comparatively rare but large events, the average event size increases to 4.6 bases, with a per-base level of genomic change equivalent to 26% of the neutral point substitution rate. The observation that microindels are a significant evolutionary force in the shaping of genomes supports similar conclusions that were reached on the basis of studies involving invertebrate sequence data (Petrov 2002).

Global Identification of Constrained Elements

Alignment of the human genome to other mammalian genomes is a powerful method to discover and annotate functional elements in the human genome (Hardison 2000; Qiu et al. 2001; Sumiyama et al. 2001; Thomas et al. 2003). Exons, regulatory elements, noncoding RNAs, and other functional elements, which tend to be difficult to predict using primary sequence alone, can be discovered by virtue of their presence in other genomes: Those sequences that function in organismal biology tend to be under purifying selection, and therefore manifest themselves in alignments as regions that are evolving slowly.

Using our whole-genome alignments, we generated an annotation of all those regions in the human genome that are evolving, on average, significantly slower than the neutral rate. We first quantified substitution events within overlapping 25-bp windows across the human genome sequence and those regions of the rodent genomes to which it aligns (see Methods and Supplemental material). We then used these scores to find all regions in the human genome that are at least 51 bp in length and that evolve at various thresholds relative to the local neutral rate (see Methods), namely, from 10% to 50% in 10% increments. This allows us to find elements evolving at various speeds, as functional elements are known to have different levels of constraint.

A false-positive analysis was also performed, to determine the rate at which stretches of truly neutral DNA would appear to evolve at the specified threshold by chance. Our error rates are upper bounds and are quite conservative (see Methods). In windows of 51 bp that evolve at 30% of the neutral rate and slower, for example, our expected false-positive rate is less than 0.2%; at 40% of the neutral rate, the error rate is under 10%. However, at 51 bp and 50%, the expected false-positive rate increases dramatically, indicating that this is the extreme limit of the resolution of comparative analyses that leverage human, mouse, and rat genomic sequence information.

We discovered 210,923 constrained elements of at least 51 bp evolving at 10% of the neutral rate. The number of elements increases steadily to >1.3 million at 40% and 2.2 million at 50% (Table 2). The average size of the elements ranges from 93–110 bp, which strongly indicates that most of the annotated elements are, in fact, real (false-positive rates drop dramatically as the size of the element increases; data not shown). Using gene annotations that include both RefSeq and predicted genes (Solovyev 2002), we categorized each of our elements as (1) overlapping an annotated exon, (2) being in the intron of an annotated gene, or (3) residing in intergenic DNA (see Methods; Table 2; Fig. 5). For all thresholds, we find that the number of nonexonic conserved segments substantially exceeds the number of segments that overlap an exon. Even at the highest level of constraint analyzed (10% of the neutral rate), we find 167,892 conserved nonexonic segments, compared with 43,031 exonic segments. Some of the nonexonic segments may be exons that have not been annotated, but we suggest that this is relatively rare given that the gene annotations used included nearly 40,000 genes from multiple annotation sources. Additionally, the relatively high abundance of “nongenic” conserved sequences in mammalian genomes has been previously documented in multiple studies (Dermitzakis et al. 2002; Hare and Palumbi 2003).

Table 2.

Distribution of Constrained Elements in the Human Genome

Ratea	Count	Total length (bp)	Average size (bp)	% genomeb
Exonic segments
10%	43,031	3,810,697	88.56	0.13
20%	100,550	11,027,423	109.67	0.37
30%	131,940	18,755,479	142.15	0.63
40%	146,855	25,128,339	171.11	0.84
50%	163,817	30,425,479	185.73	1.01
Intronic segments
10%	115,258	10,958,920	95.08	0.37
20%	259,554	27,766,537	106.98	0.93
30%	459,821	52,189,014	113.50	1.74
40%	810,279	89,257,780	110.16	2.98
50%	1,403,977	146,631,328	104.44	4.89
Intergenic segments
10%	52,634	4,898,882	93.07	0.16
20%	119,843	12,621,975	105.32	0.42
30%	213,910	23,989,791	112.15	0.80
40%	375,395	41,208,385	109.77	1.37
50%	641,700	67,363,648	104.98	2.25
All Segments
10%	210,923	19,668,499	93.25	0.66
20%	479,947	51,415,935	107.13	1.71
30%	805,671	94,934,284	117.83	3.16
40%	1,332,529	155,594,504	116.77	5.19
50%	2,209,494	244,420,455	110.62	8.15

^aExpressed as a percentage of the local neutral rate

^bAssuming a genome size of 3 billion bases

Figure 5.

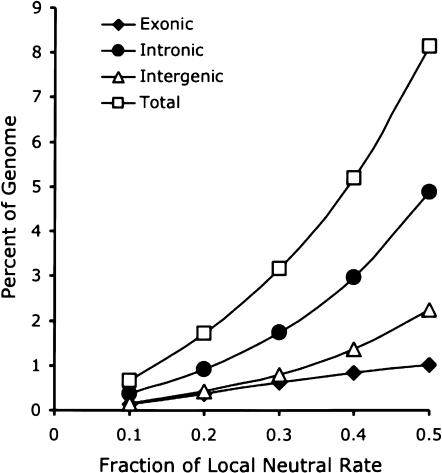
Density of constrained elements in the human genome. The fraction of the human genome annotated by our analysis as evolving at various fractions of the neutral rate, from 0.1–0.5. Total density of constrained elements are plotted (squares), in addition to being classified by type: intronic (circles), intergenic (triangles), and exonic (diamonds), based on gene annotations that include RefSeq and predicted genes.

We furthermore estimated the total amount of the human genome that is under constraint, using the conserved segments discovered (Table 2; Fig. 5). We estimate that 8% of the human genome evolves at 50% or less of the neutral rate, for example; however, given our false-positive rates reported earlier, this is likely to be an overestimate. It is estimated that 5.2% of the human genome evolves at 40% or less of the neutral rate. This may represent a more realistic, albeit conservative, estimate. It agrees with estimates reported previously using only human and mouse sequences, as well as with other estimates from human–mouse–rat comparisons that used methodology different from that used here (Rat Genome Sequencing Project Consortium 2004). The constrained 5% is distributed among more than a million functional elements evolving at various rates, and these are predominantly not identifiable as exons. Whether they are noncoding RNAs, regulatory elements, or something else, remains to be determined.

Regional Variability of Evolutionary Parameters

The estimates discussed thus far are genome-wide averages. Additional insights may be gleaned from understanding how evolutionary parameters vary across the genome, and how various types of events and phenomena are correlated with each other. The local rate of point substitution, for example, has previously been shown to vary significantly across the genome, in a pattern that is correlated with local AT content and rate of recombination (Waterston et al. 2002; Hardison et al. 2003).

To explore evolutionary variation at high resolution, we performed a sliding window analysis along rat Chromosome 1, using a window width of 2 Mb (Fig. 6). We also calculated correlations among some of the parameters on a per-alignment basis. Rates of point substitution, rates of microinsertion and microdeletion, GC and CpG content, and constrained element density all show considerable variation, and in some cases covariation, along the length of Chromosome 1 (Fig. 6).

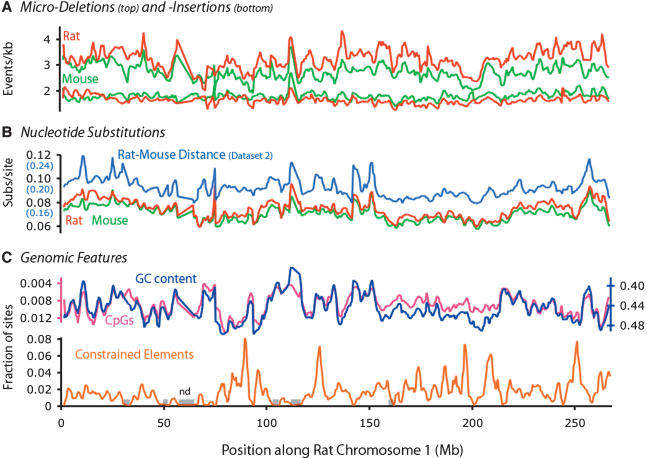
Figure 6.

Variation of various evolutionary and genomic features along rat Chromosome 1. The X-axis for all plots is the genomic coordinates along rat chromosome 1 (draft v 3.1), in megabases. Regions in which no alignment data were available (applies to all plots) are marked as gray boxes (“nd”) directly on the X-axis. (A) Rates of microinsertion (top) and microdeletion (bottom), with mouse and rat in green and red, respectively. Note the correlations among all four lines, and especially between lineages (red vs. green). (B) Rates of nucleotide substitution for the rat and mouse lineages (red and green lines, respectively). The pairwise distance between mouse and rat as estimated from rodent-specific sites is in blue. Note the correlation between the red/green and blue lines, which originate from Datasets 1 and 2, respectively. (C) GC content and CpG density are in blue and pink, respectively. Y-axes, which are inverted to show the correlation with the rate of neutral point substitution, are colored accordingly. The density of constrained elements evolving at <20% of the local neutral rate is shown in orange, and shows no significant covariation with any of the other features analyzed.

First, consider the modest-to-strong correlations between rates of microdeletion (Fig. 6A, top, R² = 0.55), microinsertion (Fig. 6A, bottom, R² = 0.21), and point substitution (Fig. 6B, R² = 0.75) in the independent lineages of mouse and rat across the length of the chromosome (Fig. 6A,B, red vs. green). Microevolutionary pressures have clearly remained substantially stable over the evolutionary time span separating mouse and rat, regardless of the type of event.

Second, consider that local variation in the rate of microdeletion correlates modestly with that of microinsertions (R² = 0.26), but that neither correlates well with point substitution. Thus, local evolutionary pressures appear to influence point substitutions and microindels differentially.

Third, consider the tight correlation between the neutral rate, estimated from rodent-specific neutral sites, with the rate of substitution in the independent lineages of mouse and rat, estimated from sites aligned to human (Fig. 6B, red/green vs. blue, R² = 0.59). The former was estimated with Dataset 2, whereas the latter was estimated from Dataset 1. The regions comprising these two data sets are interdigitated genomic neighbors, but are otherwise independent, and although the average rate of sites in Dataset 1 is lower than the average rate of sites in Dataset 2, local variation of these two rates tracks rather closely. Thus, local genomic context influences the rate of point substitution regardless of the type of site. This has been previously observed for ARs and fourfold degenerate sites, albeit at lower resolution (Waterston et al. 2002).

One interesting feature of local genomic context is GC content, which has previously been shown to correlate with rates of point substitution (Waterston et al. 2002; Hardison et al. 2003). We find very similar relationships between GC content and rates of point substitution as documented previously (Hardison et al. 2003). Finally, it is worth mentioning that the CpG content, at this level of resolution, is driven by bulk GC content and not, by inference, by the density of CpG islands (Fig. 6C). Similarly, the density of constrained elements does not correlate substantially with any of the rate estimates. In conjunction with the observation that point substitutions correlate significantly between Dataset 1 and 2, these observations support the conclusion that the correlations discussed here are not driven by the density of functional elements but by mutational parameters in the local genomic context.

DISCUSSION

Evolutionary Rates

Our estimate for the rate of evolution between the two rodents in “rodent-specific” sites, which are heavily enriched for neutral DNA, is 0.196 substitutions per site; this value can be used to estimate a gross neutral rate of 0.65 substitutions per site for the entire tree of human, mouse, and rat. These values are slightly higher than, but broadly consistent with, estimates made from different sites within different alignments that were also produced as part of the rat genome analysis effort (Rat Genome Sequencing Project Consortium 2004).

Some interesting differences have evolved in the rat and mouse lineages since their most recent common ancestor. First, there is a difference in GC content between the two species. This difference appears to have been caused by a higher tendency for substitution events to create a GC base pair in the rat lineage compared with the mouse lineage. This phenomenon is not primarily a consequence of mobile element activity: (1) comparison of the repetitive and nonrepetitive portions of the rat and mouse genomes reveal similar discrepancies in overall GC content (data not shown), and (2) the sites analyzed in this study are all shared among human, mouse, and rat, and therefore exclude recent lineage-specific insertion events. These observations indicate that differences in GC and CpG content between the rodents are largely a product of global nucleotide substitution phenomena, rather than dramatic localized differences in small subsets of the genome. Another notable difference is the slower rate of point substitution in the mouse lineage compared with the rat. This lineage-specific difference is consistent with results from similar analyses using different multiple sequence alignments of human, mouse, and rat (Rat Genome Sequencing Project Consortium 2004). Similar discrepancies between mouse and rat exist with respect to rates of microinsertion and microdeletion, with the mouse lineage having experienced slightly higher rates of microinsertion and substantially lower rates of microdeletion.

In terms of neutral evolution, these lineages have been separated only long enough for each to accumulate ∼0.1 substitutions per site. As such, the inferred shifts in evolutionary rates and genomic composition have occurred relatively recently and quickly. This is especially striking given the high degree of phenotypic similarity, in terms of anatomy, physiology, behavior, and reproduction, between the two species. Explanations for such shifts are presently confined to pure speculation. Possibilities include biochemical differences in replication or repair enzymes, selection that acts directly on genome nucleotide composition, or other forces that may influence rates and patterns of substitutions.

The effect of local genomic context on rates of evolution appears to result in correlations of local evolutionary rates between independent lineages, between classes of sites, and even between microinsertions and microdeletions. A notable exception is the relationship of microindels and point substitution rates, which are not as substantially correlated. It appears that the contextual factors that influence microindels are different from those that influence rates of point substitution.

Constrained Elements

One of the biomedical values of mammalian whole-genome sequencing efforts lies in comparative analyses for the purposes of discovering functionally important regions. Evolutionary constraint operates on those elements of the genome that serve an important role to the organism, and manifests as a deficit of substitution events within those particular elements. Whereas human–mouse comparative analyses have provided power in the past to elucidate regions of high constraint (Shabalina et al. 2001; Dermitzakis et al. 2002), the rat genome modestly increases that power by contributing 0.1 substitutions per site more neutral evolution (∼15% of the total tree length). We therefore conducted an initial search for constraint throughout the human genome.

Although the amount of divergence captured by human, mouse, and rat permits reliable quantification of constraint at a resolution of no less than 50 bp, we can learn much through such comparisons. Based on this work and other studies (Waterston et al. 2002), at least 5%, but probably less than 8%, of the human genome is under constraint, and, by inference, functional. These functional regions are distributed among more than a million discrete elements within the genome. Although many of these are exons, a majority is likely to encode other functions, such as noncoding RNA genes or elements involved in transcriptional regulation.

Conclusions

The availability of the rat genome sequence has facilitated genome-wide analyses of the variability of rates of evolution and their relationships with one another. It has also allowed a comparison of genomic and evolutionary parameters between the two closely related rodents, mouse and rat. Although some of these analyses confirmed results generated previously, a variety of new biological insights were generated. In addition, high-resolution analyses were made possible, allowing variation of evolutionary parameters to be tracked more precisely across the genome. Finally, our ability to classify rodent-specific sites and create a rich data set of neutral sites (>400 million sites) without relying on annotations was made uniquely possible by having the two closely related rodent genome sequences in addition to that of human.

As future genomes provide greater resolution for comparative analyses, estimates of the total fraction of the genome under constraint will remain relatively stable. However, the number of discrete functional elements will increase because the enhanced resolution will resolve regions that are presently annotated as a single element into multiple, distinct elements that lie close to one another. This type of analysis is perhaps one of the most exciting opportunities posed by the availability of the rat genome, and serves as a template for future comparative analyses of multiple mammalian genomes.

METHODS

Alignments

Alignments were generated as described elsewhere (Brudno et al. 2004) using the MLAGAN multiple sequence aligner (Brudno et al. 2003) and performed in collaboration with the Berkeley Genome Pipeline at LBL (Couronne et al. 2003).

Patterns of Nucleotide Substitution

GC content and CpG density were counted from the Mouse genome (February 2003) and Rat sequence draft assembly 3.1 (Rat Genome Sequencing Project Consortium 2004), that is, each nucleotide and dinucleotide was counted and normalized by the total number of each in the genome, excluding Ns. Substitution counts were obtained from our alignments. All ungapped positions were extracted from our subalignments (Dataset 1) for this purpose. As described, directionality of substitution events was inferred in all those alignment columns in which the human sequence matched only one of the rodents.

Proportions of particular changes within each lineage were determined by normalizing the observed count of each change within a lineage by the total number of observed changes within that lineage (Fig. 2A, both panels). To calculate relative rates for individual transition and transversion events (Fig. 2B), counts of the given substitution events were divided by the frequency of the departing nucleotide, and subsequently normalized such that the values for all changes from the two lineages sum to 1. These values thus constitute relative rates of the various events, averaged between the two rodent lineages. For all substitution events described, strand symmetry is assumed to account for base-pairing (e.g., counts of A to G are pooled with those of T to C).

We note that there is some potential for systematic bias introduced by violation of the parsimony assumption. To bias our estimates of the relative rates of substitution, however, such a violation would have to favor certain changes over others, which is unlikely; even if it did occur, the effect would be minimal because the species considered are closely related and multiple hits are comparatively infrequent.

For the analysis of dinucleotides, we extracted all dinucleotide pairs from Dataset 1 that aligned between the two rodents with only one nucleotide change. Counts of each potential pattern were tabulated, and differences between lineages are reported both as absolute counts (Supplemental Table 1, column 4), and values normalized by the average number (between the two species) of occurrences of the particular pattern. For example, there are 9,150,198 TC or GA dinucleotides in the mouse aligned to CC or GG dinucleotides in the rat, and 8,727,947 occurrences of the reverse pattern (Supplemental Table 1, row 7). This is an absolute difference of 422,251, and normalized by the average of the two opposite patterns this difference is 4.7%.

Global Rates of Point Substitution

“Rodent-specific” sites were extracted as described (Fig. 1) above. The criteria of a minimum length of 20 bp and a maximum of 10% gaps within the rodents were chosen for two reasons: to enrich for neutral sites by selecting for rodent-specific insertions and large human deletions, and to minimize potential alignment artifacts. Changing these criteria had little effect on the rate estimates (data not shown). The neutral divergence was estimated for each of our alignments using a Jukes-Cantor (Jukes and Cantor 1969) pairwise distance model; more sophisticated models had a negligible effect on the rate estimates (data not shown).

Ungapped sites shared by all three mammals were extracted from our subalignments (Dataset 1). These were used to construct the maximum likelihood unrooted tree relating the three species under the REV model of substitution (Yang 1994) as implemented in the Paml software package (Yang 1997). Relative branch lengths for each of the three branches of the unrooted tree were estimated by normalizing the global branch length estimates such that the rat branch was 1 unit in length. These relative branch lengths were then used to extrapolate the rodent neutral rate over the entire tree as described previously (Cooper et al. 2003), to generate neutral rate estimates for each of the three branches (Table 2).

Global Rates and Patterns of Insertion and Deletion

All gaps of <11 bp in length within Dataset 1 (Fig. 1) were tabulated. Directionality of events was inferred for the mouse and rat branches only, under the assumption of parsimony. For example, a shared human–rat gap corresponds to a mouse insertion, whereas a gap in either (but not both) rodent is identified as a deletion. Shared rodent gaps and gaps in the human sequence are identified as indels that occurred on the unrooted branch connecting human to mouse and rat (equivalent to the human and ancestral rodent branch of the rooted tree). More complicated gap scenarios, such as overlapping but not precisely shared gaps, are categorized such that (1) the number of events implied is minimized, and (2) the size of each event is minimized. These criteria are consistent with the observation that the frequency of microindel occurrence drops dramatically as the size of the event increases (Fig. 4). Because of the close evolutionary relationship between the rodents, indels inferred from these more complicated scenarios represent a minority of cases. Calculations of microindel rates are performed as described above, using the length of the alignment from which they are derived as a normalizing factor. Note that the distributions of gap event sizes are remarkably robust to the choice of gap penalties used in the process of aligning the genome sequences (data not shown).

Comprehensive Identification of Constrained Elements

All alignments are first compressed such that the human sequence is ungapped. This is consistent with the goal of searching for constraint within the human genome, and ensures consistency of alignment coordinates with annotation coordinates. We then estimate numbers of substitution events in consecutive, overlapping 25-bp windows, with a step size of 1 bp, across the length of our alignments.

We used a modified Jukes-Cantor model to measure the divergence between the nucleotide sequences of human, mouse, and rat. Gaps were treated as a fifth character, and consequently aligned gaps were considered homologous nucleotides in the analysis. Thus, the species formed a three-taxon phylogeny, with the probability of observing identical letters across a branch of length t given by

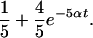The Jukes-Cantor parameter α is confounded with the branch length t, and without loss of generality we operated under the assumption that α is 1.

Branch lengths were estimated via maximum likelihood (Felsenstein 1981), and given the scope of our analysis we used a closed-form approximation to the MLEs rather than relying on numerical optimization. Specification of these heuristics, as well as a brief simulation study demonstrating their effectiveness, is available as a Supplemental material. For the purposes of estimation, the alignment was distilled into five classes of sites encoding the match/mismatch possibilities. We constructed an approximating formula based on these values that was appropriate to regions under sufficient constraint, and by excluding segments that obviously failed our constraint criteria (i.e., <50% identity between any two species, again treating gaps as a fifth character), we were able to count substitutions across the aligned genomes.

A model that treats gaps as a fifth character has been shown previously to be an effective evolutionary model, especially for alignments that contain predominantly short gaps and for building trees with relatively short branch lengths (McGuire et al. 2001). Our analysis satisfies both of these conditions, given the observed pattern of microindel events (Fig. 4) and our goal of identifying slowly evolving regions. Note also that our model assumes that the rate of gap events is equal to the rate of point substitution events. Although this is likely invalid, and a more rigorous statistical treatment would be desirable, it is a reasonable simplification for the purposes of constrained element identification.

After generating window scores, we search for consecutive stretches of windows whose total length is at least 51 bp, and whose average rate of evolution is less than the given threshold. Upon finding an initial segment that meets the given length and rate criteria (a “seed”), the seed is extended by adding windows in a greedy fashion until the threshold is met or exceeded, or a window is found in which rate estimation failed (see above). Thus, all elements reported for a given threshold have an average rate of evolution that is just slightly below the threshold, or lie immediately adjacent to a region for which the rate could not be reliably estimated. Five thresholds were used, all expressed as a fraction of the local neutral rate, ranging from 10% to 50% in 10% increments. The local neutral rate is estimated for each separate alignment of our whole-genome alignments (∼200 kb of ungapped human sequence each), using the rodent-specific sites described previously.

The gene annotations used to classify the constrained elements contain nearly 40,000 genes, including RefSeq genes and gene predictions; they are based on annotations for the human, mouse, and rat genomes made by Fgenesh++ software developed by Softberry Inc. (Solovyev 2002; http://www.softberry.com). More details are available in the paper describing our whole-genome alignments (Brudno et al. 2004).

The scope of our search made it necessary to choose parameter values that limited the number of spurious results. We constructed a null model of evolution to simulate neutral divergence between the nucleotide sequences of human, mouse, and rat as follows: Using our global estimates of interspecies neutral divergence, we considered the observed nucleotide patterns as evolving from a common ancestor under a Jukes-Cantor model with gaps treated as a fifth character. The identification of a seed here signifies a false-positive result, and we calculated the average number of consecutive alignment positions needed to obtain one false positive under the null model. Our calculation took into account the approximation used for estimating branch lengths, leading to a false-positive rate that accurately reflected the discovery process. The dependence between scores from successive windows made it prohibitive to calculate the false-positive rate exactly, and we chose a conservative estimate that bounds the value from below. These bounds were verified through simulation. These rates of false-positive occurrence are quantified at a per-nucleotide level, and are converted to total number of expected false-positive “elements” by assuming 1.3 Gb of shared human, mouse, and rat genomic DNA (see Fig. 1, Dataset 1).

Regional Variation of Evolutionary Parameters

A 2-Mb window was moved in 400-kb intervals across our alignments, within which values such as rates of substitution, GC content, and so on were calculated as described above. Before calculating these moving-window averages, any alignment that (1) covered less than ∼1% of the length of the corresponding human sequence (potentially indicative of a spurious anchor in the initial phase of alignment) or (2) had substantial overlap with a longer alignment in human or rat (potentially indicative of a segmental duplication) was eliminated from inclusion, resulting in an ∼10% reduction in the total number of alignments used. (The average rates of evolution were unaffected by this step; data not shown.)

Constrained element densities were calculated using the rat sequence as the reference sequence, that is, alignments were compressed such that all gaps in the rat sequence were eliminated. For a handful of the overlapping 2-Mb windows, no alignment data were available, and these are explicitly marked (Fig. 6). To determine correlations between the various features analyzed, data were extracted on an alignment-by-alignment basis, constituting 768 independent data points. Simple linear regressions were calculated for all pairwise relationships described, and all reported R²-values are statistically significant (p < 0.01).