Identification of Evolutionary Hotspots in the Rodent Genomes

Abstract

We describe a whole-genome comparative analysis of the human, mouse, and rat genomes to describe the average substitution patterns of four genomic regions: ancient repeats, rodent-specific DNA, exons, and conserved (coding and noncoding) regions, and to identify rodent evolutionary hotspots. In all types of regions, except the rodent-specific DNA, the rat branch is slightly longer than the mouse branch. Moreover, the mouse–rat distance is longer in the rodent-specific DNA than in the ancient repeats. Analysis of individual conserved regions with different substitution models yielded the conclusion that the Jukes–Cantor model is inadequate, and the Hasegawa–Kishino–Yano model is almost as good as the REV model. Using human as an outgroup, we identified 5055 evolutionary hotspots, which are highly conserved subalignment blocks (each consisting of at least 100 aligned sites and a small fraction of gaps) with a large and statistically significant difference in the branch lengths of the rodent species. The cutoffs used to identify the hotspots are partially based on estimates of the average rates of substitution. The fractions of hotspots overlapping with the rodent RefSeq genes, RefSeq exons, and ESTs are all higher than expected. Still, more than half of the hotspots lie in noncoding regions of the mouse genome. We believe that the hotspots represent biologically interesting regions in the rodent genomes.

The sequencing of the rat genome makes possible, for the first time, a whole-genome comparative analysis of three large mammalian genomes. Despite the exciting prospects of such an analysis, existing methods on a whole (mammalian) genome scale are scarce. Some examples include methods based on gene order comparison rather than sequence comparison (Moret et al. 2001). One of the difficulties in whole-genome comparison is that it is necessary to begin with a reliable multiple alignment of the genomes. Even pairwise whole-genome comparison is difficult (Wiehe et al. 2000; Miller 2001), and the addition of genomes significantly complicates the alignment problem with resulting consequences for the inferences that are to be made.

Three species comparison of genomic regions was first undertaken by Lee et al. (1998). Subsequent analysis of three species data (Dubchak et al. 2000) for the identification of actively conserved non-coding regions resulted in suggested percent identity cutoffs for extracting functional regions from human, mouse, and dog alignments. Recent targeted sequencing projects have yielded larger data sets for analysis (Boffelli et al. 2003; Cooper et al. 2003; Thomas et al. 2003), revealing the power of comparative analysis both for understanding sequence evolution and for identifying functional elements.

We performed a comparative analysis on a whole-genome multiple alignment of human, mouse, and rat DNA sequences, to describe the average substitution patterns of four types of DNA: ancient repeats, rodent-specific DNA, exons, and conserved regions (coding and noncoding), and to identify rodent evolutionary hotspots, which are well-conserved regions where the rodent branch lengths are very different. The data were obtained by extracting appropriate gapped subalignments, called blocks, from the whole-genome alignment. The blocks were aggregated to estimate the average substitution rates and branch lengths of the unrooted tree relating the three species (Fig. 1) for each type of DNA, by maximum likelihood on the REV substitution model (Tavaré 1986; Yang 1994). Then we investigated the effect of substitution model on branch length estimation applied to individual conserved regions. Finally, rodent evolutionary hotspots were selected from the conserved regions based on criteria that are partially motivated by the average substitution patterns.

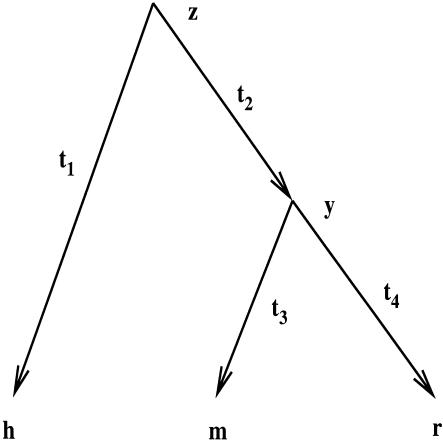
Figure 1.

The evolutionary tree relating h, m, r, the most recent rodent ancestor y, and the most recent common ancestor z. By pooling ancient repeat sites, the branch lengths are t_h = t₁ + t₂ = 0.36, t_m = t₃ = 0.070 and t_r = t₄ = 0.073 substitutions per site.

The ancient repeats (Waterston et al. 2002; Hardison et al. 2003) and rodent-specific DNA, which do not align to any human DNA (Cooper et al. 2003a), are believed to be enriched in nonfunctional sequences, hence likely to be undergoing neutral evolution. A human repetitive element, which was neither simple nor low complexity, was selected if at least 80% of its bases were aligned to both mouse and rat. Such an alignment is likely to be a good alignment between repetitive elements that descended from the same ancestor before speciation. Rodent-specific DNA were collected by selecting blocks with at least a = 50 aligned sites, flanked by gaps of length greater than g = 5, and containing gaps of length at most g = 5, with total length at most 10% of the number of aligned sites from genomic regions where rodent DNAs align to gaps in the human sequence. The conservative criteria ensured that the selected blocks had a small number of short gaps, so that we were confident that the alignments were solid. For exons, we selected human RefSeq exons with at least 80% of their bases aligned to both mouse and rat. The rationale is similar to that for ancient repeats. Finally, the criteria for conserved regions are very similar to those for rodent-specific DNA, with a = 100 and g = 10. We required at least 100 aligned sites so that the branch lengths can be estimated reliably from individual blocks. In addition, we only selected blocks where all three pairwise similarities exceeded 60%, to save computation time and to sift out spurious alignments. As will be seen, this extra requirement has little effect on the results. Although the filters are largely heuristic and arbitrary, they are conservative in the sense that most of the selected blocks are believed to represent real alignments of conserved sequences from all three species.

An evolutionary hotspot is a conserved region with the property that the human branch is shorter than 0.25 substitutions per site, the absolute difference between the rodent branch lengths is more than twice the asymptotic standard error, and the ratio of the mouse branch to the rat branch is at least 10 or at most 0.1. These are well-conserved regions, likely to contain functional elements, where the rodents have evolved at very different rates.

RESULTS

Average Substitution Patterns

Table 1 displays some statistics and the branch lengths for four types of regions: ancient repeats, rodent-specific DNA, exons, and conserved regions; the substitution patterns were aggregated in these analyses. Because the rodent-specific blocks are really pairwise alignments, the distance between the rodents, but not their respective distances to the rodent ancestor, may be estimated via the REV model. For all other regions, the mouse branch is slightly shorter than the rat branch, the ratios ranging from 0.91 to 0.95, indicating that mouse generally evolved slightly more slowly, relative to rat. The fractions of blocks with the rat branch longer than the mouse branch were 54% for long ancient repeats (>100 aligned sites), 52% for long exons (>100 aligned sites), and 55% for conserved regions. The ratio of the human branch to the mouse branch is ∼5. These are consistent with observations by others (Cooper et al. 2004; Yang et al. 2004). Ranking by any branch length gives the expected ordering

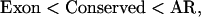because, in general, exons evolved under a lot of selective pressure, whereas the ancient repeats are likely to be enriched in nonfunctional DNA, and conserved regions are intermediate. Ordering by the mouse–rat distance yields

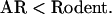Because the amount of data is so large, the discrepancy cannot be explained by statistical fluctuations but, rather, indicates a real difference. The orderings are quite robust to mild perturbations in the selection criteria. For example, the mouse–rat distances are 0.13 (at 90% threshold) and 0.15 (70%) for AR; 0.17 (a = 100, g = 10) and 0.18 (a = 20, g = 2) for rodent-specific DNA; 0.06 (90%) and 0.08 (70%) for exons; and 0.09 (70%), 0.10 (50%), and 0.12 (0%) for conserved regions. Both the parameter values a = 20, g = 2, and the mouse–rat distance 0.18 are very similar to those by Cooper et al. (2004). Perturbing other parameters for conserved regions still gave estimates within the range.

Table 1.

Statistics and Estimated Branch Lengths

Type	Blocksa	Sitesb	th	tm	tr	th/tm	tm/tr
AR	138	19	0.36	0.070	0.073	5.1	0.95
Rodent	3955	608	—	0.09c	0.09c	—	—
Exon	7	0.2	0.16	0.034	0.036	4.7	0.95
Conserved	647	52.8	0.26	0.052	0.058	5.0	0.91

^aIn units of thousand

^bIn units of million

^cOnly the sum, 0.18, was estimated. (AR) Ancient repeats; (Exon) conserved exons; (Rodent) rodent DNA that aligns to gaps in human. (t_h, t_m, t_r) Human, mouse, and rat branch length (Fig. 1), measured in average number of substitutions per site. The ratios are not exactly equal to the reported values because of rounding in the branch lengths

The estimated REV rate matrices are shown in Table 2. All rate matrices are not of the HKY type, R(C, A) being typically larger than R(T, A); the exon rate matrix is the closest to HKY. However, they are very close to being strand-symmetric, that is, the rates are invariant under complementation. For example, Q(A, C) ∼ Q(T, G). The AR and Rodent rates are remarkably similar, and they are both similar to the rates for conserved regions. Finally, all the rate matrices are more similar to each other than to those corresponding to the 4D sites and ancient repeats in Hardison et al. (2003). This could be caused by differences in data, alignment, methodology, or other factors.

Table 2.

Estimated REV Rate Matrix, Q, Its Symmetric Part, R, and Its Equilibrium Distribution π, for Four Types of Regions

Region		Q				R			π
AR	-0.87	0.18	0.52	0.18	-2.97	0.84	2.52	0.60	0.29
	0.25	-1.17	0.19	0.74	0.84	-5.64	0.90	2.52	0.21
	0.74	0.19	-1.18	0.26	2.52	0.90	-5.74	0.87	0.21
	0.18	0.52	0.18	-0.88	0.60	2.52	0.87	-3.00	0.29
Rodent	-0.88	0.17	0.53	0.19	-3.03	0.83	2.53	0.63	0.29
	0.24	-1.16	0.18	0.74	0.83	-5.55	0.84	2.54	0.21
	0.74	0.18	-1.16	0.25	2.53	0.84	-5.56	0.84	0.21
	0.19	0.53	0.18	-0.89	0.63	2.54	0.84	-3.06	0.29
Exon	-1.05	0.19	0.71	0.15	-4.53	0.72	2.60	0.64	0.23
	0.17	-0.96	0.18	0.61	0.72	-3.55	0.64	2.68	0.27
	0.60	0.17	-0.95	0.17	2.60	0.64	-3.48	0.75	0.27
	0.15	0.72	0.20	-1.07	0.64	2.68	0.75	-4.69	0.23
Conserved	-0.89	0.18	0.54	0.18	-3.09	0.83	2.51	0.61	0.29
	0.24	-1.14	0.19	0.72	0.83	-5.35	0.88	2.51	0.21
	0.72	0.19	-1.15	0.24	2.51	0.88	-5.40	0.85	0.21
	0.18	0.54	0.18	-0.89	0.61	2.51	0.85	-3.12	0.29

Sensitivity of Branch Length Estimates to Substitution Model

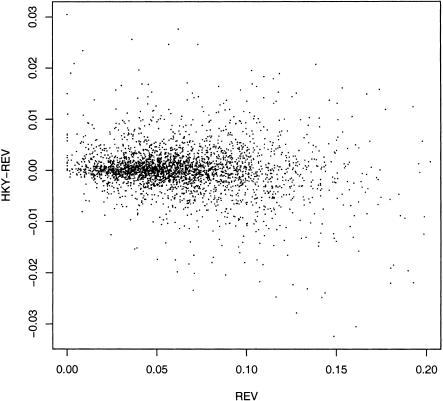
The average substitution patterns were studied using aggregated blocks, in which blocks of any size were effectively glued together to form a large block. On the other hand, to identify interesting regions for further study, it is necessary to apply the estimation procedure to individual blocks, which were required to have at least 100 aligned sites so that the estimates were not too variable. We compare the branch lengths of 646,741 conserved regions estimated via the Jukes-Cantor (JC), Hasegawa-Kishino-Yano (HKY), and general reversible (REV) models by maximum likelihood. Between JC and REV, the fractions of blocks for which the difference is <0.01 is 85% (rodents) and 27% (human). The corresponding fractions for comparing HKY and REV are 94% (rodents) and 79% (human). Thus, HKY is significantly more accurate than JC. Generally, the REV estimates are larger than the HKY estimates, which are, in turn, larger than the JC estimates. Also, the difference between REV and HKY (also REV and JC) tends to decrease modestly as the branch length (with the REV estimate as a proxy) decreases (see Fig. 2), which is consistent with the fact that the variance is larger for a longer branch. Interestingly, for very short branches, the HKY and JC estimates tend to be larger than REV. This phenomenon may partially account for the fact that the number of hotspots increases as the substitution model becomes more accurate: 3672 (JC), 4522 (HKY), and 5055 (REV). We conclude that JC should be avoided, and although HKY may be adequate for branch length estimation, the REV model is better and thus we used the latter.

Figure 2.

Plot of the difference of estimated rat branch length by the HKY and the REV against the REV branch length for the conserved regions. To present the data clearly, every 200-th block was actually plotted, yielding 3234 points. The correlation coefficient for the plot is –0.17, and for the 646,741 conserved regions is –0.18. The corresponding plot for mouse is very similar.

Evolutionary Hotspots

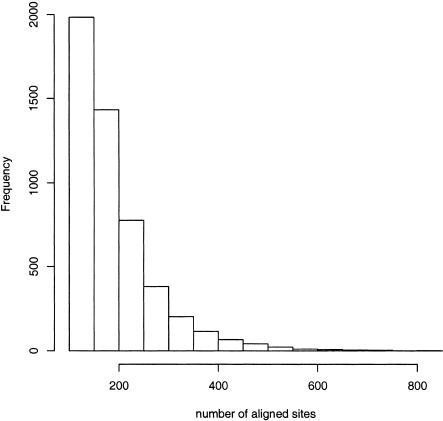
We found 5055 evolutionary hotspots among the conserved regions. The average and standard deviation (SD) of the number of aligned sites are 190 and 86, respectively (histogram in Fig. 3). If the conserved regions were not filtered by the requirement that the three pairwise similarities were at least 60%, then the number of hotspots found was 5086. Thus, the effect of the filter is rather small for identification of hotspots.

Figure 3.

Histogram of the number of aligned sites in the evolutionary hotspots.

Small fractions of the hotspots have some overlap with ancient repeats (mouse 6%, rat 5%) and simple and low-complexity repeats (mouse 9%, rat 8%). We also computed the fractions that have some overlap with RefSeq genes, RefSeq exons, and ESTs. Treating hotspots as points on the genome, if they were scattered randomly, then we would expect the fraction that landed on, say, the ESTs, to be roughly the fraction of ESTs in the genome. The observed and expected fractions are reported in Table 3. The hotspots are overrepresented in the three regions by factors ranging from 2.0 (mouse ESTs) to 6.7 (rat exons). This observation still holds for each individual chromosome. Because the mouse Ref-Seq database is more complete, we infer that about ∼37% of the hotspots lie totally in the noncoding portion of mouse genes. Assuming that the mouse ESTs cover all RefSeq genes, ∼27% are intergenic in the mouse genome. Thus, 64%, or more than half, of the hotspots are probably functional noncoding sequences in the mouse genome.

Table 3.

Observed (Expected) Fractions of Hotspots in RefSeq Genes, RefSeq Exons, and ESTs

Species	Mouse	Rat
RefSeq genes	39% (18%)	17% (8%)
RefSeq exons	2% (1%)	2% (0.3%)
ESTs	73% (37%)	49% (18%)

The smaller expected fractions for rat are due to the fact that the rat databases are less complete.

The evolutionary hotspots are available for downloading at http://baboon.math.berkeley.edu/hotrodent/. For long hotspots (>300 aligned sites, say), it is likely that the branch lengths vary considerably along the alignment. It is then desirable to perform the estimation on a sliding window for detailed study. Although it is difficult to characterize the hotspots in an automated fashion, examples we have analyzed are yielding seemingly interesting biological stories (although ones that may be difficult to verify by experiment). An example is a 505-base-long hotspot in the third intron of PEX14 (Rat Genome Sequencing Project Consortium 2004), described as peroxisomal biogenesis factor 14 in the RefSeq database. This nonrepetitive region shows remarkable heterogeneity in evolutionary rates; the 5′-end has a very short mouse branch and a long rat branch, while near the 3′-end, there is a stretch of 210 sites that are identical in all three species.

DISCUSSION

The sequencing of the rat genome has provided us, for the first time, the opportunity to compare and contrast closely related vertebrate genomes. We have specifically used the human genome as an outgroup to the rodent genomes to identify evolutionary hotspots; it is important to note that this analysis would not have been possible without the complete sequence for all three genomes. Although the phylogenetic tree for the human, mouse, and rat is rather simple, the estimation of the branch lengths is not, and, as we have shown, several interesting results emerge from a detailed analysis of the branch length estimates and their sensitivity to parameters.

One of the clearcut results is that the rat branch length is slightly longer than the mouse branch. This finding is true not only on average, but also locally across the genomes. Furthermore, this observation is confirmed by independent analyses on different alignments (Cooper et al. 2004; Yang et al. 2004). The mutually exclusive ancient repeats and rodent-specific DNA yielded two interesting findings: First, their respective substitution rate matrices are very similar, indicating that perhaps the rodent substitution processes are similar in these two regions. This is consistent with the view that both types of regions are evolving neutrally. Second, the discrepancy between the mouse–rat distances inferred from the two regions, which is quite robust to the selection criteria, seems to be fairly strong evidence that the rodent-specific DNA evolved at a faster rate than the ancient repeats. Although this suggests that there is no single average neutral rate of substitution, it is important to bear in mind that there is still no clear computational assay for identifying neutrally evolving DNA. Because blocks were conservatively selected, both distance estimates are underestimates, and one may argue that the discrepancy is not inconsistent with the existence of a common, neutral, rate of substitution.

We showed that the relatively simple HKY model worked almost as well as the general REV model, and much better than the simplest JC model. This confirms the well-known observation that base composition and substitution bias should be taken into account in branch length estimation. Furthermore, given that the HKY model is simpler than the REV model, our finding suggests that using HKY for branch length estimation can be a workable compromise between accuracy and speed when analyzing large data sets.

The close distance of rat to its common ancestor with mouse means that the total predictive power of the mouse and rat genomes for identifying conserved regions in the human genome is not that much greater than using the mouse alone. Nevertheless, as we have pointed out, treating human as an outgroup to two similar genomes (mouse and rat), allows for the targeted identification of regions in the rodent genomes that are evolving in unexpected ways. We believe that the 5055 blocks we have identified represent a conservative estimate of the number of such regions. Because we only selected hotspots with at least 100 aligned sites, we necessarily miss the shorter ones. Perhaps one way to identify them is by sliding a window along a conserved region to detect very different rodent branch lengths.

It is important to note that the cutoffs used in our methodology are motivated partly by analyses of the average substitution patterns in the human, mouse, and rat lineages. Although the estimates depend on the thresholds used, and also on the alignment, systemic patterns do emerge from independent analyses, and the universal observation that the rat lineage is evolving faster than the mouse is confirmation of that. Thus, we believe that our identified hotspots do represent biologically interesting regions, and are not merely artifacts of selected parameters and heuristic cutoffs.

The natural generalization of our study is to identify regions in a multiple alignment where the inferred tree differs substantially from the consensus tree for the genome. Recent work by Billera et al. (2001) describes the “space of trees” that has unique geodesics, and thus provides a natural framework for quantitatively assigning a distance to a pair of trees. Our method on analyzing the rodent genomes for hotspots should extend to multiple organisms using this approach.

METHODS

Alignment

A multiple alignment of the human, mouse, and rat genomes was generated by first constructing a three-way homology map between the genomes and then aligning the homologous regions with MAVID (Bray and Pachter 2003; http://babson.math.berkeley.edu/mavid). Further details are in the companion paper describing MAVID (Bray and Pachter 2004).

Ancient Repeats

The locations of the human repetitive elements were down-loaded from the UCSC Genome Browser (http://genome.ucsc.edu); simple and low-complexity repetitive elements were removed.

Exons

The locations of the human RefSeq exons were downloaded from the UCSC Genome Browser.

Rodent-Specific DNA and Conserved Regions

The criteria for rodent-specific DNA and conserved regions are more complicated because unlike the ancient repeats and exons, they have no well-defined positions. Intuitively, a block should have many aligned sites and few gaps. Our filters reflect this idea, and are similar to that used in (Yap and Speed 2003).

Evolutionary Hotspots

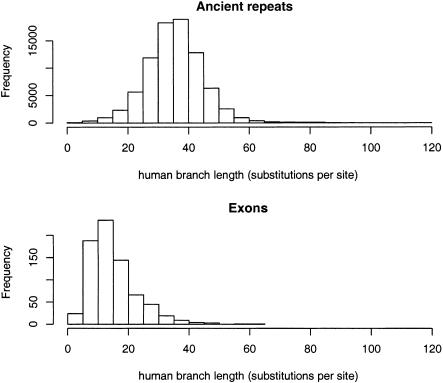
The 0.25 substitutions per site cutoff for the human branch length is natural, considering that this is a good threshold for separating exon from AR (Table 1). A more in-depth analysis of long exons and ancient repeats confirms this choice (Fig. 4). The choice to impose the cutoff on the human branch is not arbitrary. Because human is much more distant from both rodents than they are from each other, a block with a short human branch is a strong signal of conservation. On the other hand, selecting blocks with rodent branches shorter than 0.052 (mouse) and 0.055 (rat) substitutions per site gives only 3820 hotspots, 1501 of which have human branch longer than 0.25 substitutions per site.

Figure 4.

Histograms of the human branch length of blocks with at least 100 aligned sites from ancient repeats and exons. Branch lengths were estimated from each block individually without aggregation. A rough cutoff for separating the two distributions is 0.25 substitutions per site.

Estimation

To obtain the average substitution rates and branch lengths in Tables 1 and 2, we aggregated the blocks over the whole-genome alignment. We also applied the estimation procedure on individual blocks for some blocks in the ancient repeats and exons (Fig. 4) and for all conserved regions. Because aggregation is equivalent to gluing alignments into a long alignment, it suffices to explain the estimation procedure on a single block.

Let h, m, and r be the respective sequences from human, mouse, and rat. Assuming, as usual, that there was a common ancestor to human, mouse, and rat, which then split into a human lineage and a rodent lineage, which, in turn, split into mouse and rat, we then have a rooted phylogenetic tree relating the sequences as depicted in Figure 1. The branch lengths t₁, t₂, t₃, and t₄ represent the evolutionary distances between the appropriate sequences, measured in the number of evolutionary events that occurred, averaged over all possible substitution paths. Because the rate of evolution is likely to have varied across lineages, there is no general correspondence between the evolutionary distances and the chronological time intervals.

The REV rate matrix Q can be represented as

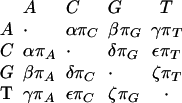The off-diagonal entries, the instantaneous substitution rates, are all nonnegative, and the diagonal entries are such that each row sums to 0. π = (π_A, π_C, π_G, π_T) is the equilibrium distribution. Equivalently, Q = RΠ, where Π is diagonal and R is symmetric:

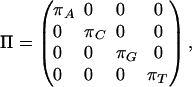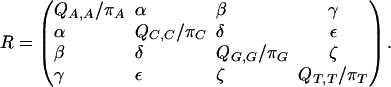If α = γ = δ = ζ and β = ε, then Q is an HKY matrix. If π is uniform and α = β = γ = δ = ε = ζ, then Q is a JC matrix. Finally, if π_A = π_T, π_C = π_G, α = ζ and β = ε, then the substitution rates are invariant under complementation; for example, Q(A, C) = Q(T, G). In this case, Q is called strand-symmetric.

Suppose that Q is calibrated, that is,

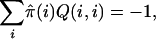or equivalently, the average number of substitutions per unit of evolutionary time is 1. The transition matrix P_t is given by

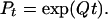The probability that an aligned site has human, mouse, and rat bases a, b, and c (see Fig. 1) is obtained by summing over all possible ancestral bases:

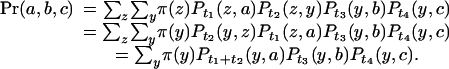Two consequences of reversibility are reflected in this expression. First, the joint probability is the same as if the rodent ancestor were the root, simplifying the calculation. Second, t₁ and t₂ are not estimable from the multiple alignment, although their sum is. We shall refer to the human, mouse, and rat branch lengths as

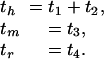Thus, we are forced to estimate branch lengths of an unrooted tree with three leaves, which is a star tree. Note that the human branch is just a mathematical convenience, but the rodent branches correspond to true lineages.

Assuming site independence and homogeneity, the probability of a subalignment (without gaps) is the product of the site-specific probabilities. This is maximized numerically to obtain estimates of the rate matrix and the branch lengths. By suitably constraining the rate matrix, we get the maximum likelihood (ML) estimates of an REV, HKY, or JC rate matrix. The whole-genome analysis for REV could be finished within 7 h on a single 2.6-Ghz processor.