Abstract
We describe a new global multiple-alignment program capable of aligning a large number of genomic regions. Our progressive-alignment approach incorporates the following ideas: maximum-likelihood inference of ancestral sequences, automatic guide-tree construction, protein-based anchoring of ab-initio gene predictions, and constraints derived from a global homology map of the sequences. We have implemented these ideas in the MAVID program, which is able to accurately align multiple genomic regions up to megabases long. MAVID is able to effectively align divergent sequences, as well as incomplete unfinished sequences. We demonstrate the capabilities of the program on the benchmark CFTR region, which consists of 1.8 Mb of human sequence and 20 orthologous regions in marsupials, birds, fish, and mammals. Finally, we describe two large MAVID alignments, an alignment of all the available HIV genomes and a multiple alignment of the entire human, mouse, and rat genomes.
The multiple-alignment problem is difficult for many reasons (for example, see Notredame 2002), and thus remains unsolved despite much progress over the past two decades. To appreciate the complexity of the problem, it is instructive to observe that five DNA sequences of length five have ∼1.05 · 1018 alignments! (Slowinski 1998). Even three sequences of length five have >14 billion alignments, and thus, it is clear that an alignment of the human, mouse, and rat genomes must be based on a relatively simple optimization criteria, and even then, must involve heuristics to reduce the complexity of the problem.
Despite the overwhelming complexity of the problem, it is important to observe that the multiple alignment problem for genomic sequences is not equivalent to the mathematical problem of producing an optimal alignment maximizing some score function (Gusfield 1997). The biological problem consists of correctly aligning homologous bases to each other, thus correctly identifying conserved noncoding regions in introns and intergenic regions, exons in orthologous genes, and groups of orthologous genes that form larger blocks of homology.
In this study, we propose a method capable of rapidly aligning multiple large genomic regions by incorporating biologically meaningful heuristics with theoretically sound alignment strategies. The core of our approach is a probabilistic ancestral alignment scheme (Feng and Doolittle 1987; Gonnet and Benner 1996; Hein 2001; Holmes and Bruno 2001; Löytynoja and Milinkovitch 2003). This involves the progressive alignment of ancestor sequences (inferred using maximum-likelihood estimation within a probabilistic evolutionary model [Felsenstein 1981]) along a phylogenetic guide tree. Although a comprehensive review of progressive alignment is beyond the scope of this work, it is important to point out that probabilistic approaches have been proposed and implemented (e.g., Hein 2001; Holmes and Bruno 2001; Holmes 2003), although existing methods are not scalable to very large problems.
To incorporate biological information into the alignment procedure, the progressive alignment is constrained by gene-based anchors. These anchors are precomputed on the basis of ab-initio gene predictions and their protein alignments and form part of the input to the program. In addition, nontrivial positional constraints (Hardison et al. 1993; Myers et al. 1997) are precomputed and ensure that the progressive alignment steps respect a precomputed homology map for the sequences.
The alignment of the ancestor sequences is based on the AVID (Bray et al. 2003) alignment method, thus allowing for the rapid alignment of very large genomic sequences even in between gene anchors that may be far apart. This fast alignment, along with the speedup obtained by using constraints, allows for an iterative alignment approach alternating between the progressive alignment step and phylogenetic tree construction (based on the alignment). In fact, as we show, it is possible to start with a random initial tree and converge to the correct guide tree, thus eliminating the need for an expensive pairwise alignment step (quadratic in the number of sequences) at the beginning of the progressive alignment (Thompson et al. 1994).
We have combined all of these ideas into a new program called MAVID, which we used to align the human, mouse, and rat genomes. We also show that MAVID is suitable for aligning very large numbers of sequences, and is therefore practical for the alignment of multiple HIV genomes (Korber et al. 2001) or hundreds of mitochondrial sequences (Hernnstadt et al. 2002). Finally, we demonstrate the accuracy of MAVID on the benchmark cystic fibrosis (CFTR) gene region (Thomas et al. 2003), and show that it compares favorably with existing alignment methods.
METHODS
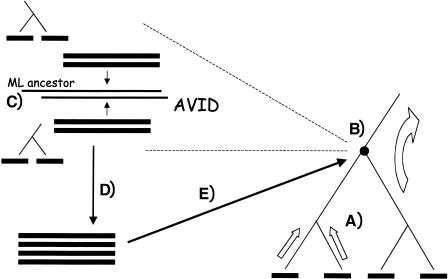
Our method consists of a core progressive ancestral alignment step, which can incorporate preprocessed constraints (see Fig. 1).
Figure 1.
MAVID architecture overview. (A) Sequences are aligned upward along a guide tree and (B) alignments of alignments are performed at internal nodes. To align two alignments (C), maximum likelihood ancestor sequences are inferred from each of the separate alignments, and (D) the ancestor sequences are aligned with MAVID. The resulting multiple alignment (E) (corresponding to a subset of leaves of the tree) is then recorded at the internal node.
To clarify the presentation of the method, we begin by defining some terminology. A match is any identified similar region between two sequences. A match does not have to be exact at the sequence level; for example, we could declare a match between two orthologous gene regions, even if the sequence does not match exactly. A maximal exact match is a match that is exact at the sequence level, and is maximal (i.e., cannot be extended on either side without creating a mismatch). An anchor is a match that is used in the alignment. A constraint ai ≤ bj in a multiple alignment means that position i in sequence a must appear before position j in sequence b in the multiple alignment.
Progressive Alignment
Let T be a phylogenetic tree, that is, a binary tree with branch lengths from an evolutionary model. To build progressive alignments, we need a root for T. Sometimes the root is known because of the availability of an outlier. In the case in which the tree T is unrooted, we use the midpoint method, select the root to be halfway in between the two leaves of T, which are farthest apart. This method produces the correct root if the molecular clock assumption holds, and a good approximation otherwise.
We associate multiple alignments to the vertices of T recursively, starting from the leaves. For a vertex x in T, let Tx be the subtree consisting of x and all of the vertices beneath x. If x is a leaf, then Tx is a trivial tree (i.e., a tree consisting of only one vertex), and we will label x with the sequence corresponding to x in the phylogenetic tree. This sequence can be considered a trivial multiple alignment (i.e., an alignment of only one sequence). If x is an internal node, then it has two children, u and v, which are labeled with the multiple alignments Au and Av, respectively. We then construct an alignment of all the sequences in Tx by aligning the two alignments Au and Av. This procedure is applied recursively, so the program works its way from the leaves of the phylogenetic tree to the root, at which point it will have constructed an alignment for all of the sequences in T.
The key difference between our progressive alignment schema and more standard methods is that instead of aligning Au and Av directly, we first infer ancestral sequences su and sv using standard phylogenetic models for inference of the common ancestor (Felsenstein 1981). We used the general reversible model, with rate matrices from Yap and Pachter (2004).
The discussion above ignores the issue of gaps. Gaps can be modeled as a fifth symbol, which is equivalent to assigning a linear gap penalty. We have implemented the procedure in this form, but affine gap penalties are preferable. Furthermore, it is desirable to infer the deletion or insertion of bases in the ancestor, and models for this already exist (e.g., TKF; Thorne et al. 1992). For the human-mouse-rat alignment, the issue of properly scoring gaps while inferring the ancestral sequence was not critical, and so we did not score with a sophisticated model; however, future work will build on probabilistic insertion/deletion models developed in Thorne et al. (1991, 1992), and which have already been used to develop multiple alignment algorithms (Holmes and Bruno 2001). It is important to note that in the MAVID alignment, scheme gaps also play a role in Smith-Waterman alignments of the ancestral sequences (see below).
After the ancestral sequence calculation, su and sv are aligned with AVID (Bray et al. 2003). AVID is a hierarchical global pairwise alignment program that iteratively anchors maximal exact matches and wobble matches (i.e., matches which are exact, except for possible mismatches every third base) until a final Smith-Waterman alignment step of remaining regions. In the Smith-Waterman phase of AVID, the match and mismatch scores are again assigned according to a substitution matrix corresponding to the branch length between u and v (using the same rate matrix as for the ancestral inference). Gap scores were assigned using the AVID protocol; however, both the gap-open and gap-extension scores were scaled according to the evolutionary distance.
The alignment of the ancestral sequences is then used to glue together Au and Av to produce a new multiple alignment, which is assigned to the vertex x. In particular, if position i in su matches position j in sv, then column i in the multiple alignment assigned to u is aligned with column j in the multiple alignment assigned to v. Gaps in the ancestral sequence alignments lead to gaps in the multiple alignment in the obvious way. The procedure terminates with a final pairwise alignment at the root node of the tree.
Exon Anchoring and Constraints
Our gene matches and constraints are based on a homology map for the sequences; this is a map that identifies the order and orientation of matching gene runs between the sequences (C. Dewey, in prep.). First, pairwise gene matches are computed between all of the sequences. Gene predictions are generated using GENSCAN (Burge and Karlin 1997), and every pair of predicted genes from every pair of sequences is aligned using the translated BLAT tool (Kent 2002). GENSCAN was selected because it is sensitive, and BLAT provides a fast way of obtaining protein alignments between large numbers of sequences. It should be noted that these programs can easily be replaced for different types of organisms, for example a viral gene-finding program is more suitable for virus alignments.
Genes are considered to match if they form a reciprocal best hit. The gene matches are assembled into runs, which then form the basis of the homology map. Genome sequence coordinates for exon matches are inferred from the protein alignments, thus producing a set of pairwise matches between all of the sequences. These matches are used in the obvious way when aligning Au and Av at node x; all matches that are between a sequence in u and a sequence in v are collected. Every such match can be converted into a match between the ancestral sequences su and sv, which is then used in the AVID alignment.
In addition to anchoring the alignment of the ancestral sequences, the exon matches can be used in more subtle ways to shape the final multiple alignment. It is illustrative to consider 1-bp anchors, that is, single matches between the sequences. Suppose we have sequences a, b, and c, and that ai is anchored to cx, and bj is anchored to cy. If we are aligning sequences a and b, then the given anchors to c do not allow us to anchor the alignment, but they do allow us to constrain it. If x is less than (resp. greater than) y, we must have that ai comes before (resp. after) bj in the alignment of a and b if we are to produce an alignment of a, b, and c, which is consistent with both of the anchors. In the language of Myers et al. (1997), the two anchors provide explicit constraints on the alignment (namely, that ai ≤ cx,ai ≥ cx,bj ≤ cy, and bj ≥ cy), but they also provide implicit constraints that are implied by transitivity; if x ≤ y, then we have ai ≤ cx ≤ cy ≤ bj, and so ai ≤ bj. This information can be used in the alignment of the ancestral sequences by requiring potential anchors between the sequences to satisfy the constraints.
Thus, when constructing the multiple alignment at node x, every triplet of sequences (a,b,c) with a in u, b in v, and c not in x provides a potential constraint for the alignment. This can lead to a combinatorial explosion of constraints. If there are n sequences in the alignment, then there are O(n3) such triplets, each of which may imply many constraints. Fortunately, we do not need to find the set of all possible constraints, many of which will be redundant. Instead, we wish to find a set of prime constraints (i.e., a set such that no constraint is implied by the others) that is equivalent to, but potentially much smaller than the set of all constraints implied by the gene matches. Such a set can be inferred from the homology map. If there are m sets of orthologous exons (not all of which will be in every sequence), then at node x there can be at most O(m) prime constraints, and a prime set that is equivalent to all possible constraints can easily be found in O(mk) time, where k is the number of leaves below x. Thus, the sets of all prime constraints can be found in O(mk2) time with a small constant factor. Matches between the ancestral sequences that are inconsistent with this set of constraints can then be filtered out in time O(Nlogm), where N is the total number of matches. For typical values of m and k, the time taken computing and utilizing the constraints is negligible.
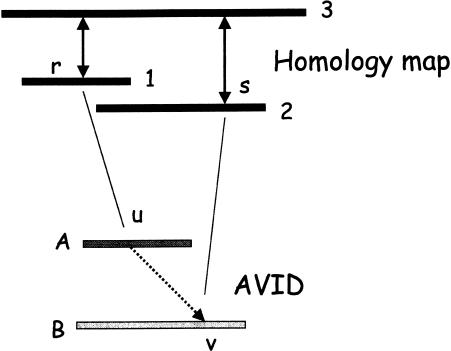
Figure 2 shows an example of a constraint, and how it is enforced in the AVID alignment of the ancestral sequences.
Figure 2.
The top half of the figure shows two exon matches determined from the homology map. In particular, exon r in sequence 1 is aligned to an exon in sequence 3, and exon s in sequence 2 is aligned to another exon in sequence 3 (double arrows). At this stage, none of the sequences have been aligned - the matches are based on the pairwise protein alignments of the predicted genes. During a MAVID alignment of ancestral sequences in the progressive multiple alignment, position r from sequence 1 maps to position u in the ancestral sequence A, and position s maps to position v in the ancestral sequence B (solid lines). Even though sequence 3 is not in the multiple alignment yet, the constraint forces position u to be aligned before position v in the final multiple alignment (broken line). The constraint is enforced by removing all the matches violating the constraint from consideration during the anchoring of the alignment.
The preprocessing step of finding all exon matches is quadratic in the number of sequences; however, as the protein alignments are gene based, they are typically computed on <5% of the sequence. Thus, the gene matching is actually significantly faster than translated match finding, which requires searching the entire sequence in all three frames and on both strands. Furthermore, by comparing only the proteins produced by a gene-prediction program, the program implicitly takes into account splice sites and other gene features in building gene anchors. It is also important to note that this approach is completely ab initio, even though a gene-finding step is necessary; no information beyond the sequences is used. For this study, we performed alignments using this strategy in order to demonstrate the performance of an ab initio approach. However, it is possible to make use of mRNA and EST data, thus incorporating known biological annotation about the sequences into the alignment.
Tree Building
Most multiple alignment programs require pairwise alignments of all of the sequences to build an initial guide tree. This step requires a quadratic number of sequence alignments and is infeasible for large numbers of sequences. We utilize an iterative method to obtain a guide tree using only a linear number of alignments.
The initial guide tree is selected randomly from the set of complete binary trees (or almost complete binary trees in the case in which the number of sequences is not a power of 2). For a given number of nodes, these are the binary trees with minimal depth, and thus, initial errors in pairwise alignments have less opportunity to propagate through the tree. The sequences are aligned using this random tree, and then a phylogenetic tree is inferred from the resulting multiple alignment. The likelihood of the tree given the alignment can be used as a quantitative measure of the quality of the tree and the process is iterated until the alignment and tree are satisfactory.
For small numbers of sequences, the inference of the tree from the multiple alignment can be done using maximum-likelihood methods and accounts for only a small percentage of the running time. However, as the number of sequences increases, we have found that ML reconstruction becomes impractical and neighbor joining must be used. Because pairwise alignments are easy to infer from a multiple alignment, we can perform neighbor-joining reconstruction rapidly, even with large numbers of sequences. We have tested MAVID with the fastDNAml (Olsen et al. 1994) program for smaller data sets and the CLUSTALW implementation of neighbor joining for larger problems.
Instead of computing all pairwise alignments, only O (nk) alignments are necessary to perform n iterations with k sequences. We found that for typical alignment problems, only a small number of iterations were necessary (see results on the HIV sequences below). It is important to note that our iterative method (multiple alignment alternating with neighbor joining) is considerably less sophisticated than ML methods such as SEMPHY (Friedman et al. 2002), or MCMC sampling methods that search through combined alignment/tree space (Hein et al. 2000). However, our approach is scalable to large problems, and as we have pointed out, appears to converge quickly in practice.
RESULTS
A Human, Mouse, and Rat Whole-Genome Multiple Alignment
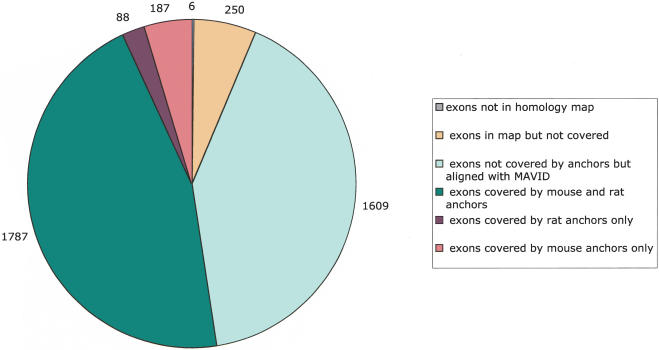
We aligned the human (April 2003), mouse (February 2003), and rat (June 2003) genomes using MAVID. A homology map for the genomes was built by C. Dewey (in prep.), and was used to generate gene anchors and constraints. Figure 3 summarizes the exon coverage of the alignment on chromosome 20; it shows how many of the RefSeq genes were covered by anchors (and, therefore, automatically aligned correctly), and how many were subsequently aligned by MAVID. Chromosome 20 was chosen because it aligns almost completely with mouse chromosome 2, and therefore, the quoted numbers should be useful for comparing MAVID to other alignment approaches that do not explicitly separate out orthologous from paralogous alignments.
Figure 3.
Coverage of human chromosome 20 RefSeq exons by the MAVID alignments. Of a total of 3927 exons, only six were not in the homology map. A total of 53.5% of the exons were covered by precomputed exon anchors in either mouse or rat. The remaining exons are mostly aligned by MAVID, resulting in 93.6% of the exons covered by alignment in either mouse or rat.
The MAVID alignments have been used to estimate evolutionary rates for the genomes and to identify evolutionary hotspots in which one of the rodent genomes has been evolving much more slowly than the other (these results are reported in a companion paper by Yap and Pachter 2004). They are also used to support the K-BROWSER (Chakrabarti and Pachter 2004; http://hanuman.math.berkeley.edu/kbrowser/), which is a new browser especially designed to view multiple genomes, their associated annotations, and alignments.
CFTR Region: 21 Organisms
We aligned 1.8 Mb of human sequence together with the homologous regions from 20 other organisms (baboon, cat, chicken, chimp, cow, dog, dunnart, fugu, hedgehog, horse, lemur, macaque, mouse, opossum, pig, platypus, rabbit, rat, tetraodon, and zebrafish) for a total of 23 Mb of sequence. This sequence has been generated by NISC as part of a comprehensive project to sequence a number of regions in the genome in multiple organisms for evolutionary and functional studies. However, it is important to note that some of the sequences remain incomplete, contributing to the difficulty of the multiple-alignment problem. A subset of this data set (13 organisms) has been used recently (Brudno et al. 2003) as a benchmark to compare pairwise and multiple alignment programs.
The map-building step takes ∼15 min on a 2.6 GhZ processor, with peak memory usage of roughly 700 Mb for GENSCAN. The subsequent MAVID alignment takes another 24 min, for a total of about 40 min. The tree reconstruction step takes less than a minute using neighbor joining. Thus, an iterative approach to building the tree is feasible, and a stable tree was constructed after only two rounds of alignment.
It is difficult to assess the overall quality of the alignment, but one feature that can be verified is the alignment of exons. To do so, we projected the alignment onto the human sequence in order to produce pairwise alignments between human and each of the other 20 sequences. This analysis was complicated by the fact that the sequencing is not complete, and so not every exon has been sequenced in every organism. To address this shortcoming, we calculated the fraction of human exons that were aligned with each of the sequences. An exon was considered to be aligned if at least 70% of it was covered by alignment, and at least 50% of the bases were matching.
The MAVID alignments were compared with MLAGAN, version 1.1 (Brudno et al. 2003). MLAGAN is the only other program we know of that is able to align the 21 sequences in a reasonable period of time (the running time of MLAGAN on the 21 sequences is roughly 6 h). DIALIGN (Morgenstern et al. 1998), also designed for large genomic regions, was too slow for processing the sequences; even with the new CHAOS/DIALIGN program, aligning only four of the sequences took 14 h. The MGA program (Höhl et al. 2002) is designed for very similar sequences only, and so was not suitable for the diverse fish, bird, marsupial, and mammal alignments.
To better understand how alignment accuracy varies with the number of sequences being aligned, we compared the MAVID and MLAGAN alignments on 21 different data sets, beginning with a pairwise alignment of the most distant organisms, and adding in one (mutually most distant) organism at a time, all the way up to a comparison on the 21 sequences. To do this, we computed the human clamped k-MST trees (Boffelli et al. 2003), that is, the subtrees on k leaves of maximum weight, with the human sequence as one of the leaves. Thus, alignments were computed first for human and zebrafish alone, then for human, zebrafish, and dunnart, and eventually all of the 21 sequences. The order in which they were added was as follows: human, zebrafish, dunnart, platypus, hedgehog, chicken, rat, fugu, cow, rabbit, dog, opossum, tetraodon, lemur, horse, pig, cat, mouse, baboon, macaque, and chimp. Exon coverage was calculated by first running TBLASTX to identify human exon homologs in the other species using the same criteria as in Brudno et al. (2003), and then computing coverage with respect to the identified exon sets.
The results of the alignments show that both programs correctly aligned mammalian sequences. The alignment of distant organisms shows much greater variability with respect to the sequences included in the alignment problem. For example, adding fugu to an alignment of human, zebrafish, and dunnart may improve the alignment, but as Table 1 demonstrates, adding platypus can degrade it. MAVID shows significant improvement over MLAGAN in this respect.
Table 1.
Comparison of MLAGAN and MAVID Multiple Alignments on the 21 Organism CFTR Alignment
| MAVID Zebrafish | 96 | 96 | 68 | 68 | 64 | 72 | 96 | 96 | 96 | 96 | 96 | 96 | 96 | 96 | 96 | 96 | 96 | 96 | 96 | 96 |
| MLAGAN Zebrafish | 96 | 32 | 12 | 12 | 8 | 8 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| MAVID Dunnart | - | 88 | 88 | 41 | 41 | 41 | 71 | 71 | 71 | 71 | 88 | 88 | 88 | 88 | 88 | 88 | 88 | 88 | 88 | 88 |
| MLAGAN Dunnart | - | 88 | 88 | 59 | 0 | 0 | 0 | 0 | 0 | 0 | 88 | 88 | 88 | 88 | 88 | 88 | 88 | 88 | 88 | 88 |
| MAVID Platypus | - | - | 51 | 51 | 52 | 51 | 49 | 51 | 49 | 51 | 51 | 51 | 52 | 52 | 52 | 52 | 52 | 52 | 51 | 51 |
| MLAGAN Platypus | - | - | 40 | 40 | 25 | 34 | 34 | 34 | 36 | 37 | 51 | 51 | 51 | 51 | 51 | 51 | 51 | 51 | 51 | 36 |
| MAVID Hedgehog | - | - | - | 46 | 46 | 46 | 56 | 57 | 57 | 57 | 67 | 67 | 64 | 66 | 66 | 66 | 66 | 67 | 60 | 60 |
| MLAGAN Hedgehog | - | - | - | 74 | 74 | 74 | 74 | 74 | 73 | 76 | 66 | 64 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 69 |
| MAVID Chicken | - | - | - | - | 79 | 86 | 90 | 79 | 83 | 83 | 81 | 71 | 71 | 76 | 76 | 71 | 71 | 71 | 69 | 69 |
| MLAGAN Chicken | - | - | - | - | 38 | 69 | 67 | 67 | 69 | 74 | 74 | 74 | 74 | 74 | 74 | 74 | 74 | 74 | 74 | 67 |
| MAVID Rat | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MLAGAN Rat | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MAVID Fugu | - | - | - | - | - | - | 84 | 84 | 85 | 85 | 85 | 88 | 88 | 88 | 88 | 88 | 88 | 88 | 85 | 85 |
| MLAGAN Fugu | - | - | - | - | - | - | 22 | 22 | 22 | 22 | 42 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 41 |
| MAVID Cow | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MLAGAN Cow | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MAVID Rabbit | - | - | - | - | - | - | - | - | 96 | 95 | 95 | 95 | 95 | 95 | 95 | 94 | 94 | 94 | 94 | 94 |
| MLAGAN Rabbit | - | - | - | - | - | - | - | - | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 |
| MAVID Dog | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MLAGAN Dog | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MAVID Opossum | - | - | - | - | - | - | - | - | - | - | 90 | 92 | 92 | 92 | 92 | 92 | 90 | 92 | 92 | 92 |
| MLAGAN Opossum | - | - | - | - | - | - | - | - | - | - | 74 | 74 | 72 | 72 | 72 | 72 | 72 | 72 | 72 | 78 |
| MAVID Tetraodon | - | - | - | - | - | - | - | - | - | - | - | 88 | 88 | 88 | 88 | 88 | 88 | 88 | 85 | 85 |
| MLAGAN Tetraodon | - | - | - | - | - | - | - | - | - | - | - | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 40 |
| MAVID Lemur | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MLAGAN Lemur | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MAVID Horse | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MLAGAN Horse | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| MAVID Pig | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 |
| MLAGAN Pig | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 | 100 |
| MAVID Cat | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 |
| MLAGAN Cat | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 | 100 |
| MAVID Mouse | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 |
| MLAGAN Mouse | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 | 100 |
| MAVID Baboon | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 |
| MLAGAN Baboon | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 | 100 | 100 |
| MAVID Macaque | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 92 | 92 |
| MLAGAN Macaque | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 96 | 96 |
| MAVID Chimp | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 |
| MLAGAN Chimp | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 100 |
Each row in the table shows the % coverage of the alignable exons in an organism as calculated by extracting the pairwise alignment with human from the multiple alignment. The different columns in the table correspond to the number of sequences in the multiple alignment. Thus, the first column corresponds to the pairwise alignment of human-zebrafish and the last column to the multiple alignment of all 21 sequences. Organisms were added according to the k-MST, so that the alignment problems are as difficult as possible (mutually most distant organisms).
HIV1/SIV: Complete Genomes From 242 Individuals
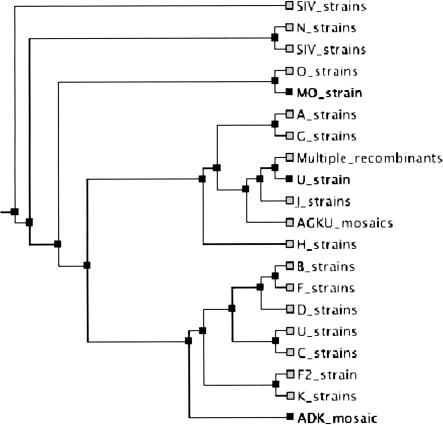
The HIV databases maintained at LANL contain a collection of HIV-1, HIV-2, and SIV sequences, carefully linked with individuals and their histories. We extracted the complete genomic sequences of HIV1 and SIV from this database (currently totaling 242) and aligned them with MAVID. The alignment of the sequences takes 2.5 min. A phylogenetic tree was constructed with neighbor joining taking an additional 30 sec. Again, it is difficult to assess the quality of the alignment, but it is accurate enough that the different strains cluster in the inferred tree (see Fig. 4). To understand the stability of the tree building/alignment iteration, we examined 100 alignment runs on a reduced sequence set with the recombinant strains removed (because recombination is not addressed by standard phylogenetic models). We found that the correct strains were grouped together within one round of alignment (starting with a random tree) in all of the 100 runs. To validate the iterative alignment/tree building procedure, we also examined the number of subtrees that were fixed with each successive round of alignment. The tree inferred after the second round of alignment has 45.87 of its subtrees in agreement with the tree after the first run (on average), and the number fixed between the second and third rounds is 54.08, on average. Starting with different random trees and aligning for three rounds, we find that 54.16 of the subtrees agree, on average. Our criteria for comparing trees (exact agreement of subtrees) is rather strict, and these numbers are very encouraging (one would expect about one nontrivial subtree to agree for two random trees). Although a MAVID multiple alignment combined with a neighbor-joining tree may not be as accurate as hand-edited alignments, followed by maximum likelihood tree building, it can serve to provide very fast results that can then form the basis for further refinement. An alignment problem of this size is not practical on a standard desktop computer if all of the pairwise alignments are computed in order to build an initial guide tree (as is done in many programs, e.g., CLUSTALW).
Figure 4.
The HIV tree as inferred from 242 sequences obtained from Los Alamos National Laboratories. The sequences are labeled by strains, and the different strains have been grouped together.
The alignments and phylogenetic trees for all the above sequences are downloadable at http://baboon.math.berkeley.edu/mavid/data.
Conclusion
As we have outlined in the introduction, we view the genomic multiple-sequence alignment problem as a biological alignment problem, rather than a purely mathematical one. That is, the incorporation of biologically relevant information (in our case ab-initio gene predictions) is critical to building accurate alignments and correctly identifying homologous relationships. Our method of incorporating constraint information into the alignments helps address one of the primary objections to progressive alignment strategies, namely, that progressive alignment is local with the alignment at each node containing only information about the sequences below it. The application of constraint information can be thought of as a look-ahead step that helps to fix potential problems.
Our approach is also consistent with a number of other ideas that we have not yet implemented, but which could be easily integrated into MAVID and will improve results. Iterative refinement, the process of realigning across an edge in the tree, fits in naturally with our framework (Gotoh 1993, 1996). Similarly, the homology map that MAVID uses can indicate information about inversions and duplications, and this can be used to correctly align regions containing rearrangements.
MAVID compares favorably with existing programs. As we have pointed out, it is significantly more accurate than MLAGAN on the alignment of the CFTR benchmark region. MLAGAN is the only other program we know of that can even align such a large data set. We also know of no other programs that can quickly align hundreds of viral or mitochondrial genomes.
A MAVID Web server has been operational for over 6 mo and processes over 1000 requests a month (Bray and Pachter 2003). Alignment requests have ranged from large genomic regions in mammals, fish, flies, and plants to alignments of viruses, mitochondria, and other bacterial genomes. MAVID can be accessed at http://baboon.math.berkeley.edu/mavid/. The program is freely available for academic and nonprofit use.
Acknowledgments
We thank Colin Dewey for providing access to his homology map-making programs. We thank Von Bing Yap for helping with the evolutionary models used in MAVID. Thanks to Ingileif Brynd's Hallgr'msdóttir for her help throughout the project and for her comments on the final manuscript. The data used in the multiple alignment of the CFTR region was generated by the NIH Intramural Sequencing Center (www.nisc.nih.gov), and was used subject to their 6-mo hold policy. The HIV sequences were downloaded from the HIV database (hiv-web.lanl.gov). Thanks also to the Rat Sequencing Consortium, both for providing the rat sequence to align, and for facilitating helpful collaborations and discussions. Finally, we thank the anonymous reviewers for their insightful comments and suggestions. This work was partially supported by funding from the NIH (grant R01-HG02362-01) and the Berkeley PGA grant from the NHLBI.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1960404.
Footnotes
[Supplemental material is available online at http://baboon.math.berkeley.edu/mavid/data.]
References
- Boffelli, B., McAuliffe, J., Ovcharenko, D., Lewis, K.D., Ovcharenko, I., Pachter, L., and Rubin, E.M. 2003. Phylogenetic shadowing of primate sequences to find functional regions of the human genome. Science 299: 1391-1394. [DOI] [PubMed] [Google Scholar]
- Bray, N. and Pachter, L. 2003. MAVID multiple alignment server. Nucleic Acids Res. 31: 3525-3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray, N., Dubchak, I., and Pachter, L. 2003. AVID: A global alignment program. Genome Res. 13: 97-102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brudno, M., Do, C.B., Cooper, G.M., Kim, M.F., Davydov, E., N.C.S. Program, Green, E.D., Sidow, A., and Batzoglou, S. 2003. LAGAN and Multi-LAGAN: Efficient tools for large-scale multiple alignment of genomic DNA. Genome Res. 13: 721-731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burge, C. and Karlin, S. 1997. Prediction of complete gene structures in human genomic DNA. J. Mol. Biol. 268: 78-94. [DOI] [PubMed] [Google Scholar]
- Chakrabarti, K. and Pachter, L. 2004. Visualization of multiple genome annotations and alignments with the K-BROWSER. Genome Res. (this issue). [DOI] [PMC free article] [PubMed]
- Felsenstein, J. 1981. Evolutionary trees from DNA sequences: A maximum likelihood approach. J. Mol. Evol. 17: 368-376. [DOI] [PubMed] [Google Scholar]
- Feng, D.F. and Doolittle, R.F. 1987. Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J. Mol. Evol. 25: 351-360. [DOI] [PubMed] [Google Scholar]
- Friedman, N., Ninio, M., Pe'er, I., and Pupko, T. 2002. A structural EM algorithm for phylogenetic inference. J. Computat. Biol. 9: 331-353. [DOI] [PubMed] [Google Scholar]
- Gonnet, G.H. and Benner, S.A. 1996. Probabilistic ancestral sequences and multiple alignments. In Algorithm theory, pp. 380-391. Proceedings of SWAT '96, Reykjavik, Iceland.
- Gotoh, O. 1993. Optimal alignment between groups of sequences and its application to multiple sequence alignment. Comput. Appl. Biosci. 9: 361-370. [DOI] [PubMed] [Google Scholar]
- ———. 1996. Significant improvement in accuracy of multiple protein alignments by iterative refinement as assessed by reference to structural alignments. J. Mol. Biol. 264: 823-838. [DOI] [PubMed] [Google Scholar]
- Gusfield, D. 1997. Algorithms on strings, trees and sequences. Cambridge University Press, Cambridge, UK.
- Hardison, R.C., Chao, K.M., Adamkiewicz, M., Price, D., Jackson, J., Zeigler, T., Stojanovic, N., and Miller, W. 1993. Positive and negative regulatory elements of the rabbit embryonic ε-globin gene revealed by an improved multiple alignment program and functional analysis. DNA Seq. 4: 163-176. [DOI] [PubMed] [Google Scholar]
- Hein, J. 2001. An algorithm for statistical alignment of sequences related by a binary tree. Proc. Pacific Symp. Biocomput. 179-190. [DOI] [PubMed]
- Hein, J., Wiuf, C., Knudsen, B., Moller, M.B., and Wibling, G. 2000. Statistical alignment: Computational properties, homology testing and goodness-of-fit. J. Mol. Biol. 302: 265-279. [DOI] [PubMed] [Google Scholar]
- Herrnstadt, C., Elson, J.L., Fahy, E., Preston, G., Turnbull, D.M., Anderson, C., Ghosh, S.S., Olefsky, J.M., Beal, M.F., Davis, R.E., et al. 2002. Reduced-median-network analysis of complete mitochondrial DNA coding-region sequences for the major african, asian, and european haplogroups. Amer. J. Hum. Genet. 70: 1152-1171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Höhl, M., Kurtz, S., and Enno, O. 2002. Efficient multiple genome alignment. Bioinformatics 18: 5312-5320. [DOI] [PubMed] [Google Scholar]
- Holmes, I. 2003. Using guide trees to construct multiple-sequence evolutionary HMMs. In Proceedings of the Eleventh ISMB conference. pp. 147-157, AAAI Press, Menlo Park, California. [DOI] [PubMed]
- Holmes, I. and Bruno, W.J. 2001. Evolutionary HMMs: A Bayesian approach to multiple alignment. Bioinformatics 17: 803-820. [DOI] [PubMed] [Google Scholar]
- Kent, W.J. 2002. BLAT—The BLAST-like alignment tool. Genome Res. 12: 656-664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korber, B.T.M., Brander, C., Haynes, B.F., Koup, R., Kuiken, C., Moore, J.P., Walker, B.D., and Watkins, D.I. (Ed.) 2001. In HIV molecular immunology, pp. 02-4663. Los Alamos National Laboratory, Theoretical Biology and Biophysics, Los Alamos, NM.
- Löytynoja, A. and Milinkovitch, M.C. 2003. A hidden Markov model for progressive multiple alignment. Bioinformatics 19: 1505-1513. [DOI] [PubMed] [Google Scholar]
- Morgenstern, B., Frech, K., Dress, A., and Werner, T. 1998. DIALIGN: Finding local similarities by multiple sequence alignment. Bioinformatics 14: 290-294. [DOI] [PubMed] [Google Scholar]
- Myers, G., Selznick, S., Zhang, Z., and Miller, W. 1997. Progressive multiple alignment with constraints. In Proceedings of the first annual international conference on computational molecular biology, pp. 220-225. Sante Fe, New Mexico. [DOI] [PubMed]
- Notredame, C. 2002. Recent progresses in multiple sequence alignment: A survey. Pharmacogenomics 3: 1-14. [DOI] [PubMed] [Google Scholar]
- Olsen, G.J., Matsuda, H., Hagstrom, R., and Overbeek, R. 1994. fastDNAml: A tool for construction of phylogenetic trees of DNA sequences using maximum likelihood. Comput. Appl. Biosci. 10: 41-48. [DOI] [PubMed] [Google Scholar]
- Slowinski, J.B. 1998. The number of multiple alignments. Mol. Phylogenet. Evol. 10: 264-266. [DOI] [PubMed] [Google Scholar]
- Thomas, J.W., Touchman, J.W., Blakesley, R.W., Bouffard, G.G., Beckstrom-Sternberg, S.M., Margulies, E.H., Blanchette, M., Siepel, A.C., Thomas, P.J., McDowell, J.C., et al. 2003. Comparative analyses of multi-species sequences from targeted genomic regions. Nature 424: 788-793. [DOI] [PubMed] [Google Scholar]
- Thompson, J.D., Higgins, D.G., and Gibson, T.J. 1994. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22: 4673-4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorne, J.L., Kishino, H., and Felsenstein, J. 1991. Evolutionary model for maximum likelihood alignment of DNA. J. Mol. Evol. 33: 114-124. [DOI] [PubMed] [Google Scholar]
- ———. 1992. Inching toward reality: An improved likelihood model of sequence evolution. J. Mol. Evol. 34: 3-16. [DOI] [PubMed] [Google Scholar]
- Yap, V.B. and Pachter, L. Identification of evolutionary hotspots in the rodent genomes. Genome Res. (this issue). [DOI] [PMC free article] [PubMed]
WEB SITE REFERENCES
- http://www.nisc.nih.gov/; NIH Intramural Sequencing Center.
- http://hiv-web.lanl.gov/; LANL HIV Databases.
- http://baboon.math.berkeley.edu/mavid/; The MAVID Web server.
- http://baboon.math.berkeley.edu/mavid/data/; Supplemental Data.
- http://hanuman.math.berkeley.edu/kbrowser/; K-BROWSER.