Whole population cell analysis of a landmark-rich mammalian epithelium reveals multiple elongation mechanisms

Abstract

Tissue elongation is a fundamental component of developing and regenerating systems. Although localised proliferation is an important mechanism for tissue elongation, potentially important contributions of other elongation mechanisms, specifically cell shape change, orientated cell division and cell rearrangement, are rarely considered or quantified, particularly in mammalian systems. Their quantification, together with proliferation, provides a rigorous framework for the analysis of elongation. The mammalian palatal epithelium is a landmark-rich tissue, marked by regularly spaced ridges (rugae), making it an excellent model in which to analyse the contributions of cellular processes to directional tissue growth. We captured confocal stacks of entire fixed mouse palate epithelia throughout the mid-gestation growth period, labelled with membrane, nuclear and cell proliferation markers and segmented all cells (up to ∼20,000 per palate), allowing the quantification of cell shape and proliferation. Using the rugae as landmarks, these measures revealed that the so-called growth zone is a region of proliferation that is intermittently elevated at ruga initiation. The distribution of oriented cell division suggests that it is not a driver of tissue elongation, whereas cell shape analysis revealed that both elongation of cells leaving the growth zone and apico-basal cell rearrangements do contribute significantly to directional growth. Quantitative comparison of elongation processes indicated that proliferation contributes most to elongation at the growth zone, but cell shape change and rearrangement contribute as much as 40% of total elongation. We have demonstrated the utility of an approach to analysing the cellular mechanisms underlying tissue elongation in mammalian tissues. It should be broadly applied to higher-resolution analysis of links between genotypes and malformation phenotypes.

INTRODUCTION

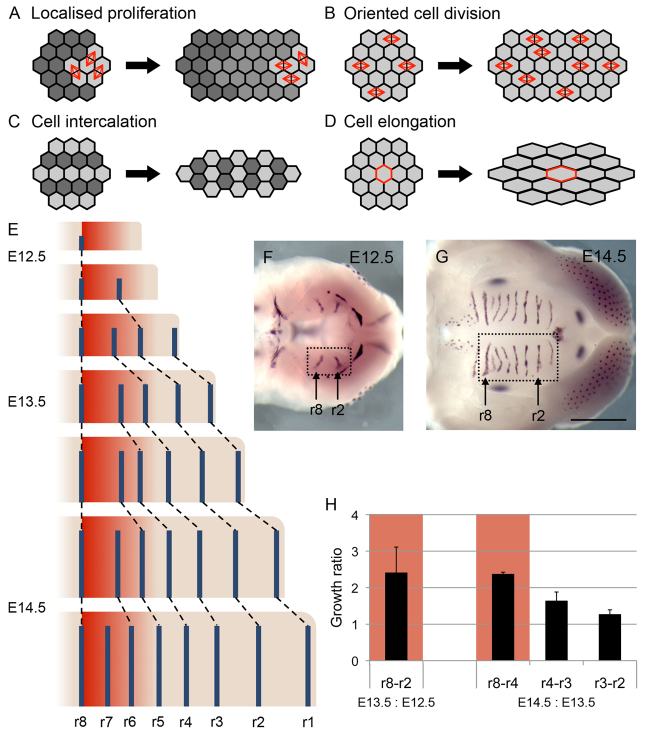
Tissue elongation is an important process in morphogenesis. As well as directly shaping tissues, elongation failure can result in many common dysmorphologies. For example, a failure of tissue elongation is one of the major causes of cleft palate, one of the most common congenital birth defects in humans (Parker et al., 2010). The cellular mechanisms for elongation have largely been described as a collection of disparate processes (Keller, 2002). We propose that tissue elongation can be rationalised into four canonical cellular processes. For tissue elongation to take place there must ultimately be an increase in either the number of cells along the axis of growth, or their size or spacing in that direction. Most simply, cell number can be increased by cell proliferation. Localised cell proliferation (Fig. 1A) is involved in the elongation of a number of tissues ranging from the vertebrate long bones to the meristems of plants. In other cases, tissue elongation is achieved through anisotropy in the orientation of cell divisions, with cell divisions throughout the tissue aligned along the axis of growth (Gong et al., 2004; Lechler and Fuchs, 2005) (Fig. 1B). An increase in the number of cells in the direction of growth can also be achieved through cell movements and rearrangements. This is most notably seen in the cell intercalation movements in convergent extension of the vertebrate body axis and elongating Drosophila germ band (Keller, 2006; Zallen and Blankenship, 2008) (Fig. 1C). Finally, tissues can elongate as a result of their component cells elongating or increasing their spacing in the direction of tissue growth (Fig. 1D), for example in the growing plant root (Baluska et al., 1996). It is becoming clear that morphogenesis often involves combinations of these processes. For example, cell shape change plays a role alongside cell intercalation in Drosophila germ band extension (Blanchard et al., 2009) and it has been shown that proliferation alone cannot account for growth in the mouse limb (Boehm et al., 2010). By contrast, studies of morphogenesis in mammalian systems, such as the mammalian palate, have generally focused heavily on proliferation. A truly mechanistic understanding of tissue elongation requires an analysis of the relative contribution of each of these canonical cellular processes.

Fig. 1.

Cellular mechanisms of tissue elongation and palatal epithelium development. (A) Localised cell division at the edge of a tissue leads to elongation at that edge. (B) Elongation occurs when daughters of cell divisions are aligned. (C) Tissue elongation through cell intercalation, where cells move perpendicular to the direction of growth, is accompanied by tissue narrowing or thinning. (D) Directional cell elongation can drive tissue elongation. (E) Schematic showing elongation in the palate [right, anterior; top, medial; posterior palate (prospective soft palate) omitted for clarity] using rugae (blue bars) as landmarks for growth. The GZ (red area) is where new rugae are added. (F,G) In situ hybridisation for sonic hedgehog (a marker of developing rugae) showing rugae in developing palate (boxed region) at E12.5 (F) and E14.5 (G) (right, anterior). Positions of ruga 8 and ruga 2 are indicated. Scale bar: 1 mm. (H) Histogram showing ratios of inter-rugal lengths between successive stages, demonstrating elevated growth in the region anterior to ruga 8 (intervals marked in red). Measurements from three samples per stage. Error bars represent s.d.

One potential difficulty in cellular analysis of morphogenesis is a lack of landmarks by which to quantify local tissue growth. For example, in the mouse limb, computationally non-trivial modelling was required to relate the patterns of tissue growth to clonal shapes (Marcon et al., 2011). By contrast, the oral palate epithelium is a tissue that undergoes considerable anteroposterior (AP) elongation and is rich in landmarks. It is marked by a series of transverse ridges (rugae) spaced evenly, ruler-like, along its AP axis, with mouse having a full complement of eight. These rugae form sequentially as the palate is elongating (Fig. 1E-G) with their earliest appearance consisting of epithelial thickening and expression of Sonic hedgehog (Shh). Throughout growth, the rugae remain approximately parallel and mediolateral (ML) growth is largely uniform along the AP axis, making it an ideal system to study the cellular contribution to differential AP growth rates along the AP axis. Genetic labelling of cells in the rugae has shown that they are stable once formed. Specifically, Shh-expressing cells were pulse labelled during ruga formation (using a tamoxifen-dependent Cre recombinase under the control of an Shh promoter) (Thirumangalathu et al., 2009). Cre recombinase activated lacZ expression in the forming rugae. The resulting labelled cells were restricted entirely to the rugal stripes (Thirumangalathu et al., 2009), indicating that cells do not move out of the forming rugae.

New rugae appear in association with AP elongation, mostly in a mid-palate rugal ‘growth zone’ (GZ) just anterior to ruga 8 (Fig. 1E) (Pantalacci et al., 2008; Welsh and O’Brien, 2009; Economou et al., 2012). [Ruga 1 is added out of sequence, in association with ML growth (Economou et al., 2012) and will not be considered further.] Tissue in the GZ more than doubles in length every 24 hours compared with much less elongation more anteriorly (Fig. 1H). The cellular basis of this growth distribution is not understood: studies looking at the distribution of cell proliferation rates appeared to show little or no net elevation in the GZ compared with more anterior regions (Pantalacci et al., 2008; Welsh and O’Brien, 2009). This suggests involvement of proliferation rate-independent elongation mechanisms. We therefore set out to understand the mechanism underlying the non-uniform growth distribution.

Methods for high-resolution growth analysis are not well established. The gradual improvement of tools for imaging and image analysis have allowed the automated identification of nuclei and segmentation of cell shapes for the thousands of cells that make up a tissue (Truong and Supatto, 2011). Such studies have largely focused on optically accessible non-mammalian species, such as Drosophila (e.g. Butler et al., 2009; Aigouy et al., 2010; Bosveld et al., 2012), zebrafish (e.g. England et al., 2006; Keller et al., 2008; Blanchard et al., 2009; Olivier et al., 2010), Caenorhabditis elegans (e.g. Bao et al., 2006) and ascidian (e.g. Sherrard et al., 2010). Most of these studies have tracked cells over time, relating cell movements to morphogenesis, but very few have associated changes in cell shape with tissue morphogenesis. This has largely been restricted to studies in Drosophila, in which cell shapes are largely based on apical markers rather than full three-dimensional segmentations (Butler et al., 2009; Aigouy et al., 2010; Bosveld et al., 2012). Studies of cell shape in other systems, such as invagination in ascidian gastrulation, consider far fewer cells (Sherrard et al., 2010).

Very few studies have considered the cellular basis of morphogenesis in mammalian systems, which can be very useful for understanding human dysmorphologies. This is partly due to difficulties in culturing tissue ex utero and so live imaging is limited. Although there has been some progress in imaging the limb (Gros et al., 2010; Wyngaarden et al., 2010), the methods are not generally applicable to other tissues. Moreover, resolution is limited, preventing the detailed analysis of cell shape possible in the systems described above. For the palate in particular, we have found that existing explant culture methods fail to give normal growth (Economou et al., 2012) and so are not useful for live imaging for growth analysis. Even automated capture of cellular processes on a large scale in fixed material is not widespread, with a few studies of the heart looking at patterns of proliferation (Soufan et al., 2006; van den Berg et al., 2009) and polarity (Le Garrec et al., 2013; Pop et al., 2013). However, owing to the complex patterns of tissue morphogenesis in this system the relationship between the patterns of the cellular behaviours described and morphogenesis is not clear.

We have therefore applied quantitative methods to fixed material (in a manner applicable, in principle, to many tissues) to obtain cellular statistics from all cells and thus to allow inferences to be made about the cellular mechanisms. We have taken advantage of the rectilinear and landmark-rich nature of the palate to validate our methods. We show that, contrary to previous reports, the GZ is a region of net elevated proliferation relative to the rest of the palate, with transient phases of proliferation associated with ruga formation. However, by a comprehensive quantitative analysis we also show the importance of considering other mechanisms, demonstrating that cell elongation, spreading by vertical intercalation (epiboly) and cell rearrangements in the inter-rugal regions make significant contributions to AP growth.

RESULTS

Whole cell segmentation

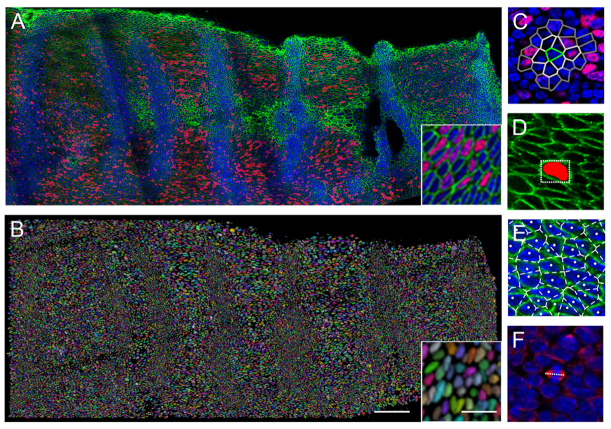
For localised elongation in the mid-palate rugal GZ to occur, one or more of the cellular mechanisms of tissue elongation must be taking place at a higher rate within the GZ than outside it. We took the approach of quantifying the different cellular processes throughout the epithelium, allowing comparison between different regions. Palatal shelves were collected from mice previously injected with bromodeoxyuridine (BrdU) and imaged as confocal stacks of entire fixed palatal epithelia, using immunofluorescence to identify BrdU-incorporating cells and DAPI to identify nuclei, allowing a measure of proliferation (Fig. 2A). To understand better the role of cell size and shape in palate epithelial growth, we used immunofluorescence for beta-catenin, which stains cell junctions, demarcating cell outlines (Fig. 2A). As the older [embryonic day (E)14.5] shelves contain over 20,000 cells, it was not feasible to measure a significant proportion of all cells manually. We therefore used the imaging software package FIJI (Schindelin et al., 2012) to write a set of macros automating the identification and segmentation of cells based on the localisation of beta-catenin (Fig. 2B) and the identification of BrdU-incorporating cells. This allowed the measurement of local cell proliferation, shape and size across the palate epithelium (Fig. 2C-E). In addition, to examine the orientation of cell divisions, we visualised mitotic spindles by immunofluorescence for alpha-tubulin (Fig. 2F). Orientations of mitotic spindles, which are at any one time rather few in number owing to the shortness of this cell cycle phase, were determined manually.

Fig. 2.

Imaging and quantifying cellular parameters. (A) Single z slice from stitched confocal stacks of E14.5 palatal shelf (anterior to the right, medial at the top) using DAPI to label nuclei (blue), and immunofluorescence for BrdU (red) and beta-catenin (green) with detail in inset. (B) 3D rendering of segmented cell volumes in random pseudocolour of the specimen shown in A (inset showing detail). Scale bar: 100 μm; inset, 20 μm. (C) Local BrdU index for a cell (green) includes successive sets of neighbours (shades of grey), shown as Voronoi polygons overlaid on a confocal slice stained for nuclei (blue) and BrdU (red). (D) Cell shape measured from segmented volume (red) by a bounding rectangle at the level of the centroid (white box), shown on a beta-catenin stained (green) confocal slice. (E) Cell territory measured by Voronoi polygons of tessellation of cell centroids (white), shown overlaid on a confocal slice stained for nuclei (blue) and beta-catenin (green). (F) Orientation of mitotic spindle (white line) following immunofluorescence for alpha tubulin marking spindles (red), with DAPI-labelled nuclei (blue).

Proliferation elevation in the GZ is pulsatile

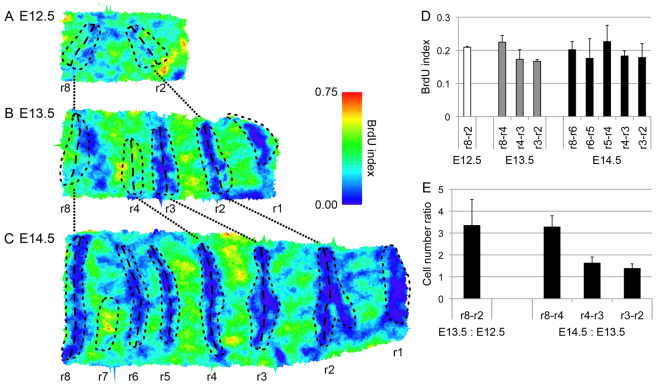
Previous studies of the GZ reported contrasting proliferation patterns: Pantalacci et al. (Pantalacci et al., 2008) demonstrated elevation of proliferation (mitotic index) at the anterior of the GZ (defined as the space just anterior to ruga 8) whereas Welsh and O’Brien (Welsh and O’Brien, 2009) showed elevated proliferation (BrdU/mitotic index) at the posterior of the GZ. We therefore re-examined proliferation in the palate epithelium to determine whether these differing observations could be reconciled. We constructed a time series of E13.5 epithelia with the same number of rugae, but of different ages as evidenced by the different lengths of GZ and the inter-rugal distances, which we have shown to be closely correlated with age (Economou et al., 2012). In younger palates, we observed elevated proliferation in the newest ruga at the anterior of the GZ, similar to the pattern described by Pantalacci et al. (Fig. 3A,B,D). In slightly older palates, proliferation was reduced in the newest ruga, but elevated more posteriorly in the GZ where the next ruga was due to form, similar to the pattern described by Welsh and O’Brien (Fig. 3C,D). Thus, the two reported proliferation distributions are not contradictory but reflect alternating situations: there is a burst of proliferation in the ruga-free part of the GZ, which then declines as the ruga thickens and a new burst more posterior to it begins. Each burst thus initiates at the posterior of the GZ and is displaced towards the anterior of the GZ as growth proceeds.

Fig. 3.

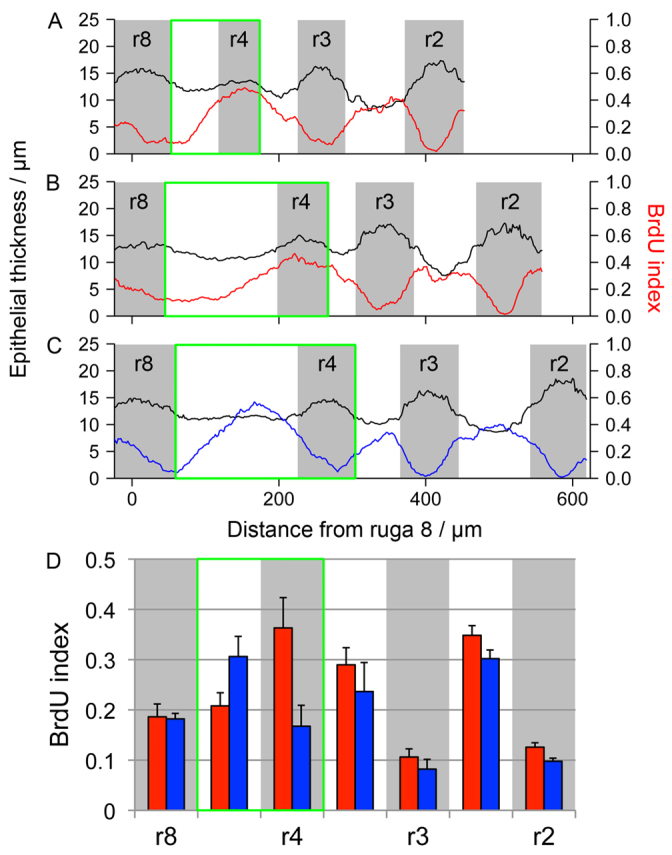
Ruga formation is associated with elevated proliferation. (A-C) Line graphs of epithelial thickness (black line, left-hand scale) and local BrdU incorporation (red/blue lines, right-hand scale) along the AP axis showing ruga 4 (r4) forming in a series of three closely aged E13.5 specimens (positions of rugae marked in grey). In younger specimens (A,B), BrdU incorporation is high in r4, whereas in the older specimen (C) BrdU incorporation is lower in r4 but high more posteriorly. (D) Histogram of BrdU index in rugal (grey) and inter-rugal (white) regions in three younger specimens (red) compared with three older specimens (blue). Error bars represent s.d. In all plots, the GZ is marked by a green box.

However, these results do not appear to show an elevation in proliferation in the GZ as a whole relative to more anterior tissue. Mapping the BrdU index showed this pattern at all stages examined (Fig. 2C; Fig. 4A-C): BrdU incorporation is low in established rugae, high in the inter-rugae. In the GZ, proliferation is high in the newly forming rugae and low in and anterior to ruga 8. Rather than subdividing the GZ into rugal and inter-rugal regions, we examined BrdU incorporation throughout our growth regions, i.e. we measured mid-ruga to mid-ruga. We observe a slight net elevation in the GZ at E13.5, although not at E14.5 (Fig. 4D). One possible explanation for these observations is that the BrdU index does not accurately reflect cell proliferation rate, because BrdU incorporation depends on the length of the S phase, and this could vary. We therefore used an independent measure to assess cell proliferation: we were able simply to count the number of cells in each region (defined from mid-ruga to mid-ruga) because we had segmented every cell. We could thus quantify proliferation directly as an increase in cell number between stages. By this analysis, there was clearly higher proliferation in the GZ than in the rest of the palate (Fig. 4E). Indeed, the increase in cell number was nearly proportional to the AP tissue growth (compare Fig. 4E with Fig. 1H). However, this might be a somewhat misleading coincidence because, as is clear from the thickness data above, the proliferation also contributes to the thickening of the forming rugae. At the same time, cells in the rugae are smaller and more closely packed (see below). Both thickening and cell packing would tend to reduce the effect of proliferation on AP growth.

Fig. 4.

Distribution of proliferation in the palatal epithelium. (A-C) Maps of BrdU index at E12.5 (A), E13.5 (B) and E14.5 (C) showing little obvious elevation in the GZ, anterior to ruga 8 (anterior to the right, medial at the top). Maps show representative palatal epithelia for each stage with cellular BrdU indices calculated over a cell and its three sets of neighbours. Positions of rugae are marked with black dashed lines with the middle of rugae marked with long dashes. (D) Histogram of BrdU index across epithelia, divided into regions bounded by the rugal midlines (as marked in A-C) showing a largely uniform BrdU index with a slight elevation in the GZ at E13.5. (E) Cell number ratio between successive stages confirms elevated proliferation in the GZ compared with the anterior palate. For each interval in histograms D and E, measurements were calculated across three palates. Error bars represent s.d.

Cell division orientation is greater outside the GZ than within it

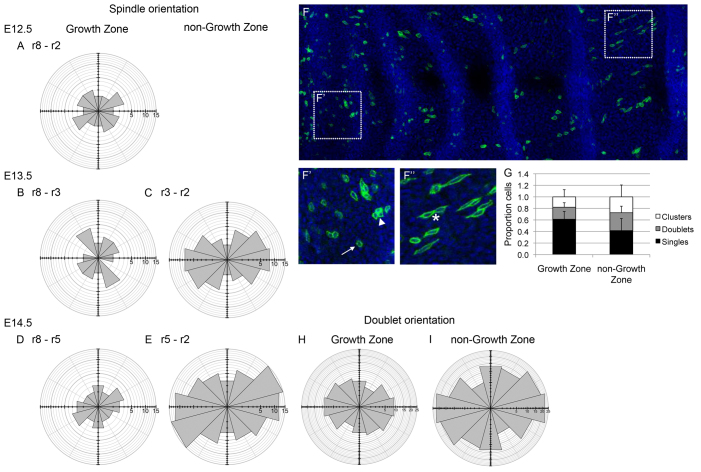
We therefore examined other cellular processes to see if they could be contributing to the pattern of growth. First, we examined the possible contribution to elongation of oriented cell division. On measuring angles of mitotic spindles (Fig. 2F), the orientation of cell division within the GZ could not be distinguished from a uniform distribution (Fig. 5A,B,D, no significant directional bias, Watson U² test, P>0.05). In contrast in the anterior non-GZ palate, cell division orientation showed a significant bias orientation along the AP axis (Fig. 5C,E, Watson U² test, P<0.05). To confirm that our measures of spindle orientation reflected the orientation of pairs of daughter cells, we pulse-labelled cells using low dose tamoxifen to drive tamoxifen-dependent Cre recombinase-mediated GFP expression in small cell clones (Fig. 5F-F′). Intriguingly, we found that the proportion of labelled cell doublets versus single cells was lower in the GZ than elsewhere (Fig. 5G), despite higher proliferation rates. This suggests that there is more cell mixing in the GZ that separates pairs of daughter cells. This is consistent with planar cell intercalation being higher in the GZ (see below). We also found that the orientation of labelled cell doublets (i.e. touching cell pairs, most or all of which could be assumed to be sister cells given the overall sparseness of the labelling and that our counts of cell number between stage suggest that inter-rugal cells would have gone through at least one division) was similar to that of spindles (Fig. 5H,I): outside the GZ there was a significant AP bias in doublet orientation (Fig. 5I, Watson U² test, P<0.05) whereas within the GZ there was no statistically significant difference from a uniform distribution (although there was a weak AP trend) (Fig. 5H, Watson U² test, P>0.05). Thus, bias in orientation is inversely correlated with elongation rate and is therefore unlikely to be a significant factor in tissue growth.

Fig. 5.

Cell division orientation shows no anteroposterior bias in the GZ. (A-E) Radial plots of spindle orientation at E12.5 (A), E13.5 (B,C) and E14.5 (D,E) with spindles grouped as GZ (A,B,D) and non-GZ (C,E), only show bias along the AP axis in the non-GZ at both E13.5 (C) and E14.5 (E). Axes indicate cell numbers. For each interval, orientations are pooled from three palates. (F-F′) Average projection of an E14.5 epithelium, showing DAPI-stained nuclei (blue) and sparse GFP-labelled cells (green) induced by low tamoxifen dose given at E12.5. Details of GZ (F′) and non-GZ (F′) illustrating single cells (arrow), doublets (asterisk) and clusters of more than two cells (arrowhead). Doublet orientation was the angle of the line drawn between the centres of such touching cell pairs. (G) Histogram quantifying cell group sizes in inter-rugal epithelium. The proportion of single cells in the GZ is significantly higher than that in the non-GZ (paired t-test, P<0.05). Error bars represent s.d. n=8 palates. (H,I) Radial plots showing orientation of inter-rugal doublets in GZ (H) and non-GZ (I). Orientations are pooled from eight palates. The GZ shows a slight bias in orientation, whereas outside the GZ is a strong bias in orientation along the AP axis. For all radial plots, scale shows number of cell divisions in given direction (anterior to the right, medial at the top).

Cell elongation contributes to directional growth

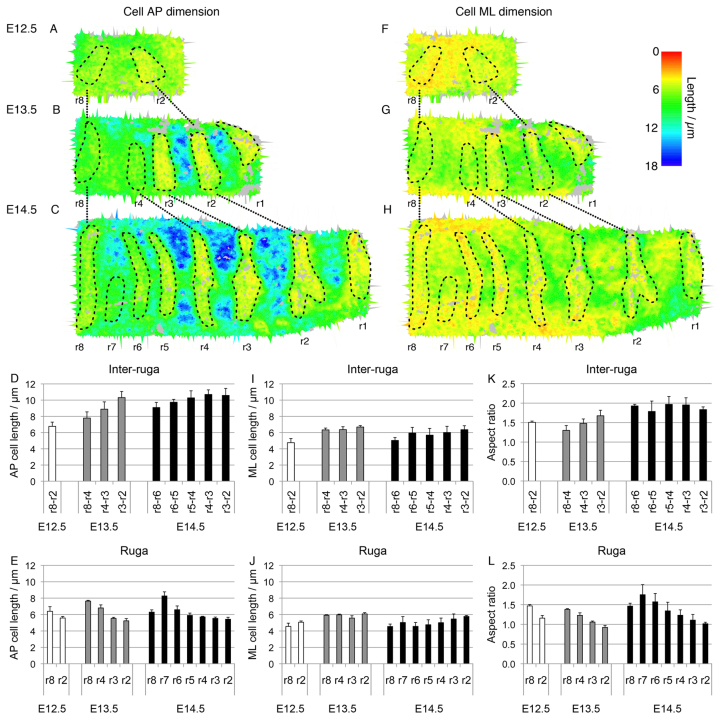
We next examined the potential contribution from changes in cell shape. We first took a simple measure of cell AP length, namely the dimensions of the xy bounding boxes of the segmented cell volumes (Fig. 2D). Maps of AP cell length thus obtained (Fig. 6A-C) reveal a clear difference between GZ and non-GZ inter-rugae, with increasing AP cell length from GZ to anterior tissue. This indicates that cells elongate as tissue in the GZ gets progressively displaced into more anterior positions. For example, the AP cell length in the GZ at E12.5 (ruga 8-2) was on average 6.8±0.5 μm (mean±s.d.) whereas the length of inter-rugal cells that had left the GZ by E13.5 (ruga 3-2) increased to 10.3±0.8 μm. This was then maintained (10.5±0.9 μm at E14.5; Fig. 6D). Similar results were obtained when using the bounding rectangle at the level of the centroid to measure cell length.

Fig. 6.

The epithelial GZ is a region of cell elongation. (A-C) Maps of AP cell length at E12.5 (A), E13.5 (B) and E14.5 (C) showing cell elongation in inter-rugal regions of the palate (anterior to the right, medial at the top) where tissue elongation is occurring, and cell shortening in the rugae. Maps were smoothed by averaging measurements over each cell and its immediate neighbours. (D,E) Histograms of average AP cell length across inter-rugal regions (D) and rugae (E) (rugae bounded as marked on maps) summarising this pattern. (F-H) Maps of ML cell length at E12.5 (E), E13.5 (F) and E14.5 (G) showing a small increase in ML cell length with tissue growth between E12.5 and E13.5, but little ML growth between E13.5 and E14.5, and little change in ML cell length in the rugae either. (I,J) Histograms averaging ML cell length across inter-rugal regions (I) and rugae (J) summarising this pattern. (K,L) Histograms of average cell aspect ratio across inter-rugal regions (K) and rugae (L). Inter-rugal AP increase is associated with an increase in AP/ML aspect ratio (K). Ruga maturation is associated with cells becoming more isotropic (L). For each interval in histograms (D,E,I-L), spacing calculated across three palates. Error bars represent s.d.

To confirm that this was indeed an elongation of cells and not an isotropic expansion, we examined both the ML dimension of the bounding boxes and the principal axes of fitted ellipses. Unlike the AP length, the ML cell width is nearly uniform throughout the palate, although it does increase throughout the palate between E12.5 and E13.5 and decreases slightly in the E14.5 GZ (Fig. 6F-I). Fitted ellipses revealed that cell elongation is highly aligned with the AP axis, deviating by less than 30° in the E13.5-14.5 GZ (supplementary material Fig. S2). Importantly, aspect ratios of both bounding boxes and fitted ellipses are greater in cells that have left the GZ (Fig. 6K; supplementary material Fig. S2D), confirming cell elongation. Interestingly, the occurrence of the AP-aligned cell division spindles described above occurs in the most elongated cells, suggesting that the spindle orientation is a response to cell shape rather than a cause of elongation, with cell division tending to bisect the elongated axis of a cell, as observed in some other model systems (Gibson et al., 2011; Morin and Bellaïche, 2011).

In contrast to cell elongation in the inter-rugae, cells giving rise to the rugae undergo an AP contraction relative to the length of cells in the GZ at earlier stages (they become rounder and more tightly packed; Fig. 6E,J,L).

Cell rearrangement via vertical intercalation (epiboly) contributes to tissue elongation

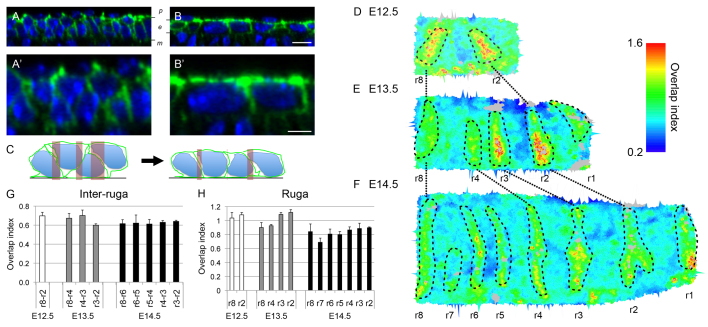
Inspection of sagittal projections of our image stages revealed not only that cells become bigger and more elongated as they leave the GZ but also that vertical intercalation might also be contributing to planar growth by reducing cell overlap in the xy plane (Fig. 7A-B′). This is comparable to the process of epiboly described in Xenopus (Keller, 1980) and zebrafish (Warga and Kimmel, 1990). To estimate the quantitative contribution of epiboly to growth, we needed a relative measure of the change in cell overlap in the xy plane (Fig. 7C). To do this, we compared the xy area of each cell (the cross-section at the level of the centroid of each cell) to the contribution of each cell to tissue size in the plane of the epithelium measured by its Voronoi area (Fig. 2E). Voronoi areas do not reflect cell shape, but by geometrically tiling an area according to cell spacing, they provide a measure of the absolute contribution of each cell to total area, i.e. cell ‘territory’ or ‘effective cell size in the plane’. Dividing the segmented area by the Voronoi area gives a cell level overlap index: the greater the overlap, the greater the value of the index. This analysis reveals a subtle reduction in overlap in cells in the anterior palate compared with those in the GZ (Fig. 7D-F). For example, cells in the GZ at E12.5 (ruga 8-2) have on average an overlap of 0.70±0.04, whereas in cells that had left the GZ by E13.5 (ruga 3-2) the index has dropped to 0.60±0.01. This was then maintained (0.63±0.01 at E14.5; Fig. 7G). [Note that these overlap values are <1 because our cell shapes represent the inside volumes of the cells and so there are gaps between them (see Fig. 2B, inset).] In cellular terms, this index change corresponds to a subtly pseudostratified epithelium becoming a simple epithelium, i.e. epiboly. Consistent with this, the cell area increase seen on exiting the GZ is associated with ∼20% thinning of the inter-rugal epithelium (data not shown). By contrast, the condensation of the rugae requires an increase in overlap. For example, cells in ruga 3 at E13.5 have an overlap of 1.09±0.03, compared with the 0.70±0.04 seen in the E12.5 GZ inter-rugal cells (Fig. 7H). As well as a shortening in cell length, ruga formation consists of a stratification of cells.

Fig. 7.

The epithelial GZ is associated with an apicobasal cell rearrangement. (A-B′) Orthogonal (apicobasal) slices of confocal stacks showing different arrangements of cell packing in the palatal epithelium (DAPI in blue, beta-catenin in green). (A,A′) Cells in the GZ (shown for E13.5 r8-r4 interval) are tightly packed with cell bodies overlapping in the x axis (detail in A′). (B,B′) Equivalent cells that have left the GZ (shown for E14.5 r5-r4 interval) are more squamous with less overlap (detail in B′) and the epithelial layer is thinner [epithelial cells (e) lying between mesenchymal (m) and peridermal (p) cells]. Scale bars: 10 μm (B); 5 μm (B′). (C) Schematic illustrating how a reduction in x overlap (pink shaded areas) can lead to tissue elongation without cell shape change. (D-F) Maps of overlap Index (segmented cell area/Voronoi cell area; see text for details) at E12.5 (D), E13.5 (E) and E14.5 (F) showing a slight decrease in cell overlap in inter-rugal regions where tissue elongates, whereas ruga formation is associated with an increase in cell overlap (anterior to the right, medial at the top). (G,H) Histograms of overlap index across inter-rugal regions (G) and rugae (H) summarising this pattern. For maps, measurements for each cell were averaged over that cell and two sets of neighbours. For each interval in histograms (G,H), overlap index was calculated across three palates. Error bars represent s.d.

Relative contributions of cellular processes to tissue elongation

The results described above show that proliferation, cell elongation and cell rearrangement all contribute to epithelial elongation in the palate. However, to establish a mechanistic understanding of growth, it was necessary to establish whether these processes were sufficient to account for gross growth or whether there was ‘missing mass’. In particular, could we determine a contribution from the one elongation process that we did not directly measure, namely ML cell intercalation? As mentioned above, greater labelled cell dispersion in our clonal labelling experiments indicated that this might be occurring in the GZ, but the question remained whether this was making a quantitatively significant contribution to growth. Using our quantifications described above, we were able to estimate the quantitative contribution of planar cell rearrangement using the following calculations.

From gross measurements, we defined directional growth, G, as

i.e. the ratio of tissue lengths (L_t at time t). We know that G is the product of increase in cell number, increase in cell length, orientation of cell division and cell rearrangement when these are appropriately defined. From cell counting, we can define proliferational growth (P) in a given direction as

This is defined here as the contribution of the fold change in cell number of a clonal cell population (compartment) to tissue size in a given axis. Cell number is isotropic (orientation of cell division is considered below) and, therefore, in an epithelium, growth in a given axis is the square root of the fold change in total cell number (n_t). (For a tissue volume, the cube root would be used.)

From segmented volumes, we can measure cell elongation, E, as

i.e. the fold-change of average cell length (l_t).

Cell rearrangement as a whole is much harder to quantify. However, one component of it can be quantified, namely tissue growth as a result of decreasing overlap in the xy plane. This can be defined as V where

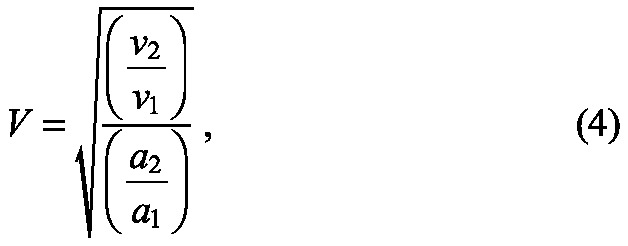derived from dividing the ratio of Voronoi areas (v_t) at successive times (a growth measure that includes the reduction in overlap as well as cell size change) by the segmented area (a_t) ratio (which does not account for changes in overlap). As these measures are based on areas, and assuming that overlap is isotropic, the square root gives the contribution of this process to growth in a given axis.

We combined the above terms to describe overall growth as a product,

where A is the contributions of the orientation of cell division and anisotropic cell rearrangement (i.e. ML cell intercalation). As we have shown that oriented cell division is not correlated with AP growth in the GZ, this term here largely or exclusively describes ML cell intercalation.

Although these processes are multiplicative, we find it conceptually helpful to work in log space where the processes become additive:

This allows the fractional contribution of a given process to be calculated; for example, that of proliferation is thus given by logP/logG, that of cell elongation by logE/logG, etc.

Because cells in and between rugae clearly behave differently, we performed this analysis separately on rugal tissue, inter-rugal tissue and tissue in the GZ in the process of forming new rugae (the initial extent of which is estimated from the width of the unthickened but highly BrdU-positive region in the GZ, as in Fig. 3). The results of this analysis are shown in Fig. 8. Our growth breakdown shows us that proliferation is the dominant growth process in the GZ (Fig. 8A,B), accounting for ∼60% of growth in inter-rugal and 70% in forming-rugal tissue at each stage. In inter-rugal tissue, cell elongation makes 18-20% contribution (higher at earlier stages) whereas epiboly adds a further 2-4% (higher at later stages). By contrast, in the formation of rugae, cell rounding (negative elongation) and cell stacking (negative epiboly) reduces local tissue elongation, making a negative 20% growth contribution. Finally, we are left with remaining processes that account for 20-30% of the growth (fold change in tissue length), indicating that these processes, mostly ML cell intercalation, contribute substantially to tissue growth. Existing rugae undergo no growth or even a slight shortening as cellular processes cancel each other out (Fig. 8C). Overall, non-proliferation processes contribute ∼40% of elongation in this tissue.

Fig. 8.

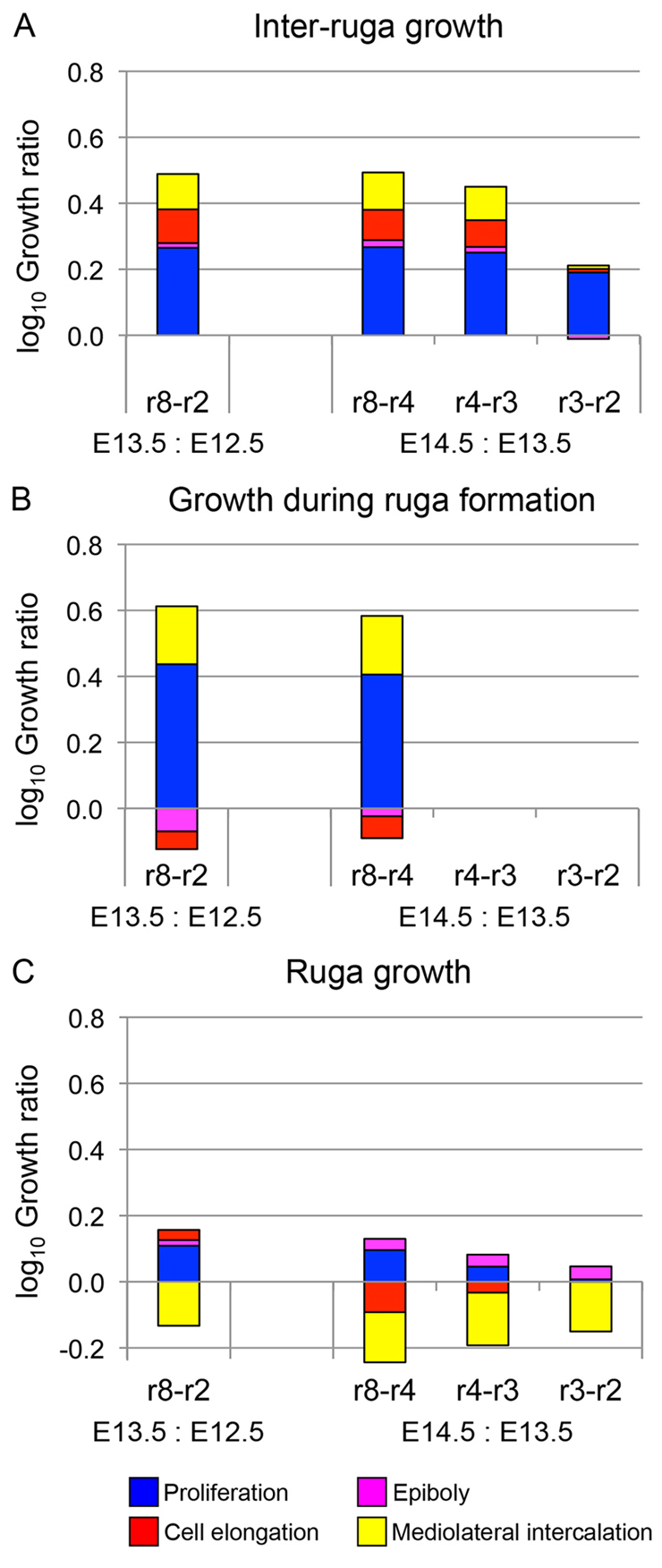
Contribution of different cellular processes to tissue elongation. (A-C) Histograms showing log₁₀ growth ratio of tissue growth in inter-rugae (A), newly forming rugae from inter-rugal primordia (B) and existing rugae (C). Colours indicate contribution of each cellular process. Negative values indicate processes leading to tissue shortening. For both inter-rugal growth (A) and ruga formation (B), proliferation is the dominant process, with ML cell intercalation contributing too. Inter-rugal growth also has a contribution from cell elongation and a small contribution from vertical intercalation. In mature rugae, there is no net growth or even tissue shortening and processes balance out. Data are from three palates for each stage.

DISCUSSION

In this study, we have analysed all possible tissue growth processes in the developing palate epithelium by measuring cell parameters in fixed specimens. We hope this will serve as a paradigm for analysis of morphogenesis in other tissues in which live imaging is difficult or impractical. We have captured contributions from cell proliferation, cell elongation, oriented cell division and cell rearrangement without live imaging or extensive clonal labelling. Of these, the most difficult to capture is cell rearrangement in the epithelial plane. However, by subtracting out the other processes, we have been able to calculate the contribution of cell rearrangement processes to growth. We can conclude, for this tissue, that although proliferation dominates growth (perhaps unsurprisingly), cell elongation and cell intercalation make significant contributions. ‘Significant’ in this instance means not only statistically significant, but also significant enough to be the sole cause of a clinically relevant dysmorphology (e.g. ML growth failure in palate mesenchyme causing cleft palate). Phenotypic analysis of, for example, cleft palate models, should not therefore be restricted to analysis of cell proliferation (and apoptosis) alone, as is often the case in the literature to date, but should also include analysis of cell shape and cell rearrangement. In mesenchymal tissues, in which extracellular matrix can contribute significantly to volume, a further measure of cell spacing would be appropriate. Taken together, we have demonstrated that growth processes can be mapped and gross phenotypes analysed to the cellular level, even in tissue that cannot easily be imaged live (as is the case for many mammalian tissues).

This study reduces growth to a set of cellular mechanisms, but it does not address mechanisms at the mechanical or molecular level. One might speculate, for example, that the epithelial growth is at least in part driven by elongation forces from underlying mesenchyme. Preliminary investigation of the underlying mesenchyme shows no evidence of similar distributions of cell size or proliferation (supplementary material Fig. S3). This suggests that the midpalate GZ does not arise as a passive response to cell properties in the underlying bulk tissue but reflects properties inherent in the epithelium itself. The GZ is associated with a region of elevated fibroblast growth factor gene expression (Welsh and O’Brien, 2009) and our findings point to this having an effect on cell architecture as well as cell division, making cells more columnar/pseudostratified rather than squamous. The mechanisms that control the columnar-cuboidal-squamous cell shape spectrum are not well understood, but this system suggests a new avenue for investigation.

In that a periodic pattern is generated in a region of growing tissue, the palatal epithelium has a certain similarity to vertebrate somitogenesis. However, we see no sign of the oscillating gene expression that is the hallmark of somitogenesis and we therefore believe that the patterning mechanisms differ (reaction diffusion in the rugae, clock and wavefront in the somites). Regarding growth, although there has been some investigation into the role of cell movement in pre-somitic axis elongation (Bénazéraf et al., 2010), a comprehensive examination of all cellular mechanisms would be of interest. The same is true for the growing limb for which there are now several lines of evidence for cell movement rather than pure proliferation being the mechanism of tissue elongation (Boehm et al., 2010; Gros et al., 2010; Wyngaarden et al., 2010).

Our study is also an attempt to contribute to what is a currently small but growing effort to quantify cell ensemble behaviour at a statistical level to link gross tissue changes to single cell and ultimately molecular genetic and epigenetic mechanisms. Without such quantitative kinematic descriptions, integration of genotype and phenotype is not possible. However, although our simple summations have given us insight into the cellular basis of growth, it is also apparent that with so many variables to be accounted for, computational models (numerical simulations) are needed to understand fully the cellular basis of growth. We have demonstrated that the oral palate rugae provide a useful starting point for developing the relevant imaging and computational methods, but these can and should be extended to three-dimensional morphogenesis in other contexts.

MATERIALS AND METHODS

Mouse strains and tissue labelling

Wild-type CD1 mice were injected with BrdU at 50 mg/kg body weight 2 hours before sacrifice. Palatal shelves were dissected out in PBS and fixed overnight in 4% paraformaldehyde in PBS at 4°C. Antigen retrieval for BrdU was carried out by 2 hours DNase treatment at 37°C (Tkatchenko, 2006). Specimens were then blocked for 1 hour at room temperature in PBT (0.1% Triton X-100 in PBS) with 10% goat serum and 1% bovine serum albumin followed by incubation overnight at 4°C in rabbit anti-beta-catenin (1:200; H-102, Santa Cruz Biotech) and rat anti-BrdU (1:400; BU1/75, Abcam). Specimens were subsequently washed in PBT for 1 day before incubation in blocking buffer of 1 hour at room temperature followed by incubation overnight at 4°C in anti-rabbit Alexa488 and anti-rat Alexa568 (1:400; Invitrogen). Finally, specimens were washed in PBT for at least 1 day.

Immunostaining for alpha tubulin followed the protocol described above except that dissected palatal shelves were fixed overnight in Dent’s fix (20% DMSO, 80% methanol) at -20°C before rehydration through a methanol series. Specimens were incubated with the primary antibody anti-alpha-tubulin (1:400; T-9026, Sigma) for 48 hours. In situ hybridisation was performed as previously described (Economou et al., 2012).

Clonal labelling was achieved by injecting 150-200 μl of 20 mg/ml tamoxifen into a pregnant female mT/mG mouse [Gt(ROSA)26Sor^{tm4(ACTB-tdTomato,-EGFP)Luo/J} (Jackson Laboratories strain 007576)] crossed with a tamoxifen-inducible Cre male B6.Cg-Tg^{(CAG-cre/Esr1*)5Amc/J} (Jackson Laboratories strain 004682).

Imaging and image processing

Specimens were mounted in Mowiol for imaging on a Leica SP5 confocal microscope. Images were captured using a HCX PLAN APO CS N.A. 1.25 ×40 oil immersion lens. As the specimens were larger than the field of view, they were captured using a motorised stage driven by the Tile Scan application, and stacks were subsequently stitched together using the Grid/Collection Stitching plug-in in FIJI (Preibisch et al., 2009). Mitotic spindle orientations were measured using the line tool in Volocity (Perkin-Elmer).

Image analysis

Stitched confocal stacks contained, in addition to epithelial cells, the underlying mesenchymal cells and an overlying layer of peridermal cells. The segmentation of the images to identify and obtain volume data (including bounding box and fitted ellipse measurements) for specifically the epithelial cells was achieved using macros written by us for FIJI (Schindelin et al., 2012). Details of these are available on request but are summarised as follows.

Slices of confocal stacks containing epithelial cells but not mesenchymal and peridermal cells were identified by exploiting the local alignment of cells in these different layers. Specifically, acquired stacks were subdivided in the xy plane such that each xy ‘tile’ had layers well aligned in the z plane. Layers of cells could then be separated by the two xy planes in which there was a minimum of total DAPI staining and, apically, a maximum of total beta-catenin staining (supplementary material Fig. S1A). Periderm and mesenchyme could then be removed by cropping the stacks above the upper and below the lower of these planes, respectively. The upper and lower cropping positions also gave local measures of epithelial thickness.

Individual epithelial cells were identified as local minima in beta-catenin intensity. Because intensity of this signal and background varied within and between samples, these could not be identified with a single intensity threshold. Instead, using ImageJ plug-ins 3D object counter (Bolte and Cordelières, 2006) and 3D ROI manager (Ollion et al., 2013), we applied successively decreasing intensity thresholds in each image. Initially, such thresholds identified below-threshold objects consisting of large areas of several cells. As the thresholds were lowered, smaller regions were identified. Eventually, at different levels in different places, single cell voids (i.e. areas surrounded by beta-catenin) were identified. To ensure that these were indeed single cell voids, only below-threshold objects larger than 100 voxels in volume with uniform (background) intensity (i.e. that disappeared after a single threshold decrement) were scored. A further filter required the objects also to be DAPI positive. The above steps identified single cells with high reliability (supplementary material Fig. S1B,C; see below). BrdU-positive cells were also identified at this stage as having BrdU channel intensity above a threshold, which was itself determined as one above the local auto-threshold level that would not generate noise (objects of two pixels or fewer).

Once all cells were identified, the Active Contours method in the Level Sets segmentation protocols provided with FIJI (Schindelin et al., 2012) was used to fill cell volumes bounded by beta-catenin immunofluorescence. The active contours were seeded from the centroids of the identified cell minima. Parameter values were chosen to give the best segmentation of elongated objects without the contour bleeding through to neighbouring cells as a result of gaps in the beta-catenin staining (e.g. supplementary material Fig. S1D). Cell volumes that exceeded a realistic maximum cell size or overlapped several neighbours were assumed to be segmentation errors and not used for further analyses of cell shape (grey pixels in Figs 6 and 7).

Cell identification was validated against a set of 2079 manually identified cells. Cells were identified with a sensitivity [true positives/(true positives + false negatives)] of 0.97 and a positive predictive value (ppv) [true positives/(true positives + false positives)] of 0.96. Considering GZ inter-ruga, non-GZ inter-ruga and rugal regions separately, cells were still identified with a sensitivity of >0.95 and ppv of >0.95 except for the non-GZ where ppv fell to 0.91. Identification of BrdU positive cells was validated over a set of 2119 manually identified cells from a range of stages and AP positions. The proportion of correctly identified cells was 0.98. Considering GZ, non-GZ and rugal regions separately, the proportion of correctly identified cells was >0.95 for each.

Cell shape measurements were validated against a set of 240 cells from a range of stages and AP positions as follows. Cells were manually segmented in three dimensions by outlining the cell boundary as defined by beta-catenin immunofluorescence in successive xy slices of z stacks (a total of 9324 slices). Measures of cell shape were compared between the manual and automated volumes as dimensions of the bounding rectangle at the level of the centroid (a measure of shape where the cell bulk is highest).

We found that automated shapes were systematically larger than manual outlines by 1.3 pixels in both AP and ML dimensions. We attribute this to in the need in the manual outlining to mark the inner edge of the (sometimes quite thick) beta-catenin staining whereas the automated segmentation uses an arbitrary unbiased intensity gradient steepness that was within the stained region. A correction factor of 1.3 pixels was therefore applied to all automated shape values. Automated shapes were also more spherical (i.e. less elongated) than manual shapes. This discrepancy is expected because the volume-filling level-set algorithm limits surface contour curvature (to prevent bleeding, see above), which is higher for more elongated cells. We found this discrepancy to be highly correlated with aspect ratio (R²=0.80). We therefore applied an aspect-ratio-dependent correction factor (empirically optimised to 1.30 AR - 0.30, where AR is the outline aspect ratio) to all automated shape values. With doubly corrected automated cell shape values matched the manual values to within <5% for all regions and cell shapes sampled.

Map generation

Quantified data were represented as maps to show the spatial distribution of measurement at a cellular level. Maps used a Voronoi tessellation of xy coordinates of segmented cell centroids, with each cell-tile coloured according to the parameter in question (i.e. tiles were used to display the quantitative data for or around each cell rather than reflecting the actual cell shapes). Voronoi tessellations and colourings were performed using the statistical package ‘R’ (R Core Team, 2012) using a dedicated package (http://cran.r-project.org/package=deldir). Cells for which segmentation errors (size out of range or overlapping with neighbours) had occurred in >40% of neighbours were assumed to lie in regions of poor image quality and so were greyed out.