Prediction of heterosis using genome-wide SNP-marker data: application to egg production traits in white Leghorn crosses

Abstract

Prediction of heterosis has a long history with mixed success, partly due to low numbers of genetic markers and/or small data sets. We investigated the prediction of heterosis for egg number, egg weight and survival days in domestic white Leghorns, using ∼400 000 individuals from 47 crosses and allele frequencies on ∼53 000 genome-wide single nucleotide polymorphisms (SNPs). When heterosis is due to dominance, and dominance effects are independent of allele frequencies, heterosis is proportional to the squared difference in allele frequency (SDAF) between parental pure lines (not necessarily homozygous). Under these assumptions, a linear model including regression on SDAF partitions crossbred phenotypes into pure-line values and heterosis, even without pure-line phenotypes. We therefore used models where phenotypes of crossbreds were regressed on the SDAF between parental lines. Accuracy of prediction was determined using leave-one-out cross-validation. SDAF predicted heterosis for egg number and weight with an accuracy of ∼0.5, but did not predict heterosis for survival days. Heterosis predictions allowed preselection of pure lines before field-testing, saving ∼50% of field-testing cost with only 4% loss in heterosis. Accuracies from cross-validation were lower than from the model-fit, suggesting that accuracies previously reported in literature are overestimated. Cross-validation also indicated that dominance cannot fully explain heterosis. Nevertheless, the dominance model had considerable accuracy, clearly greater than that of a general/specific combining ability model. This work also showed that heterosis can be modelled even when pure-line phenotypes are unavailable. We concluded that SDAF is a useful predictor of heterosis in commercial layer breeding.

Introduction

Heterosis or hybrid vigour is the observed increase in growth, productivity, fertility and vigour of a hybrid organism over that of its parents (Shull, 1914; Dobzhansky, 1950). This genetic phenomenon is an essential element of commercial poultry, pig, sheep and plant breeding schemes. In poultry breeding, heterosis was exploited even as early as 1893 (Warren, 1942). Over the years, poultry breeders have established pure lines (not necessarily homozygous) that when crossed produce F₁ hybrids with superior performance in traits of economic importance like growth, egg production and survival. In plant breeding, hybrid cultivars are produced by crossing inbreds from opposite and complementary heterotic groups (Bernardo, 1994). The wide application of such breeding designs demonstrates that the benefits of heterosis are widely exploited by breeders.

In practice, selecting lines to be used as parents in crossbreeding programmes is a challenge because testing all possible line combinations is expensive and time consuming. Also, predicting the F1 performance from per se phenotypic records of pure lines has failed (Duvick, 1999; Hallauer et al., 2010), and prediction methods based on microsatellite markers have not been very conclusive (Gavora et al., 1996; Minvielle et al., 2000; Atzmon et al., 2002; Jagosz, 2011; Di et al., 2012). Therefore, there is the need to find reliable methods for predicting heterosis because it has the potential to substantially increase the efficiency of crossbreeding schemes, by identifying optimal parental combinations and reducing costs of field-testing.

Some hypotheses have been put forward as possible explanations for the genetic mechanisms underlying heterosis: the dominance hypothesis attributes heterosis to the masking of deleterious recessive alleles from one parental line by dominant alleles in the other parental line; the overdominance hypothesis attributes heterosis to advantageous combinations of alleles at heterozygous loci; and the epistasis hypothesis assumes that interactions among loci lead to heterosis (Lynch and Walsh, 1998; Crow, 1999; Goodnight, 1999; Lamkey and Edwards, 1999).

In a single locus model, heterosis is solely due to dominance and is proportional to the squared difference in allele frequency (SDAF) between the parental lines (Falconer and Mackay, 1996). This finding has triggered research into predicting F1 heterosis and overall performance based on microsatellite marker information from parental pure lines. In poultry, evidence to support the theory that heterosis is higher in offspring from more genetically distant parents has been found (Gavora et al., 1996; Haberfeld et al., 1996; Atzmon et al., 2002). Also, many prediction studies have been carried out on commercial crops such as maize, rapeseed, sunflower, chick pea and carrot. Some of these studies reported correlations between genetic distances (GD) and heterosis (Reif et al., 2003; Balestre et al., 2009), but others concluded that GD is not a reliable predictor of heterosis (Dias et al., 2004; Krishnan et al., 2013).

Because of inconsistencies in the results from previous studies, one cannot conclude whether the prediction of heterosis based on molecular marker information has been a success or not, as pointed out in reviews by Dias et al. (2004) and Krishnan et al. (2013). The former authors reviewed several studies in plants and suggested that the number of molecular markers (averages of 160 random amplified polymorphic DNAs, 281 restriction fragment length polymorphisms and 25 simple sequence repeats) should be increased for accurate predictions. Gavora et al. (1996) and Minvielle et al. (2000) reported studies on poultry using ∼85 DNA fingerprint bands. Nowadays, genotyping technologies have advanced, producing large amounts of genome-wide marker information and creating opportunities to reinvestigate the genetic basis of heterosis, and methods for its prediction.

A further difficulty in the study of heterosis, particularly in livestock populations, is that phenotypic values on pure-bred individuals are often recorded only in specific environments that differ systematically from the environments in which crossbred phenotypes are recorded. In those cases, heterosis cannot be observed because it is fully confounded with the environment. Although an analysis of crossbred data using a specific vs general combining ability model is feasible in such cases, this provides estimates of combining ability rather than heterosis. In contrast to heterosis, general and specific combining ability (GCA/SCA) depend on the set of crosses included if the crossing scheme is incomplete, and this is generally the case in animal populations. Dependency of results on the set of crosses included hampers the comparison of results with the literature, and the prediction of future crosses. Hence, animal breeders are interested primarily in heterosis and hybrid performance, rather than combining ability, but are faced with the problem that pure-bred phenotypes are unavailable.

The aim of this study was to determine whether genome-wide difference in allele frequencies between pure lines can be used to predict heterosis for egg number, egg weight and survival days in white Leghorn crosses. For this purpose, we used allele frequencies on 60 K single nucleotide polymorphism (SNP) loci from 11 pure lines of white Leghorns, and phenotypic data on 47 crosses between those lines, representing ∼400 000 individuals. No phenotypic data were available on the pure lines. In animals, this is the largest data set ever used for the prediction of heterosis and the first to utilise genome-wide SNP-marker data. We performed a cross-validation to test how accurately we could predict heterosis in crosses for which phenotypic records were unavailable. Moreover, we investigated the estimation of heterosis in the absence of phenotypic data on pure lines, and compared the predictive ability of heterosis vs combining-ability modelling.

Materials and methods

Population structure

Phenotypic records of crossbred hens originating from 11 pure-bred white Leghorn layer lines (5 sire- and 6 dam-lines) were obtained from the Institut de Sélection Animale B.V. (ISA). Phenotypic records were available on crossbreds only; phenotypic records on pure lines reared under similar conditions were not available. Coding of the pure lines was as follows: S1, S2, S3, S4, S5 represented sire-lines and D1, D2, D3, D4, D5, D6 represented dam-lines. A cross produced by an S1 sire and a D1 dam is referred to as S1 × D1 and its reciprocal as D1 × S1. Within each line there were multiple sires and dams, resulting in full- and half-sibs within a cross. The mating scheme shown in Table 1 produced a total of 47 crosses, some being reciprocal crosses. Phenotypic records were from routine performance tests carried out on test farms in the Netherlands, Canada and France from 2004 through 2010. On the test farms, each henhouse had several rows of cages, and each row had three tiers: bottom, middle and top. Crossbreds were kept in group cages of a mix of full- and paternal half-sibs which were assigned randomly to a row and tier within the henhouse, but ensuring that the different crosses and families were randomized across all rows and tiers. On average, there were ∼5 hens per cage. All hens had been beak-trimmed.

Table 1. The mean and number of records (given in brackets) per cross for egg number, egg weight and survival days.

		Father line
		S1	S2	S3	S4	S5	D1	D2	D4	D5	D6
Egg number	Mother line
	S1				329 (42)	321 (75)	343 (4899)	340 (1854)	334 (4104)		315 (46)
	S2						339 (865)	340 (896)	333 (380)
	S4									329 (189)	331 (1381)
	S5									329 (336)	329 (1479)
	D1	337 (4823)	337 (1321)	329 (2983)	333 (723)	340 (641)			337 (3025)		331 (531)
	D2	338 (5996)	337 (927)	330 (3178)	335 (350)	340 (487)
	D3	340 (4519)	337 (457)	336 (3729)	336 (264)	344 (435)
	D4	334 (5085)	334 (1189)	323 (2187)		326 (41)	341 (3348)
	D5	330 (208)		306 (20)	325 (3678)	335 (2783)			331 (100)
	D6	336 (212)	335 (99)	325 (117)	326 (3808)	333 (2770)			304 (20)	295 (40)
Egg weight	S1				60.1 (28)	61.3 (58)	60.8 (3516)	62.8 (1363)	61.5 (3085)		61.0 (28)
(in grams)	S2						61.4 (671)	63.0 (618)	62.8 (278)
	S4									63.5 (188)	61.3 (1177)
	S5									64.1 (336)	61.8 (1288)
	D1	62.4 (3553)	63.0 (912)	63.0 (2298)	62.1 (492)	62.6 (411)			63.3 (2207)		62.5 (360)
	D2	60.5 (4448)	61.2 (668)	60.1 (2275)	61.2 (273)	60.9 (317)
	D3	60.2 (3371)	61.2 (324)	60.7 (2994)	60.4 (216)	60.8 (283)
	D4	61.3 (3772)	62.5 (874)	61.5 (1683)		61.2 (34)	62.1 (2525)
	D5	61.9 (142)		62.6 (14)	61.0 (2820)	62.9 (2219)			60.8 (81)
	D6	60.7 (161)	61.4 (80)	60.7 (95)	60.0 (2937)	61.1 (2254)			60.6 (13)	63.8 (19)
Survival	S1				526 (42)	536 (75)	564 (4899)	556 (1854)	535 (4104)		522 (46)
days	S2						563 (865)	543 (896)	583 (380)
	S4									551 (189)	555 (1381)
	S5									558 (336)	555 (1479)
	D1	543 (4823)	559 (1321)	549 (2983)	534.8 (723)	549 (641)			539 (3025)		546 (531)
	D2	541 (5996)	553 (927)	549 (3178)	528 (350)	554 (487)
	D3	544 (4519)	540 (457)	544 (3729)	506 (264)	549 (435)
	D4	539 (5085)	569 (1189)	544 (2187)		556 (41)	560 (3348)
	D5	550 (208)		533 (20)	548 (3678)	559 (2783)			552 (100)
	D6	549 (212)	546 (99)	543 (117)	550 (3808)	560 (2770)			518 (20)	504 (40)

All records were taken on a cage-basis. The rows for S3 and column for D3 did not have any observations so were omitted from the table.

Phenotypic data

Traits studied were egg number, egg weight and survival days.

Egg number

Hens were kept in cages and all records were taken at the cage level (rather than at the level of the individual hens). Hen-day records of eggs produced from 100 through 504 days of age were used. Hen-day egg number was calculated as the total number of eggs laid in the cage divided by the total number of days that a hen was present (days are summed for all hens that were placed in the cage), and then multiplied by the maximum number of days the production period lasted. As an example, consider a production period lasting 410 days. If total number of eggs laid is 1650 in a cage that started with five hens, and all hens survived until the end of the production period, then summed hen days are 5 × 410 days=2050 days. Hen-day egg number is (1650/2050) × 410=330 eggs. In a case where the same egg numbers were reached, but one hen died 50 days before the end of the period, the summed hen days would be 2000 days. This would give a hen-day egg number of (1650/2000) × 410=338.25 eggs. This cage-based value represents one record and in this paper we will simply refer to this trait as ‘egg number'. After descriptive statistics of the data on egg number, we discovered that three consecutive performance tests conducted by the same farmer had ∼9% of the records above the biological limit of one egg per hen per day. We studied hen-day egg number, so those unusually high records could be because of mistakes in recording the duration of the production period or mortality records. We therefore decided to eliminate all of that farmer's tests from further analysis. For other performance tests with only a few (<3%) of the records above the biological limit, we only excluded those particular records but kept the other records from that performance test in the analyses. No two tests in this category were from the same farmer. Also, total egg number records that were less than 150 eggs were considered to be errors (personal communication Jeroen Visscher, ISA poultry breeders) and therefore excluded. Excluded records represented 7.6% of the total record count. The final data set used had 76 640 records.

Egg weight

Approximately five times throughout the production period (at around 25, 35, 45, 60 and 75 weeks of age), for each cage, the average weight of all eggs laid on a particular day was recorded. At the end of the production period, these five averages were again averaged to give one value for egg weight per cage for the entire production period. The data set used was the same as that for egg number but there were some missing records for egg weight, leaving 57 759 records.

Survival days

The trait survival days is the average number of days that the hens within each cage survived. For example, if a cage started with five hens, three of which survived for 410 days, one for 405 days and the other for 400 days, the record for that cage would be ((3 × 410)+405+400)/5=407 days. Fractions were truncated. There were 76 640 records on survival days.

Allele frequency data

For each pure line, blood from 75 randomly chosen males was pooled, and DNA was extracted for genotyping. The Illumina chicken 60 K SNP BeadChip was used (Groenen et al., 2011). The same array was used for all genotyping. Quality control criteria were call rate and visual inspection of the clustering of the three genotypes at each SNP. The total number of SNPs used in this study was 53 582, after excluding the sex chromosomes. The sex chromosomes were excluded because females are the heterogametic sex in chickens (ZW), thus the sex chromosomes do not contribute to heterosis by dominance in females. Estimated allele frequencies were corrected for unequal amplification by ‘k-correction', using the relative allele signal of heterozygous individuals (Hoogendoorn et al., 2000), and then normalised with respect to the two homozygotes (Craig et al., 2005). Correction factors were obtained from 288 individually genotyped animals across all lines. On average, estimation of allele frequencies from the DNA pooling technique has an accuracy of 0.993, with a range of 0.986 to 1 (Hoogendoorn et al., 2000).

Statistical analyses

Allele frequencies

Our statistical analysis rests on two assumptions. The first assumption is that heterosis is due to dominance. Under this assumption, the heterosis due to a single locus, say l, is proportional to the SDAF between the parental lines at that locus,

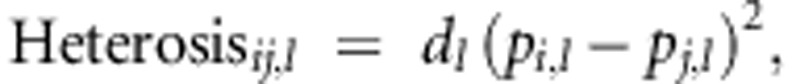where d_l is the dominance deviation at locus l, p_i,l is the allele frequency at locus l in parental line i, and p_j,l is the allele frequency at locus l in parental line j (Falconer and Mackay, 1996). Under the assumption that heterosis is due to dominance, total heterosis is simply the sum of heterosis at each locus,

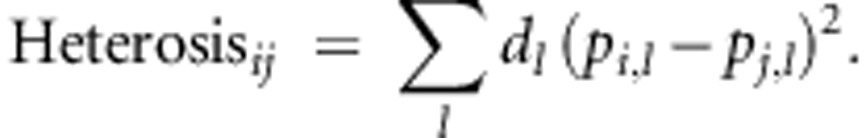The second assumption is that the dominance deviation at a locus is independent of the SDAF between parental lines at that locus, so that 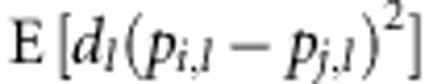=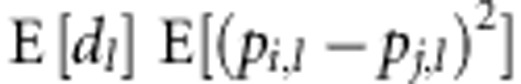. Under this assumption, expected heterosis: 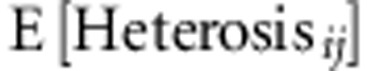=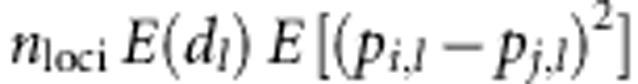, where n_loci is the total number of loci. Thus, under this assumption, heterosis is linear in the SDAF between parental lines, averaged over all loci, with a coefficient of proportionality of n_loci E(d₁), which will be higher with directional than ambidirectional dominance. We therefore used the genome-wide average of SDAF as a predictor of heterosis. For any two parental lines, say i and j, SDAF_ij was calculated as

where 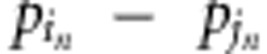is the difference in allele frequency between pure lines i and j at SNP n, and N is the total number of SNPs.

We also calculated Nei's standard GD (Nei, 1972) from the allele frequencies using the PHYLIP software (Department of Genetics, University of Washington, Seattle, WA, USA) (Felsenstein, 1993). Nei's standard GD is given by

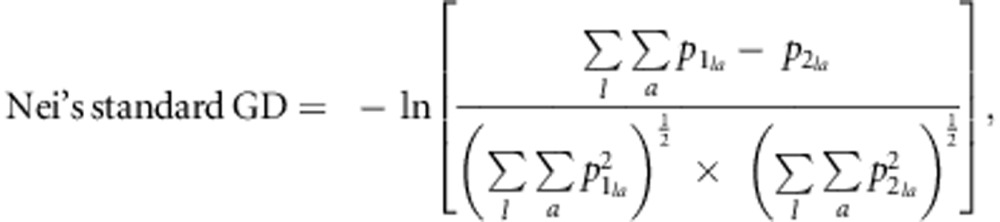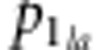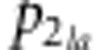where is the allele frequency of the a-th allele at the l-th locus in line 1, and is the allele frequency of the a-th allele at the l-th locus in line 2. To visualise the genetic differences between the pure lines, we constructed a phylogenetic tree using MEGA (Tamura et al., 2011).

Prediction of heterosis

To test the significance of SDAF for predicting heterosis, we fitted a linear mixed model where we regressed the phenotypes of crossbreds on the SDAF between both pure lines producing the cross:

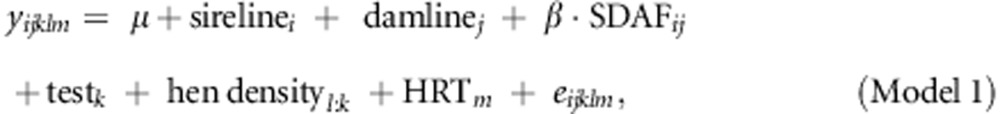where y_ijklm was a phenotypic record, sire-line_i and dam-line_j were the fixed effects of the ith sire-line and jth dam-line of each cross (i, j=1–10), β was the regression coefficient of y on SDAF, test_k was the fixed effect of each performance test (k=1–50); test is a factor that represents the year in which the test was carried out, and on which farm. Hen density_l was a fixed effect accounting for the initial number of hens within a cage. It had 205 levels, and was nested within the test because the physical size of cages differed across some performance tests. The combined effect of the henhouse, row and tier of the cage was accounted for by including the term ‘HRT_m' as a random effect (m=1–1088) and e_ijklm was the random residual error term. Data were analysed using the MIXED procedure in SAS version 9.2. This model was used for all three traits. Under the assumptions given above, Model 1 is a heterosis model, where the estimates of sire-line and dam-line are estimates of the pure-line performance, whereas the estimate of β × SDAF_ij is an estimate of heterosis. (See Discussion and Supplementary Information).

Predicted heterosis was calculated by multiplying the estimated regression coefficient of the phenotypes on SDAF (obtained from Model 1) by the SDAF between the lines in each cross,

For example, predicted heterosis for egg number in an S1 × D1 cross was.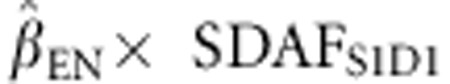

Note that as SDAF_ij is the same as SDAF_ji, the predicted heterosis for reciprocal crosses is the same, although their trait values may differ.

Egg number had a markedly skewed distribution; a characteristic that causes model assumptions of normally distributed residuals to fail. Also, P-values obtained from the statistical analyses may not be valid. To correct for this, a Box-Cox transformation (Box and Cox, 1964) is commonly applied before the analysis (Ibe and Hill, 1988, Besbes et al., 1993). We therefore applied this transformation to the egg number records. The general form of the Box-Cox transformation equations is:

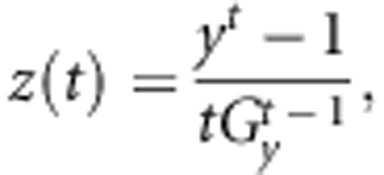where y is the original variable, z(t) is the standardized variable, G_y is the geometric mean of the data and t is the parameter by which data are normalised. We used an empirically selected ‘optimum' t=4 based on the minimal residual variance of the model used to describe the transformed records. We also considered the minimum test statistic for the Kolmogorov–Smirnov normality test.

We fitted our models on both the transformed and original scale, however, to facilitate interpretation, the estimated effects are given only on the original scale in the Results.

Accuracy of predicted heterosis

To evaluate the accuracy of predicted heterosis, we used two approaches. First, we calculated Pearson's correlation coefficient between predicted and observed heterosis; second, we used cross-validation to assess the accuracy of predicted heterosis for crosses not included in the estimation of β.

Correlations between observed and predicted heterosis

We calculated Pearson's correlation between observed and predicted heterosis. As we did not have phenotypic records of the pure lines, we did not have true observed heterosis. We therefore used the following strategy to obtain values of ‘observed heterosis'.

Observed heterosis, y^#, was obtained by correcting all records for effects of sire-line, dam-line, test, hen density and HRT (henhouse-row-tier) using estimates from Model 1,

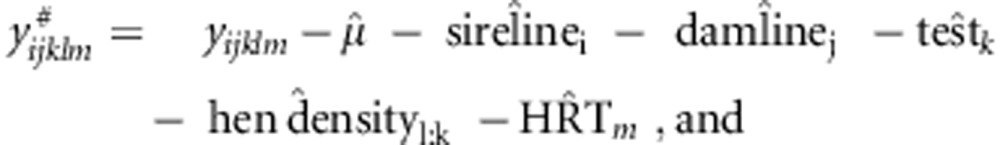There are two issues in relation to y^#. First, the correction factors in the expression for y^#_ijklm were estimated from Model 1, which includes the SDAF term. Under a dominance hypothesis, therefore, y^# is an estimate of heterosis, rather than of SCA (see Discussion and Supplementary Information for more details). Second, to obtain independent estimates for correction, Model 1 was fitted separately for each of the crosses, and each time the cross for which observed heterosis was to be calculated was omitted from the data set. Thus, correction factors for each cross were obtained without using data on that cross, so as to avoid that correction factors would be biased towards the data to be validated. As we had 47 crosses, we obtained 47 different sets of factors for correction, each based on data of 46 crosses.

Finally, accuracy was taken as Pearson's correlation between observed and predicted heterosis.

Cross validation

The measure of accuracy presented above describes the fit for the current data set, but may not reflect the accuracy of predicted heterosis in an independent data set. To investigate the accuracy with which a cross that was not in the data set could be predicted, we performed a ‘leave-one-cross-out' cross-validation, in which one cross at a time was left out of the estimation of β. As we had 47 crosses in our data set, this resulted in 47 different estimates of the regression coefficient, 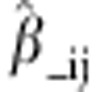, for each trait. We then predicted heterosis for each i × j cross that had been left out as:

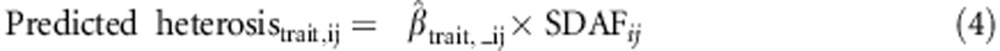where 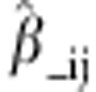is the estimated regression coefficient when the i × j cross is omitted from the training data set. Accuracy was taken as Pearson's correlation between observed (y^#) and predicted heterosis. To quantify the bias of SDAF as a predictor of heterosis, we also calculated the regression coefficient of observed heterosis on both the ‘regular' (equation 2) and cross-validated predictions (equation 4).

Selection of crosses based on predicted heterosis

To quantify the benefits of selecting crosses based on genomically predicted heterosis, we considered a two-step selection process. In the first step, heterosis was predicted for all crosses, and a subset of crosses was selected based on the prediction. In the second step, only crosses selected in the first step were field-tested and a final selection was made based on the observed (that is, true) heterosis and hybrid performance. Compared with a selection based entirely on observed/true heterosis, this two-step selection will yield lower heterosis after the final selection, because the truly best cross may have been discarded based on predicted heterosis in the first step.

The methodological problem is to predict true heterosis after the two-step selection, as a function of the selected proportion in the first step. To enable prediction, we assumed that the predicted and observed heterosis approximately follow a bivariate normal distribution. Then the standardized response in true heterosis after the two-step selection can be obtained from the moment generating function of the truncated bivariate normal distribution (Tallis, 1961), and is given by:

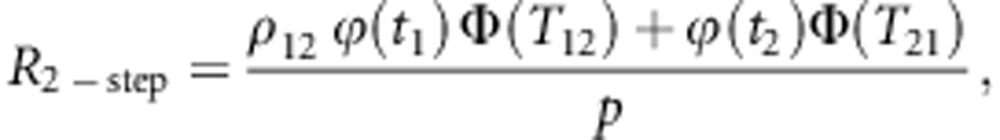where t₁ is the standardized truncation point applied in the first step of selection, t₂ is the standardized truncation point used in the second step (relative to the original distribution), p=p₁p₂ is the overall selected proportion (10% in Figure 4), ρ₁₂ is the correlation between both normal variates (that is, the accuracy of predicted heterosis), 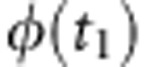is the standard univariate normal density function evaluated at t₁, Φ(T₁₂) is the (cumulative) univariate normal distribution function evaluated at T₁₂, and

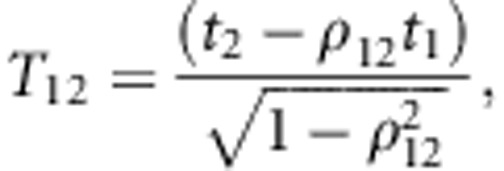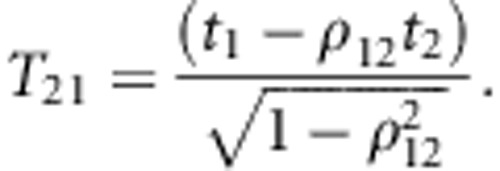The standardized maximum response in heterosis, that is, heterosis obtained when the selection is based entirely on true heterosis, so that p₁=1 and p₂=p, is given by:

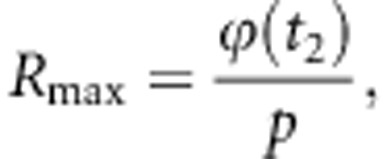where t₂ is the standardized truncation point belonging to a selected proportion p in a univariate normal distribution. Finally, the proportion of maximum heterosis obtained in a two-stage selection is given by:

Application of the expressions for R_2-step and R_max requires values for the truncation points t₁ and t₂ corresponding to the selected proportions p₁ and p₂ of a bivariate standard normal distribution with correlation ρ₁₂. Those can be obtained using algorithms for the integration of multivariate normal distributions, such as the Dutt's algorithm (Dutt, 1973, Ducrocq and Colleau, 1986). From the %R_max, we calculated the amount of heterosis lost due to preselecting animals based on genomically predicted heterosis as %loss=100%−%R_max.

Results

Descriptive statistics

Table 1 shows the means and number of records per cross for egg number, egg weight and survival days.

Egg number

Egg numbers ranged from 150.9 to 375.3 eggs, with a mean of 334.7 eggs (s.d.=18.2), which translates to an average of 0.83 eggs per hen per day over the entire laying period. The S5 × D3 cross had the highest mean of 343.6 eggs, whereas the D5 × D6 cross had the lowest of 294.7 eggs. Egg number had a markedly skewed distribution (not shown).

Egg weight

Records ranged from 48.6 to 76.7 g, with a mean of 61.4 g (s.d.=2.7). The D5 × S5 cross had the highest mean egg weight of 64.1 g, whereas the S4 × D6 cross had the lowest of 60 g. Egg weight records were normally distributed (not shown).

Survival days

Records ranged from 240 to 620 days, with a mean of 548.4 days (s.d.=34.5). Mortality was relatively low, with 89.6% of the hens (cage averages) surviving till the end of the production period used in this study (from 100 to 504 days). The D4 × S2 hens had the highest record of 583.2 days, whereas the lowest survival record was 503.6 days for D5 × D6 hens. Survival days had a negatively skewed distribution (not shown).

Difference in allele frequency between parental lines

Table 2 shows the SDAFs for all crosses. Of the 47 crosses for which we had phenotypic records, the lowest SDAF was 0.05 for D5 × D6, and the highest was 0.113 for S4 × D1. SDAFs between lines that were both dam-lines were slightly lower (mean=0.075) than for those between sire-line × dam-line (mean=0.084) and sire-line × sire-line (mean=0.088).

Table 2. Squared differences in allele frequencies (SDAFs) between white Leghorn pure lines.

	S1	S2	S3	S4	S5	D1	D2	D3	D4	D5	D6
S1		0.004	0.095	0.094	0.082	0.089	0.082	0.072	0.085	0.082	0.073
S2			0.094	0.094	0.080	0.085	0.080	0.070	0.083	0.079	0.071
S3				0.105	0.099	0.112	0.095	0.091	0.098	0.101	0.090
S4					0.085	0.113	0.092	0.089	0.089	0.101	0.085
S5						0.103	0.056	0.060	0.058	0.089	0.057
D1							0.096	0.078	0.096	0.048	0.068
D2								0.032	0.029	0.083	0.061
D3									0.041	0.066	0.055
D4										0.081	0.060
D5											0.050
D6

SDAFs in bold font represent those for which phenotypes were available. In some cases, reciprocal crosses were made, so although the bold SDAFs are 35 in number, we actually had phenotypes for 47 crosses. Because reciprocal crosses had the same SDAF, only the upper diagonal is presented.

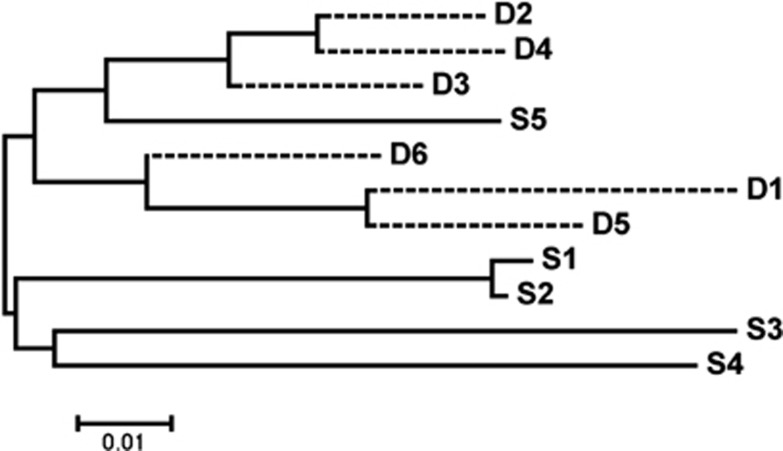
Figure 1 shows a phylogenetic tree of the 11 white Leghorn pure lines used in this study. The first branch clearly shows the separation of the sire-lines (solid lines) from the dam-lines (dashed lines), which is expected because sire- and dam-lines are selected and bred for different traits. The only sire-line that was grouped together with the dam-lines was the S5 line; however, it branched off from the dam-lines relatively early, still making this sire-line distinct from the dam-lines. The most closely related sire-lines were S1 and S2, they share the most recent common ancestor than any other two lines. The most closely related dam-lines were D2 and D4. This pattern of relatedness corresponds with the SDAF values in Table 2.

Figure 1.

 Phylogenetic tree for the 11 white Leghorn pure lines in our study based on Nei's standard genetic distance calculated from allele frequencies of 53 582 SNPs. Dashed-lines represent dam-lines and solid-lines represent sire-lines.

Predicted heterosis

Table 3 shows the estimated regression coefficients for SDAF from the full data, their standard errors (s.e.) and P-values for egg number, egg weight and survival days. All fixed effects in the models were significant (P<<0.05, results not shown).

Table 3. Estimated regression coefficients (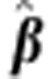) of egg number, egg weight and survival days on SDAF, s.e.'s and P-values.

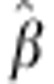
Trait		s.e.(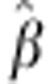)	P value
Egg numbera	103.5	16.8	7.07 E−10
Egg weight	22.3	2.2	2.35 E−19
Survival days	−42.06	25.9	1.04 E−01

^aEstimates for egg number are on the original (untransformed) scale. The P-value on the transformed scale=6.76 E−11.

The estimated regression coefficient of egg number on SDAF was 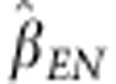=103.5, showing a positive and highly significant association between SDAF and egg number. Thus, parental lines with larger SDAFs produce offspring with higher levels of heterosis for egg number. Of the 47 crosses in our study, the lowest predicted heterosis was 5.2 eggs for D5 × D6 and the highest was 11.7 eggs for S4 × D1. When we include SDAFs of potential crosses but of which no phenotypic data were available (see Table 2), the range of predicted heterosis is much wider (0.4–11.7 eggs), showing that some of the crosses with lower predicted heterosis were not part of our data set.

The estimated regression coefficient of egg weight on SDAF was 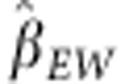=22.3, showing a positive and highly significant association between SDAF and egg weight. From the 47 crosses in our data set, the lowest predicted heterosis was 1.1 g for D5 × D6 and the highest was 2.5 g for S4 × D1.

The estimated regression coefficient of survival days on SDAF was negative, but not significantly different from zero (P=0.104). Results for survival days will therefore not be presented further.

Accuracy of predicted heterosis

Correlation between observed and predicted heterosis

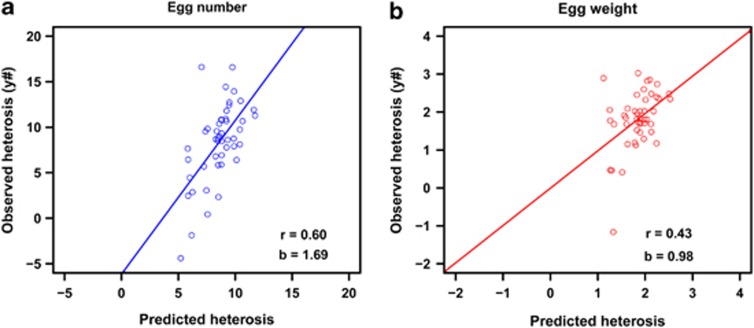
Figure 2 shows correlations between observed and predicted heterosis for egg number (2a) and egg weight (2b). The correlation between observed and predicted heterosis was 0.60 for egg number and 0.43 for egg weight.

Figure 2.

 Observed (y^#) vs predicted heterosis for egg number (a) and egg weight (b). r=Pearson's correlation between observed (y^#) and predicted heterosis; b=regression coefficient of observed (y^#) on predicted heterosis. The line represents the regression of observed on predicted heterosis.

Cross-validation

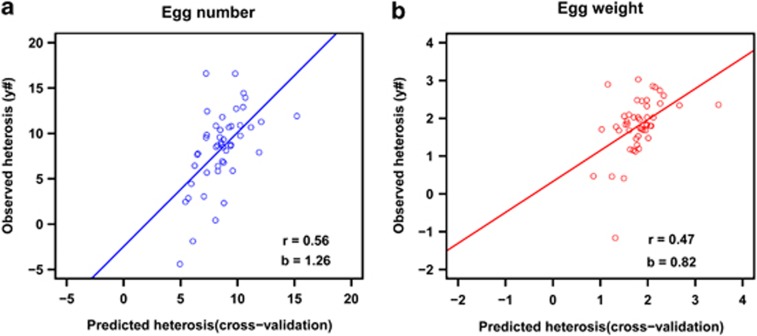
For egg number, the estimates of β in the leave-one-cross-out cross-validation ranged from 73.1 when the S5 × D5 cross was omitted to 135.3 when the S3 × D1 cross was omitted. Despite the large number of crosses included, the large fluctuations in the estimated regression coefficients imply high dependence on which crosses are present in the training data set. Figure 3a shows plots of observed vs cross-validated predicted heterosis for egg number. The correlation was 0.56, which is slightly lower than the correlation for the ‘regular' predictions (Figure 2a).

Figure 3.

 Observed (y^#) vs cross-validated predicted heterosis for egg number (a) and egg weight (b). r=Pearson's correlation between observed (y^#) and cross-validated predicted heterosis; b=regression coefficient of observed (y^#) on cross-validated predicted heterosis. The line represents the regression of observed on cross-validated predicted heterosis.

For egg weight, the estimates of β in the leave-one-cross-out cross validation ranged from 11.5 when the S5 × D5 cross was omitted to 33.9 when the S5 × D1 cross was omitted. As with egg number, there were large fluctuations in the estimated regression coefficients. Figure 3b shows plots of observed vs cross-validated predicted heterosis for egg weight. The correlation was 0.47, which is slightly higher than that for the ‘regular' predictions (Figure 2b). For both traits, the lowest regression coefficient was obtained when the S5 × D5 cross was omitted.

Bias in predicting heterosis

The regression coefficient of observed on ‘regular' predicted heterosis was 1.69 for egg number and 0.98 for egg weight. That for the cross-validated predicted heterosis was 1.26 for egg number and 0.82 for egg weight. This indicates that the differences in heterosis between crosses were under-predicted for egg number and over-predicted for egg weight.

Selection of crosses based on predicted heterosis

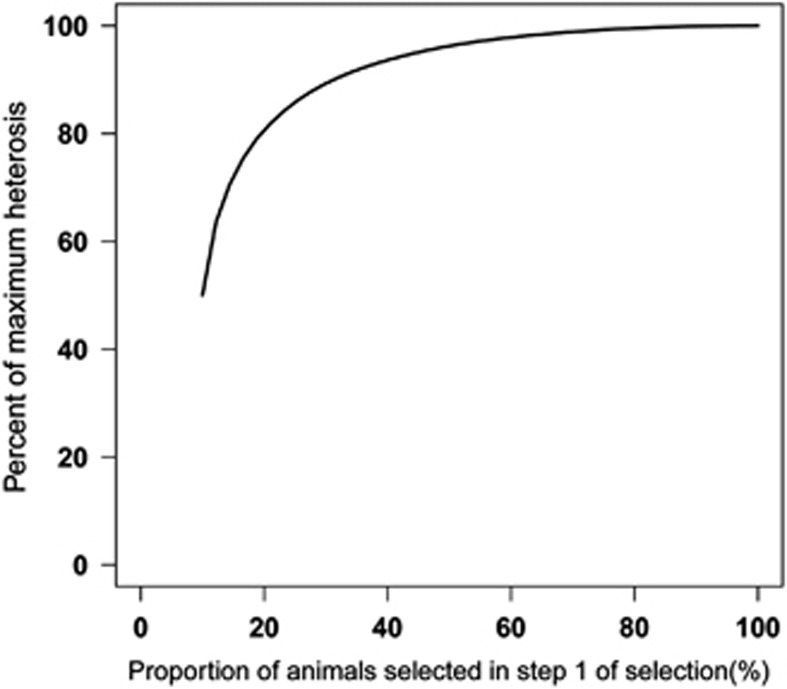
Figure 4 shows a plot of the per cent of maximum heterosis (%R_max, equation 5) as a function of the proportion of animals selected in the first step of the two-step selection. Results show that considerable preselection can be applied with little loss of heterosis in the final selection. For example, when the top 50% crosses with the highest genomically predicted heterosis are selected in the first step, the resulting heterosis equals 96% of the heterosis that could have been obtained by field-testing all potential crosses. Hence, a 50% cost saving (on field-testing) can be achieved with only 4% loss in heterosis.

Figure 4.

 Percent of maximum heterosis exploited in a two-step selection program as a function of the proportion of animals selected in step 1. In step 1 animals are selected based solely on predicted heterosis (accuracy of prediction=0.5). In step two the pre-selected animals are field-tested and a final selection is made based on true/observed heterosis. The overall proportion of selected animals is 10% (see Materials and Methods).

Discussion

We investigated whether the SDAF between parental lines predicts heterosis in egg number, egg weight and survival days in domestic white Leghorn crosses, using data on ∼400 000 individuals from 47 crosses and allele frequencies on ∼53 000 SNP loci spread across the genome. Moreover, we quantified the accuracy of this prediction using cross-validation methods. Results show that SDAF predicted heterosis for egg number and egg weight with an accuracy of ∼0.5, whereas SDAF did not predict heterosis for survival days in our data.

Magnitude of heterosis

Predicted heterosis for egg number ranged from 5.2 to 11.7 eggs for the 47 crosses in our study. Though the difference of 6.5 eggs between highest and lowest predicted heterosis may seem small, it equals two to three generations of response to selection, corresponding to∼4–6 years in a practical layer breeding programme (personal communication Jeroen Visscher, ISA poultry breeders). Moreover, when considering all possible combinations of sire-lines and dam-lines, predicted heterosis ranged from 0.4 to 11.7 eggs. For egg weight, predictions ranged from 1.1 to 2.5 g for the 47 crosses in our study, and from 0.09 to 2.5 g when all possible crosses were considered. Our results agree with the findings of Gavora et al. (1996) and Haberfeld et al. (1996), who found that heterosis for egg production traits and body weight in white Leghorns increases with GD estimated from DNA fingerprints. They did not, however, state the range of predicted heterosis, which could have served as a basis of comparison for our estimates.

We did not find a significant effect of SDAF on survival days (P=0.104). Two factors may account for this result. First, the limited variation in survival days: as most hens survived until the end of the testing period, there were many right-censored records. The censoring was not accounted for in the linear model we used (Model 1). A survival analysis model could have accounted for this, but would have required individual survival records which were not available (cage-means were used). Second, when fitting a sire-line × dam-line interaction in the model, this effect turned out to be very small, suggesting that heterosis for survival days under the current housing conditions and recording period is small, and thus difficult to estimate.

Accuracy of predicted heterosis

In general, the accuracy of heterosis prediction obtained in this study was moderate for both traits (∼0.5). We cannot clearly compare these accuracies with those reported in previous research in this area, because they reported accuracies as correlations between observed heterosis and GD obtained from the fit of the model, and one study (Gavora et al., 1996) also reported R² values of their prediction models. To our knowledge, none of the studies that predicted heterosis based on the molecular marker divergence of parental lines have reported correlations between observed and predicted heterosis, or performed cross-validation.

Judging the prediction of heterosis based on the fit of the model, that is, by using correlations between observed values and values predicted from the same rather than independent data, may overestimate the accuracy of prediction. To investigate this issue, we calculated the correlation between predicted heterosis and observed heterosis when both were estimated from a single analysis on the full data. This resulted in an accuracy of predicted heterosis of 0.72 for egg number and 0.61 for egg weight. These values are clearly higher than accuracies obtained when either y^# (Figure 2) or both y^# and β (Figure 3) were estimated from independent data. Hence, the accuracy of predicted heterosis based on the fit of the model overestimates the accuracy with which future crosses can be predicted.

In the present study we have used the SDAF averaged overall SNPs. To increase the accuracy of predicted heterosis, it has been suggested to preselect ‘significant' markers instead of using all markers for prediction (Gavora et al., 1996; Shen et al., 2006). Results from studies on genomic selection and genome-wide association studies, however, point towards a highly polygenic nature of many traits in livestock. If those results extend to dominance effects, it will be difficult to identify the relevant loci and estimate their contribution to heterosis. Nevertheless, the use of genome-wide marker information together with methods for genome-wide evaluation (also known as ‘genomic selection' Meuwissen et al., 2001) may enable more accurate prediction of heterosis in the future.

Selection of crosses based on predicted heterosis

An interesting question for practical applications of the prediction of heterosis in breeding programmes would be how well one can predict future crosses. To address this question, we performed a cross-validation using Model 1, where heterosis for each cross was predicted using a regression coefficient estimated from data that excluded that cross. Note that observed heterosis (y^#) for each cross was also obtained by correcting observations for the model effects, where model effects were estimated by leaving out the cross of interest. Hence, both predicted heterosis and y^# for each cross were obtained without making use of the data on that cross. Finally, the accuracy of prediction was calculated as the correlation between predicted heterosis and y^#, resulting in a value of ∼0.5 for both egg number and egg weight (Figure 3). With this accuracy, considerable preselection can be performed based on predicted heterosis with limited loss of total heterosis. Figure 4 shows that by reducing the amount of field-testing by about 50%, the loss in total heterosis would only be 4%. This would significantly reduce the cost of field-testing in crossbreeding programs.

Heterosis vs combining ability modelling

The true heterosis for a particular cross is defined as the mean phenotype of the cross expressed as a deviation from the mean of both parental lines; it does not depend on other crosses that may or may not be included in the analysis. In contrast, the true general combining ability (GCA) of a line and the true SCA of a particular cross do depend on which lines are included in the analysis (Hallauer et al., 2010). This occurs because SCA is defined as a statistical interaction-term, which is zero on average by virtue of the model. Consequently, in a GCA/SCA model, the average heterosis in the data is included in the main-effects of the model, which are the GCA-estimates. Thus, the estimates of GCA and SCA will change when crosses are added or removed from the analysis, even when the model fits the data perfectly.

The dependency of GCA/SCA-estimates on the set of crosses included causes fluctuation of estimates when breeding companies evaluate additional crosses. Moreover, the genetic basis of combining ability is complex, even under a simple dominance hypothesis. Although the true values of GCA and SCA can be derived for a single locus model, the result is a complex function of additive and dominance effects and the allele frequencies of the lines included in the analysis. Heterosis, in contrast, has a simple genetic basis under a dominance hypothesis, in which case it is proportional to SDAF. We therefore opted for a heterosis model in this study.

To calculate the accuracy of predicted heterosis, we required a measure of observed heterosis. However, we were faced with the problem that data on the pure lines were available only on individuals kept in high quality breeding environments, and no crossbred records were available from those environments. Thus, pure-bred performance was fully confounded with environment, so that we could not calculate classical observed heterosis. This is a common problem in heterosis studies in livestock: large data sets are available only within breeding companies, in which purebred and crossbred individuals are usually kept in environments that are systematically different.

In the current study, we addressed this issue by hypothesising that heterosis is solely due to dominance and that the dominance effect at a locus is independent of the SDAF at that locus. Under those two assumptions, heterosis is proportional to the SDAF between both parental lines, averaged over loci. (See Falconer and Mackay, (1996), and the derivation in Materials and Methods). Under these assumptions, therefore, the estimate of the β × SDAF term in Model 1 is an estimate of heterosis, and 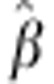is an estimate of n_lociE(d). Consequently, because the β × SDAF term is included in Model 1, the estimates of the sire-line and dam-line effects from Model 1 are estimates of the pure-line values, rather than of GCA. We confirmed this finding by analysing simulated data in which heterosis was due to dominance. 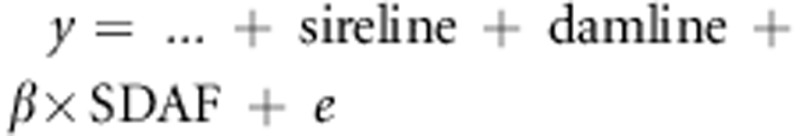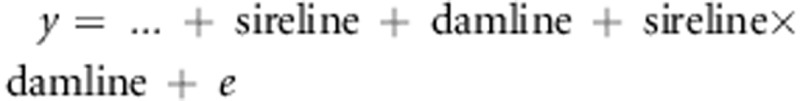Thus, under the hypothesis that heterosis is solely due to dominance, a model yields estimates of pure-line averages and heterosis, whereas a model yields estimates of GCA and SCA. Hence, with Model 1, we could model heterosis even though we did not have phenotypes of the pure lines. To further clarify that Model 1 yields estimates of pure-line values and heterosis, rather than of combining abilities, we constructed a three-locus model in an Excel file which is available as Supplementary Information with this manuscript. This file also illustrates the difference between a heterosis model and a GCA-SCA-model, particularly when a diallel-cross is incomplete.

At first glance, one might expect that estimating sire and dam effects from a model y=…+ sire-line+dam-line+e, and subsequently defining observed heterosis as 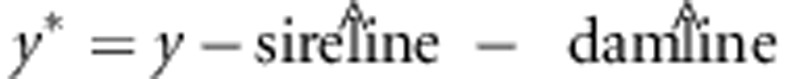would give similar results as using y^# as observed heterosis. We, however, observed that y* shows much lower correlation with predicted heterosis than with y^#. Correlations of predicted heterosis with y* were only 0.32 for egg number and 0.02 for egg weight, whereas correlations with y^# were 0.56 and 0.47, respectively, (using values from the cross-validation). Note that the higher accuracies for y^# are not an artefact of model fitting, as we used independent data for estimating both y^# and β in the cross-validation. The difference in accuracy occurs because correction factors used for y* come from a combining ability model, so that y* is an estimate of SCA rather than heterosis. The higher accuracies found for y^# than for y* illustrate the benefit of using a statistical model that has a solid genetic basis.

We based our modelling approach on the hypothesis that heterosis is due to dominance. If that assumption is true, one would not expect 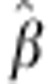to fluctuate significantly when leaving out one cross at a time in the cross-validation. However, 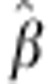for egg number ranged from 73.1 to 135.3, and 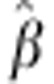for egg weight ranged from 11.5 to 33.9 in the cross validation. 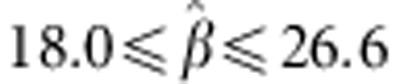For comparison, the 95% confidence interval for the estimated regression coefficient from the full data was for egg number and for egg weight. The fluctuation in 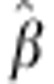suggests that dominance does not fully explain heterosis in our data, particularly for egg weight. Gavora et al., (1996) also found that heterosis predicted with a dominance model was more accurate for egg number than for egg weight. Fairfull et al., (1987), in contrast, reported that heterosis in egg weight ‘closely approximated that expected due to dominance alone'. Although dominance may not have fully explained heterosis in our data, the dominance hypothesis allowed us to estimate observed heterosis and to achieve a considerably higher accuracy of predicted heterosis than with a combining ability model (see results for y^# vs y* in the previous paragraph).

The complexity of modelling heterosis shows that further research is needed before scientists can reach a consensus on the genetic bases of heterosis. A review on the study of heterosis by Chen (2010) gave the following reasons for the difficulty of modelling heterosis: (1) epistatic effects are difficult to explain with statistical models; (2) heterosis is affected by genetic backgrounds; (3) the role of paternal and maternal effects of genetic loci; and (4) the fact that heterosis is affected by many genetic loci, each with differing contributions. In support of the need for further research, Kaeppler (2012) states that ‘the final answer to the basis of heterosis will be the accumulation of results of many and diverse studies and not a singular, unifying, novel discovery'.

GD and SDAF

The prediction of heterosis based on the molecular marker information from pure lines has been studied extensively in both plants and animals. Approaches reported in the literature are (1) the regression of either hybrid performance or heterosis on molecular GD, and/or the estimation of correlations between those variables (Gavora et al., 1996; Haberfeld et al., 1996; Cheres et al., 2000; Minvielle et al., 2000; Jordan et al., 2003; Dias et al., 2004; Balestre et al., 2009; Gärtner et al., 2009) or (2) the estimation of marker effects or associations of markers with hybrid performance, heterosis or SCA (Vuylsteke et al., 2000; Gärtner et al., 2009). Although some of these studies mentioned the theory that heterosis is proportional to SDAF between the parental populations (Falconer and Mackay, 1996), they rather used various measures of GD as predictors of heterosis, without theoretical justification. Only Reif et al. (2003), who used the square of modified Roger's distance, stated that it is linearly related to SDAF, and thus yields equivalent predictions of heterosis.

We therefore investigated the similarity between SDAF and GD by calculating Pearson's correlations between SDAF and the commonly used measures of GD: Nei's, Rogers', modified Rogers' and Cavalli-Sforza (Cavalli-Sforza and Edwards, 1967, Nei, 1972, Wright, 1984). Correlations between the GDs as well as with SDAF were >0.98, indicating that the ranking of pure-line combinations is very similar for all measures. Furthermore, we investigated the accuracy of predicted heterosis using the GD showing the lowest correlation with SDAF (Roger's and modified Roger's distance; both had correlation=0.98), and found almost identical results as with SDAF. Hence, whether heterosis is predicted using GD or SDAF does not appear to be crucial. Nevertheless, for reasons of scientific consistency, the use of SDAF is to be preferred because the relationship between heterosis and SDAF has a sound theoretical basis.

Data archiving

Data are available upon request. Contact Jeroen Visscher by email: Jeroen.Visscher@hendrix-genetics.com.

The authors declare no conflict of interest.