Magnitude and control of mitochondrial sensitivity to ADP

Abstract

The transduction function for ADP stimulation of mitochondrial ATP synthesis in skeletal muscle was reconstructed in vivo and in silico to investigate the magnitude and origin of mitochondrial sensitivity to cytoplasmic ADP concentration changes. Dynamic in vivo measurements of human leg muscle phosphocreatine (PCr) content during metabolic recovery from contractions were performed by ³¹P-NMR spectroscopy. The cytoplasmic ADP concentration ([ADP]) and rate of oxidative ATP synthesis (Jp) at each time point were calculated from creatine kinase equilibrium and the derivative of a monoexponential fit to the PCr recovery data, respectively. Reconstructed [ADP]-Jp relations for individual muscles containing more than 100 data points were kinetically characterized by nonlinear curve fitting yielding an apparent kinetic order and ADP affinity of 1.9 ± 0.2 and 0.022 ± 0.003 mM, respectively (means ± SD; n = 6). Next, in silico [ADP]-Jp relations for skeletal muscle were generated using a computational model of muscle oxidative ATP metabolism whereby model parameters corresponding to mitochondrial enzymes were randomly changed by 50–150% to determine control of mitochondrial ADP sensitivity. The multiparametric sensitivity analysis showed that mitochondrial ADP ultrasensitivity is an emergent property of the integrated mitochondrial enzyme network controlled primarily by kinetic properties of the adenine nucleotide translocator.

the metabolic regulation underlying energy balance in mammalian cells has long been the subject of investigation, in particular regulation of mitochondrial ATP synthesis (1). At first, a relatively straightforward picture emerged from studies in isolated mitochondria; a feedback control loop involving transduction of changes in the extramitochondrial concentrations of the ATP hydrolysis products ADP and P_i to the intramitochondrial ATP synthetic network during cellular work explained energy balance (10, 13). ³¹P-NMR spectroscopy (11) and computational modeling (28) later showed that mitochondrial sensing of concentration changes in ADP alone sufficed to explain energy balance in skeletal muscle. However, in cardiac muscle, near-constant phosphocreatine (PCr), and thereby ADP, concentrations were measured during work jumps (3). This observation led to the proposition of a second, if not alternative, mitochondrial metabolic control mechanism in excitable cells such as cardiac muscle, i.e., a feedforward control loop involving direct or indirect transduction of intracellular calcium concentration changes to the mitochondrial ATP synthetic network (1). More recently, yet another alternative respiratory control mechanism of particular relevance to energy balance in the heart has been identified (2). It involves a mix of feedforward and feedback kinetic effects of P_i on multiple reactions in the oxidative ADP phosphorylation pathway (7).

What has been relatively lacking for each of the postulated respiratory control signals, in particular calcium, is a thorough kinetic characterization of the corresponding mitochondrial transduction function f([X],Jp), where [X] is the extramitochondrial concentration of signal molecule X and Jp equals the rate of mitochondrial ATP synthesis. The need for explicit knowledge of these transduction functions in respiratory control model validation has recently become all the more pressing due to a surge in availability of computational models of mitochondrial oxidative metabolism that require proper validation criteria (4, 15, 31, 33, 42, 46). Of these wanting kinetic functions, the transduction function f([ADP],Jp) has been investigated most thoroughly (10, 13, 17, 23, 24, 29). Characterized initially as “approximately hyperbolic” with a “K_m” in the range of 20–30 μM (10, 13), it was later reported that this function is in fact sigmoidal with an apparent kinetic order of at least two (24). Two independent studies have since, albeit indirectly, confirmed the non-Michaelis-Menten (MM) nature of the ADP stimulation of mitochondrial ATP synthesis (14, 45).

According to Koshland et al.'s (27) classification of biological sensory systems, a sigmoidal ADP transduction function with a Hill coefficient (n_H) >1 would indicate that mitochondria are ultrasensitive to variations in extramitochondrial ADP concentration changes. Normal sensitivity was defined as the sensitivity corresponding to a hyperbolic input-output function such as in MM kinetics (i.e., n_H = 1) (27). Importantly, mitochondrial ultrasensitivity, but not normal sensitivity to ADP, was shown to explain energy balance by feedback respiratory control for a range of mammalian cell types, including skeletal and cardiac muscle (24). However, the hypothesis of mitochondrial ADP ultrasensitivity has generally not been embraced. Quantitative formalisms based on MM kinetics of ADP stimulation of mitochondrial ATP synthesis have continued to be used in the field of muscle energetics to evaluate mitochondrial function on the basis of ³¹P-NMR spectroscopy measurements (34). A possible explanation may be the lack of any verified mechanistic basis for second-order kinetic behavior of ADP stimulation of mitochondria. Non-MM kinetics of ATP/ADP exchange across the inner membrane catalyzed by the adenine nucleotide translocator (ANT) has been proposed but not confirmed as the origin of mitochondrial ADP ultrasensitivity (24).

Here, the magnitude and control of mitochondrial ADP sensitivity are investigated further. We collected multiple high-time resolution ³¹P-NMR spectroscopy data sets on PCr concentration dynamics in human muscle during recovery from exercise to reconstruct the in vivo mitochondrial ADP transduction function with a high number of data points for accurate kinetic characterization. The result confirmed second-order kinetics of ADP stimulation of mitochondrial respiration. Next, we investigated the control of mitochondrial ADP sensitivity by conducting a network analysis of a computational model of mitochondrial oxidative ADP phosphorylation in muscle (46). Hereto, a multiparametric sensitivity analysis (MPSA) was performed, which involved generation of multiple random sets of parameter values for all mitochondrial enzymes in the model followed by reconstruction and characterization of the mitochondrial ADP transduction function for each set. The results indicated that mitochondrial ADP ultrasensitivity is an emergent property of the integrated mitochondrial metabolic network determined primarily by the kinetic properties of the ANT.

MATERIALS AND METHODS

Reconstruction and Analysis of the In Vivo Mitochondrial ADP Transduction Function in Muscle

Subjects.

Six healthy normally active subjects (4 males, 2 females; mean age ± SD 31 ± 12 yr) participated in the study. The nature and the risks of the experimental procedures were explained to the subjects, and all gave their written informed consent to participate in the study, which was approved by the local Medical Ethics Committee of the Máxima Medical Center, Veldhoven, The Netherlands.

³¹P-magnetic resonance spectroscopy.

³¹P-magnetic resonance spectroscopy (MRS) was performed at 1.5 Tesla (Gyroscan S15/ACS; Philips Medical Systems, Best, The Netherlands), as described previously (41). Briefly, after localized shimming, ³¹P signals were collected using a 6-cm-diameter surface coil placed over the m. vastus lateralis (spectral width, 2,000 Hz; no. of data points, 1,024). From the dimension of the coil and the size and geometry of a typical upper leg, it was estimated that the majority of the signal in the unlocalized ³¹P-MRS measurements originated from the m. vastus lateralis, with minimal contaminations from the adjacent m. rectus femoris and underlying m. vastus intermedius. Spectra were acquired during a rest-exercise-recovery protocol, with a repetition time of 3 s and 2 scans yielding a time resolution of 6 s. The first 20 spectra (2 min) were measured at rest, after which the subjects started the exercise. Exercise consisted of dynamic, single-leg extensions every 1.5 s in the supine position using a home-built MR compatible ergometer (41). The initial workload varied per subject and ranged between 7.5 and 12.5 W. This level was maintained for the first minute, and the workload was then increased by 5 W each minute. Subjects performed exercises of different durations, and eight to 12 data sets were collected per subject during four to eight different sessions, with ≥15 min rest between different protocols within one session. The position of the ³¹P surface coil was marked on the leg during the first session, and the coil was placed at the same location in subsequent sessions.

³¹P-MRS data analysis.

Spectra were fitted in the time domain by using a nonlinear least squares algorithm (43) in the jMRUI software package (32), as described previously (41). PCr, P_i, and ATP signals were fitted to Lorentzian line shapes. Absolute concentrations of the phosphorylated metabolites were calculated after correction for partial saturation and assuming that [ATP] is 8.2 mM at rest (39). Intracellular pH was calculated from the chemical shift difference between the P_i and PCr resonances (38). All data sets had an end-exercise pH of ≥6.7. The free cytosolic ADP concentration ([ADP]) was calculated from pH and [PCr] using a creatine kinase equilibrium constant (K_eq) of 1.66 × 10⁹ M⁻¹ (30) and assuming that 15% of the total creatine is unphosphorylated at rest (8), using the following equation (Eq. 1):

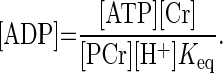(1)

The molar free energy of cytosolic ATP hydrolysis was calculated according to Eq. 2,

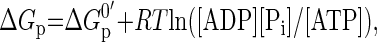(2)

where ΔG_p^0′ is −31.8 kJ/mol at 37°C (21).

The PCr recovery time course, PCr(t), was fitted to a monoexponential function (Eq. 3):

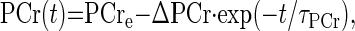(3)

where PCr_e is the PCr level after recovery, ΔPCr is the difference between the PCr levels after recovery and at the end of exercise, and τ_PCr is the time constant for PCr resynthesis. The PCr resynthesis rate at time t [V_PCr(t)] was calculated from the derivative of the fitted PCr recovery time course (Eq. 3). During recovery from exercise, PCr is resynthesized purely as a consequence of oxidative ATP synthesis (35, 37, 38). Because the creatine kinase reaction is much faster than oxidative ATP production (45), V_PCr(t) reflects mitochondrial oxidative phosphorylation flux. Covariations of V_PCr(t) with thermodynamic (ΔG_p) and kinetic ([ADP]) adenine nucleotide concentration functions were analyzed by nonlinear curve fitting of a Hill function of the form (Eq. 4):

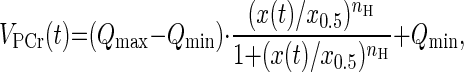(4)

with Q_max and Q_min the maximal and minimal net ADP phosphorylation fluxes¹ , x_0.5 the ΔG_p or [ADP] value at half-maximal V_PCr, and n_H the Hill coefficient (24). This analysis was performed for each subject separately, using the pooled data from all the exercise protocols of that subject (8–12 data sets/subject). Only data points with V_PCr(t) > 0.02 mM/s were included in the analysis. All nonlinear curve fitting was performed using Matlab (version 7.3; Mathworks, Natick, MA).

Statistical analysis.

All data are expressed as means ± SD. Statistical analyses were performed using the SPSS 15.0 software package (SPSS, Chicago, IL). Because of the small number of subjects, the nonparametric Wilcoxon signed-rank test was used for paired comparisons of the data. The level of significance was set at P < 0.05.

Simulation and Analysis of In Silico Mitochondrial ADP Transduction Functions in Muscle

The computational model of skeletal muscle oxidative ATP metabolism featuring a detailed biophysical model of mitochondrial oxidative ADP phosphorylation by Wu et al. (46) was used as platform for all in silico investigations of the origin of mitochondrial ADP ultrasensitivity. First, an analysis of the sensitivity of the macroscopic parameters Q_max, K₅₀, and n_H of in silico-reconstructed [ADP]-Jp relations for muscle toward 19 mitochondrial parameters in the Wu et al. (46) model was performed (Table 1). This particular set consisted of 15 mitochondrial parameters of which the value had previously been estimated by model fitting (denoted by Ref. 5c in Table 2 of Ref. 46) and four mitochondrial parameters (k_O2, K_m,ADP, θ, and β, respectively) of which the value had been taken from a computational model (denoted by Ref. 26 in Table 2 of Ref. 46). The design of this MPSA was based on methods described elsewhere (47), including statistical analysis (20). Next, the MPSA results were used to investigate whether any set of model parameter values that would give rise in silico to mitochondrial ADP ultrasensitivity existed. Hereto, the model was fitted to an in vivo [ADP]-Jp data set from an individual muscle, whereby only model parameters with a significant Kolmogorov-Smirnov (K-S) test score in the MPSA (see below) were varied.

Table 1.

Overview of the mitochondrial model parameters tested in the multiparametric sensitivity analysis of the Wu et al. (46) model of oxidative ATP metabolism in muscle

Parameter No.	Model Parameter	Description
1	R	Dehydrogenase parameter
2	kPi,1	Dehydrogenase parameter
3	kPi,2	Dehydrogenase parameter
4	XDH	Dehydrogenase parameter
5	XC1	Complex I activity
6	XC3	Complex III activity
7	kPi,3	Complex III parameter
8	kPi,4	Complex III parameter
9	XC4	Complex IV activity
10	kO2	Complex IV parameter
11	XF1	F0F1-ATPase activity
12	XANT	ANT activity
13	Km,ADP	Michaelis constant ANT
14	θ	ANT parameter
15	kPiHt	H+/Pi− cotransporter parameter
16	XPiHt	H+/Pi− cotransport activity
17	XKH	K+/H+ antiporter activity
18	XHle	H+ leak activity
19	β	Mitochondrial matrix buffering capacity

ANT, adenine nucleotide translocator.

Table 2.

Results of the unconstrained curve fitting of Eq. 4 to the (ΔG_p, V_PCr) data for the 6 subjects

	Qmax, mM/s	Qmin, mM/s	ΔGp,0.5, kJ/mol	nH
Subject
1	0.81	−0.04	−58.1	24.9
2	0.76	−0.02	−58.9	25.9
3	0.69	−0.09	−58.8	21.8
4	0.70	−0.04	−57.9	23.5
5	0.86	−0.03	−57.8	23.8
6	0.65	−0.03	−57.9	22.7
Means ± SD	0.74±0.08	−0.04±0.02	−58.2±0.5	23.8±1.5

Q_max, maximal net phosphocreatine (PCr) resynthesis flux; Q_min, minimal net PCr resynthesis flux; ΔG_p,0.5, molar free energy of cytosolic ATP hydrolysis at half-maximal V_PCr; n_H, Hill coefficient.

MPSA

Generation of random sets of parameter values.

Multiple random samples were taken from a 50–150% range of the default value for each of the 19 kinetic parameters of the mitochondrial enzymes in the model (Table 1) plus five dummy parameters yielding multiple random sets of parameter values for simulation and analysis of in silico [ADP]-Jp relations for muscle. The introduction of dummy parameters in this analysis (but not in the model) was necessary to dissect the contribution of sensitive vs. insensitive model parameters in a particular set to any changes in Q_max, K₅₀, and n_H of the corresponding in silico [ADP]-Jp relation. An optimized Monte Carlo sampling scheme was used to sample from the multidimensional distribution while guaranteeing that individual parameter ranges were evenly covered. In this case, the parameters were sampled from a logarithmic uniform distribution within the defined range. The vectors containing the parameter samples were combined to obtain N parameter combinations. It was verified that the number of Monte Carlo runs, N, was sufficiently large to guarantee a good representation of all possible parameter value combinations (see below). The sampling and combination process was done with Latin hypercube sampling, whereby each parameter range was divided into N equally probable intervals from which only one sample was drawn. These samples were permuted and stored in a vector (with N samples for each parameter). Subsequently, these permuted vectors of all p parameters were combined in an N-by-p matrix. After the initial combination process, the minimum distance between the sample points was maximized. The Latin hypercube was generated using the function lhsdesign of the Statistics Toolbox from Matlab. The number of Monte Carlo runs (N) was 5,000.

Simulations.

The model was simulated for each set of parameter values and characterized with respect to the particular Q_max, K₅₀, and n_H of the corresponding in silico [ADP]-Jp relation by fitting of a three-parameter Hill function (Eq. 4 with Q_min set at 0; in this case, x_0.5 = [ADP]_0.5 = K₅₀). This particular Hill function rather than Eq. 4 was used for computational ease on the grounds that Q_min was very small compared with Q_max and not significantly different from 0 (see results and Table 2). To quantify the similarity of each of the simulations with respect to the reference simulation, the sum of squared differences was calculated as criterion function. Each set of parameter values was then classified as either “unacceptable” or “acceptable” by comparing the value of the criterion function to a certain threshold. Specifically, the set of parameter values was scored unacceptable if the criterion function value was greater than the threshold and acceptable in all other cases. The average value of the criterion function for the total ensemble of simulations was used as threshold value (20).

Sensitivity analysis.

The influence of each parameter on the model output was evaluated statistically using the K-S test (20). Hereto, the distributions of the individual parameter values associated with the unacceptable and the acceptable cases were compared. For each parameter, the cumulative frequency was calculated for all unacceptable and acceptable cases. The sensitivity is evaluated by a measure of the separation of the two cumulative frequency distributions. The K-S test for the ith parameter is represented as Eq. 5,

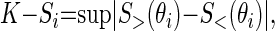(5)

where S_> and S_< are the cumulative frequency functions corresponding to unacceptable and acceptable cases, respectively, and θ_i is the parameter. The value of K-S is determined as the maximum vertical distance between the cumulative frequency distribution curves for n unacceptable and m acceptable cases, n + m = N. A larger K-S score indicates that the model is sensitive to variation in that parameter. The highest K-S score of the dummy parameters was used as threshold for statistical significance; i.e., parameters with a K-S score above the threshold were classified as sensitive. Finally, the K-S scores were summarized in a ranking of the sensitive parameters. This ranking was also used to verify that the number of Monte Carlo runs, N, was sufficiently large to guarantee a good representation of all possible parameter value combinations. For sufficiently large N, the ranking of the sensitive parameters is independent of the exact number of samples (47).

Model Fitting

To test whether any set of model parameter values existed that would give rise in silico to mitochondrial ADP ultrasensitivity, the model was fitted to an in vivo [ADP]-Jp data set from an individual muscle (subject 2) whereby only model parameters with a significant K-S score were adjusted. Model fitting was performed using a nonlinear least-squares optimization method employing the lsqnonlin algorithm in the parameter estimation toolbox in Matlab. Subsequently, in silico [ADP]-Jp covariations were computed for the model with the fitted parameter values and kinetically characterized by curve fitting of Eq. 4.

RESULTS

Reconstruction and Analysis of the In Vivo Mitochondrial ADP Transduction Function in Muscle

Figure 1 shows typical examples of ³¹P-MR spectra obtained from the vastus lateralis muscle of an individual subject 1) at rest (Fig. 1A), 2) at the end of exercise (Fig. 1B), and 3) at two time points during recovery (Fig. 1, C and D). Figure 2, solid line, shows the corresponding plot of the PCr concentration against recovery time together with the monoexponential fit of the recovery data. The PCr resynthesis rate was calculated from the derivative of the fitted PCr recovery time course for each time point sampled during recovery. For this particular population of six subjects, the maximal PCr resynthesis rate was 0.73 ± 0.05 mM/s. End-exercise ADP concentration (maximal) and molar Gibbs free energy of cytosolic ATP hydrolysis (lowest) were 86 ± 8 μM and −52.8 ± 0.4 kJ/mol, respectively.

Fig. 1.

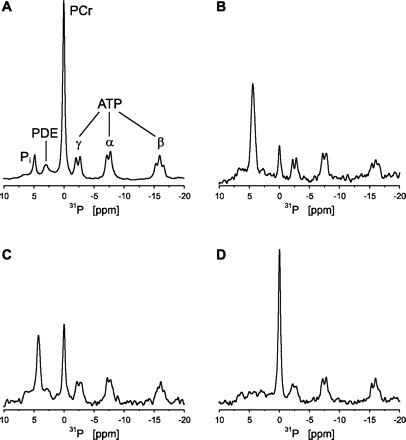
Typical m. vastus lateralis ³¹P-MR spectra for 1 subject at rest (A; no. of scans = 60), at the end of exercise (B: no. of scans = 2), and at 15 and 117 s of recovery (C and D, respectively; no. of scans = 2). Spectra were processed with 5 Hz line broadening. PDE, phosphodiesters; PCr, phosphocreatine. α, β and γ indicate the 3 phosphate groups of ATP. For this subject the PCr depletion at the end of exercise (B) was 81%, and the corresponding end-exercise pH was 6.72.

Fig. 2.

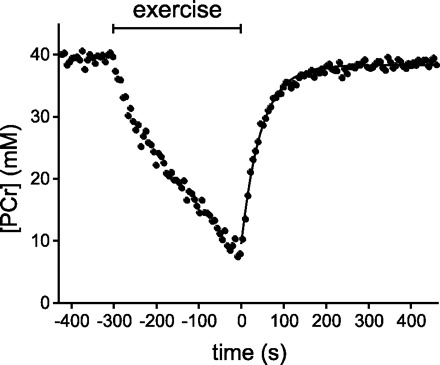
PCr concentration during rest, exercise, and recovery obtained from the corresponding data set shown in Fig. 1 (time resolution 6 s). The recovery of PCr (starting at t = 0) was fitted to a monoexponential function (solid line). The time constant for PCr recovery was 46.8 s.

To estimate the PCr resynthesis rate asymptotes Q_max and Q_min in the muscle cells, we analyzed the thermodynamic flow-force relation of PCr resynthesis (36, 40). This relation was characterized by unconstrained fitting of Eq. 4 to the (ΔG_p, V_PCr) data (Fig. 3). Almost the full range of sustainable energy balance states was covered by the experimental data points, resulting in accurate estimation of the flux asymptotes Q_max and Q_min (Table 2). The group mean value for ΔG_p at half-maximal V_PCr was −58.2 ± 0.5 kJ/mol.

Fig. 3.

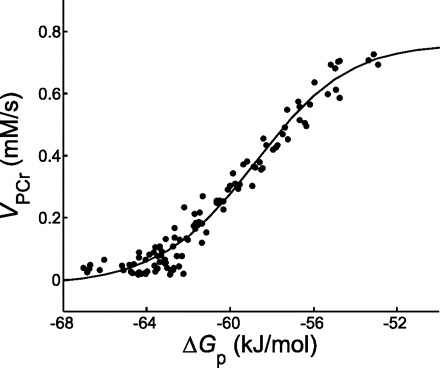
PCr resynthesis rate as a function of the molar free energy of cytosolic ATP hydrolysis (•) for an individual muscle (subject 2). The unconstrained, 4-parameter fit of Eq. 4 to the data is shown by the solid line.

The values for Q_max and Q_min determined from the thermodynamic flow-force relation were next imposed as constraints on the fit of Eq. 4 to the ([ADP], V_PCr) data (Fig. 4, solid line) to determine the apparent affinity and kinetic order of mitochondrial ADP sensing. The results of the analysis for each of the subjects studied are summarized in Table 3. Group mean values for [ADP]_0.5 and n_H were 22 ± 3 μM and 1.9 ± 0.2, respectively. Eq. 4 was also fitted to the ([ADP], V_PCr) data without imposing any constraints on the flux asymptotes (Fig. 4, dotted line, and Table 4). The fitted values for Q_max and Q_min were similar to the values obtained from the thermodynamic flow-force relation (Table 2), except for one muscle (subject 3). Fitted estimates of [ADP]_0.5 and n_H were not different from the values obtained from the constrained fit (Table 3). Last, the PCr resynthesis rate, V_PCr(t), was also correlated with the ADP concentration at each measurement point using a hyperbolic function (n_H = 1 in Eq. 4) corresponding to the classic MM ADP respiratory control model (12). The result for a single muscle is shown in Fig. 4 (dashed line). The MM ADP control model was incompatible with the experimental data at high flux values, causing overestimation of the maximal net PCr resynthesis flux Q_max [0.98 ± 0.13 vs. 0.74 ± 0.08 mM/s (Table 2), P < 0.05]. In addition, the MM ADP control model predicted a sevenfold higher net mitochondrial ATP hydrolysis rate at low ADP concentrations than the second-order control model [Q_min −0.27 ± 0.04 vs. −0.04 ± 0.02 mM/s (Table 2); P < 0.05].

Fig. 4.

PCr resynthesis rate as a function of ADP concentration (•) for an individual muscle (subject 2). Eq. 4 was fitted to the data: 2-parameter fit with maximal (Q_max) and minimal net ADP phosphorylation fluxes (Q_min) constrained to the values obtained from the thermodynamic flow-force relation (solid line), unconstrained 4-parameter fit (dotted line), and 3-parameter fit with Hill coefficient (n_H) constrained to 1 (dashed line).

Table 3.

Results of the curve fitting of Eq. 4 to the ([ADP], V_PCr) data for the 6 subjects with Q_max and Q_min constrained to the values obtained from the thermodynamic flow-force relation (Table 2)

	[ADP]0.5, μM	nH
Subject
1	25	1.9
2	19	2.1
3	18	1.7
4	23	1.9
5	24	1.8
6	22	1.7
Means ± SD	22±3	1.9±0.2

[ADP]_0.5, ADP concentration at half-maximal V_PCr.

Table 4.

Results of the unconstrained curve fitting of Eq. 4 to the ([ADP], V_PCr) data for the 6 subjects

	Qmax, mM/s	Qmin, mM/s	[ADP]0.5, μM	nH
Subject
1	0.78	−0.03	24	2.1
2	0.72	−0.03	18	2.3
3	0.62	−0.01	18	2.3
4	0.65	−0.05	21	2.0
5	0.83	−0.07	22	1.7
6	0.64	−0.05	21	1.7
Means±SD	0.71±0.09	−0.04±0.02	21±2	2.0±0.3

Simulation and Analysis of In Silico Mitochondrial ADP Transduction Functions in Muscle

MPSA.

The results of the MPSA are summarized in Fig. 5. The K-S scores with respect to the Q_max, ADP affinity (K₅₀), and n_H of the mitochondrial ADP transduction function for each of the 19 mitochondrial kinetic parameters and five dummy parameters (parameters 20–24; Table 1) are shown in Fig. 5, A, B, and C, respectively. The threshold score for significant sensitivity determined by the dummy parameter K-S scores (20) was 0.03–0.04 (Fig. 5, A–C). On this basis, all three macroscopic kinetic parameters of the mitochondrial ADP transduction function were found to exhibit significant sensitivity to the particular kinetic properties of three mitochondrial enzymes in the model, i.e., the lumped tricarboxylic acid dehydrogenase activity (TCA-DH; parameters 1–4), respiratory chain complex III (CIII; parameters 6–8), and the ANT (parameters 12–14) (Fig. 5, A–C). Within this subset, the ANT parameter sensitivity was dominant (Fig. 5, A–C). Specifically, the Q_max of the mitochondrial ADP transduction function exhibited significant sensitivity to parameters 1–4, 7, 12, and 14 corresponding to TCA-DH parameters k_Pi,1 and k_Pi,2 and r and X_DH, CIII parameter k_Pi,3, and ANT parameters X_ANT and θ, respectively (Table 1), whereby the sensitivity to the ANT parameter X_ANT was dominant (K-S score 0.46 vs. 0.05–0.07 for TCA-DH and CIII parameters, respectively; Fig. 5A). Likewise, the apparent kinetic order of the ADP transduction function (n_H) exhibited significant sensitivity only to all TCA-DH parameters (parameters 1–4; Table 1) and all ANT parameters (parameters 12–14; Table 1), whereby the sensitivity to ANT parameter θ was dominant (K-S score 0.63 vs. 0.09–0.13 for all other ANT and TCA-DH parameters, respectively; Fig. 5B). Finally, the overall mitochondrial ADP affinity K₅₀ exhibited significant sensitivity to the TCA-DH parameters k_Pi,1, r, and X_DH (parameters 1, 3, and 4, respectively; Table 1), CIII parameters X_C3 and k_Pi,3 (parameters 6 and 7, respectively), and ANT parameters K_m-ANT and θ (parameters 13 and 14, respectively), whereby the sensitivity to θ was again dominant (K-S score 0.47 vs. 0.04–0.07 for all other significant parameters) (Fig. 5C).

Fig. 5.

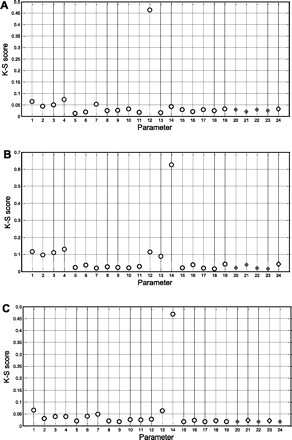
Kolmogorov-Smirnov (K-S) scores of the 19 model parameters (○) and 5 dummy parameters (◊) from the multiparametric sensitivity analysis of the model for each of the 3 macroscopic kinetic parameters of the mitochondrial transduction function: Q_max, (A) n_H (B), and K₅₀ (C). Shaded areas indicate the threshold of significance set by the K-S scores of the 5 dummy parameters in each graph.

Model fitting.

The MPSA results were next used to investigate whether any set of model parameter values that would give rise to in silico mitochondrial ADP ultrasensitivity existed. First, the transduction function for the default parameterization of the model (46) was characterized. Figure 6A shows the [ADP]-Jp covariation computed for the default set of model parameter values together with a set of experimental [ADP]-Jp data points obtained in an individual muscle. By scaling X_ANT and X_DH, the in silico Q_max of oxidative phosphorylation was adjusted to 0.8 mM/s, corresponding to the in vivo estimate for this particular muscle (subject 2; Table 2). This required a twofold increase of X_ANT and a threefold increase of X_DH to 0.016 and 0.260 mM/s, respectively. Curve-fitting of Eq. 4 to the simulated data showed that the ADP transduction function for the default parameterization of the model was hyperbolic (n_H 1.06) with Q_max and Q_min of 0.80 and −0.02 mM/s, respectively, and a K₅₀ of 0.16 mM. Clearly, the first-order in silico mitochondrial ADP sensitivity for the default model parameterization was incompatible with the measured in vivo response of Jp to [ADP] changes in muscle (Fig. 6A). Figure 6, B and C, shows the computed variations of the mitochondrial membrane potential (Δψ_m) and redox potential {([NADH]/[NAD])_m}, respectively, with [ADP] for the default parameterization. Both potentials were predicted first to rapidly increase at very low [ADP] and subsequently gradually drop toward limit values of 170 mV and 1.3, respectively (Fig. 6, B and C).

Fig. 6.

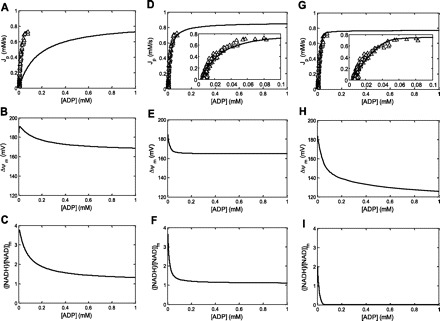
Simulations of the covariation of Jp (in mM/s), ΔΨ_m (in mV), and ([NADH]/[NAD])_m with cyoplasmic ADP concentration (in mM) for 3 different model parameterizations. Open triangles correspond to measured in vivo ADP concentration ([ADP])-Jp covariation in an individual muscle (subject 2). A–C: default model parameterization with X_ANT and X_DH is 0.016 and 0.269 mM/s, respectively. A: the simulated relation was kinetically characterized by unconstrained, 4-parameter curve fitting of Eq. 4 yielding fitted estimates for with Q_max, Q_min, n_H, and K₅₀ of 0.80 mM/s, −0.02 mM/s, 1.06, and 0.16 mM, respectively. D–F: fitted model parameterization I; X_ANT = 0.41 mM/s and θ = 1.0. X_DH was kept at 0.269 mM/s. D: the simulated relation was kinetically characterized by unconstrained, 4-parameter curve fitting of Eq. 4 yielding fitted estimates for with Q_max, Q_min, n_H, and K₅₀ of 0.82 mM/s, −0.02 mM/s, 1.50, and 0.025 mM, respectively. G–I: fitted model parameterization II; X_ANT = 0.32 mM/s, X_DH = 0.12 mM/s, and r = 3.1. G: the simulated relation was kinetically characterized by unconstrained, 4-parameter curve fitting of Eq. 4 yielding fitted estimates for with Q_max, Q_min, n_H, and K₅₀ of 0.81 mM/s, −0.02 mM/s, 2.10, and 0.023 mM, respectively.

Figure 6, D–I, shows the results of the model fitting to the same in vivo [ADP]-Jp data set for two cases. In the first case, only the model parameters with the highest MPSA K-S score (i.e., ANT parameters X_ANT and θ; Fig. 5, A–C) were adjustable parameters in the fitting yielding X_ANT = 0.041 mM/s and θ = 1.0 mM/s (vs. 0.016 and 0.35 mM/s, respectively, in the default case). Figure 6D shows the corresponding fit of Eq. 4 to the computed [ADP]-Jp covariation for this particular model parameterization compared with the measured [ADP]-Jp covariation in the individual muscle. The in silico ADP transduction function in this case was sigmoidal with a n_H of 1.5 and a K₅₀ of 0.025 mM corresponding to ADP ultrasensitivity (27). The fitted estimates for Q_max and Q_min were 0.82 and −0.02 mM/s, respectively. Figure 6, E and F, shows the computed variations with [ADP] of Δψ and ([NADH]/[NAD])_m for this particular model parameterization. Both potentials exhibited a steeper drop over the physiological range of ADP concentration changes in muscle compared with the default model parameterization (but without any initial rise at low [ADP]) followed by a more rapid stabilization at 165 mV and 1.1, respectively, at ADP concentrations >0.2 mM. Figure 6, G–I, shows the results for an alternative model fitting. In this case, all model parameters with a significant K-S score except θ were adjustable parameters in the fitting, yielding X_ANT = 0.32 mM/s, X_DH = 0.12 mM/s, and r = 3.1 (vs. 0.016 mM/s, 0.26 mM/s, and 4.6, respectively, for the default case in Fig. 6A). The ADP transduction function for this model parameterization was likewise sigmoidal with fitted estimates of Q_max, Q_min, and K₅₀ of 0.81 mM/s, −0.02 mM/s, and 0.023 mM, respectively (Fig. 6G). The n_H was in this case even higher than in the former case (i.e., 2.1 vs. 1.5, respectively). However, for this particular model parameterization, ([NADH]/[NAD])_m collapsed over the physiological range of ADP concentration changes in muscle accompanied by ΔΨ falling <150 mV (Fig. 6, H and I).

DISCUSSION

The present in vivo and in silico investigations of the magnitude and origin of mitochondrial sensitivity to cytoplasmic ADP concentration changes in human skeletal muscle have yielded two main results. First, it was found by ³¹P-MRS that the in vivo affinity and kinetic order of ADP stimulation of mitochondrial oxidative ADP phosphorylation in human skeletal muscle were 0.022 ± 0.003 mM and 1.9 ± 0.2, respectively. Second, it was found by computational analysis that these kinetic characteristics of mitochondrial ADP sensing and transduction are determined primarily by the kinetic properties of the mitochondrial adenine nucleotide transporter. Below, these results and aspects of the underlying analysis are discussed.

In Vivo Mitochondrial ADP Transduction Function: Analysis

The previous investigation of the mitochondrial ADP transduction function used, among others, in vivo data sets on the covariations of the mitochondrial ATP synthesis rate (Jp) with cytosolic ΔG_p and [ADP] in contracting forearm muscle (24). Hereto, muscle PCr, P_i, and ATP concentrations and pH were measured in individual subjects typically at six electrical nerve stimulation frequencies (24). As such, the ΔG_p-Jp and [ADP]-Jp relations in individual subjects were only sparsely sampled (7 points in each data set). In the present study, sampling of these relations was highly improved when an alternative approach was taken. First of all, the relationship between mitochondrial ATP synthesis flux and ΔG_p and [ADP] was reconstructed from the densely sampled (6-s time resolution) PCr recovery time course following muscle contractions (Figs. 3 and 4). Second, multiple data sets were obtained from each subject, resulting in individual data sets containing 100+ (range: 109–206) data points, including improved sampling of the ΔG_p-Jp covariation at very low fluxes (Figs. 3 and 4). As a result, accurate estimation of the mitochondrial flux asymptotes (and therefore n_H) was achieved in individual subjects (Tables 2 and 3). In fact, fully unconstrained fitting of a sigmoidal relation to individual ([ADP], Jp) data sets yielded the same results as two-parameter fits with flux asymptotes fixed at values obtained from the thermodynamic flow-force analysis (n_H: 2.0 ± 0.3 vs. 1.9 ± 0.2; Tables 3 and 4, respectively). These values were not different from the value obtained previously for skeletal muscle [i.e., 2.1 (24)].

A second methodological difference with the previous investigation of the mitochondrial ADP transduction function regarded the calculation of the mitochondrial ATP synthesis rate (Jp) corresponding to each [ADP] data point. In both cases, the derivative of the exponential fit to the time course of PCr was used to compute the net ATP turnover flux at each time point. However, in the previous study, a subsequent subtraction step was necessary to correct for any nonoxidative ATP synthesis flux evidenced from progressive acidification of the contracting muscle fibers (24). The magnitude of this flux was estimated from the pH time course. In the present study, no such correction was necessary because the muscle was electrically silent during recovery. It has previously been shown that anaerobic ATP synthesis flux is negligible under these conditions (5, 16, 35, 37, 38). Indeed, fitting of a biexponential function to the PCr time course during recovery failed to detect any significant second source of ATP synthesis (data not shown). If anything, only the first PCr concentration time point at 3 s into metabolic recovery may have had a contribution from nonmitochondrial ATP synthesis (19). In that case, the data points in Fig. 4 at the highest ADP concentrations would need to be correlated with lower mitochondrial Jp values. If anything, this would render the fitted transduction function even more, not less, sigmoidal.

In Vivo Mitochondrial ADP Transduction Function: Magnitude of the Apparent Kinetic Order (n_H)

The first main result of the present investigation of the magnitude and origin of mitochondrial ADP ultrasensitivity is that the apparent kinetic order of the in vivo mitochondrial transduction function f([ADP],Jp) in skeletal muscle is 1.9 ± 0.02 (range: 1.7–2.1; Table 3). This value is in close agreement with the outcome of a previous investigation of the precise value of this macroscopic kinetic parameter in isolated mitochondria and human forearm muscle (2.4 and 2.1, respectively) (24). As such, the present investigation constitutes the first direct in vivo confirmation of the previously formulated hypothesis that mitochondria are ultrasensitive to extramitochondrial ADP concentration changes (24). Previous confirmations had come only from indirect evidence (14, 45).

This result impacts the field of bioenergetics in two ways. First, after having previously been dismissed as an irrelevant regulatory mechanism in cardiac energetics (3), feedback control of mitochondrial ATP synthesis has recently returned to the center of attention (2). This renewed interest has been spurred by the discovery of multiple stimulatory effects of P_i on the mitochondrial metabolic network involved in oxidative ADP phosphorylation in cardiac and skeletal muscle (7). Indeed, a recent review of contemporary knowledge of cardiac energetics elaborately discusses the impact of this discovery on understanding energy balance in the heart (2). However, no mention was made of the other ATP hydrolysis product, ADP, and its particular role in feedback control of ATP synthesis in the heart (2). Yet it was shown previously that mitochondrial ADP ultrasensitivity may in large part explain the measured covariation of [ADP] and myocardial oxygen consumption (24). Therefore, the present affirmation of the hypothesis of mitochondrial ADP ultrasensitivity suggests that both this particular mechanism as well as the multiple stimulatory roles of P_i contribute to the efficacy of feedback respiratory control in striated muscle energetics. Importantly, the apparent allosteric stimulatory effects of ADP and P_i on mitochondrial ATP synthesis appear to operate independently. This conclusion is based on the finding that the magnitude of mitochondrial ADP ultrasensitivity quantified by n_H of the transduction function (27) was sensitive only to a subset of the parameters in the mitochondrial metabolic network model whereby the multiple stimulatory roles of P_i were mathematically implemented (Fig. 5B). Second, the result impacts computational modeling of mammalian cell energetics. Specifically, the affirmation of second order for the mitochondrial ADP transduction function provides a firm and tractable validation criterion for evaluation of past (4, 15, 31, 33, 42, 46) and future computational models of mitochondrial oxidative metabolism.

In Vvo Mitochondrial ADP Sensing and Transduction: Origin of ADP Ultrasensitivity

Koshland identified three distinct generic biochemical mechanisms that may endow a biological network with ultrasensitivity (27). For the particular case of mitochondrial ultrasensitivity to cytoplasmic ADP concentration changes, concrete indications exist for the possible involvement of two of these mechanisms, i.e., the presence of allosteric network elements and multisite network activation (27). Specifically, three alternative biochemical implementations of multisite activation have been demonstrated in mitochondria, i.e., multisite kinetic activation by calcium (1), multisite kinetic activation by P_i (7), and multisite phosphorylation (22). Likewise, in vitro evidence has been obtained for non-MM kinetics of ADP-ATP exchange catalyzed by the ANT (9, 18). The latter mechanism was previously invoked to explain mitochondrial ADP ultrasensitivity in the original communication (24). However, that particular hypothesis for the origin of mitochondrial ADP ultrasensitivity has awaited validation. The present investigation has yielded new evidence that the kinetic properties of ANT indeed principally determine the macroscopic mitochondrial property of ADP sensitivity. This is the second main result of the investigation.

The evidence for this conclusion that was obtained in this study was twofold. First, the MPSA of the computational model of skeletal muscle oxidative ATP metabolism, including a detailed biophysical model of mitochondrial oxidative ADP phosphorylation (46), identified an ANT parameter as the primary determinant of mitochondrial ADP sensitivity with respect to both ADP sensing (K₅₀) and transduction (n_H) (Fig. 5, B and C). This particular parameter, θ, is a phenomenological parameter in the rate equation for the ADP-ATP exchange reaction catalyzed by ANT of the model that was analyzed (see Ref. 46 and appendix). The K-S scores for this parameter were one order of magnitude higher than the statistical threshold and five- to 10-fold higher than any other model parameter (Fig. 5, B and C). Second, the results of the model fitting to an in vivo [ADP]-Jp data set from an individual muscle showed that mitochondrial ultrasensitivity to ADP concomitant with homeostasis of the mitochondrial membrane and redox potentials could be obtained in silico if and only if the ANT parameter θ was included in the set of adjustable parameters in the model fitting (Fig. 6).

The default ADP sensitivity of the mitochondrial network in the model was insufficient, as indicated by the hyperbolic nature of the simulated [ADP]-Jp relation for the default model parameterization (Fig. 6A). Changing θ from its default value of 0.35 to the fitted optimum of 1.0 concomitant with a 2.5-fold increase of the V_max of ANT resulted in an almost fivefold increase in mitochondrial ADP sensitivity compared with the default parameterization of the model (n_H 1.5 vs. 1.06 mM and K₅₀ 0.025 vs. 0.16 mM, respectively; Fig. 6, A and D). Importantly, these specific values of in silico mitochondrial ADP affinity and transduction closely agreed with the experimentally determined values of these macroscopic mitochondrial kinetic parameters in muscle (Table 3). Furthermore, simulation showed that homeostasis of the mitochondrial membrane and redox potential at high ADP concentrations was superior compared with the default model parameterization (Fig. 6, B and C vs. E and F, respectively). In contrast, ΔΨ_m and particularly ([NADH]/[NAD])_m collapsed at physiological ADP concentrations in muscle for the alternative combination of fitted model parameters (including the V_max of ANT but not θ) that yielded mitochondrial ADP ultrasensitivity (Fig. 6, H and I, respectively). Specifically, simulation showed that ([NADH]/[NAD])_m in this case near-instantaneously collapsed to almost zero when mitochondria were activated by cytoplasmic accumulation of ADP and ΔΨ_m dropped below the critical value of 150 mV at an only moderately elevated cytoplasmic ADP concentration for muscle of 0.07 mM (Fig. 6, H and I). It has been well established that the reaction catalyzed by mitochondrial F1-ATPase reverses from net ATP synthesis to ATP hydrolysis for ΔΨ_m values below 150 mV (31).

Finally, it could perhaps be argued that the maximal n_H for in silico mitochondrial ADP transduction that was obtained by fitting of θ and X_ANT falls short of reproducing the in vivo estimate of this macroscopic parameter [1.5 vs. 1.9 ± 0.02 (range: 1.7–2.1), respectively; Table 3]. In that case, there would maximally be need for another twofold increase in sensitivity by some kinetic mechanism that remained unidentified in the present computational studies likely because it was not included in the particular mitochondrial computational model that was analyzed. Since multisite kinetic activation of the mitochondrial network by P_i has been explicitly incorporated in the model (46), another kinetic mechanism must be involved. In that case, some form of kinetic regulation by calcium may appear to be a tenable first hypothesis for several reasons. First of all, the computational mitochondrial model platform for our computational studies did not yet include implementation of calcium balance [nor of any metabolic regulatory effect of calcium (46)]. Second, it has been well established that calcium can modify TCA-DH activity in mitochondria (1). Third, the kinetic parameters of the TCA-DH were found to have significant control, albeit small compared with θ, of the n_H of the mitochondrial ADP transduction function (Fig. 5B). However, we were unable to further increase n_H above 1.5 by additionally changing any of the TCA-DH parameter values within a 10-fold range (data not shown), indicating that, if anything, none of the known calcium effects on TCA-DH activity (1) would be involved. Any significant contribution of calcium activation of other enzymes in the mitochondrial network [e.g., direct activation of ATP synthase (1) or indirect activation of the redox proton pumps via covalent modification by kinases (22)] also appears unlikely since none of these mitochondrial enzymes had any significant MPSA K-S scores (Fig. 5B). As such, it may well prove difficult to identify any ancillary kinetic mechanisms and their biochemical implementation in the mitochondrial metabolic network that may further increase the macroscopic kinetic order of ADP transduction from 1.5 to 1.9. However, the present study illustrates that computational modeling and network analysis provide powerful tools to conduct such an investigation.

Implications for Kinetic Modeling of ANT

The adjustment of the value of ANT parameter θ from 0.35 to 1.0 that, together with a 2.5-fold increase in V_max of ATP/ADP exchange, transforms the ADP sensitivity of the mitochondrial metabolic network in the Wu et al. (46) model from normal to ultrasensitivity represents not merely an arbitrary model optimization. Instead, it has a significant mechanistic implication. In the Wu et al. (46) model, θ is a phenomenological partition coefficient that determines the magnitude of the effective ΔΨ_m components on the intermembrane space and matrix sides of the inner membrane (ΔΨ_m–i and ΔΨ_m–x, respectively) with respect to the transport of ADP and ATP across the inner membrane (see appendix). The phenomenological partitioning of ΔΨ_m into ΔΨ_m–i = θ × ΔΨ_m and ΔΨ_m–x = (1-θ) × ΔΨ_m was originally introduced in the kinetic modeling of the ATP/ADP exchange reaction catalyzed by the ANT by Korzeniewski and Froncisz (26) and later parameterized by fitting of in vitro mitochondrial adenine nucleotide uptake data yielding θ = 0.35 (25). It has since been used in other computational models of mitochondrial ATP synthesis, including the model analyzed here (44, 46).

The results of the present investigation invalidate this particular kinetic model of mitochondrial ATP/ADP exchange as a suitable component of any computational model that seeks to simulate the behavior of mitochondria in living cells. Specifically, the result of the model fitting that θ should be 1 rather than 0.35 to adequately simulate ATP metabolism in muscle indicated that the partitioning of ΔΨ_m into any cytoplasmic and matrix component introduced on the basis of in vitro data is not appropriate in vivo and should be omitted. The adjusted ANT rate equation is shown in the appendix (Eq. A3). The mechanistic implication of this result is that the kinetic effect of the mitochondrial membrane potential on the ATP⁴⁻/ADP³⁻ exchange rate supported by the ANT can be mathematically accounted for by its effect in the matrix.

APPENDIX

The rate equation for ATP/ADP exchange across the inner mitochondrial membrane catalyzed by the ANT in the model of Wu et al. (46) is

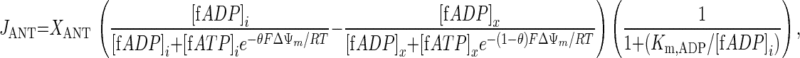(A1)

where [fX]_i and [fX]_x are the magnesium-unbound species of ATP and ADP in the mitochondrial intermembrane space and matrix, respectively, and ΔΨ_m is the mitochondrial membrane potential (46). The kinetic parameters X_ANT and K_m,ADP (parameters 12 and 13 in Table 1, respectively) correspond to the ANT activity (in mol·s⁻¹·l mito⁻¹) and the ANT Michaelis constant (in M), respectively (46). Parameter θ is a phenomenological coefficient introduced by Korzeniewski and Froncisz (26) that determines the magnitude of the effective ΔΨ_m components on the intermembrane space and matrix sides of the inner membrane (ΔΨ_m–i and ΔΨ_m–x, respectively) with respect to the transport of ADP and ATP across the inner membrane according to Eqs. A2a and A2b:

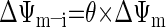(A2a)

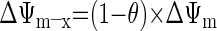(A2b)

The default value of θ in the Wu model was 0.35 (46) and identical to the value derived previously by Korzeniewski (25) on the basis of model fitting to in vitro data of adenine nucleotide uptake in isolated mitochondria.

For the case θ = 1, Eq. A1 reduces to:

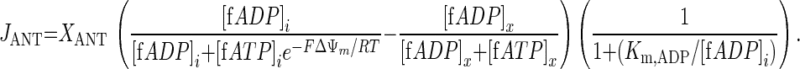(A3)

GRANTS

This research was funded in part by the National Heart, Lung, and Blood Institute through a subcontract of grant HL-072011.